A Comparison of Efficiency of Life Insurance Companies in Mainland China and Taiwan Using Bootstrapped Truncated Regression Approach

Abstract

For strategic and competitive insights, this study measures and benchmarks the comparative operating efficiencies of insurance companies in Taiwan and mainland China. We employ the two-stage DEA with the bootstrapped truncated regression approach to examine the overall efficiency of insurance companies in Taiwan and mainland China during 2005-2011. Empirical results reveal that the savings rate, elderly population percentage, and business freedom positively affect the managerial efficiency of life insurance companies in Taiwan and mainland China, while GDP growth rate, inflation rate, corruption index, and climate risk negatively affect their managerial efficiency.

Keywords:

• efficiency
• two-stage DEA
• bootstrap
• truncated regression model
• insurance industry

PUBLIC INTEREST STATEMENT

For strategic and competitive insights, this study measures and benchmarks the comparative operating efficiencies of insurance companies in Taiwan and mainland China. Due to financial crisis (or called financial tsunami) of 2008, we aim to understand the differences and effect before and after 2008 financial tsunami, and decide to adopt within 3 years before and after 2008, that is 2005–2011, as the time frame of this study. This study employs the two-stage bootstrapped truncated regression approach, proposed by Simar and Wilson (2007), and aims to analyze the insurance corporations’ efficiencies of two economies during 2005–2011. Empirical results reveal that the savings rate, elderly population percentage, and business freedom positively affect the managerial efficiency of life insurance companies in Taiwan and mainland China, while GDP growth rate, inflation rate, corruption index, and climate risk negatively affect their managerial efficiency. In the end, appropriate recommendations have been forwarded in this paper.

1. Introduction

Most industries faced the fierce challenge, insurance industry with no exception, by the unstable economic and financial market recently. The low interest rate environment continued to put downward pressure on insurers’ profitability, particularly on the life insurance. According to the Swiss Re research report, global life insurance premiums increased by 2.3% in 2012 after contracting by 3.3% the previous year. However, the growth rates still remain below the average pre-crisis rate (before 2008). Over the past decade, in Asia, insurance industry has experienced rapid expansion and the share of premiums has strongly increased, especially in mainland China. Mainland China's insurance market is continuing to grow unabated and will have usurped the US to become the world’s largest insurance market in the near future. However, there is still in the lower insurance density and the insurance penetration in mainland China, the world ranking is 61 and 46. Therefore, regardless of culture difference between western and eastern, most international insurance companies are still highly interesting to develop their business in mainland China.

Taiwan is also an important insurance market in the world. Due to financial market liberalization and permissions that banks and foreign firms participate in life insurance management, insurance industry has seen explosive development in Taiwan. Taiwan insurance density and penetration rank 1 in the world; however, in 2011, Taiwan insurance premium growth faced a first recession since 2000. Due to the IFRS17 will be formally adopted in 2026, the authority has introduced a number of new systems to encourage and require the life insurance industry to strengthen protections for citizens. Moreover, the low interest rate environment is unfavorable for savings insurance sales, etc., so the life insurance market of Taiwan is highly competitive and approaching saturation.

The paper explores an interesting topic that compares the efficiency of life insurers in mainland China and Taiwan. Especially, these two markets share common cultures, but different in economic institutions. In general, the time range used in the study is from 1 to 3 years before and after the targeted (e.g., Tsoutsoura, 2004; Wibowo, 2019). Due to financial crisis (or called financial tsunami) of 2008, we aim to understand the differences and effect before and after 2008 financial tsunami, and decide to adopt within 3 years before and after 2008, that is 2005–2011, as the time frame of this study. This study employs the two-stage bootstrapped truncated regression approach, proposed by Simar and Wilson (2007), and aims to analyze the insurance corporations’ efficiencies of two economies during 2005–2011.

2. Literature review

2.1. Two-stage DEA

Data envelopment analysis (DEA) was first introduced by Farrell in 1957, Charnes et al. (abbreviated as CCR) developed the frontier efficiency concept in 1978 and further modified by Banker et al. (abbreviated as BCC) in 1984. DEA is essentially a linear programming model and a nonparametric technique, calculates the best multiplier for inputs and outputs and then evaluates efficiencies of decision-making units (DMUs). DMUs generally treat the production system as a black-box when measuring efficiency and ignore its internal structure in conventional DEA analysis (Cook et al., 2010; Kao, 2014), and one of the drawbacks is the neglect of intermediate products or linking activities (Tone & Tsutsui, 2014).

DEA can deal with multiple inputs and outputs without assuming any particular functional frontier form and does not require the specification of a specific functional form relating inputs to outputs or the setting of weights for the various factors (Lee, 2011), so it has been widely applied in insurance industry (e.g., Seiford & Zhu, 1999; Banker et al., 2010; Fukuyama & Weber, 2010; Curi et al., 2013; Juo, 2014; Curi & Lozano-Vivas, 2015; Chen et al., 2016). Many studies employ two-stage DEA, obtain efficiency scores in the first stage and then regress the efficiency scores on environmental variables in the second stage, to explore how environmental variables influence efficiencies, especially in using the Tobit model (Chen et al., 2016; e.g., Dusanksy & Wilson, 1994; Kooreman, 1994; De Borger & Kerstens, 1996; Luoma et al., 1996; Carrington et al., 1997; Kirjavainen & Loikkanen, 1998; Fried et al., 1999; Jackson & Fethi, 2000; Mukherjee et al., 2001; Rączka, 2001; Ralston et al., 2001; Isik & Hassan, 2002; Okeahalam, 2004; McDonald, 2009; Li & Hu, 2010; Merkert & Hensher, 2011; Jha et al., 2013; Afzal, 2014; Chang et al., 2014; Samut & Cafrı, 2016).

However, Simar and Wilson (2007) argue that it is not the property of latent variables to decide whether efficiency equals one and is primarily an artifact of the finite samples of the DEA model. DEA is sensitive when outliers exist and has long been criticized for lacking in statistical power and being deterministic (Lee, 2011). Carrington et al. (2005) further indicated that the limitation is caused by the regression analysis on the Tobit model, when employing a two-stage DEA approach. Furthermore, the dependent variable estimated by the DEA model is serially correlated, and the random distance is correlated with environmental variables in the second stage (Chen et al., 2016). To overcome the above problems, Simar and Wilson (2007) regard that the truncated regression model is more appropriate approach than the Tobit model in the second stage. Therefore, they suggested an alternative approach involving a second-stage truncated regression model and bootstrap method to estimate confidence intervals. Based on a bootstrap approach, they also proposed an alternative estimation and statistical inference procedure. Lee (2011) indicated that this approach can solve the dependency problem and produce valid estimates for the parameters in the second-stage regression. Hence, this study employs the two-stage bootstrapped truncated regression approach by Simar and Wilson (2007) to examine the overall efficiency of insurance companies in Taiwan and mainland China.

2.2. Efficiency in insurance industry

X. Hu et al. (2009) explore the relationship between ownership structure and the efficiencies of insurers in mainland China. The empirical results revealed that the average efficiency values of all insurance companies are cyclical. Employing Tobit regression can explain that the insurance company’s market power and ownership structure may be the cause of differences in efficiency values.

Eling and Luhnen (2010) used both SFA and DEA methods to assess the efficiency of international insurance industry. The results pointed out that technical and cost efficiency of international insurance markets grow steadily from 2002 to 2006. In general, Asia and Europe countries’ efficiency scores are higher than the emerging market countries. The highest average efficiency is Denmark and Japan, whereas the most inefficient is Philippines.

Grmanová and Strunz (2017) used DEA models and the Tobit regression model to explore the relationship between technical efficiency and profitability of 15 commercial insurance companies in Slovakia in the period of 2013–2015. Their results show the relationship between the technical efficiency score in the CCR and BCC models and all the groups formed on the basis of both ROA and ROE was not confirmed.

Nourani et al. (2018) employs a dynamic network DEA for performance evaluation of insurer (life, general and composite insurers) and ownership (domestic and foreign), the period of 2007–2014, in Malaysia. Compared to their foreign counterparts, the findings show that domestic insurers lack of efficiency in the investment capability function. Furthermore, the general segment achieves better efficiency in the premium accumulation function, and in the investment capability function, the composite or non-specialized segment performs better.

Hong and Xu (2019) use DEA-Tobit two-step method to examine the relationship between Internet insurance and the efficiency of insurance companies. The findings show that the development of Internet insurance industry and the development of Internet insurance business have a significant role in promoting the efficiency of insurance companies and the impact is heterogeneous. Besides, the efficiency of Chinese-funded insurance companies is higher than that of foreign-funded (joint venture) insurance companies.

Naushad et al. (2020) employs DEA to estimate the managerial efficiency of 30 insurance companies listed on the Saudi stock exchange including both conventional and Takaful insurance companies from 2015 to 2018. Their study reveals that most insurance companies operating are efficient on managerial efficiency scale and no company is found with zero or negative efficiency.

3. Mehodology

In this study, we employ a DEA bootstrapping model, proposed by Simar and Wilson (2007), to measure efficiency of insurance companies in mainland China and Taiwan from 2005 to 2011. Bootstrapped DEA scores, derived in the first stage analysis, are regressed against a set of environmental variables using the maximum likelihood method to explain efficiency drivers. Wijesiri et al. (2015) pointed out that the results obtained in this study are more meaningful than those from the past literature based on conventional DEA models.

Based on a bootstrap set with 2,000 replications, in the study we combine two-stage DEA model with the bootstrapped truncated regression approach, proposed by Simar and Wilson (2007), and employ annual panel data. This method could have a better explanation for drivers of efficiency while producing standard errors and confidence intervals for these scores simultaneously.

Assume that there are N DMUs. Each DMU employs K inputs $\left(x_1,\cdots ,x_N\right)\in {\mathrm{\Re }}_{+}^N$, to produce M outputs $\left(y_1,\cdots ,y_M\right)\in {\mathrm{\Re }}_{+}^M$. Charnes et al. (1978) proposed the input-oriented CCR model for DMU j as follows:

(1) $\underset{{\theta }_j,{\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_H}{min}\begin{array}{cc}\hspace{0.17em}& {\theta }_j\end{array}$(1)

Subject to

${\theta }_j{x}_{kj}-{\sum }_{n=1}^N{\lambda }_n{x}_{kn}\ge 0,\begin{array}{cc}\hspace{0.17em}& k=1,2,\cdots ,K\end{array}$

$-y_{mj}+{\sum }_{n=1}^N{\lambda }_n{y}_{mn}\ge 0,\begin{array}{cc}\hspace{0.17em}& m=1,2,\cdots ,M\end{array}$

${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_H\ge 0.$

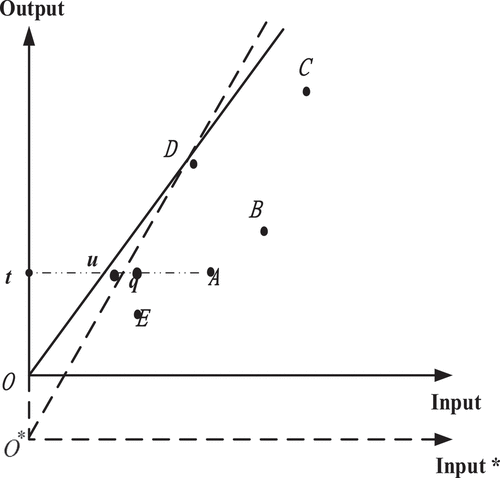
The optimal value of ${\theta }_j$, denoted by ${\hat{\theta }}_j$, is the input-oriented technical efficiency of DMU j. The CCR model assumes that the production exhibits CRS and thus, cannot handle negative outputs. Suppose that there are five DMUs, A, B, C, D and E. In Figure 1, the solid line, passing through the origin O and the point D, is the CCR efficient frontier. The input-oriented TE of DMU A is measured by the ratio $\overline{tu}/\overline{tA}$. If we translate the output value by a given amount such that the origin moves to O*, the CCR efficient frontier becomes the dotted line passing through the new origin O* and the point D. The input-oriented TE of DMU A, based on the new coordinate system, turns out to be the ratio $\overline{tq}/\overline{tA}$, which differs from the old value $\overline{tu}/\overline{tA}$.

Figure 1. The CCR model with translation of output.Source: created by authors.

Banker et al. (1984) relaxed the CRS constrain in the CCR model by allowing production to be VRS, known as the BCC model. 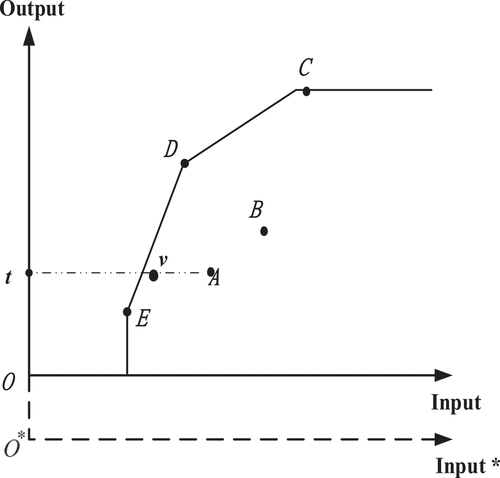Mathematically, it is easy to extend the BCC model from the CCR model by adding the convexity constraint ${\sum }_{n=1}^N{\lambda }_n=1$ in equation (1)(1) $\underset{{\theta }_j,{\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_H}{min}\begin{array}{cc}\hspace{0.17em}& {\theta }_j\end{array}$(1) . Furthermore, the input-oriented BCC model is invariant under the translation of outputs (Ali & Seiford, 1990). We described this in Figure 2. The efficient frontier of the BCC model is the bold line connecting point C, D, and E. The input-oriented TE of A is measured by the ratio $tv/tA$, regardless of the coordinate systems O or $O{ }^{\mathrm{\prime }}$. Hence, it is translation invariant with respect to outputs.

Figure 2. The BCC model with translation of output.Source: created by authors.

Many studies have used the two-stage approach to investigate how environmental variables $\left(z_1,\dots ,z_p\right)\in {\mathrm{\Re }}^p$ affect technical efficiencies. They computed the estimates $\hat{\theta }$ by the BCC model (or the CCR model) in the first stage and then regressed $\hat{\delta }=1/\hat{\theta }$ (or $\hat{\theta }$) on environmental variables in the second stage:

(2) ${\hat{\delta }}_n={\beta }_0+{\beta }_1{z}_{1n}\cdots +{\beta }_p{z}_{pn}+{\epsilon }_n\ge 1,n=1,2\dots ,N$(2)

where βs are unknown parameters, and ε_n is a continuous i.i.d. random variable with mean zero and constant variance σ². Most studies observed that several efficiencies are equal to unity, so they used the Tobit regression method to estimate equation (2)(2) ${\hat{\delta }}_n={\beta }_0+{\beta }_1{z}_{1n}\cdots +{\beta }_p{z}_{pn}+{\epsilon }_n\ge 1,n=1,2\dots ,N$(2) . It means a probability mass at one and a concept of latent variables.

Simar and Wilson (2007) indicated that an artifact of the finite samples of the DEA model decides whether efficiency equals one, not the property of latent variables. Therefore, they suggest that the second stage should employ the truncated regression and also mentioned that not only are the dependent variable ${\hat{\delta }}_n$ serially correlated, but the random disturbance ε_n in equation (2)(2) ${\hat{\delta }}_n={\beta }_0+{\beta }_1{z}_{1n}\cdots +{\beta }_p{z}_{pn}+{\epsilon }_n\ge 1,n=1,2\dots ,N$(2) is also correlated with environmental variables since ${\hat{\delta }}_n$ cannot be observed directly and has to be estimated by the BCC model in the first stage. Under mild assumptions, the final DEA estimator obtained from the BCC model is consistent; however, it converges slowly at the rate $N^{-2/(K+M+1)}$ known as the curse of dimensionality (Kneip et al., 2003). It implies that they are unlikely to obtain reliable estimates, even though the maximum likelihood estimators of βs are consistent in the second stage regression.

Simar and Wilson (2007) proposed a double-bootstrap procedure to overcome the above problems. We summarize this procedure as follows:

[1] Use all DMUs to calculate ${\hat{\delta }}_n$ (n = 1, 2, … , N) by the BCC model.

[2] Acquire the ML estimates $\left({\hat{\beta }}_0,\dots ,{\hat{\beta }}_p,\hat{\sigma }\right)$ of $\left({\beta }_0,\dots ,{\beta }_p,{\sigma }_{\epsilon }\right)$ in the truncated regression ${\hat{\delta }}_n={\beta }_0+{\beta }_1{z}_{1n}\cdots +{\beta }_p{z}_{pn}+{\epsilon }_n\ge 1$ where ε_n are iid $N(0,{\sigma }^2)$ with left-truncation at $(1-({\beta }_0+{\beta }_1{z}_{1n}\cdots +{\beta }_p{z}_{pn}))$ by all inefficient DMUs where ${\hat{\delta }}_n>1$, n = 1, 2, … , J (< N).

[3] For each DMU (n = 1, … , N), loop the following four steps ((3.1)~(3.4)) L₁ times to obtain a set of bootstrap estimates $\{{\hat{\delta }}_{nb}^{\ast }{\}}_{b=1}^{L_1}$:

(3.1) Draw ${\epsilon }_n^{\ast }$ randomly from $N(0,{\hat{\sigma }}^2)$ with left truncation at $(1-({\hat{\beta }}_0+{\hat{\beta }}_1{z}_{1n}\cdots +{\hat{\beta }}_p{z}_{pn}))$.

(3.2) Compute ${\delta }_n^{\ast }\mathit{=}{\hat{\beta }}_0+{\hat{\beta }}_1{z}_{1n}\cdots +{\hat{\beta }}_p{z}_{pn}+{\epsilon }_n^{\ast }$.

(3.3) For each DMU, set $x_{kn}^{\ast }=x_{kn}{\delta }_n^{\ast }/{\hat{\delta }}_n,k=1,\dots ,K$ and $y_{mn}^{\ast }=y_{mn},m=1,\dots M.$

(3.4) Calculate ${\hat{\theta }}_n^{\ast }(x_{1n},\dots ,x_{Kn},y_{1n},\dots ,y_{Mn})$ by the BCC model with technology $\{(x_{1n}^{\ast },\dots ,x_{Kn}^{\ast },y_{1n}^{\ast },\dots ,y_{Mn}^{\ast }){\}}_{n=1}^N$.

[4] For each DMU (n = 1, … , N), compute the bias-corrected estimate ${\widehat{\widehat{\delta }}}_n\text{=}{\widehat{\delta }}_n-\text{B}\widehat{\text{IA}}\text{S}\left({\widehat{\delta }}_n\right)$, where $\mathrm{B}\widehat{\mathrm{I}\mathrm{A}}\mathrm{S}\left({\hat{\delta }}_n\right)=\frac{1}{L_1}{\sum }_{b=1}^{L_1}{\hat{\delta }}_{nb}^{\ast }-{\hat{\delta }}_n$.

[5] Get the ML estimates $({\widehat{\widehat{\beta }}}_0,\dots ,{\widehat{\widehat{\beta }}}_p,\widehat{\widehat{\sigma }})$ in the truncated regression ${\widehat{\widehat{\delta }}}_n={\beta }_0+{\beta }_1{z}_{1n}\cdots +{\beta }_p{z}_{pn}+{\epsilon }_n\ge 1$ with left-truncation at $(1-({\beta }_0+{\beta }_1{z}_{1n}\cdots +{\beta }_p{z}_{pn}))$

[6] Loop the following three steps ((6.1)~(6.3)) L₂ times to obtain a set of bootstrap estimates ${\left\{{({\widehat{\widehat{\beta }}}_0^{*},\dots ,{\widehat{\widehat{\beta }}}_p^{*},{\widehat{\widehat{\sigma }}}^{*})}_b\right\}}_{b=1}^{L_2}$:

(6.1) For each DMU (n = 1, … , N), draw ${\epsilon }_n^{\ast \ast }$ randomly from $N(0,{\widehat{\widehat{\sigma }}}^2)$ with left truncation at $(1-({\widehat{\widehat{\beta }}}_0+{\widehat{\widehat{\beta }}}_1{z}_{1n}\cdots +{\widehat{\widehat{\beta }}}_p{z}_{pn}))$.

(6.2) For each DMU (n = 1, … , N), compute ${\delta }_n^{**}={\widehat{\widehat{\beta }}}_0+{\widehat{\widehat{\beta }}}_1{z}_{1n}\cdots +{\widehat{\widehat{\beta }}}_p{z}_{pn}+{\epsilon }_n^{**}$.

(6.3) Obtain the ML estimates $({\widehat{\widehat{\beta }}}_0^{*},\dots ,{\widehat{\widehat{\beta }}}_p^{*},{\widehat{\widehat{\sigma }}}^{*})$ in the truncated regression ${\delta }_n^{\ast \ast }={\beta }_0+{\beta }_1{z}_{1n}\cdots +{\beta }_p{z}_{pn}+{\epsilon }_n\ge 1$ with left-truncation at $(1-({\beta }_0+{\beta }_1{z}_{1n}\cdots +{\beta }_p{z}_{pn}))$

[7] Use the estimates $({\widehat{\widehat{\beta }}}_0,\dots ,{\widehat{\widehat{\beta }}}_p,\widehat{\widehat{\sigma }})$ and the bootstrap values obtained from the step [6] to construct estimated confidence intervals for each element of $\left({\beta }_0,\dots ,{\beta }_p,{\sigma }_{\epsilon }\right)$.

4. Empirical analysis

4.1. Input and output variables

In this study, we adopt three inputs and two outputs to assess the efficiency of insurance companies in mainland China and Taiwan. The selection of inputs and outputs is based on past studies. The operating variables are collected from the China Insurance Regulatory Commission and Taiwan Insurance Institute, and annual data cover the period from 2005 to 2011. Due to merger and acquisition, the number of insurance companies varies every year and we use unbalanced panel data from the period 2005 to input-output specification and generate new frontier to measure the efficiency.

Alizezaee et al. (1998) suggest that the minimum number of DMUs should be greater than three times the total number of inputs plus outputs. Raab and Lichty (2002) also noted that it has been regarded as DEA convention. DEA uses the total number of insurance observations in association with the total number of insurance input and output variables. This study meets this requirement with a sample size of 552 DMUs, from a total of five insurance variables (3 inputs and 2 outputs) for the DEA model.

Table 1 shows the numbers of observations from 2005 to 2011 in mainland China and Taiwan, and Table 2 describes the definitions of these variables.

Table 1. Number of observations during 2005 to 2011

Economy	2005	2006	2007	2008	2009	2010	2011
mainland China	40	41	46	49	54	57	57
Taiwan	29	29	29	30	28	30	30

Source: created by authors.

Table 2. Definitions of input and output variables

Variables	Definitions	Unit
Input Variables
Total asset (x1)	Total assets in the balance sheet, including insurance premium, property and other	Million USD in 2005
Employee (x2)	Total employees involved in the operation of Insurance company, including executive, administration staff, sales and other.	Person
Total Equity (x3)	Total equity in the balance sheet, including paid-in capital, retained earnings and other.	Million USD in 2005
Output Variables
Insurance revenues (${\mathrm{y}}_1$)	Incomes from the insurance premium	Million USD in 2005
Investment revenues (${\mathrm{y}}_2$)	Incomes from the financial operation	Million USD in 2005

Source: created by authors.

Many empirical results indicated that an increase in total assets can cause a firm’s operation to be more efficient (e.g., Berger et al., 1993; Gardner & Grace, 1993; Yuengert, 1993). Therefore, total asset is an important index to measure an insurance company’s scale and is an input variable in this study.

Total equity can be generally as a reserve fund to pay the premium loss and the capability of facing risk; therefore, we use it to be one of the three input variables. Besides, the insurance industry is a labor-intensive industry because that the insurance product is an intangible commodity and needs a lot of salesmen and office staffs (Berger et al., 1993; Cummins et al., 2010). This study use employee to the third input variables.

For every insurance company, premium insurance is the main and vital revenue, so we choose the premium insurance for the output variable (Noulas, 2001; Cummins et al., 2010). Besides, based on the previous literature, investment revenue is the second revenue source for the insurance company (Noulas, 2001; Hwang & Kao, 2006). Therefore, this study chooses the investment revenue for another output variable.

In this study, all nominal variables in monetary units are transformed into real USD by annual exchange rates using the U.S. GDP deflators with 2005 as the base year. Table 3 illustrates the descriptive statistics for all variables in this study.

Table 3. Summary statistics of input and output variables

	Name	Mean	SD	Maximum	Minimum
	Output Variables
$y_1$	Insurance revenues	2725.63	8629.939	110,636.4	0.010983
$y_2$	Investment revenues	557.736	2036.325	22,534.92	−135.796
	Input Variables
$x_1$	Total asset	12,130.73	41,107.44	550,625.7	2.496918
$x_2$	Employee	18,849.09	68,330.46	818,241	9
$x_3$	Total Equity	1523.731	4956.75	67,700.98	0.758677

Source: created by authors.

These increased inputs cannot reduce outputs in the DEA model is to satisfy the property of isotonicity. Table 4 shows the correlation matrix of inputs and outputs, revealing that all the correlation coefficients between any pair of an input and an output are positive, satisfying the isotonicity property. That is, an output will increase as an input increases.

Table 4. Correlation matrix for inputs and outputs, 2005–2011

	Input			Output
	Total asset	Employee	Total equity	Insurance revenues	Investment revenues
Total asset	1
Employee	0.798***	1
Total equity	0.656***	0.422***	1
Insurance revenues	0.946***	0.788***	0.607***	1
Investment revenues	0.915***	0.769***	0.661***	0.859***	1

Notes: ***, ** and * denote rejection of the zero null at the 1%, 5%, and 10% significance levels, respectively.

Source: created by authors.

4.2. Environmental variables

Based on the previous studies, we use 10 environment variables in the study including country GDP growth rate, inflation rate, savings rate, re-discount rate, financial leverage, elderly population, business freedom index, insurance penetration rate, corruption index, and climate risk index. The further explanations are as follows:

Lee et al. (2013) pointed out that a 1% increase in the real-life premium will raise real GDP by 0.06%. And GDP represents the market value of all final goods and services produced within a country. Therefore, GDP growth rate (GDP) should have a significant relationship with operation efficiency.

Some literature suggested that the insurance sector should pay more attention in macroeconomic policy sector. A significant impact between the interest rate and the level of economic development on the insurance-growth (Haiss & Sümegi, 2008). Beck and Webb (2003) revealed that the higher saving rate and higher interest rate associated with higher life insurance consumption. Furthermore, the inflation rate has a negative correlation to the life insurance consumption (Browne & Kim, 1993). Therefore, we choose the inflation rate (IR), savings rates (SV), and re-discount rate (DR) as environmental variables to explore their relationships with efficiency.

Financial leverage (FL) described a business or investor is using the borrowed money and its formulation is total debt/shareholders equity. Hwang and Kao (2006) indicated that the use of funds will affect the operating efficiency of insurance company.

According the official definition in mainland China and Taiwan, elder population (EP) is the population of over 65 years old. Due to a large share of older population has higher of life insurance premium (Beck & Webb, 2003); therefore, the increased of the elder population will bring a big effect to the life-insurance industry.

Business freedom (BF), proposed by the heritage foundation, can measure the efficiency of country regulations. A country with lower score is to imply that there exist burdensome and redundant regulations in his economy, and vice versa. Thus, the regulations should have a significant relationship with the operation efficiency.

Insurance penetration rate (IPR) is the ratio of the percentage of total insurance premiums to GDP and represents the level of development of insurance industry in a country. Butler et al. (1998) indicated that the higher the IPR could come about the more moral hazard and the more resource dissipation. So, this study chooses the penetration rate to be one of environment variables.

According to the definition of the heritage foundation, corruption index (CI) denoted the freedom from corruption. In general, corruption will bring insecurity and uncertainty into economic relationships, further erode economic freedom and have a negative effect to efficiency. Therefore, in the study, we use CI to be an environment variable.

Climate risk index (CR), gauged by the German watch, is the score of the impacts of weather-related loss events. The climate crisis may lead people to feel life-threatening and be willing to buy insurance. We adopt CR to be another environment variable because it has a positive relationship with business operating. Table 5 describes the definitions of these variables.

Table 5. Definitions of environmental variables

Variables

Definitions

GDP growth rate (GDP) Inflation rate (IR) Financial leverage (FL) Savings rate (SV) Rediscount Rate (DR) Elderly population (EP) Insurance penetration rate (IPR) Business freedom (BF) Corruption Index (CI) Climate risk Index (CR)

GDP growth rates in Taiwan and mainland China.^1 Inflation rates in Taiwan and mainland China.^1 Total debt/ Shareholders Equity. National saving rate in Taiwan and mainland China.^2 Rediscount Rate announced by Central Bank in Taiwan and People’s Bank in mainland China.^1 Population of over 65 years in Taiwan and mainland China.^3 the ratio of the percentage of total insurance premiums (in US dollars) to gross domestic product.^1 The higher the level of regulation barriers, the lower a country’s score.^4 The higher the level of corruption, the lower the level of overall economic freedom and the lower a country’s score. ^4 The score of the impacts of weather-related loss events. The higher the level of risk, the lower a country’s score.^5

1. Swiss Re World Insurance Report from 2005–2011.

2. IMF.

3. The Ministry of Internal Affairs of Taiwan and National Bureau of Statistics of mainland China.

4. The Heritage Foundation.

5. Germanwatch Global Climate Risk Index Report from 2005 − 2011.

Source: created by authors.

In summary, all environmental variables used in this study are ratios such that there is no need for price level adjustments. Hence, the empirical model can be specified as follows:

(3) ${\widehat{\widehat{\delta }}}_n={\beta }_0+{\beta }_1{z}_{1n}+{\beta }_2{z}_{2n}+{\beta }_3{z}_{2n}+{\beta }_4{z}_{2n}+{\beta }_5{z}_{5n}+{\beta }_6{z}_{6n}+{\beta }_7{z}_{7n}+{\beta }_8{z}_{8n}+{\beta }_9{z}_{9n}+{\beta }_{10}{z}_{10n}+{\epsilon }_n$(3)

where ε_n is distributed $N(0,{\sigma }^2)$ with left-truncation at ${\widehat{\widehat{\delta }}}_n\ge 1$ for each n.

4.3. Empirical results

Based on the suggestions of Simar and Wilson (2007), the study uses 2,000 replications to construct estimates of confidence intervals in the bootstrapped procedure. Table 6 illustrates the truncated regression results. If the coefficient is negative, the covariate in the empirical model can improve technical efficiency or reduce $\widehat{\widehat{\delta }}$. In Table 6, Columns 2–8 show the estimated result for the bootstrapped truncated regression model, among which Column 5 reveals an average of 2,000 estimated values via the bootstrapping method.

Table 6. Bootstrapped truncated regression results

Variables	Lower bound			Mean		Upper bound
	0.5%	2.5%	5%			95%	97.5%	99.5%
Constant	–281.286	–259.307	–247.456	–178.658	***	–107.718	–89.536	–39.9106
GDP	–157.850	–131.274	–120.155	–62.561	*	–0.180	16.262	44.637
IR	–312.110	–281.750	–272.207	–204.563	***	–113.695	–93.784	–46.468
FL	–19.739	–10.042	–6.141	7.883		19.383	22.035	25.158
SV	–29.096	5.080	23.963	99.127	**	168.750	181.897	210.705
EP	0.651	1.030	1.220	1.902	***	2.440	2.534	2.700
IPR	–1.874	–1.645	–1.438	–0.495		0.453	0.630	1.029
BF	0.041	0.068	0.079	0.123	***	0.154	0.157	0.164
CI	–4.494	–4.051	–3.800	–2.561	**	–0.909	–0.413	1.054
CR	–0.9182	–0.874	–0.842	–0.635	***	–0.381	–0.278	–0.062
DR	–9.630	–6.856	–5.234	1.074		6.924	8.403	11.670
${\hat{\sigma }}_{\epsilon }$	9.733	11.096	11.647	14.820	***	17.130	17.463	18.283

1. ^{*, **}, and *** represent the 10%, 5%, and 1% levels of significance, respectively.

2. Mean (in column 5) is the average estimate obtained from MLE estimates and the bootstrap set with 2,000 replications.

According to Table 6, this study’s main empirical results are as follows:

The GDP growth rate negatively affects the managerial efficiency of a life insurance company. That is, life insurance companies in Taiwan where the GDP growth slows down are compelled to be more efficient. Otherwise, it will be more difficult to survive in a slowing down economy.

The inflation rate has a negative effect on managerial efficiency. Because a higher inflation rate effectively reduces the real liability of a life insurance company. A life insurance company located in mainland China hence may not need to be so efficient because a higher inflation rate helps reduce its real liability.

The savings rate significantly increases the managerial efficiency. A higher savings rate helps an insurance company operate efficiently. This implies that mainland China, where the savings rate is relatively high, helps a life insurance company run efficiently.

The elderly population significantly helps a life insurance company operate efficiently. Taiwan has a relatively higher percentage of elder population which needs the aid of life insurance. The mainland economy is a relatively young economy. A higher elderly population percentage helps life insurance companies in Taiwan operate efficiently.

The business freedom significantly promotes the managerial efficiency. Taiwan has higher business freedom than mainland China, making the life insurance more efficient since it has to face more severe market competition.

The corruption index significantly reduces the managerial efficiency, which fits our expectation. This is because corruption increases the transaction costs of firms to do business. In recent years both Taiwan and mainland China have been crashing down corruptions.

The climate risk index significantly reduces efficiency, which is against our expectation. Financial leverage, insurance penetration rate, and re-discount rates have no significant effects on the managerial efficiency.

5. Conclusion

The findings show that the savings rate, elderly population percentage, and business freedom positively affect the managerial efficiency of life insurance companies in mainland China and Taiwan, while GDP growth rate, inflation rate, corruption index, and climate risk negatively affect their managerial efficiency. In the study, the efficiency scores derived for the period 2005–2011 are new findings on operating performance of insurance companies in mainland China and Taiwan. These constructive findings will benefit the development and formulation of more effective and competitive strategies and policies for insurance companies in mainland China and Taiwan. It is still important to note that more work can be done by improving on the study by introducing qualitative data.

In this study, we use efficiency analysis and then try to help the insurance companies in mainland China and Taiwan to make better strategic decisions to survive and gain in the dynamic and hyper-competitive market. Wijesiri et al. (2015) suggested that the underperformers could take their peers who are successful as a benchmarking and try to adjust their market strategies. The empirical results could provide useful and constructive information for policymakers to implement appropriate regulatory mechanisms from the policy-making point of view, to streamline the operation process and to improve and enhance the performance of the insurance companies in mainland China and Taiwan. Overall, the analysis of the findings not only reveals strategic implications for practitioners in the insurance industry in mainland China and Taiwan but also provides future perspectives and directions to policy-makers for further reforming and liberalizing the commercial insurance industry. Nevertheless, Chaabouni (2019) points out that the study could provide a valuable source of evidence for policy when using data from different countries to conduct a quantitative transnational comparison rigorously.

Finally, according to the study of Du et al. (2018), due to the changes in the frontiers that are typically unobserved in practice, the development of a proper test to measure the significance of any change would be an important direction in future research. Therefore, it is important to note that this study is not without limitations. For future research, other variables may have different impacts on technical, allocative, and cost efficiencies as well as ultimately operational efficiency. Besides, other different environment variables and approaches can also be applied for such an operational efficiency evaluation. Applying the other recently developed methods to analyze larger or different data sets may produce more interesting and valuable strategic implications.

Disclosure statement

The authors have no relevant financial or nonfinancial relationships to disclose..

Additional information

Funding

The authors received no direct funding for this research.

Notes on contributors

Hwai-Shuh Shieh

Hwai-Shuh Shieh completed his PhD in Management Science from National Chiao Tung University, Taiwan. His research interests major in strategy management, social innovation and sustainable issues, and he has published more than 30 articles in both national and international journals. He is now an Associate Professor in Shih Chien University, Taiwan.

Yang Li

Yang Li received a Ph.D. degree in economics from Iowa State University, USA and is Professor at Newhuadu Business School, Minjiang University, China. His research interests include productivity and efficiency, foreign direct investment, and bank efficiency.

Jin-Li Hu

Jin-Li Hu is Professor at the Institute of Business and Management, National Yang Ming Chiao Tung University, Taiwan. He received a Ph.D. degree in economics from State University of New York at Stony Brook, USA. His research interests include efficiency and productivity, regional studies, and sustainable development.

Yong-Ze Ang

Yong-Ze Ang completed his Master in Business Management from National Chiao Tung University, Taiwan. His research interests major in productivity and efficiency.