Extended Validity of the Energy Dependent Scattering Kernel within the Boltzmann Transport Equation

Abstract

The scattering term within the Boltzmann equation was for decades approximated either through the Legendre polynomial for deterministic solvers or by $S(\alpha ,\beta )$/free gas model approach for Monte Carlo solvers. This, to some extent, inaccurate approach led to the assumption in several cases that the scattering term can be further “tuned” to simplify complex mathematical solver of the transport equation, mainly by reducing considerably the computation time, assuming no consequences on the physical results.

The introduction of the resonant dependent scattering kernel to MONTE CARLO code and in particular the experimental validation within the resolved resonance range for Uranium and Thorium, in RPI (Renselear Polytechnic Institute), pointed out that the scattering term cannot be taken as a second order negligible term, but rather should be accurately regarded for any solution of the transport equation.

Corollary to the considerable high impact of that “physical” scattering kernel, this study extends its importance beyond the epithermal resolved resonance range and aims to proof that the scattering kernel can and should be accurately dealt also at higher energies at least up to about several tens of keV. Moreover, in the debate between the purely quantum mechanics treatment known as the Optical Model -OM and the Doppler broadening based classical approach, the latter seems to be correct for this extended energy range. Strictly speaking, Newton’s Laws for the scattering kernel evaluation remain intact, yet in accordance to their quantum mechanics based integrated scattering cross section values as was shown for example by the well-known fundamental Breit Wigner formula.

Keywords:

• DBRC
• Optical model potential
• scattering kernel

Introduction

The theoretical prediction of the characteristics of a nuclear reactor, in particular its nuclear inventories, decay heat and radiation levels in operation and shut-down, and the production rate of plutonium is – more than 80 years after the discovery of fission and despite the availability of ever more powerful computers – still not satisfactorily possible. The crucial problem is the modeling of the scattering source term (distribution of the scattering kernel over all directions), in particular in view of newly enhanced requirements for accurate estimations.

A pragmatic solution is to derive correction/normalization factors (Macfarlane and Muir 1994) from the deviations between the integrated scattering cross section- XS on the left-hand side and its differential part on the right-hand side of the transport equation. In view of the dissatisfying inaccuracy there were even attempts to tune this mathematical complicated scattering term in favor of other terms in the transport solution, which often allows saving of computing time.

In their critical essay “How Accurately Can We Calculate Neutrons Slowing Down In Water?”

Cullen et al. (2006) posed the question: “Aren’t our Monte Carlo codes more or less perfect?” with the provoking, yet correct answer: “Far from it. Compared to deterministic codes, Monte Carlo codes have the advantage of being able to more accurately model geometry, but they are still limited by the accuracy of the nuclear data they use, how data are presented to them by nuclear data processing codes, and ultimately how they interpret data. …”

Cullen et al. pointed out quantitatively that the scattering term can change the results in a much meaningful manner than expected in accordance with the way it had been introduced.

Huge effort was dedicated since for handling scattering kernels, appearing in the Boltzmann equation, albeit “annoying” as the scattering term is also the implicit differential part $\frac{d{\sigma }_s}{\mathit{\text{dΩdE}}}$ of the integral scattering term ${\sigma }_s$ as mentioned above. Consequently, neutron balance becomes more cumbersome. For deterministic solutions based on NJOY, the energy group structure was “artificially” corrected in a sense that at least neutron balance was kept, yet with false energy loss and angular distribution (Macfarlane and Muir 1994).

The need for accurate evaluation of the disposed nuclide inventory at the end of a fuel cycle poses a challenging demand on the nuclear data processing and their interpretation as pointed out by Cullen et al. for thermal neutrons. This study extends the discussion on the validity of scattering kernel treatment to fast neutrons, up to several tens of keV.

This work is sequential to former studies by Ousiloumen and Sanchez (1991), Rothenstein and Dagan (1998) and Becker, Dagan, and Lohnert (2009). Those studies dealt mainly with the low epithermal energy range, emphasizing the energy and temperature impact on scattering kernels in the vicinity of pronounced resonances. In particular, the dominating up-scattering effect necessitated eventually the development of the Doppler Broadening Rejection Correction (DBRC) (Becker, Dagan, and Lohnert 2009), a solver technique which replaces the nonphysical asymptotic scattering model and is applicable for Monte Carlo transport codes. For deterministic codes, Arbanas et al. (2012). showed that the order of Legendre Moments needed to represent accurately a temperature and energy dependent scattering kernel could be impractical high, above 15. Thereafter, an alternative approach is to introduce probability tables (Ravetto 2009) such as the resonance dependent $S(\alpha ,\beta )$ (Dagan 2005) which could replace, in a dedicated form, the use of Legendre moments as well as the DBRC approach.

The current study analyses the energy dependent treatment of the elastic scattering term at higher energies/several tens of (keV) for Iron (which is important for the safety disposal of nuclear waste) and tungsten (¹⁸²W- important in the fusion research fields) as representative examples.

At very high energies, the Optical Model (OM) (Hodgson 1971) is often used which is based upon a specific form of the well-known Schrödinger equation. Strictly speaking, the very complex multiple Schrödinger Equations nucleons-system of a nuclide of a neutron-target interaction is simplified by one representative potential for the whole Nucleons within the nucleus. In this procedure the scattering cross section and its derivative, namely the angular scattering kernel are obtained by using additional fitting parameters. Experimental based fitted parameters allow then for a better determination of the integrated elastic cross section, albeit lacking the energy dependent secondary distribution $\frac{d{\sigma }_s}{dE}.$

The current study investigates the double differential cross sections for exact energy shapes in tens of keV range. The work compares the approach, verified for the resonance energy range, including the temperature against the OM, which can only deal with averaged cross sections at actually 0 K, as mentioned above.

The next section presents the two scattering models followed by their implementation for an iron and a tungsten isotope and the consequential scattering kernel different forms.

Energy and temperature dependent scattering kernels

The change of energy and flight direction of a neutron after an interaction with a given nuclide is commonly evaluated in accordance with the neutron’s energy. For low energy neutrons up to 10 eV, the intermolecular forces are significant; thereafter a phonon expansion approximation is widely used as is extensively explained in (Macfarlane and Muir 1994; Williams 1966). Above those energies, one uses the free gas model, based on the assumption that the nuclei behave like an ideal gas as far as their thermal agitation is concerned. This approach, originated already in 1944 by Wilkins and Wigner (1944) was further pursued by (Brown and John 1954; Blackshaw and Murray 1967) and finally was written in an cumulative form, namely the resonance and temperature dependent energy secondary distribution (over all angles) by Ousiloumen and Sanchez (1991). More important, Gunsing et al. (2012) proved this model experimentally.

Rothenstein and Dagan (1998) extended the solution of (Ousiloumen and Sanchez 1991) to include the angular distribution, namely, to add the momentum in addition to the energy conservation law of (Ousiloumen and Sanchez 1991). Y. Danon verified experimentally their model in two different experiments up to 210 eV including the 6 first S resonances of U238 (Ro et al. 2009) as well as the pronounced resonance of thorium at 69.2 eV of Thorium 232 (Dagan et al. 2011).

Equation (1)(1) $$\begin{array}{c}{\sigma }_s^T\left(E\to E\prime ,\overrightarrow{\Omega }\to \overrightarrow{\Omega }\prime \right)=\frac{1}{2\pi }{\sigma }_s^T\left(E\to E\prime ,{\mu }_0^{\mathit{lab}}\right)=\frac{1}{2\pi \mathrm{v}}{\left(\frac{A+1}{A}\right)}^4{\left(\frac{A}{\pi }\right)}^{3/2}\\ \int 2\pi u^{2}du\int d{\mu }_u\int c^{2}dc\int {(u\prime )}^{2}du\prime \int d{\mu }_{u\prime }\int \frac{2}{\hspace{0.17em}\text{sin}\hspace{0.17em}\phi }\frac{\delta (u\prime -u)}{{(u\prime )}^2}\text{exp}\hspace{0.17em}\left[{\mathrm{v}}^2-(A+1)\left(\frac{u^2}{A}+c^2\right)\right]\\ \frac{1}{u\mathrm{v}c}\delta \left[{\mu }_u-\frac{({\mathrm{v}}^2-c^2-u^2)}{2uc}\right]\frac{1}{2u\prime c{k}_{B}T}\delta \left[{\mu }_{u\prime }-\frac{{(\mathrm{v}\prime )}^2-{(u\prime )}^2-c^2}{2u\prime c}\right]\\ \frac{4\text{vv}\prime c^2}{B_0^{\prime }}\delta (\hspace{0.17em}\text{cos}\hspace{0.17em}\phi -\hspace{0.17em}\text{cos}\hspace{0.17em}\widehat{\phi })u{\sigma }_s(E_r)\frac{P(u,{\mu }_0^{cm})}{2\pi }d\hspace{0.17em}\text{cos}\hspace{0.17em}\phi \end{array}$$(1) presents the energy and angular dependent free gas kernel where the momentum conservation is applied by the delta functions dealing with the velocities of the neutron and the nuclide before and after an interaction. The energy and temperature dependency of the cross section is shown in the last raw of Equation (1)(1) $$\begin{array}{c}{\sigma }_s^T\left(E\to E\prime ,\overrightarrow{\Omega }\to \overrightarrow{\Omega }\prime \right)=\frac{1}{2\pi }{\sigma }_s^T\left(E\to E\prime ,{\mu }_0^{\mathit{lab}}\right)=\frac{1}{2\pi \mathrm{v}}{\left(\frac{A+1}{A}\right)}^4{\left(\frac{A}{\pi }\right)}^{3/2}\\ \int 2\pi u^{2}du\int d{\mu }_u\int c^{2}dc\int {(u\prime )}^{2}du\prime \int d{\mu }_{u\prime }\int \frac{2}{\hspace{0.17em}\text{sin}\hspace{0.17em}\phi }\frac{\delta (u\prime -u)}{{(u\prime )}^2}\text{exp}\hspace{0.17em}\left[{\mathrm{v}}^2-(A+1)\left(\frac{u^2}{A}+c^2\right)\right]\\ \frac{1}{u\mathrm{v}c}\delta \left[{\mu }_u-\frac{({\mathrm{v}}^2-c^2-u^2)}{2uc}\right]\frac{1}{2u\prime c{k}_{B}T}\delta \left[{\mu }_{u\prime }-\frac{{(\mathrm{v}\prime )}^2-{(u\prime )}^2-c^2}{2u\prime c}\right]\\ \frac{4\text{vv}\prime c^2}{B_0^{\prime }}\delta (\hspace{0.17em}\text{cos}\hspace{0.17em}\phi -\hspace{0.17em}\text{cos}\hspace{0.17em}\widehat{\phi })u{\sigma }_s(E_r)\frac{P(u,{\mu }_0^{cm})}{2\pi }d\hspace{0.17em}\text{cos}\hspace{0.17em}\phi \end{array}$$(1) where ${\sigma }_s(E_r)$ is within the integral and is a function of the relative (temperature dependent) energy Er of the neutron for target nucleus at rest. It should be noticed that ${\sigma }_s(E_r)$- the scattering integrated cross section- is point-wise calculated and includes the exact resonance shape as developed from the early formula of Breit-Wigner (Bell and Glasstone 1970)

Further notations appearing in the Equation (1)(1) $$\begin{array}{c}{\sigma }_s^T\left(E\to E\prime ,\overrightarrow{\Omega }\to \overrightarrow{\Omega }\prime \right)=\frac{1}{2\pi }{\sigma }_s^T\left(E\to E\prime ,{\mu }_0^{\mathit{lab}}\right)=\frac{1}{2\pi \mathrm{v}}{\left(\frac{A+1}{A}\right)}^4{\left(\frac{A}{\pi }\right)}^{3/2}\\ \int 2\pi u^{2}du\int d{\mu }_u\int c^{2}dc\int {(u\prime )}^{2}du\prime \int d{\mu }_{u\prime }\int \frac{2}{\hspace{0.17em}\text{sin}\hspace{0.17em}\phi }\frac{\delta (u\prime -u)}{{(u\prime )}^2}\text{exp}\hspace{0.17em}\left[{\mathrm{v}}^2-(A+1)\left(\frac{u^2}{A}+c^2\right)\right]\\ \frac{1}{u\mathrm{v}c}\delta \left[{\mu }_u-\frac{({\mathrm{v}}^2-c^2-u^2)}{2uc}\right]\frac{1}{2u\prime c{k}_{B}T}\delta \left[{\mu }_{u\prime }-\frac{{(\mathrm{v}\prime )}^2-{(u\prime )}^2-c^2}{2u\prime c}\right]\\ \frac{4\text{vv}\prime c^2}{B_0^{\prime }}\delta (\hspace{0.17em}\text{cos}\hspace{0.17em}\phi -\hspace{0.17em}\text{cos}\hspace{0.17em}\widehat{\phi })u{\sigma }_s(E_r)\frac{P(u,{\mu }_0^{cm})}{2\pi }d\hspace{0.17em}\text{cos}\hspace{0.17em}\phi \end{array}$$(1) can be found in (Rothenstein and Dagan 1998) (1) $$\begin{array}{c}{\sigma }_s^T\left(E\to E\prime ,\overrightarrow{\Omega }\to \overrightarrow{\Omega }\prime \right)=\frac{1}{2\pi }{\sigma }_s^T\left(E\to E\prime ,{\mu }_0^{\mathit{lab}}\right)=\frac{1}{2\pi \mathrm{v}}{\left(\frac{A+1}{A}\right)}^4{\left(\frac{A}{\pi }\right)}^{3/2}\\ \int 2\pi u^{2}du\int d{\mu }_u\int c^{2}dc\int {(u\prime )}^{2}du\prime \int d{\mu }_{u\prime }\int \frac{2}{\hspace{0.17em}\text{sin}\hspace{0.17em}\phi }\frac{\delta (u\prime -u)}{{(u\prime )}^2}\text{exp}\hspace{0.17em}\left[{\mathrm{v}}^2-(A+1)\left(\frac{u^2}{A}+c^2\right)\right]\\ \frac{1}{u\mathrm{v}c}\delta \left[{\mu }_u-\frac{({\mathrm{v}}^2-c^2-u^2)}{2uc}\right]\frac{1}{2u\prime c{k}_{B}T}\delta \left[{\mu }_{u\prime }-\frac{{(\mathrm{v}\prime )}^2-{(u\prime )}^2-c^2}{2u\prime c}\right]\\ \frac{4\text{vv}\prime c^2}{B_0^{\prime }}\delta (\hspace{0.17em}\text{cos}\hspace{0.17em}\phi -\hspace{0.17em}\text{cos}\hspace{0.17em}\widehat{\phi })u{\sigma }_s(E_r)\frac{P(u,{\mu }_0^{cm})}{2\pi }d\hspace{0.17em}\text{cos}\hspace{0.17em}\phi \end{array}$$(1)

At higher energies the scattering kernel is often simplified by employing a so called asymptotic kernel, which approximates the scattering kernel at unphysical temperature of 0 K and constant cross sections. Those “short cuts” in the scattering handling allows obviously for a faster solution of the transport solvers. However, the impact of the resonances and the temperature is of rather larger importance and goes far beyond this energy range (up to several tens of keV) as is shown in the next section.

Another option is the OM (Hodgson 1971), which is mainly valid for very high energies above 1 MeV.

The OM-Optical Model solution for the so-called shape elastic cross section (Koning and Delaroche 2003) uses the Schrödinger wave equation: (2) $${\nabla }^2\Psi +(2m/{\mathit{\hslash }}^2)(E-V(r))\Psi =0$$(2)

This equation is transformed to its radial form including the orbital angular momentum quantum number L. Its solution leads to the definition of the momentum dependent shift factor $S_L,$ which defines the scattering amplitude $f(\theta )$. The differential cross section, namely the scattering kernel is obtained by: (3) $$\frac{d\sigma }{d\Omega }={\left|f(\theta )\right|}^2$$(3)

The procedure depends obviously on the chosen potential V(r) of the outgoing wave of the nuclear “disturbance” and evolves very complex optimized parameters. The obtained cross section is then compared to available data and the parameters are re-adjusted.

As far as the physics is concerned one talks here about average cross section at 0 K as the temperature does not appear explicitly in the Schrödinger equation. Hence, the range of applicability of the OM is at energies where temperature effects and sharp resonance structures are neglected. The applicability of such models is in MeV energy range where also direct or pre-equilibrium processes are dominant. However, at the range of tenth KeV one should use R- Matrix theory which can handle resonant structures. In addition, as the OM is based actually on fitting experimental data for each nuclide separately, it depends strongly on the evaluation procedure, which is sometime not so good (see Figure 1 for Fe56), and sometime is better(see Figure 2 for W182).

Figure 1. Comparison between total cross section based on the OM (Koning and Delaroche 2003) and ENDF/B-VIII library for Fe56.

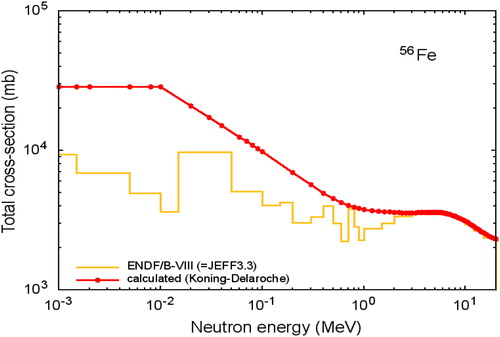
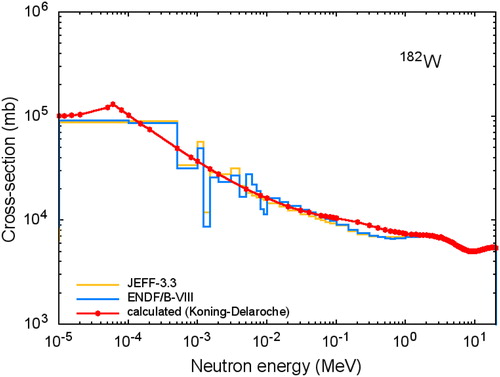
Figure 2. Comparison between the OM (Koning-Delaroche) and ENDF/B-VIII (Brown et al. 2018) and JEFF (JEFF 2017) libraries for W182.

Cross sections evaluations for Fe56 and W182 by the two different scattering kernel treatments

Starting with the total cross section of iron Fe56 it can be seen that below 100 keV (Figure 1) the difference between the OM based on (Koning and Delaroche 2003) and the nuclear data based libraries (Chadwick et al. 2006; Brown et al. 2018) reaches factor 5 at some high energies. This emphasizes clearly that at several cases, i.e. iron, the accuracy of the OM is doubtful below already at 1 MeV. For tungsten W182 (Figure 2) the OM can estimates to some extent well average values, yet cannot deal the resonances nor their temperature dependency. In particular, this is true for the elastic scattering shown in Figure 3.

Figure 3. Elastic scattering cross section of the ENDF/B-VII library (Chadwick et al. 2006) for W182.

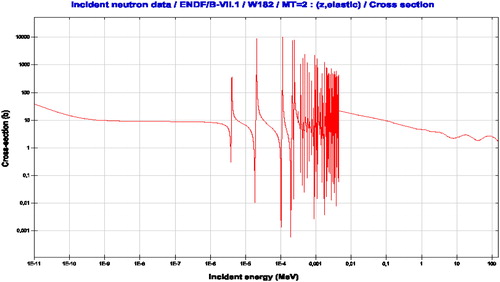
Thereafter one can expect that the scattering kernels would be quite different, depending on their originate physics models.

Scattering kernel calculations for Fe56 and W182

The angular differential part of the scattering kernel at keV energy range is introduced, comparing the two approaches discussed above. Mathematically speaking the scattering kernel, obtained by Equation (3)(3) $$\frac{d\sigma }{d\Omega }={\left|f(\theta )\right|}^2$$(3) , is compared to the energy-integrated scattering kernel of Equation (1)(1) $$\begin{array}{c}{\sigma }_s^T\left(E\to E\prime ,\overrightarrow{\Omega }\to \overrightarrow{\Omega }\prime \right)=\frac{1}{2\pi }{\sigma }_s^T\left(E\to E\prime ,{\mu }_0^{\mathit{lab}}\right)=\frac{1}{2\pi \mathrm{v}}{\left(\frac{A+1}{A}\right)}^4{\left(\frac{A}{\pi }\right)}^{3/2}\\ \int 2\pi u^{2}du\int d{\mu }_u\int c^{2}dc\int {(u\prime )}^{2}du\prime \int d{\mu }_{u\prime }\int \frac{2}{\hspace{0.17em}\text{sin}\hspace{0.17em}\phi }\frac{\delta (u\prime -u)}{{(u\prime )}^2}\text{exp}\hspace{0.17em}\left[{\mathrm{v}}^2-(A+1)\left(\frac{u^2}{A}+c^2\right)\right]\\ \frac{1}{u\mathrm{v}c}\delta \left[{\mu }_u-\frac{({\mathrm{v}}^2-c^2-u^2)}{2uc}\right]\frac{1}{2u\prime c{k}_{B}T}\delta \left[{\mu }_{u\prime }-\frac{{(\mathrm{v}\prime )}^2-{(u\prime )}^2-c^2}{2u\prime c}\right]\\ \frac{4\text{vv}\prime c^2}{B_0^{\prime }}\delta (\hspace{0.17em}\text{cos}\hspace{0.17em}\phi -\hspace{0.17em}\text{cos}\hspace{0.17em}\widehat{\phi })u{\sigma }_s(E_r)\frac{P(u,{\mu }_0^{cm})}{2\pi }d\hspace{0.17em}\text{cos}\hspace{0.17em}\phi \end{array}$$(1) .

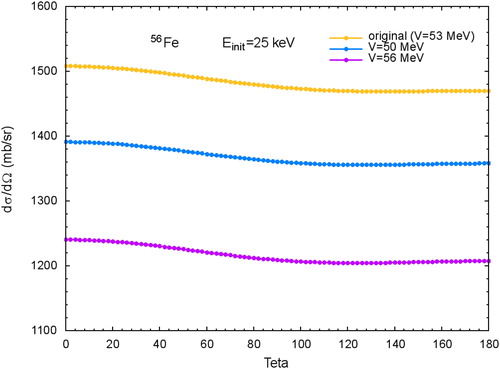
Figure 4 presents the OM based kernel for Fe56 at 25 keV. The yellow line presents the original suggested (Koning and Delaroche 2003) potential, while the two other curves show arbitrary potentials examined in this work for the sensitivity of slight changes of the same potential model. The results show that the shape of all curves is very similar. However, the amplitude of the scattering kernel is quite sensitive to arbitrary, albeit close to each other, alternative potentials, 50 and 56 MeV instead of the correct one, 53 MeV. The OM emphasizes, thereafter, the ability to adjust the kernel to available data, but on the other side, it shows the complexity of its phenomenological approach. It lacks the secondary distribution of the energy based on resonances, as well as the temperature impact, (assumed to be 0 K) effects which generally causes enhanced anisotropy.

Figure 4. OM based angular scattering kernel for Fe56 at 25 keV for the original.

Potential (53 MeV) and two arbitraries at 50 and 56 MeV. The scattering is almost isotropic for all cases.

The “classical” angular distribution for Fe56 based on the energy, momentum conservation laws and temperature dependency scattering cross sections in shown in Figure 5. In contrary to the OM, one can observe a clear enhanced scattering around 90° and a slight increase toward forward scattering in comparison to back scattering.

Figure 5. “Classical” momentum and energy dependent angular scattering kernel (Equation 1(1) $$\begin{array}{c}{\sigma }_s^T\left(E\to E\prime ,\overrightarrow{\Omega }\to \overrightarrow{\Omega }\prime \right)=\frac{1}{2\pi }{\sigma }_s^T\left(E\to E\prime ,{\mu }_0^{\mathit{lab}}\right)=\frac{1}{2\pi \mathrm{v}}{\left(\frac{A+1}{A}\right)}^4{\left(\frac{A}{\pi }\right)}^{3/2}\\ \int 2\pi u^{2}du\int d{\mu }_u\int c^{2}dc\int {(u\prime )}^{2}du\prime \int d{\mu }_{u\prime }\int \frac{2}{\hspace{0.17em}\text{sin}\hspace{0.17em}\phi }\frac{\delta (u\prime -u)}{{(u\prime )}^2}\text{exp}\hspace{0.17em}\left[{\mathrm{v}}^2-(A+1)\left(\frac{u^2}{A}+c^2\right)\right]\\ \frac{1}{u\mathrm{v}c}\delta \left[{\mu }_u-\frac{({\mathrm{v}}^2-c^2-u^2)}{2uc}\right]\frac{1}{2u\prime c{k}_{B}T}\delta \left[{\mu }_{u\prime }-\frac{{(\mathrm{v}\prime )}^2-{(u\prime )}^2-c^2}{2u\prime c}\right]\\ \frac{4\text{vv}\prime c^2}{B_0^{\prime }}\delta (\hspace{0.17em}\text{cos}\hspace{0.17em}\phi -\hspace{0.17em}\text{cos}\hspace{0.17em}\widehat{\phi })u{\sigma }_s(E_r)\frac{P(u,{\mu }_0^{cm})}{2\pi }d\hspace{0.17em}\text{cos}\hspace{0.17em}\phi \end{array}$$(1) ) at 25 keV for Fe56 with temperature of 1200 K the angle dependent anisotropy is well pronounced.

Figures 6 and 7 introduce the differential cross section for W182 at 1000° K for an incident neutron at 10 keV. In this case, the scattering cross section is near a pronounced resonance shown in Figure 3. The scattering kernels of the two models differ strongly from each other. The averaged based approach of the OM shows, as for the case of Fe56 in Figure 4, an almost isotropic scattering. The difference between lowest and highest value is only about 6%. Contrarily, the “classical” model of Equation (1)(1) $$\begin{array}{c}{\sigma }_s^T\left(E\to E\prime ,\overrightarrow{\Omega }\to \overrightarrow{\Omega }\prime \right)=\frac{1}{2\pi }{\sigma }_s^T\left(E\to E\prime ,{\mu }_0^{\mathit{lab}}\right)=\frac{1}{2\pi \mathrm{v}}{\left(\frac{A+1}{A}\right)}^4{\left(\frac{A}{\pi }\right)}^{3/2}\\ \int 2\pi u^{2}du\int d{\mu }_u\int c^{2}dc\int {(u\prime )}^{2}du\prime \int d{\mu }_{u\prime }\int \frac{2}{\hspace{0.17em}\text{sin}\hspace{0.17em}\phi }\frac{\delta (u\prime -u)}{{(u\prime )}^2}\text{exp}\hspace{0.17em}\left[{\mathrm{v}}^2-(A+1)\left(\frac{u^2}{A}+c^2\right)\right]\\ \frac{1}{u\mathrm{v}c}\delta \left[{\mu }_u-\frac{({\mathrm{v}}^2-c^2-u^2)}{2uc}\right]\frac{1}{2u\prime c{k}_{B}T}\delta \left[{\mu }_{u\prime }-\frac{{(\mathrm{v}\prime )}^2-{(u\prime )}^2-c^2}{2u\prime c}\right]\\ \frac{4\text{vv}\prime c^2}{B_0^{\prime }}\delta (\hspace{0.17em}\text{cos}\hspace{0.17em}\phi -\hspace{0.17em}\text{cos}\hspace{0.17em}\widehat{\phi })u{\sigma }_s(E_r)\frac{P(u,{\mu }_0^{cm})}{2\pi }d\hspace{0.17em}\text{cos}\hspace{0.17em}\phi \end{array}$$(1) shows enhanced scattering at the range of 60 to 120 degrees as obtained in Figure 7. The backscattering and forward scattering angles in Figure 7 exhibit an oscillating behavior, which to some extent is reminiscent of the behavior of the resonance range by heavy nuclides (Becker, Dagan, and Lohnert 2009). This range should be verified by dedicated experiments to ensure its validity. Nevertheless, as far as this paper is concerned, the shape of the scattering spectrum of the “classical” model are clearly different in shape, differential and integrated value (the scattering cross section) from the OM.

Figure 6. OM based angular scattering kernel forW182 at 10 keV. The scattering is quite isotropic. The difference between lowest and highest value is about 6%.

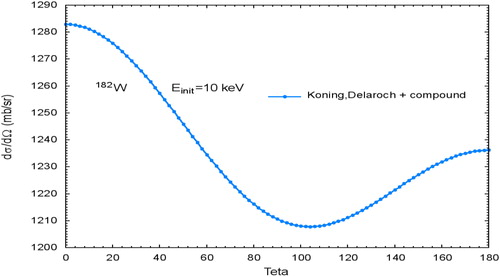
Figure 7. Momentum and energy dependent angular scattering kernel (Equation 1(1) $$\begin{array}{c}{\sigma }_s^T\left(E\to E\prime ,\overrightarrow{\Omega }\to \overrightarrow{\Omega }\prime \right)=\frac{1}{2\pi }{\sigma }_s^T\left(E\to E\prime ,{\mu }_0^{\mathit{lab}}\right)=\frac{1}{2\pi \mathrm{v}}{\left(\frac{A+1}{A}\right)}^4{\left(\frac{A}{\pi }\right)}^{3/2}\\ \int 2\pi u^{2}du\int d{\mu }_u\int c^{2}dc\int {(u\prime )}^{2}du\prime \int d{\mu }_{u\prime }\int \frac{2}{\hspace{0.17em}\text{sin}\hspace{0.17em}\phi }\frac{\delta (u\prime -u)}{{(u\prime )}^2}\text{exp}\hspace{0.17em}\left[{\mathrm{v}}^2-(A+1)\left(\frac{u^2}{A}+c^2\right)\right]\\ \frac{1}{u\mathrm{v}c}\delta \left[{\mu }_u-\frac{({\mathrm{v}}^2-c^2-u^2)}{2uc}\right]\frac{1}{2u\prime c{k}_{B}T}\delta \left[{\mu }_{u\prime }-\frac{{(\mathrm{v}\prime )}^2-{(u\prime )}^2-c^2}{2u\prime c}\right]\\ \frac{4\text{vv}\prime c^2}{B_0^{\prime }}\delta (\hspace{0.17em}\text{cos}\hspace{0.17em}\phi -\hspace{0.17em}\text{cos}\hspace{0.17em}\widehat{\phi })u{\sigma }_s(E_r)\frac{P(u,{\mu }_0^{cm})}{2\pi }d\hspace{0.17em}\text{cos}\hspace{0.17em}\phi \end{array}$$(1) ) at10 keV for W182 with temperature of 1000 K. The difference between lowest and highest value is almost factor 6.

The different results of the scattering kernels based on Equation (1)(1) $$\begin{array}{c}{\sigma }_s^T\left(E\to E\prime ,\overrightarrow{\Omega }\to \overrightarrow{\Omega }\prime \right)=\frac{1}{2\pi }{\sigma }_s^T\left(E\to E\prime ,{\mu }_0^{\mathit{lab}}\right)=\frac{1}{2\pi \mathrm{v}}{\left(\frac{A+1}{A}\right)}^4{\left(\frac{A}{\pi }\right)}^{3/2}\\ \int 2\pi u^{2}du\int d{\mu }_u\int c^{2}dc\int {(u\prime )}^{2}du\prime \int d{\mu }_{u\prime }\int \frac{2}{\hspace{0.17em}\text{sin}\hspace{0.17em}\phi }\frac{\delta (u\prime -u)}{{(u\prime )}^2}\text{exp}\hspace{0.17em}\left[{\mathrm{v}}^2-(A+1)\left(\frac{u^2}{A}+c^2\right)\right]\\ \frac{1}{u\mathrm{v}c}\delta \left[{\mu }_u-\frac{({\mathrm{v}}^2-c^2-u^2)}{2uc}\right]\frac{1}{2u\prime c{k}_{B}T}\delta \left[{\mu }_{u\prime }-\frac{{(\mathrm{v}\prime )}^2-{(u\prime )}^2-c^2}{2u\prime c}\right]\\ \frac{4\text{vv}\prime c^2}{B_0^{\prime }}\delta (\hspace{0.17em}\text{cos}\hspace{0.17em}\phi -\hspace{0.17em}\text{cos}\hspace{0.17em}\widehat{\phi })u{\sigma }_s(E_r)\frac{P(u,{\mu }_0^{cm})}{2\pi }d\hspace{0.17em}\text{cos}\hspace{0.17em}\phi \end{array}$$(1) and those based on Equation (3)(3) $$\frac{d\sigma }{d\Omega }={\left|f(\theta )\right|}^2$$(3) emphasize the importance of further measurements. The OM uses an approximated approach with representative potential, adjusted parameters, unrealistic 0 K, only averaged cross section and in its basic approach ignores the secondary energy distribution. An alternative for the energy range discussed in this study could be the Blatt Biedenharn angular distribution (Blatt and Biedenharn 1952). It uses the basic approach of Equations (2)(2) $${\nabla }^2\Psi +(2m/{\mathit{\hslash }}^2)(E-V(r))\Psi =0$$(2) and (3)(3) $$\frac{d\sigma }{d\Omega }={\left|f(\theta )\right|}^2$$(3) , accounts for momentum conservation; and hence is in particular suitable for cases where there are no changes in the energy of the emitted particle. For other cases as seen in (Blatt and Biedenharn 1952) a “direct comparison with experiments “is available with consequent adjustments. Further on the procedure is embedded also within the R-matrix theory (Gunsing 2018), which as mentioned above is crucial for handling resonant structures. Recently this option became also possible within the new ENDF library VIII (Brown et al. 2018). It is evident that dedicated experiments are needed to compare this quantum mechanics based approach with the theoretical classical approach of Equation (1)(1) $$\begin{array}{c}{\sigma }_s^T\left(E\to E\prime ,\overrightarrow{\Omega }\to \overrightarrow{\Omega }\prime \right)=\frac{1}{2\pi }{\sigma }_s^T\left(E\to E\prime ,{\mu }_0^{\mathit{lab}}\right)=\frac{1}{2\pi \mathrm{v}}{\left(\frac{A+1}{A}\right)}^4{\left(\frac{A}{\pi }\right)}^{3/2}\\ \int 2\pi u^{2}du\int d{\mu }_u\int c^{2}dc\int {(u\prime )}^{2}du\prime \int d{\mu }_{u\prime }\int \frac{2}{\hspace{0.17em}\text{sin}\hspace{0.17em}\phi }\frac{\delta (u\prime -u)}{{(u\prime )}^2}\text{exp}\hspace{0.17em}\left[{\mathrm{v}}^2-(A+1)\left(\frac{u^2}{A}+c^2\right)\right]\\ \frac{1}{u\mathrm{v}c}\delta \left[{\mu }_u-\frac{({\mathrm{v}}^2-c^2-u^2)}{2uc}\right]\frac{1}{2u\prime c{k}_{B}T}\delta \left[{\mu }_{u\prime }-\frac{{(\mathrm{v}\prime )}^2-{(u\prime )}^2-c^2}{2u\prime c}\right]\\ \frac{4\text{vv}\prime c^2}{B_0^{\prime }}\delta (\hspace{0.17em}\text{cos}\hspace{0.17em}\phi -\hspace{0.17em}\text{cos}\hspace{0.17em}\widehat{\phi })u{\sigma }_s(E_r)\frac{P(u,{\mu }_0^{cm})}{2\pi }d\hspace{0.17em}\text{cos}\hspace{0.17em}\phi \end{array}$$(1) in the relevant energy range.

Nevertheless, at high energies, in particular above 1 MeV the OM procedure or other processes, mentioned above, are inevitable in order to replace the unpractical complex full quantum mechanics solution of the cross section and its derivatives. It cannot and therefore should not replace validated existing scattering models. In energies up to several tens of keV, the cross section evaluation methods such as the R Matrix theory used successfully also in the unresolved resonance range and often used in the common nuclear data libraries (Brown et al. 2018) (Chadwick et al. 2006), (JEFF 2017), should be utilized. The differential part, which is through all lower energy range detached from the cross section itself, should involve the experimental approved (for low energies) Equation (1)(1) $$\begin{array}{c}{\sigma }_s^T\left(E\to E\prime ,\overrightarrow{\Omega }\to \overrightarrow{\Omega }\prime \right)=\frac{1}{2\pi }{\sigma }_s^T\left(E\to E\prime ,{\mu }_0^{\mathit{lab}}\right)=\frac{1}{2\pi \mathrm{v}}{\left(\frac{A+1}{A}\right)}^4{\left(\frac{A}{\pi }\right)}^{3/2}\\ \int 2\pi u^{2}du\int d{\mu }_u\int c^{2}dc\int {(u\prime )}^{2}du\prime \int d{\mu }_{u\prime }\int \frac{2}{\hspace{0.17em}\text{sin}\hspace{0.17em}\phi }\frac{\delta (u\prime -u)}{{(u\prime )}^2}\text{exp}\hspace{0.17em}\left[{\mathrm{v}}^2-(A+1)\left(\frac{u^2}{A}+c^2\right)\right]\\ \frac{1}{u\mathrm{v}c}\delta \left[{\mu }_u-\frac{({\mathrm{v}}^2-c^2-u^2)}{2uc}\right]\frac{1}{2u\prime c{k}_{B}T}\delta \left[{\mu }_{u\prime }-\frac{{(\mathrm{v}\prime )}^2-{(u\prime )}^2-c^2}{2u\prime c}\right]\\ \frac{4\text{vv}\prime c^2}{B_0^{\prime }}\delta (\hspace{0.17em}\text{cos}\hspace{0.17em}\phi -\hspace{0.17em}\text{cos}\hspace{0.17em}\widehat{\phi })u{\sigma }_s(E_r)\frac{P(u,{\mu }_0^{cm})}{2\pi }d\hspace{0.17em}\text{cos}\hspace{0.17em}\phi \end{array}$$(1) , as it gives a full theoretical, albeit classical, solution. As mentioned above, the use of Blatt Biedenharn angular distribution in the tenth KeV range is a better option than OM. However, the role and a practical solution of the quantum mechanics concerning the secondary energy and angular distribution remain an open question, in particular, in the above relevant energy range.

Conclusions

This work points out the importance of the energy and temperature dependent differential scattering term of the Boltzmann equation also in the tens of keV energy range. Simplification or unjustified homogenization of the scattering term in favor of a smoother mathematical solver leads promptly to erroneous results, which are often beyond expectations.

The theory of the scattering kernels has been significantly improved in the last decades in particular in the thermal and resonance energy range. The experimental confirmation led in this work to the analysis of higher energies relevant still for nuclear reactors. The validity of those scattering models in the energy range of tens of keV-collide with the OM, which is mostly applicable only at energies above 1 MeV.

The outcome of this work is clearly in favor of using the resonant dependent scattering approach which is based on the classical momentum and energy conservation law (Equation 1(1) $$\begin{array}{c}{\sigma }_s^T\left(E\to E\prime ,\overrightarrow{\Omega }\to \overrightarrow{\Omega }\prime \right)=\frac{1}{2\pi }{\sigma }_s^T\left(E\to E\prime ,{\mu }_0^{\mathit{lab}}\right)=\frac{1}{2\pi \mathrm{v}}{\left(\frac{A+1}{A}\right)}^4{\left(\frac{A}{\pi }\right)}^{3/2}\\ \int 2\pi u^{2}du\int d{\mu }_u\int c^{2}dc\int {(u\prime )}^{2}du\prime \int d{\mu }_{u\prime }\int \frac{2}{\hspace{0.17em}\text{sin}\hspace{0.17em}\phi }\frac{\delta (u\prime -u)}{{(u\prime )}^2}\text{exp}\hspace{0.17em}\left[{\mathrm{v}}^2-(A+1)\left(\frac{u^2}{A}+c^2\right)\right]\\ \frac{1}{u\mathrm{v}c}\delta \left[{\mu }_u-\frac{({\mathrm{v}}^2-c^2-u^2)}{2uc}\right]\frac{1}{2u\prime c{k}_{B}T}\delta \left[{\mu }_{u\prime }-\frac{{(\mathrm{v}\prime )}^2-{(u\prime )}^2-c^2}{2u\prime c}\right]\\ \frac{4\text{vv}\prime c^2}{B_0^{\prime }}\delta (\hspace{0.17em}\text{cos}\hspace{0.17em}\phi -\hspace{0.17em}\text{cos}\hspace{0.17em}\widehat{\phi })u{\sigma }_s(E_r)\frac{P(u,{\mu }_0^{cm})}{2\pi }d\hspace{0.17em}\text{cos}\hspace{0.17em}\phi \end{array}$$(1) ) as it was, albeit for lower energies, experimentally proven in three different laboratories (Ro et al. 2009; Dagan et al. 2011; Gunsing et al. 2012). Those experiments emphasized the prevalence of the classical scattering laws – the differential scattering cross section- in accordance (as shown in Equation (1)(1) $$\begin{array}{c}{\sigma }_s^T\left(E\to E\prime ,\overrightarrow{\Omega }\to \overrightarrow{\Omega }\prime \right)=\frac{1}{2\pi }{\sigma }_s^T\left(E\to E\prime ,{\mu }_0^{\mathit{lab}}\right)=\frac{1}{2\pi \mathrm{v}}{\left(\frac{A+1}{A}\right)}^4{\left(\frac{A}{\pi }\right)}^{3/2}\\ \int 2\pi u^{2}du\int d{\mu }_u\int c^{2}dc\int {(u\prime )}^{2}du\prime \int d{\mu }_{u\prime }\int \frac{2}{\hspace{0.17em}\text{sin}\hspace{0.17em}\phi }\frac{\delta (u\prime -u)}{{(u\prime )}^2}\text{exp}\hspace{0.17em}\left[{\mathrm{v}}^2-(A+1)\left(\frac{u^2}{A}+c^2\right)\right]\\ \frac{1}{u\mathrm{v}c}\delta \left[{\mu }_u-\frac{({\mathrm{v}}^2-c^2-u^2)}{2uc}\right]\frac{1}{2u\prime c{k}_{B}T}\delta \left[{\mu }_{u\prime }-\frac{{(\mathrm{v}\prime )}^2-{(u\prime )}^2-c^2}{2u\prime c}\right]\\ \frac{4\text{vv}\prime c^2}{B_0^{\prime }}\delta (\hspace{0.17em}\text{cos}\hspace{0.17em}\phi -\hspace{0.17em}\text{cos}\hspace{0.17em}\widehat{\phi })u{\sigma }_s(E_r)\frac{P(u,{\mu }_0^{cm})}{2\pi }d\hspace{0.17em}\text{cos}\hspace{0.17em}\phi \end{array}$$(1) ) to a quantum mechanics based integral scattering cross section ${\sigma }_s(E_r).$

The OM is the optimal theoretical approach for energies beyond 1 MeV where the temperature, the exact cross section shape and the secondary energy distribution are of minor importance. Hence, the single differential cross section introduced in Equation (3)(3) $$\frac{d\sigma }{d\Omega }={\left|f(\theta )\right|}^2$$(3) is acceptable. However, for nuclear reactors relevant energies, in particular, up to several tens of keV, the OM should not be employed, due to its deficiencies as far as its double differential scattering cross section treatment is concerned.

In summary, the experimental evidence of the models of a resonant scattering kernel (Ousiloumen and Sanchez 1991; Rothenstein and Dagan 1998) pronounced a unique phenomenon. The mathematical formula of an energy dependent cross section cannot be directly differentiated to get the scattering kernel or vice versa (as is done in the OM) because the fundamental physics is completely different. The scattering cross section is based on derivation of the Schrödinger equation whereas the differential scattering part originates from Newton laws or Einstein’s specific relativity, albeit adopting the integrated value of the scattering cross section.

Can equation (1) with its energy and temperature dependency be exchanged or reevaluated, if not by OM, then by a resonance specific orbital moments? The attempt by Blatt Biedenharn (Blatt and Biedenharn 1952) was introduced only for cases without energy change. As mentioned above other cases are still too complex to handle. It remains that the only experimental approved theory is the Newton or Einstein laws, which show a non-negligible effect also in the high energies, as discussed in this work. Further experiments, which are planned in the GELINA facility in Geel (Schillebeeckx 2020), could illuminate the applicability range of the classical model in view, among others, of the Blatt Biedenharn approach. In any case, the scattering term within the Boltzmann equation indeed has an enhanced importance as shown by (Ousiloumen and Sanchez 1991; Rothenstein and Dagan 1998) and should be considered accordingly.

Acknowledgments

The paper is dedicated to Wolfgang Rothenstein whose work and ideas supplied the basis for this paper.

The authors would like to thank Manfred Popp for his fruitful discussions and valuable remarks.