Radiation emission processes and properties: synchrotron, undulator and betatron radiation

Abstract

Synchrotron, undulator and betatron radiations are generated from last generation and novel concept sources. The achievement of unprecedented radiation properties opens new opportunities in various research fields as well as novel potential applications. In particular, bright coherent X-rays and -rays have been recently obtained thanks to enormous efforts in technological advancements and research activities. We give in this work a uniform argumentation and comparison of the main fundamental emission processes and radiation properties of synchrotron, undulator and betatron radiations. Emphasis is given to spatial coherence and related diagnostics, a fundamental property for any ‘modern light source’ and a basis for recent important advancements.

Graphical Abstract

Keywords:

• Synchrotron radiation
• undulators
• betatron radiation
• laser-plasma acceleration
• coherence

PACS:

• 41.60.Ap Synchrotron radiation
• 41.75.Jv Laser-driven acceleration
• 41.50.+h X-ray beams and x-ray optics
• 42.25.Kb Coherence

1. Introduction

‘Modern light sources’ are nowadays of increasing interest for the development of bright, highly coherent and short-wavelength radiation. Such performances can be obtained exploiting synchrotron emission from high-energy particles accelerated in large facilities available around the world. Huge advantages are expected since these performances can be of fundamental interest in many disciplines, from life science to medicine, chemistry, physics and material science, across a wide range of dimensional scales. In parallel with the development of sources with superior performances, it becomes essential to achieve suitable diagnostics, playing a fundamental role in effectively monitoring the state-of-the-art and for pushing further improvements.

This works provides an overview on the fundamental emission processes and radiation properties. Starting from the synchrotron emission (Section 1), which is at the basis of the modern light sources, we give emphasis on the properties of transverse spatial coherence and related diagnostics tools in the last generation synchrotrons. We present both the state-of-the art and advancements of undulators (Section 3) since they represent the fundamental devices in ‘conventional accelerators’ to produce diffraction-limited radiation with high degree of coherence and high brilliance. We finally extend our discussion to novel concept sources.

In particular, a promising compact source is envisioned to be based on the relativistic laser-plasma interaction that provides a synchrotron-like emission exploiting a completely novel technique to accelerate particles. Betatron radiation is emitted by particles during the acceleration process in an ultra-short X-ray burst (tens of fs) with a degree of coherence much higher than conventional X-ray sources. The emission process, the properties of betatron radiation and the diagnostics techniques will be presented and discussed in Section 4.

Finally, we collect our conclusions in Section 5.

2. Synchrotron radiation

Synchrotron radiation is produced in laboratory and observed in several astrophysical phenomena in a broad range of wavelengths from radio-waves [1] to -rays [2–5]. For example, it is produced from neutron stars and pulsars [6,7], dwarf stars [8,9], planets [10], galaxies [11,12], interstellar medium [13] as well as from cosmological sources [14].

Nowadays, medium and high energy facilities are present around the world [15] to produce high brilliance and highly polarized radiation, characterized by a broad spectrum, intrinsically low divergence and transverse spatial coherence.

Third-generation synchrotrons produce radiation close to the diffraction limit with unprecedented coherence properties, thereby constituting a precious resource in different fields of research as in biology [16], life sciences [17], chemistry [18] physics and material sciences also due to the wide applicability and to investigate matter at the nanometer and sub-nanometer scale. A comprehensive coverage of properties of synchrotron and undulator radiation was given in [19], while an earlier and more basic coverage of the properties of bending magnet, undulator and wiggler radiation was made in [20]. A very simple and clear explanation of radiation emission processes has been given in [21], who gave an effective approach accessible to non-specialists. The emission process from a single-particle characterizes the common properties of many cases of interest. However, the multi-particle case must be taken into account to describe radiation properties such as transverse emittance and coherence, which are the crucial properties of the particle beam and radiation in synchrotrons of last generation we are mainly interested here.

2.1. Emission process and relativistic beaming in a arbitrary boost

Synchrotron radiation must be described in the theoretical framework of the Special Relativity due to the high particle energy involved during the emission process.

We define for clarity two reference frames with relative normalized velocity , the frame where particles are at rest and all quantities referred to this frame are primate. The lab frame K with the axis parallel to frame and with the origin of the axes coinciding at . All quantities referred to frame K are not primate.

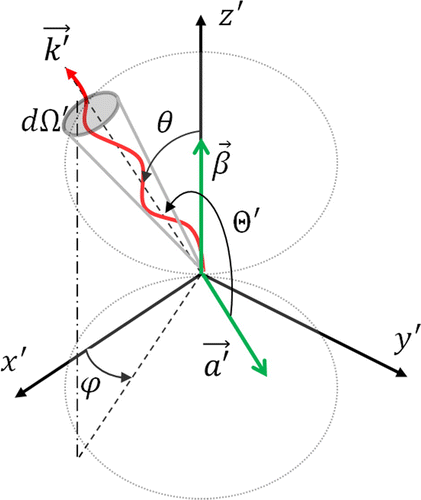
Figure 1. Geometry of the emission process of the electromagnetic radiation from a single particle with acceleration in the frame .

The synchrotron emission can be explained transforming the emission process from the frame in the classical limit to the frame K, where the observer sees the particle approaching the speed of light. The radiation power per unit solid angle emitted by a particle with initial zero velocity in , but with non-zero acceleration , is given by the Larmor formula:(1)

where is the energy per unit solid angle and unit time, q is the charged particle and is the angle between the particle acceleration and the wavevector as sketched in Figure 1. Since the total power is by its very nature an invariant quantity, it is written in spherical coordinates in both frames as(2)

The argument of the second integral can be written in the following form (see Appendix 1)(3)

where and are the momentum energy four vector and the four wavevector, respectively. are geometrical functions depending on and and is the matrix of the Lorentz transformations.

Equation (3(3) ) provides a very interesting picture of what occurs if passing from the rest frame to the lab frame K. In fact, it can be used to separately show geometrical and kinematic quantities involved in the transformations from to K for any arbitrary boost. A similar formulation was also applied to the relativistic Thomson scattering as shown in [22,23]. In the relevant case of collinear motion between K and , the observer (in the lab frame) sees the particle moving with normalized velocity along the z axis. The matrix of the Lorentz transformations takes the form

where has been assumed. The power per unit solid angle in K is computed from Equation (3(3) ) with the acceleration perpendicular to the electron velocity as(4)

This equation is the product of four factors with the following physical meaning. The first term is the classical Larmor formula, whose acceleration in K introduces the extra-factor , that becomes for parallel to . The second term is the light aberration due to the conversion of of the Larmor formula from to K. The third factor is due to time dilatation and transformation of the momentum energy four vector from to K. 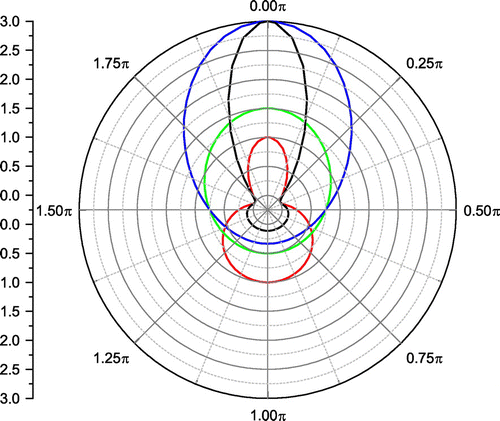Finally, the last term is due to the transformation of the solid angle from to K using the spherical coordinates defined in the lab frame. In Figure 2, we separately compare the three factors which are dependent on and . Notice that in the ultra-relativistic case the second and third terms (red and green curves ) are upper limited to 1 and 2, respectively, while the last factor (blue curve) due to the contraction of the solid angle can increase indefinitely.

Figure 2. Polar diagram of the geometrical factors (as a function of ) which generate the beaming of synchrotron radiation as described in Equation (4(4) ) for and . Red is light aberration. Green is the transformation of the momentum energy four vector and time dilatation. Blue is the contraction of the solid angle from to K. The black curve is the product of all the three factors normalized to the maximum value of the blue curve.

The two fundamental consequences of the beaming into a cone of semiaperture are bright radiation and broad spectrum.

The brightness of radiation has a huge increment related to the concentration of the emitted power along the direction of the electron velocity, passing from the classical limit to relativistic case. All emitted power is concentrated in a very small angle (order of rad in recent synchrotrons), despite the total power is kept constant, since it is a Lorentz invariant.

The broad spectrum is due to the impulsive nature of the radiation observed in the K frame that can be easily derived by means of a Fourier transformation of P(t). The spectrum of radiation extends up to the critical frequency , where is the radius of curvature of particle due to the transverse acceleration. The shorter wavelengths currently achievable in laboratories are in the hard X-ray range. A proper frequency band, with frequencies less than , can be selected using filters or monochromators, depending on application.

2.2. Transverse emittance and coherence of diffraction-limited radiation

The beaming effect explains many of the fundamental properties of synchrotron radiation. However, the emission process from a single particle cannot provide a satisfactory explanation to understand the practical limitations related to the generation of high-quality radiation beams in actual machines. An important role in the multi-particle system is played by the beam emittance , where are the particle beam rms sizes and are the particle beam rms divergences in horizontal and vertical directions, respectively.

Enormous efforts have been made in the last decade in order to decrease the beam emittance in conjunction with a substantial increment of the beam energy as reported in Figure 3. In recent synchrotrons, emittances of few nm rad are obtained [24,25] with electron beam energies of a few GeV. There is nevertheless a physical limit to the increase of the brilliance by exploiting only the particle beam quality. It can be seen considering the brilliance defined in terms of the beam emittance(5)

where F is the photon flux. As shown in Equation (5(5) ), the beam emittance is an essential parameter in order to increase the radiation brilliance. However, in third-generation synchrotrons, the diffraction-limited radiation implies(6)

where is the radiation emittance in the horizontal and vertical directions, respectively. Since the brilliance in terms of the radiation beam emittance satisfies

we obtain from Equation (6(6) ). Notice that in such a condition the brightness cannot be increased from the transverse electron beam properties except for the particle beam energy.

Figure 3. Beam emittance and energy of many high and intermediate energy synchrotron light sources worldwide as reported in [24].

Another important implication of a diffraction-limited beam on the radiation properties is related to its transverse spatial coherence. It is generally assumed that an incoherent quasi-homogeneous source of transverse size D produces radiation with a certain degree of coherence when observed at a sufficiently far distance . The degree of coherence of the radiation field is the key quantity that describes such property(7)

where:

and is a time delay.

For example, taking as typical parameters: nm, m and m, the corresponding transverse spatial coherence will be in the range m (in accordance with the Van Cittert–Zernike theorem), which is a coherence area applicable in many experiments.

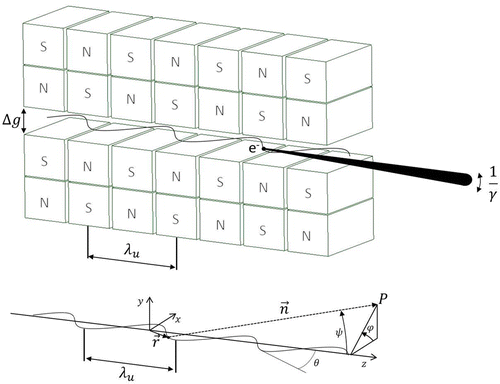
Figure 4. Sketch of a planar undulator. Electrons oscillate in the gap between two periodic arrays of permanent magnets. The characteristic period of electron oscillation is characterized by the magnetic structure defined by the undulator period . Synchrotron radiation is emitted in a cone due to the continuous deflection of particles. Geometry of undulator radiation emission (bottom).

An appreciable deviation from this theory must be taken into account in the diffraction-limited case when the beam emittance becomes comparable or lower than the photon emittance or when the source is not quasi-homogeneous. For example, in third-generation synchrotrons, the vertical emittance is typically two orders of magnitude lower than the horizontal emittance which is in the range 1–3 nm, corresponding to a vertical emittance 0.1–0.3 Å. This implies that, remarkably, the Van Cittert–Zernike theorem cannot be applied, aside for the hard X-ray limit at wavelengths shorter than 0.1 Å[26].

There is a close connection between the state of coherence of the source and the angular distribution of the radiant intensity [26]. The Van Cittert–Zernike theorem is applicable to sources that are correlated over the minim distance (which is order of the wavelength) [27]. More precisely, the applicability of the Van Cittert–Zernike theorem can be explicitly described for undulator radiation and depends on two diffraction parameters of the beam [28](8) (9)

where is the undulator length. The real effect of and has been experimentally verified only very recently in [29], demonstrating that in the diffraction-limited case, the coherence area deduced using the Van Cittert–Zernike theory would indeed be overestimated. Further investigations are necessary to understand and manipulate coherent radiation close to the diffraction limit.

From these considerations, it is evident that the experimental characterization of coherence is of fundamental importance for its practical applicability, especially in those applications where the stability of the transverse coherence is essential or even when the coherence must be known shot by shot due to the high variability of the radiation source.

To partially solve this fundamental problem, several diagnostics techniques have been recently developed to measure the degree of coherence of radiation. Such techniques have the capability to provide a precise determination of the modulus of the complex degree of coherence using interference and diffraction [30–36].

A completely statistical approach to measure in single shot was also reported in the visible and X-ray regime [37,38,45]. It exploits the speckle field from a colloidal suspension interposed between the radiation exit-port and a CCD camera equipped with scintillators.

3. Synchrotron radiation from undulators

Radiation generated in bending magnets and wigglers is broadband due to the high ratio between the emission angle and the radiation cone . This is also described by the strength parameter . On the contrary, in undulators, the particle beam is deflected several times (as sketched in Figure 4), but the maximum deflection angle is lower or comparable to the radiation cone. In such a way, undulator radiation is obtained with spectral density characterized by narrow harmonics with wavelengths(10)

where is the undulator wavelength, is the observation angle, m is the harmonic number and . The width of each harmonic is reduced as the number of undulator periods N increases: .

More in detail, the spectral properties of a linear undulator can be derived from the Lienard–Wiechert integral(11)

where is the spectral intensity per unit angle, and are the unit vectors of observation and the particle position, respectively, as shown in Figure 4. Taking contributions up to the order and since , we can split the integral in Equation (11(11) ) (see Ref. [39]) in three terms(12) (13) (14)

corresponding, respectively, with the three components(15) (16) (17)

where functions and are defined, respectively, as(18) (19)

and(20)

Here, is the generalized Bessel function of first kind, and . Combining Equations (11(11) )–(14(14) ), we obtain the spectral brightness in the form(21)

where .

Figure 5. Spectral brightness of a linear undulator normalized to for , and for different K. Only odd harmonics are irradiated.

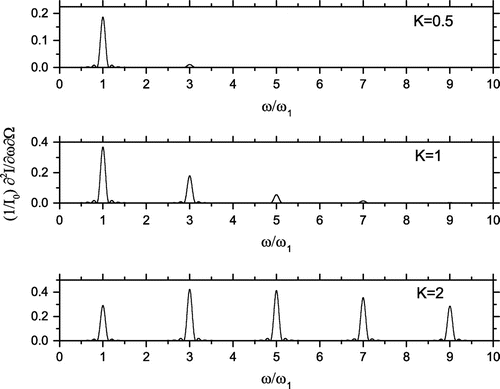
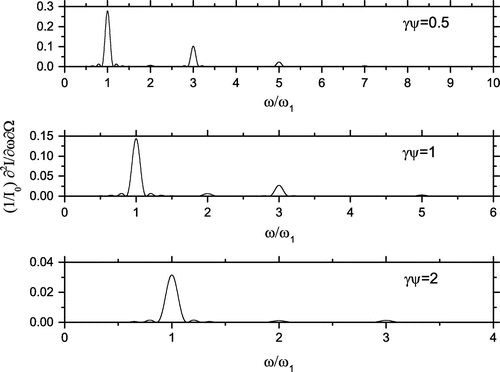
Figure 6. Spectral brightness of a linear undulator normalized to for , , and for different . Even harmonics are also irradiated but with lower intensity with respect to odd harmonics.

Spectral brightness as a function of is shown in Figures 5 and 6 for different K and , respectively. Notice that for a filamentary beam only odd harmonics are irradiated on-axis . Using the same approximations, we can similarly derive the spectral brightness of a helical undulator with magnetic dependence on z (22)

which gives(23)

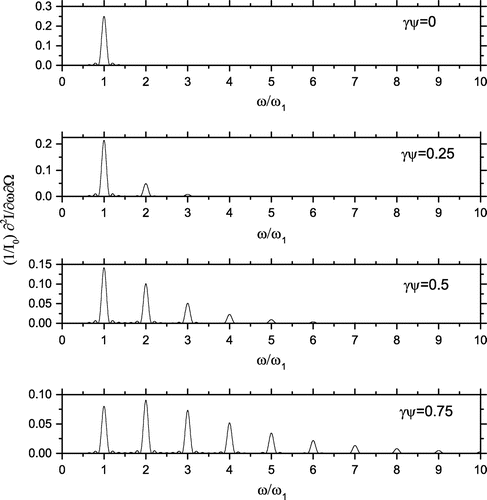
where . An example of spectra is shown in Figure 7. Thebrightness of a helical undulator is azimuthally independent and only the fundamental is irradiated on-axis.

The analytical approach provides an ideal reference for high-quality undulator beams. Nevertheless, several limitations must be considered for finite emittance beams with longitudinal energy spread that can only be addressed through numerical approaches. In particular, one finds that harmonics exhibit increments in the spectral tails at lower frequencies due to both the angular dependence of wavelength on and the finite emittance of the particle beam. As a consequence, the calculated spectral peaks are drastically reduced, thus reducing the beam quality in terms of emittance and energy spread.

Figure 7. Spectral brightness of a helical undulator normalized to for , and for different . The spectra are independent on .

Currently, the minimum wavelength obtained at the fundamental harmonic is limited to hard X-rays due to the difficulty of obtaining short undulator wavelengths with high magnetic fields. Cryogenic permanent magnets undulators with relatively short period ( mm) have been recently proposed [41,42] to increase the magnetic field strength with respect to conventional permanent magnets.

Millimeter-wave undulators using micro pulsed undulators or RF undulators are also reported [43,44]. A different approach has been proposed that exploits the field periodicity of the lattice structure inside a crystal. This introduces a natural ultra-short period undulator [40,46] for generating hard X-rays and -rays. In such configuration, electrons (or positrons) are sent with grazing incidence onto the crystallographic planes or axis of a bent crystal. Particles are deflected several times and axially confined similarly to a conventional undulator, but with higher efficiency due to the strong electric fields inside the crystal.

A fundamental property of the undulators with a high number of periods is of course the quasi-monochromaticity of radiation. However, in actual undulators, such condition is not easily obtained since the spectrum is characterized by higher order harmonics. Several techniques are proposed to suppress the unwanted harmonics and to improve the power at the fundamental: by altering the characteristic periodic structure of a conventional undulator in order to obtain a quasi-periodicity of the magnetic field [47,48]; by detuning the photon energy; by dividing the undulator into several segments and detuning the optical phase in between [49].

The undulator acts as a low curvature sequence of dipole sources that emits along the acceleration axis. The beaming effect increases the brightness of each source concentrating the radiation power in a angle as in a bending magnet, but with increased power due to the higher number of sources. Moreover, the undulator is realized in such a way the radiation from the oscillation periods interferes constructively with each other, increasing the power by a factor proportional to . Thus, the brightness of radiation from undulator is typically several orders of magnitude higher than for bending magnets. For a fixed undulator length, the decrease in the undulator periods is the fruitful way to increase brilliance and to reduce radiation wavelength. The realization of in-vacuum cryogenic short-undulators is the future challenge in ultimate storage rings [50].

Radiation divergence and emittance are quite different in the horizontal and vertical directions since the deflection of particles is usually imposed in the horizontal plane. As discussed in Section 2.2, the diffraction parameters , characterize the coherence properties of radiation close to the diffraction limit. This occurs in third-generation synchrotrons along the vertical direction. Conversely, in the horizontal plane, the Van Cittert–Zernike theorem can be applied since . The transverse coherence and thus the beam size can be determined. In the opposite limit of a filamentary beam, the diffraction provides a value close to the minimum photon emittance, which depends on the undulator configuration. For example, it is reached at least theoretically in an undulator with Lorentzian profile [51].

The magnetic field configuration determines the state of polarization of light since the radiation field is related to the electron motion in the magnetic field: planar undulator substantially provides linearly polarized light. Several solutions and configurations have been also proposed to produce arbitrary polarized radiation. The crossed-planar scheme [52] initially proposed by [53] consists of two pairs of planar permanent magnet arrays above and below the electron orbit plane. The state of polarization can be changed by shifting the pair of opposite magnetic arrays.

Elliptical undulators have been also designed to generate linear, elliptical and circular polarizations [54,55]. Circular polarization can be naturally obtained from helical undulators [56,57], and they also introduce Orbital Angular Momentum (OAM) to light [58,59], i.e. generate optical vortices. Different approaches have also been proposed to produce light with OAM from relativistic beams by up conversion of a Gaussian laser beam through an electron beam exploiting inverse Compton scattering or free electron laser [60,61].

4. Betatron radiation

Large distances are necessary to accelerate particles at very high energy in conventional synchrotrons. There is no chance to realize high energy compact accelerators because of the technical impossibility to produce electric fields in the GeV/m range using RF cavities in vacuum. A different approach that follows the early original idea of [62] is the generation of high strength electric fields exploiting dense plasmas in a gas.

Basically, total or partial separation of ions from electrons is induced by a high power laser (Laser Wake Field Acceleration LWFA) or external relativistic beams (Plasma Wake Field Acceleration PWFA). The loss of the quasi-neutrality condition provides local fields of the order of tens of GeV/m that propagate close to the speed of light in the plasma medium.

The advancement and development of tera- and peta-watt lasers [63,64] offers new perspectives for effective and compact accelerators and a new generation of radiation sources. In recent years, several compact sources of X-rays [65] have been realized using this concept with the aim to serve for many applications [66].

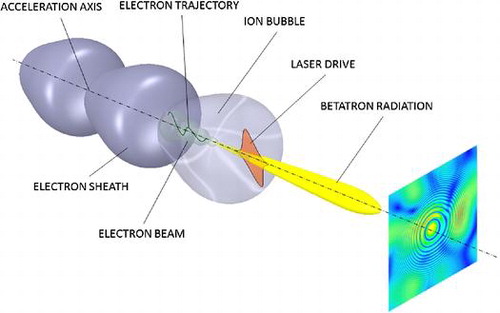
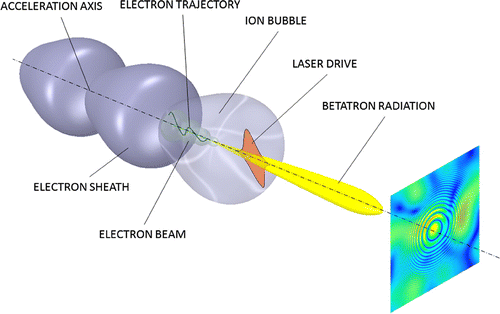
The possibility to produce X-ray radiation is guaranteed by the high field strength that forces electrons to oscillate in betatron motion with high transverse acceleration. The potential well is generated by the ions cloud with the minimum close to the acceleration axis as sketched in Figure 8. The entire beam is modulated by a characteristic envelope composed by the incoherent superposition of all electrons.

Figure 8. Representation of the emission process of betatron radiation and basic principle for transverse coherence measurement. The ion bubble produces a high gradient field which accelerates electrons along the direction of the laser pulse at very high energy. Electrons initially expelled from the bubble (electron sheath) are again self-injected on the back. Betatron radiation with a certain degree of coherence is emitted with a synchrotron-like process within a narrow cone. The interference pattern (on the right) is a time-resolved in-line Gabor hologram used to measure the coherence properties by means of the interference of radiation with a spherical wave scattered by a test micro-particle (interposed between the source and the detector). The speckles at a given instant are shown with false colours. This represents in principle the basis of the NFS technique applicable up to hard X-ray radiation.

Betatron radiation is basically a synchrotron-like emission. Nevertheless, substantial differences must be taken into account with respect to SR emitted in bending magnets and undulators, where all the particles are deflected one time or many times by magnetostatic fields.

4.1. Emission process and radiation properties

Several experiments have been considered in the past which involve quite different emission processes. In fact, depending on the experimental parameters, different regimes of betatron emission can occur: linear (cold fluid) regime [67,83], weakly or fully non-linear regimes [68–71], blowout or bubble regimes [72,73], self-focusing [74,75], self-trapping [76,77] and self-modulated regimes [78]. In addition, different experimental configurations can be adopted: (i) using relatively long capillaries to guide the laser beam at longer distances [79,80], or (ii) by exploiting the external injection of the electron beam instead of the self-injection scheme [81,82] or (iii) using multiple beams to enhance the wakefield amplitude [83,84].

Several theories have been proposed in order to describe the basic properties of betatron emission [72,85–87]. In many schemes, particle moves in a fixed-shaped parabolic potential , which propagates almost at the speed of light. Here, and are constants. For a particle in the (x, z) plane, the orbit is given by [87](24) (25)

where is the betatron wavenumber, is a constant amplitude, , is the initial axial momentum of the electron, and is a constant.

The electrostatic potential is related to the plasma density as , where is the ion density in a uniform background, is the electron density and is the plasma wavenumber. In the blowout regime, , which gives .

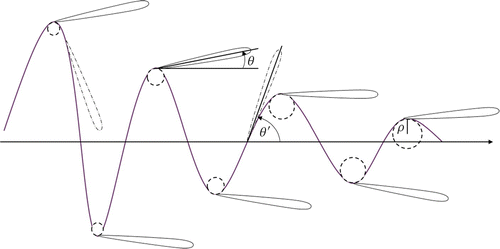
Equations 24(24) and 25(25) give a useful representation of the particle motion in the (x, z) plane; however, the amplitude in the transverse direction is assumed constant. A time-dependent betatron amplitude should be considered introducing the dumping factor in the equation of motion as in [88] (where is derived by ). Thus, the single particle trajectory appears as in Figure 10 where both amplitude and frequency of the particle trajectory reduce during evolution.

In the linear case, the maximum amplitude of the plasma wave is much smaller than the non-relativistic wavebreaking field () , which produces a simple sinusoidal electrostatic potential, e.g. [89], where is the electron plasma frequency and is the phase velocity determined by the drive. On the contrary, the plasma wave becomes highly non-linear when .

Several calculations are reported in both one and two dimensions [67,90–92] in order to consider non-linear effects as the laser intensity increases and the wakefield exhibits a substantial deviation from the linear case. However, a complete and more realistic description of the three-dimensional, fully non-linear evolution of the plasma wakefield as well as the electron trajectories requires numerical simulations. Several Particle In Cell (PIC) codes as Vorpal, Osiris, Q-fluid, are developed to this aim, also exploiting paralleling computing and GPU architecture [93–100].

Following this generalization in three dimensions, the radiative emission process can be treated as two distinct problems: (i) Solving the laser and plasma evolution with relative trajectories, (ii) Solving the emission process from the electron trajectories. The two are couplet when radiation interacts with plasma or beam.

The radiated field from the electron trajectories is generally estimated numerically using the Lienard–Wiechert formulas [101] in the time domain or in the frequency domain [102,103]. The emission is a synchrotron-like process due to the high energy of the accelerated particles and the radiation is beamed along the electron velocity with an angle with respect to the acceleration axis. The strength parameter is then and the spectrum is quite broad, with critical harmonic , where .

In the limit , the single particle with constant parameters K, and exhibits a synchrotron-like emission spectrum which can be approximated by the asymptotic limit as [104]:(26)

where is the observation angle, is the radius of curvature of the electron trajectory, , are modified Bessel functions and .

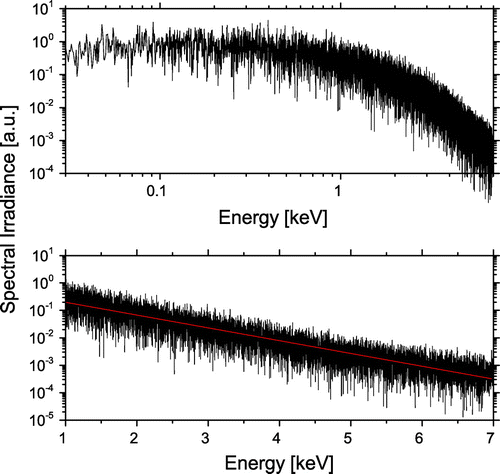
Integrating over angles is , where is the modified Bessel function of the second kind and is the critical frequency. Due to the variability of the motion parameters and different electrons, the radiation spectrum can be calculated numerically with the methods discussed above. A typical on-axis spectral irradiance of a 78 MeV, 3.5 m size electron beam accelerated in a  cm plasma channel is shown in Figure 9. The similarity with the synchrotron-like distribution can be shown at fitting the exponential tail with a straight line in a log-linear scale. The matching between the synchrotron spectral distributions and experimental spectra was also experimentally verified in [105].

Equation (26(26) ) shows that the peak frequency is lower for larger . Experimental measurements of the angular dependence of betatron X-ray spectra in a LWFA scheme were given in [104]. They observed that the peak energy vs. the observation angle decreases slower than that predicted by Equation (26(26) ) since the overlapping of radiation emitted from different electron trajectories tends to make uniform the photon energy over angles.

Figure 9. Numerical simulation of the spectral irradiance of a 14 pC beam undergoing betatron oscillations (top). Broadband emission occurs in the soft X-rays with critical energy 1 keV. The exponential drop of the spectrum can be shown in log-linear scale (bottom). The red curve is the better linear fit.

Recently, the possibility to extend the spectrum up to -rays with peaking between 20 and 150 keV [106] has been demonstrated exploiting a resonant coupling between the laser frequency and a harmonic of the betatron frequency. This opens new perspectives in isotope production, probing dense matter, homeland security and nuclear physics [107].

While the spectrum is already extended beyond the hard X-rays, the brightness cannot be easily extended over the photons per bandwidth. This value is comparable with that of third-generation synchrotrons. The main limitation in both LWFA and PWFA is the beam emittance, which cannot be easily reduced during the beam formation. This is due to the low external control on the beam quality in comparison with the photoinjectors, despite several techniques proposing to improve the beam emittance to about 0.2 mm mrad [108,109]. Such limitation is partially compensated by the high peak current of the self-injected electron beam in comparison with conventional storage rings.

Figure 10. Osculation circle approximation for a two-dimensional single particle trajectory. Trajectories can be approximated at the maxima with the respective osculation circles, thus radiation (on the axis) can be seen for as the superposition of emitters from circular trajectories with radius .

A total different scheme was recently proposed to decrease emittance exploiting the external injection instead of self-injection [98,110]. In this case, the laser-plasma stage acts as a compact insertion device that takes advantage from the beam energy produced by a photoinjector.

4.2. Coherence

Ultimately, betatron radiation is not diffraction limited because of the high emittance, about three orders of magnitude larger than synchrotrons of third generation. However, brightness and low divergence considerably improve the source performances with respect to a conventional X-ray tube while maintaining acceptable compactness and providing a certain degree of coherence as recently demonstrated [99,111].

The synchrotron-like emission can be used to estimate the spatio-temporal coherence in the framework of the theory exposed in Section 2.1 using the osculation circle approximation [112–114]. This method can be applied for small oscillations and for small angles of observation in such a way the observer sees only the radiation coming from the maximum of the betatron oscillations as sketched in Figure 10. Each electron acts as a dipole source with transverse acceleration given by the curvature of the osculation circle around each maximum. This provides the analytic solution of Equation (3(3) ).

Because the phases are mixed due to the stochastic motion of electrons, the dipole sources are uncorrelated in space, acting as an incoherent source. However, a certain degree of spatial coherence exists due to the small transverse size of the electron beam (a few m) in agreement with the van Cittert–Zernike theorem as reported in [115]. For a typical 5 m beam size, a coherence area m is generated at 1 meter of distance from the source and for 1 nm wavelength.

A peculiar behaviour of the coherence due to the different emissions of particles at different radii was recently demonstrated [112–114]. Multiple oscillations on the modulus of the coherence factor depending on the transverse non-uniformity of emission can be observed using an asymmetric detection method.

A completely different mechanism to generate spatially coherent radiation can be observed at THz frequencies where the radiation wavelength is larger than the longitudinal size of the beam (femtosecond beams) [116,117].

Different techniques to characterize the coherence properties of radiation have been recently developed. One of the main limitations of betatron radiation in comparison with the diagnostics of coherence in conventional synchrotrons is the instability of the beam. An ideal diagnostics for these types of sources should measure the coherence shot by shot to avoid miss-interpretation due to the rapid fluctuations of the radiation beam properties. Coherence was measured in single shot using Fresnel diffraction from calibrated wires or foils together with the beam size characterization [106,111,118]. Recent techniques exploit the heterodyne near field scattering of radiation from a colloidal suspension of microparticles to map in single shot and in two dimensions (vertically and horizontally) the transverse coherence [99,119–121].

5. Conclusions

We have shown that the development of radiation sources based on synchrotron or synchrotron-like emissions is oriented to achieve bright radiation by exploiting large or relatively compact facilities. The technological advancement and the new scientific frontiers have extended the applicability at the lower wavelength: from hard X-rays in conventional accelerators up to -rays in novel concept accelerators.

Starting from a basic description of synchrotron emission, we have discussed about the coherence properties of radiation generated in third-generation synchrotrons which produce diffraction-limited radiation, exploring recent models and experimental techniques about this fundamental topic. We have shown the important advancements of undulators to generate bright, arbitrarily polarized radiation, which also opens important perspectives for exotic properties of light such as X-ray vortices. We have discussed about novel concept sources that use quite different methods to produce synchrotron radiation. Despite these sources generating bright radiation comparable to that produced in conventional accelerators, the higher emittance remains an open problem although radiation is characterized by a certain degree of coherence.

The achievement of high brilliance sources naturally introduces the need to explore the coherence properties since, ultimately, the increase in brilliance brings a corresponding reduction of emittance, hence an enhancement of spatial coherence. Nevertheless, beam emittance can be reduced below the photon emittance . This occurs in undulator radiation of last generation where is close to the wavelength, i.e. close to the so-called ‘diffraction limit’ where the source becomes ‘fully coherent’.

Coherence is also important in the opposite condition, when radiation is far from the diffraction limit, as emerged in recent years with the novel concept accelerators as in the case of LWFA or PWFA schemes. According to the Van Cittert–Zernike theorem, any incoherent source generates partially coherent radiation when observed far enough. For a conventional source as an X-ray vacuum tube, this implies a rampant intensity reduction. On the contrary, new generation sources exploit the relativistic beaming to concentrate radiation in a very small solid angle.

Finally, another important resource of synchrotron or synchrotron-like radiation is the wealth of information available to investigate phenomena in the microscopic and macroscopic world.

Additional information

Funding

Italian Ministry for University and Research (MIUR) ‘FIRB 2012’ funds [RBFR12NK5K].

Notes

No potential conflict of interest was reported by the authors.

Appendix 1

Derivation of the radiation power with arbitrary boost

The derivation of Equation (3(3) ) is applied to transform the radiation power from to K in any arbitrary boost. The argument of the second integral of Equation (2(2) ) can be written in terms of the momentum energy four vector as(A1)

where the factor at the denominator is due to time dilatation , is the matrix of the Lorentz transformation for a boost in any arbitrary direction :

and

is the determinant of the Jacobian of the transformation represented by the matrix

Notice that through we conceptually show how the geometry (in the space–time) changes passing from (where the emission is a dipole-like radiation) to the frame K (where we want to know how radiation will appear). It can be estimated in a general way (arbitrary boost) by introducing the four vector of the emitted radiation with unit vector , which is represented in spherical coordinates as .

The components of can be written as a function of , using the transformations(A2) (A3) (A4)

Thus, the determinant in Equation (A1(A1) ) becomes(A5)

where is

Defining now the quantities , , () as(A6)

the Equation (A5(A5) ) is written as(A7)

with the coefficient

or by(A8)

with the definitions , ().

Equation (A8(A8) ) substituted in Equation (A1(A1) ) gives Equation (3(3) ).