Quantum spin models for measurement-based quantum computation

Abstract

Measurement-based quantum computation is different from other approaches for quantum computation, in that everything needs to be done is only local measurement on a certain entangled state. It thus uses entanglement as the resource that drives computation. We give a pedagogical treatment on the basics, and then review some selected developments beyond graph states, including Affleck–Kennedy–Lieb–Tasaki states and more recent 2D symmetry-protected topological states. We point out some open questions along the way.

Graphical Abstract

Keywords:

• Measurement-based quantum computation
• entanglement
• cluster state
• AKLT state
• symmetry-protected topological order
• quantum spin models

PACS:

• 03.67.Bg Entanglement production and manipulation
• 03.67.Lx Quantum computation architectures and implementations
• 64.60.ah Percolation
• 75.10.Jm Quantized spin models

1. Introduction

Quantum computation exploits massive parallelism of many quantum bits under the unitary evolution [1]. Measurement is only necessary at the last step of reading out the result of computation. However, it was realized that local measurements alone on certain many-qubit entangled states can simulate arbitrary unitary gates and hence universal quantum computation [2]. The price to pay is the use of one spatial dimension as the simulated time direction and entanglement as the enabling resource. For example, an array of entangled qubits can be used to simulate a sequence of one-qubit gates. With some entanglement between two such arrays, two-qubit gates such as the Controlled-NOT (CNOT) gate can be simulated. Measurement in quantum mechanics generally gives outcomes randomly, but quantum computation is to implement certain fixed gigantic unitary operation. How do we deal with such randomness to yield a ‘deterministic’ unitary evolution? The framework of measurement-based quantum computation (MBQC) [3,4] is to exploit useful entanglement structure and to deal with randomness in measurement to enable quantum computation, and is the focus of this review.

The main MBQC framework was proposed by Rassendorf and Briegel in the ‘One-way quantum computer’ [2] using the cluster state [5]. One of the important precursory works is the teleportation-based quantum computation by Gottesman and Chuang [6], which also helps to provide an alternative understanding of the cluster-state quantum computation via the valence-bond or projected entangled pair states (PEPS) by Verstraete and Cirac [7]. Subsequently, a framework using matrix-product states and PEPS called quantum computation in the correlation space was developed by Gross and Eisert [8].

Entanglement is the enabling resource in MBQC and thus it is important to know what aspect of entanglement makes computation possible. It is natural to regard states with litte entanglement as being useless and those with high entanglement as potentially useful [9,10]. However, it was shown that if a state possesses a high amount of entanglement, any particular outcome in the measurement-based scheme will occur with low probability. This means that the distribution of measurement outcomes will be so random that it can be efficiently simulated by classical random coin tossing [11,12]. Thus, it is the structure of the entanglement that matters for MBQC.

With classification of entanglement into short-range and long-range types in recent condensed-matter literature [13], one may wonder whether that perspective can give us any insight for the resourcefulness of entanglement. Long-range entanglement is a property of intrinsic topological order [14], such as exhibited in the Kitaev’s toric code [15], gapped spin liquids [16], or fractional quantum Hall states [17,18]. Their utility for quantum computation originates from a very different perspective, i.e. using anyonic properties to enable quantum gates [19], and not much is focused on the entanglement structure, except from the point of view of topological entanglement. Most of the so-called resource states for MBQC belong to the so-called short-range entangled states, such as the cluster states [5] and the Affleck–Kennedy–Lieb–Tasaki (AKLT) states [20,21]. However, even local measurements can convert a short-range entangled state to a long-range entanglement state, as demonstrated in the work by Bravyi and Raussendorf, where a cluster state can be converted to a surface code (a planar version of the toric code) [22]. This later led to the fault tolerance of MBQC using a 3D cluster state [23,24], where each 2D slice is used to simulate a time step in the operation of anyons in a 2D surface code [25,26].

Although not much further progress has been made in connecting intrinsic topological order to MBQC [22,27], recently a connection of the type of topological order protected by symmetry to MBQC was unveiled. This symmetry-protected topological (SPT) order possesses only short-range entanglement instead. Else et al. recognized [28] that both the 1D cluster and the 1D AKLT states, capable of supporting arbitrary single-qubit gates, belong to a 1D nontrivial SPT phase protected by on-site symmetry. Moreover, any ground state in the entire phase also supports a protected identity gate operation for transmission of quantum information. But the ability for the entire SPT phases for arbitrary qubit or qudit gates is only established recently by Miller and Miyake [29] and Stephen et al. [30,31]. However, the status in 2D has not been explored much, with only some results on fixed-point wave functions [32–34], and certain result slightly beyond fixed points [35]. Future development may strengthen the notion of computational phases in SPT and other phases of matter.

There are other reviews on MBQC and related subjects [3,36–38]. Due to space limitation, we can only cover a few selected topics. In Section 2, we discuss cluster/graph-state based quantum computation. In Section 3, we review the status of using the AKLT family of states and some deformations from AKLT states for the purpose of MBQC. In Section 4, we cover aforementioned works on 2D SPT states for quantum computation. In Section 5, we make some concluding remarks, commenting on some experimental proposals and progress.

Why the framework of MBQC is restricted to local measurements only? If we can perform any two-qubit measurement, then universal quantum computation can be achieved even with product states. Therefore, MBQC separates entanglement as its resource and local measurements can only decrease the entanglement in the system, hence the name ‘one-way’ quantum computer [2]. However, one can also imagine adding certain limited two-qubit measurements or couplings to extend the framework, but we will not consider that in this review.

2. MBQC using cluster/graph states

We discuss cluster/graph states and the construction of the universal set of gates, which is done on the Hilbert space of qubits. An alternative framework in the correlation space was proposed by Gross and Eisert [8,39], however, it is not covered here.

Figure 1. Gate teleportation: (a) a single one, (b) cascade of (a) four times.

2.1. 1D cluster state

Consider one qubit in the state and another in the state . Note that and are the +1 and –1 eigenstates, respectively, of the Pauli Z matrix . In the following, the normalization may be dropped for ease of notation. The Controlled-Z gate , despite the expression, is actually symmetric, , as the nontrivial action is only a phase shift: . Applying it to the two qubits: , where  ; entanglement is thus created between qubits 1 and 2.

2.1.1. Unitary evolution by local measurement

Imagine we perform a projective measurement on the first qubit, described by the observable , where and are the Pauli X and Y matrices, respectively. This is equivalent to measurement in the basis , with eigenvalues (and ). Depending on s, the second qubit is projected to

(1)

where an overall phase factor is omitted. Such a procedure of (1) entangling an arbitrary input qubit with a fixed , followed by (2) measuring the first qubit in basis, results in the quantum information teleported to the second qubit, with an additional outcome-dependent unitary gate , where H is not a Hamiltonian but the so-called Hadamard gate

(2)

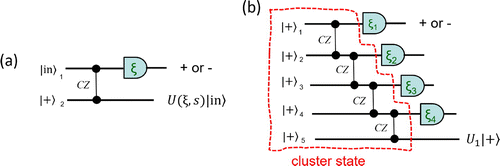
Such a gate teleportation [40] is schematically shown in Figure 1.

2.1.2. Arbitrary single-qubit gate implemented on a segment of qubits

Cascading the above procedures four times gives the gate . One can show that by choosing

(3)

the gate is

(4)

where . We see here that an arbitrary SU(2) rotation up to by-product Pauli operators is possible and randomness can be dealt with by adapting later measurement axes.

2.1.3. Cluster and graph states

We have seen in the above that with a linear array of cluster states, arbitrary rotation can be achieved. Therefore, instead of an arbitrary input state, we may as well set it to , as we can rotate to any desired input state. Then we can separate all the CZ gates acting on all ’s and define a 1D cluster state (with an open-boundary condition) [5]

(5)

which allows for simulation of a sequence of arbitrary single-qubit rotations. The one dimensionality of the cluster serves as a discrete time direction of an effective qubit evolution.

Generalizing the cluster state, we can define the so-called graph state, where a qubit resides on each vertex (in V) and each edge (in E) of the graph G indicates a CZ gate:

(6)

Then there is a stabilizer operator associated with each vertex u,

(7)

such that . A trivial observation is that the graph state is the unique ground state of the Hamiltonian .

2.1.4. Connection to SPT order

SPT order [41–46] has been identified and characterized recently, whose origin dates back to Haldane’s work on the spectral gap of integer-spin antiferromagnetic Heisenberg chains [47,48]. In the context of quantum computation, it was first revealed in the 1D SPT phase by Else et al. [28], where protection of certain quantum gates in MBQC arises due to the SPT order. Examples include the 1D cluster state and the 1D spin-1 AKLT state [8,39,49]. The connection is recently strengthened [29–31,50], but below we will instead focus on recent yet limited progress in 2D.

2.2. Cluster state on square and other lattices are universal resource

Briegel and Raussendorf invented the cluster state on the square lattice [5], which then led to their one-way quantum computers [2]. Further advancing the result, Van den Nest et al. showed that all the graph states defined on 2D regular lattices are interconvertible by using only local Pauli measurements, thus possessing the same computational power [9].

Figure 2. Conversion of graph states: (a) Square lattice; (b) Brickwork lattice. Solid black circles indicate Z measurements and meshed red circles indicate Y measurement.

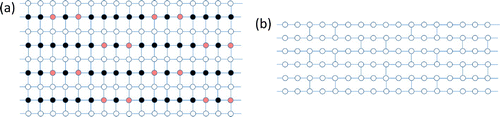
Universal gates can be realized on the square lattice cluster state [2]. But here we introduce the specific brickwork lattice as illustrated in Figure 2(b), as it also offers an interesting application: blind quantum computation [51,52]. Even though we are not going to discuss blind quantum computation here, the universal gates discussed below will help readers understand the original proposal in Ref. [51]. In Figure 3(a), a pair of arbitrary single-qubit gates, , can be implemented, up to local correctable byprouct operators,

(8)

Similarly, the CNOT gate can be proved by translating Figure 3(b) to

(9)

Placing these gate patterns appropriately on the brickwork lattice, universal quantum computation can be achieved. Figure 2(a) illustrates that local Pauli Z and Y measurements [53] can convert the square-lattice cluster state to the brickwork state. Since all 2D graph states on regular lattices can be converted by local measurements to the square lattice, then they are all universal resources.

Figure 3. Gates implementation: (a) two independent one-qubit gates; (b) CNOT gate. The symbols inside the circles indicate the measurement angles.

2.3. Random planar graph states

Going beyond the regular lattices, Browne et al. considered faulty square lattices, namely, each site is occupied with a probability p [54]. As long as p is above the site percolation threshold , the resultant graph state is still universal, due to sufficient connectivity in the graph. This subsequently led to the general connection of percolation to universality of random planar graph states [54,55], whose graphs reside in the supercritical phase of percolation. Thus, the quantum computational universality is well understood in the cluster/graph state family.

2.4. Nielsen’s no-go theorem

If cluster/graph states appear as the exact unique ground state of ‘naturally occurring physical system’, then cooling the system could lead to creation of the universal resource states. However, Nielsen proved that this cannot happen for qubit Hamiltonians with two-body interactions [40,56]. Van den Nest et al. proved this generally for graph states [57]. Chen et al. later gave a general proof for such a no-go theorem for any qubit two-body frustration-free Hamiltonian [58,59]. This was discussed in a recent review [37] and will not be elaborated further here.

The above no-go theorem applies only to the exact ground state. If we allow an approximate ground state, there can be such a two-body Hamiltonian, according to a perturbative construction by Rudolph and Bartlett [60]. Van den Nest et al. also showed how to obtain two-body Hamiltonians such that graph states are the approximate nondegenerate ground states [57]. Motivated by the no-go results, Chen et al. constructed the so-called spin-5/2 TriCluster state [61], such that it is both (i) the unique ground state of a two-body Hamiltonian and (ii) a universal resource for MBQC. The above no-go results and the results on the TriCluster state stimulated the quest for searching other two-body interacting ground states that are universal. So far, such states have the smallest local Hilbert-space dimension being 4 (i.e. spin-3/2), including the spin-3/2 AKLT state. Whether a universal resource state is of spin-1 entity and the unique ground state of a two-body interacting Hamiltonian remains open.

3. AKLT family of states

The first member of 2D AKLT family shown to be a universal resource for MBQC is the spin-3/2 one on the honeycomb lattice [62,63]. Subsequent works have led to a better understanding of the universality [64–66], albeit still incomplete.

3.1. 1D AKLT state

Below we will explain why the spin-1 AKLT chain [20,21] is useful for simulating arbitrary one-qubit gates. The bond state used to form the AKLT state is the singlet and the projection from virtual qubits to the physical spin is , where the physical spin is in the spin-1 Hilbert space. Since the construction is via singlets, the maximal spin magnitude of two neighboring sites cannot exceed unity and thus the AKLT state must be annihilated by the spin-2 projector. This leads to a gapped parent Hamiltonian for the AKLT state (as the unique ground state) [20,21,67]

(10)

 

Figure 4. From AKLT to a graph state. (a) A spin-1 chain; (b) Spin-3/2 case on the honeycomb lattice. Encoding is indicated by shapes with the same color. The new edges are derived from the original edges in a mod-2 fashion, as can be seen in (b).

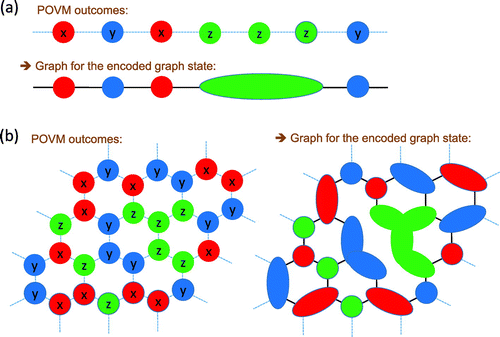
It turns out that by performing local measurements, the 1D AKLT state can be converted to the 1D cluster state, with reduced number of sites. The key point is that there is a two-dimensional subspace spanned by and or equivalently by the two virtual qubits and , which also holds similarly for and subspaces. One therefore considers

(11)

(12)

(13)

as projections that preserve a two-dimensional subspace, where we suppress the label . Note that the completeness relation in the spin-1 Hilbert space holds:

(14)

The above F’s constitute the so-called generalized measurement or POVM, characterized by . Their physical meaning is to define a two-dimensional subspace and to specify a preferred quantization axis x, y or z. In principle, the POVM can be realized by a unitary transformation U jointly on a spin-1 state, denoted by , and a meter state such that

(15)

where for the meter states . A measurement on the meter state will result in a random outcome , for which the spin state is projected to [1].

After the POVM on all sites, with denoting the measurement outcomes (x, y or z), the resulting state

(16)

is an ‘encoded’ 1D cluster state [55,62]. The encoding of a logical qubit can effectively be represented by a few sites, but, if desired, it can be reduced to a single site by further local measurements. For example, for three consecutive sites with outcome z, the logical qubit spans only a subspace by and ; see Figure 4(a). To establish that the post-POVM state is the cluster state, it was shown [55,62] that for each logical qubit u, there is an logical stabilizer as in Equation (7).

An alternative measurement scheme for such a conversion was first used by Chen et al. [68], but the POVM here can be extended to two dimensions in the honeycomb and square lattices, allowing proof of universality of AKLT states on these lattices, as discussed below.

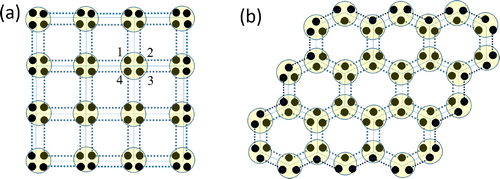
Figure 5. AKLT states on graphs or 2D lattices. (a) Arbitrary graph: showing virtual qubits on each site. The physical spin is a projection from the symmetric subspace of the virtual qubits to a spin S Hilbert space. (b) Honeycomb lattice. (c) Square-octagon lattice. (d) Cross lattice. (e) Hexagon-square lattice. (f) Square lattice.

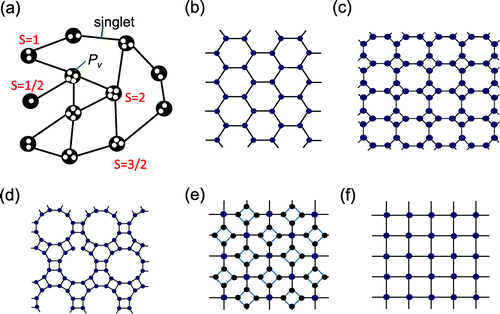
3.2. 2D AKLT states

It is natural to ask whether 2D AKLT states can be useful for quantum computation, especially due to their uniqueness as ground states of two-body AKLT Hamiltonians. One- and two-dimensional AKLT states are characterized as some kind of disordered states, having no local magnetizations and no breaking of lattice translation, and their construction is via the valence-bond approach, described above. However, AKLT states on three dimensions need not be disordered, they can possess Néel order, depending on the lattice [69]. Even spin glass can appear in AKLT models on random graphs [70]. Ordered states, such as ferromagnetic or Néel states, are conjectured not to possess sufficient entanglement structure for universal MBQC.

3.2.1. Spin-3/2 case

The spin-3/2 AKLT state on any trivalent lattice is a ground state of the following Hamiltonian

(17)

where an irrelevant constant term has been dropped. To show that it is a universal resource, a suitable POVM (for ) is as follows:

(18)

(19)

(20)

Note that the prefactor differs from that of in the case and that the completeness relation still holds:

(21)

which means that a generalized measurement with outcome , converts a state to .

Similarly to the 1D case, the post-POVM state

(22)

is an ‘encoded’ graph state, whose graph is modified from the original trivalent lattice, e.g. the honeycomb, in a way determined by . As illustrated in Figure 4, the encoding means that a logical cluster state qubit can effectively be represented by a few spin-3/2 sites, but, if desired, can be reduced to a single site by further local measurements. See Refs. [55,62] for details. A sufficient condition for quantum computational universality is thus to check to see if the resulting random graphs are, with nonzero probability, in the supercritical phase of percolation. Numerical simulations indeed confirmed this [55,62].

3.2.2. Spin-2 and higher

We note that Equation (22) will give a graph state even for any spin-S AKLT state, where

(23)

However, for and higher S, is not proportional to the identity operator. But for one only needs a second round of measurements to obtain 2D planar graph states. It requires a few more technicalities, which we do not have space to discuss here, to demonstrate that the spin-2 AKLT state on the square lattice (as well as on the diamond lattice) is a universal resource [66].

How do we know which AKLT states are universal? Those involving any combination of spin-2, spin-3/2, spin-1 and spin-1/2 (the last can appear at the boundary) are universal if the lattice they reside on is frustration-free (Figure 5). Here ‘lattice’ is used loosely to denote a 2D periodic titling which can have boundary. AKLT states on frustrated lattices may not be universal. The extension to general higher spins remains an open question. One technical issue is the lack of generic local measurements for universal gates or state reduction. One may want to use criteria in Refs. [9,10] to exclude those whose entanglement does not scale with the system size. However, any AKLT state can be probabilistically (which can be exponentially small in the system size) converted to a cluster state on the same lattice, this means that the AKLT state has at least the same entanglement as the cluster state using any strong entanglement measure. Therefore, one cannot use the amount of entanglement to rule out candidates for universal resource in the AKLT family.

3.2.3. Other bond states and spectral gap issue

Besides the singlet state as the valence bond, one may as well use other states, e.g. or . For bipartite lattices, these AKLT states are inter-convertible locally, so the quantum computational capability is identical [71]. But on non-bipartite lattices they cannot be inter-converted. AKLT states using different bonds on these may have different capability for quantum computations, which is not much explored. Evidence from correlation functions indicates that the AKLT models on both the honeycomb and square lattices are gapped [21], but no rigorous proof has been given. Recent developments in tensor-network methods have allowed estimation of these gaps in the thermodynamic limits, providing strong numerical evidence of the gaps [72,73].

3.3. Away from the AKLT point

Darmawan, Brennen and Bartlett studied the deformed AKLT states by Niggemann, Klümper and Zittarz (NKZ) [74] on the honeycomb lattice:

(24)

where in the spin basis, with . For a certain range of a, the universality still persists, but terminates at the Néel transition [75]. This is also the case for other bipartite trivalent lattices [71]. However, for , the quantum computational power has not been explored due to some technicality.

Darmawan and Bartlett also considered specific patterns of and thus the associated projectors, and constructed a one-parameter family [76]

(25)

where . The parent Hamiltonian is gapped if for some [77]. The seemingly non-universal AKLT state on the star lattice [64] can thereby be deformed to a universal state.

4. 2D SPT states for quantum computation

Given the success of relating 1D SPT states for quantum computation [29–31], it is important to extend this to 2D and inquire whether they lead to universal MBQC.

Figure 6. Fixed-point SPT states: (a) on the square lattice; (b) on the honeycomb lattice.

4.1. CZX state and generalizations

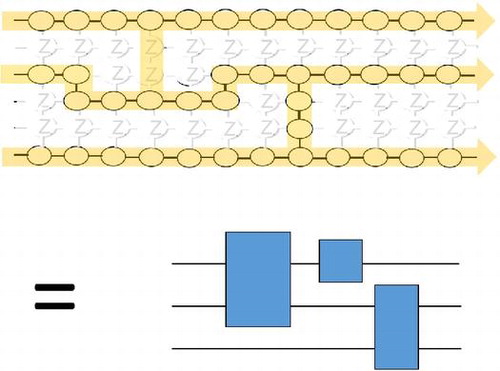
The first discovered 2D bosonic SPT order was exhibited in the CZX model [78], where each site contains four qubits or ‘partons’ and each qubit forms with corresponding ones on neighboring sites in the GHZ states . The ground state is essentially composed of product of such GHZ states; see Figure 6(a). The on-site nontrivial action is , where and . As argued in Ref. [78], the 2D SPT order can be seen from the symmetry action at a boundary, whose degrees of freedom reside on the half GHZ plaquettes. It is non-onsite and there are nontrivial 3-cocycles emerging from composing a sequence of three symmetry actions in different ways.

Generalizing to arbitrary 2D planar graphs, these GHZ-like plaquettes still exhibit nontrivial SPT order and serve as universal resource; the latter holds provided the graphs are in the supercritical phase (and regular 2D lattices certainly are).

4.1.1. Nontrivial SPT order

The GHZ-like state on a plaquette p is

(26)

where G is the on-site symmetry group and is the number of ‘partons’ within a plaquette (e.g. on the square lattice), not necessarily constant. To demonstrate nontrivial SPT order, the idea is to construct an appropriate local action using group 3-cocyles, and as long as the 3-cocycle is nontrivial, is a nontrivial SPT state w.r.t. G [46].

The action , , on site i within the ‘sublattice’ I is then given by

(27)

where is a fixed element in G and

(28)

The sublattices I can be chosen arbitrarily, but for regular lattices, the colors in the graph colorability is a choice. For details, see Ref. [33].

One can indeed verify that is a valid local symmetry, i.e.

(29)

Furthermore, is a global on-site symmetry. Thus, the state is a SPT state w.r.t. the on-site symmetry U(g), and if the 3-cocycle is nontrivial, then the SPT order is nontrivial [33].

Figure 7. Entanglement concentration: converting the SPT state to a known universal resource state.

4.1.2. Quantum computational universality

To see how the universality arises we use entanglement concentration. (i) An n-qubit GHZ state: after measurement of qubit 1 in the X basis, the remaining state becomes , where sign depends on the outcome of X measurement. One can continue this and concentrate to a Bell state between any two qubits. (ii) If a site contains two qubits that are respectively part of two GHZ states, then by local measurement on this site the two GHZ states is merged into one. Using these one can show that as long as the underlying graph for is in the supercritical phase of percolation, then it is a universal resource [33]. Figure 7 illustrates the conversion of the CZX state to a valence-bond state.

Percolation arises due to the requirement to have sufficient or macroscopic number of universal gates for universal quantum computation. One drawback of using these fixed-point wave functions for MBQC is that the dimension of local Hilbert space is not small, e.g. 16 for the CZX state or 8 for the extension to the honeycomb lattice. A different construction by Miller and Miyake achieves qubit SPT states for universal MBQC [32], which will be discussed below.

4.1.3. Away from fixed points

Is quantum computational universality a property of only SPT fixed points or more general? In Ref. [35], it was shown that by deforming these wavefunctions away from fixed points there is a finte region such that quantum computational universality persists [35]. Moreover, its disappearance in one direction seems coincide with the phase transition to a symmetry-breaking phase. A potential breakthrough is to establish an entire SPT phase supporting universal MBQC, which remains open.

4.2. Miller–Miyake states

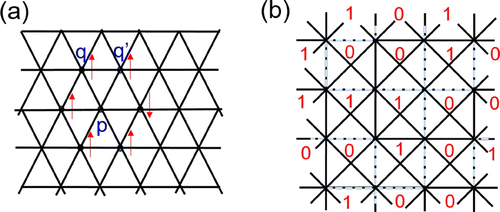
Miller and Miyake provided a fixed-point SPT wavefunction that is invariant under symmetry and universal for MBQC [32,34]. It is defined on the Union-Jack lattice, see Figure 8, but can certainly be defined on any triangulation. Due to the 3-cocyle construction, it manifestly has SPT order. It is easily defined in terms of the CCZ gate:

(30)

where

(31)

with p, q, and r, sitting on the vertices of a triangle . As the CCZ gate is diagonal, it is symmetric under permutation of qubits p, q and r. One can show that the Miller–Miyake state is ‘stabilized’ by operators of the form , where , i.e. . This gives rise to a parent Hamiltonian such that is the unique ground state. The connection of to the trivial Hamiltonian is given the global operator

(32)

and one has .

4.2.1. Universal MBQC

There are two approaches for the universality [32]. One is to construct universal gates, and in this case, they constructed measurement patterns that yield both Toffoli and Hadamard gates, which together form a universal set. Another is to use state reduction. Observe that the three qubits p, q and r are acted by a CCZ gate, and if one of the qubits, say p, is measured in the Z basis, then the effective action on qubits q and r is either identity when the outcome on p is or when the outcome is , respectively. All ‘cross’ sites are measured as shown in Figure 8(b). An edge in the square sublattice has two such sites on opposite sides, there is a net CZ if and only if the two outcomes are different. Thus, the remaining unmeasured qubits form a graph state, whose graph depends on whether an edge is occupied (with a net CZ), indicated by the dashed lines in Figure 8(b). They showed that the resultant random graphs, with high probability, belong to the supercritical phase of bond percolation; thus the state on the Union-Jack lattice is universal [32]. They later generalized to 3-cocycle states where cocycle functions are tri-linear and each site can contains multiple qubits, and showed that these ‘fractional-symmetric’ states are also universal [34].

The works by Miller and Miyake present exciting advancement in connecting 2D SPT phases to MBQC. The entities are qubits, instead of higher-dimensional ones. Nevertheless, the parent Hamiltonian involves multiple-qubit interactions, similar to that of graph states. Interestingly, Pauli measurements suffice to achieve quantum gates that are in the 3rd-level of the Clifford hierarchy [79]. However, the universality may not exist on other simple lattices, such as the triangular lattice.

Figure 8. (a) Triangular lattice; (b) Union-Jack Lattice.

4.3. The Levin–Gu model

Levin and Gu constructed another interesting symmetric Hamiltonian (invariant under ) on the triangular lattice (see Figure 8(a)),

(33)

(34)

They showed that and represent two distinct 2D SPT phases (with being nontrivial) [80]. Here, one may also ask whether the Levin–Gu state is also universal for MBQC.

4.3.1. Connection of different states

First we note that the above factor can be rewritten as

where denotes neighbors of site p and was defined earlier in the Miller–Miyake model. As seen above, one can transform away the factor by :

(35)

where we have used the definition of from Equation (7). The right-hand side is just the negative of the cluster-state Hamiltonian. Moreover, with , we can bring it to the simple form,

(36)

The ground state of the r.h.s. is a product of the negative eigenstate of : or equivalently , where . If the sign in the Hamiltonian were the opposite, we would have instead. Summarizing the above analysis in terms of states, we have

(37)

(38)

(39)

4.3.2. Complement of edges in graphs

From the above equations, we have found the relation between the ground states of and defined on the same lattice of triangulation,

(40)

We thus conclude that the graph of the graph state after the measurement in the Miller–Miyake state is actually the ‘complement’ of that in the Levin–Gu case. It would be interesting to see whether it may happen that the Miller–Miyake state on some particular lattice is not universal whereas the Levin–Gu state on the same lattice is, due to this complementary relation. Alternatively, could both states on the same lattice possess the same quantum computational power? It was commented in Ref. [32] that defined on the triangular lattice was not likely universal, and we also expect that would not be universal on this lattice. In a recent work [81], it was shown that the generalization of to qudit SPT states on the triangular lattice can indeed be universal.

5. Concluding remarks

We have reviewed the measurement-based approach for quantum computation, in which specific types of entanglement are known to provide a resource and only local measurement is needed. It remains one central open question as to what the complete characterization of universal resource states is. The study of computational universality in different families of states, such as the cluster/graph, the AKLT, and the SPT states, and how it relates to physical properties may pave the road for such a complete characterization. Specifically, whether the entire phase with certain 2D SPT order can be quantum computationally universal is an open question relevant to the notion of quantum computational phases of matter, for which the connection to the 1D SPT order has been substantiated recently [29–31].

Although cluster-state one-way computation is an abstract model of computation, it helps to make certain physical implementations more feasible. Knill, Laflamme and Milburn (KLM) [82] showed that quantum computation is possible with linear-optical elements with single-photon sources and detectors. Nielsen later combined the KLM and the cluster-state approaches and developed an alternative optical quantum computation scheme that has less demanding resource requirement than KLM [83]. Browne and Rudolph developed another scheme without using teleported gates and achieved a more resource-efficient linear-optical quantum computation [84]. Cluster/graph states of small photons number have been nondeterministically generated (e.g. using downcoversion photons) [85,86]. Another notable contribution of MBQC is the high error threshold in the surface-code quantum computation [25,26].

There have also been schemes for deterministically generating cluster states of photons, e.g. using the coupling to quantum dots [87,88]; several important aspects have recently been demonstrated [89]. Certain graph states of phase-flip code were also created using trapped ions, with up to seven physical qubits [90].

One natural setting for MBQC is the cold-atom system [91]; creation of cluster-state cold atoms was realized some time ago [92]. But the challenge is the local measurement; significant progress has since been made to detect and image single atoms [93–95]. One advantage of utilizing this system is the ability to scale up. Another impressive achievement in realizing large-scale cluster states, from of order 100 to million modes [96–98], employs the continuous-variable quantum-optical system [99,100]. The challenge to implement MBQC there is to perform local optical-mode measurement.

Recent rapid development in quantum simulations using cold atoms, Rydberg atoms, trapped ions, cavities, photonics, superconducting qubits, etc. have been proposed and developed to emulate spin Hamiltonians, and possible exotic Hamiltonians (such as topological orders) not necessarily existing naturally [93,95,101,109]. If Hamiltonians of those universal resource ground states can be engineered, then the resource states can be created by ‘cooling’ the system. An experimental simulation of such a cooling was recently done for cluster states [110]. Alternatively, some resource states may be created by simple acitve entangling procedure [92].

Less experimental realization has been explored for other resource states. However, a short 1D AKLT chain was simulated with photons [111] and several quatum gates were demonstrated. A proposal was made for the spin-3/2 state on the honeycomb lattice and for implementing the POVM [112]. Small-scale entangled-photon implementation is within the reach of current technology, but scaling up can be an issue. On the other hand it was recently proposed to realize AKLT and general valence-bond states using electrons in Mott insulators [113]. The ground state is not the exact AKLT state, but in the same phase; thus the theoretical study of quantum computational universality away from the exact wavefunctions and even the entire phase is important. SPT states in quantum computation is also mostly limited to theoretical consideration. However, it is possible that the above mentioned quantum simulations in various systems may provide useful avenue for realization.

Note added in proof. After this manuscript was accepted, the author learned of an exciting work by Raussendorf et al. [114], who established a 2D cluster phase that is universal for quantum computation.

Acknowledgements

The author acknowledges useful discussions with Ian Affleck, Akimasa Miyake, Abhishodh Prakash, Hendrik Poulsen Nautrup, Robert Raussendorf, David Stephen, Dongsheng Wang.

Additional information

Funding

This work was supported by the National Science Foundation [grant number PHY 1620252].

Notes

No potential conflict of interest was reported by the authors.