Photonic flat band dynamics

ABSTRACT

During the last decades, researchers of different scientific areas have investigated several systems and materials to suggest new ways of transporting and localizing light. These problems are probably main goals in any search for new configurations and new emerging properties, independently of the degree of complexity of suggested methods. Fortunately, fabrication techniques in photonics have consolidated during the last decades, allowing the experimental implementation of different theoretical ideas which were neither tested nor validated. Specifically, we will focus on recent advances in the implementation of Flat Band (FB) photonic systems. FB periodical structures have at least two bands in their linear spectrum, with one of them completely flat. This implies the emergence of linear photonic states which are completely localized in space and that can be located in different regions across the lattice. This localization occurs as a result of destructive interference, what naturally depends on the particular lattice geometry. In addition, flat band systems also posses dispersive states which make possible the observation of ballistic transport as well. Therefore, FB photonic lattices constitute an unique platform for studying localization and transport, without requiring the inclusion of any sophisticated interaction/effect, rather a smart and simple geometry.

Graphical abstract

KEYWORDS:

• Photonic lattices
• flat Bands
• light Localization
• discrete systems
• integrated optics
• image propagation

Introduction

Transport and localization, considering different geometries and interactions, have been key goals in general physics. Most of the nowadays well known solid-state phenomena is based essentially on the understanding of electronic transport and localization in diverse materials. Therefore, the idea of using photonic platforms to evidence or visualize otherwise occulted electronic phenomena is of great fundamental relevance and interest [1]. In addition, the study of photonic systems also guarantees finding solutions for optical communications and photonic chip structures, in order to improve the steering and generation of optical data [2]. Considering this fundamental and applied view, the question about which kind of photonic structure could become the ideal setup for controlling light on a single optical chip is still open. Waveguide arrays (WA) are such a nice example of Photonic lattices (PL), where many different effects could be investigated, due to their similarities with solid-state physics [1]. The ability of directly imaging the wave-function by using a simple CCD camera (something forbidden for electronic systems) is probably one of the key advantages of waveguide arrays, allowing to check directly the dynamics on a micrometer scale.

At the end of the 90’s, different results started to appear rapidly, showing a good agreement between theoretical models and experimental observations. At the very beginning, most of the experiments were performed using deposition and lithographic techniques and, therefore, limited to 1D spatial configurations. Important results were the observation of the first discrete optical soliton [3], after being predicted by Christodoulides and Joseph in 1988 [4]. Bloch oscillations [5] and band-gap structure [6] were observed as well, showing a close relation with condensed matter problems. These similarities were crucial to speed up the progress in this area of research, where a natural experimental improvement was demanded. In 2003, a new technique was suggested using photorefractive SBN crystals to induce 1D photonic lattices [7] and, some years later, to observe Anderson localization in two-dimensional (2D) hexagonal induced structures [8]. In 2005, the femtosecond (fs) waveguide writing technique on silica glass [9] was proposed [see figure 1(a)], as a high-quality and simple method to fabricate photonic lattices inside a transparent media (see a Lieb photonic lattice as an example in figure 1(b) [10]). In this technique, a femtosecond laser is focused inside a glass material, which slightly modifies the refractive index ($\sim {10}^{-4}-{10}^{-3}$) at the focusing region, while sample is translated in XYZ directions. Dynamical localization [11], relativistic analogs [12], and topological insulators [13] are just some exciting examples using this fabrication method. Very recently, a kind of mixture between both previous fabrication techniques was developed [14,15], opening new possibilities for photonic lattices research. The idea essentially consists, as sketched in figure 1(c), on performing a site-to-site induction on a SBN photorefractive crystal. A light object is generated on a spatial light modulator (SLM) which is then imaged inside the crystal. This allows the generation of arbitrary lattices that can be erased and written again depending on the particular implemented experiment.

Figure 1. (a) fs-laser-writing technique and (b) fabricated photonic Lieb lattice, as an experimental platform to observe flat band compact localized states. (c) Experimental setup for site-to-site induction writing technique on photorefractive SBN crystals. (d) Scanning Electron Microscope image of a photonic Stub lattice made of engineered coupled micropillars (reproduced with permission from reference [16])

Both previous fabrication methods produce waveguide photonic structures, where the basic element is, in general, a single-mode optical waveguide. However, other photonic methods use different basic units to study lattice configurations as well. An interesting example of this consists of coupled micropillar arrays [16], which are grown by molecular beam epitaxy, as the example shown in figure 1(d). One of the key advantages of this experimental platform is the possibility of imaging the excited energies during the dynamics, allowing a direct observation of the linear and nonlinear lattice spectrum [17]. Another – completely – different photonic lattice setup consists of coupled octagon resonators, which strongly couple to each other forming nanophotonic lattice structures [18]. There, every unit cell is formed by several resonators, allowing the emulation of periodically driven systems and the study of associated topological properties.

A few years ago, photonic Flat Band (FB) lattices emerged as a good solution for transport and localization problems, due to its simplicity and clear results [15,19]. In principle, any FB lattice will induce localization on a linear level, while some of them will show good transport conditions on a nonlinear regime. Before the appearance of FB photonic lattices most of the efforts were concentrated on finding conditions for localization on a given lattice and study the stability of localized states. In this context, impurity modes [20,21], discrete solitons [3], Anderson states [22] showed a way to localize energy on a given lattice region, but requiring the inclusion of some inhomogeneities through the system. The first result on FB systems for the photonic community was on nonlinear vortex states on a kagome lattice [23], in the limit of strong nonlinearity. Interestingly, in that paper authors overlooked the linear spectrum and the possible connection between FB linear modes and nonlinear vortices. After that, some works studied defect solitons in kagome optical lattices with saturable nonlinearity [24] and nonlinear localization in kagome ribbons [25], without considering the bifurcation of these localized states from the FB. Nonlinear kagome states, occupying few lattice sites, bifurcate at zero power exactly at the FB [26]. This was completely opposite to the general idea of requiring a power threshold to excite nonlinear localized states for dimensions larger than one [27], something that was an indication of a new phenomenology appearing due to the special linear spectrum found in FB lattices.

FB research in photonics had a nonlinear origin which was not initially focused on the most crucial and relevant aspect of this kind of photonic lattices; that is, the total absence of transport for a large set of linear eigenmodes, that form a complete degenerated band. In this work, we will describe the main results obtained during the last decade on Flat Band photonic lattices and we will also show some perspectives for future research on this marvelous and promising fundamental and applied topic.

FB photonic lattices and main properties

Linear spectrum

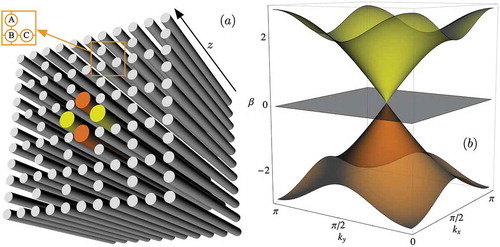
We will use a Lieb lattice [10,28,29] as a generic example to explain some general properties of FB systems. We sketch this photonic lattice in figure 2(a), where every cylinder represents an optical waveguide. The geometry of this lattice is quite similar to a rectangular system, excepting the absence of some waveguides every two lattice sites and every two rows, commonly defined as a face-centered or depleted square lattice. In general, the study of light propagation on lattice structures is performed by using an approach coming from coupled mode theory [1], which is also known as tight-binding approximation in solid-state physics. This approach describes a weak interaction between neighboring waveguides, located at different lattice positions, which evanescently couple with each other. Final equations are known as discrete nonlinear Schrödinger equations (DNLSE) and are written, in a generic form, as

(1) $-i\frac{d{\psi }_{\vec{n}}}{dz}={\beta }_{\vec{n}}{\psi }_{\vec{n}}+\sum _{\vec{m}\ne \vec{n}}{V}_{\vec{n},\vec{m}}{\psi }_{\vec{m}}+\gamma |{\psi }_{\vec{n}}{|}^2{\psi }_{\vec{n}}.$(1)

Figure 2. (a) A Lieb photonic lattice, which is composed of straight waveguides represented by gray cylinders. A FB state is sketched in this figure, which propagates along the $z$ direction. Different colors indicate a different phase, being 0 or $\pi$ for yellow and orange colors, respectively. Inset specifies the Lieb unit cell, which is formed by sites A, B and C. These sites couple to nearest-neighbor sites only. (b) The linear spectrum of a Lieb lattice is shown in the first Brillouin zone, where we clearly observe two dispersive and symmetric (yellow and orange) bands, including a completely flat (grey) band at the very center of the spectrum

Here, ${\psi }_{\vec{n}}(z)$ represents the electric field mode amplitude at site $\vec{n}$. $z$ is the propagation coordinate (dynamical variable), and ${\beta }_{\vec{n}}$ corresponds to the propagation constant at the $\vec{n}$-th site (we set ${\beta }_{\vec{n}}=0$ for an homogeneous lattice). Coupling between lattice sites $\vec{n}$ and $\vec{m}$ is given by term $V_{\vec{n},\vec{m}}$, which contains the full lattice structure. We also include a Kerr (cubic) nonlinearity controlled by coefficient $\gamma$, which is a standard nonlinear response in diverse optical materials (for low level of power, saturable nonlinearities also reduce to a similar cubic term). This model has only two conserved quantities, the total power $P$ and the Hamiltonian $H$ [1].

We study the linear properties of a given lattice by analyzing matrix elements $V_{\vec{n},\vec{m}}$, which includes the unit cell definition. We obtain the linear spectrum by solving linear ($\gamma =0$) coupled equations using a plane wave ansatz ${\psi }_{\vec{n}}(z)={\varphi }_{\vec{n}}exp[i({\vec{k}}_{\mathrm{\perp }}\cdot d\vec{n}+\beta z)]$, where ${\vec{k}}_{\mathrm{\perp }}\equiv \{k_x,k_y\}$ represents the transversal propagation vector, $\beta$ the longitudinal propagation constant, and d a lattice constant. By inserting this ansatz into model (1), and considering the number of sites per unit cell, the linear problem is analytically or numerically solved. In our example, a Lieb lattice has three sites per unit cell (sites A, B, and C in figure 2(a)-inset) and, therefore, the linear spectrum (band structure) consists of three bands

(2) $\beta (k_x,k_y)=0,\pm 2V\sqrt{{cos}^2(k_{x}d)+{cos}^2(k_{y}d)}.$(2)

Here, we have assumed a symmetric Lieb lattice with a single nearest-neighbor coupling V. We plot these bands in figure 2(b), in the first Brillouin zone. We clearly notice two dispersive (orange and yellow) bands, having a particle-hole symmetry [30], connected at $k_z=0$ by one Dirac cone. Additionally, we observe in figure 2(b) a perfect flat band (gray) located at $k_z=0$. Band curvature defines the associated dispersion properties of any lattice. Specifically, group transversal velocity is proportional to the gradient of $\beta (k_x,k_y)$ which separates slow from fast propagating linear waves. Typical/conventional lattices have a dispersive spectrum only. This means that different modes at different transversal wave vectors have a different propagation velocity, been this proportional to the slope of the respective band. For FB lattices, transport properties strongly depend on the particular site excited as we have clearly shown for Lieb [28], Sawtooth [31], and Stub [32] photonic lattices. When a B site is excited on a Lieb lattice the observed transport is maximum [see figure 3(a)]. Light travels through the whole lattice and the energy is very well disseminated, because the dispersive part of the spectrum is excited the most.

Figure 3. Output intensity profiles for a Lieb photonic lattice [see Figure 1(a)], after a propagation distance of 10 cm. (a) B-site excitation (input position denoted by yellow circle) using a focused 633 nm (red) laser beam. (b) 532 nm (green) laser excitation modulated – in amplitude and phase – using a SLM setup: (b1) A FB linear mode profile, (b2) Two FB modes in a diagonal configuration, (b3)–(b6) four FB mode superpositions. Yellow symbols in (b) indicate the relative phase of each superposed ring mode

A flat band has a null group velocity and null diffraction coefficient, implying that linear modes of that band are completely static and do not diffract upon propagation [10,29]. In the Lieb example, 1/3 of the linear spectrum corresponds to this zero dispersion band. We can construct these FB states by using some construction techniques [33], which consider specific boundary conditions and extended line mode states. In the case of a Lieb lattice, these line states consist of staggered ($\dots ,+,-,+,-,\dots$) diagonal straight lines satisfying a site relation A = -c and $B=0$, for an isotropic system (this explains why exciting a B site produces mostly transport as figure 3(a) shows). They can be superposed on the whole lattice and finally form a very compact entity called ‘compact localized state’ or ‘FB mode’. These states have only 4 sites different to zero and they are perfectly localized in space, without any tail, as sketched in figure 2(a). This example shows very clearly the main ingredient for having localization on a FB linear system. As we see from site relations and different colors in figure 2(a), we notice a $\pi$ phase difference between sites A and C, such that the amplitudes at B sites are exactly zero. When light couples to the corner B sites receive light from A and C sites simultaneously, and an exact destructive interference at these connector sites occurs. Therefore, light transport is completely forbidden and the energy remains trapped in the form of a FB compact state. In 2015, we performed a challenging experiment to show, for the first time ever in any physical system, the existence of a FB mode on a Lieb lattice. That experiment coincided with the efforts from another experimental group and results were published in the same journal issue [10,29]. In our experiment, we were able to fabricate a Lieb lattice and excite it with a FB input condition, which consisted on four sites with alternated phases. We used a SLM to, first, modulate in amplitude a wide light beam and, then, to imprint a $\pi$-phase difference between different sites. The output profile, after traveling a distance of 10 cm, is shown in figure 3(b1). In this picture we observe a FB state, which is perfectly localized in space and constitutes a clear experimental proof for FB phenomenology. In micropillar arrays, a Lieb photonic lattice was experimentally studied as well [34,35], where fundamental and excited flat band modes were observed separately. Spatial profiles clearly show the spatial ordering of a Lieb FB excitation, and the direct imaging of the spectrum shows the characteristic flatness expected for zero dispersion bands.

Considering the ‘compacton’ definition [36], a FB mode constitutes a perfect linear compacton. This is a very important property, because linear/nonlinear localized states of discrete lattices always possess an exponential-like tail which strongly depends on the strength of a system parameter (propagation constant detuning, power, nonlinear coefficient, etc.) [1]. This compacton linear concept is probably one of the most important for FB systems, in terms of fundamental results and possible applications. For years, researchers were looking for conditions to find localized and stable modes on a lattice and, suddenly, the solution for this major goal was simply solved by considering new lattice geometries. FB systems, as for example a Lieb lattice, possess dispersive and localized linear waves without requiring any additional interaction neither special effect in the system. We can observe a nice ballistic transport [see figure 3(a)] as well as a perfect localized profile [figure 3(b1)], both, in a linear regime for low level of power.

A flat band is composed for as many localized states as closed rings in the lattice. All these modes have exactly the same longitudinal propagation constant $\beta$ and, therefore, any linear combination of them will also be a solution of the system. This perfectly coherent superposition will propagate along the $z$ direction without experiencing any diffractive detriment, being a perfect solution for diffraction-free image transmission schemes [37,38]. In Ref [39]., we studied this concept in the framework of a kagome photonic lattice. That system possesses one FB at the bottom of the spectrum and linear localized FB states have six sites different to zero, with a staggered phase structure. By linearly combining these states we were able to propagate numerically images (words) formed by a superposition of FB states. The first experiment showing that concept was performed in a Lieb photonic lattice [10] where we generated several linear combinations as the examples shown in figure 3(b). As we implemented an SLM-based technique, we got a perfect control of the input excitation and we were able to excite a Lieb lattice with different optical patterns. Figure 3(b2)–(b6) show some examples for FB linear combinations, considering different phases and different FB modes. The number of possible combinations increases depending on the number of combined rings, and the different amplitudes and phases of every mode [32]. This concept was experimentally corroborated for induced Lieb [14,40] and kagome [41] photonic lattices. We patented [42] this idea as a way of transmitting information, codified in optical patterns, for any FB photonic lattice, idea that certainly could be implemented in any physical context having lattices as a framework.

FB construction technique

In 2016, we developed a simple method to generate arbitrary lattices presenting at least one flat band in their spectrum [43]. After analyzing the literature, we found some methods to construct FB lattices, however no one was direct neither simple neither general. For example, Ref [44]. shows a method to construct partial line graphs without studying the respective physics of the sublattices, which we consider a crucial aspect in our method. Ref [45]. briefly mentions that the wave function may be zero at some connecting sites, in order to cancel the transport across the lattice. However, although this is an important requirement, it is not the only one. To observe localization, destructive interference will cancel the amplitudes at some connecting sites and transport will simply not occur. Therefore, a FB lattice can be designed by selecting different geometrical configurations to assure a phase cancellation in specific lattice sites. Additionally, our method proposes the construction of a lattice starting with a simple miniarray as elementary unit, which could be connected to other miniarrays and form a full lattice.

To illustrate this idea, we will use the simplest miniarray: a dimer. A photonic dimer, as sketched in figure 4(a), consists of two waveguides with a separation that allows an evanescent coupling between the modes at every site. In this case, coupling between waveguides is determined by parameter V, and normal modes of this system are sketched in figure 4(b). These modes are standard: one in-phase (left) and one out-of-phase (right), with propagation constants $\beta =+V$ and $\beta =-V$, respectively. Naturally, if all coupling constants are positive (for example, if we consider fundamental modes only [46]), there is no way to observe destructive interference using an in-phase mode. On the other hand, the out-of-phase mode could allow phase cancellation if, for example, an extra site is inserted. We sketch this idea in figure 4(c) by adding an extra/connector site to the right of a first dimer, including a new diagonal coupling constant $\bar{V}$. We also add a second dimer to the right, in order to show how to increase the system size. We notice that by exciting the out of phase normal mode, for example in the left dimer, the light gets immediately trapped. While light tries to jump into the connector site both dimer sites contribute and interfere destructively, cancelling each other perfectly. Therefore, light gets localized at the original region and is never able to jump into a neighbor dimer. So, the initial out-of-phase normal mode of a single dimer becomes also an exact solution for a larger system, as the one sketched in figure 4(c). The rest of the method is quite simple, we add several connector sites and several dimers and construct a full diamond lattice, as shown in figure 4(d). By continue doing this we are, in fact, constructing a flat band by hand, because all the out-of-phase modes located in all the dimers will have exactly the same propagation constant – V and will form a complete degenerated flat band. We can compute the linear spectrum as we did for the Lieb lattice using a plane wave ansatz, but considering the quasi-1D nature of a diamond lattice and its unit cell with three sites [47,48], getting

(3) $\beta (k_x)=-V,\left(V\pm \sqrt{V^2+32{\bar{V}}^2{cos}^2(k_{x}d)}\right)/2.$(3)

Figure 4. (a) Photonic dimer with coupling constant V. (b) Symmetric ‘++’ (left) and asymmetric ‘+ -’ (right) dimer normal modes. Here, + and – signs indicate 0 and $\pi$ phases, respectively. (c) FB construction technique based on miniarrays linked by connector sites, where a new diagonal coupling $\bar{V}$ has been included. (d) A diamond lattice formed by connecting several dimers following the construction technique. (e) Linear spectrum of a diamond lattice in the first Brillouin zone for $V=\bar{V}$, having two dispersive and one flat bands

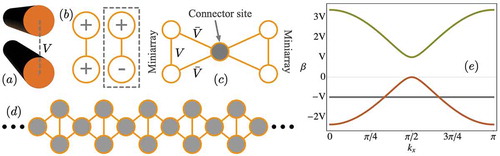
We plot the linear spectrum in figure 4(e), where we clearly notice two dispersive bands and one completely flat band at $\beta =-V$, which is exactly the same value of the out-of-phase dimer normal modes. So, that means that we can construct a flat band lattice just by adding miniarrays connected by connector sites and know exactly the flat band $\beta$ value. It is important to mention that for many cases there is no need to include a connector site, but visualizing some normal modes having zero amplitudes. For example, a Lieb lattice can be composed by adding miniarrays formed by 8 sites on a square, and considering a mode $A,0,-A,0,A,0,-A,0$, which has a zero propagation constant. Then, we can add miniarrays sharing, for example, the corner site and construct a full lattice having a perfect flat band at $\beta =0$, as shown in figure 2(b).

Nonlinear flat band compactons and mobility

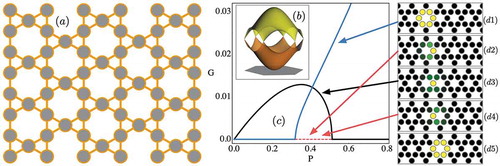
It is important to discuss the effect of considering nonlinearity in FB lattices for a historical as well as a practical reason. As described above, discrete lattices were studied from a nonlinear perspective for decades as a way to localize energy, on a homogenous system, due to a balance between linear diffraction and nonlinear self-focusing processes [49]. In particular, the first work in the FB context was about vortices and multipole solitons on a kagome lattice [23]. However, not much attention was given to this area of research afterwards in waveguide arrays. Experimental efforts have been mostly concentrated in exciton-polariton photonic lattices, where the combination of nonlinearity and flat bands has been experimentally reported [16,50]. Only very recently, the observation of topological Floquet solitons [51,52] has renewed the interest for studying different lattice configurations and nonlinear interactions. Self-trapping transition in presence of disorder and a FB geometry was studied recently as well [53], where the degenerary of FBs have shown to have a strong impact in transport properties. In Ref [26]. we studied in detail a kagome lattice [see figure 5(a)] including a defocusing Kerr-like nonlinearity. This lattice possesses three sites per unit cell and, therefore, three bands in the linear spectrum, given by

(4) $\beta (k_x,k_y)=-2V,V\left(1\pm \sqrt{1+8f(k_x,k_y)}\right),$(4)

Figure 5. (a) A kagome photonic lattice structure. (b) Linear spectrum with two dispersive (yellow and orange) and one flat (gray) bands. (c) Stability diagram for nonlinear fundamental solutions: maximum unstable eigenvalue G versus power P, for a ring (blue), one-peak (black), and intermediate (red) solutions. (d) Intensity profiles $|{\psi }_{\vec{n}}(z){|}^2$ at different $z$-values for an initially kicked ring, where black, green and yellow colors correspond to zero, middle and maximum intensity. We can observe how the FB mode is able to junp into a neighbor lattice ring, while spatially transforming its profile: ring→intermediate→one-peak→intermediate→ring. Arrows indicate the relation with stationary solutions

with $f(k_x,k_y)=1+2{cos}^2(k_x/2){cos}^2(\sqrt{3}{k}_y/2)+2{cos}^4(k_x/2)-3{cos}^2\text{break}(k_x/2)-{cos}^2(\sqrt{3}{k}_y/2)$. The FB is located at $\beta =-2V$ and touches a single point of a dispersive band at $k_x=k_y=0$ as shown in figure 5(b), where modes have a staggered phase structure. In this case, FB linear modes are composed of only six amplitudes different from zero, forming a staggered ring [26,39]. As the flat and the dispersive bands touch each other exactly where an extended fundamental $\pi$-phase mode exists, a natural question arises with respect to the existence of fundamental single-peaked discrete solitons. As it is well known for 2D nonlinear cubic lattices [27], single-peak localized solutions bifurcate at the linear band exactly at the fundamental mode located at the band edge, preserving the phase structure of the original normal mode, but diverging in power immediately. Therefore, how these fundamental nonlinear solutions bifurcate for a kagome lattice has no a straightforward solution.

We derived analytically [26], for the first time ever, a perfect nonlinear compact (ring) solution which can be written as $P=6(\beta +2V)/\gamma$, obtained from (1) for a kagome geometry. In general, for lattices having perfectly compact symmetric FB modes $P=R(\beta -{\beta }_{FB})/\gamma$, with R the participation ratio and ${\beta }_{FB}$ the FB propagation constant [43]. The participation ratio is an indicator of the numbers of effective excited sites of a given solution. Nonlinear discrete lattices of more than three sites are typically non-integrable and, therefore, it is only possible to obtain approximate or numerical solutions. So, this result is quite important because we obtained an analytical expression for a nonlinear solution, but also because this is a perfectly compact nonlinear mode, something that was a whole subject of research some years ago [36,54]. We studied the stability of this six-sites (ring) solution [blue line in figure 5(c)] and found, surprisingly, that was stable at low level of power and always compact being, therefore, a perfectly localized ground state of the system (a nonlinear ground state is typically very broad when it bifurcates from the linear band [27]). G = 0 and G > 0 correspond to stable and unstable solutions, respectively, in the stability diagram of figure 5(c). While increasing the solution power, we noticed that it suddenly gets unstable and never stabilizes again. So, a new stable ground state may appear in the lattice; in this case, a single-peaked fundamental solution [black line in figure 5(c)]. However, by decreasing now the power of the single peak discrete soliton, we found that both solutions were simultaneously unstable for $P\sim \{0.3,0.5\}$, as figure 5(c) shows. This was an indication of an additional stable solution, which connects both unstable modes [55,56]. For nonlinear lattices, this mode is ussually called intermediate solution (IS) [red line in figure 5(c)] and corresponds to a spatially asymmetric ground state, something very rare considering a perfectly homogenous lattice. Additionally, we also noticed that the single peak solution bifurcates at exactly zero power, without any divergence and without any power threshold [27]. By continue digging in the mystery of this lattice, we found that the single peak fundamental mode does not bifurcate from the dispersive band, but from the flat band. By linearly combining two kagome FB linear modes a single peak state is formed and, therefore, when increasing the power this solution gets more and more localized. At zero power, a FB linear mode has R = 6, while a state formed by two linearly combined FB modes has R = 7.5. As the Hamiltonian is proportional (in the low power regime) to the number of excited sites, the ring mode has the lower Hamiltonian and, therefore, it must be the lattice ground state. However, when increasing the power, the single-peak solution reduces its participation ratio, and it transform into the system ground state (the compacton has always R = 6 for any level of power). Therefore, a Hamiltonian crossing occurs and the stability properties are exchanged, as shown in figure 5(c). All this description shows how a simple change in geometry introduces completely different properties on, both, linear and nonlinear regimes. From a practical point of view, the described phenomenology implies something very important in terms of dynamics. Stability exchange mechanisms [55,56] have shown to be connected with the reduction of the so-called Peierls-Nabarro barrier [1]. This immediately implies an enhanced mobility through the lattice on a nonlinear regime, what in the kagome case corresponds to mobile compactons. Figures. 5(d1)–(d5) show intensity profiles at different propagation distances z, for a horizontally kicked ring mode. We observe how this compact state adiabatically transforms into an IS, then to a one-peak profile, to a IS again and, finally, to a ring mode.

We continued investigating this idea (nonlinear compactons and mobility) on different nonlinear FB lattices, but we found neither good mobility nor clear dynamical picture as the one described for the kagome geometry. For example, for a nonlinear kagome ribbon [57] the mobility is considerably diminished compared to the 2D full case. The dimensional reduction decreases the degrees of freedom and prevents transport of localized modes across the lattice, due to the impossibility of radiating energy to the rest of the system. For a nonlinear Lieb lattice [58,59], we found a tendency to have stability inversion regions but not as clear or complete as in kagome. As a consequence, we observed good mobility only for narrow regions in parameter space, what changes abruptly depending on the system size. Stability conditions for fundamental and compact spatially localized states have also been studied from a more theoretical perspective for a nonlinear diamond/rhombic lattice [60,61]; however, no coherent mobility was reported. Very recently, we explored octagonal-diamond lattices [62], a system presenting two flat bands. We were not able to observe mobility, but oscillation around the input position. In this case, we did not find the real ground state of the system which may connect the FB modes at the bifurcation point. One and two peaks solutions have always a smaller participation ratio than FB modes in this lattice, therefore it was not possible to find stability inversion conditions as in previous systems. We also studied the persistence of asymmetric FB modes in a Sawtooth geometry [63] including a general on-site nonlinearity. This lattice has a FB only for a very specific ratio between coupling constants, something that can be tuned in a nonlinear regime, while keeping the compactness of the nonlinear compact mode. Very recently [64], a plus-like geometry was considered as well, a system presenting only one FB. However, nonlinearity immediately destabilizes the FB modes and dynamics can not preserve the energy localized on narrow regions as, for example, in kagome or Lieb lattices. Therefore, there is still an open question about what are the necessary conditions for a FB lattice to become a good lattice in terms of nonlinear mobility. Up to now, only some lattice examples have been explored, but there is a lack of a rigorous and general theory to explain the theoretical and numerical findings. Additionally, no experiment showing FB nonlinear mobility has been performed to this date, which could be of relevance to increase the advantages of FB systems for steering optical codified information.

Flat bands for higher-order photonic modes

Graphene ribbon

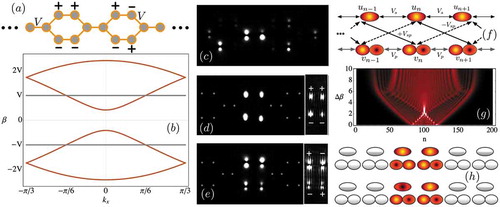
As it is well known from waveguide theory [65], if shorter wavelengths are used on a given photonic waveguide higher-order modes could be excited along the structure [46]. In particular, we studied the existence of flat bands excited with fundamental and excited modes (photonic dipoles) on a graphene ribbon lattice [66], as the one shown in figure 6(a). This lattice was constructed following the method described above [43], but specifically looking for a robust system when next-nearest neighbor interactions are included as well, an important requirement for a successful experimental observation. The linear spectrum is composed of six bands, four of them dispersive and two perfectly flat at $\beta =\pm V$ [see figure 6(b)]. Both FB modes have only four sites different from zero [as sketched in figure 6(a)] and a lateral staggered phase structure, satisfying the destructive interference condition at connector sites (lattice central row). In this case [66], we were interested on studying a photonic system having two FB, as a first experimental evidence of such a lattice but, also, on observing the first ever dipolar FB state. In figure 6(c) a bulk excitation shows dipolar diffraction due to the excitation of dispersive waves from the linear spectrum. Figure 6(d) shows, quite clearly, a $\beta =V$ flat band mode formed by individual fundamental modes only, while figure 6(e) shows the $\beta =-V$ flat band state composed of four dipoles. Insets in figures 6(d) and (e) show interferograms between the FB modes and a wide light beam, where the relative phases between different amplitudes are observed. In these figures, we observe, quite clearly, localized linear FB states of two different flat bands, which occupy only four sites of the lattice.

Figure 6. (a) A graphene ribbon lattice, including a sketch of FB modes profiles where ‘+’ and ‘–’ mean a 0 and $\pi$ phase, respectively. (b) Linear spectrum formed by four dispersive (orange) and two flat (gray) bands. Output intensity profiles for a 633 nm (red) modulated laser excitation: (c) Single dipolar bulk excitation; (d) fundamental FB mode at $\beta =V$; (e) dipolar FB mode at $\beta =-V$. Gray dots in (d) and (e) indicate waveguide positions. Insets in (d) and (e) are interferogram images showing the relative phases between different waveguides. (f) Hybrid SP 1D model. (g) S mode numerical output profiles versus detuning $\mathrm{\Delta }\beta$, after propagating a given distance $z_{max}$. Color code: black, red and white correspond to zero, middle and maximum intensity. (h) FB modes at $+2V_s$ (top) and $-2V_s$ (bottom), for a zero detuning condition

Hybrid 1D lattices

Considering the terminology used in quantum mechanics, we call S and P modes to the fundamental and dipolar states, respectively. We can ask the question about what would happen on a lattice presenting, simultaneously, S and P modes, and how linear properties can be modified [67]. In 2019, we explored [68] a 1D binary lattice having fundamental and dipolar modes at every lattice site, transforming the system into an effective ladder-like quasi-1D hybrid model [69]. As our binary lattice considered horizontal and vertical waveguide orientations, the excitation of a P mode at vertical waveguides generated, immediately, a perfect flat band with propagation constant $\beta =0$. Although the origin of this FB is trivial (P states at those sites do not interact with the rest of the lattice), this very simple model offers the possibility to observe perfect localization with a FB state occupying a single site, what corresponds to the more localized FB state ever (before this result, the ‘record’ was for the diamond lattice [47], with FB states occupying only 2 sites). On the other hand, by exciting the same vertical waveguide but now with an S mode, we simply observe transport across the lattice. Therefore, the same lattice offers perfect localization and diffusive transport just by exciting the system with different orthogonal states. Additionally, if we allow coupling between S and P states at different sites, we can find an analytical condition for a second flat band, with highly localized modes occupying approximately two lattice sites.

Very recently, we studied an even simpler model consisting on a 1D lattice on a row, with horizontally oriented waveguides only [70]. Again, we allowed inter-site coupling in between S-S ($V_s>0$), P-P ($V_p<0$), and S-P ($V_{sp}$, sign depends on orientation) modes, including a propagation constant detuning $\mathrm{\Delta }\beta$. By assuming two modes per waveguide, the system dimension increases and an effective hybrid ribbon (ladder) structure is obtained [see figure 6(f)]. When considering a standard coupling relation $|V_s|<|V_{sp}|<|V_p|$, we observe that for some specific value of detuning $\mathrm{\Delta }\beta$, one of the two bands flattens and transport is reduced quite importantly for S modes as figure 6(g) shows (bright peak at $\mathrm{\Delta }\beta \sim 2$). Therefore, there is a tendency of generating a FB in the linear spectrum but, however, it never becomes perfectly flat for $\mathrm{\Delta }\beta \ne 0$. Nevertheless, by considering zero detuning and a symmetric coupling condition $|V_s|=|V_p|=|V_{sp}|$, the two originally dispersive bands of this model become both perfectly flat at $\beta =\pm 2V_s$, with the corresponding hybridized FB modes sketched in figures 6(h). Although this symmetric condition could be thought to be quite artificial and not related to real physics, we are currently working on its experimental implementation, that could become the first observation of an hybridized FB, something that up to now is still a theoretical promise. The idea of studying lattices presenting different orbital states seems to be an interesting route for increasing complexity on rather trivial and even conventional geometries due to the presence of positive and negative coupling constants. For example, a honeycomb (graphene) lattice could show excellent transport conditions for fundamental modes, while having two FB when injecting P states [71].

Flat bands: non-direct mechanisms

The inclusion of artificial gauge fields on lattices allows the appearance of an effect known as Aharonov-Bohm (AB) caging [72,73], where due to a perfect cancellation of phases the dispersive part of the spectrum becomes completely flat [74,75]. Therefore, the excitation of any lattice site is simply decomposed on the excitation of FB modes only and, therefore, energy remains trapped on a reduced lattice region. This effect has been experimentally observed in femtosecond laser written diamond lattices by modulating waveguides along the propagation direction [76], or by inserting auxiliary waveguides [77] to effectively induce negative coupling interactions. Some proposals also offer the possibility to explore the interaction between AB caging, FB and nonlinearity in diamond lattices, where the persistence of localization phenomena and breathing has been numerically predicted [78,79].

Flat bands in Floquet topological insulators has been also observed in fs written bipartite lattices [80,81]. Here, a driving protocol was implemented such that waveguides couple to each other on a modulated and controlled way, allowing the generation of localized trapped profiles after a given dynamical cycle. This finally generates two effective degenerated flat bands at zero energy (with a Chern number equal to zero), with completely localized bulk states and, as expected from topological insulators physics [82], only transport along the edges. Very recently Floquet solitons has been observed as well in modulated fs written photonic arrays [51,83]. As FB naturally enhances interactions at very reduced spatial regions, the addition of nonlinearity allows the observation of soliton-like structures at arbitrary low power, something that was theoretically predicted several years ago [26], as described in previous section.

Finally, we describe the effect of considering non-hermitian lattices in the formation of FBs. It has been shown that a simple quasi-1D $\mathcal{P}\mathcal{T}$ symmetric lattice [84], having three sites per unit cell (with gain, loss and passive waveguides) could show the appearance of a FB transition when increasing the gain/loss parameter. This exactly occurs at a lattice exceptional point, where a pair of eigenstates coalesce and the Hamiltonian becomes defective, exhibiting non-Hermitian degeneracies [85–87]. An experimental verification of this idea was reported recently [88], where an interesting degree of freedom was marvelously added to the fs laser written technique. By changing the concentration of scattering centers along the waveguides, which are created by slowing down the writing velocity at very specific positions, authors were able to introduce controlled losses at selected waveguides. This is certainly an important step forward in the study of non-hermitian photonic lattices and their connection with FB localization. The appearance of FBs due to the existence of one or more exceptional points, on a given photonic system, is believed to be a promising solution for waveguide lasing [88–92], due to the possibility of producing a huge amplification on a reduced spatial region.

1. Summary and outlook

To summarize, we have described a general picture about FB photonic lattices up to now. Specifically, we have described the main linear properties of flat band systems, with a clear focus on the possibility of exciting localized states as well as of observing good transport using different input conditions, both on a linear regime (low level of power). We described the main dynamical results for a Lieb photonic lattice. There, the first ever FB state was observed [10,29], something that was crucial to speed up the interest and impact on diverse areas of research [19]. We explained in detail the application in image transmission schemes, where every FB lattice constitutes a perfect candidate for transporting images and codified information along a given optical system. Then, we showed a very simple method to generate FB lattices starting from miniarrays, where the understanding of their normal modes gives the possibility to create a full lattice having one or more FB. We described nonlinear results specifically for a kagome lattice, where many 2D nonlinear fundamental properties become not valid any more. For example, the existence of highly localized states bifurcating at zero power threshold, asymmetric intermediate ground states, perfectly analytical nonlinear compacton solutions and, quite importantly, nonlinear mobility at very low power.

We also focused on a new research direction where hybridized interactions offer different possibilities for lattice dynamics. In particular, we showed the observation of the first FB dipolar state on a graphene ribbon presenting two FB. We also discussed how the inclusion of inter-mode coupling allows the existence of FB on conventional lattice structures. This idea seems to be quite general on different lattice models due to the presence of positive and negative coupling interactions, adding for free destructive interference mechanisms. We consider this topic a crucial one for future FB research due to the possibility of observing FB dynamics on rather trivial geometries. Positive and negative coupling constants could generate effective magnetic fields also, where FB and topological properties could meet and give us new and exotic results.

At the very end, we gave a general overview of more complex mechanisms for FB generation; i.e, AB caging, Floquet topological insulation and non-hermiticity. All these systems naturally produce FB in the linear spectrum as well as spatial localization. Therefore, as we wrote at introduction, transport and localization properties remain to be the more important topics in lattice physics, independently of the specific geometry, interaction or complex selected mechanism. Flat bands are quite a generic topic in photonic lattices and, as we have already pointed out, their appearance and use can be achieved in conventional and non-conventional lattice geometries. The main challenge is to find good conditions for having destructive interference mechanisms, which is – at the end – the fundamental requirement for having FB localization and related phenomenology. Future research in photonic lattices will continue exploring new interactions and new effects by mixing different areas of knowledge, that will probably give us new recipes and new ingredients for novel FB photonic platforms. Fortunately, the best is yet to come.

Acknowledgments

This work was supported in part by Programa ICM Millennium Institute for Research in Optics (MIRO) and FONDECYT Grant No. 1191205. Special thanks to all my collaborators in flat bands research, with an important emphasis in my master students L. Morales-Inostroza, C. Cantillano, B. Real, G. Cáceres and I. Salinas. I would like to also thank to Alexander Szameit and Robert Thomson groups which fabricated high quality samples for our experimental research and development.

Disclosure statement

No potential conflict of interest was reported by the author.

Additional information

Funding

This work was supported by the Fondo Nacional de Desarrollo Científico y Tecnológico Grant No 1191205 and Programa ICM Millennium Institute for Research in Optics (MIRO).