Assessing membrane material properties from the response of giant unilamellar vesicles to electric fields

ABSTRACT

Knowledge of the material properties of membranes is crucial to understanding cell viability and physiology. A number of methods have been developed to probe membranes in vitro, utilizing the response of minimal biomimetic membrane models to an external perturbation. In this review, we focus on techniques employing giant unilamellar vesicles (GUVs), model membrane systems, often referred to as minimal artificial cells because of the potential they offer to mimick certain cellular features. When exposed to electric fields, GUV deformation, dynamic response and poration can be used to deduce properties such as bending rigidity, pore edge tension, membrane capacitance, surface shear viscosity, excess area and membrane stability. We present a succinct overview of these techniques, which require only simple instrumentation, available in many labs, as well as reasonably facile experimental implementation and analysis.

GRAPHIAL abstract

KEYWORDS:

• Membrane electroporation
• vesicle electrodeformation
• pore edge tension
• bending rigidity
• membrane capacitance
• membrane surface shear viscosity

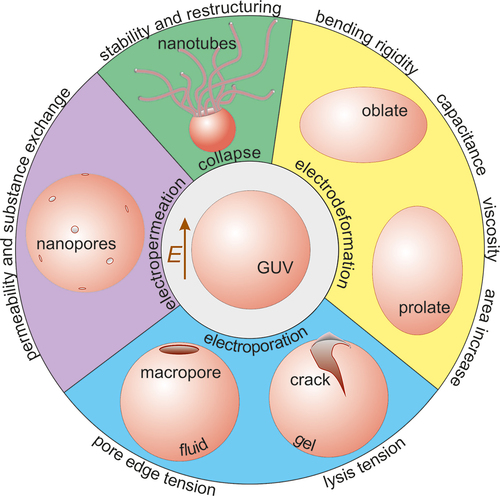
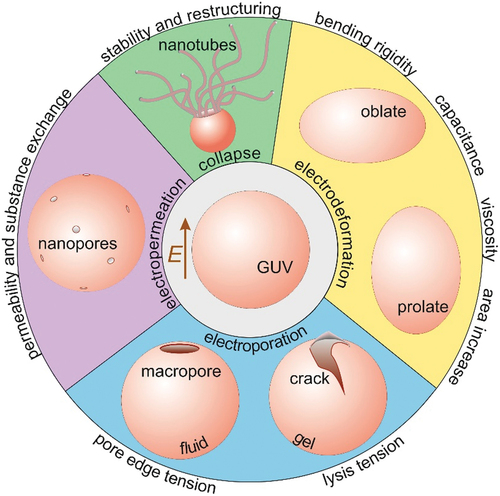
1 Introduction

Biological membranes are essential for the maintenance of cellular homeostasis and changes in their physiology have been associated with several pathological conditions [1]. The plasma membrane is relatively flexible and can adopt complex (and highly curved) morphologies during key cellular processes such as endocytosis [2] and exocytosis [3], cell migration [4], cytokinesis [5], trafficking [6] and signaling [7] pathways. The membrane mechanics, rheology and stability are the determinants of the cell response to external perturbations. Understanding this response is justified by the ever increasing quest for techniques in biomedical engineering and treatment. The response of cells to electric fields has received significant attention as means for the development of novel therapeutic strategies. For example, electrofusion has been used for the production of monoclonal antibody and cancer vaccines [8] and it has been reported as a promising approach towards treatment of diabetes [9]. Other examples include electroporation in tumor ablation [10], electrochemotherapy [11,12], exogenous cell engraftment [13], gene and drug delivery [14], cell transfection [15] and inactivation of microorganisms [16]. However, because of the high complexity of cells, the complete bioelectrochemical mechanisms and functions of individual cell components such as the plasma membrane during these electromicromanipulation methods remain poorly understood.

Giant unilamellar vesicles (GUVs) as cell-sized, simple biomembranes are one of the most convenient cell-mimetic models for membrane characterization [17–21]. Mechanical, rheological and electrical properties such as bending rigidity, stretching elasticity, lysis tension, edge tension, viscosity and capacitance, can be directly assessed from microscopy observations of GUVs [18]. Deformation and poration of vesicles exposed to electric fields have contributed substantially to increasing our understanding of electric-field-based applications on cells as well as for resolving membrane physical characteristics [22–25]. This review focuses on recent developments in the characterization of these membrane properties (considering the short size of the review, the references will be far from exhaustive). Typical values of various material properties of lipid membranes (in fluid and gel phases) deduced from such studies are given in Table 1. In the following sections, we shortly introduce fundamental membrane material properties and provide a summary of the available practical methods for assessing them. We also indicate advantages and limitations of these methods. Finally, we discuss the application of electric fields to assess membrane area stored in fluctuations and address one last membrane property that is unique for the application of electric fields, namely increased membrane permeation, i.e. electropermeability.

Table 1. Typical membrane material properties of lipid membranes in the fluid and gel phases deduced from manipulation of GUVs. Example techniques used to assess these properties are indicated with emphasis on approaches employing electric fields. For more references with data on specific properties, see respective sections.

Property (symbol)	Example methods of assessment	Typical values and trends
Bending rigidity	Electrodeformation [23,40,141], Fluctuation analysis [40,141], Micropipette aspiration [26], Tube pulling [27,28,102], Optical dynamometry [29] (for review on techniques, see [44])	Liquid disordered phase: 10–20 kBT [27,75]; Liquid ordered phase: 80–200 kBT [27,75]; Gel phase: ∼350 kBT [29]; Dramatic decrease close to the main phase transition temperature [29,30]; Variations with chain length and saturation of lipid bilayers [26,75]
Stretching elasticity (Ka)^a	Micropipette aspiration [26]	Fluid phase: ∼200 mN/m [31,32]; Gel phase: ∼300 mN/m [31,32]
Lysis tension (σlys)	Micropipette aspiration [33,97], Electroporation – critical transmembrane potential [33,59,98]	Fluid phase: 5–10 mN/m [33,59,97]; Gel phase: ≥ 15 mN/m [97]
Edge tension ()	Electroporation – pore closure dynamics [59,61]	Liquid disordered phase: 10–50 pN [34,59,61]; Liquid ordered phase: ∼150 pN [34]; Decrease with increasing lipid charge and unsaturation [60]
Surface shear viscosity, (ηs)	Electrodeformation [35,36,75], Domain rheology [76–79], Falling-ball viscosimetry [29,37,38] (for review on techniques, see [75])	Liquid disordered: ∼10^−9 N.s/m [35,75]; Liquid ordered: ∼10^−8 N.s/m [35,75]; Critical behavior near the fluid-to-gel transition [29]
Critical transmembrane potential (Vm)	Electroporation – detection of pores [59,107]	Fluid phase: ∼1 V [59]; Gel phase: ∼10 V [107]
Membrane capacitance (Cm)	Electrodeformation under AC field (frequency sweep) [35,39,45,72–74], Fast Fourier transform electrochemical impedance spectroscopy [74], Electroporation [39], Patch clamp [68]	∼1 μF/cm^2 [35,72,73]

^aCurrently, there is no systematic approach for measuring the stretching elasticity of membranes using electric fields, but we include this property for completeness.

2 Membrane bending rigidity

The membrane bending rigidity () defines the energy needed to change membrane curvature. It can be assessed using diverse approaches based on microscopy observation of GUVs such as fluctuation spectroscopy (see e.g [40–43].) and response to external stimuli (for a review see [44]). The latter approach includes employing electric fields, e.g. alternating current (AC) or direct current (DC) electric square pulses applied to a quasi-spherical vesicle to create a mechanical force. This force gently pulls area stored in suboptical membrane undulations and deforms the GUVs into ellipsoids. Shape deformation and relaxation of vesicles can then be analyzed to extract membrane bending rigidity.

2.1 Bending rigidity from vesicle electrodeformation

Vesicle electrodeformation to assess membrane bending rigidity is an experimentally less-demanding method compared to approaches, which rely on complex setups, for example, micropipettes (requiring very precise measurement of the differential pressure in the region of small membrane tensions) or optical tweezers (see overview in [44]). In this approach, GUVs are exposed to an uniform AC field. This generates electrical stresses in the membrane suppressing thermal undulations and deforming a quasi-spherical vesicle into ellipsoid shapes [45–48], see Figure 1a. In the experiments, the field frequency generally ranges between 1 and 300 kHz and the field amplitude is increased stepwise typically by 0.4–1 kV/m when the suspending medium contains 1 mM NaCl (note that for low conductivity solutions low frequency can cause poration [49], which should be avoided). The electric stress induced on the membrane is known to depend quadratically on the amplitude of the applied electric field [46,50]. The flattening of the membrane fluctuations triggers an increase in the apparent area of the vesicle [40,45,46,51]:

Figure 1. Membrane bending rigidity obtained from different types of vesicle electromanipulation. (a) Electrodeformation of giant vesicles subjected to an AC field. Upper panel: Phase contrast images of a GUV at 300 kHz and field amplitudes of 2, 10 and 20 kV/m (left to right). The scale bar corresponds to 25 µm. Reproduced from [40]. Lower panel: Change in the area of a GUV as a function of increasing electric field strength (the field strength is in V/m, and the curvatures in 1/m). From the slope of the data (solid line), one obtains the bending rigidity following Eq. (1)(1) . Adapted from supplementary material of [51]. (b) Relaxation of GUVs exposed to a DC pulse. Upper panel: The shape factor is shown in real time for 8 different vesicles denoted by different colors; time zero corresponds to the end of the DC pulse. The insert shows a sketch of a GUV deformed into a prolate ellipsoid and the two vesicle semi axes and (the field direction is along ). Lower panel: Time normalization (by see text and [58] for notations) and translation by a constant leads to collapse of the data form all 8 vesicles. The solid curve is the theoretical prediction in [58]. The bending rigidity is calculated from the intial part of the relaxation curve, also referred to as ‘entropic’ regime. Reprinted with permission from [58] Copyright (2015) by the American Physical Society.

(1)

where is the projected surface area of the vesicle, is the initial vesicle area, is the Boltzmann constant, is the temperature, is the electric field and the curvatures at the equator () and pole () of the vesicle are , , , and are the vesicle semi-axes along and perpendicular to the field direction (see sketch in Figure 1b); refers to a constant frequency-dependent factor. Thus, the membrane bending rigidity can be obtained from the slope of the plot of the logarithmic term as a function of the area change , see Figure 1b. The theory for vesicle electrodeformation has been developed in [52–55].

Among others, the method has been employed to quantify the effect of cholesterol on the bending rigidity of membranes prepared from binary mixtures of cholesterol with dioleoylphosphatidylcholine (DOPC) or with sphingomyelin [40]. The effect was found specific to lipid structure: the bending rigidity of DOPC-based membranes was not altered by cholesterol while sphingomyelin-based ones become softer with increasing cholesterol fraction [40]. The bending rigidity of phase-heterogeneous membranes such as GM1-doped ones, exhibiting gel-like domains in fluid environment, have also been explored through fluctuation analysis, vesicle electrodeformation and micropipette aspiration [51]. Both fluctuation spectroscopy and vesicle electrodeformation experience the signature of the gel-like domains while the micropipette aspiration technique only allowed exploring the rigidity of the fluid phase. Recently, we utilized the electrodeformation method to measure the bending rigidity of asymmetric vesicles exhibiting tubes. This system is difficult to characterize using conventional methods such as flickering spectroscopy due to lack of excess area for fluctuations. These asymmetric membranes were found to be stiffer than symmetric ones [45].

GUV electrodeformation is a very practical and easy to implement method for measuring the membrane bending rigidity. Compared to the micropipette aspiration technique, it can access more easily and probe more extensively the low tension regime, because tension changes can be applied and regulated more finely with the electric field. However, the electrodeformation approach also has some limitations. It cannot be applied for analysis of membranes containing charged lipids (such as phosphatidylserine or phosphatidylglycerol) or vesicles prepared in solutions of high salt concentrations (where the field is screened). Accumulation of excess charges and absorbance of ions on the membrane surface resulting in transmembrane asymmetry and spontaneous curvature effects [56,57], could be enhanced at the vesicle poles upon electric field application, which may interfere in the analysis.

2.2 Bending rigidity from vesicle relaxation dynamics after the application of DC pulses

Bending rigidity can also be deduced from the relaxation dynamics of giant vesicles after application of square DC pulses [58]. In this approach, a spherical vesicle is exposed to a strong DC field of 100–160 kV/m amplitude and duration of 50–100 µs, which causes the vesicle to deform into an ellipsoid. After switching off the electric field, the ellipsoidal vesicle relaxes back to a sphere. The ellipticity of a vesicle is defined by the shape factor . The relaxation process is governed by the membrane bending rigidity , and the medium viscosity , and depends on the initial tension and the radius of the particular vesicle. At large deformation (high ), the relaxation is entropy driven followed by a regime of constant tension at lower values of the shape factor . Yu et al. [58] demonstrated that upon normalizing the time by , the relaxation follows a unique solution. The values of both (to calculate ) and can be obtained by minimizing the error between data sets from different vesicles and the theoretical solution. The time normalization coupled with translation allows collapsing the data from different vesicles (with different radii and initial tensions) into a master curve, see Figure 1b, lower panel. The theoretical predictions were validated with experimental results from the relaxation dynamics of cholesterol-doped vesicles. The model is applicable only for membranes with moderate surface shear viscosity.

3 Edge tension from pore dynamics

Upon pore formation, the edge tension is the energetic cost per unit length of the pore rim to reorient the amphiphilic lipid molecules and shield the hydrophobic bilayer core from water. The edge tension can be determined from monitoring the closing of micron-sized pores (macropores) induced by the application of strong DC pulses on GUVs [59–61].

The theoretical model describing pore dynamics in giant vesicle was introduced by Brochard-Wyart et al. [62,63], who considered the interplay of pore opening and leak-out of internal solution caused by the Laplace pressure. The pore evolution was found to consist of four successive stages [62–64]: (i) fast growth, in which the pore nucleates and then opens exponentially, (ii) the pore reaches its maximum radius followed by (iii) a quasi-static leak-out, in which the internal solution of the vesicle slowly leaks through the pore, and finally (iv) fast closure, during which the size of the pore becomes very small while the pore closes at a constant velocity. Within these four stages, the quasi-static leak-out (stage three) covers the majority of the pore lifetime. The theoretical model describing the third leak-out stage sets the basis of a fast and easily applicable experimental method for deducing the membranes edge tension [59], see Figure 2a,b. In this method, a strong DC pulse, either millisecond long (20–80 kV/m for 5 ms) or shorter (300 kV/m for 150 μs), can be applied to induce micron-sized pores in GUVs. These macropores are then monitored under a phase contrast microscope using fast camera imaging and pore sizes are determined. According to the hydrodynamic model, in the third leak-out regime, the porated region described by the quantity shows a linear decrease as a function of time [62]:

Figure 2. Pore edge tension analysis. (a) Response of a POPC GUV exposed to a DC pulse (3 kV/cm, 150 μs). Macropores are first visualized in the third frame. The field direction is illustrated with a white arrow. The scale bar is 10 µm. Reproduced from [59]. (b) Characterization of the porated region time dependence of another vesicle shown in the insert (phase contrast image and binarized image of the right vesicle half). The red open circles show experimental data. The solid line is a linear fit and the edge tension is deduced from its slope following the dependence in Eq. (2)(2) . Adapted from Biophys. J., 99, T. Portet and R. Dimova,A new method for measuring edge tensions and stability of lipid bilayers: effect of membrane composition, pp. 3264–3273, Copyright (2010), with permission from Elsevier. (c) Main window of the pore edge tension analysis software PoET illustrating the experimental setting and a processed video in the left panel with detected pore rim and indicated pore diameter. Reproduced from [61].

(2)

Here is the GUV radius, is the current pore radius, is time, is viscosity of the solution and is the edge tension. Thus, the edge tension can be deduced from the slope of the time dependence of , Figure 2b. The relatively fast process of pore closure (in the range of a few hundred milliseconds) requires fast digital imaging (e.g. at 1000 frames per second) to resolve the pore for edge tension analysis. This yields hundreds of images for analysis. Leomil et al. [61] designed a user-friendly, free and open-source software (PoET) in Python for completely automated image processing for edge tension analysis, see Figure 2c. The method was applied to investigate the role of cholesterol and charged lipids on pore stability as well as medium conditions such as the presence of ions, GM1 or detergents affecting the edge tension [59–66].

This experimental approach cannot be applied to deflated or tubulated vesicles, and in principle to vesicles, which deform excessively. Pore closure should not be obstructed and the method is not applicable to multilamellar vesicles either.

The edge tension can also be roughly estimated from the macropore lifetime and size provided that knowledge of the membrane viscosity is available [67]. In this approach, the pore lifetime is described to depend on the pore size as where is the membrane viscosity, and is the maximal pore radius. The edge tension can be then obtained from the slope of pore radius versus pore lifetime plot [62,67].

4 Membrane capacitance

Lipid bilayers are impermeable to ions. Application of an electric field leads to accumulation of charges near the membrane surfaces. Thus, the membranes act as a capacitor shielding the cell content from an external electric field. However, charging of the bilayer occurs in a finite time interval and during this period, the cell interior is exposed to the field. This can destabilize the structural integrity and lead to cell death. Hence, accurate knowledge of the charging time, which depends on the membrane capacitance, is desirable. Various methods exist to measure membrane capacitance, for example patch-clamp and dielectrophoresis [68–71]. However, complex analysis and low throughput have limited the application of such methods. A simpler GUV-based method was introduced in [72]. If the solution conductivity inside the vesicle is less than that outside, the GUV experiences a prolate to oblate shape transition under AC electric field as the frequency is increased [47,48,52]. The critical frequency, , of this transition can be used to extract the membrane capacitance [47,72]

(3)

where is the size of the vesicle, is the ratio between solution conductivity inside to outside. The critical frequency, , can be determined from performing a frequency sweep, as shown in Figure 3a, and with all other parameters set experimentally, the membrane capacitance, , can be determined from Eq. (3)(3) non-invasively. Using this approach, it was found that increasing the sugar concentration in solutions increases the bilayer capacitance [73,74]. Faizi et al. [45] developed the method further by showing that the same data in Figure 3a can be used to simultaneously determine membrane capacitance and bending rigidity in one step. Like the classical Kummrow-Helfrich electrodeformation method [46], instead of plotting the area strain as a function of electric field strength at a fixed frequency like in Figure 2b or also Figure 1a (lower panel), the plot of area strain with frequency dependent prolate shape at a fixed field strength can also be utilized to yield the bending rigidity, as given in Figure 3c. Both approaches yield the same bending rigidity but the frequency-dependent analysis yields capacitance and bending rigidity simultaneously. The method has higher accuracy for thicker membranes. At low frequencies, electrokinetic flows may arise causing vesicle motion, and thus hindering the experiments.

Figure 3. Electrodeformation of GUVs to measure membrane capacitance. (a) Frequency-dependent deformation of a POPC vesicle exposed to a uniform AC electric field at kV/m. The critical frequency is used to determine the membrane capacitance from Eq. (3)(3) . (b) Area strain dependence on the applied electric field strength for the same vesicle in (A) at a fixed frequency 0.2 kHz. The size of the vesicle is 26 m and the conductivity ratio is . The electric field amplitude is changed from 2 to 10 kV/m in steps of 0.25 kV/m. The obtained bending rigidity is 12.67 . (c) Area strain dependence on the applied field frequency at a fixed field strength 6 kV/m. The expression of the electric stress can be found in [45]. The data is fitted in the prolate regime, , from panel (A). The obtained bending rigidity is 14.97 . Reproduced from [45] by permission of John Wiley and Sons.

5 Surface shear viscosity

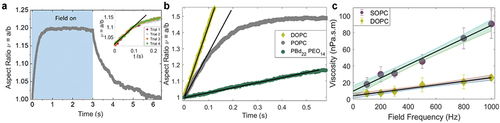
Self-assembled lipids in bilayer membranes are held together by non-covalent bonds. As a result, a bilayer behaves as a two-dimensional viscous fluid to in-plane deformation. Viscosity is a key property of cell membranes that influences transport of biomolecules and membrane remodeling. Experimentally measuring the membrane viscosity using GUVs has remained challenging due to complex experimental designs and models with complicated analysis, e.g. see for review [75]. The implementation of some methods is limited to few specific membrane compositions; for example domain-based methods are limited to phase separated membranes and diffusion-based methods are probe dependent [76–79]. Recently, Faizi et al. [75] demonstrated that membrane viscosity can be obtained from transient deformation of GUVs in electric fields. The method is non-invasive, high throughput, probe independent and able to measure membrane viscosity of a wide range of compositions and phase state. Briefly, upon application of a uniform electric field, a quasi-spherical vesicle at conductivity condition deforms into a prolate ellipsoid, Figure 4a. The method analyzes the initial deformation rate of the vesicle aspect ratio, , as the AC electric field is turned on at a particular frequency , see Figure 4b. The slope depends on the membrane viscosity:

Figure 4. Electrodeformation of GUVs as a method to measure membrane viscosity. (a) A uniform AC electric field deforms a GUV into a prolate ellipsoid as shown by the evolution of the aspect ratio Here, time zero refers to turning on the field. The inset shows that repeated deformation of the same GUV does not alter the membrane structure. (b) Vesicles made of different composition (DOPC, POPC, and diblock-copolymer) deform at a different rate revealing different shear viscosities; the field strength and frequency are 8 kV/m and 1 kHz. (c) Viscosity measured at different frequencies at a fixed field strength. Extrapolation to the vertical intercept yields the zero-frequency shear viscosity corresponding to the viscosity in the absence of field. Reprinted from Biophys. J. 121, H.A. Faizi, R. Dimova, P.M. Vlahovska, A vesicle microrheometer for high-throughput viscosity measurements of lipid and polymer membranes, pp. 910–918 Copyright (2022), with permission from Elsevier.

(4)

where is the characteristic rate-of-strain imposed by the electric field with being the permittivity of the solution, and is the dimensionless surface viscosity, and are the viscosities of the membrane and the bulk solution; the expression of the electric stress can be found in [75]. The apparent viscosities are measured at different frequencies in the range 0.1–1 kHz. Linear extrapolation yields the zero-frequency viscosity, which corresponds to the viscosity in the absence of electric field (Figure 4c). The data provided new insights into the relation between membrane viscosity, composition, and structure [75]. The only current limitation of the method is that it is not yet developed to probe charged membranes.

6 Assessing membrane area stored in fluctuations

Vesicle shapes are defined by the membrane spontaneous curvature and the ratio of the vesicle area and volume [80,81]. Chemical and physical triggers such as temperature [80], osmotic deflation/inflation [82], light [83,84], incorporation of amphiphilic molecules [85,86] and fusion [87] can change the membrane surface area, see examples in Figure 5. When excess membrane area is stored in fluctuations or protrusions in the form of buds or tubes, manipulation techniques are needed to quantify the area changes. The two common methods to resolve the excess area stored in thermal fluctuations are micropipette aspiration and AC-field electrodeformation of GUVs, the latter being easier in terms of experimental implementation, as discussed in detail below. Furthermore, the application of a weak DC field to a vesicle resting on an electrode (for example, indium tin oxide coated glass) can be used to pull out fluctuations. The vesicle overall shape and contact curvature detected with confocal microscopy (see Fig. 5a,b) can be used to assess the adhesion energy and membrane tension [88].

Figure 5. Vesicle electrodeformation and assessment of hidden area stored in membrane fluctuations. (a,b) Modulating vesicle adhesion by DC field. Confocal vertical cross sections of a non-adhering (a) and adhered (b) GUV (green). The scale bar represents 20 µm. Upon switching on the field, the vesicle adheres to the electrode (red) viewed in reflection. White arrows point to the contact curvature (left arrows) and membrane undulations (right). Undulations get suppressed after applying the DC field (1 V) in panel (b). (a,b) Reprinted from Biophys. J. 111, J. Steinkühler, J. Agudo-Canalejo, R. Lipowsky and R. Dimova, Modulating vesicle adhesion by electric fields, pp. 1454–1464, Copyright (2016), with permission from Elsevier [88]. (c) Area increase and budding of a vesicle caused by photo-isomerization of an azo-benzene derivative (F-azo) incorporating in the membrane upon UV-light irradiation (purple region in graph). The area increase is assessed from simultaneous application of an AC field (10 kV/m, 1 MHz). Phase contrast images and degree of deformation plots over time are shown for 0.25 mM F-azo. The time stamps are indicated on the images upper left corners; 0 corresponds to turning the field on. The UV irradiation (violet region in the plot) starts after 7.1 s (image 2A). The scale bar is 10 μm. Reproduced from [83]. (d-f) GUV area increase caused by insertion of Triton TX-100 just before membrane solubilization. Phase contrast sequences of POPC (d) and POPC/cholesterol (e) GUVs under an AC field (20 kV/m, 200 kHz) after addition of an aliquot of a concentrated Triton X-100 solution (80 mM). Scale bars are 10 μm. (f) Relative area increase (ΔA/A₀) measured from the maximum aspect ratio using Eq. (5)(5) displayed by the vesicle before contrast loss and membrane solubilization. Each data point represents one GUV. Mean values with standard deviation are shown in green. (d-f) Adapted with permission from Langmuir, 31, 378–386, B. Mattei, A.D.C. França, K.A. Riske,Solubilization of Binary Lipid Mixtures by the Detergent Triton X-100: The Role of Cholesterol. Copyright 2015 American Chemical Society.

For freely suspended GUVs, whose internal solution has higher conductivity than the external one, moderate AC fields pull out the excess membrane area stored in thermal fluctuations by deforming the vesicles into prolate ellipsoids [48]. The vesicle surface area, can be then calculated from measuring the vesicle semi-axes:

(5)

This approach was used to quantify the area increase from fusion of small cationic liposomes to anionic GUVs and quantify the efficiency of a newly developed method for protein-free fusion [87]. Light-induced shape changes and membrane mechanics of GUVs was evaluated via electrodeformation under photodamage in the presence of lipids with a porphyrin group [89], methylene blue [85] and azobenzene-containing photoswitchable molecules [83,84,90] (Figure 5c), establishing a platform for reversible light-induced modulation of membrane shape and mechanics. Electrodeformation of GUVs allowed also the quantitatively montior the dynamics of incorporation of the detergent Triton X-100 into membranes of different compositions [86], see Figure 5d-f.

There are some requirements for applying GUV electrodeformation to assess membrane area changes. The membrane should not be in the gel phase or permeable to ions, otherwise the vesicle will not deform under electric field. When GUVs undergo large deformations, they may attain non-elliptical shapes and form buds and tubes at the poles (as in Fig. 5c, image 4a). In such cases, the area increase cannot be calculated by the expression for an ellipsoid Eq. (5)(5) .

7 Membrane electropermeabilization and stability

Lipid membranes are permeable to water but practically impermeable to ions, hydrophilic molecules and nanoparticles (permeability to water can be directly measured on GUVs, see e.g [91]). Electric fields are used to enhance membrane permeability to these species, by opening pores in the membrane (as demonstrated above for micron-sized pores). Membrane stability during electroporation is of crucial importance for the optimization of applications in medicine [92,93] and food processing [16]. Loss of membrane integrity can be associated with formation of a pore, which can continue to expand until the vesicle collapses, i.e. vesicle bursting [60,94]. The vesicle response could also consist of developing long-lived submicroscopic pores while restoring the spherical vesicle shape [95,96]. These pores allow the transport of molecules that would otherwise not cross the membrane, i.e. electropermeabilization. Poration occurs above a critical tension called lysis tension (see example values in Table 1). It is typically assessed by micropipette aspiration of vesicles [97]. Vesicle electroporation can also serve to estimate the lysis tension [59,98].

7.1 Membrane instability and vesicle bursting in electric fields

Membrane stability in electric fields is sensitive to composition, especially presence of charged lipids, and phase state. Lira et al. [60] studied the influence of medium and lipid charge on the stability of multicomponent GUVs in more detail. Upon exposure to shorter DC pulses (300 kV/m, 150 µs), negatively charged GUVs exhibited complete or partial bursting, or gradual permeation through submicroscopic pores, see Figure 6a-c. Both partially and completely bursting vesicles revealed internal and external tubes. The latter are a signature of membrane asymmetry (and substantial spontaneous curvature [99]) which could result from the asymmetric distribution of charged lipids in the membrane [57].

Figure 6. Evaluation of membrane stability through electroporation and electropermeabilization. Examples of bursting vesicles observed under phase contrast (a) and epifluorescence (b) microscopy. (c) Phase-contrast images of an electropermeabilized vesicle showing macropore closure but loss of optical contrast over time because of remaining submicroscopic pores. The GUVs were subjected to a DC pulse (300 kV/m, 150 μs). The field direction is indicated with an arrow. The scale bars are 10 µm. The time relative to the beginning of the pulse is shown on each snapshot. (a,b and c) are reproduced from [60]. (d) Differential interference contrast (a, d) and confocal (b, c, e, f) images of vesicles forming cracks and wrinkles (folds) after exposure to a DC pulse (600 kV/m, 300 μs). The folds and cracks are indicated with arrows. The electrode polarity is indicated with a plus and a minus sign in (a). Images are reproduced from [107].

Stability of pores strongly depends on the composition, molecular shape and chain saturation of the lipids in the membrane as well as the presence of salts and other solutes in the GUV internal and external solutions [59,60,100,101]. Incorporation of cone-shaped molecules such as phosphatidylinositol [101], GM1 ganglioside [66,102], detergent Tween20 [64] and α-hemolysin [103] are reported to increase the lifetime of macropores whereas inverted-cone shape molecules such as cholesterol [64] and phosphatidylethanolamine [101] reduce the electroporation threshold and result in shorter pore lifetimes. Studies with actin filaments [104,105] and agarose hydrogels [100,106] present in the membrane vicinity demonstrated that such polymer networks slow down the resealing process of macropores and result in more permeabilized GUVs.

Vesicle stability under the influence of electric pulses has been explored also for membranes in the gel phase. Because of the increased stiffness and toughness of these membranes (see Table 1), stronger field strength (roughly fivefold) is needed to deform such vesicles compared to those with membrane in the fluid state [107]. Furthermore, gel-phase vesicles undergo intra-pulse shape relaxation and exhibit wrinkles parallel to the field direction. Exposure to even stronger DC pulses, induces membrane cracks leading to irreversible rupture of the gel-phase vesicles, see Figure 6d, whereby requiring much higher transmembrane potentials for poration compared to fluid-phase vesicles [107], see also Table 1.

Perrier et al. [108] took the electroporation studies with gel-phase vesicles one step further by investigating GUVs exhibiting gel and fluid phase coexistence. Exposure of such vesicles with domain to porating electric pulses resulted in expelling fluid-phase lipids and associated decrease in vesicle size (this effect was observed earlier also for completely fluid vesicles exposed to repeated pulses [109]). Furthermore, the gel-phase domains were observed to buckle [108], consistently with the wrinkling detected in entirely gel-phase membranes [107], see Figure 6d.

The limitations of such observations is imposed by the resolution of detail that can be detected for the membrane restructuring. On the one hand, while observations under transmission microscopy (e.g. phase contrast or bright field) can reach unprecedented speed of 20,000 frames per second (fps), they are not able to resolve the resulting membrane structures. On the other hand, epifluorescence and confocal microscopy have improved resolution, especially in the porated area, which can restructure into lipid nanotubes, but these approaches are significantly slower with acquisition frequency of maximum around 300 fps and 30 fps, respectively. None of the currently available imaging approaches allows for live detection of nano-sized pores in the membrane.

7.2 Quantifying membrane electropermeabilization

Vesicle electropermeabilization reflects the long-term stability and the dynamic structural changes in the membrane after exposure to DC pulses. When membrane components are reorganized or chemically modified by the electric field, submicroscopic defects can develop, affecting the structural integrity of the lipid bilayer and leading to increased membrane permeabilization [95,110]. Recent studies demonstrated that electric-field induced chemical modifications are particularly triggered in unsaturated lipids due to peroxidation [111–113]. Strong electric fields can generate reactive oxygen species in the vesicle media, which can initiate multistep oxidative damage mechanisms on unsaturated lipids thus prompting the phospholipids to undergo primary or secondary oxidation. These changes enable the influx and efflux of ions, small molecules or even macromolecules such as nucleic acids [114]. In the absence of chemical changes, transport of molecules in electropermeabilized membranes is not completely diffusive [115–117]; electrostatic interactions of the transported molecules with the membrane and pore interface play a significant role in the kinetics of electropermeabilization. In order to assess electropermeabilization dynamics of GUVs, a number of imaging and characterization techniques including phase contrast, epifluorescence and confocal microscopy, amperometry, patch clamp, electrochemiluminescence and coherent anti-Stokes Raman scattering (CARS) microscopy have been applied previously [60,66,68,100,118–121].

One of the least demanding methods to visualize membrane permeability in GUVs is to generate a sugar asymmetry between the interior and exterior solutions by dispersing GUVs grown in sucrose solution into iso-osmolar glucose solution and monitor the associated contrast [122–124]. The refractive index difference between the two media results in the generation of a sharp vesicle contour under phase contrast microscopy, see first image in Figure 6c. Upon the formation of electric-field induced submicroscopic pores, the sharp optical contrast decreases in time due to the passage of sugar molecules across the membrane. This membrane leakage can be characterized through analysis of the intensity profile of a line crossing the vesicle [60,100,121,125]. Similarly to sugars, various aqueous fluorescent dyes and/or labeled macromolecules such as dextran and nucleic acids can also be added in the external or internal GUV media for monitoring electropermeation dynamics under epifluorescence or confocal microscopy [100,104,126], see Figure 7a. For example, sulforhodamine B (SRB) was encapsulated in GUVs immobilized in agarose gel to monitor diffusion kinetics [100]. The fluorescence signal of SRB added to the external vesicle solution was used to investigate the electric-field response of GUVs encapsulating actin cortex mimetic [104]. Addition of calcein to the outer media of GUVs exposed to a train of ultrashort unipolar and bipolar nanosecond pulses allowed comparison to the response of cells through experimental and simulation data [127]. Leakage and long-term stability of GUVs doped with GM1 has also been characterized by adding calcein to the outer vesicle solution [66]. In addition to assessing long-term electropermeation kinetics of GUVs, labeled molecules of different sizes can be used to estimate the size of the nanopores in the electropermeabilized membrane [60].

Figure 7. Electropermeabilization monitored with different approaches. (a) GUV internalization of dyes introduced at different times (before pulse, t ≈ 0, and 5–10 min after macropore resealing) reveals three types of vesicle response (membrane in red): pores reseal (no permeation; first column), short-living pores reseal within 1–2 minutes (middle column) and long-living pores persist (last column). Calcein (green) is added prior to poration (time ≈ 0, upper row) and shows the immediate dye permeation occurring in the first 1–2 min after the pulse as well as long-term permeability in the presence of long-living pores (last column). Atto-647 (cyan, lower row) is added 5–10 min after electroporation and reports the presence of long-lived pores only (last column). Scale bars: 20 µm. Reproduced from [60]. (b) Electropermeabilization of a GUV imaged under CARS microscopy. Images N = 1, 10, 20 and 30 are part of a time series acquired with an interval between each image of 310 ms. White arrows indicate nanotubes shed from the GUVs upon electropermeabilization. The yellow arrow indicates the electric field direction. The scale bar is 10 µm. (b) Reprinted from Bioelectrochemistry, 87, C. Mauroy, T. Portet, M. Winterhalder, E. Bellard, M.-C. Blache, J. Teissié, A. Zumbusch, M.-P. Rols, Giant lipid vesicles under electric field pulses assessed by non invasive imaging, pp. 253–259, Copyright (2012), with permission from Elsevier.

Another important application of electropermeabilization of vesicles is that it allows exploring the electric-field-based delivery of genes [128] and nucleic acids [129]. Contradictions between proposed mechanisms of gene and nucleic acid electrotransfer in cells [96,130–132] have made it necessary to simplify the studies through less complex membrane models like GUVs. By staining DNA (fragments) and siRNA, it is possible to monitor their entry in GUVs from confocal images and fluorescence intensity analysis, characterizing the electrophoretic force for DNA translocation [110,133], efficiency or translocation and dependence on pore and DNA size [134,135].

Another effective way of monitoring passive transport of molecules is using patch clamp and amperometry [119]. Messina et al. [118] combined amperometry with the patch clamp technique to investigate the transport of redox-tagged molecules through GUV and cellular membranes, while monitoring patch quality and sealing via electrochemical impedance spectroscopy and measuring the coefficients of partition and diffusion of the redox-tagged molecules. Combining amperometry, epifluorescence imaging and electrochemiluminescence allowed the characterization of release from GUVs ruptured on electrodes via surface polarization [120]. Amperometry has a millisecond range temporal resolution to quantify the release dynamics of electroactive species, however it lacks spatial resolution [136,137]. This can be compensated by combining the method with electrochemiluminescence and epifluorescence imaging. Garten et al. [68] established a technique based on whole-GUV patch-clamping, which allowed investigating how membrane composition and tension modulate permeation through the ion channel gramicidin. The technique holds promises for electrophysiological studies of ion channels and transporters at physiologically relevant range of membrane tensions. Stability of the vesicles in patch-clamp techniques presents a challenge and needs optimization for the specific membrane composition.

Electropermeabilization and lipid loss in the membrane can also be detected through coherent anti-Stokes Raman scattering (CARS) microscopy [96]. This is a dye-free and non-invasive optical technique, in which the samples are monitored by the intrinsic vibrational resonances of the constituting molecules [138]. Mauroy et al. [121] used this technique to investigate the effect of pulse parameters on the membrane permeabilization in terms of lipid loss and shape deformations, see Figure 7b. CARS signals can be collected via a suitably adapted confocal microscope. For lipid bilayers, CH-stretching vibrations are recorded to generate optical contrast [139]. The technique is beneficial in preventing imaging artefacts stemming from the use of fluorescence dyes and enables the visualization of pure lipid bilayers in the absence of any exogenous molecules. However, imaging multicomponent vesicles is very difficult because of overlap of the multiple vibrational bands [138].

8 Outlook

Giant vesicles under the influence of electrical field provide a complete toolbox to probe the membrane elastic, electrical and rheological properties as summarized in Figure 8. Most of the reviewed methods have been utilized for simple or multi-component bilayers as well as polymer membranes. Climbing up the ladder of bottom-up synthetic biology approaches, the next step would be to probe membranes with increasing complexity. Examples include membranes with several components, including membranes with reconstituted proteins, and cell-derived plasma membranes (blebs) as their compositional and structural complexity closely represents the lipidomics and proteomics of plasma membrane. The electrodeformation methods can be utilized to explore other synthetic systems such as polymersomes, protein condensates and shells, hybrid polymer-lipid vesicles, asymmetric membranes or dendrimersomes with scarcely assessed material properties. Increasing the system complexity will require expanding the theoretical description of some of the approaches to account for charges, both in the membrane and in the solution.

Figure 8. An overview of the spectrum of techniques for assessing membrane material properties and characteristics from exposing giant GUVs to elelctric fields as reviewed in this work: bending rigidity, capacitance, membrane surface shear viscosity, area stored in fluctuations, lysis tension, pore edge tension, permeability and stability after poration.

Despite significant progress in our understanding of the interaction of vesicles with electric fields, there are still open questions. Extreme vesicle shapes such as the transient sharp edges [140] in GUVs remains an unsolved mystery. The electromechanics of biomembranes undergoing phase transition and domain formation remains poorly understood [54,141]. While the effect of intrinsic lipid charges on membrane rigidity is well understood both theoretically and experimentally [142–144], the rheology of charged membranes is not explored. Membrane elastic properties such as rigidity, stretching modulus, tension and spontaneous curvature can all be modulated by the transmembrane potential across the membrane. The theoretical models are limited to planar membranes [145–146], and the experimental verification is lacking.

We close this review by reiterating that the described experimental approaches for characterizing the membrane from monitoring the response of GUVs to electric fields are simple and high throughput. The experimental setup, requiring two electrodes and a standard signal generator, can be easily implemented in a moderately equipped lab. Simple squeezing, tearing, deforming and electrocuting giant vesicles offers facile access to unravelling material characteristics of membranes.

Acknowledgments

M.A. acknowledges support from the International Max Planck Research School (IMPRS) on Multiscale Bio-Systems. H.A.F., P.M.V. and R.D. acknowldege support by the National Science Foundation under grant NSF PHY-1748958. K.A.R. acknowledges financial support of FAPESP (2016/13368-4). P.M.V and H.A.F acknowledge financial support by NIGMS award 1R01GM140461.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Correction Statement

This article has been republished with minor changes. These changes do not impact the academic content of the article.

Additional information

Funding

This work was supported by the Max Planck Society [IMPRS on Multiscale Bio-Systems]; NSF [NSF PHY-1748958]; National Institute of General Medical Sciences [1R01GM140461]; Sao Paulo Research Foundation (FAPESP) [2016/13368-4].