Pore-scale viscous fingering as a mechanism for pattern formation – a historical overview, application, and the ways of controlling it

ABSTRACT

Viscous fingering instability, as one of the numerous fluid instabilities and mechanisms of pattern formation, is very common in different fields of research. First studied experimentally in an apparatus called a Hele-Shaw cell in 1898, it has been widely used, for example, as a model for porous media in laboratory testing. This paper provides a brief insight into the mathematical model of the Saffman–Taylor instability (pore scale viscous fingering) and the situations in which viscous fingering can be encountered. Since it is a morphogenetic instability, it is usually considered a nuisance and in recent decades many scientists and researchers have focused on the ways to avoid its occurrence. For instance, the petroleum industry has been continuously trying to discover the best solution for its control since viscous fingering limits oil recovery in porous media. The review provides a historical overview of the phenomena and various methods that have been used to control this instability. The final part of the paper gives a summary and the conclusions that have been drawn as the results of diverse studies.

KEYWORDS:

• Viscous fingering
• Hele-Shaw cell
• suppression
• Saffman-Taylor instability

1. Introduction

If we look more closely at the creations of nature that surround us, we can rarely see straight lines or regular geometric shapes that we studied throughout the entire period of our schooling. In contrast, a large number of irregular or nonlinear shapes, curves or patterns are present in almost every form in nature, such as plants, dunes [1], snowflakes, cracks, waves, foams, meanders, etc. Some of these can be modelled and solved mathematically, but science still does not have the answer to the essence of as nearly as many phenomena we encounter on a daily basis.

Since the 19th century, scientists have examined different pattern formation phenomena – the Belgian physicist Plateau researched soap films, thus describing the idea of a minimal surface [2]; the German biologist Haeckel coloured plenty of microscopic marine organisms in order to point out their symmetry [3]; the Scottish biologist D’Arcy Thompson was the first to analyse the form and growth of patterns in animals and plants [4,5]. Every single pattern is the result of physical processes – e.g. in biological systems and chemistry, one of the mechanisms for pattern formation is the reaction-diffusion model given by Turing [6]; in physics, the processes of solidification and precipitation can result in various patterns such as those in crystals of a dendritic form and snowflakes (self-similarity being the main characteristic of this pattern type).

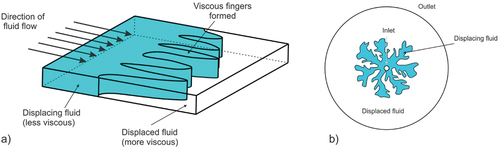
However, pattern formation is also very common in fluid mechanics and it represents a direct result of numerous fluid instabilities. Considering these factors, various examples can be named: the Kelvin–Helmholtz instability (such as in cloud formation) (Figure 1a), the Plateau-Rayleigh instability (widely used in ink jet technology) [13], coilings (viscous, gravitational, and inertial coiling) (Figure 1b) [13,14], the Rayleigh–Taylor instability (such as in mushroom clouds from volcanic eruptions and nuclear explosions (Figure 1c)) [13], printer’s instability (occurring during the coating processes when a thin layer of fluid uniformly covers a solid surface) [4], tears of wine or wine legs (the Marangoni effect) (Figure 1d), immiscible and miscible viscous fingering (Figure 1e,f) etc.

Figure 1. (a) The Kelvin-Helmholtz instability [7]; (b) from left to right, viscous, gravitational and inertial coiling respectively [8]; (c) the Rayleigh–Taylor instability [9]; (d) wine tears [10]; (e) and (f) immiscible [11] and miscible [12] viscous fingering, respectively.

Viscous fingering belongs to the group of interfacial instabilities, and has been widely studied since the 1950s. Even though the flow between two rigid plates was first mentioned at the end of the 19th century, great interest in this phenomenon started with the research of Sir Geoffrey Taylor.

1.1. Historical background

Once a viscous fluid is injected into a narrow gap between two parallel plates (i.e. a Hele-Shaw cell) previously filled with gas, the boundary between fluids will remain stable; in other words, the interface will be flat in a rectangular geometry, whereas in a radial geometry it will be circular. If the reverse experiment is conducted, i.e. a less viscous fluid (air or gas) is injected into a fluid of higher viscosity (glycerine or oil) occupying the space between plates, the interface becomes linearly unstable and develops rapidly into a large-amplitude fingerlike structure (Figure 2). Viscous fingering, also known as– the Saffman–Taylor instability (at a pore scale), is a phenomenon that occurs when a less viscous fluid displaces a more viscous fluid in a confined or shallow geometry [15,16]. Such boundary conditions commonly occur in porous media, for instance, during oil recovery. Actually, the interfacial instability described in the 1958 paper ‘The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid’ was named after the authors of the publication Philip Geoffrey Saffman and Sir Geoffrey Ingram Taylor [17]. The study was conceived by Sir G. I. Taylor in 1956 after he had paid a visit to the Humble Oil Company [17,18].

Figure 2. Viscous fingering in Hele-Shaw cell with a planar channel geometry (a) and radial geometry (b).

However, Saffman and Taylor were not the first to encounter this phenomenon. Morris Muskat, an American petroleum engineer, developed in 1937 the model based on the assumption that the displacement of oil by water was piston-like [19,20]. He refined Darcy’s law for single-phase flow and, with the help of his colleague Milan W. Meres, he generalised it so it could cover the multiphase flow of gas, oil, and water in the porous medium [20]. A few years later, Sidney E. Buckley and Miles C. Leverett developed the Buckley–Leverett equation, a conservation equation used to model two-phase flow in porous media that describes an immiscible displacement process [19,21]. The term ‘viscous fingering’ was used for the first time in 1951 referring immiscible oil/water fingering. A simple case of packed unconsolidated grains of nearly uniform size has been used to study the formations made by water displacing oil in porous media [22]. In 1952, Hill [23], reported the presence of viscous fingering on packed columns filled with charcoal, for vertical downward flows during sugar refining operations involving the displacement of sugar liquors with water. He conducted a series of experiments and found that the critical displacement velocity measured via flow visualization was in quantitative agreement with a simple one-dimensional stability analysis. This study is considered the first scientific investigation of viscous fingering [23,24]. The first mathematical expressions and theories for explaining viscous fingering were developed by Saffman, Taylor [17], and Chouke [25]. Using Hele–Shaw system, Chouke [25] studied the linear displacement of two immiscible fluids, and the one-dimensional model he proposed was validated against experimental data. The theoretical analysis developed by Saffman and Taylor [17] focused on the growth and development of a single finger, as well as the penetration of a liquid into a more viscous fluid, resulting in a mathematical expression of how viscous fingering grows in a one-dimensional space [19]. Almost two decades later, McLean and Saffman (1981) and Vanden Broeck (1983) solved the steady free-boundary problem numerically for finite capillary numbers and examined the limit of large capillary numbers. They found an infinite family of discrete solutions which tend toward the same shape with the ratio of the finger width to the characteristic macroscopic length equal to one-half as the capillary number approaches infinity [24,26,27]. The study of Bensimon et al. in 1986 provided a comprehensive review of viscous flows in two dimensions, including the stability of viscous fingering. It discussed the theoretical investigations on finger growth by linear and weakly nonlinear stability analysis [24,28]. Regarding viscous fingering in non-Newtonian fluids, considerable interest in this type of instability has appeared in mid-1980s [29–32].

When it comes to the studies of viscous fingering in porous media, Chouke, van Meurs, and van der Paul conducted early visualizations of viscous fingering in porous media using fluids with matched refractive indices in 1959. They used refractive index matched oil and beads to construct high permeability bead packs, and when water was injected into the oil, the resulting fingers could be clearly observed [24,25]. These experiments showed the processes of shielding, spreading, and splitting that determine fingering patterns [25]. A year later, in 1960, Habermann published experiments on viscous fingering in five-spot patterns, showing the development of long-wavelength fingers [24,33]. These patterns were later reproduced in lattice simulations by Sherwood in 1987 [24,34]. In 1963, Slobod and Thomas used X-ray absorption to visualize viscous fingering in porous media, comparing the results to Hele-Shaw cell experiments [24,35]. In 1985, a simple computer model of viscous fingering was presented along with experiments in etched-glass networks. The model demonstrated that a wide distribution of pore sizes leads to chaotic fingering with a fractal dimension, in a qualitative agreement with experiments [24,36]. A breakthrough article written by Homsy in 1987 represents the first comprehensive review of viscous fingering in porous media. He discussed both continuum and discrete approaches to modelling, noting the close similarity between the Hele-Shaw and porous media results in the limit of isotropic dispersion [24,37].

Nevertheless, it is of crucial importance to make a difference between viscous fingering in the Hele-Shaw cell and porous media. According to King and Dunayevsky [38,39] and Yortsos and Hickernell [38,40], there are actually two different types of the instability mechanisms in porous media: a short-wavelength instability (the Saffman–Taylor instability) addressing fingering at the pore scale [38,41–43], and a long-wavelength instability that is pertinent to fingering at the Darcy scale [39,40,44]. In both cases, the instability is caused by a contrast in mobility; however, capillary forces have different effect on the finger width or wavelength at pore-scale and Darcy scale. In the Hele-Shaw apparatus, capillarity related to the fingertip curvature is inversely proportional to its radius R, resulting in the concept that could be applied to the short-wavelength viscous fingering in porous media [38]. The curvature tends to prevent finger formation and it is of the equivalent order as the finger wavelength λ. The wavelength of viscous fingers is characterized by a most unstable wavelength which depends on the viscosity difference between two immiscible fluids and sets the characteristic width of the fingers [45]. However, when it comes to long wavelength viscous fingering in porous media, capillary forces act longitudinally along the interface, creating a capillary dispersion zone that reduces the mobility contrast at the shock front [38,40,44]. These capillary pressure gradients lead to a capillary-driven flow that mixes the fluids, thus counteracting the development of viscous fingering instability [38,40,46]. Therefore, in a Hele-Shaw cell, there is a clear separation between displacing and displaced fluid (upstream and downstream, respectively) due to the fixed composition and saturation of the fluids, while in porous media at Darcy scale, a Buckley-Leverett shock front appears with a saturation gradient upstream as a consequence of a fractional flow physics [38].

Finally, as saturation and its distribution are concepts that are typically non-uniform in Darcy scale porous media, the Saffman–Taylor formalism is unable to offer a trustworthy criterion for the commencement of viscous fingering. Contrary to previously mentioned researchers who discussed the criteria for the onset of the fingering [38–40,47], Skauge, and Sorbie [48–51] presented an alternative picture, arguing that the instability alters the relative permeability-saturation function.

When it comes to the suppression of viscous fingering in porous media and stability analysis of one-dimensional solutions, the studies begun in 1980s [47,52,53]. Yortsos et al. [24,40,54] have proposed a design of structured porous media that can either suppress or trigger the instability without modifying fluid properties or wettability. They utilized pore-scale direct numerical simulations, state-of-the-art experiments, and analysis to derive predictive tools for evaluating the effects of various parameters on controlling viscous fingering in porous media. The study conducted by Yortsos et al. suggests that a gradual and monotonic variation of pore sizes along the front path can suppress viscous fingering during immiscible displacement. This seemingly contradicts the conventional expectation of enhanced instability with pore size variability. The results provide insights into ways to suppress unwanted interfacial instabilities in porous media and offer design principles for engineered porous media such as chromatography columns, fabric, paper, and membranes with respect to their desired immiscible displacement behaviour [40,47,54].

To conclude, viscous fingering can be equated with Saffman–Taylor instability when it comes to short wavelength viscous fingering in porous media and to a related phenomenon studied in Hele-Shaw cells. On the other hand, viscous fingering at Darcy scale has significantly different features in terms of wavelength and scaling with interfacial tension, which is much more relevant for most application scenarios than the fingering at the pore scale. Unfortunately, researchers whose works are of great importance for complete understanding of viscous fingering in porous media (i.e. King and Dunayevsky, Yortsos, and Hickernel) are not recognized enough. However, the focus of this paper is on a pore scale viscous fingering and methods that enable its control and suppression.

1.2. Significance and application

At the beginning of a typical experiment carried out in a Hele-Shaw cell, a small gas bubble is initially placed in the centre of the system. The gas is then injected into the bubble at a constant flow rate, thus causing its expansion, and the interface between fluids turns into finger-like bulks, which are inherently unstable. As the fingers grow, their tips commence to split into two or more new fingers, and these tip-splitting events repeat, resulting in the patterns of fractal form (i.e. the fractal form is more common for a smaller gap width h) [55] (Figure 2b). On the other hand, the interface at the finger roots remains relatively stable. The answer to finger formation (as well as to electrochemical deposition and growth of bacterial colonies) lies in the growth in the Laplacian field. Since the difference in fluid viscosities is pretty large, a strong pressure gradient is generated in the fluid confined between the plates (the initially flat interface between fluids is now perturbed), while the pressure in displacing the fluid (bubble) remains basically the same (if the injected fluid, e.g. air, has negligible viscosity and density) [4,56,57]. Moreover, for the finger width, capillary, and viscous forces are of the greatest importance – capillary forces are likely to widen it, while viscous forces tend to tighten it [4,24,58].

This hydrodynamic instability can be observed in both immiscible and miscible fluids (Figure 1e,f). However, viscous fingering in immiscible fluids has been investigated more than in the miscible ones. One of the primary distinctions between those is that the immiscible finger is of a greater width than the equivalent miscible finger due to the interfacial tension. According to recent research, effective interfacial tension can exist even in miscible viscous fingering when a gradient in the concentration of chemical species at the interface is present [59]. Nonetheless, it is unknown what physicochemical process triggers the tip-splitting events and controls the flow state’s transition point. By computing the momentum transport and entropy production, the latest study examined the interfacial instability transition in miscible displacement from a thermodynamic point of view [60]. When it comes to non-Newtonian fluids, it was found that shear-thinning can significantly affect finger width – fingers become narrower for stronger shear-thinning [30]. Furthermore, numerous experiments were conducted with ferrofluids confined within the Hele-Shaw cell too. As liquids, ferrofluids respond to magnetic fields paramagnetically. As colloidal suspensions of microscopic permanent magnets, ferrofluids flow when magnetic forces are applied [61,62]. First, it was considered in a rectangular flow geometry, it was deduced that the asymmetry at the fluid interface was driven solely by viscosity contrast. Moreover, tip – splitting events, which do not occur in the rectangular geometry for ordinary fluids, are generated by magnetic repulsion within the ferrofluid [63,64].

Viscous fingering, as one of the mechanisms for pattern formation, belongs to the group of free-boundary problems [24] and, surprisingly, it is present in many processes. It has been researched for both scientific and industrial purposes. For instance, the process during which an external fluid (gas or water) is injected into the reservoirs through injection wells placed in rock and connected with production wells, is called secondary oil recovery. The aim of secondary recovery is to preserve the pressure in reservoirs and displace hydrocarbons to the wellbore, and it is used when the pressure inside the well drops to the level that makes primary recovery no longer viable. The most frequent techniques are water flooding (when water is injected to displace residual oil) and gas injection. The tertiary or enhanced oil recovery (EOR) uses more efficient techniques that modify the original properties of oil. Its function is to increase the pressure and permeability through three types of EOR processes (chemical flooding, miscible displacement, i.e. miscible viscous fingering and thermal recovery) [65]. During the secondary and tertiary oil recovery, the presence of viscous fingering lowers the efficiency of oil production. Recent studies have been based on the enhancement of oil recovery using different fluids to achieve it, i.e. nanoparticles, polymers, etc [66,67], and vertical vibrations, as the external periodic forcing [68]. There is a tendency to lower the mobility ratio M (the ratio of the displacing and displaced fluid during the EOR process) below one, because the displacement then becomes stable (Figure 3). Mobility ratio, which is the ratio of the viscosities of the displacing and displaced fluid, plays a crucial role in the growth of fingers as such. When M is greater than one, viscous fingers form, leading to earlier solvent breakthroughs and poorer oil recovery [70]. In contrast, when mobility ratio is less or equal to unity, the displacement front remains stable, and the displacing fluid displaces the displaced fluid efficiently without significant fingering.

Figure 3. Oil recovery during the secondary and tertiary phases without and with the presence of viscous fingering (a comparison of displacement front stability). Adapted from [69].

However, according to Sorbie et al. [50], the immiscible viscous fingering is better characterized by viscosity ratio rather than mobility ratio M. The viscosity ratio is used to describe the relative mobility of the oil and water phases during immiscible displacement processes. It represents an important parameter in understanding the behaviour of viscous oils and the impact of polymer injection on their recovery. For instance, in the context of tertiary polymer flooding, the viscosity ratio determines the relative permeability of the oil and water phases. Higher viscosity ratios indicate that the oil is more viscous than the water, which can lead to unstable displacements and reduced recovery [49,71].

In coating processes, viscous fingering can hinder the uniformity of the coating and affect the quality and performance of the final product, especially in applications where uniform coatings are critical, such as in the production of semiconductors or medical devices [72]. Many studies were conducted regarding the enhancement of the process itself. Some polymers, such as tertiary polymers, have been shown to be effective in suppressing viscous fingering [49], cross-linking reactions can affect the viscosity profile at the interface, leading to changes in flow stability [49,72], particle-laden fluids, where the interaction between the particles and fluid–fluid interface can achieve desired surface properties [73], etc.

In addition to the previously mentioned difficulties during oil recovery, viscous fingering can also cause other issues in the oil and gas industry. If the rock in the immediate vicinity of the injection well, where the fluid pressure can be high, is not well-consolidated, sand may be forced out of the rock at this location. The displacing fluid then transports the sand to the production well and related equipment thus causing their erosion. This phenomenon is called ‘sand production’ and can be very detrimental for oil extraction machinery. To prevent sand production, a chemical treatment fluid is often used to consolidate the rock surrounding the injection well. However, chemical treatment has the potential to clog the pore throats close to the injection well [74].

Viscous fingering is a ubiquitous hydrodynamic instability in liquid chromatography and ground contamination. Liquid chromatography is utilized to separate the chemical components of the studied sample by running it through a porous medium. In preparative or size-exclusion chromatography, the viscosities of a sample and displacing fluid (eluent) are usually significantly different. Viscous fingers form at the interface of the two fluids, thus deforming the initial interfacial front. This instability is detrimental for the separation process since it provides the peak broadening and distortions [75,76]. With regard to groundwater and soil contamination, the spill’s fluid is often of different viscosity and/or density than that of water, thus forming the fingering phenomenon. From an ecological point of view, it is of great importance to predict the extent to which fingers will develop in time since they represent the mechanism for spill’s fluid expansion [75,77].

This phenomenon plays a significant role in the process of CO₂ sequestration (Figure 4) into deep aquifers. It is relevant in the context of carbon sequestration as it can enhance the mixing of CO₂ with surrounding saline aquifer, leading to more effective storage of the carbon dioxide [4,24,79]. This is particularly important for the long-term storage of CO₂, as it helps to reduce the risk of leakage and maintain the integrity of the storage site [78,79]. A more uniform distribution of CO₂ in the aquifer can be achieved when carbon dioxide is injected into a deep saline aquifer, where it displaces the brine by controlling the injection rate and pressure [80].

Figure 4. MR (Magnetic resonance) signal intensity with flow rate 0.03 ml/min, pressure 6MPa and temperature 295 K shows the displacement process in quartz glass sands BZ-02. The CO₂ distribution is uneven prior to breakthrough, however, the displacement achieves a balance after some time, thus stabilizing the water and CO₂ distribution [78].

Furthermore, there is an excellent example of viscous fingering occurrence at Terra Nova Intrusive Complex (TNIC) in northern Victoria Land, Antarctica (represents the result of widespread magmatism during Early Palaeozoic Ross Orogeny) during the replenishment of felsic magma (rich in lighter elements such as silicon, oxygen, aluminium) chambers fossilized by continuous intrusions of a mafic magma (rich in magnesium and iron). This process is characterized by the intrusion of mafic magma (less viscous fluid) into a felsic magma (more viscous fluid) chamber, resulting in the development of finger-like structures at the interface between the two magmas [81].

In turbulent fluid flows, the chaotic velocity field enables efficient mixing of fluids due to the high values of the Reynolds number when the dominance of the inertial forces over the viscous ones is present. However, at low values of the Reynolds number, the inertia is negligibly small, and mixing of the fluids can be achieved only by the diffusion process. Nevertheless, this process can be accelerated, even in the absence of inertia, if viscous fingering is induced at the interface between the two fluids (this mechanism has recently become very popular with the development of microfluidics) [82–84]. The newest research compared directly experiments and simulations of density-driven convective mixing in 3D porous media, thus finding excellent agreement between the model and experiment in terms of convective fingering pattern and the fluid mixing average rate [85].

Viscous fingering in biological fluids is not an omnipresent phenomenon; however, its occurrence in certain biological processes has been studied. In 1992, a group of researchers described the development of viscous fingering in the mammalian stomach, referring to the process by which hydrochloric acid (HCl) secreted by the gastric glands traverses the protective layer of gastric mucus through narrow fingers without acidifying it. This phenomenon is stomach’s ability to digest food while protecting its own epithelial lining from damage [86].

The Saffman–Taylor instability can also be encountered in the research of spreading tumours (Figure 5). Generally speaking, metastatic tumours do not maintain a straight front line while spreading. Their growth has been intensely studied in the last few decades in order to find out what are the mechanisms controlling the tumours morphogenesis [87,88]. The latest findings describe them as finger – like protrusions developing from the cancer mass, thus attacking the healthy neighbouring tissue [87]. In summary, the active traction forces generated by tumour cells, which increase with metastatic potential, are a key mechanical driver of viscous fingering instabilities at the tumour boundary [89].

Figure 5. Model of growing tumour and invading neighbouring tissue; Adapted from [87].

At the beginning of every human being’s life, when one takes their first breath (or inspiration) after birth, the airways reopen. The first breath differs from ‘breathing’ activities in the uterus, where mother’s placenta enables the baby to receive oxygen and carbon dioxide through the blood placed in the placenta. In other words, there is no gas exchange while foetus resides in utero and at birth, baby’s lungs are filled with liquid. With the first breath, the air displaces the liquid in bronchus and bronchiole, thus forming a long finger [90,91]. The experimental study of air displacing a more viscous fluid in a collapsed, compliant channel can be used as a model for pulmonary airway reopening [92].

Even though the majority of patterns are rich in multiple fingers, single fingers can be encountered in certain cases. For instance, pulmonary airway reopening involves the propagation of an air finger into fluid-filled collapsed airways, which can be modelled as a viscous fingering process in a compliant channel [93–97]. If viscous effects dominate, the air finger branches asymmetrically and tends to reopen a single path through the airway network [98]. Conversely, if the air finger propagates slowly enough and/or the airway wall elasticity is sufficiently high, the fingers tend to branch symmetrically [98]. Understanding these complex fluid–structure interactions is crucial for developing effective treatments for respiratory diseases involving airway occlusion [93]. Furthermore, a single finger viscous fingering is used to manipulate ion transport and dendritic instability in electrochemical systems. It is caused by electroconvective vortices below the interface, which are initiated by selective ion rejection through a charge-selective surface [99].

Section 2 provides an overview of typical apparatus for experimental analysis of the Saffman – Taylor instability (pore scale viscous fingering), as well as the story behind it. Commonly used mathematical model for the description of this fluid instability, as well as the linear stability theory, is presented in Section 3, followed by different research methodologies (theoretical, numerical, and experimental) for control of pore scale immiscible viscous fingering phenomenon (Saffman–Taylor instability) in Section 4. The last Section (Section 5) gives a summary with conclusions, as guidelines for future experiments essential for better understanding of finger formation and its suppression.

2. The Hele-Shaw cell

Although it is well-known that this apparatus is widely used in the experimental analysis of porous media, it is of great importance to explain in detail the Hele-Shaw cell itself [17,18,56,100–102]. Since there are variations of the apparatus used in numerous types of research, it is vital to mention the historical development of the Hele-Shaw cell as a necessary background in the study of the viscous fingering phenomenon.

Originally, the Hele-Shaw cell was not of the same form as it is known today. It was named after Henry Selby Hele-Shaw (1854–1941), an English mechanical engineer, and inventor. The most significant outcome of Hele-Shaw’s longstanding scientific work occurred completely fortuitously in 1897 – he wanted to present the character of the flow of water past an object placed in a lantern slide to his students in Liverpool, where he served as a professor of engineering. To demonstrate the stream lines of the flow, Hele-Shaw first injected the colouring liquid (following the example of the Osborn Reynolds’ famous experiment [103]), but it turned out to be unsuccessful since the injected fluid mixed with the water in the slide at once. Secondly, he tried it with sand, but numerous eddies were formed (the places where the particles of sand accumulated), thus changing the nature of the flow [100,101]. Eventually, the goal was achieved when the slide created a small coincidental leak providing little air bubbles that served as persistent tracers. This experiment enabled him to visualize the streamlines past different obstacles he used in later studies [100,101,104,105]. The new method was presented by Hele-Shaw himself in 1897 at the Royal Institution of Naval Architects and he was awarded the Gold Medal in 1898 for his streamline method [100]. The most important outcome of Hele-Shaw’s experiment was that if the glass plates were close enough (approximately 0.02 inch), the flow became laminar at all velocities [100].

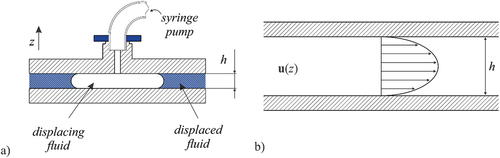
Today, the Hele-Shaw cell is an apparatus consisting of two parallel glass (or acrylic) plates with a very small fixed gap (the constant gap width is commonly provided with spacers) between them (only a few millimetres) and a viscous fluid filling the gap and wetting the plates (the viscous fluid is spread on the upper surface of the bottom plate and afterwards the plates are clamped together). After the plates have been set up, the less viscous fluid is injected through a small hole drilled through the overlying plate. Lower flow rates can be achieved via a syringe pump, while the higher flow rates can be reached via gas bottles.

Different geometries of Hele-Shaw cells have been used since an interest in viscous fingering emerged. Initially, the greatest number of the conducted experiments were performed in flat Hele-Shaw cells with a planar channel geometry (Figure 2a) or, later, planar radial geometry (Figure 2b) [4,17,18,56]. Moreover, in the past few years, a number of experiments included flat tapered (diverging and converging) Hele-Shaw cells [106] (Figure 6a,b). Regarding the non-flat environments, spherical and conical Hele-Shaw geometries were examined as well [107] (Figure 6c,d).

Figure 6. Cross sections of the flat convergent (a) and divergent (b) Hele-Shaw cells [106]; Spherical (c) and conical (d) Hele-Shaw cell. Adapted from [107].

Thereafter, the Hele-Shaw cell can be considered as the simplest system in which two-dimensional convection is present [100,104,108]. The advantage of such a system is that the gap width is significantly smaller compared to a characteristic length scale (shallow geometry) in the flow direction and the Reynolds number is very low (creeping flow), thus the Navier–Stokes equations can be simplified to a linear velocity relation identical to the inviscid potential flow and the flow through a porous medium (Darcy’s law).

However, real-world porous media are three-dimensional, which introduces additional complexities not captured by the Hele-Shaw cell model. These complexities include the three-dimensional flow patterns, turbulence and effects of inertia (which cannot be neglected in vertical and rotating Hele-Shaw cells, etc.). Moreover, real porous media are often heterogeneous, meaning that the permeability and other properties vary spatially; the boundary conditions are far more complex, pressure gradients, fluid properties and permeability are not uniform [17,109,110]. The Hele-Shaw cell typically assumes a homogeneous porous medium and simple boundary conditions, and it is commonly used to study flow behaviour at a specific scale, whereas porous media can exhibit flow behaviour at various scales, from microscopic to macroscopic [109,111]. For higher Reynolds numbers, the Hele-Shaw cell model may not accurately capture the flow behaviour in porous media, meaning that the convective terms in the Navier–Stokes equations become significant, and the model’s assumptions are no longer valid [111].

3. Mathematical model of the Saffman–Taylor instability

Even though several mathematical solutions were used to simulate this phenomenon (Hele-Shaw model, Darcy’s law), the most successful one has arisen from the conservation equations of fluid flow. The Hele-Shaw equation is obtained by averaging the Navier–Stokes equations across the vertical direction, while the continuity equation directly generates the Laplace equation for pressure [19,100,112].

Regarding mathematical modelling, it is very important to point out that single finger is a common approach used in models for viscous fingering. This method involves simulating the behaviour of a single finger or a small number of fingers in a Hele-Shaw cell or other similar setup. The goal is to capture the fundamental physics and dynamics of viscous fingering, which can be scaled up to larger systems [17,24].

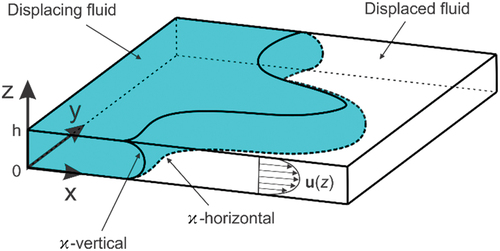
First, we consider the flow in a horizontal flat Hele-Shaw cell and its frame of reference, which are given in Figure 7.

Figure 7. The Hele-Shaw flow in a planar channel geometry within the frame of reference.

The motion of Newtonian, incompressible fluids can be described by the momentum (Navier-Stokes) equation [113]:

(1) $\mathit{\rho }\left[\frac{\mathit{\partial }{\mathbf{u}}^{\ast }}{\mathit{\partial }{t}^{\ast }}+\left({\mathbf{u}}^{\ast }\cdot {\mathrm{\nabla }}^{\ast }\right){\mathbf{u}}^{\ast }\right]=-{\mathrm{\nabla }}^{\ast }{p}^{\ast }+\mathit{\rho }{\mathbf{g}}^{\ast }+\mathit{\mu }{\mathrm{\nabla }}^{\ast 2}{\mathbf{u}}^{\ast }$(1)

where ${\mathbf{u}}^{\ast }$ is the vector of fluid velocity, $\mathit{\rho }$ the fluid density, $p^{\ast }$ the pressure field, $\mathit{\mu }$ the dynamic viscosity, and ${\mathbf{g}}^{\ast }$ the gravitational acceleration. Asterisks indicate dimensional physical quantities. By using the characteristic scaling parameters and the fact that the gap width h is very small in comparison to the dimensions of the cell in flow direction, the momentum equation (1)(1) $\mathit{\rho }\left[\frac{\mathit{\partial }{\mathbf{u}}^{\ast }}{\mathit{\partial }{t}^{\ast }}+\left({\mathbf{u}}^{\ast }\cdot {\mathrm{\nabla }}^{\ast }\right){\mathbf{u}}^{\ast }\right]=-{\mathrm{\nabla }}^{\ast }{p}^{\ast }+\mathit{\rho }{\mathbf{g}}^{\ast }+\mathit{\mu }{\mathrm{\nabla }}^{\ast 2}{\mathbf{u}}^{\ast }$(1) becomes significantly simplified. After the simplification of (1), one comes to the conclusion that the Reynolds number, the dimensionless ratio of inertial and viscous forces, is negligibly small, i.e. the convective terms in the Navier–Stokes equations are significantly reduced [17,55]. Furthermore, inertia can also be neglected since the Bond or Eötvös number, the dimensionless ratio of gravitational forces and surface tension forces, is far smaller than the capillary number. Regarding the vertical Hele-Shaw cells, the Bond number must be taken into account [114,115]. Moreover, inertial effects cannot be neglected in the case of fluids of low viscosity and for large gap width between the plates in Hele-Shaw cell [58]. Finally, under all these assumptions, the nonlinear terms disappear, thus reducing the Navier–Stokes equation to the linear Stokes equation:

(2) $\mathrm{\nabla }\mathit{p}=\mathit{\mu }{\mathrm{\nabla }}^2\mathbf{u}$(2)

where p represents the dimensionless pressure of the displaced fluid, µ dynamic viscosity and u the dimensionless velocity vector.

Concerning a shallow geometry, two horizontal components of velocity vector are taken into consideration (the components parallel to the plates) and their dominant variation is in the z-direction, so that (2) can be written in the following form:

(3) $\mathrm{\nabla }\mathit{p}=\mathit{\mu }\frac{{\partial }^2\mathbf{u}}{\mathit{\partial }{z}^2}$(3)

which then transforms, after the integration, into the expression for the parabolic velocity field of the same form as of the plane Poiseuille flow (Figure 8):

Figure 8. Expanding air bubble displacing the fluid between the plates (left) and velocity profile (right).

(4) $\mathbf{u}=\frac{1}{2\mathit{\mu }}\left(z^2-\mathit{zh}\right)\mathrm{\nabla p}.$(4)

Now, we can integrate (4) through the cell thickness in order to obtain the depth-averaged velocity that is governed by the potential law:

(5) $⟨\mathbf{u}⟩=-\frac{h^2}{12\mathit{\mu }}\mathrm{\nabla p}.$(5)

Equation (5) has the same form as the governing equation of fluid motion in porous media (Darcy’s law), written as $\mathbf{u}=-\mathit{k}\nabla \mathit{p}$, where k represents permeability of the medium [116]. When investigating the instability partially responsible for coning in the process of secondary oil recovery, Sir Taylor realized that this two-dimensional flow could be simulated with the flow in the Hele-Shaw cell [18].

Since the fluid in a Hele-Shaw cell and in the porous medium is incompressible, $\mathrm{\nabla }\cdot \mathbf{u}=0$, by taking the divergence of equation (2)(2) $\mathrm{\nabla }\mathit{p}=\mathit{\mu }{\mathrm{\nabla }}^2\mathbf{u}$(2) , one comes to the expression for pressure in the Laplacian field [4]:

(6) ${\mathrm{\nabla }}^2\mathit{p}=0.$(6)

Moreover, the constant volumetric flux Q can be defined as

(7) $\mathit{Q}={\int }_0^h\mathbf{u}\mathit{dz}=⟨\mathbf{u}⟩\mathit{h}=-\frac{h^3}{12\mathit{\mu }}\mathrm{\nabla p}.$(7)

After the substitution of (7) in the continuity equation $\mathrm{\nabla }\cdot \mathit{Q}=-\frac{\mathit{\partial h}}{\mathit{\partial t}}$, one obtains the Reynolds lubrication equation in the displaced fluid:

(8) $\mathrm{\nabla }\cdot \left(\frac{h^3}{12\mathit{\mu }}\mathrm{\nabla p}\right)=\frac{\mathit{\partial h}}{\mathit{\partial t}}.$(8)

When there is no mass transfer across the boundary between two fluids, a simple kinematic outcome is that the normal components of the injected fluid velocity must be equivalent to the normal component of the displaced fluid velocity [117]:

(9) $\frac{\mathit{\partial }\mathbf{R}}{\mathit{\partial t}}\cdot \mathbf{n}\text{ = }⟨\mathbf{u}⟩\cdot \mathbf{n}$(9)

where $\mathbf{n}$ is the outward normal unity vector and $\mathbf{R}\left(\mathit{\theta },\mathit{t}\right)=\mathit{R}\left(\mathit{\theta },\mathit{t}\right){\mathbf{e}}_{\mathbf{r}}$ the radius vector that describes the fluid–fluid interface.

The dynamic boundary condition refers to the surface tension that acts at the interface and it is governed by the Young-Laplace equation:

(10) $\mathrm{\Delta }\mathit{p}=\mathit{\gamma \kappa }$(10)

where $\mathit{\gamma }$ represents the surface tension, $\mathit{\kappa }$curvature of the interface and $\mathrm{\Delta p}$ pressure drop across the interface. Curvature $\mathit{\kappa }$ can be divided into two components – horizontal ${\kappa }_{\mathit{horizontal}}$ and vertical ${\kappa }_{\mathit{vertical}}$. The only obstacle to the formation of infinitely sharp fingers is surface tension, which tends to reduce the pressure gradient near the fingertip. Furthermore, as the curvature is larger, the effect of surface tension is more significant, i.e. smaller radii of curvature result in sharper fingertips [18,118].

In order to predict whether a flow is stable or not, one has to apply linear stability analysis. The stability of an axisymmetric interface to small perturbations (Figure 9) is firstly taken into consideration, and thereafter the nonlinear dynamics of late phases is examined [120]. After the equations for the unperturbed, axisymmetric expanding interface are derived, the growth rate of small sinusoidal perturbations is studied [4,121]. By solving the system of equations for base (unperturbed) flow, e.g. in a radial Hele-Shaw cell, one obtains the expressions for the pressure inside and outside the bubble [119]:

Figure 9. A perturbed interface in a radial flat rigid wall Hele-Shaw cell; Adapted from [119].

(11) $p_B=-\mathit{log}\bar{R}(\mathit{t})+\frac{1}{12}\frac{A}{\mathit{Ca}}\left(\frac{A}{\bar{R}(\mathit{t})}+\frac{2}{h}\right),$(11)

(12) $\bar{p}=-\mathit{log}\mathit{r}$(12)

where $p_B$ is pressure in the bubble, $\bar{R}$ the radius of the bubble for axisymmetric flow, Ca capillary number, $\mathit{A}=h_0/R_{\mathit{out}}$ aspect ratio (ratio of the initial gap width and outer radius of the Hele-Shaw cell), and $\bar{p}$ base-flow pressure in the fluid (pressure outside the bubble). For a rigid flat Hele-Shaw cell, $\mathit{h}=1$, while in the lifting, tapered and compliant cell, $\mathit{h}$ changes over time.

Hereafter, the system is perturbed by substituting the ansatzes for the position of the interface $\mathit{R}\left(\mathit{t},\mathit{\theta }\right)$and fluid pressure $\mathit{p}\left(\mathit{r},\mathit{t},\mathit{\theta }\right)$ of the form:

(13) $\mathit{R}\left(\mathit{t},\mathit{\theta }\right)=\bar{R}\left(\mathit{t}\right)+\mathit{\epsilon }{R}_N\mathit{sin}\left(\mathit{N\theta }\right)\wedge \mathit{p}\left(\mathit{r},\mathit{t},\mathit{\theta }\right)=\bar{p}\left(\mathit{t}\right)+\mathit{\epsilon }{p}_N\mathit{sin}\left(\mathit{N\theta }\right)$(13)

into the governing equations, where $\mathit{N}$ represents an integer that defines the number of fingers in the perturbation, $\mathit{\epsilon }$ small parameter $\mathit{\epsilon }\ll 1$ and hats indicate perturbation amplitudes [4,24,119]. The solutions of the system of equations with substituted ansatzes that are obtained and considered are the growth rate [119]:

(14) ${\sigma }_N=\frac{1}{R_N}\frac{\partial R_N}{\mathit{\partial t}}$(14)

and the wavenumber of the maximum growth rate [119]:

(15) $N_{max}\simeq \sqrt{\frac{1}{3}\left(1+\frac{12Ca{R}_0^3}{A^2}\right)}$(15)

where $R_0$ represents the radius of the initial bubble.

The obtained equations describe viscous fingering in a flat rigid cell, i.e. the simplest system used to examine this instability. According to linear stability analysis, surface tension fails to control the evolution of minor disturbances at the fluid–fluid interface as the radius of the interface expands [122].

The linear perturbation theory assumes that the interface or displacement front of a base state is perturbed in a wavelike manner with exponential growth rate. The way of analysing perturbations through the Fourier decomposition was previously introduced by Lord Rayleigh who derived the onset criterion based on density gradients [38,123]. Following Lord Rayleigh’s work, G. I. Taylor developed a theoretical approach (1949) to set up a criterion for the onset of immiscible displacement instability taking only density difference into the account [38,124]. The validity of Taylor’s theoretical work was proved through experiments by D. J. Lewis the same year [125]. Almost a decade later, the milestone article written by Saffman and Taylor (1958) introduced the effect of interfacial tension showing that viscous fingers could be counteracted by the Laplace pressure [17,38]. Despite being closely related to Saffman and Taylor, Chouke et al. (1959) focused specifically on porous media, thus identifying a wavelength of maximum instability growth rate (also referred to as the most dangerous wavelength) [25,38,52,126,127]. More than a decade later, Hagoort (1974) continued to study linear perturbation theory and he derived a stability criterion [38,128]. Based on the Buckley–Leverett shock front saturation theory, he assumed that saturation occurs upstream of the instability front [21] and came to the conclusion that the instability occurs when a mobility ratio between the fluids behind and ahead of the shock front is greater than 1, providing a shorter wavelength than the canal width [128]. A final extension of Chouke et al.’s work (1959) was provided by Peters and Flock (1981). According to them, fluid displacement through a circular or rectangular cross-section system could be governed by spatial boundary conditions, thus introducing a discrete spectrum of wavelengths [38,129].

However, linear stability theory is limited and can be applied until the amplitude of the interfacial instability significantly increases. Then linearizing assumptions are violated and nonlinear theory is required [130]. Once the fingers have reached sufficiently large amplitude, they start to interact nonlinearly. There are some generic features that appear in all radially growing Laplace unstable systems as a result of this interaction. The most commonly observed and studied generic features are finger competition and tip-splitting events. The finger tends to stop growing if it lags behind the other fingers since the growth is always fastest at the tips of larger amplitude fingers that consume all the driving forces. Moreover, smaller fingers usually withdraw due to the surface tension. Finger competition is likely to reduce the number of viable growing fingers before the nonlinear regime is fully established [4,24,121]. The tip-splitting events create new fingers from existing ones, thus increasing the number of fingers, and the whole process of finger competition is repeated [131]. Eventually, the result is a very complex pattern that reminds of a fractal structure (Figure 10). It is pointed out that viscous fingering in radial cells, to a certain limit, can be simulated by diffusion-limited aggregation (DLA clusters), one of the most commonly used models that describes the production of fractal objects [13,132–135].

Figure 10. A complex bifurcation pattern of viscous fingering simulated by the DLA model; the patterns’ ages are indicated by their colours, with the first generated region being blue and the newly formed being red [132].

4. Control of immiscible viscous fingering at a pore scale

Viscous fingering, as a morphogenetic instability, is often thought to be an undesirable phenomenon [4] and, in the last few decades, scientists have been examining the ways to control it. There are various methods to achieve this – by changing the geometry of the cell or boundaries of the cell, types of fluids wetting the plates, injection rates, etc [94,136–152]. Moreover, there are researches that are based on the control of viscous fingering beyond the onset [153]. This paper deals with the control of immiscible viscous fingering instability before it becomes fully established.

Regarding the rearrangement or modification of the geometry of the classic Hele-Shaw cell, recent studies have shown that the Saffman–Taylor instability can be stabilized. Numerous theoretical and experimental studies were carried out in tapered Hele-Shaw cells, either of a rectangular or radial geometry, since the problem of fluid displacement in such cells has a similar geometry with various problems that include two-phase flows in channels with fluctuations in shape (i.e. printer’s instability) [136,154,155]. This type of cell was first introduced in 1992 [156], and single-finger instability was observed. In a divergent cell, the fingertip was flatter and more unstable in comparison to the cell without the depth gradient. On the other hand, in a convergent cell, the fingertip was sharper and more stable [136,154,156,157].

Furthermore, Al-Housseiny and Stone [136] theoretically described viscous fingering in a tapered Hele-Shaw cell, with a constant depth gradient, in the direction of fluid flow. They reached a conclusion that the depth gradient can affect the stability of the interface and that the expansion of perturbation can be suppressed due to capillary stresses. Moreover, Dias and Miranda [158] focused their research on the examination of the interface behaviour between two fluids – one was of negligible viscosity and density, while the other was denser and more viscous – in a radially tapered rotating Hele-Shaw cell. They showed that the depth gradient had a major impact on the stability of the interface, i.e. it could favour or restrain the emergence of centrifugally induced instabilities by altering the sign and amplitude of the gap gradient. According to Bongrand and Tsai [144], the instability can be completely suppressed using a converging passage with a suitable flow rate. On the other hand, by increasing Q, the viscous fingering can change from stable to unstable for every converging gradient. To summarise, the suppression of viscous fingering in rectangular [159] and circular geometries [136,158,160] can be achieved by a negative taper, while in the case of rotating plate, with sufficiently large rotating rates, the instability can be completely stabilised (the centrifugal force tends to stabilize interface) [147].

According to Anjos et al. [106], the increase of capillary number in a radially tapered Hele-Shaw cell (Figure 6a and b) leads to the changes of the interface relative to the parallel plate cell. These authors noticed that at lower Ca values the interface in a converging cell was more stable than in a zero depth gradient cell, whereas it appeared to be considerably destabilized at the higher values of the capillary number. When it comes to a divergent cell, the situation is completely the opposite – at lower values of Ca the fluid–fluid interface becomes more unstable than at higher values. Additionally, the value of Ca affected the shape of emerging fingers – in both types of radially tapered cells, fingers had the tendency to split at higher Ca, while at lower Ca they tended to be rounded. At transitional Ca, fingers got flattened.

Considering the nonflat Hele-Shaw cell geometries, Brandão et al. [107] conducted experiments in the spherical and conical ones. It was concluded that viscous fingering could be reduced in such geometries by manipulating a time-dependent injection flow rate $\mathit{Q}\left(\mathit{t}\right)$. The constant injection rate led to the appearance of fingers and tip-splitting events, while the time-dependent flow rate resulted in completely different patterns (perturbations of interface were significantly minimized). The most interesting outcome of this study is that the desired injection rate utterly depends on the geometry of curved cells, more specifically, it depends on the radius of curvature and the aperture angle of the spherical and conical cell, respectively.

The time-dependent strategies were used to control viscous fingering as well. Considering the work of Cardoso and Woods [148], it was found that the injection profile $\mathit{Q}\left(\mathit{t}\right)={\alpha }_c{t}^{-1/3}$ resulted in complete stabilization of an axisymmetric displacement, where $\mathit{Q}\left(\mathit{t}\right)$ is the time-dependent injection flow rate and ${\alpha }_c$the constant of proportionality. The constant was chosen in such a way that mode 2 appeared to be the fastest growing mode for the value which was stabilized throughout the injection [149]. With reference to Dias and Miranda [150], it was demonstrated through the application of weakly nonlinear analysis that the suppression of tip-splitting events can be achieved via the damping of the harmonic perturbation at a time-dependent injection rate $\mathit{Q}\sim t^{-1/3}$. In the lifting Hele-Shaw problem, when the cell’s gap width increases linearly over time, various patterns appear, thus resulting in strong competition among the inward developing fingers that define the interface structure [149]. The finger competition can be suppressed via subharmonic perturbations at certain time-dependent gap width [150]. However, from a perspective of a control theory, the governing equations under time-varying flow rates cannot be handled easily since the boundary expands geometrically (the truncated Fourier series describe the shape of the interface) and the modes equations are changing over time [161].

More recently, Zheng et al. [162] have shown theoretically and numerically that the suppression of viscous fingers can be managed by manipulating the gap width in a lifting Hele-Shaw cell in the power-law form $\mathit{h}\left(\mathit{t}\right)=h_0{t}^{1/7}$, where $h_0$ represents the initial gap width of the cell. The viscous fingering instability can be completely restrained or a series of tip splitting events can be avoided by selecting a single dimensionless time-independent control parameter $\mathit{J}=6\mathit{\mu }{Q}^{3/2}/\left({\pi }^{3/2}\mathit{\gamma }{h}_0^{7/2}\right)$. Therefore, the growth rate becomes time independent too. Moreover, Vaquero-Steiner et al. [119] modified a simplified analysis obtained by Zheng et al. [162] in order to demonstrate that the plate separation delays the start of non-axisymmetric instabilities by carrying out a linear stability analysis of an interface expansion in a radial Hele-Shaw cell with time-dependent depth.

Heretofore, different types of rigid plate Hele–Shaw cells were considered. A more complicated variation of the Hele–Shaw problem, when the upper plate is replaced with a thin elastic membrane, was studied theoretically [12,137,145,146], numerically [12,138,163,164] and experimentally [145,163,165] in the past decade. The problem known as a fluid–structure interaction (FSI) problem links fluid and mechanical solid instabilities, and it was concluded that it had different regimes due to the sheet’s elasticity. The fluid – fluid interface is unstable for stiff sheets, thus causing the elastic sheet to bend passively with regard to the fingering of the injected bubble. On the other hand, very flexible sheets suppress the FSI instability However, the solid becomes mechanically unstable and starts to buckle, thus causing the interface to deform passively [166]. Intermediate sheet elasticity was shown to be the most favourable solution for the stability of both the elastic sheet and interface between fluids. The suppression of instability in the Hele – Shaw cell can be explained through a theoretical model that couples the Reynolds lubrication equation and Föppl-von Kármán equations, a set of nonlinear partial differential equations that describe the deflection of thin plates. The study of Pihler-Puzovic et al. [137], in addition to dealing with the mechanism for viscous fingering suppression, also serves to link the Saffman–Taylor instability in a Hele – Shaw cell with the rigid walls with the printer’s instability in roll and slot coating flows. The quantitative study of pattern formation regarding both instabilities is described in the work of Ducloué [167]. Al-Housseiny et al. [145] discovered that the membrane’s compliance facilitates the inhibition of viscous fingering. Due to the gas injection at the center of the elastic cell, the membrane deflects and forms a tapered geometry, thus enabling the suppression of the instability. Moreover, the late-time viscous fingering suppression in [138] could be the result of the decrease in the capillary number [159], although this is not sufficient to prevent instability for small values of volumetric flux [146].

In the latest research [168–170], viscous fingering was observed in a Hele–Shaw cell consisting of two thin parallel plates and the cylindrical rigid mould glued to the lower plate (Figure 11). The mould was filled with an elastomer which deformed due to the constant flow rate (both low and high), thus making contact with upper plate of the apparatus and interrupting the flow (known as “choking”). This kind of FSI problems can be applied in further development of microfluidic devices since the deformable components in such tools do not need external actuation. Microfluidic devices employ the physical and chemical properties of fluids at the microscale and are widely used in agriculture, food safety, tissue engineering, etc [171]. So far, it has been perceived that viscous fingering in a compliant Hele-Shaw cell is not significantly suppressed; however, two mechanisms that can lessen the choking tendency were spotted – either with the proximity of the inviscid bubble to the cell rim or with the compression of the injected gas (choking cannot occur with a compressible gas) [170]. Choking, as an undesirable phenomenon, can be encountered when a fluid forced through a deformable porous medium compresses the medium against the outlet due to the pressure gradient, thus reducing the permeability [172], and in the two-phased gas-driven displacement of a mixture of aqueous liquid and hydrophilic solid grains in a capillary tube [173].

Figure 11. Schematic diagram of an elasto-rigid Hele-Shaw cell: a narrow gap between a rigid horizontal top plate and an elastomer confined within a rigid mould (left); fluid injected into the compliant Hele-Shaw cell at a constant flow rate spreads outwards, with a radial front position $r_f$, deforming the elastomer and displacing fluid resident in the cell; Adapted from [168].

When considering the incompressible displacing and displaced fluid, the capillary number represents the crucial parameter that governs the severity of the viscous fingering instability. However, if the injected gas is compressible, the gas injection rate becomes unsteady and another non – dimensional parameter, the compressibility number, affects the pattern formation as well. In [174], researchers came to the conclusion that the increasing compressibility number delays the onset of finger expansion compared to the corresponding incompressible variant. Moreover, they showed that the increasing compressibility number orderly decreases the severity of the finger development at high capillary numbers.

Regarding the wettability of the Hele-Shaw cell walls, the changes in wettability can significantly impact viscous fingering in the cell itself and porous media too. Increasing the wettability (making the walls water-wet) tends to stabilise the interface and suppress the Saffman–Taylor instability [175,176]. The fingers become broader and more rounded since the wetting fluid preferentially flows along the walls, creating a more stable displacement front [176]. However, the relationship between wettability and displacement efficiency (saturation at breakthrough) is more complex. In some cases, an optimal wetting angle that maximises saturation exists, with up to 30% higher saturation compared to the non-wetting case. Nevertheless, in other cases, increasing wettability does not always improve displacement [176,177].

When it comes to non-Newtonian fluids confined between plates, the properties of complex fluids can extremely modify viscous fingering instability [178,179]. Complex fluids can be either surfactants or polymers, where one can modify capillary or viscous forces, respectively. Regarding complex fluids, the dynamic surface tension and viscosity lead to much wider and larger fingers, thus enabling more efficient displacement of i.e. crude oil during oil recovery. Actually, in order to alter the wetting properties and reduce the amount of immobile oil remaining in a reservoir following waterflooding, surfactants are used. To reduce the viscosity difference in the displacing fluid, polymers are commonly added, while polymer gels are utilized to seal bigger pores in the porous medium [179].

The viscous fingering instability was also examined in the presence of two immiscible fluids being under the simultaneous action of the pressure gradient and electric field [180]. The electrokinetic (EK) phenomenon was included and, surprisingly, this interfacial instability was controlled by changing the injection ratio of the electric current to volumetric flux. For instance, Gao et al. have showed that by adjusting the direction and strength of the electric field, both stable and unstable displacements are possible for any viscosity ratio in a Hele-Shaw cell. However, when a critical injection rate has been exceeded, interfacial stability becomes independent of the viscosity ratio and it is affected only by the relative direction of the flow and current. When the electro-osmotic flow is in the same direction as the hydraulic flow, the overall resistance is reduced, resulting in an apparent decrease in viscosity, known as ‘electrokinetic thinning’, thus stabilizing the interface motion (Figure 12). According to the researchers, it can be potentially applied in electrical oil recovery and the EK remediation of contaminated soils [175].

Hydrodynamically unstable displacement ($\mathit{M}<1$) can be stabilized by electrokinetic control; an electro-osmotic flow can be stabilized by a positive current (electrokinetic thinning), however, a negative current of the same magnitude makes the displacement front unstable, resulting in the finger patter of smaller wavelengths [175].

Furthermore, partial miscibility can significantly contribute to the control of finger formation and finger propagation [181]. However, previously mentioned approaches might not be applicable when it comes to miscible viscous fingering phenomenon [83,182–185].

5. Summary and conclusion

Viscous fingering, as a morphogenetic instability, is often considered as an impediment to certain industrial processes, e.g. in the petroleum industry, it limits the efficiency of oil recovery in porous media. Furthermore, in the coating process, due to the occurrence of the Saffman – Taylor instability, the fluid cannot be spread uniformly onto a solid surface. However, the existence of this instability can also be beneficial. Fluid mixing at low Reynolds numbers can be improved by employing the hydrodynamic instability that is the result of unstable displacement of fluids with different viscosities.

Since the control of this hydrodynamic instability is of a crucial importance, especially in industry, numerous scientists have been trying to theoretically, experimentally and numerically determine how to achieve it. Immiscible systems have been studied extensively over the years, and as the subject of this paper, the control mechanisms of immiscible viscous fingering at a pore scale have been thoroughly examined. Moreover, it is important to mention that these control mechanisms may not be directly applicable to miscible viscous fingering.

Based on a thorough analysis of the previously published results of the control approach, we came to the conclusion that the methods can be grouped in the following way:

• With regard to control by changing the geometry, in 1992, it was shown that a small tapering angle to the cell gap (convergent cell) can stabilize the single-finger instability. Almost two decades later, in 2013, it was concluded that viscous fingering can be suppressed in a tapered Hele–Shaw cell with constant width gradient due to the capillary forces. The radially tapered rotating Hele – Shaw cell also proved that the gap width gradient altered the stability of the fluid – fluid interface. Overall, whether the geometry is rectangular or radial, rotating or not, the negative taper enables the suppression of viscous fingering instability, while the positive one amplifies it. Regarding the non-flat Hele-Shaw cells, the spherical and conical ones, finger development and tip-splitting events were present. It was concluded that viscous fingering instability in such geometries can be minimized only by manipulating the time-dependent injection rate.

• When it comes to time-dependent strategies, it has been detected that the injection power law $\mathit{Q}\left(\mathit{t}\right)\sim t^{-\frac{1}{3}}$ leads to the complete stabilization of an axisymmetric interface displacement. Dias et al. provided insight into a mode-coupling analysis to determine the criterion that controlled the selection of the fastest growing mode. This work was broadened by Zheng et al., who revealed that the fastest growth mode could be chosen by the introduction of a time-dependent gap width instead of an injection flow rate.

• Considering the elastic cell boundaries instead of the rigid ones, the authors of certain papers showed that replacing of the upper plate with an elastic membrane could delay the onset of viscous fingering. Therefore, the perturbations in pressure before the progressive interfacial front can be decreased by sheet bending. Intermediate sheet elasticity has proven to be the best solution for ensuring the stability of both the fluid and solid relative to very flexible and stiff membranes. On the other hand, by replacing the bottom plate of the Hele–Shaw cell with a rigid mould filled with the elastomer, the suppression of fluid instability was not achieved. Nevertheless, the soft slab deformed due to the constant injection flow rate thus causing the interruption of the fluid flow, i.e. ‘choking’. The choking effect can be applied in the development of a microfluidic device; still, in the oil recovery process, it is an undesirable phenomenon, which can be reduced by the mechanisms given in.

• With reference to wettability of cell walls, the stability and saturation of viscous fingering depend on the interplay between wettability, viscosity ratio, and capillary number. At low capillary numbers, increasing the wettability gradient can suppress viscous fingering and improve displacement efficiency in porous media. In summary, while increasing wettability tends to stabilize the interface, the effect on displacement efficiency is more nuanced and depends on the specific flow conditions. Careful control of wettability, viscosity ratio, and capillary number is needed to optimize the displacement process.

• The Saffman–Taylor instability can be suppressed by using complex (yield-stress) fluids, surfactants, and polymers, since one has the possibility to significantly modify viscous and capillary forces. It was shown that the reduction of viscous fingers could be achieved by altering the selection mechanism (depending on the type of complex fluid) in specific ways.

• The presence of an electric field in viscous fingering was also applied to the control of instability. By changing the injection ratio of the electric current to the volumetric flux, the deformation of the interface was successfully suppressed, making it possible to enhance secondary oil recovery, improve mixing efficiency in microfluidics, and even control drug delivery in layered bodily tissues.

• When replacing the incompressible displacing fluid with compressible gas, the injection flow rate becomes unsteady. Then the effect of the otherwise important capillary number appears to be negligible in comparison to the compressibility number. With the increase of the compressibility number, the pattern formation is delayed and viscous fingers are suppressed even at high values of capillary numbers.

Abbreviation and nomenclature

DLA	=	Diffusion – limited aggregation
EK	=	Electrokinetic phenomena
EOR	=	Enhanced oil recovery
FSI parameter	=	Fluid structure interaction parameter
HCl	=	Hydrochloric acid
$\mathit{\mu }$	=	Dynamic viscosity
$\mathit{k}$	=	Permeability of the medium
$\mathbf{u}$	=	Vector of fluid velocity
$\mathbf{n}$	=	Outward normal unity vector
$\mathbf{g}$	=	Gravitational acceleration
$\mathbf{R}$	=	Radius vector
${\mathbf{e}}_{\mathbf{r}}$	=	Radial unity vector
$\mathit{p}$	=	Pressure field
$\mathit{Q}$	=	Volumetric flux
N	=	Number of fingers in perturbation
$\mathit{\rho }$	=	Fluid density
$\mathit{\kappa }$	=	Curvature of the interface
$\mathit{\gamma }$	=	Surface tension
$\mathrm{\Delta p}$	=	Pressure drop across the interface
$p_B$	=	Pressure in the bubble
Ca	=	Capillary number
A	=	Aspect ratio
${\sigma }_N$	=	Growth rate
$R_0$	=	Radius of initial bubble
h	=	Gap width
$\mathrm{\nabla }$	=	Hamilton operator
M	=	Mobility ratio
$\bar{R}$	=	Radius of the bubble for axisymmetric flow
$\bar{p}$	=	Base-flow pressure in the fluid
J	=	Dimensionless time-independent control parameter
t	=	Time
λ	=	Finger wavelength
CO2	=	Carbon dioxide
MR signal	=	Magnetic Resonance signal

Funding

The presented research was supported by the Ministry of Education, Science and Technological Development of the Republic of Serbia through the project “Integrated research in micro-, macro- and nano-mechanical engineering” (contract no. 451-03-47/2023-01/200105 dated February 3, 2023).

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

The work was supported by the Ministarstvo Prosvete, Nauke i Tehnološkog Razvoja [451-03-47/2023-01/200105].