A new modified wavelet-based ECG denoising

Abstract

Purpose: Wavelet denoising is one of the denoising methods commonly used for ECG signals. However, due to the frequency overlap between the EMG and ECG, the feeble characteristics of ECG signals exists the risk of being weakened in the process of filtering noise. This paper presents a method of modified wavelet design and applies it to the denoising of ECG signals.

Materials and methods: The optimized filter coefficients are obtained by approximating the amplitude-frequency response of the ideal filter, and the wavelet is constructed with the optimized filter coefficients. The algorithm is tested by clinical ECG data.

Results: The results show that the proposed denoising method can remove the high-frequency noise effectively and enhance the characteristic information of P waves and T waves, and retain the characteristic information of the atrial fibrillation signals simultaneously. Compared with db4 and sym4 wavelets, the proposed wavelet can improve the signal to noise ratio and reduce the mean square error effectively at the same time.

Conclusion: The modified wavelet design method proposed in this paper can effectively remove high-frequency noise while retaining and enhancing weak features. It provides a theoretical guidance for the de-noising of ECG signals in mobile medicine and also provides a way for other types of weak feature signal denoising.

Keywords:

• ECG signals
• atrial fibrillation signals
• modified wavelet
• wavelet denoising
• EMG interference

1. Introduction

ECG signals, which are the most important bio-electricity signals of the human body, reflect the cardiac electrical activity and other reliable features in various aspects. Therefore, these signals can serve as vital clinical references for the diagnosis and treatment of cardiological diseases. However, noises are inevitable when ECG signals are being collected. The subsequent results would be tampered if those noises are left untreated. The noises in ECG signals generally come from three sources: interference of power frequency, electromyography (EMG) interference, and baseline drift. Among them, EMG denoising is a troublesome problem, because its frequency range is overlapped with ECG’s [1].

EMG is often eliminated as high-frequency noise. Empirical mode decomposition (EMD) [2,3] decomposes the signal into a sum of intrinsic mode functions (IMFs) arranged in order of frequency and then eliminates EMG adaptively. However, the drawback of this method is that the end effects must be restrained effectively to achieve better performance. Digital filtering [4] and adaptive filtering [5,6] have the strong performance of removing noise. But when they are used to remove EMG, these two methods ignore the fact that the frequency between noise and ECG features is overlapped. The principal component analysis (PCA) [7] is based on the idea that the useful parts are uncorrelated with noise, and the denoising is accomplished by eliminating the less correlated components in the signal. However, it can only process aligned signals or multi-channel signals, otherwise, the denoising effect will be weakened. The wavelet transform (WT) [8] has good time-frequency localization properties and can provide signal analysis in time and scale. At the same time, its multi-resolution property can depict the non-stationary characteristics of signals. Therefore, it has become one of the denoising methods commonly used for ECG signals [9–11].

When the wavelet is used for ECG denoising, the selection of mother wavelet could be a crucial procedure. The Daubechies wavelet has a largest vanishing moment, but it sacrificed its symmetry at the same time. The Symlet wavelet obtains the symmetry by reducing the vanishing moment [12]. In recent years, some scholars have proposed some optimized methods to construct wavelets for specific applications [13–17]. In [13], a class of 4-band symmetric biorthogonal wavelet bases is constructed. They proposed that the high-pass filters can be determined by exchanging position and changing the sign of the two low-pass filters in any wavelet system. D Wang and X Zhang [14] have designed simultaneously two scaling low-pass filters with the flat group delay arbitrarily specified to obtain orthogonal and almost symmetric complex wavelets.

These wavelets are designed to satisfy orthogonality and symmetry. However, P waves and T waves which are important signals used in the clinic, expressing the characteristics of the heart function, are not obvious in some leads. The wavelets with orthogonality and symmetry still exist the risk that the characteristics of the P and T waves will be blurred and weaken after denoising. Particularly, when the subject is the atrial fibrillation (AF) signal, the F wave will be weakened (for example, in [18], the F wave is treated as the interference in the ECG signal, and the discrete packet wavelet transform (DPWT) method is used to extract the F wave).

Therefore, a method of modified wavelet design is proposed in this paper. By optimizing the filter coefficients to approximate the ideal filter, a nearly symmetric orthogonal wavelet is obtained and applied to ECG signal denoising. The main contents of the paper are as follows: in the second section, the method of wavelet denoising and the design of modified wavelet are proposed. The third section presents the results of experiments and tests the performance of the proposed method. In the fourth section, we discuss the experiment and summarize the advantages of the modified wavelet design. The fifth section gives the conclusion. Finally, the sixth section gives the acknowledgment.

2. Materials and methods

2.1. Wavelet denoising for ECG

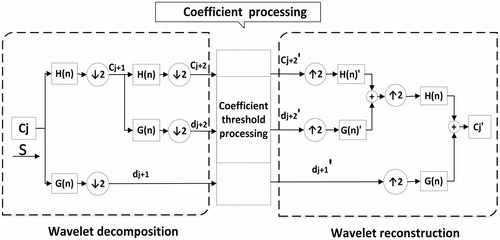
As shown in Figure 1, the algorithm of wavelet denoising mainly contains three steps: wavelet decomposition, coefficient processing, wavelet reconstruction (the figure is based on [16]).

Figure 1. Schematic diagram of wavelet denoising algorithm.

In the process of wavelet decomposition, two-scale equations are used to realize the dilation and translation of time, and then the scale coefficients and wavelet coefficients at any scale are obtained. The Fourier transform of the scaling function and the wavelet function have the properties of low pass and high pass filtering respectively. Therefore, the wavelet transform and wavelet denoising can be realized by the Mallat algorithm [19] as shown in Figure 1. Where ‘S’ is the input signal, and ‘H(n)’ and ‘G(n)’ are low-pass and high-pass filters respectively. H(n) and G(n) form a dual-channel filter bank as a pair of mirror filters. The filter coefficients h(n) and g(n) are determined by the scaling function and the wavelet function respectively. In the process of coefficient processing, the threshold is estimated according to the characteristics of EMG noise and is used to deal with the decomposed wavelet coefficients. For the wavelet reconstruction, the processed wavelet coefficients are reconstructed by the mirror filter, and the denoised ECG signal is obtained.

2.2. Modified wavelet design

2.2.1. The principle of design

As for the denoising of clinical ECG signals, in order to achieve reconstruction of signals accurately, the requirements for the performance of filters are very high. The ideal filter can reduce the frequency components in the stopband to zero and filter the noise effectively. However, it is not available. Filters often exist aliasing-distortion with energy loss in practical applications.

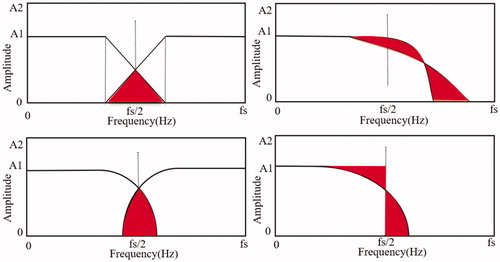
Therefore, when the dual-channel filter decomposes the noisy signal into multiple frequency bands, the characteristic information is easily weakened and lost in the frequency crossing bands. The amplitude-frequency response (AFR) of different aliasing types in the decomposition of signals are shown in Figure 2. If the frequency components of characteristic signals are exactly in the red regions as shown in

Figure 2. AFR of different frequency aliasing types.

Figure 2, the characteristic signal will be divided into details and contour parts when the nonideal filter as the wavelet coefficient decomposes the signal. Moreover, if the characteristic signal itself is weak, the coefficient will become smaller in the different parts. When the wavelet decomposition coefficients of the characteristic signal are processed by the threshold method, they are more likely to be estimated to be noise parts and be removed, thus increasing the risk of denoising. Therefore, in order to reduce the risk of eliminating the feeble features of ECG signals in denoising, this paper proposes to construct an optimized filter by approximating the ideal filter, thus the modified wavelet can be designed.

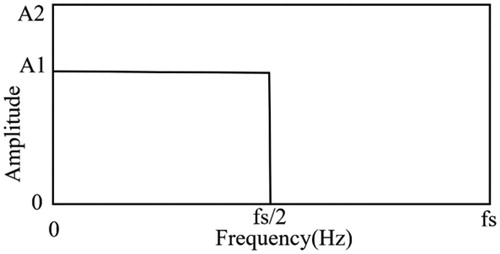
An ideal filter with AFR is shown in Figure 3. Considering that the scale function also has the similar AFR, each detail or approximation level contains only certain frequency components supposed to exist in the exact level. In addition, using the ideal filter can build orthogonal wavelets, so it would be a good idea to use symmetric coefficients to approximate the ideal filter.

Figure 3. AFR of the ideal filter.

The disparity between the filter and ideal filter determines the filtering performance directly. In order to minimize the gap, we define an error function as in Equation (1)(1) $$\min \left(\mathit{\text{Eamp}}\right)=\min \left(\sum _{w=0}^{\pi /2}\left(1-{\left|H\left(w\right)\right|}^2\right)+\sum _{w=\pi /2}^{\pi }{\left|H\left(w\right)\right|}^2\right)$$(1) . (1) $$\min \left(\mathit{\text{Eamp}}\right)=\min \left(\sum _{w=0}^{\pi /2}\left(1-{\left|H\left(w\right)\right|}^2\right)+\sum _{w=\pi /2}^{\pi }{\left|H\left(w\right)\right|}^2\right)$$(1)

$\mathit{\text{Eamp}}$ presents the error between the filter and the ideal filter and $H(\omega )$ is the AFR of the filter. Minimum $\mathit{\text{Eamp}}$ in Equation (1)(1) $$\min \left(\mathit{\text{Eamp}}\right)=\min \left(\sum _{w=0}^{\pi /2}\left(1-{\left|H\left(w\right)\right|}^2\right)+\sum _{w=\pi /2}^{\pi }{\left|H\left(w\right)\right|}^2\right)$$(1) is tantamount to optimize the AFR of the filter and make the wavelet nearly orthogonal. However, it is intractable to minimize $\mathit{\text{Eamp}}$. Therefore, using filter coefficients to express the problem turns out to be a good choice. Given an L-length filter, the AFR can be expressed as: (2) $${\left|H\left(w\right)\right|}^2=\frac{1}{2}\left[{\left|\sum _{n=0}^{L-1}h\left(n\right)\hspace{0.17em}\text{cos}\hspace{0.17em}nw\right|}^2+{\left|\sum _{n=0}^{L-1}h\left(n\right)\hspace{0.17em}\text{sin}\hspace{0.17em}nw\right|}^2\right]$$(2)

Where $h(n)$ are symmetric filter coefficients in a form of $[a,b,c,\dots ,c,b,a]$. In order to satisfy the needs of wavelet filters, $h(n)$ is set up to be: (3) $$\sum _{n}h\left(n\right)=\sqrt{2}$$(3)

Now the design goal becomes to a minimum $\mathit{\text{Eamp}}$ in Equation (1)(1) $$\min \left(\mathit{\text{Eamp}}\right)=\min \left(\sum _{w=0}^{\pi /2}\left(1-{\left|H\left(w\right)\right|}^2\right)+\sum _{w=\pi /2}^{\pi }{\left|H\left(w\right)\right|}^2\right)$$(1) under the constraint of Equation (3)(3) $$\sum _{n}h\left(n\right)=\sqrt{2}$$(3) . It makes the objective function a multivariate polynomial equation and quadratic for all filter coefficients by inserting Equation (2)(2) $${\left|H\left(w\right)\right|}^2=\frac{1}{2}\left[{\left|\sum _{n=0}^{L-1}h\left(n\right)\hspace{0.17em}\text{cos}\hspace{0.17em}nw\right|}^2+{\left|\sum _{n=0}^{L-1}h\left(n\right)\hspace{0.17em}\text{sin}\hspace{0.17em}nw\right|}^2\right]$$(2) to Equation (1)(1) $$\min \left(\mathit{\text{Eamp}}\right)=\min \left(\sum _{w=0}^{\pi /2}\left(1-{\left|H\left(w\right)\right|}^2\right)+\sum _{w=\pi /2}^{\pi }{\left|H\left(w\right)\right|}^2\right)$$(1) . To solve this problem, the trust-region-reflective quadprog algorithm which is a simple yet powerful tool for optimization is chosen. Subsequently, we can get the filter coefficients of different lengths.

2.2.2. Realization of modified wavelet

Considering that the coefficient is symmetric, the filter length must be even. By setting the length of the filter H(n) to 8, the wavelet filter coefficients as shown in Table 1 can be obtained by solving the Equation (1)(1) $$\min \left(\mathit{\text{Eamp}}\right)=\min \left(\sum _{w=0}^{\pi /2}\left(1-{\left|H\left(w\right)\right|}^2\right)+\sum _{w=\pi /2}^{\pi }{\left|H\left(w\right)\right|}^2\right)$$(1) .

Table 1. Fibr wavelet coefficients.

Length	Coefficients: h(n)
8	0.001590, −0.056193, 0.056736, 0.493436, 0.493436, 0.056736, −0.056193, 0.001590

The scaling function is obtained by iterative numerical convolution of optimized filter coefficients and is also called the wavelet father function. The wavelet function called mother wavelet can be obtained by scaling function according to the two-scale equation, then the wavelet is defined by these two functions. Afterward, the approximate orthogonal wavelet which is constructed by the coefficients is named fibr wavelet and the diagrams of a scaling function and wavelet function are shown in Figure 4.

Figure 4. The result of wavelet design (fibr wavelet). From the left to right: (a) The scaling function diagram (b) The wavelet function diagram.

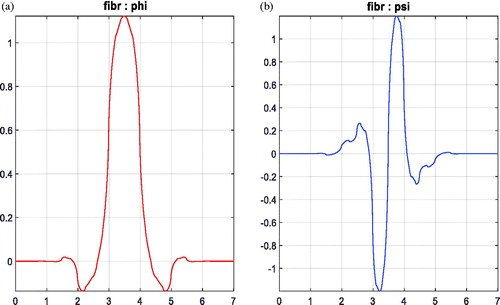
Figure 4 shows the scaling function diagram and wavelet function diagram of fibr wavelet. We can observe that a wavelet with the symmetry scaling function and anti-symmetry wavelet function is obtained by setting $h(n)$ in form of $[a,b,c,\dots ,c,b,a]$.

2.3. Denoising evaluation

In order to test the denoising effect of the modified wavelet, the signal to noise ratio (SNR) and the mean square error (MSE) are used [1]. The SNR and MSE are defined as follows： (4) $$SNR=10\lg \left(\frac{\sum _{n=1}^N{x}^2\left(n\right)}{\sum _{n=1}^N{\left[x\right(n)-y(n\left)\right]}^2}\right),\hspace{1em}MSE=\frac{\sum _{n=1}^N{\left[x\right(n)-y(n\left)\right]}^2}{N}$$(4)

In the Equation (4)(4) $$SNR=10\lg \left(\frac{\sum _{n=1}^N{x}^2\left(n\right)}{\sum _{n=1}^N{\left[x\right(n)-y(n\left)\right]}^2}\right),\hspace{1em}MSE=\frac{\sum _{n=1}^N{\left[x\right(n)-y(n\left)\right]}^2}{N}$$(4) , $x(n)$ is the original signal, $y(n)$ is the reconstructed signal after wavelet denoising, and N is the length of the signal. The bigger the SNR value is, the better the effect is, while the MSE value needs to be smaller to get the better effect.

3. Results

3.1. Data sources

In this paper, we test our methods by using the normal clinical ECG data as well as simulated AF signals.

The clinical data used in this paper comes from the standardized database which is collected and processed by SID Medical Technology Co. Ltd. This corporation specializes in ECG medical science and technology. Moreover, its huge clinical database is the diagnosis data which comes from consecutive patients in the Department of Cardiology in several authoritative hospitals in Shanghai. After the doctor's accurate diagnosis and desensitization processing, all the data are stable and standard, which can be used for signal processing and disease automatic diagnosis.

In the experimental 3.2.1 and 3.2.2, the data used is normal ECG data which contains 87 consecutive normal ECG records from the database mentioned. Each record lasted 10 s with 12 leads, and acquisition equipment parameters of ECG signals are shown in Table 2 (the parameters are provided by the technology company). All these records represent the consecutive patients in the Department of Cardiology of hospitals respectively. According to the statistics of these patients, the age range is from 30 to70 years old, and the proportion of women is greater than that of men.

Table 2. Parameters of the acquisition equipment.

Parameters	Values
Defibrillation protection voltage	5000 V
DC polarization voltage	±300 mV, ±5%
Frequency response	1–75 HZ, +0.5 dB, −3.0 dB
Dynamic input range	20 mV
Calibration voltage and accuracy	1 mV, ±5％
CMRR（Common mode rejection ratio）	>60 dB
System noise	≤15 $\mu \mathrm{V}$
Nonlinear error	±10％
Baseline drift	≤1 mm (5－40 °C )
A/D resolution	13 byte, 2.44/bit
Digital sampling rate	500 Hz
Signal length/sampling point	5000

In the experimental 3.2.3, the data is derived from the simulated AF signals synthesized by the simulated F waves and clinical normal ECG signals mentioned. The F waves are generated by the method that is shown in [20]. The parameters [20] used in this paper are shown in Table 3.

Table 3. Parameters using for generating F waves.

Parameters	Values
Frequency, $f_0$	6 Hz
Frequency variation, $\Delta f$	0.2 Hz
Frequency variation frequency, $f_f$	0.1 Hz
Harmonics, M	3
Amplitude, am [ II V1 V5 ]	[150 75 45]$\mu v$
Amplitude variation, Δam [ II V1 V5 ]	[50 25 15]$\mu v$
Amplitude variation frequency, $f_a$	0.08 Hz

3.2. Denoising results

In order to test the denoising effect of fibr wavelet, the following denoising experiments for different ECG signals are carried out.

3.2.1. Denoising results on normal ECG

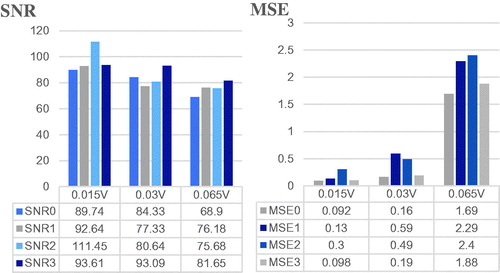
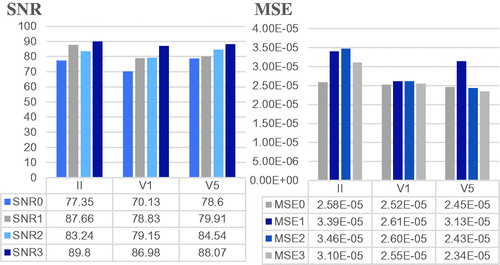
Based on the normal ECG signals of 87 records mentioned in the data sources, the random white Gaussian noise (WGN) with an expected amplitude of 0.3 V is added. The average SNRs are shown in row SNR0 in data sheets of Figure 5. Sym4 and db4 wavelets are used for comparison with fibr wavelet.

Figure 5. The average denoising effects on normal ECG.

According to the frequency characteristics of EMG, the number of decomposition level is set to 8. The threshold is the sure threshold obtained by the unbiased risk estimate of Stein. For a given threshold T, the likelihood estimation is obtained and minimize the likelihood function, then the selected threshold can be obtained. Subsequently, the high-frequency coefficients are processed by soft threshold quantization [1] under each decomposition scale. The wavelet can be reconstructed based on the lowest low-frequency coefficients of wavelet decomposition and the high-frequency coefficient of each layer. And this processing methods are also used in the experiments of section 3.2.2 and section 3.2.3.

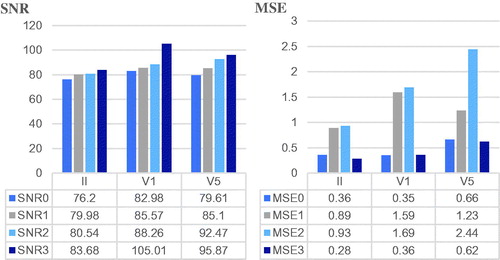
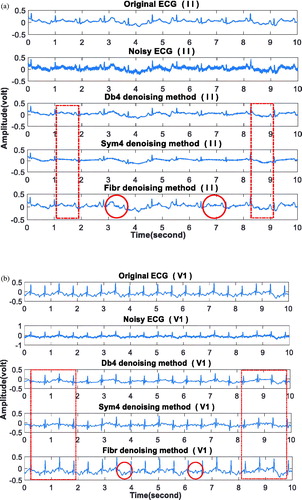
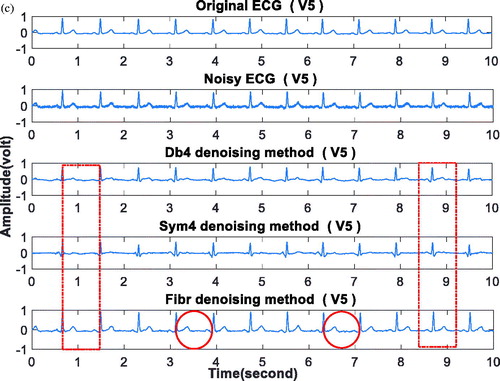
The result for a normal record with II, V1 and V5 leads are shown in Figure 6. And the average denoising effects evaluated by SNR and MSE, are shown in Figure 5.

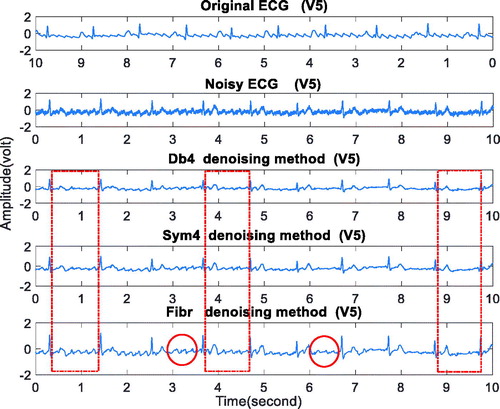
Figure 6. The denoising result on normal ECG. From top to bottom: (a) lead II (b) leadV1 (c) lead V5.

The Original ECG in Figure 6 represents the normal ECG signal mentioned in section 3.1. The Noisy ECG is the signal synthesized by adding the random white Gaussian noise (WGN) with an expected amplitude of 0.3 V on the Original ECG. The denoising results by db4, sym4, fibr wavelets are shown in following three Figures entitled Db4 denoising method, Sym4 denoising method, Fibr denoising method. In the data sheet of Figure 5, the row SNR(i) and row MSE(i) (i = 0,1,2,3) represent the SNR and MSE of noisy signal, db4 wavelet, sym4 wavelet and fibr wavelet denoising respectively.

Figure 6 shows that, for II, V1 and V5 leads, the proposed method can retain the P wave and T wave information as shown in the red tagging parts. It demonstrates that fibr wavelet outperforms db and sym wavelets for ECG denoising. Figure 5 gives the bar charts of mean values of SNR and MSE and data sheets. It shows that the SNR of the fibr wavelet denoising is the largest and the MSE is the smallest in the three leads, indicating that the fibr wavelet is more capable than the db4 and sym4 wavelets to suppress the noise.

3.2.2. Denoising results on ECG signals under different noise levels

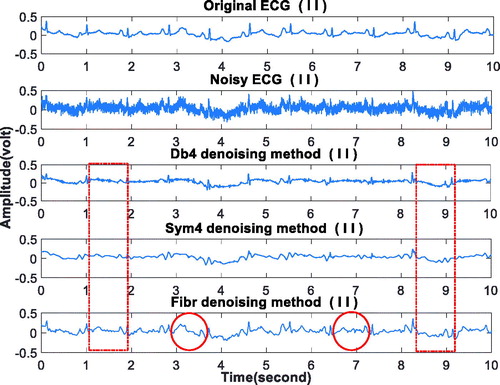
The random WGN with expected amplitudes of 0.015 V, 0.03 V, and 0.065 V are added to 87 records respectively. The result for a normal record with II lead is shown in Figure 7. And the average denoising effects evaluated by SNR and MSE, are shown in Figure 8.

Figure 7. The denoising result under the noise with expected amplitude of 0.065 V.

Figure 8. The average denoising effects at different noise levels.

The specific meanings of Original ECG, Noisy ECG, Db4 denoising method, Sym4 denoising method, and Fibr denoising method in Figure 7 are the same as those in the experiment of Section 3.2.1. Moreover, the specific meanings of the values of SNR(i) and MSE(i)(i = 0,1,2,3) in Figure 8 are the same as those in the experiment of Section 3.2.1.

Figure 7 shows that when the noise expected amplitude reaches 0.065 V, the proposed method can still retain the P wave and T wave information as shown in the red tagging parts. It demonstrates that fibr wavelet outperforms db and sym wavelets in ECG denoising once again. Meanwhile, Figure 8 gives the average denoising results of at different noise levels. It shows that when the noise expected amplitude reaches 0.065 V, the SNRs for the db4 wavelet, the sym4 wavelet, and the fibr wavelet denoising methods are calculated to be 76.18, 75.68, and 81.65 dB, respectively. It can be seen that the SNR of the fibr wavelet denoising is the largest and the MSE is the smallest generally, indicating that the fibr wavelet denoising method is superior to the db4 and sym4 wavelets.

3.2.3. Denoising results on the simulated AF signals

Based on the normal ECG signals, firstly add the F waves generated according to the parameters in Table 2 and then the random WGN with an expected amplitude of 0.1 mv is added. The average SNRs are shown in row SNR0 in the data sheets of in Figure 9. Sym4 and db4 wavelets are used for comparison. The result for a simulated AF signal with V5 lead is shown in Figure 10. Also, the average denoising effects evaluated by SNR and MSE are presented in Figure 9.

Figure 9. The average denoising effects on simulated AF signals.

Figure 10. The denoising result on the simulated AF signal.

The specific meanings of Original ECG, Noisy ECG, Db4 denoising method, Sym4 denoising method, and Fibr denoising method in Figure 10 are the same as those in the experiment of Section 3.2.1. The specific meanings of the values of SNR(i) and MSE(i)(i = 0,1,2,3) in the data sheets of Figure 9 are the same as those in Section 3.2.1.

Figure 10 shows that when the subject is the atrial fibrillation ECG signal, the proposed method can retain the F wave information as shown in the red tagging parts. It demonstrates that fibr outperforms db and sym wavelets for denoising on simulated AF signals. Figure 9 gives the average denoising results on simulated AF signals. It shows that the SNR of the fibr wavelet denoising is the largest and the MSE is the smallest, which confirms the superior performance of the proposed method when applied to the noise of AF signals. These results further demonstrate that the proposed method is not only applicable to ECG denoising but also suitable for denoising on AF signals.

3.3. Discussion of results

The 12-lead ECG signals are usually used in clinical. Sometimes, P waves and T waves are not obvious in some leads. When it happens, the start and end of P wave and T wave are usually determined by observing good leads. However mobile ECG monitoring devices usually have only three leads: II, V1, and V5 leads.

While denoising for these three-lead ECG signals, the fibr wavelet preserves the P wave and T wave characteristic information as shown in the Figure 6 and Figure 7, showing that the proposed denoising method is potentially useful for the three-lead ECG equipment. In Figure 10, the proposed wavelet retains recurrent F wave information during denoising, demonstrating the advantages of fibr wavelet denoising for AF signals.

Figure 5, 8, and 9 show that, with the increase of the noise amplitude, the values of MSE becomes larger up to 10 times and the effects of denoising obviously becomes worse. This demonstrates that the larger the noise is, the greater the risk of eliminating useful information is. However, Figure 7 shows that compared to db and sym wavelets, fibr wavelet can still retain the waveform characteristics of P waves and T waves.

4. Conclusion

In order to reduce the weakening of the feeble features in the ECG signals by wavelet denoising, an optimized design method of the mother wavelet is proposed. The optimized filter coefficients are obtained by approximating the amplitude-frequency response of the ideal filter, and the wavelet is constructed with the optimized filter coefficients and applied to the denoising of ECG signals.

The proposed method is tested by clinical ECG data and compared with db4 and sym4 wavelet, the modified wavelet can retain the feeble features such as P waves, T waves and recurrent F waves in the process of denoising. Meanwhile, it can improve the signal to noise ratio and reduce the mean square error for the denoising effectively.

The method proposed in this paper provides theoretical guidance for the ECG signal denoising in mobile medical treatments and also provides a way to denoise other types of signals with feeble features.

Disclosure statement

The authors report no potential conflict of interest.

Additional information

Funding

This work was supported by Natural Science Foundation of Zhejiang province [Grant No. LQ18F010006] and National Natural Science Foundation of China [Grant No. 61801454].