Shewhart control charts for dispersion adjusted for parameter estimation

ABSTRACT

Several recent studies have shown that the number of Phase I samples required for a Phase II control chart with estimated parameters to perform properly may be prohibitively high. Looking for a more practical alternative, adjusting the control limits has been considered in the literature. We consider this problem for the classic Shewhart charts for process dispersion under normality and present an analytical method to determine the adjusted control limits. Furthermore, we examine the performance of the resulting chart at signaling increases in the process dispersion. The proposed adjustment ensures that a minimum in-control performance of the control chart is guaranteed with a specified probability. This performance is indicated in terms of the false alarm rate or, equivalently, the in-control average run length. We also discuss the tradeoff between the in-control and out-of-control performance. Since our adjustment is based on exact analytical derivations, the recently suggested bootstrap method is no longer necessary. A real-life example is provided in order to illustrate the proposed methodology.

KEYWORDS:

• S control chart
• adjusted control limits
• parameter estimation
• Phase I
• Phase II

1. Introduction

The limits of a control chart depend on the in-control value(s) of the parameter(s) of the process. In the more typical situation where these parameter values are unknown, estimates are obtained from an in-control Phase I sample and used in their place. However, as Phase I samples vary across practitioners, the estimated control limits also vary. This variation is referred to as practitioner-to-practitioner variation. As a consequence, chart performance differs across practitioners, even when the same nominal in-control performance measure, such as the in-control Average Run Length (ARL) value, is used in the construction of the charts. The variation and degradation in chart performance as a result of parameter estimation has been highlighted by several researchers. Until very recently, the performance of a control chart was generally measured in terms of the unconditional run length (RL) distribution and its associated attributes, such as the unconditional ARL or the unconditional False Alarm Rate (FAR). For reviews of work performed up to 2006 see Jensen et al. (2006), and for more recent developments see Psarakis et al. (2014). One way to improve the performance of a Phase II control chart is to increase the amount of Phase I data. For example, in the context of standard deviation, early research (Chen, 1998)) recommended the use of around 75 subgroups of size 5 in Phase I for Shewhart charts, whereas Maravelakis et al. (2002) recommended using 100 subgroups of size greater than 20 or 200 subgroups of smaller size. However, these results were based on unconditional performance measures and do not take into account the practitioner-to-practitioner variability, as the unconditional formulation averages out such effects.

Motivated by this observation, recent research has advocated the use of the conditional RL distribution in the construction and implementation of control charts. From this perspective, Chakraborti (2006) and Saleh, Mahmoud, Keefe, and Woodall (2015), for the case of the chart, and Epprecht et al. (2015), for the case of the S chart (where S is the sample's standard deviation), evaluated the effects of parameter estimation on the in-control conditional RL distribution. Because the conditional RL distribution is geometric, it can be characterized by the probability of success, the so-called Conditional False Alarm Rate (CFAR), or its reciprocal, the in-control Conditional Average Run Length (CARL). Since the CFAR (CARL) is a random variable, Epprecht et al. (2015) proposed a prediction bound formulation to determine the number of Phase I subgroups required such that a minimum in-control performance based on the CFAR or CARL of the one-sided S chart is guaranteed with a pre-specified probability. However, it was seen that based on this approach, the number of subgroups required to guarantee a practically attractive in-control chart performance is in the order of several hundreds or thousands, depending on the choice of the estimators. These numbers are substantially higher than the values recommended by previous authors based on the unconditional in-control ARL. Saleh, Mahmoud, Keefe, and Woodall (2015) reached similar conclusions with respect to the and X charts.

This presents a dilemma for the practitioner. Working with the conditional RL distribution and its various attributes (such as the CFAR or the CARL) makes more sense from a practitioner's point of view. However, the amount of Phase I data required is often huge, to the point of being almost impractical. Thus, from a practical standpoint, another approach is necessary. One such recent proposal is to adjust the control limits to guarantee a minimum in-control chart performance based on the CFAR (or CARL; see, e.g., Albers and Kallenberg (2004), Gandy and Kvaløy (2013), and Goedhart et al. (2017)) with a given probability. This is the idea pursued in this article. Note that in this context, bootstrap methods have already been proposed (e.g., Gandy and Kvaløy (2013), Faraz et al. (2015), Salah, Mahmoud, Jones-Farmer, Zwetsloot, and Woodall (2015), and Saleh, Mahmoud, Keefe, and Woodall (2015)) to find the adjusted control limits. Although this computer-intensive method eventually leads to the desired results and is more broadly applicable, analytical expressions give more insight into the required adjustments and are, in general, easier to implement.

The choice between analytical and bootstrap methods depends on what assumptions one can reasonably make about the underlying process distribution. Here we assume normality, as that is the most common assumption in practice. Moreover, since an increase in the process dispersion is deemed more important to detect (this indicates process degradation), we consider the upper one-sided chart (where is the sample charting statistic of dispersion), equivalent to Epprecht et al. (2015) and derive the corresponding adjusted upper control limits. These adjusted limits guarantee that the CFAR exceeds a pre-specified tolerated bound with only a small probability, for a given number of Phase I samples of a given size. The adjusted control limits are obtained by replacing the coefficient of the traditional Phase I control limit by an adjusted coefficient. This adjusted control limit coefficient is obtained analytically, as opposed to using the bootstrap approach as in Faraz et al. (2015), and its efficacy also depends on the type of estimator used to estimate the in-control process dispersion from the given Phase I data. Our formulation and derivations allow the use of different estimators for the process dispersion. We illustrate the concepts using one well-known estimator of Phase I standard deviation, namely, the square root of the pooled variances. Note further that the adjusted control limit can also be obtained for control charts based on monotone-increasing functions of the process dispersion , such as or log(), by taking the corresponding monotone-increasing function of the adjusted limit for the chart. Furthermore, our framework is applicable for the range charts. See also the tutorial on estimating the standard deviation written by Vardeman (1999).

After determining the adjustment coefficient, we examine the impact of using the resulting adjusted control limits on charts' out-of-control performances. To this end, performance comparisons are made between charts with the adjusted and the unadjusted control limits for detecting increases in σ. As previously mentioned, Faraz et al. (2015) also considered the problem of adjusting the S and S² chart control limits. They used the bootstrap method of Gandy and Kvaløy (2013) to obtain the adjusted coefficients. However, their out-of-control performance analysis was restricted to a pair of boxplots of the distribution of a chart's out-of-control CARL with the adjusted and unadjusted control limits.

Our contributions are as follows. We consider the problem of adjusting the control limits for the Phase II control charts for dispersion so that a minimum in-control chart performance (in terms of CFAR or CARL) can be guaranteed with a pre-specified probability. We provide an analytical solution that enables a straightforward calculation of the adjusted control limit for any combination of parameters, which include the number of available reference samples m, sample size n, a desired performance threshold (to be defined later), and a specified probability of this threshold being exceeded. We give tables of the adjustment coefficients for a wide range of these parameter values. Also, we provide a formula for computing the out-of-control CARL of the resulting chart for any increase in the process dispersion. This is compared with the out-of-control CARL for the chart with the unadjusted limits, in order to assess the impact of the adjustment on the chart's out-of-control performance. A practitioner has to balance two things: controlling the in-control performance versus the deterioration in the out-of-control situation. We provide some guidelines on how a practitioner can balance this tradeoff. Our derivations are based on Shewhart-type control charts for dispersion. For a comparison of other control chart designs, such as the CUSUM and the EWMA, we refer to Acosta-Mejia et al. (1999).

This article is structured as follows. We present the analytical derivations of the adjusted limits in Section 2 and of the resulting chart's power (the probability that the chart gives a true signal in the case of an increase in process dispersion) in Section 3. Then in Section 4, the adjusted limits, as well as the resulting power and the out-of-control ARL of the resulting chart, are tabulated for a comprehensive spectrum of cases and the results are discussed. In Section 5 we present and discuss a practical example as an illustration. Finally, general conclusions are summarized in Section 6.

2. Determination of the adjusted coefficients

Assume that after a Phase I analysis, m samples of size n each are available to produce an estimate of the in-control standard deviation (σ₀) and that the observations come from a N(μ, σ₀) distribution. In Phase II, samples of size n from a N(μ, σ) distribution, where both parameters are assumed unknown, are available and their standard deviations are monitored at each time period i on the basis of a statistic . Note that σ may differ from the in-control value σ₀. Our methodology works for all monitoring statistics (Phase II estimators of σ) that have a distribution either exactly or approximately proportional to a chi-square distribution (where the approximation is based on Patnaik (1950)). For example, we can take (i.e., the ith Phase II sample's standard deviation) and since it is well-known that  (n − 1)S²_i/σ_i² ∼ χ²_{n − 1} exactly, it follows that (where ∼ denotes distributed as) exactly under the normal distribution. On the other hand, if we consider then we approximate the distribution of by based on the approach of Patnaik (1950). We elaborate on this point later, in Section 2.4.

Note that when monitoring the process dispersion, it is generally of interest to detect and signal increases, as these situations indicate process degradation. Hence, we consider only an upper control limit, in line with other research (e.g., Epprecht et al. (2015)).

2.1. Unadjusted control limit

In this section we discuss the traditional (unadjusted) α-probability limits for the Phase II control chart for dispersion. Consider a monitoring statistic such that for suitable values a > 0 and b > 0. This means that given a desired nominal FAR α, the traditional estimated upper control limit of the chart is set at (1) with (2) where χ²_{[ν, p]} denotes the 100p-percentile of a chi-square distribution with ν degrees of freedom, and is the estimator of σ₀, which is the standard deviation of the in-control process in Phase I. Note that, for the specific case that is equal to the sample's standard deviation S, we know that a = 1 and b = n − 1, so that Equation (2(2) ) corresponds to Montgomery ((2013), p. 267). This standard control limit does not account for either parameter estimation or practitioner-to-practitioner variability and is referred to as the unadjusted control limit.

Note that, as previously mentioned, one can consider various estimators for that have a distribution proportional to the chi-square distribution. We consider this general point of view in our presentation. In order to find an expression for the probability of a signal, define the standard deviation ratio (3) where σ is the current (Phase II) process standard deviation. When the process is in control, σ = σ₀, so that  γ = 1. When special causes result in an increase in the process standard deviation, σ > σ₀ and consequently  γ > 1. Similarly, with a reduction in the standard deviation of a process, we have  γ < 1. However, we do not consider this latter case here, as the meaning and usefulness of detecting decreases in the process dispersion are totally different. Of course, one may consider a lower control limit using the same methodology as in our approach to study this behavior.

Next, define the error factor of the estimate as the ratio (4)

As it is assumed that the data come from a normal distribution, it is easy to see (Epprecht et al., 2015) that in Phase II, the Conditional Probability of an Alarm (denoted CPA) of the upper one-sided chart is given by (5)

since bL² = χ²_{[b, 1 − α]} from Equation (2(2) ), and where denotes the cumulative distribution function (cdf) of the chi-square distribution with b degrees of freedom. Note that Equation (5(5) ) holds for both the in-control case (γ = 1), in which case it corresponds to CFAR, and in the out-of-control case (γ > 1), where it represents the CPA of the chart, both in Phase II. Thus, (6)

The CPA of the chart in Equation (5(5) ) is also the CPA of the chart with equal to the square of the chart's in Equation (1(1) ). These two charts are equivalent: one will signal if and only if the other signals. In this article, we use the chart for illustration, but all analyses, numerical results, and conclusions equally apply to the chart. In fact, these observations hold for any monotone-increasing function of , such as log(), which is sometimes used in practice. In summary, for any monotone-increasing function of , is equivalent to . Therefore, the adjusted limits proposed for the chart can be applied to any monotone-increasing function g( of , by applying the same transformation to the obtained for the chart.

The CFAR shown in Equation (6(6) ) is a function of the error factor of the estimate W and, as a result, is also a random variable. Thus, the value of the CFAR will be different for different values of W, corresponding to different values of the estimator, from different Phase I samples obtained by practitioners. This is true unless W = 1, which is the case for consistent estimators when the number of reference samples tends to infinity, which implies the known parameter case. The finite sample distribution of W depends on the distribution of the estimator used for σ₀. In the case of normally distributed data, the most common estimators of the standard deviation of a process available in the literature follow, either exactly or approximately, a scaled chi-square distribution. Thus, in a general formulation, we consider estimators such that either exactly or approximately for suitable a and b. To distinguish between Phase I and Phase II estimators, we use a₀ and b₀ for Phase I and a and b for Phase II. This formulation allows a more general and comprehensive treatment of Phase II monitoring of σ, covering most common estimators of the standard deviation used: (i) in the Phase I control limit and (ii) as a plotting statistic in Phase II. For example, a commonly used estimator of σ₀ in the Phase I control limit is the square root of pooled variances (also recommended by Mahmoud et al. (2010)), defined as (7)

Since it is well known that m(n − 1)S²_p/σ₀² follows a chi-square distribution with m(n − 1) degrees of freedom, it follows that exactly, where a₀ = 1 and b₀ = m(n − 1). The plotting statistic for the Phase II S chart is the sample's standard deviation and since it is well known that (n − 1)S²_i/σ² ∼ χ_{n − 1}², it follows that , again exactly, where a = 1 and b = n − 1.  Other Phase I estimators of σ₀ such as where and c₄ is an unbiasing constant (see Montgomery (2013)) can be considered, but we do not pursue this here and use the estimator S_p for illustration throughout this article. Note further that other monitoring statistics and charts, such as the R chart, can also be considered under this framework. We make some comments about these points later in Section 2.3.

As in Epprecht et al. (2015), the cdf of the CFAR (denoted as F_CFAR) of the upper one-sided chart with the traditional as in Equations (1(1) ) and (2(2) ), set for a nominal FAR α, can be shown to be equal to (8)

Equation (8(8) ) thus implies that the cdf of the CFAR also depends on the distribution of this estimator.

Epprecht et al. (2015) also showed that the CFAR has a non-negligible probability of being much larger than the specified nominal value α, unless the number of Phase I samples is prohibitively high. Motivated by this observation, and with a practical point of view, we derive the adjusted control limit in order to guarantee a minimum performance based on the CFAR with a specified probability, for given values of m and n.

2.2. Adjusted control limit

We are interested in finding an adjustment to the traditional UCL in Equation (1(1) ), such that the probability that CFAR exceeds a tolerated upper bound (α_TOL) is controlled at a small value p. Formally, we want to determine an adjusted coefficient L* to be used to calculate the Phase I upper control limit such that (9) where (10)

Equation (9(9) ) requires a little explanation. The formulation in Equation (9(9) ), introduced in Epprecht et al. (2015), recognizes parameter estimation and practitioner-to-practitioner variability in working with the distribution of the random variable CFAR. The adjusted coefficient L* that solves Equation (9(9) ) guarantees that the CFAR is larger than the specified value α_TOL with probability p. Note that α_TOL thus serves as a lower bound to the CFAR  where ϵ (0 ⩽ ϵ < 1) is introduced to determine an appropriate value for α_TOL. The traditional nominal value α is obtained for ϵ = 0. Thus, practitioners can choose their own ϵ—for example, 0.10 (10%) or 0.20 (20%)—to determine an appropriate minimum performance threshold α_TOL, in order to relax the demands on the in-control performance. Thus, for example, if α =  0.005  and one chooses ϵ = 0.10, we obtain α_TOL = 0.0055. Note that Equation (9(9) ) can be rewritten as P(CFAR(t, L*) ⩽ α_TOL) = F_CFAR(α_TOL; L*) = 1 − p, so that the interval [0, α_TOL] can be interpreted as a 100(1 −p)% prediction interval for the CFAR. This interpretation may help in better understanding the proposed formulation.

Note also that Equation (9(9) ) is equivalent to writing P(CARL_in-control < 1/α_TOL) = p. Thus, solving Equation (9(9) ) is equivalent to finding the L* that guarantees a minimum in-control CARL equal to CARL_tol = 1/α_TOL, the minimum in-control CARL performance threshold, with a specified probability 1 − p. Due to this equivalence, our further derivations are based on CFAR. Note that the interval [1/α_TOL, ∞) can be interpreted as a 100(1 − p)% prediction interval for the CARL_in-control.

In order to determine L* from Equation (9(9) ), we need the cdf of CFAR. Similar to Equation (5(5) ), we can write the CFAR when using the adjusted limits as (11)

Thus, the cdf is obtained, similar to Equation (8(8) ), for 0 < t < 1 as (12)

since we assume that in general so that .

Now L* is determined so that (13)

Hence, using Equation (12(12) ), we obtain (14) which leads to the general solution (15)

We emphasize that Equation (15(15) ) is a general expression for the adjusted control limit coefficient that can be applied with any Phase I estimator for which and for which the Phase II monitoring statistic satisfies . Note that, if one would be interested in the equivalent correction for the , the only changes required are to substitute α_TOL for 1 − α_TOL and 1 − p for p in Equation (15(15) ).

2.3. Use of different estimators in Phase II

Until now we have considered general Phase I and Phase II estimators and , respectively. However, it is possible to use a wide range of estimators in both Phase I and Phase II. Consider, for example, the use of the pooled standard deviation in Phase I and the standard deviation in Phase II. We then have a₀ = 1, b₀ = m(n − 1), a = 1, and b = n − 1. Implementing these values in Equation (15(15) ) then gives us the required control limit for this special case as (16)

Note that this special case is equal to the result of Tietjen and Johnson (1979), who determined tolerance intervals for this specific example. However, our approach is more generally applicable, as we allow a wide range of estimators in both Phase I and Phase II. For more information on estimators of dispersion, we refer to Vardeman (1999).

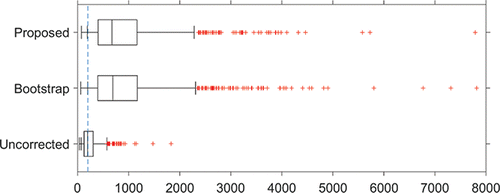
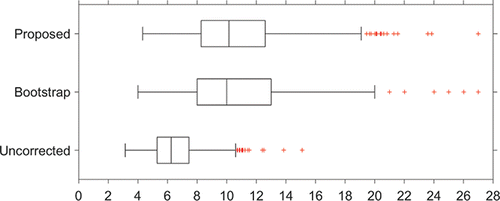
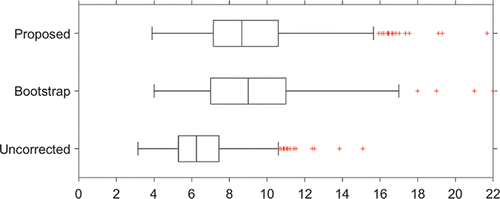
To illustrate the application and the consequences of implementing the adjusted control limits, ^{Figure 1, Figure 2}Figures 1 and 2 show boxplots of 1000 simulated CARL values for the in-control (γ = 1) and an out-of-control (γ = 1.5) situation, respectively, with m = 50, n = 5, α = 0.005, ϵ = 0.1, and p = 0.1, so that α_TOL = 0.0055. We have used S_p as estimator of the Phase I standard deviation and S as estimator in Phase II. In the in-control situation (Fig. 1), CARL_tol = 1/α_tol = 1/0.0055 = 182. For comparison purposes, the boxplots also show the results of using the bootstrap method of Gandy and Kvaløy (2013) and Faraz et al. (2015) and of the chart with unadjusted limits. The minimum tolerated CARL of 182 is indicated with a vertical dashed line, and the p-quantile of the CARL distribution is indicated in each boxplot with an added short vertical line. As can be seen, the p-quantile coincides with CARL_TOL = 182 for the adjusted control limits. Note that the difference between the proposed method and the bootstrap approach is negligible. However, the proposed control limits are analytical expressions that are easier to implement, and the required adjustments are found more directly through the use of statistical distribution theory. For additional insight into the effect of the choices of ϵ and p, Figures 3 and 4 illustrate, equivalent to Figures 1 and 2, respectively, this effect for ϵ = 0  and p = 0.05. There the p-quantile coincides with CARL_TOL = 200.

Figure 1. Boxplots of 1000 simulated values of in-control (γ = 1) CARL. Parameter values are m = 50, n = 5, α = 0.005, ϵ = 0.1, and p = 0.1. The dashed vertical line indicates CARL_tol = 1/α_tol = 182, and the p-quantiles are indicated with an added vertical line in the boxplots.

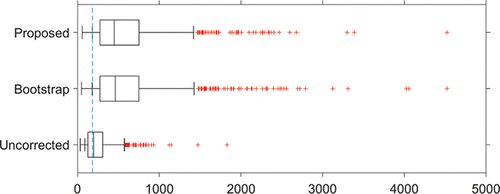
Figure 2. Boxplots of 1000 simulated values of out-of-control (γ = 1.5) CARL. Parameter values are m = 50, n = 5, α = 0.005, ϵ = 0.1 , and p = 0.1.

Figure 3. Boxplots of 1000 simulated values of in-control (γ = 1) CARL. Parameter values are m = 50, n = 5, α = 0.005, ϵ = 0, and p = 0.05. The dashed vertical line indicates CARL_tol = 1/α_tol = 200, and the p-quantiles are indicated with an added vertical line in the boxplots.

Figure 4. Boxplots of 1000 simulated values of out-of-control (γ = 1.5) CARL. Parameter values are m = 50, n = 5, α = 0.005, ϵ = 0 , and p = 0.05.

2.4. Distributions of different estimators of the standard deviation

We have noted that in general we can consider any estimator such that either exactly or approximately. We make a few comments here in this direction. First, the estimator used in Phase I usually dictates the chart to be used in Phase II. Thus, if is estimated by a function of the Phase I sample standard deviations, we use an S chart in Phase II for consistency, whereas if is estimated by a function of the Phase I sample ranges, we use an R chart in Phase II for monitoring the standard deviation. For some estimators such as S_p, as shown above, this distribution theory is exact, but that is not the case for all estimators that have been proposed in the literature for the standard deviation of a normal distribution. However, for many of the available estimators, their distribution can be approximated. One common approach to do this is by equating the first two moments of W with those of (see, for example, Patnaik (1950)). We consider such an approximation based on Patnaik (1950), as used in Roes et al. (1993). For an estimator such that E[W] = 1, so that is an unbiased estimator of σ₀, Roes et al. (1993) showed that the required values of a₀ and b₀ must equal: (17) where^{Table 1}V[W] denotes the variance of W. Recognizing the fact that practitioners might use other estimators of the standard deviation, we summarize three popular estimators of the Phase I standard deviation σ₀ along with the corresponding values of a₀ and b₀ in Table 1. Of course, the same approach can be used for the Phase II estimators. Note that we have also indicated the corresponding Phase II plotting statistic and its corresponding values of a and b in Table 1.

Table 1. Required values of a and b (and a₀ and b₀) for different estimators used in the calculation of the adjusted control limit.

Phase II plotting statistic	Values of a and b	Phase I estimator	Values of a0 and b0	V[W]
	a = 1,b = n − 1	Pooled sample standard deviation	a0 = 1b0 = m(n − 1)	1 − c^24(m(n − 1) + 1)
	a = 1, b = n − 1	Average sample standard deviation
		Average sample range

Note that the constants c₄(n), d₂(n), and d₃(n) can be found in Appendix VI in Montgomery (2013).

2.5. Deviations from the proposed model

The derivations as shown in this section are based on one-sided control charts for dispersion under normality. In the case where the normality assumption is violated, the adjustments are less accurate in terms of providing a specified in-control performance. However, a suitable alternative is to apply a Box–Cox transformation (see Box and Cox (1964)) or a Johnson-type transformation (see Chou et al. (1998)) to the data first and determine the control limits afterwards using this transformed data. Of course, the Phase II data need to be transformed in the same way during the monitoring stage.

Another way to investigate deviations from normality is to use robust estimators, in order to deal with contaminations. However, this means that an investigation as in Schoonhoven and Does (2012) is required, which may be the subject of a future study.

Whereas the problem with deviations from normality can be addressed in practice by applying a Box–Cox transformation, the proposed adjustments for the one-sided charts cannot be generalized directly to the two-sided control charts for dispersion. A common first guess when implementing the two-sided control chart is to calculate the upper and lower control limits using α/2 instead of α. However, in that case the guaranteed in-control performance results provided for the one-sided charts will no longer hold (see, for example, Goedhart et al. (2017)), so that the two-sided case needs to be analyzed separately. However, note that in practice, it is highly important to detect increases in process dispersion. By focusing on control charts with an upper control limit only, we provide control limits that are more sensitive to detecting these increases. Two-sided control charts would require a different approach, and their ability to detect increases would suffer from the addition of the lower control limit, while the benefits (detecting decreases in variation) are of minor importance in practice.

3. Out-of-control performance of the chart

By analogy with the power of a hypothesis test, the power of a control chart can be defined to be the probability that the chart gives a true signal. As the conditional RL distribution of the chart is geometric, the reciprocal of the conditional probability of a true signal, the CPA (or the conditional power), is the conditional out-of-control ARL, denoted CARL. As with the CFAR, the power (and the reciprocal of this power, the out-of-control CARL) of the chart with the adjusted limit depends on the realization (w) of the (unknown) error factor of the estimate, the random variable W. Note that the same is also true for the (or some other similar) chart with the unadjusted limit (see Equation (5(5) )). The power of the chart in the unknown parameter case will be larger (smaller) than the power for the known parameter case if w < 1; that is, when σ₀  is under-estimated (or if w > 1, that is, when σ₀ is over-estimated). The gain or loss in the out-of-control performance of the chart due to the use of the adjusted limit (relative to that of the chart using the unadjusted limit) will thus vary based on the realization of W. That is, the gain/loss of an out-of-control performance is also a random variable. See Zwetsloot (2016) for a more detailed comparison of the effect of estimation error in control charts for dispersion.

In order to examine the implications of using the adjusted limits on the out-of-control performance (power) of the chart, we evaluate the chart performance for the case when the estimation error is zero (w = 1; the known parameter case) and for increases of 50% and 100% in the standard deviation σ (γ = 1.5 and γ = 2.0, respectively). This is because the conditional probability of an alarm depends only on the ratio between w and γ and not on their absolute values (as can be seen from Equation (5(5) )).

To calculate the out-of-control CARL, recall from Equation (5(5) ) that the conditional probability of an alarm (or a signal; CPA) with the adjusted limit is given by (18) which, for the estimators and equals, using Equation (16(16) ) (19) where

The out-of-control (γ ≠ 1) CARL is the reciprocal of CPA(γ, L*) in Equation (18(18) ) in general and of Equation (19(19) ) in particular for the estimators . The probability in Equation (18(18) ) can be calculated for various values (quantiles) from the distribution of Y and the out-of-control performance can be examined. Thus, from Equation (18(18) ) it is also possible to determine the distribution of the CPA for given values of γ and L*.

4. Results and discussion

4.1. Out-of-control performance evaluation

Tables 2 and 3 show, for several values of m and n, the values of the adjusted control limit coefficient L* for the estimator S_p, for a nominal FAR of α = 0.005, and the combinations of two values of ϵ (0.10 and 0.20) and two values of p (0.05 and 0.10). Table 2 corresponds to ϵ = 0.10 and Table 3 ϵ = 0.20. For each value of n, the first row gives the values of L* and the second row gives in italics the adjustment factor, which is the ratio between these values and the unadjusted control limit coefficient L. Other estimators of σ₀ can be considered in a similar manner.

Table 2. Control limit coefficients: Unadjusted and adjusted for S_p with ϵ = 0.10 (α = 0.005). Every second row (in italics) gives the ratio between the adjusted and the unadjusted limit.

					L*
			L*/L
p	n	L	m = 25	50	100	200	500
0.05	3	2.302	2.736	2.584	2.487	2.422	2.368
			1.188	1.123	1.080	1.052	1.029
	5	1.927	2.167	2.086	2.032	1.996	1.965
			1.125	1.082	1.054	1.035	1.019
	10	1.619	1.746	1.704	1.675	1.655	1.638
			1.079	1.052	1.035	1.023	1.012
	15	1.496	1.588	1.557	1.537	1.522	1.510
			1.062	1.041	1.027	1.018	1.009
	20	1.425	1.499	1.475	1.458	1.446	1.436
			1.052	1.035	1.023	1.015	1.008
	25	1.378	1.441	1.420	1.406	1.396	1.387
			1.046	1.031	1.020	1.013	1.007
	30	1.343	1.399	1.381	1.368	1.359	1.352
			1.042	1.028	1.018	1.012	1.006
0.10	3	2.302	2.627	2.513	2.440	2.390	2.349
			1.141	1.092	1.060	1.039	1.020
	5	1.927	2.108	2.046	2.005	1.977	1.953
			1.094	1.062	1.040	1.026	1.013
	10	1.619	1.715	1.683	1.660	1.645	1.632
			1.059	1.039	1.026	1.016	1.008
	15	1.496	1.565	1.542	1.526	1.515	1.505
			1.047	1.031	1.020	1.013	1.006
	20	1.425	1.481	1.462	1.449	1.440	1.432
			1.039	1.026	1.017	1.011	1.005
	25	1.378	1.426	1.410	1.398	1.391	1.384
			1.035	1.023	1.015	1.009	1.004
	30	1.343	1.386	1.371	1.362	1.355	1.349
			1.031	1.021	1.014	1.008	1.004

Table 3. Control limit coefficients: Unadjusted and adjusted for S_p with ϵ = 0.20 (α = 0.005). Every second row (in italics) gives the ratio between the adjusted and the unadjusted limit.

					L*
			L*/L
p	n	L	m = 25	50	100	200	500
0.05	3	2.302	2.713	2.562	2.501	2.466	2.402
			1.178	1.113	1.087	1.071	1.044
	5	1.927	2.153	2.072	2.018	1.982	1.951
			1.117	1.075	1.047	1.028	1.012
	10	1.619	1.737	1.695	1.666	1.647	1.630
			1.073	1.047	1.029	1.017	1.007
	15	1.496	1.581	1.551	1.530	1.516	1.503
			1.057	1.037	1.023	1.013	1.005
	20	1.425	1.494	1.469	1.452	1.441	1.431
			1.048	1.031	1.019	1.011	1.004
	25	1.378	1.436	1.415	1.401	1.391	1.382
			1.042	1.027	1.017	1.010	1.003
	30	1.343	1.395	1.376	1.364	1.355	1.347
			1.038	1.025	1.015	1.009	1.003
0.10	3	2.302	2.605	2.492	2.446	2.419	2.370
			1.132	1.083	1.063	1.051	1.030
	5	1.927	2.094	2.033	1.992	1.964	1.940
			1.086	1.055	1.033	1.019	1.006
	10	1.619	1.706	1.674	1.652	1.637	1.624
			1.054	1.034	1.020	1.011	1.003
	15	1.496	1.558	1.535	1.519	1.508	1.498
			1.042	1.026	1.016	1.008	1.002
	20	1.425	1.475	1.457	1.444	1.435	1.427
			1.035	1.022	1.013	1.007	1.001
	25	1.378	1.421	1.405	1.394	1.386	1.379
			1.031	1.019	1.011	1.006	1.001
	30	1.343	1.381	1.367	1.357	1.350	1.344
			1.028	1.018	1.010	1.005	1.001

As can be seen, and as might be expected, the adjusted limit converges to the unadjusted limit when n or m (or both) increases. This happens due to the variance of the estimators decreasing with the increase in the number of observations. Also, keeping m and n fixed, the adjusted limit decreases (becoming closer to the unadjusted limit) with increases in ϵ and p, which means a greater tolerance to FARs larger (or to CARL values smaller) than the nominal.

Tables 4 and 5 give the out-of-control CARLs of the charts for γ = 1.5 and γ = 2.0, respectively. They correspond, as said in the previous section, to the case w = 1. In these tables, the column “Unadjusted” gives the out-of-control CARL of the chart with the unadjusted control limit. The values indicate that, with the traditionally recommended numbers of preliminary samples (m between 25 and 75 samples) and the usual sample sizes (less than 10 observations), the adjustment made for the guaranteed in-control performance entails substantial deterioration of the out-of-control performance. For example, with less than 50 Phase I subgroups each with a sample size of five, the out-of-control CARLs of the chart with adjusted limits are 40% to 100% larger than the ones of the chart with unadjusted limits. Even with m = 100, the out-of-control CARLs for γ = 1.5 and n = 3 are 30% to 50% larger than the ones for the chart with the unadjusted control limit. However, if the increase in the process standard deviation that is relevant to detect quickly is a little bigger, γ = 2.0, the increases in the out-of-control CARLs due to the adjustment become less substantial, except for the smaller values of n (three and five) and m (25 and 50; see Table 5). With larger sample sizes, the CARL values are already close to one with or without the adjustment. However, if the user considers, for example, 100 or 200 Phase I subgroups (a number much smaller and far more practical than the several hundreds to thousands found to be required in Epprecht et al. (2015)), the increase in the CARL (relative to the chart with unadjusted limits) is of the order of 25% or less; that is, the adjustment yields, in this case, a good compromise between the guaranteed in-control performance, the out-of-control performance, and the number of Phase I subgroups.

Table 4. Out-of-control CARL for γ = 1.5 of the S chart with and without the adjusted limits, when W = 1 (α = 0.005).

			CARL
				Adjusted with estimator Sp
ϵ	p	n	Unadjusted	m = 25	50	100	200	500
0.10	0.05	3	10.5	27.8	19.4	15.6	13.6	12.1
		5	6.3	12.6	9.8	8.4	7.6	7.0
		10	3.2	4.9	4.2	3.8	3.6	3.4
		15	2.2	3.0	2.7	2.5	2.4	2.3
		20	1.7	2.2	2.0	1.9	1.8	1.8
		25	1.5	1.8	1.6	1.6	1.5	1.5
		30	1.3	1.5	1.4	1.4	1.4	1.3
0.10	0.10	3	10.5	21.5	16.6	14.1	12.7	11.6
		5	6.3	10.5	8.8	7.8	7.2	6.8
		10	3.2	4.4	3.9	3.7	3.5	3.3
		15	2.2	2.8	2.5	2.4	2.3	2.3
		20	1.7	2.1	1.9	1.9	1.8	1.8
		25	1.5	1.7	1.6	1.5	1.5	1.5
		30	1.3	1.4	1.4	1.4	1.3	1.3
0.20	0.05	3	10.5	26.3	18.5	14.9	13.0	11.6
		5	6.3	12.0	9.4	8.1	7.3	6.7
		10	3.2	4.8	4.1	3.7	3.5	3.3
	0.05	15	2.2	2.9	2.6	2.4	2.3	2.2
		20	1.7	2.1	2.0	1.9	1.8	1.8
		25	1.5	1.7	1.6	1.6	1.5	1.5
		30	1.3	1.5	1.4	1.4	1.3	1.3
0.20	0.10	3	10.5	20.4	15.8	13.5	12.1	11.1
		5	6.3	10.1	8.4	7.5	7.0	6.5
		10	3.2	4.3	3.8	3.6	3.4	3.2
0.20	0.10	15	2.2	2.7	2.5	2.4	2.3	2.2
		20	1.7	2.0	1.9	1.8	1.8	1.7
		25	1.5	1.6	1.6	1.5	1.5	1.5
		30	1.3	1.4	1.4	1.3	1.3	1.3

Table 5. Out–of-control CARL for γ = 2.0 of the S chart without and with adjusted limits, when W = 1 (α = 0.005).

			CARL
				Adjusted with estimator Sp
ϵ	p	n	Unadjusted	m = 25	50	100	200	500
0.10	0.05	3	3.8	6.5	5.3	4.7	4.3	4.1
		5	2.2	3.1	2.8	2.6	2.4	2.4
		10	1.3	1.5	1.5	1.4	1.4	1.4
		15	1.1	1.2	1.2	1.1	1.1	1.1
		20	1.0	1.1	1.1	1.1	1.0	1.0
		25	1.0	1.0	1.0	1.0	1.0	1.0
		30	1.0	1.0	1.0	1.0	1.0	1.0
0.10	0.10	3	3.8	5.6	4.9	4.4	4.2	4.0
		5	2.2	2.9	2.6	2.5	2.4	2.3
		10	1.3	1.5	1.4	1.4	1.4	1.4
		15	1.1	1.3	1.3	1.3	1.2	1.2
		20	1.0	1.1	1.1	1.0	1.0	1.0
		25	1.0	1.0	1.0	1.0	1.0	1.0
		30	1.0	1.0	1.0	1.0	1.0	1.0
0.20	0.05	3	3.8	6.3	5.2	4.6	4.2	4.0
		5	2.2	3.1	2.7	2.5	2.4	2.3
		10	1.3	1.5	1.4	1.4	1.4	1.3
		15	1.1	1.2	1.2	1.1	1.1	1.1
		20	1.0	1.1	1.1	1.0	1.0	1.0
		25	1.0	1.0	1.0	1.0	1.0	1.0
		30	1.0	1.0	1.0	1.0	1.0	1.0
0.20	0.10	3	3.8	5.5	4.7	4.3	4.1	3.9
		5	2.2	2.8	2.6	2.4	2.3	2.3
		10	1.3	1.5	1.4	1.4	1.4	1.3
		15	1.1	1.2	1.1	1.1	1.1	1.1
		20	1.0	2.0	1.9	1.8	1.8	1.7
		25	1.0	1.0	1.0	1.0	1.0	1.0
		30	1.0	1.0	1.0	1.0	1.0	1.0

Note that Faraz et al. (2015, p. 4412) concluded that “adjusting the S² control limit did not have too much an effect on the out-of-control performance of the chart.” By contrast, as we have seen, this effect can be significant for small values of m and n. Clearly, the user should seek a combination of a number of preliminary samples, m, and a level of adjustment (through the specification of the values of α_TOL and p) that result in an appropriate compromise between the risk of a large FAR and a poor out-of-control performance. The ideal compromise depends on the particular situation. The tables in this article provide guidance to the user's decision, and the formulae in Sections 2 and 3 enable the calculation of the adjusted control limit and the of the out-of-control CARL for any particular situation (for specified values of m, n, ϵ, p, and α and for known γ).

4.2. Balancing in-control and out-of-control performances

The aim of the proposed correction is to guarantee a minimum in-control performance. However, the resulting out-of-control performance should not be ignored, as detecting out-of-control situations is still the main purpose behind the use of control charts. To examine this issue, we define the cdf of the CPA, which can be used to evaluate the out-of-control performance more closely. First, recall that the CPA as in Equation (18(18) ) can be rewritten as

Consequently, in a similar way as in Equation (11(11) ), we can write the cdf of CPA(γ, L*) as

Note that  F_CPA(t; 1, L*) is equal to  F_CFAR(t; L*) from Equation (12(12) ). In the out-of-control situation, it is desired to obtain a signal as quickly as possible. This means that in the out-of-control situation the CPA (CARL) is preferred to be large (small). For a given increase in standard deviation γ and adjusted control limit coefficient L* one can use  F_CPA(t; γ, L*) to determine the probability of obtaining a CPA smaller than a specified value t. Of course, F_CPA(t; γ, L*) is desired to be small for γ > 1, as this means that a low probability of an alarm (high CARL) is unlikely in the out-of-control situation. Based on the situation (e.g., what sizes of shifts may be desired to be detected), one may argue whether or not such an out-of-control performance is sufficient.

For example, consider the case that m = 50 samples of size n = 5 each are available in Phase I and that we use as the Phase I estimator and as the plotting statistic. Moreover, consider α = 0.005, ϵ = 0.1 (such that  α_tol = 0.0055), and p = 0.05. Finally, suppose that we are interested in detecting changes in process dispersion such that γ = 1.5. The required value of L* can be found to be equal to 2.086 (from Table 2 or Equation (16(16) )). This control limit coefficient guarantees that the CFAR is less than α_tol = 0.0055 (or the CARL is greater than 1/α_tol = 182 when γ = 1) with probability 1 − p = 0.95. From Table 4 we conclude that, in the absence of estimation error, the CARL of this chart will be 9.8 when γ = 1.5. Of course, the out-of-control CARL for practitioners depends on the estimation error. Suppose that we are interested in the probability of having CPA less than 0.067 (or, equivalently, CARL greater than 15) when γ = 1.5. For that specific case, one can calculate this probability to be  F_CPA(0.067 ; 1.5, 2.086) = 0.091, which is an indication of the out-of-control performance.

If the performance is not deemed sufficient, then two alternatives are possible. The first is to increase the amount of Phase I data, and the second is to be more lenient on the guaranteed in-control performance. Gathering more data will provide more accurate estimates of the in-control process in Phase I, which is incorporated in the adjusted control limits. As there is less uncertainty to account for, the adjusted limit coefficient will be smaller, resulting in lower out-of-control CARL values. However, often this amount of data is not available or is costly to collect. If increasing the amount of used Phase I data is not an option, one may have to choose to be more lenient on the adjustment. Using larger values of α_TOL means that we choose a less strict minimum performance threshold, whereas using a larger value of p means that there is a larger probability obtaining CARL values below the minimum threshold. Both of these lead to lower adjusted control limit coefficients and consequently to lower CARL values in both the in-control and out-of-control situations. In the example discussed in the previous paragraph, consider adjusting our values of p and ϵ to p = 0.1 and ϵ = 0.2, while leaving the rest as before. This changes α_tol to 0.006 and CARL_tol to 1/0.006 = 167, which indicates a deterioration in the in-control performance. We would then find (from Table 2 or Equation (16(16) )) that L* = 2.033, which results in  F_CPA(0.067 ;  1.5, 2.033) = 0.030. This is substantially smaller than the 0.091 obtained previously, which illustrates the balancing of the in-control and out-of-control performance.

5. Application of the proposed control chart

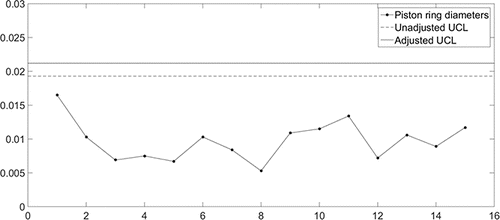
In this section we illustrate how the proposed control limits should be implemented in practice, by means of a practical example. We consider a data set provided in Montgomery (2013) that contains the inside diameters of forged automobile engine piston rings. In Phase I, the control limits are constructed based on m = 25 samples of size n = 5 each. These obtained limits are then used for monitoring the process standard deviation in Phase II. As an example, the application of the control chart is illustrated using m = 15 samples of size n = 5 each, obtained in Phase II. The corresponding Phase I and Phase II data can be found in Table 6.3 and Table 6E.8 of Montgomery (2013), pages 260 and 283, respectively.

Before the control limits are constructed, we check whether the Phase I data used to calculate them follow a normal distribution. From the Shapiro–Wilk test for normality we find no reason to reject the normality assumption, as the p-value is close to 0.9. This means that we can continue with the construction of the control limits, which is done through the following steps:

1.	First, we determine our parameters. We have m = 25 and n = 5, and we choose α = 0.005. p = 0.1, and ϵ = 0. Note that for this case αtol = (1 + ϵ)α = 0.005 and consequently CARLtol = 1/αtol = 200. Combined with p = 0.1, this means that a minimum in-control CARL of at least 200 is guaranteed with 100(1 −p)% = 90% probability.
2.	Second, we need to determine our estimator and plotting statistic and their corresponding values of a, b, a0, and b0. We consider as the Phase I estimator and as the plotting statistic, which means that we have a = 1, b = n − 1 = 4, a0 = 1, and b0 = m(n − 1) = 100. As a Phase I estimate we find Sp = 0.0100.
3.	The values from 1 and 2 are implemented in Equation (15(15) ) to obtain L* = 2.124. As a comparison, using Equation (2(2) ) we find L = 1.928. We can now calculate the adjusted and unadjusted control limits as and , respectively.

The obtained limit can now be used to monitor the process standard deviation, as is illustrated in Figure 5 for the provided Phase II data set. For comparison purposes, we have also added the unadjusted control limit to this figure. As can be seen in the figure, the adjusted limit is larger than the unadjusted limit to prevent low in-control CARL values. Note that, for this specific data, neither of the control limits indicate an out-of-control situation, since all observations are below both limits.

Figure 5. Application of the proposed control chart to the piston ring data set. Both the unadjusted and adjusted control limits are indicated.

6. Conclusions

Not accounting for the effects of parameter estimation can cause substantial deterioration in control chart performance, both in the in-control and out-of-control cases. The in-control performance at some nominal value is very important when it comes to implementing and using a control chart that can be relied upon. A Phase I data set is typically required to estimate the unknown parameters, and as the Phase I data set will differ across practitioners, so will the control chart limits and, consequently, the control chart performance. Increasing the amount of available Phase I data will improve the control chart performance and decrease the performance variation among practitioners. However, the required amount of Phase I data to achieve a good (close to nominal) in-control control chart performance is typically infeasible (see Epprecht et al. (2015)). Thus, for a practical implementation, we propose the use of adjusted control chart limits for Shewhart control charts for dispersion under normality adopting an alternative point of view. The idea is in line with recent research (e.g., Faraz et al. (2015), Salah, Mahmoud, Jones-Farmer, Zwetsloot, and Woodall (2015), Saleh, Mahmoud, Keefe, and Woodall (2015), and Goedhart et al. (2017)). The adjusted control limits are determined such that a minimum in-control chart performance is guaranteed with a pre-specified probability. However, whereas Faraz et al. (2015) use a bootstrap approach following Gandy and Kvaløy (2013), we derive analytical expressions to determine the adjusted limits that are easier to implement and give more insight in the required adjustment. Our adjusted limits allow different available estimators of the standard deviation to be used in the analysis and are easily applicable to any monotone-increasing transformation of S.

Due to the formulation based on the CFAR, the adjusted control chart (limit) accounts for parameter estimation and yields a better in-control performance compared with the unadjusted chart, which does not account for parameter estimation. The in-control performance of the unadjusted chart suffers from parameter estimation and the practitioner-to-practitioner variability and therefore is unreliable. However, note that this gain in the in-control performance of the adjusted chart is seen to lead to a deterioration of the out-of-control performance for smaller numbers of Phase I subgroups. Thus, a tradeoff has to be made in practice to balance the in-control and out-of-control performance properties of the control chart, depending on the amount of Phase I data at hand. We recommend using the adjusted limits, as the in-control (stability) performance of a control chart is deemed more important in practice and our results show that the loss of some out-of-control performance can be tolerable, particularly for larger amounts of Phase I data.

Acknowledgements

We are very grateful to the Department Editor and the referees for their comments and suggestions, which have resulted in an improved version of this article.

Funding

This research was partly supported by CAPES (Brazilian Coordination for the Improvement of Higher Education Personnel, Ministry of Education) through a master scholarship for the 2nd author, and by CNPq (Brazilian Council for Scientific and Technological Development, Ministry of Science, Technology and Innovation) through projects numbers 308677/2015-3 (4th author), 401523/2014-4 (5th author) and 309756/2014-6 (last author).

Additional information

Notes on contributors

Rob Goedhart

Rob Goedhart is a Ph.D. student in the Department of Operations Management and consultant at the Institute for Business and Industrial Statistics of the University of Amsterdam, The Netherlands. His current research topic is control charting techniques with estimated parameters.

Michele M. da Silva

Michele M. da Silva holds a master's degree in electrical engineering from the Pontifical Catholic University of Rio de Janeiro, Brazil. Her current research activities include the design of control charts with estimated parameters.

Marit Schoonhoven

Marit Schoonhoven is an Associate Professor at the Department of Operations Management and senior consultant at the Institute for Business and Industrial Statistics of the University of Amsterdam, The Netherlands. Her current research interests include control charting techniques and operational management methods.

Eugenio K. Epprecht

Eugenio K. Epprecht is a Professor in the Department of Industrial Engineering at the Pontifical Catholic University of Rio de Janeiro. He is a member of ASQ. His major research interest is in statistical process control.

Subha Chakraborti

Subha Chakraborti is a Professor of Statistics in the Department of Information Systems, Statistics and Management Science, University of Alabama. He is a Fellow of the ASA and an elected member of the ISI. His research interests are in nonparametric and robust statistical inference, including applications in statistical process/quality control.

Ronald J. M. M. Does

Ronald J.M.M. Does is a Professor of Industrial Statistics at the University of Amsterdam, Director of the Institute for Business and Industrial Statistics, Head of the Department of Operations Management, and Director of the Institute of Executive Programs at the Amsterdam Business School. He is a Fellow of the ASQ and ASA, an elected member of the ISI, and an Academician of the International Academy for Quality. His current research activities include the design of control charts for nonstandard situations, healthcare engineering, and operational management methods.

Álvaro Veiga

Álvaro Veiga is an Associate Professor of the Department of Electrical Engineering at the Pontifical Catholic University of Rio de Janeiro. His current research activities include nonlinear statistical modeling and high-dimensional statistics with application to quantitative finance, energy, and marketing.