Integrated maintenance and spare part optimization for moving assets

ABSTRACT

We consider an integrated maintenance and spare part optimization problem for a single critical component of a moving asset for which the degradation level is observable. Degradation is modeled as a function of the current operating mode, mostly dictated by the actual location of the moving asset. The spare part is stocked at the home base that the moving asset eventually visits. Alternatively, the spare part can be stocked on-board the moving asset to prevent costly expedited deliveries. The costs associated with spare part deliveries and part replacements depend on the operating mode. Our objective is to minimize the expected total discounted cost of spare part deliveries, part replacements, and inventory holding over an infinite planning horizon. We formulate the problem as a Markov decision process and characterize the structure of the optimal policy, which is shown to be a bi-threshold policy in each operating mode. Our numerical experiments show that the cost savings obtained by the integrated optimization of spare part inventory and part replacement decisions are significant. We also demonstrate the value of the integrated approach in a case study from the maritime sector.

KEYWORDS:

• Maintenance
• replacement
• spare parts
• moving assets
• inventory
• maritime
• condition-based maintenance

1. Introduction

Maintenance and spare parts holding costs are known to be significant contributors to the overall operating costs for many moving assets, such as maritime assets (e.g., ships, vessels, submarines), aircraft, commercial vehicles (e.g., trucks, buses, trains), and military equipment (e.g., frigates, strike-fighters). For maritime assets, maintenance activities can constitute between 25 and 35% of the operating costs (Turan et al., 2009). For commercial airlines, maintenance accounts for around 10% of an airline's total costs (Lam, 1995). The total spare parts inventory in the aviation industry was estimated to be 45 billion U.S. dollars in 1995 (Flint, 1995). In addition to the significant costs associated with maintenance and spare parts inventory, unexpected downtimes can lead to a significant loss of revenue and can affect health, safety, and the environment. For instance, daily shipping operation of a tanker can yield as much as $20 500, which would be lost during downtime (United Nations Conference on Trade and Development, 2013). Downtime of naval ships can seriously affect national security. For such assets, maintenance and spare parts optimization is essential to decrease overall operating costs and to increase asset availability.

A component is called critical when the consequences associated with its failure are significant. In practice, such components are usually maintained by the so-called repair-by-replacement strategy; i.e., the component is removed from the asset and replaced by a new or as-good-as-new spare part. This reduces the maintenance execution time and the resulting downtime (Van Houtum and Kranenburg, 2015). In this setting, the availability of spare parts is crucial, as emergency shipments and the downtime associated with waiting for the spare parts may be very costly. Traditionally, maintenance and spare parts inventory decisions are made separately. However, a separate optimization may lead to poor solutions, as it ignores the interdependencies between the two decisions. In general, integrated optimization provides remarkable improvement in terms of cost and availability compared with separate optimizations (Kabir and Al-Olayan, 1996; van Horenbeek et al., 2013).

For many technical systems, it is possible to measure parameters of the critical components that reveal the actual degradation behavior (van Houtum and Kranenburg, 2015). This enables the prevention of failures by means of Condition-Based Maintenance (CBM); i.e., by executing a preventive replacement at the moment that a pre-specified degradation threshold is exceeded. In practice, measurements can be performed via periodic inspections or advanced sensor technologies. Physical degradation models investigate the quantitative relation between degradation, usage, and environment (see, e.g., Tinga (2010) and Tinga and Janssen (2013)). In this article, we consider a critical component of a moving asset for which the degradation level is observable and can be modeled as a function of the current operating mode. Operating modes represent the current location of the moving asset, how the component is used, and under what environmental conditions it operates. For many moving assets, the sequence and duration of operating modes are more realistically modeled as random variables (see, e.g., Alam and Al-Saggaf (1986) and Çekyay and Özekici (2015)).

Under the commonly used repair-by-replacement strategy, the spare part must be on-board the moving asset to allow replacement of the component. In practice, the spare part is usually available at a fixed location in the home base, which is taken to be a location that the moving asset is expected to eventually visit. Depending on the application, the home base can be a harbor, hangar, or garage. Typically, the cost associated with delivering a spare part is negligible when the moving asset is already in the home base. However, the cost of the delivery of a spare part can become significant when the asset is operating at a remote location. Such a delivery is made by means of an aircraft, helicopter, boat, dedicated vehicle, etc. To prevent expensive deliveries, the spare part can be stocked on-board the moving asset. A holding cost is incurred if the spare part is kept on-board the asset. This holding cost can become relatively high, due to several factors including the spare part's unit-value, the risk of obsolescence, and limited space availability on-board the asset.

The work reported in this article is motivated by our collaboration with Fugro Marine Services (FMS). Fugro is the world's largest integrator of geotechnical, survey, subsea, and geosciences services. A major part of its turnover relates to exploration of the seafloor. For these operations, survey vessels are employed. The availability of these vessels is of major importance, as the activities performed generate significant revenues. FMS is Fugro's in-house vessel management company. FMS manages maintenance-related activities on survey vessels and other types of vessels. We considered a critical component of one of these vessels in the case study presented in Section 6. FMS considered the component under consideration to be reliable, based on the specifications of the Original Equipment Manufacturer (OEM). Thus, the replacement of this component was planned to be performed on a time-based schedule and it was decided to not to hold the spare part on-board the vessel. However, the component failed before its preventive replacement time while the vessel was operating at a remote location. The expedited delivery of the spare part incured an approximate cost of €10 000. In addition, the downtime cost due to a 1-day delay in operations, which significantly varied over time, was within the range €20 000–€50 000 in this case. This situation could have been avoided if the spare part of this relatively cheap component was held on-board the vessel. On the other hand, it was neither realistic nor economic to always hold spare parts on-board a vessel. First of all, the available space on-board a vessel is usually very limited. Some of the critical components are very expensive, resulting in significant holding costs. This shows that there is a need for a structured approach to make the decisions on when to put a spare part on-board a vessel and when to replace the component just-in-time. Such an approach should take into account the randomness in the sequence and the duration of operating modes, as well as the relation among operating modes, component degradation, and cost parameters. To the best of our knowledge, this problem has not been studied in the literature.

We formulate the above-presented problem as a Markov decision process model, in which the objective is to minimize the expected total discounted cost. Given that many moving assets have very long service times, we develop an infinite-horizon model. We characterize the structure of the optimal policy, which is found to be a bi-threshold policy in each operating mode. Moreover, we provide insights regarding the performance of the optimal policy compared with four benchmark policies. In these benchmark policies, replacement decisions are optimized and spare part inventory decisions are pre-defined as follows: never keep a spare part on-board a vessel or always keep a spare part on-board a vessel. Our numerical experiments show that, compared with the considered benchmark policies, the cost savings obtained by the optimal policy can be significant.

This article is organized as follows. Section 2 presents the related literature. Section 3 formulates the problem as a Markov decision process model. Section 4 characterizes the structure of the optimal integrated policy. Section 5 provides numerical experiments and several insights regarding the performance of the optimal policy compared with four benchmark policies. Section 6 presents a case study for demonstration purposes. Section 7 draws some conclusions and suggests potential future research directions.

2. Literature review

This article relates to three main research streams, namely, CBM optimization for components subject to Markovian degradation, maintenance optimization of mission-based systems, and integrated maintenance and spare parts inventory optimization.

A large body of the CBM literature models degradation as a Markov process (Elwany et al., 2011). The earliest and basic replacement models for components subject to Markovian degradation can be found in Kolesar (1966), Derman (1970), and Kawai et al. (2002). For these models, it is shown that under some monotonicity assumptions the optimal replacement policy that minimizes the expected total discounted cost in an infinite time horizon is a threshold-type policy. This means that there exists a threshold with respect to the degradation level above which the optimal decision is to replace the component and below which the optimal decision is to do nothing. Over the last decades, the structure of optimal replacement policies have been investigated in different problem settings (see, e.g., Makis and Jiang (2003), Kurt and Kharoufeh (2010); Elwany et al. (2011)). Çekyay et al. (2011) reviewed CBM models with Markovian degradation, for which threshold-type policies are optimal. They showed that these policies are not necessarily optimal in a variety of cases and the optimal policy may have a rather complex structure.

There is a vast literature on systems performing missions that are composed of different phases or stages. In the literature, these systems are called phased-mission systems or mission-based systems. These systems are analogous to those that are subject to different operating modes and mission environments. Many papers have focused on reliability and availability analysis for such systems (see, e.g., Esary and Ziehms (1975), Kim and Park (1994), Mura and Bondavalli (1999), and Kharoufeh et al. (2010)). To the best of our knowledge, maintenance and replacement models for mission-based systems and for systems subject to randomly varying environments are limited. Waldmann (1983) investigated the structure of an optimal replacement policy for a system subject to stochastic degradation in a random environment. The author provided sufficient conditions to establish the optimality of threshold-type policies. Özekici (1995) modeled the environment using a semi-Markov process and used the intrinsic aging concept for degradation. The intrinsic age represents the cumulative hazard accumulated over time during the operation of the component in the randomly varying environment. Under increasing failure rate distribution functions in all environments and reasonable cost structures, the author showed that the threshold-type intrinsic age replacement and repair policies are optimal. In a similar setting, Zhang et al. (2013) and Çekyay and Özekici (2015) provided extensions to deal with the multi-component case. Ulukus et al. (2012) modeled the environment as a finite-state Markov process. They assumed that the system accumulates degradation at a linear rate whose value depends on the environment. They showed that there exists an optimal threshold-type replacement policy for each environment. Considering similar degradation dynamics, Flory et al. (2015) extended the work of Ulukus et al. (2012) to partially observable environments. Çekyay and Özekici (2012) defined both the mission process and the degradation process as finite-state Markov processes where the generator of the degradation process depends on the phases of the mission. They discussed optimal repair and replacement problems and characterized the optimal policies under some monotonicity assumptions. In this article, our assumptions regarding mission and degradation processes are similar. The mission process (operating modes) is described as a finite-state Markov process. The degradation process of the component is defined by another finite-state Markov process and is modulated by the mission process. Different from the existing papers in this research stream, we investigate an integrated problem by taking the spare part inventory decision into account.

In the last decades, several integrated maintenance and spare parts inventory optimization models have been developed. Many papers in this research stream rely on the assumption that components' lifetime/reliability distributions are given. Armstrong and Atkins (1996) considered a single component subject to age-based replacement. They investigated the optimal combination of replacement and ordering time that minimizes the total replacement and inventory costs. Armstrong and Atkins (1998) provided several extensions to the previous work, generalizing the cost terms and the replenishment time of spare parts. Kabir and Al-Olayan (1996) proposed a policy for integrated optimization of age-based replacement and spare parts ordering. They considered a number of identical components. Their simulation model reported a remarkable improvement on the total cost compared with separate optimization. To the best of our knowledge, only a few articles are available for components subject to CBM. Wang et al. (2008) considered a number of identical components and developed a condition-based replacement and spare parts ordering policy. They modeled the degradation of components as discrete-time Markov chains. They used Monte Carlo simulation to evaluate the performance of the proposed policy. Wang et al. (2009) combined Monte Carlo simulation and a genetic algorithm to determine the optimal parameters of the condition-based replacement and spare parts ordering policy. Elwany and Gebraeel (2008) enabled the use of sensor information and proposed a method that dynamically updates replacement and ordering decisions based on the physical condition of the equipment. They highlighted the advantages of using the proposed methodology compared with that of Armstrong and Atkins (1996). We refer the reader to van Horenbeek et al. (2013) for a complete review of this research stream. Unlike our work, existing research does not investigate an integrated maintenance and inventory optimization problem from a moving asset perspective. To the best of our knowledge, none of these models incorporates the relation among operating modes, component degradation, and cost parameters.

3. Markov decision process formulation

In this section, we present the Markov decision process formulation of our integrated maintenance and spare part optimization problem.

Let I be a non-empty finite set representing different operating modes of the moving asset. Operating modes dictate the current location of the moving asset, how the component is used, and under which environmental conditions it operates. For example, operating modes can be defined as “wait in the home base,” “transit to location l,” “perform mission m in environment e,” etc. We assume that the operation process evolves as a Continuous-Time Markov Chain (CTMC), X ≡ {X_t, t ⩾ 0}, on the discrete state space I. Therefore, the duration of operating mode i ∈ I is assumed to be exponentially distributed with rate μ_i. The probability that the system jumps from operating mode i ∈ I to operating mode k ∈ I is denoted by Q(i, k). Generally, Q(i, i) = 0 for all i ∈ I, but technically one can allow Q(i, i) to be larger than zero. As further demonstrated in Section 6, the operation process of a real-life system can be well represented by such a Markov process.

The degradation of the component also evolves as a CTMC, Y ≡ {Y_t, t ⩾ 0} on a discrete state space J ≡ {0, 1, …, F}, representing degradation levels from perfect (0) to failure state (F), where F > 1. Transitions between degradation levels are from j to j + 1 for , where The degradation process is modulated by the operation process; i.e., transition rate λ_ij for the transition from j to j + 1 depends on the current operating mode i ∈ I. We note that the number of degradation levels and operating modes can be arbitrarily large. Therefore, this constitutes a fairly general degradation process.

We assume that at most one spare part can be stocked on-board the moving asset. This assumption is not unrealistic considering the limited space availability on-board the vessel. Moreover, the component lifetime is usually much higher than the time between two successive home base visits; i.e., in practice, it is not likely to observe two or more failures during one mission. We denote the number of spare parts on-board the vessel by u ∈ U, where U ≡ {0, 1}.

We define the state of the Markov decision process as (i, j, u) ∈ I × J × U, a realization of the joint process (X, Y, Z) where X denotes the current operating mode, Y is the current level of degradation, and Z is the number of spare parts on-board the vessel. We restrict our attention to a model where decisions are only made at transition instants. A decision maker observes the system at each decision epoch (i.e., each time instant at which a transition occurs) and makes decision a ∈ {0, 1, 2}, which can be one of the following:

0:	Do nothing
1:	Deliver a spare part
2:	Replace the part

The set of possible actions A(i, j, u) in state (i, j, u) ∈ I × J × U is defined as

At a decision epoch, action 0 (do nothing) can be chosen if the component has not failed. Action 1 (spare part delivery) is possible if there is no spare part on-board the vessel. Action 2 (part replacement) can be performed only if the spare part is already on-board the vessel.

We assume that a part replacement or a spare part delivery can be scheduled to occur immediately and instantaneously. Therefore, action 1 brings the system from state (i, j, 0) to state (i, j, 1) immediately. Similarly, action 2 brings the system from state (i, j, 1) to state (i, 0, 0) immediately. After each transition, a new action can be taken. That is, a spare part delivery can be immediately followed by a part replacement and vice versa. For example, if the component failed when the spare part was not on-board the vessel, a spare part delivery and a part replacement should take place consecutively, bringing the system from state (i, F, 0)  to state (i, F, 1)  and then from state (i, F, 1)  to state (i, 0, 0)  instantaneously. In this case, both actions take place at the same time instant.

The assumption of instantaneous replacements and deliveries is reasonable when the duration of these actions is much shorter than the mean component lifetime. In practice, even short downtimes can lead to significant costs. In this model, the downtime is translated into cost parameters. We distinguish a part replacement cost and a spare part delivery cost. At the time that a preventive replacement occurs in operating mode i ∈ I, the replacement cost c^pr_i > 0 is charged. If the system is found to be failed, then a corrective replacement must be performed at a corrective replacement cost c^cr_i, where c^cr_i ⩾ c_i^pr for i ∈ I. The replacement cost parameters c^pr_i and c^cr_i include the cost of labor and the cost of downtime due to preventive and corrective replacement actions, respectively.

For a spare part delivery that takes place when the system is in operating mode i ∈ I, a preventive spare part delivery cost c^pd_i ⩾ 0 is incurred. The cost of a preventive delivery includes the price of the spare part and the transportation cost. The transportation cost depends on the location of the moving asset; i.e., on the operating mode. We assume that a spare part is always available at the home base. By definition, the moving asset eventually visits the home base. When the moving asset is at its home base, the spare part can be directly put on board with a negligible transportation cost (regular delivery). If the moving asset is at a remote location at the moment a spare part is requested, the delivery should be made by means of an aircraft, helicopter, boat, dedicated vehicle, etc. (expedited delivery). We translate the difference between regular and expedited deliveries into cost terms, by differentiating the spare part delivery cost with respect to operating modes. In principle, preventive deliveries do not cause downtime if the component has not failed. If the component has failed, additional costs may be incurred, due to the cost of an emergency shipment and the cost of downtime while waiting for the spare part. To represent these additional costs, we introduce a corrective spare part delivery cost c^cd_i, where c^cd_i ⩾ c_i^pd for i ∈ I. Moreover, holding the spare part on-board the moving asset incurs a holding cost h > 0 per time unit.

We apply uniformization to convert the continuous-time Markov decision problem into an equivalent discrete-time Markov decision problem. We add fictitious transitions from state to itself, ensuring that the total rate out of a state is equal for all states . The latter refers to the so-called uniformization rate (see Alagoz and Ayvaci (2010)). We select a positive uniformization rate v such that where v_ij = μ_i + λ_ij. In our Markov decision model, how long the system stays in a state depends on the action taken. Under uniformization, if action 0 is taken, the next transition (and decision epoch) is after an exponentially distributed time with mean 1/v in each state . In this case, one of the following transitions can occur at the subsequent transition instant: (i) the system can jump from degradation level to j + 1 with probability λ_ij/v; (ii) the system can jump from operating mode i ∈ I to operating mode k ∈ I, k ≠ i with probability μ_iQ(i, k)/v; or (iii) the system can occupy the same state after transition with probability 1 − v_ij/v. If action 1 or 2 is taken, the transition to the subsequent state is instantaneous. Due to the latter, our formulation is slightly different from the standard Markov decision process formulation in Puterman (1994), in which all transitions are as described for action 0. For illustration purposes, we depict an exemplary process in Appendix A.

We assume a continuous discount rate α > 0 so that any cost incurred at some future time t is discounted by a factor e^{− αt}. Hence, the discount factor in the uniformized process can be defined as

The discounted holding cost of keeping a spare part on board during t time units is

If there is a spare part on-board the vessel and action 0 is taken, then the expected discounted holding cost between two decision epochs in the uniformized process is

The expected total discounted cost between two decision epochs in the uniformized process r(i, j, u, a) if action a is taken in state (i, j, u) is equal to where H(i, j, u, a) is the lump sum equivalent of the continuous cost and C(i, j, u, a) is the lump sum cost of action a ∈ A(i, j, u) in state (i, j, u):

We note that the uniformized process and the original process have the same lump sum cost under instantaneous transitions. Let V(i, j, u) be the value function representing the minimum expected total discounted cost using the optimal policy if the operating mode is i, the degradation level is j, and the number of spare parts on-board the vessel is u. The optimal replacement problem can be formulated by the following dynamic programming equation: (1) where operators Γ₀, Γ₁, and Γ₂ refer to the actions of doing nothing, a spare part delivery, and a part replacement, respectively: (2) (3) (4)

Equation (2(2) ) models possible future random events following the decision to do nothing. It consists of three types of transitions. The first one is the transition in operating modes, bringing the system from state (i, j, u) to (k, j, u) where i, k ∈ I, i ≠ k. The second one represents the component's degradation, bringing the system from state (i, j, u) to (i, j + 1, u) where The third one represents the transitions from state (i, j, u) to itself, which is a consequence of the uniformization procedure. Equation (3(3) ) corresponds to the decision to deliver a spare part, in which case the system jumps immediately from state (i, j, 0)  to state (i, j, 1). Finally, Equation (4(4) ) represents the replacement decision that resets the number of spare parts on-board the vessel and the degradation level to zero. Under Equations (3(3) ) and (4(4) ), at each decision epoch, a part replacement can immediately follow a spare part delivery and vice versa. We note that the state space of the model is discrete, the action space A(i, j, u) ∈ {0, 1, 2} is finite for each (i, j, u) ∈ I × J × U. The model satisfies the conditions of Theorem 6.2.10 in Puterman (1994), which establishes the existence of an optimal deterministic stationary policy and the convergence of the value iteration algorithm to the optimal value. A value iteration algorithm that is designed to deal with immediate and instantaneous actions is given in Appendix B.

4. Optimal policy

In this section, we analyze the structure of the optimal policy. We start by stating three theorems that establish monotonicity results related to the component's degradation level. From this, we derive the structure of the optimal policy, which is an operating mode–dependent bi-threshold policy. The proofs of the theorems are given in Appendices C to E.

Theorem 1.

V(i, j, u) is non-decreasing in j ∈ J for each i ∈ I and u ∈ U.

This theorem states the following. Consider two components in operating mode i ∈ I while u ∈ U spare parts are on-board the vessel. If the degradation level of the first component is higher than the second one, then the minimum expected total cost of the first component cannot be less than the minimum expected total cost of the second component.

Theorem 2.

V(i, j, u) is submodular in (j, u) ∈ J × U; that is,

In Theorem 2, we consider the difference between the two cases: (i) there is a spare part on-board the vessel and (ii) there is no spare part on-board the vessel. We show that in a certain operating mode, when a component's degradation increases, the increase in the minimum expected total cost in case (i) cannot be greater than that of case (ii). In other words, if the spare part is not on-board the vessel, the cost increase resulting from the component's degradation is higher compared with the case where the spare part is on-board the vessel.

Theorem 3.

In each i ∈ I, there exists an optimal part replacement threshold ψ(i) ⩽ F and an optimal spare part delivery threshold ξ(i) ⩽ F such that

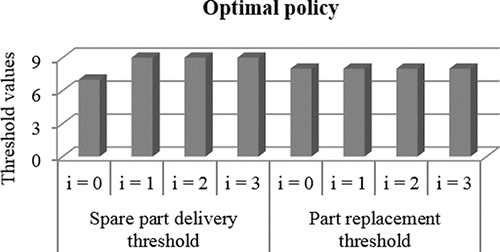
This theorem shows that the optimal policy is an operating mode–dependent bi-threshold policy on the degradation level.

Remark 1.

The spare part delivery threshold can be greater than or equal to the part replacement threshold, which may seem counterintuitive in the sense that one would expect a spare part delivery to precede a part replacement in all operating modes. This is because whether a replacement decision is made or not depends on the number of spare parts on-board the vessel. If there is no spare part on-board the vessel at a certain degradation level and operating mode, the additional cost of delivering a spare part may not repay the risk of a failure. However, if there is already a spare part on-board the vessel for the same degradation level and operating mode, it may be optimal to replace the component. Appendix F provides an example supporting this remark.

5. Numerical experiments

In this section, we execute numerical experiments in order to test the performance of the optimal policy and to assess the value of integrated spare part and maintenance optimization. We compare the optimal policy to four benchmark policies, in which replacement decisions are not integrated with spare part optimization. These policies simplify spare part inventory decisions by “never” or “always” keeping the spare part stock on-board the vessel. Replacement decisions are optimized in all benchmark policies.

In the first benchmark policy, the spare part stock^{Table 3}is never kept on-board the vessel. That is, a spare part delivery is always ^{Table 1, Table 2}followed by a part replacement. In addition, preventive deliveries are not allowed when the moving asset is away from its home base. As a consequence, preventive part replacements can only occur at the home base. We refer to this policy as never spare part policy (NP). Denoting the home base by i = 0, spare part delivery and part replacement thresholds in NP are such that ξ(i) = ψ(i) = F for all i ∈ I\{0} and ξ(0) = ψ(0) ⩽ F. The second policy is similar to NP, the only difference being that preventive deliveries are allowed when the moving asset is away from the home base. We call this policy a never spare part policy with preventive deliveries (NPP). In NPP, the spare part delivery threshold becomes equal to the part replacement threshold in each operating mode; i.e., ξ(i) = ψ(i) ⩽ F for all i ∈ I. In the third policy, the spare part is put on-board the vessel whenever the asset is at its home base (if it is not already on-board). We refer to this policy as always spare part policy (AP). In AP, preventive deliveries in operating modes other than the home base are not allowed. That is, the spare part delivery threshold is zero at the home base and is equal to the failure threshold in all other operating modes; i.e., ξ(0) = 0 and ξ(i) = F for all i ∈ I\{0}. Finally, we relax AP to allow preventive deliveries outside the home base and call this policy as the always spare part policy with preventive deliveries (APP). As such, APP enables more than one preventive replacement in between home base visits. In APP, ξ(0) = 0 and ξ(i) ⩽ F for all i ∈ I\{0}. The setup of the experiments is described in Section 5.1 and the results are discussed in Section 5.2.

5.1. Setup

We consider a critical component with four operating states I ≡ {0, 1, 2, 3} where 0 represents the home base of the moving asset, 1 and 3 intermediate states, and 2 the mission state. Intermediate states may correspond to transit states from the home base to the mission site or vice versa. The operating mode transition probability matrix is defined as in Table 1, representing a deterministic cyclic sequence of operating modes.

Table 1. Operating mode transition probability matrix.

Q(i, k)	0	1	2	3
0	0.00	1.00	0.00	0.00
1	0.00	0.00	1.00	0.00
2	0.00	0.00	0.00	1.00
3	1.00	0.00	0.00	0.00

Three alternatives are considered regarding the operating mode transition rates (see Table 2). Alternative 1 fits to a commercial setting similar to the real-life case that we present in Section 6. In that case, missions and home base visits have short durations. Alternative 2 reflects our observations from the defense industry (Navy ships) where mission durations and home base visits are long. To enrich our comparative analysis, we also consider Alternative 3, in which mission durations are very long compared with home base visits.

Table 2. Operating mode transition rates.

Operating mode transition rate (per year): μi	0	1	2	3
High	180	720	90	720
Low	6	26	6	26
Low in mission	180	52	6	52

Depending on the component, degradation can be uniform in different operating modes, high during missions, or high during home base visits. For example, power on/off switching has a significant influence on degradation for some electronic components; in this case, degradation rates may be higher at the home base where the systems are often switched on/off. On the other hand, if the degradation is linearly related to operating time and the component mostly operates during missions, the degradation would be higher in missions (cf. the case study in Section 6). In these numerical experiments, we consider 10 degradation levels J ≡ {0, 1, …, 9} and different degradation profiles for each operating mode i ∈ I as given in Table 3.

Table 3. Degradation rates.

	j
Degradation rates (per year): λij	i	0	1	2	3	4	5	6	7	8	9
Uniform	0	2	2	2	2	4	6	8	10	12	—
	1	2	2	2	2	4	6	8	10	12	—
	2	2	2	2	2	4	6	8	10	12	—
	3	2	2	2	2	4	6	8	10	12	—
High in mission	0	2	2	2	2	4	6	8	10	12	—
	1	4	4	4	4	8	12	16	20	24	—
	2	6	6	6	6	12	18	24	30	36	—
	3	4	4	4	4	8	12	16	20	24	—
High in home base	0	6	6	6	6	12	18	24	30	36	—
	1	4	4	4	4	8	12	16	20	24	—
	2	2	2	2	2	4	6	8	10	12	—
	3	4	4	4	4	8	12	16	20	24	—

We take the same preventive replacement costs c^pr_i = €1000 for all operating modes i ∈ I. The cost parameters considered for corrective replacement c^cr_i, transportation c^tr_i, and the spare part's price c^sp are^{Table 5}given in Table 4. We note that the preventive spare part delivery cost consists of the cost of transportation and the spare part's price; i.e., c^pd_i = c_i^tr + c^sp in operating mode i ∈ I. The additional spare part delivery cost in the case of failure c^ad_i is the difference between preventive and corrective deliveries, reflecting a possible downtime cost or the additional cost of an emergency shipment; i.e., c^cd_i = c_i^pd + c^ad_i in operating mode i ∈ I. Three alternatives are considered for the annual holding cost rate h^ra, 10% (low), 25% (medium), and 50% (high). The annual holding cost is calculated by multiplying the annual holding cost rate with the cost of the spare part; i.e., h = h^rac^sp. The annual discount rate of money is taken as 2%, resulting in the continuous rate α = −ln (0.98). We note that the considered cost ranges are based on our observations from real-life cases that consist of both commercial (survey vessels) and defense equipment (the Navy ships) in the maritime sector. Overall, we obtain 3⁶ × 2 = 1458 instances with the combination of different alternatives considered. The value iteration algorithm given in Appendix B was coded in C on a DELL computer with Intel Core i5-4300U processor (1.90 – 2.50 GHz) and 4.00 GB RAM.

Table 4. Cost parameters in thousand €.

		Operating mode i
Cost parameters (€ (x10^3))	Alternatives	0	1	2	3
Transportation cost (c^tri)	Low	0	0.1	0.2	0.1
	Medium	0	1	2	1
	High	0	10	20	10
Additional delivery cost (c^adi)	Yes	0	25	50	25
	No	—
Corrective replacement cost (c^cri)	Low	1.5
	Medium	5
	High	50
Spare part's price (c^sp)	Low	0.05
	Medium	5
	High	50

5.2. Results

We assess the value^{Table 4}of the integrated approach by comparing its performance with the four benchmark policies in terms of average and maximum cost increase. The cost increase was calculated by CS = (C − C*)/C*, where C is the expected total discounted cost under the benchmark policy and C* is the optimal cost obtained by our integrated maintenance and spare part optimization model. In addition, we calculated the percentage of instances for which the expected total discounted cost obtained under the benchmark policy coincides with the optimal cost (denoted by OC %).

Our numerical experiments show that the integrated approach has significant value. As shown in Table 5, the average cost increases under the benchmark policies NP, NPP, AP, and APP are 78, 20, 30, and 27%, respectively. The benchmark policies are not very likely to give the optimal cost. The percentage of instances for which the optimal cost coincides with the cost obtained by NP, NPP, AP, or APP is 5, 22, 2, or 12%, respectively. Not surprisingly, NP and AP are outperformed by NPP and APP, respectively. The average cost performance of NPP is found to be better than that of APP. In addition, the never spare part policies (NP and NPP) are more likely to give the optimal cost than the always spare part policies (AP and APP) for most of the cases. Nevertheless, the maximum cost increases in the never spare part policies are significantly higher compared with always spare part policies, meaning that the latter are usually more robust. In what follows, we summarize our observations regarding the performance of benchmark policies in different parameter settings.

Table 5. Cost increases under the benchmark policies compared to the optimal policy.

		Never spare part policies						Always spare part policies
		NP			NPP			AP			APP
Parameter	Alternative	Avg. (%)	Max. (%)	OC (%)	Avg. (%)	Max. (%)	OC (%)	Avg. (%)	Max. (%)	OC (%)	Avg. (%)	Max. (%)	OC (%)
Degradation rates	Uniform	40	199	7	13	108	31	41	140	2	41	140	6
	High in mission	154	1057	2	33	264	14	23	74	2	14	62	23
	High in home base	41	200	4	14	108	22	26	105	2	25	105	7
Operating mode transition rates	High	9	34	8	5	32	22	31	140	0	31	140	0
	Low	108	950	3	25	243	29	29	134	3	24	134	17
	Low in mission	119	1057	2	29	264	15	30	132	3	25	132	19
Corrective replacement cost	Low	56	613	10	19	264	18	29	140	4	27	140	12
	Medium	62	645	2	20	264	25	29	137	2	27	137	12
	High	117	1057	1	20	264	24	32	137	0	27	137	12
Transportation cost	Low	78	1057	7	3	14	45	35	140	0	32	140	5
	Medium	76	1034	4	13	73	16	31	136	0	28	136	7
	High	82	963	3	44	264	5	23	129	6	21	129	24
Add. exp. cost in case of failure	No	47	617	8	19	264	25	29	140	4	27	140	12
	Yes	109	1057	1	20	264	19	31	137	0	27	137	12
Spare part's price	Low	170	1057	0	48	264	0	8	74	5	1	6	33
	Medium	51	283	3	10	85	20	35	115	1	33	115	4
	High	15	73	10	2	18	47	47	140	0	47	140	0
Holding cost rate	Low	81	1057	3	22	264	15	13	74	2	10	32	15
	Medium	78	1051	3	20	263	19	27	74	2	24	73	14
	High	75	1041	7	18	260	33	50	140	1	47	140	8
Overall Avg./Max.		78	1057	5	20	264	22	30	140	2	27	140	12

Observation 1.

Our numerical experiments show that APP is near-optimal when the spare part is cheap. NPP is well-performing if the spare part is expensive or the operating mode transition rates are high or transportation costs are low. For the above-mentioned cases, the associated benchmark policy could be preferred, due to its practical benefits (e.g., ease of implementation and communication of the spare part inventory decisions). For all other cases, the optimal policy is advisable, as the benchmark policies would lead to significant cost increases.

Observation 2.

When the spare part is never stocked on-board the vessel, relying on preventive replacements at the home base significantly deteriorates the cost performance. The cost performance of NP is significantly worse compared with NPP when the transportation costs are low, corrective replacement and corrective delivery costs are high, degradation is fast during missions, and the moving asset is mostly performing a mission. Moreover, the cost performance of NP is non-monotonous with respect to transportation costs. This can be explained as follows. When transportation costs are low, preventive deliveries are favorable away from the home base; i.e., we often observe that ξ(i) < F for i ∈ I\{0} in the optimal policy. Since NP is restricted to ξ(i) = F for i ∈ I\{0} (i.e., no preventive spare part deliveries away from the home base), it performs poorly for low transportation costs. On the other hand, when transportation costs are high, preventive deliveries away from the home base are much less favorable. Nevertheless, NP becomes more expensive since the spare part cannot be stocked on-board the vessel.

Observation 3.

When the spare part is put on-board the moving asset whenever it is at its home base, the cost saving resulting from preventive deliveries performed away from the home base is usually very limited. This can be seen by looking at the difference between AP and APP in terms of average cost increase (3%). Enabling more than one replacement in between home base visits leads to significant cost benefits only under extreme conditions (e.g., the combination of high corrective costs, low price of the spare part, long mission durations, and high degradation rates during missions).

Observation 4.

The cost performance of all benchmark policies is very sensitive to the structure of the degradation rates. The performance of never spare part policies deteriorates when a component's degradation is fast during missions. On the other hand, the always spare part policies perform relatively poorly when degradation is fast at the home base. For the uniform degradation rates that we consider, the component's lifetime is longer compared with other alternatives. This is shown to cause a very poor performance in always spare part policies.

Observation 5.

Different from the always spare part policies, the performance of the never spare part policies is very sensitive to changes in the operating mode transition rates. This is because, when the spare part is not stocked on-board the vessel, the total cost of spare part deliveries is highly dependent on the operation process. In particular, NPP performs very well when the operating mode transition rates are high; i.e., when the home base visits are frequent. These cases greatly improve the average performance of NPP.

Observation 6.

The cost performances of NPP, AP, and APP are almost insensitive with respect to corrective replacement and corrective delivery costs. This is due to the trade-off between preventive and corrective costs being taken into account while optimizing replacement thresholds ψ(i) for all i ∈ I. This does not hold for NP, as preventive deliveries and replacements cannot be performed away from the home base, by the definition ξ(i) = ψ(i) = F for all i ∈ I\{0} under NP.

Observation 7.

In our numerical experiments, the average computation time of the optimal policy (47 seconds) is comparable to those of AP (31.1 seconds) and APP (30.8 seconds). NP (1.8 seconds) and NPP (1.7 seconds) outperform the other policies in terms of computation time. This is because the state information that indicates the number of spare parts on-board the vessel is irrelevant in NP and NPP, resulting in smaller action and state spaces. The difference in terms of computation time will become significant for problems with larger state spaces or higher degradation/transition rates, due to the structure of the solution algorithm (cf. Appendix B). For cases where one of the benchmark policies is known to be well-performing (cf. Observation 1) and the optimal policy is computationally expensive, a near-optimal solution can be found using that benchmark policy.

6. Case study: Cooling fan of a survey vessel

In this section, real-life data acquired from FMS are utilized to demonstrate our integrated maintenance and spare part optimization model. As briefly introduced in Section 1, a major part of Fugro's business activity relates to exploration of the seafloor, for which survey vessels are used. These vessels use Diesel Electric Propulsion (DEP) systems that produce thrust and create movement. The DEP system consists of several subsystems. The centrifugal cooling fan of the frequency convertor is a part of the DEP system. The frequency converter generates heat as a consequence of its operation and needs to be cooled down by a cooling fan. As the failure of the cooling fan can lead to a fire, the DEP system needs to be stopped if the cooling fan fails, which results in downtime. The cooling fan can be easily replaced at all locations and a stock of spare parts can be kept either on-shore or on-board the vessel.

The daily reports of survey vessels contain information about the duration of different states, such as length of stay in a harbor, sailing to a location, performing operations, or waiting for suitable weather conditions. For the case of unsuitable weather conditions, the vessel sails to a location near the shore and waits there for improved weather conditions. When this happens the vessel sails back to its operation site. Otherwise, the vessel returns back to the harbor. There also exist consecutive missions; i.e., a mission can be followed by another mission with a transit phase in between. Based on the daily reports, we have categorized the operating modes as follows: “harbor,” “transit-to-mission,” “mission,” “transit-to-harbor,” and “weather.” We have analyzed a data set of 3 years regarding the sequence of these operating modes and their duration. As for the appropriateness of the Markovian model, we have also tested whether the durations of operation modes are well represented by exponential distributions. For all operating modes, except for the transit-to-mission state, the exponential distribution assumption is not rejected by the Kolmogorov–Smirnov test at the 95% confidence level. The corresponding transition rates and the transition probability matrix are given in Table 6. Based on the failures experienced by FMS, the failure of the ball bearing is found to be the main reason for the failure of the cooling fan. According to the OEM, the service life of the bearing system mainly depends on the thermal load on the bearing; i.e., the thermal fatigue. The OEM provides the L₁₀ fatigue life of the bearing, which is the time at which 10% of the bearings can be expected to have failed. The OEM states that the L₁₀ fatigue life is approximately 40 000 operating hours at an ambient temperature of 40°C. Based on this information, FMS treats cooling fans as reliable and holds no spare parts on-board a vessel. The current policy employed by FMS corresponds to a time-based block replacement policy. The replacement is done during dry-dock maintenance, which is mandatory every 5 years. Corrective maintenance is performed if the cooling fan has failed before dry-dock maintenance.

Table 6. Transition rates and the transition probability matrix.

Transition matrix: Q(i, k)	Harbor	Transit-to-mission	Mission	Transit-to-harbor	Weather	Transition/year: μi
Harbor	0.00	1.00	0.00	0.00	0.00	151
Transit-to-mission	0.00	0.00	1.00	0.00	0.00	1039
Mission	0.00	0.19	0.00	0.46	0.35	102
Transit-to-harbor	1.00	0.00	0.00	0.00	0.00	924
Weather	0.00	0.61	0.00	0.39	0.00	194

Over the last 3 years, FMS has observed significantly shorter service lives. The earliest failures have occurred within the range of 2000–5000 operating hours. In the pursuit of better representing the expected failure times of the ball bearing, we used the fatigue life prediction model presented in Harris and Barnsby (2001): (5) where L_na is the adjusted bearing fatigue life and a₁, a₂, and a₃ are life adjustment factors for the selected reliability level, material, and operating conditions, respectively. As the vessel under consideration always operates in the same geographical region, environmental conditions were assumed to be similar for all the different operating modes. After applying Equation (5(5) ) (based on the qualitative information obtained from FMS), the adjusted fatigue life of the ball bearing was found to be 4300 operating hours. The adjusted fatigue life is consistent with the failures that FMS has observed.

The degradation^{Table 6, Table 7, Table 8, Table 9Figure 1}process was modeled based on our service life estimation in Equation (5(5) ) and considering how the cooling fan is used in different operating modes. We note that the cooling fan is in use only when the bow thruster is operating. This is required to make the vessel more maneuverable in the mission, harbor, and weather states. Using expert knowledge, we have assessed the operating time of the cooling fan in different operating modes. Assuming that the degradation is linearly correlated with the operating time, the cooling fan is expected to degrade 17 times faster during missions than during harbor or weather states. In transit states, the degradation of the cooling fan is assumed to be negligible, as it is never utilized. Based on this information, we built an Erlangian degradation process for each operating mode where F = 10 and the rates out of each state to the next degradation state are 0.41, 0.00, 7.13, and 0.41 for harbor, transit, mission, and weather states, respectively. By doing this, we divided the lifetime of the component in 10 equal parts (see Table 7). There is a small amount of data to statistically support the degradation process that we propose. Nevertheless, this degradation process is found to reflect actual operation based on the observations of FMS.

Table 7. Degradation rates.

	j
	i	0	1	2	3	4	5	6	7	8	9
Degradation rates (per year): λij	Harbor	0.41	0.41	0.41	0.41	0.41	0.41	0.41	0.41	0.41	0.41
	Transit-to-mission	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
	Mission	7.13	7.13	7.13	7.13	7.13	7.13	7.13	7.13	7.13	7.13
	Transit-to-harbor	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
	Weather	0.41	0.41	0.41	0.41	0.41	0.41	0.41	0.41	0.41	0.41

The cost parameters differ between operating modes and are as listed in Table 8. The preventive replacement costs mainly consist of the cost of labor. The preventive delivery costs include the spare part's price, which is €3600 and the cost of transportation, which is €10 000 (applied if the vessel is in transit or on a mission). During a bad weather situation, the vessel takes shelter near the shore, which results in lower transportation costs. During a harbor stay, the cost of transportation is negligible. The corrective replacement and delivery costs can be significant during mission and transit-to-mission states, due to the resulting downtime. A corrective replacement was estimated to take 4 hours and an expedited delivery lasts almost 1 day. The downtime cost associated with the delay in operations is an intangible parameter and can vary to a major extent over time. In this case study, we took the downtime cost as €30 000 per day; however, this should not be taken as the actual cost incurred by FMS. We refer the reader to Section 5 for the impact of the downtime cost on the solution performance (this is reflected in corrective costs). In this case study, the holding cost rate was taken as 25% per year and the continuous rate is set to α = −ln (0.98).

Table 8. Cost parameters.

Operating mode	Preventive replacement cost c^pri	Corrective replacement cost c^cri	Preventive delivery cost c^pdi	Corrective delivery cost c^cdi
	(€)	(€)	(€)	(€)
Harbor	100	400	3600	3600
Transit-to-mission	100	5400	13 600	43 600
Mission	100	5400	13 600	43 600
Transit-to-harbor	100	400	13 600	13 600
Weather	100	400	8600	8600

Considering the degradation information given in Table 7, we adapted the replacement interval of the current policy. Indeed, the initial service life of the component was overestimated and the current policy excludes the relation between operating modes and degradation. The replacement interval was adjusted using the bisection method. Under the adjusted policy, the component is replaced at fixed time intervals of 1.5 years instead of 5 years and the spare part is never stocked on-board the vessel.

Table 9 summarizes the performance of different policies in terms of cost. We note that the total cost obtained by the current policy is coherent considering what FMS has faced for the last few years. Assuming that the degradation model that we have built reflects the degradation of the cooling fan, the current policy performs significantly worse compared with the adjusted policy. The adjusted policy is found to be 47% more expensive than the optimal policy. This is mainly a result of the operating modes and condition information being neglected and the replacements are made in a time-based manner under the adjusted policy.

Table 9. Cost performance of different policies.

	Expected total discounted cost over an infinite horizon	Cost increase compared to the optimal policy
	(€)	(%)
Current policy	804 933	—
Adjusted policy	139 765	47
Never spare part policies	105 784	11
(NP and NPP)
Always spare part policies	131 736	38
(AP and APP)
Optimal policy	95 290	—

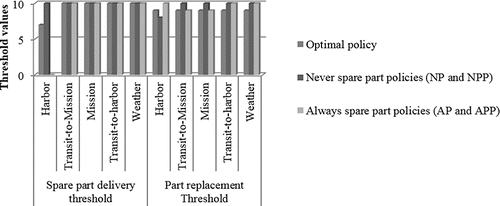
Figure 1 demonstrates the threshold values obtained by the optimal policy and the benchmark policies. We observe that the never spare part policies encourage early replacements in the harbor to deal with the risk of corrective deliveries/replacements in non-harbor states. On the other hand, the always spare part policies postpone the replacement in the operating modes in which the corrective replacement costs are relatively low (harbor, transit-to-harbor, and weather states). Moreover, NP and AP give the same solution as NPP and APP, respectively. This is due to the fact that preventive delivery costs are high in non-harbor states and the frequency of harbor visits is very high compared with the frequency of failures. This makes preventive deliveries unfavorable in non-harbor states.

Figure 1. Threshold values obtained for different policies.

We observe that the never spare part policies outperform the always spare part policies. This is due to harbor visits being very frequent, offering many opportunities for cheap preventive replacements in the harbor. Nevertheless, compared with the optimal policy, both simple policies are shown to be very costly. Total cost increases of about 11 and 38% are observed under the never spare part policies and the always spare part policies, respectively. Even under very frequent harbor visits, it is not optimal to “never” keep a stock of the spare part on-board the vessel. The optimal policy provides a solution in which the component is stocked on-board the vessel when the risk of failure is high, providing a trade-off between spare part deliveries, part replacements, and holding costs.

7. Conclusions

In this article, we have considered an integrated maintenance and spare part optimization problem for a single critical component of a moving asset. We have proposed a Markov decision model and analyzed the optimal integrated policy. We have shown that the optimal policy is an operating mode–dependent bi-threshold policy. Numerical experiments have been provided to assess the value of the optimal policy compared with four benchmark policies. In these benchmark policies, replacement decisions are optimized but not integrated with spare part inventory decisions. These policies simplify spare part inventory decisions by “never” or “always” keeping a stock of the spare part on-board the vessel. Through a comparative analysis, we have shown that our integrated approach has significant value. Simplifying spare part inventory decisions results in an average cost increase of at least 20%. The benchmark policies are unlikely to be optimal, except under some specific conditions such as very high or very low prices of the spare part or transportation costs.

The problem studied in this article was motivated by a real-life problem faced at FMS. From our collaboration with the maritime sector, we observed that failure-related historical data are usually limited. This makes the characterization of the degradation process challenging. In modeling the degradation and failure behaviors of the components, physical models are known to be less data demanding than data-driven models. Moreover, the difference associated with operating modes can be incorporated into physical models, using the quantitative relation between usage, environment, and degradation. Nevertheless, considerable effort is generally needed to develop such models.

We considered a single critical component and at most one spare part kept on-board of the moving asset. Our numerical experiments show that under extreme conditions, performing more than one replacement in between home base visits would be cost-effective. Therefore, allowing a stock of more than one spare part on-board a vessel can potentially lead to a better solution. In this direction, extension of our model requires the consideration of fixed costs associated with delivering multiple spare parts at a time; i.e., the economies of scale in spare part deliveries. This can be captured by extending the state and the action space of our model. The investigation of the optimal policy structure would be an interesting topic in this extension. We note that if a non-consumable and critical component has to be replaced more than one time in between home base visits, one can question the existence of a design problem. For such cases, one should consider increasing reliability by redesign or built-in redundancy. Existing research considers CBM and inventory optimization problems for identical and independent components (see, e.g., Wang et al. (2008), (2009) and Xie and Wang, (2008)). These works take non-zero lead times, fixed ordering costs, and shortage costs for spare parts into account. As these aspects increase problem complexity, the proposed solution methods are approximate, combining techniques such as simulation and genetic algorithms. To the best of our knowledge, there exists no work in the literature that considers non-identical components (see also van Horenbeek et al., (2013)). The consideration of economic, structural, and stochastic dependencies between multiple components has a great practical relevance for moving assets. In practice, there exist fixed costs associated with maintenance and ordering spare parts, which would promote clustering or opportunistic policies. In this respect, a direct extension of our Markov decision process would be affected by the curse of dimensionality. In order to solve such real-life problems, the application of approximate dynamic programming can be investigated (Powell, 2007).

In this article, we assumed that spare parts are always available at the home base. In practice, the home base is a central warehouse where the stock of spare parts is limited and pooled to serve several moving assets. If spare parts are directly assigned to moving assets and stocked on-board, the benefit of inventory pooling at the central warehouse vanishes. In particular, this happens if lateral transshipments from one asset to another are not allowed. In our model, this effect can be taken into account implicitly, by inflating the holding cost rate. However, this approach is approximate. An exact approach would be to analyze this problem from multi-echelon spare parts inventory perspective, considering a number of moving assets served by a central warehouse (see, e.g., Muckstadt (2005) and van Houtum and Kranenburg (2015)).

Furthermore, in this article, the consequences associated with system failure have been translated into cost parameters. In practice, estimating intangible corrective cost terms is not straightforward, in particular, when failures affect people's health, safety, and environment. If modeling the trade-off between preventive and corrective costs is not obvious, the focus should lie on availability and reliability measures. The relation between system design and availability–reliability requirements needs to be closely investigated in the design phase of a system.

We note that although our motivation came from a maritime application, the model and the results presented in this article may be applied to other moving assets such as aircraft, commercial vehicles, and military equipment. The rapid development of advanced sensor technologies is making the condition monitoring of components more affordable and feasible. The condition information provided by sensors can be especially useful for critical systems operating in environments that vary randomly over time. This is due to the changes in environmental conditions and system usage being related to the rate at which degradation accumulates (Ulukus et al., 2012). The model that we propose is highly valuable considering the trend of shifting from time-based maintenance to CBM. Moreover, repair-by-replacement is a common practice for high-value capital assets in general (Driessen et al., 2015). Our model can be of value when there is an option of stocking the spare part on-board a moving asset. Depending on the application to be performed, the model can be easily tailored to adjust to the number of operating modes, their duration/sequence, associated costs, and degradation parameters.

Acknowledgements

The authors gratefully acknowledge the support of Fugro Marine Services and the discussions with Roy van Hugten and Fred Schulte.

Additional information

Funding

This research is funded by Dutch Institute for Advanced Logistics (Dinalog, 2011-4-085-R).

Notes on contributors

Ayse Sena Eruguz

Ayse Sena Eruguz is a Post-doctoral Researcher at Eindhoven University of Technology and is working on joint university–industry research projects, namely, integrated maintenance and service logistics concepts for maritime assets (MaSeLMa) and pro-active service logistics for capital goods—the next steps (ProSeLoNext). She received her Ph.D. in industrial engineering from Ecole Centrale Paris, France, in 2014. Her current research interests include service logistics, maintenance optimization, and multi-echelon inventory optimization.

Tarkan Tan

Tarkan Tan is an Associate Professor of sustainable operations management in the School of Industrial Engineering at Eindhoven University of Technology, The Netherlands. He received his Ph.D. from the Middle East Technical University, Ankara, Turkey, in 2002. He spent a year at Columbia University, New York, as a Fulbright Scholar. He joined Eindhoven University of Technology in 2003 and he is currently the director of the operations management and logistics M.Sc. program at this university. He has visited the University of California, Los Angeles, and the University of Sydney as a visiting scholar. He is an executive board member of the European Supply Chain Forum. His research interests include inventory theory, capacity management, spare parts management, and supply chain management with a particular focus on sustainability.

Geert-Jan van Houtum

Geert-Jan van Houtum is a Professor of maintenance and reliability at the School of Industrial Engineering, Eindhoven University of Technology. He is the scientific director of the BETA Research School for Operations Management and Logistics. His research is focused on spare parts management, production-inventory systems, maintenance and availability management of capital goods, and the effect of design decisions on the total cost of ownership of capital goods.

Appendix

Appendix A: Markov decision process with immediate transitions

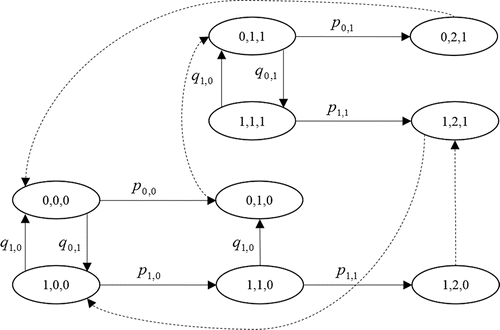
For illustration purposes, we depict an exemplary process in Figure A1. We consider two operating modes I ≡ {0, 1} and three degradation levels J ≡ {0, 1, 2}. We assume that the system operates under the following policy. In operating mode i = 0, a spare is delivered when degradation level j is greater than one. In operating mode i = 1, spare part delivery is performed when the component has failed. In both operating modes, the component is replaced only correctively. In the uniformized process, when action 0 is taken under the given policy, the probability that the system jumps from degradation level to j + 1 is p_ij = λ_ij/v and the probability that the system jumps from operating mode i ∈ I to k ≠ i is q_ik = μ_iQ(i, k)/v. In Figure A1, transitions from a state to itself are not depicted for ease of exposition (the corresponding probabilities are q_ii = 1 − v_ij/v). Immediate transitions under the given policy are shown by dotted arcs.

Figure A1. Markov chain illustrating the uniformized process under a given policy.

Appendix B:

Value iteration algorithm

Let V_n(i, j, u) be the expected total discounted cost over a time horizon of n periods, where each period has an expected length 1/v. Without loss of generality, we select V₀(i, j, u) as follows: (A1)

We introduce an additional notation σ_a to represent the instantaneous part replacements and spare part deliveries:

For (i, j, u) ∈ I × J × U and n ∈ ℕ₀, where ℕ₀ is the set of non-negative integers, V_{n + 1}(i, j, u) can be computed by (A2) where is defined as follows for a = 0, a = 1, and a = 2, respectively: (A3) (A4) (A5)

Due to instantaneous part replacements and spare part deliveries, value iteration should substitute updated values of V_{n + 1}(i, j, u) at the (n + 1)th iteration. In state (i, 0, 1), if the optimal decision is to replace the part, this decision will not be immediately followed by a spare part delivery. This is because V_{n + 1}(i, 0, 1) = c^pr_i + c^pd_i + V_{n + 1}(i, 0, 1) cannot hold since c^pr_i > 0 and c^pd_i ⩾ 0 for each i ∈ I. Therefore, V_{n + 1}(i, 0, 1) is equivalent to (A6)

Starting with Equation (A6(A6) ), V_{n + 1}(i, j, u) can be evaluated in decreasing order of u ∈ U and increasing order of j ∈ J using Equation (A2(A2) ). As such, Equations (A4(A4) ) and (A5(A5) ) can be indirectly expressed in terms of V_n(i, j, u) for each (i, j, u) ∈ I × J × U. This overcomes instantaneous transitions for all states. What follows presents the value iteration algorithm that is designed to solve Equation (1(1) ). We refer to Puterman (1994, Theorem 6.3.1., p. 161) for further details about the convergence of such a value iteration algorithm to the optimal value of the infinite-horizon problem.

• Step 1: Set n = 0 and ϵ = 0.0001. Select V₀(i, j, u) as Equation (A1(A1) ).

• Step 2: For each (i, j, u) ∈ I × J × U, compute V_{n + 1}(i, j, u) in decreasing order of u ∈ U and increasing order of j ∈ J: If (j, u) = (0, 1) use Equation (A6(A6) ). Otherwise, use Equation (A2(A2) ).

• Step 3: If for each (i, j, u) ∈ I × J × U, |V_{n + 1}(i, j, u) − V_n(i, j, u)| < ϵ(1 − β)/2β, then go to Step 4. Otherwise, increment n by one and return to Step 2.

• Step 4: For each (i, j, u) ∈ I × J × U, choose the optimal stationary policy by

  and stop.

Appendix C:

Proof of Theorem 1

In order to prove Theorem 1, we first introduce Lemmas A1 to A4.

Lemma A1.

For each i ∈ I and n ∈ℕ₀, if Γ₀V_n(i, j, 1) is non-decreasing in , then V_{n + 1}(i, j, 1) is non-decreasing in .

Proof of Lemma A1.

From Equation (A2(A2) ), V_{n + 1}(i, j, 1) can be re-written as follows for each i ∈ I, , and n ∈ℕ₀: (A7)

For each i ∈ I, the cost of preventive replacement c^pr_i + V_{n + 1}(i, 0, 0) and the term (β/v)h are constant and do not depend on . Therefore, if Γ₀V_n(i, j, 1) is non-decreasing in , then Equation (A7(A7) ) is also non-decreasing in .■

Lemma A2.

For each i ∈ I and n ∈ ℕ₀:

(a)	Vn(i, j, 1) is non-decreasing in j ∈ J.
(b)	Γ0Vn(i, j, 1) is non-decreasing in .

Proof of Lemma A2(a).

We first prove Lemma A2(a) by induction.

Basis: Lemma A2(a) holds for n = 0 by Equation (A1(A1) ).

Induction Step: For each i ∈ I, assume that V_n(i, j, 1) is non-decreasing in j ∈ J for a given n > 0 (induction hypothesis). From Equation (A3(A3) ), we have the following for : (A8)

The second equality follows from the definition of v_ij and v_{i, j − 1}, which are equal to μ_i + λ_ij and μ_i + λ_{i, j − 1}, respectively. We note that v ⩾ max {v_ij|i ∈ I, j ∈ J} by definition. Therefore, Equation (A8(A8) ) is greater than or equal to zero for each i ∈ I and under the induction hypothesis. Thus, Γ₀V_n(i, j, 1) is non-decreasing in for each i ∈ I. Using Lemma A1, V_{n + 1}(i, j, 1) is non-decreasing in for each i ∈ I.

It remains to prove that V_{n + 1}(i, F, 1) − V_{n + 1}(i, F − 1, 1) ⩾ 0 for all i ∈ I. For j = F, we have (A9)

The first inequality follows from the definition of preventive and corrective cost parameters. The second inequality holds by the definition of V_{n + 1}(i, F − 1, 1). Thus, for each i ∈ I, V_{n + 1}(i, j, 1) is non-decreasing in j ∈ J, completing the induction and the proof of Lemma A2(a).

From Lemma A2(a), Equation (A8(A8) ) is greater than or equal to zero for each i ∈ I, , and n ∈ ℕ₀, implying that Lemma A2(b) holds. □

We note that Lemma A2(b) is required to prove Theorem 2.

Lemma A3.

For each i ∈ I and n ∈ ℕ₀, if Γ₀V_n(i, j, 0) is non-decreasing in , then V_{n + 1}(i, j, 0) is non-decreasing in .

Proof of Lemma A3.

From Equation (A2(A2) ), V_{n + 1}(i, j, 0) can be re-written as follows for each i ∈ I,, and n ∈ ℕ₀: (A10)

From Lemma A2(a), V_{n + 1}(i, j, 1) is non-decreasing in j ∈ J for each i ∈ I and n ∈ ℕ₀. Lemma A3 follows from Equation (A10(A10) ), in which V_{n + 1}(i, j, 0) is the minimum between two non-decreasing terms in ■

Lemma A4.

For each i ∈ I and n ∈ ℕ₀:

(a)	Vn(i, j, 0) is non-decreasing in j ∈ J.
(b)	Γ0Vn(i, j, 0) is non-decreasing in .

Proof of Lemma A4.

The proof of Lemma A4 is along the same lines as the proof of Lemma A2, replacing u = 1 by u = 0, Lemma A1 by Lemma A3, Lemma A2 by Lemma A4, and Equation (A9(A9) ) by

The first inequality follows from Equation (A9(A9) ) and c^cd_i ⩾ c_i^pd. The second equality follows from Equation (A10(A10) ). ■

We note that Lemma A4(b) is required to prove Theorem 3.

Proof of Theorem 1.

Theorem 1 follows from Lemma A2(a) and Lemma A4(a). Since they hold for all n ∈ ℕ₀, they also hold for the infinite-horizon function V(i, j, u) where n tends to infinity.■

Appendix D:

Proof of Theorem 2

In order to prove Theorem 2, we first introduce Lemmas A5 to A7.

Lemma A5.

For each i ∈ I,, and n ∈ ℕ₀, if action 2 is optimal in state (i, j − 1, 1), then action 2 is also optimal in state (i, j, 1).

Proof of Lemma A5.

Fix operating mode i ∈ I and n ∈ ℕ₀. Suppose that .

From Equation (A7(A7) ), the optimality of action 2 means that the cost associated with action 2 is less than or equal to the cost associated with action 0. Hence, if action 2 is optimal in state (i, j − 1, 1), then

From Lemma A2(b), we have

Thus, action 2 is also optimal in state (i, j, 1), completing the proof. ■

Proof of Lemma A6.

The following inequality holds for all i ∈ I, , and n ∈ ℕ₀: (A11)

Proof of Lemma A6.

Fix operating mode i ∈ I and n ∈ ℕ₀. Suppose that .

From Equation (A10(A10) ), we have V_{n + 1}(i, j − 1, 0) ⩽ Γ₀V_n(i, j − 1, 0). Similarly, from Equation (A7(A7) ), we have

Therefore, if then Equation (A11(A11) ) holds. Otherwise, if V_{n + 1}(i, j − 1, 1) = c^pr_i + V_{n + 1}(i, 0, 0), then V_{n + 1}(i, j, 1) − V_{n + 1}(i, j − 1, 1) = 0 by Lemma A5. From Lemma A2(b), Γ₀V_n(i, j, 1) − Γ₀V_n(i, j − 1, 1) ⩾ 0 and, thus, Equation (A11(A11) ) holds.■

Lemma A7.

For each i ∈ I and n ∈ ℕ₀, the following inequalities hold: (A12) (A13)

Proof of Lemma A7.

We first prove Lemma A7(a) by induction.

Basis: Lemma A7(a) holds for n = 0 under Equation (A1(A1) ).

Induction Step: For each i ∈ I and j ∈ J\{0}, assume that Lemma A7(a) holds for a given n > 0 (induction hypothesis).

•	Case 1: j = F.

By definition, V_{n + 1}(i, F, 0) = c^cd_i + V_{n + 1}(i, F, 1). Hence, for n + 1, the left-hand side of Equation (A12(A12) ) is (A14)

Equation (A14(A14) ) is less than or equal to zero since V_{n + 1}(i, F − 1, 0) ⩽ V_{n + 1}(i, F − 1, 1) + c^pd_i and c^pd_i ⩽ c_i^cd.

•	Case 2: and Vn + 1(i, j, 0) = cpdi + Vn + 1(i, j, 1).

For n + 1, the left-hand side of Equation (A12(A12) ) is (A15)

From Equation (A10(A10) ), Equation (A15(A15) ) is less than or equal to zero.

•	Case 3: and Vn + 1(i, j, 0) = Γ0Vn(i, j, 0).

For n + 1, the left-hand side of Equation (A12(A12) ) becomes (A16)

From the definition of operator Γ₀, we have the following: (A17)

From the induction hypothesis, Equation (A17(A17) ) is less than or equal to zero for each i ∈ I and . Lemma A6 implies that Equation (A16(A16) ) is less than or equal to Equation (A17(A17) ). Hence, Equation (A16(A16) ) is less than or equal to zero for each i ∈ I and , completing the induction and the proof of Lemma A7(a).

From Lemma A7(a), Equation (A17(A17) ) is less than or equal to zero for each i ∈ I, , and n ∈ ℕ₀, implying that Lemma A7(b) holds.■

Proof of Theorem 2.

Theorem 2 follows from Lemma A7(a). Since Equation (A12(A12) ) holds for all n ∈ ℕ₀, it also holds for the infinite horizon function V(i, j, u) where n tends to infinity. ■

Appendix E:

Proof of Theorem 3

Lemma A8.

For each i ∈ I,, and n ∈ ℕ₀, if action 1 is optimal in state (i, j − 1, 0), then action 1 is also optimal in state (i, j, 0).

Proof of Lemma A8.

Fix operating mode i ∈ I and n ∈ ℕ₀. Suppose that .

From Equation (A10(A10) ), the optimality of action 1 means that the cost associated with action 1 is less than or equal to the cost associated with action 0. Hence, if action 1 is optimal in state (i, j − 1, 0), then (A18)

From Lemma A4(b), we have

If V_{n + 1}(i, j − 1, 1) = c^pr_i + V_{n + 1}(i, 0, 0), then V_{n + 1}(i, j, 1) = c^pr_i + V_{n + 1}(i, 0, 0) = V_{n + 1}(i, j − 1, 1) from Lemma A5. In this case, it holds that c^pd_i + V_{n + 1}(i, j, 1) = c^pd_i + V_{n + 1}(i, j − 1, 1) ⩽ Γ₀V_n(i, j, 0) and, thus, action 1 is optimal in state (i, j, 0).

Otherwise, if V_{n + 1}(i, j − 1, 1) = (β/v)h + Γ₀V_n(i, j − 1, 1), then Equation (A18(A18) ) can be re-written as (A19)

From Lemma A7(b), we have (A20)

Inequalities (A19(A19) ) and (A20(A20) ) imply

From Equation (A7(A7) ), V_{n + 1}(i, j, 1) ⩽ (β/v)h + Γ₀V_n(i, j, 1). Thus,

In this case, action 1 is optimal in state (i, j, 0), completing the proof.■

Proof of Theorem 3.

The existence of an optimal replacement threshold ψ(i) ⩽ F in operating mode i ∈ I follows from Lemma A5. The existence of an optimal spare part delivery threshold ξ(i) ⩽ F in operating mode i ∈ I follows from Lemma A8. Since both lemmas hold for all n ∈ ℕ₀, they also hold for the infinite-horizon problem where n tends to infinity.■

Appendix F:

Illustrative example for Remark 1

As an illustrative example to Remark 1, we use one of the instances of the test bed described in Section 5. We consider the combination given in Table A1. Figure A2 demonstrates the threshold values obtained by the optimal policy. For this example, under the optimal policy, a preventive spare part delivery would not be performed away from the home base since ξ(i) = F = 9 for all i ∈ I\{0}. That is, if the spare part is not on-board the vesssel, a preventive part replacement would not be optimal. However, if the spare part has already been delivered at the home base, it is optimal to perform a preventive part replacement in i ∈ I\{0} since ψ(i) ⩽ F.

Table A1. Illustrative example parameters.

Degradation rates	Uniform
Operating mode transition rates	High
Corrective replacement cost	Medium
Transportation cost	High
Add. exp. cost in case of failure	No
Spare part's price	High
Holding cost	Medium

Figure A2. Threshold values of the optimal policy.