Robust Optimization Approaches in Inventory Management: Part A - The Survey

Abstract

This work, the first part (Part A) of a comprehensive study, presents a survey on Robust Optimization (RO) in inventory management, highlighting its role in addressing uncertainties. This survey reviews various modeling frameworks, types of uncertainties, decision-making criteria, and decision rules essential to RO. The subsequent part (Part B) offers a comparative study, analyzing robust inventory models and highlighting key analytical and numerical contributions. This survey critically evaluates the effectiveness of RO in managing model uncertainty, enhancing decision-making processes, deriving structural insights, and boosting computational efficiency. Additionally, it discusses the limitations and challenges of applying RO to inventory management. While acknowledging the foundational role of traditional inventory literature in establishing essential theories, optimal policies, and efficient algorithms, this paper addresses a significant gap by focusing on inventory management through the lens of RO methodology. Together with the comparative study, these works encapsulate the current state of robust inventory management, shedding light on future research directions and ongoing challenges in this evolving field.

Keywords:

• Robust optimization
• Decision rules
• Model uncertainty
• Decision criteria
• Inventory management

Disclaimer

As a service to authors and researchers we are providing this version of an accepted manuscript (AM). Copyediting, typesetting, and review of the resulting proofs will be undertaken on this manuscript before final publication of the Version of Record (VoR). During production and pre-press, errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal relate to these versions also.

1 Introduction

Inventory control in particular stochastic inventory management is a critical issue in operations management and has been extensively studied since the pioneering work of Scarf (1958) on the single-period newsvendor problem and Scarf et al. (1960) on the multi-period stochastic inventory model. Traditional research typically assumes complete information about the probability distribution of random parameters (Clark and Scarf, 1960; Veinott Jr, 1966). However, these assumptions often do not hold in practical situations where the distribution is unknown and only historical data is available. As demonstrated by Liyanage and Shanthikumar (2005), three methodological streams—parametric, non-parametric, and partially known information about the underlying probability distribution—can be utilized to address inventory management problems with an unknown distribution of model parameters. Under the parametric methods, it is assumed that the distribution belongs to a parametric family of distributions, and the parameters specifying the distribution are estimated using historical data. Once the probability distribution is identified, the inventory problem is solved based on the estimated distribution (Conrad, 1976; Nahmias, 1994; Agrawal and Smith, 1996).

In the context of multi-stage decision-making, the parametric approach can utilize the Bayesian method to incorporate realized information about uncertain parameters, thereby updating the prior distribution for the unknown parameters (Scarf, 1959; Karlin, 1960; Azoury, 1985). Applications of the Bayesian approach to the censored demand case are provided by Lariviere and Porteus (1999) and Ding et al. (2002). In contrast, within the non-parametric approach, either the empirical distribution or the bootstrapping method can be applied to historical data to obtain an inventory policy (Bookbinder and Lordahl, 1989). Despite their wide usage and promising implementability, both parametric and non-parametric methods rely on estimating the probability distributions of random parameters. However, the estimated distributions may not be accurate, and thus, the approach of fitting the distribution and optimizing inventory decisions sequentially may not work as expected (Liyanage and Shanthikumar, 2005). Moreover, the misspecification of the true probability distributions of random parameters when estimated using historical data is not uncommon (Bertsimas and Thiele, 2006; Klabjan et al., 2013).

Robust inventory models, which do not assume a parametric family of distributions, only require partial information about the random parameters, such as moments and lower and upper bounds. These models provide a third alternative for dealing with unknown probability distributions. For example, when the unknown demand distribution is characterized by the first two moments, Scarf (1958) adopts a min-max approach that aims to minimize the worst-case expected cost, maximized over the set of distributions that meet the known information of the first two moments of the demand. Advancements in Robust Optimization (RO) since the 1990s further present viable solutions for inventory control challenges involving uncertain parameters with ambiguous probability distributions. However, compared to the classical parametric and non-parametric methods, robust models based on partial information of the probability distribution may miss important information conveyed in the historical data set, such as the shape of the distribution, which is fully utilized in the classical approach (Klabjan et al., 2013).

The first general RO model was investigated by Soyster (1973), who proposed a linear optimization model to yield a feasible solution for all data residing in a convex set. Over the past two decades, there has been explosive growth in the development of RO, driven by a series of breakthroughs in theory and methodology. Some of the important works include but are not limited to Ben-Tal and Nemirovski (2000), Bertsimas and Sim (2004), and Gorissen et al. (2014) for robust linear programming, Ben-Tal et al. (2015a), Bertsimas et al. (2023), and Zhen et al. (2023) for robust convex optimization, and Bertsimas and Sim (2003) and Kouvelis and Yu (2013) for robust discrete optimization. These advancements have quickly led to extensive inventory and supply chain management applications. Despite the increasing number of research studies in robust inventory management, specific review literature for this area remains scarce.

Our study bridges existing knowledge gaps through an extensive exploration of RO applications in inventory management, covering a wide range of contexts. To achieve this, we employed a systematic approach based on the PRISMA (Preferred Reporting Items for Systematic Reviews and Meta-Analyses) method (Mishra and Mishra, 2023). Specifically, our method includes several key components: We searched multiple academic databases, including Google Scholar, Science Hub, and Scopus, using primary keywords such as “Robust Optimization,” “Inventory Management,” “Newsvendor,” and “Lot-sizing.” Papers were selected based on their relevance to robust inventory management, focusing on two types of studies: 1) Methodological Studies exploring RO methodologies applicable to inventory management problems, and 2) Applied Studies covering single-period and multi-period issues, as well as scenarios involving single and multiple suppliers. The first stream of studies was representatively selected and served as the cornerstone for the second stream, which was comprehensively reviewed. We conducted an initial screening of titles and abstracts to identify relevant studies, followed by a full-text review to ensure they met our inclusion criteria. To ensure comprehensiveness, we tracked citations by reviewing the literature sections of recently published works and recent review papers. In total, 150 papers were included when this paper was revised in May 2024.

This study distinguishes itself from prior reviews, like those by Zemzam et al. (2017) and Lu and Shen (2021), which mainly concentrate on sources of uncertainty, such as demand and lead time, or delve into general theories and specific applications (Gabrel et al., 2014; Yan ikoğlu et al., 2019). Our research distinctively focuses on the critical elements of decision-making, accurately representing uncertainty, establishing decision criteria, and formulating decision rules. These components are fundamental to our study, as they form the basis for developing robust optimization models in inventory management.

To the best of our knowledge, this work is the first to offer a comprehensive review exclusively dedicated to robust inventory management. While related literature, such as Lu and Shen (2021), covers a wider range of robust operations management, including inventory management, production planning, and revenue management, it tends to lack depth in the specific area of inventory management, potentially falling short in providing detailed guidance for researchers in this field. In contrast, our study intently focuses on inventory management, thoroughly surveying and comparing the latest developments and trends, from both structural and algorithmic perspectives.

Importantly, this survey lays the groundwork for the subsequent comparative study in Part B, providing essential context and framing in several key aspects:

1. Identification of Key Approaches: The survey categorizes RO methods in inventory management, providing a framework for comparative analysis with selected metrics like worst-case objective value and solution robustness.

2. Baseline Knowledge Establishment: The survey offers a comprehensive overview of RO in inventory management, forming a solid foundation for the comparative study and aiding in understanding its nuances and implications.

3. Comparison Areas Highlighting: The survey identifies key areas for closer investigation in RO, such as uncertainty representation, decision criteria, and adaptability, which become focal points in the comparative study.

4. Identification of Challenges and Opportunities: This survey recognizes challenges in the existing literature and underscores potential avenues for innovation. It steers the direction of the ensuing comparative study, which aims to delve deeply into these challenges and contribute further to the advancement of the field.

In conclusion, Part A’s survey serves as both a foundation and a guide for Part B. It establishes a framework for a detailed comparative analysis, grounded in a thorough understanding of the field. The insights from this survey will inform a focused comparison in Part B, enhancing the comprehension of RO in inventory management. Note that while this paper focuses on the theoretical aspects and methodological foundations of robust optimization in inventory management, detailed discussions on computational speed, time, and effectiveness of specific approaches are reserved for Part B of this study. Part B will provide a comprehensive analysis of the computational performance of various robust inventory models, highlighting their practical implications and efficiency.

The structure of the remainder of this paper is as follows: Section 2 provides a historical overview of various stochastic inventory models, outlining their respective strengths and applicable contexts. Section 3 explicitly introduces the leading modeling frameworks in RO, emphasizing their applications in inventory management. Section 4 discusses various decision criteria utilized in robust inventory models, providing insights into their practical implications. In Section 5, we examine a spectrum of decision rules fundamental to RO, and highlight their importance in the context of inventory management. The paper concludes with Section 6, which synthesizes key findings and sets the stage for the subsequent comparative study.

2 Stochastic Inventory Management

Before delving into the framework and technical details of robust inventory models, it is essential to provide a historical overview of stochastic inventory theory and position RO within the context of stochastic inventory methods. Note that this section does not aim to present an exhaustive overview of the vast literature on stochastic inventory models but rather to offer a representative picture of the influential studies and prevalent methods in the field. Specifically, our goals are twofold: 1) to present and compare the strengths and applicable contexts of inventory models employing various stochastic optimization (SO) methods; and 2) to specify the prevailing application environment of robust inventory models, demonstrating how they can complement traditional stochastic inventory methods. For a comprehensive overview of stochastic inventory theory, we refer to handbooks such as Porteus (2002) and Zipkin (2000) for developments up to the early 2000s, and Song (2023) for recent advancements over the past two decades. We also recommend interested readers refer to the latest surveys by Perera and Sethi (2023a) and Perera and Sethi (2023b) and the references therein.

2.1 Historical Overview

As a cornerstone of stochastic inventory research, the seminal work by Arrow et al. (1951) marked a significant departure from deterministic models by introducing random demand into both the single-period newsvendor problem and the multi-period dynamic inventory setting. For the newsvendor model, the authors proposed the renowned critical fractile solution, where the optimal ordering quantity is defined in closed form using the demand distribution function and cost parameters. For the dynamic model, they introduced the celebrated (s,S) policy, where $s$ is the reorder point and $S$ is the order-up-to level. The details of both the critical fractile solution and the (s,S) policy are explicitly covered in the companion Part B. Despite their fundamental contributions to the literature, the pioneering work of Arrow et al. (1951) left two major gaps: their critical fractile solution depends on full knowledge of the demand distribution, and the optimality of the (s,S) policy was not proved in their work.

2.1.1 Static Inventory Model

To ease the assumption of a known demand distribution, several research directions have addressed the newsvendor model under unknown demand distribution. In particular, we discuss the following streams of literature: (1) the data-driven newsvendor, (2) the newsvendor model with operational statistics, where estimation and optimization are performed jointly, and (3) the distributionally robust newsvendor model.

Data-Driven Newsvendor. Building on data-driven techniques, the newsvendor model can be solved using only historical data, without making any assumptions about the form of the demand distribution. As mentioned in the introduction, this is a type of nonparametric method to address unknown distributions. Kleywegt et al. (2002) designed the sample average approximation (SAA) method, which uses available data to create an empirical demand distribution. The optimal order quantity is then found at the critical fractile of this distribution in the newsvendor context. Levi et al. (2007) showed that in the newsvendor model, the SAA method provides a solution that is provably near-optimal with high probability, a result that was improved by Levi et al. (2015), who introduced an additive bias into the order quantity. Ban and Rudin (2019) further extended the approach of Levi et al. (2015) to include explanatory variables that influence the demand distribution using machine learning algorithms.

The data-driven newsvendor model does not require assuming a parametric family of distributions, thereby reducing the risk of misspecifying the actual probability distribution compared to parametric methods. Additionally, the data-driven approach can fully utilize historical data, an area where RO may fall short. However, the solution quality of the data-driven model largely depends on the accuracy of the estimated distribution, and suboptimal solutions may result (Liyanage and Shanthikumar, 2005; Siegel and Wagner, 2021). Recently, Siegel and Wagner (2023) pointed out that in the newsvendor model, if the empirical distribution is used to estimate the expected profit, this estimate exhibits a positive and statistically significant bias.

Operational Statistics. As demonstrated in Liyanage and Shanthikumar (2005), operational statistics refers to integrating estimation and optimization to directly estimate the optimal operational policy. Liyanage and Shanthikumar (2005) considered the newsvendor model under a parametric demand distribution with available data to estimate parameters. Assuming demand is exponentially distributed, the authors intentionally bias the order quantity to obtain higher expected profit through a joint estimation–optimization approach. Chu et al. (2008) studied the operational statistics approach using Bayesian analysis for parametric distributions characterized by location and scale parameters, deriving closed-form solutions for both exponential and uniform demand distributions. Siegel and Wagner (2021) extended the results of Liyanage and Shanthikumar (2005) and Chu et al. (2008) to a broad array of distributional families, deriving closed-form asymptotic expressions for the profit’s expected estimation error, which can be used to correct the error.

The operational statistics method can reduce estimation bias compared to nonparametric methods like data-driven newsvendor models, which separate estimation and optimization, potentially yielding better solutions. However, this parametric method requires assuming a specific class of probability distribution initially, which may deviate from the true distribution.

Distributionally Robust Newsvendor. In a distributionally robust newsvendor model, the probability distribution of demand is assumed to be ambiguous. Seminal research by Scarf (1958) assumed that the only available information on demand is the mean and the variance, for which he developed a closed-form expression for the optimal order quantity. Ben-Tal and Hochman (1976) extended this result by developing a closed-form optimal order quantity when the mean and the mean absolute deviation are known. Gallego and Moon (1993) provided extensions and a review of similar work. With the explosive development of RO methodology, the distributionally robust newsvendor model has been well-investigated over the last two decades. Representative works will be explicitly introduced and compared in the following sections and in the companion Part B.

2.1.2 Dynamic Inventory Model

Building on the (s,S) policy introduced by Arrow et al. (1951), Scarf et al. (1960) proved the optimality of this policy in dynamic inventory problems by developing and utilizing the concept of K-convexity. Three years later, Iglehart (1963) extended Scarf’s work to an infinite-horizon setting, proving the existence of a stationary optimal (s,S) policy for the infinite-horizon problem. The early research by Scarf et al. (1960) and Iglehart (1963) assumed that the random demand in each period follows a known distribution and is independent of demands in other periods and environmental factors. This restriction has since been relaxed by subsequent studies using various demand generalizations. Here, we focus on three key approaches: 1) Markovian demand, 2) demand updates with forecasting techniques, and 3) demand characterized by uncertainty sets.

Markovian Demand. In practice, many environmental factors, such as fluctuating economic conditions and uncertain market dynamics, can significantly impact demand (Sethi and Cheng, 1997). In the Markov chain approach, these environmental factors are represented by a demand state for each period. Over the planning horizon, these demand states constitute a Markov chain with a given finite-dimensional transition matrix. The demand in each period has a distribution function that depends on the demand state of that period. Kalymon (1971) provided the first proof of the optimality of (s,S)-type policies when demand is governed by a Markov process. He extended the results of Scarf et al. (1960) and Iglehart (1963) to cases where the demand distribution in each period depends on the price of the inventoried item, with the price being a random variable governed by a Markov process.

Song and Zipkin (1993) considered a single-item inventory model with nonstationary demand, assuming the demand process is Poisson with a rate governed by a Markov process. They formulated a dynamic program to characterize the optimal policy. Recently, Avci et al. (2020) modeled an inventory system as a Markov decision process with an uncountable state space, consisting of both the inventory position and a conditional probability mass function about the actual state of the world. Assuming the state of the world evolves as an ergodic Markov chain, they proved the existence of an optimal average cost that is independent of the initial system state.

Markovian demand models are adept at capturing demand correlations across periods and the impact of external environmental factors. These models allow for the adjustment of inventory policies based on the current state of demand, leading to more responsive and flexible inventory management (Beyer et al., 2010). However, Markovian demand models can become complex as the number of states increases. Additionally, accurately estimating transition probabilities requires extensive historical data, which poses a challenge for implementing Markovian demand models in practice (Xin and Goldberg, 2022).

Demand Updates. In real-world operations, forecasts based on time series data, such as weighted moving averages, can help inventory managers better manage inventories. Exponential smoothing, as discussed by Brown (2004), was widely used in early research for demand forecasting in inventory control because it is relatively simple to compute and easy to explain (see Packer (1967) and Jacobs and Wagner (1989) and references therein). With the advancement of forecasting techniques, the incorporation of autoregressive integrated moving average (ARIMA) processes, as discussed by Box et al. (2015), into inventory management has garnered substantial attention (Johnson and Thompson, 1975; Badinelli, 1990). Graves (1999) considered a single-item inventory control problem in both single-stage and supply chain contexts, where the demand was assumed to follow a nonstationary ARIMA process. They proved that the optimal ordering policy under the nonstationary ARIMA process behaves significantly differently from the stationary demand case.

Another stream of research for forecasting demand in inventory planning is the application of advance demand information (ADI), where customers place orders for future demand. In their seminal work, Sethi et al. (2001) described how the process of multiple forecast updates can be modeled in an appealing way, analogous to peeling layers of an onion. Specifically, in their model, the demand in any period (hidden at the core of the onion) has several sources of randomness (layers of the onion). These uncertainties are resolved successively over periods leading up to the period in which the demand materializes (peeling the onion layers to get to the core). In a related study, Gallego and Özer (2001) considered additive demand information updates, a particular case of the forecast updating process introduced by Sethi et al. (2001). They showed that state-dependent (s,S)-type policies are optimal for finite- and discounted infinite-horizon problems. Further extensions in this direction include incorporating fixed order costs (Sethi et al., 2003), considering delivery flexibility (Wang and Toktay, 2008), and advance purchase discounts (Gan et al., 2019).

Forecasting techniques can effectively aid inventory managers in optimizing ordering decisions. ARIMA models are adept at capturing underlying trends and seasonal patterns in time series data, while using ADI can significantly enhance forecast accuracy by providing real-time insights. However, both of these techniques rely heavily on the quality of the data. Inaccurate or delayed information, which is common in practice, can lead to poor inventory decisions (Zhao et al., 2002; De Gooijer and Hyndman, 2006).

Uncertainty Set. RO offers an alternative approach for incorporating demand generalizations into inventory models. By characterizing uncertain demand using an uncertainty set, robust inventory models can derive optimal ordering decisions without relying on specific demand distributions. Research on dynamic robust inventory management is relatively new compared to the robust newsvendor problem. In their seminal work, Bertsimas and Thiele (2006) proposed robust optimal (s,S) policies for both single-stage and supply chain network cases. Since then, extensive research and extensions have been conducted, including dual sourcing settings (Sun and Van Mieghem, 2019), uncertain lead times (Thorsen and Yao, 2017), and target-oriented objective functions (Lim and Wang, 2017). These works, alongside other representative works, are discussed in more detail in the following sections and in the companion Part B.

2.2 Specific Inventory Systems

Our work primarily focuses on basic inventory systems, such as the classical newsvendor model considered by Scarf (1958) and the multi-period single-stage and tree-structure supply chain network considered by Bertsimas and Thiele (2006), where most robust inventory literature is centered. Nevertheless, for completeness, we briefly introduce several widely studied inventory systems and various methodologies to model them. In particular, we review three types of stochastic inventory systems: 1) distribution systems, 2) assemble-to-order (ATO) systems, and 3) dual-sourcing inventory systems. We then present a summary table (Table 1) listing the representative references for each type of inventory system, highlighting their contributions to both the research community and practical applications. For research focused on other inventory systems, such as reverse logistics and perishable inventory systems, we refer to the latest handbook by Song (2023) for a comprehensive overview.

Distribution System. The landmark paper by Clark and Scarf (1960) proved the optimality of the base-stock policy for a multi-echelon inventory system under stochastic demand by modeling the problem using dynamic programming. Clark and Scarf’s seminal contribution was to propose the Clark-Scarf decomposition, a method that decomposes a multi-dimensional objective function into single-dimensional component functions. This approach resolves the curse of dimensionality inherent in Dynamic Programming (DP) formulations, making the model efficiently solvable. Since then, DP has become a standard tool for addressing supply chain inventory management problems and has inspired numerous extensions. Key developments include the incorporation of expediting orders (Lawson and Porteus, 2000; Shen et al., 2022), lateral shipments (Angelus, 2011; Gong and Wang, 2021), and reverse logistics (Angelus and Özer, 2021). For further extensions, such as assembly supply chain systems, refer to the book chapter by Angelus (2023) and the survey by De Kok et al. (2018).

Building upon Clark and Scarf (1960), Bertsimas and Thiele (2006) proposed robust inventory theory for multi-echelon supply chain networks. They proved the optimality of the (s,S) policy in the RO version for a serial supply chain where uncertain demand is characterized by a polyhedral uncertainty set. Subsequent extensions include the works of Ben-Tal et al. (2005), de Ruiter et al. (2017), and Lim et al. (2021), among many others.

ATO System. ATO systems are a manufacturing strategy where components are stocked based on forecasted demand, but the final assembly of the product is only completed upon receipt of a customer order. This strategy allows companies to respond quickly to customer demands while maintaining lower levels of finished goods inventory. Despite these benefits, the complex two-stage replenishment and allocation decisions make ATO models challenging to solve by classic approaches like stochastic programming (SP), even for a single-period case without lead time considerations. The difficulty in solving one-period ATO models has motivated various heuristics, such as decomposition (Lu and Song, 2005; DeValve et al., 2020) fractional rounding (van Jaarsveld and Scheller-Wolf, 2015; DeValve et al., 2020), and discrete convex optimization (Doğru et al., 2017; Zipkin, 2016).

Unlike the one-period model, multi-period ATO models involve the consideration of component lead times, which further complicates their formulation. The optimal policy for these models remained largely unknown until recently. Researchers have turned to specific classes of policies commonly seen in practice, such as independent base-stock replenishment policies and first-come, first-served allocation rules. Examples include Song (1998, 2002); Song et al. (1999); Song and Yao (2002); van Jaarsveld and Scheller-Wolf (2015). Despite the general lack of knowledge about the optimal control policy for ATO systems, certain specially structured ATO systems under cost symmetry conditions have been solved, as demonstrated by Song and Zhao (2009) and Lu et al. (2010). Additionally, asymptotically optimal policies have been developed and analyzed under conditions such as large component lead times (Reiman and Wang, 2015; Reiman et al., 2023). For more information about various ATO systems, please refer to the book chapter by DeValve et al. (2023).

The application of RO in ATO systems has been largely unexplored. The only relevant reference we found is Long et al. (2024). The authors address a single-period ATO problem defined in Song and Zipkin (2003), assuming zero lead time. They provide a necessary and sufficient condition for determining whether the objective function of the ATO model has the supermodularity property. Additionally, they prove that certain ATO systems, such as the binary tree family introduced in Zipkin (2016), possess supermodularity and can therefore be efficiently solved using the proposed approach.

Dual-Sourcing System. The dual-sourcing inventory model typically assumes that one regular source is inexpensive, while the other express source is fast but costly. Its objective is to offer a high service level at a low cost by strategically ordering from the two sources. The seminal work by Fukuda (1964) proved the optimality of a single-index, dual-base-stock policy when the difference in lead time between the two sources equals a review period. The” index” here refers to the regular inventory position (i.e., the sum of net inventory and outstanding orders), and the optimal policy is a function of this index. However, for general lead time cases, Fukuda’s result may not hold optimal, and the optimal policy remains largely unknown until recently.

Dual-index dual-base-stock policies have been proposed to improve upon the work of Fukuda (1964). The dual-index policy considers both the regular inventory position and the expedited inventory position, which includes net inventory and all orders due to arrive in the next number of periods equal to the lead time of the express source. The superiority of dual-index over single-index policies was demonstrated in the work of Li and Yu (2014) and Hua et al. (2015). Another family of policies widely employed in practice is the Tailored Base-Surge (TBS) policy, first proposed by Allon and Van Mieghem (2010). In the special case where demand follows a two-point support distribution, Janakiraman et al. (2015) established the optimality of TBS policies. For more comprehensive reviews on dual-sourcing inventory systems, see the latest survey by Svoboda et al. (2021) and the book chapter by Xin and Van Mieghem (2023).

The application of RO to dual-sourcing inventory models has gained increasing attention. The main challenge lies in the curse of dimensionality in DP. To address this, Sun and Van Mieghem (2019) used RO to tackle the dual-sourcing problem with general lead times, proposing a robust optimal policy called the capped dual-index policy, which includes a constraint on the slow order. Recently, data-driven RO methods have been proposed to address dual-sourcing inventory models, with the structural properties of the optimal policy characterized by Xiong et al. (2022) and Kim and Do Chung (2024).

Summary. We summarize the representative papers within the three reviewed inventory streams in Table 1, emphasizing the problem setting, modeling method, theoretical contribution, solution approach, and practical implication. This table highlights the contributions of these papers to both the research community and practical applications, showcasing the capabilities of various methodologies in addressing different system features.

2.3 The Strengths and Limitations of RO

Traditional stochastic inventory methods have established fundamental theories, optimal policies, and efficient algorithms, as introduced in previous sections and summarized in Table 1. Specifically, RO complements traditional approaches that rely on known or historically estimated probability distributions of uncertain parameters in two cases: (i) It is effective when only partial information about the probability distribution is available, and (ii) It ensures higher feasibility of model solutions with respect to realized uncertain parameters, addressing the decision-makers’ need for robustness.

In case (i), traditional approaches are not feasible because the accurate probability distribution cannot be obtained. For instance, for new products, it is impossible to estimate demand distribution from historical data (Qiu et al., 2017). In case (ii), although traditional approaches can be used, their solutions may have a higher probability of constraint violations with respect to realized uncertain parameters. For example, when a decision-maker requires a high service rate or faces significant penalties for backlogging or lost sales, RO significantly outperforms traditional approaches (Bandi et al., 2019; Das et al., 2021).

Although RO is more robust than traditional stochastic optimization approaches, its computational tractability heavily depends on the structure of the uncertainty/ambiguity set. Typically, convex uncertainty sets (e.g., interval, ellipsoidal, general polyhedral) are required to ensure that robust models can be reformulated as equivalent convex optimization models and solved efficiently. This requirement may somewhat limit the application of RO (Jaillet and Wagner, 2010). The increased computational complexity incurred by robust constraints makes RO challenging to implement in complex inventory systems, such as ATO systems and inventory models considering stochastic lead times. For more information about the computational challenges associated with RO due to constraints on the uncertainty, see Mutapcic and Boyd (2009) and Ben-Tal et al. (2015b).

Another common concern regarding RO is its over-conservatism, as RO solutions are derived by optimizing the worst-case scenario of the uncertain parameters. This drawback can result in the average-case performance of robust optimal inventory policies underperforming compared to their nominal counterparts; e.g., models without uncertainty (Qiu et al., 2014). However, advancements in RO methodology have mitigated this issue to a large extent. Incorporating powerful convex analysis tools, such as the perspective function (Zhen et al., 2023; Bertsimas et al., 2023) and the Fenchel duality theorem (Ben-Tal et al., 2015a), as well as connecting RO with statistical theorems Bandi and Bertsimas (2012); Wagner (2023), has made RO less conservative. Additionally, leveraging historical data (e.g., empirical demand distributions) via data-driven techniques (Delage and Ye, 2010; Mohajerin Esfahani and Kuhn, 2018) has further improved RO’s performance. Efficient decision rules have also been developed to enhance RO’s performance (Ben-Tal et al., 2004; Chen et al., 2008). The applications of these tools in inventory management settings will be explicitly introduced in the following sections and in the companion Part B.

3 Robust Modeling Framework

In this section, we provide a concise introduction to the elements of RO modeling frameworks and their applications in inventory management. Unlike traditional Stochastic Programming (SP) or Dynamic Programming (DP) methods, which assume complete knowledge of the probability distribution information of uncertain parameters, RO incorporates uncertain parameters into optimization models by relaxing this assumption. RO utilizes well-defined deterministic uncertainty sets, encompassing all potential values of uncertain parameters. By doing so, optimization models with these parameters can be reformulated into a tractable robust counterpart via worst-case analysis, which ensures the feasibility of constraints for all possible realizations of uncertain parameters (Gabrel et al., 2014). A brief comparison of these three methods is presented in Table 2.

The formulation and type of robust counterparts are significantly influenced by the definition of the worst-case scenario, which depends on the representation of uncertainty. In this review, we mainly focus on the representation of uncertainty using continuous uncertainty sets. The scenario-based uncertainty representation is not included in our study, as its application in inventory management is scarce. For further information on scenario-based uncertainty and related literature, we recommend referring to the books and surveys by Ben-Tal et al. (2009) and Gabrel et al. (2014).

3.1 Parameter Uncertainty

Representing uncertainty as deterministic sets of parameters, rather than as probability distributions, marks the difference between RO and SP/DP. Uncertainty sets must be chosen appropriately to achieve a trade-off between sufficient protection against uncertainty and desired system performance.

In practical scenarios, estimates or forecasts are often accompanied by confidence or prediction intervals. This situation naturally leads to the use of box uncertainty sets, where each uncertain parameter is restricted within a specified interval. For example, consider a single-item, multi-period inventory management problem spanning a T-period planning horizon. The uncertain demand for each period, represented as $\tilde{\mathbf{d}}=({\tilde{d}}_1,\dots ,{\tilde{d}}_T)$, can be effectively described within an uncertainty set defined by these intervals.(1) $${\Omega }_{\text{BOX}}=\{{\tilde{\mathbf{d}}}_{\mathbf{t}}\in {ℝ}_{+}^T|{\tilde{d}}_t\in \left[{\overline{d}}_t-{\widehat{d}}_t,{\overline{d}}_t+{\widehat{d}}_t\right],\forall t\},$$(1) where ${\overline{d}}_t$ represents the demand forecast (i.e., the nominal value), and ${\widehat{d}}_t$ denotes the forecast error bound (i.e., the maximum deviation from the nominal value) for period t.

Considering interval uncertainty for inventory management can be traced back to Kasugai and Kasegai (1960), who derived a dynamic ordering policy using a max-min method for classical multi-stage games with concave payoff functions. Similarly, in Lin and Ng (2011), the authors presented a robust model with interval demand data to address a single-period newsvendor problem, aiming to determine the optimal order quantity and the targeted market. Expanding on the box uncertainty set, Kang et al. (2015) addressed inventory control problems with service-level constraints using a distribution-dependent robust linear optimization approach. Their study demonstrates that incorporating additional distributional information results in solutions that are equally robust, yet less conservative and more cost-effective, compared to those derived from RO approaches that solely rely on box uncertainty sets. The box uncertainty set has also been utilized in inventory-related research conducted by Qiu et al. (2014); Qiu and Shang (2014); Qiu et al. (2017).

Despite the advantage of having tractable reformulations for many optimization problems, interval-type uncertainty sets often lead to over-conservative solutions (Bertsimas and Sim, 2004; Bertsimas and Thiele, 2006), as it is not likely for multiple uncertain parameters to take on their extreme values (i.e., corners of the interval) simultaneously.

To mitigate the excessive conservatism inherent in the box uncertainty set, it is imperative to regulate the degree of deviation from the nominal value. To achieve this objective, two distinct lines of research have been established. Firstly, the ellipsoidal-type uncertainty set was introduced by Ben-Tal and Nemirovski (1999) as a pioneering approach to address this issue,(2) $${\Omega }_{\text{EL}}=\{{\tilde{\mathbf{d}}}_{\mathbf{t}}\in {ℝ}_{+}^T|{\tilde{d}}_t\in \left[{\overline{d}}_t-{\widehat{d}}_t,{\overline{d}}_t+{\widehat{d}}_t\right],\sqrt{\sum _{i=1}^T{\left(\frac{{\tilde{d}}_i-{\overline{d}}_i}{{\widehat{d}}_i}\right)}^2}\le \theta \},$$(2) where the parameter θ is a subjective value chosen by the decision maker to control the level of conservatism. Note that for θ = 0, ${\Omega }_{\text{EL}}$ shrinks to the singleton where ${\tilde{d}}_t={\overline{d}}_t$ $\forall$ t; for θ = 1, $\sqrt{T},{\Omega }_{\text{EL}}$ is the largest or smallest volume ellipsoid contained in ${\Omega }_{\text{BOX}}$, respectively.

Robust linear programs incorporating ellipsoidal-type uncertainty sets can be transformed into conic quadratic programs, thereby enabling resolution via commercial solvers. Owing to its tractability, ${\Omega }_{\text{EL}}$ has found extensive application in tackling challenges in inventory management and newsvendor problems. In the work of Qiu et al. (2014), the uncertain demand is postulated to lie within either ellipsoidal or box uncertainty sets. They developed a multi-period robust inventory model, incorporating the conditional value-at-risk measure, specifically tailored for risk-averse decision-makers. In a parallel context, Qiu et al. (2017) proposed a robust dynamic programming methodology to address the multi-period inventory model, with both box and ellipsoid uncertainty sets being examined in their work.

While robust linear programs with ellipsoidal uncertainty sets offer reduced conservatism and can lead to tractable formulations, they nonetheless result in nonlinear, albeit convex, models. These models, despite their advantages, are computationally more demanding than their nominal counterparts, which are typically simpler linear models. In response to this challenge, Bertsimas and Sim (2004) proposed the budget uncertainty sets:(3) $${\Omega }_{\text{BT}}=\{{\tilde{\mathbf{d}}}_{\mathbf{t}}\in {ℝ}_{+}^T|{\tilde{d}}_t\in \left[{\overline{d}}_t-{\widehat{d}}_t,{\overline{d}}_t+{\widehat{d}}_t\right],\sum _{i=1}^t\left|\frac{{\tilde{d}}_i-{\overline{d}}_i}{{\widehat{d}}_i}\right|\le {\Gamma }_t,\forall t\},$$(3) where the thresholds, ${\Gamma }_t\le t,\forall$ t, trade-off the objective value against protection against the uncertainty. In Bertsimas and Sim (2004), the authors showed that by suitably adjusting the values of Γ_t , the robust model’s performance can be substantially enhanced, while maintaining an acceptable upper bound on the probability of constraint violation. This type of uncertainty has the appealing property of preserving the complexity of the nominal problem (i.e., without uncertainty) in the robust counterpart.

Inspired by this approach, Bertsimas and Thiele (2006) tackled the single-item, multi-period inventory control problem, involving both single installation and supply chain settings. The authors demonstrated that an optimal solution exhibits a base-stock structure, and this finding can be extended to a supply chain with capacity constraints. Using a similar budget uncertainty set, Bienstock and Özbay (2008) developed procedures for setting the basestock levels for a buffer in a supply chain subject to demand uncertainty, using a Benders-like two-phase decomposition algorithm. More related works can be found in Adida and Perakis (2006), Klabjan et al. (2013), Ahmadi and Majumdar (2016), and Bandi et al. (2019).

Both ellipsoidal and budget uncertainty sets mitigate over-conservatism by leveraging the fact that uncertain parameters are less likely to simultaneously reach the corner values of the uncertainty set, specifically, ${\tilde{d}}_t={\overline{d}}_t+{\widehat{d}}_t/{\overline{d}}_t-{\widehat{d}}_t,\forall t$. The probability bounds of constraint violation for robust counterparts employing either ellipsoidal or budget uncertainty sets can be found in the works of Ben-Tal and Nemirovski (1999) and Bertsimas and Sim (2004), respectively.

To derive the probability bounds of constraint violation based on statistical theorems, Bandi and Bertsimas (2012) proposed the central limit theorem (CLT) uncertainty set,(4) $${\Omega }_{\text{CLT}}=\{{\tilde{\mathbf{d}}}_{\mathbf{t}}\in {ℝ}_{+}^T|{\tilde{d}}_t\in \left[{\mu }_t-{\widehat{\Gamma }}_t{\delta }_t,{\mu }_t+{\widehat{\Gamma }}_t{\delta }_t\right],\left|\sum _{i=1}^t\frac{{\tilde{d}}_i-{\mu }_i}{{\delta }_1^t}\right|\le {\Gamma }_t,\forall t\}$$(4) where μ_t and δ_t are the mean and standard deviation of ${\tilde{d}}_t$, respectively. ${\delta }_1^t$ is the standard deviation of the partial sum demands ${\sum }_{i=1}^t{\tilde{d}}_i$. Meanwhile, Γ_t , ${\widehat{\Gamma }}_t$ are tunable parameters similar to the thresholds in budget uncertainty set ${\Omega }_{\text{BT}}$. Particularly, the larger these values are, the more conservative the robust solution will be.

The CLT uncertainty sets provide an intuitive link between robust and stochastic optimization, leading to tractable robust counterparts of SO problems that suffer from the curse of dimensionality. Consequently, RO with a CLT uncertainty set has already been applied to solve problems in supply chain and inventory management. Mamani et al. (2017) present closed-form solutions for the same single installation robust inventory management problem, similar to the work of Bertsimas and Thiele (2006). Utilizing a CLT uncertainty set, Sun and Van Mieghem (2019) examines a dual sourcing inventory management problem. More recently, Xie et al. (2021) resolved the robust inventory management problem with multiple supply sources. The closed-form solutions are obtained in the case that uncertain demand belongs to the CLT uncertainty sets.

3.2 Distribution Ambiguity

When incomplete distribution information is available, uncertainty can be represented using ambiguous probability distributions. The Distributionally Robust Optimization (DRO) approach addresses this by assuming that uncertainties follow a distribution within a predefined set of distributions. These sets can be based on moment constraints (Delage and Ye, 2010), $\varphi$-divergences (Ben-Tal et al., 2013), or Wasserstein metrics (Mohajerin Esfahani and Kuhn, 2018) to enable tractable reformulations.

When the first moment (i.e., mean) μ and second moment (i.e., variance) ${\delta }^2$ of demand are known, the moment-based ambiguity set can be presented as follows:(5) $${\mathcal{A}}_{\text{MB}}=\{P\in \mathcal{P}|{\mathbb{E}}_P\left[\mathbf{D}\right]=\mu ,{\mathbb{E}}_P\left[{\mathbf{D}}^2\right]={\mu }^2+{\delta }^2\},$$(5) where demand D is a random variable with probability distribution P, $\mathcal{P}$ is the set including all possible demand distributions P.

The first moment-based ambiguity model for the newsvendor problem was investigated by Scarf (1958) and later extended by Gallego and Moon (1993). A resurgence of interest in this approach was sparked by Delage and Ye (2010), who incorporated support information, covariance, and uncertain moments into the model, connecting it with data-driven techniques, such as confidence region estimate. Motivated by research advances in DRO and conic optimization, the application of the moment-based ambiguity model and its various variants in inventory management has witnessed explosive growth in recent years (Natarajan et al., 2018; Das et al., 2021; Qiu et al., 2022).

Returning to newsvendor problems, Hanasusanto et al. (2015) developed a multi-dimensional newsvendor model for products with correlated, trend-driven demands and multimodal, yet incomplete, demand distributions. By minimizing worst-case risk over compatible distributions, the NP-hard distributionally robust optimization problem was efficiently solved using quadratic decision rules, yielding conservative, accurate solutions with strong stress-test performance. Wang et al. (2016) introduced the likelihood robust optimization (LRO) model for decision-making in uncertain environments with unknown input distributions and limited historical data. They applied the LRO model to the newsvendor problem, yielding desirable solutions by excluding unrealistic distributions and maintaining robustness for statistically likely outcomes.

Recent studies have been investigating the asymmetry of probability distributions in the distributionally robust newsvendor problem. Natarajan et al. (2018) enhanced the classical model by integrating distribution asymmetry measures like semivariance. They showed that a three-point distribution yields the worst-case expected profit and provided a closed-form solution for univariate demand order quantities, along with a tractable lower bound for multivariate demands. Their numerical results suggest that incorporating asymmetric information significantly reduces expected profit loss, especially in heavy-tailed distributions.

Similarly, Das et al. (2021) expanded Scarf’s (1958) newsvendor problem by establishing a heavy-tail optimality property for the distributionally robust order quantity within an ambiguity set defined by the first and αth moments (for any real α > 1). They demonstrated that this order quantity is optimal for regularly varying distributions with parameter α and outperforms the original distribution’s optimal order quantity in high service level scenarios, even with slight contamination by a regularly varying distribution.

In multi-period inventory management, Wang and Chen (2020) developed a two-stage DRO model for blood supply network optimization in disaster scenarios with limited historical data. Using a moment-based ambiguity set, they optimized blood inventory prepositioning and relief activities, enhancing disaster response efficiency and effectiveness. Qiu et al. (2021) introduced a distributionally robust approach for inventory management, tackling uncertainties in product demands and yields for budget-constrained retailers sourcing from multiple suppliers. This model, focusing on worst-case expected profit maximization, was converted into a tractable convex program. Similar moment-based ambiguity set applications in inventory management are found in Xin and Goldberg (2021), Xue et al. (2022), Qiu et al. (2022), and Li et al. (2023).

When the actual distribution is believed to be close to a known nominal distribution (e.g., a distribution fitted from the historical data), an ambiguity set can be developed by using divergence (“distance”) measures or metrics between distributions. For instance, when the nominal distribution Q and the actual distribution P, have probability density function f_Q and f_P , respectively, the variation distance divergence from Q to P is given by$$I_V(P,Q)=\int |f_P(x)-f_Q(x)|dx.$$

One can construct the following divergence-constrained ambiguity set(6) $${\mathcal{A}}_{\text{DC}}=\{P\in \mathcal{P}|I_V(P,Q)\le \rho \},$$(6) where the parameter ρ serves as a regulator for the degree of ambiguity, and $\mathcal{P}$ is the set including all possible demand distributions P.

Various $\varphi$-divergence functionals, including Hellinger distance, Kullback-Leibler divergence, and Chi-squared divergence, offer diverse options for constructing ambiguity sets. For an in-depth understanding, refer to Ben-Tal et al. (2013), Love and Bayraksan (2015), Jiang and Guan (2016), and Lam (2019). Ben-Tal et al. (2013) utilized single and multiple item newsvendor problems to demonstrate the effectiveness of ambiguity sets based on $\varphi$-divergences.

Lam (2019) used the newsvendor problem to illustrate the application of Burg-entropy divergence balls in ambiguity sets. They showed that these sets can restore the asymptotic statistical guarantees of the central limit theorem, maintaining the feasibility of expected value constraints under ambiguous distributions, a feature not commonly found in other $\varphi$-divergence-based sets.

Despite their prevalent application, ambiguity sets predicated on $\varphi$-divergence exhibit several limitations. A notable drawback of $\varphi$-divergence balls is their potential inadequacy in encompassing distributions that are frequently relevant, or conversely, their propensity to hedge against distributions that are excessively extreme (Gao and Kleywegt, 2023). In response to this challenge, the Wasserstein distance, a metric within the realm of probability measures that quantifies the cost associated with transmuting one distribution into another, has been harnessed to formulate the ambiguity set within the framework of DRO (Mohajerin Esfahani and Kuhn, 2018; Zhao and Guan, 2018; Gao and Kleywegt, 2023).

The Wasserstein distance, denoting the discrepancy between the nominal distribution Q and the actual distribution P, is defined as follows:$${\mathrm{d}}_w(P,Q)=\text{inf}\int ||x_P-x_Q||\Pi (d{x}_P,d{x}_Q).$$where Π is a joint distribution of x_P and x_Q with marginals P and Q, respectively. $\left|\right|·\left|\right|$ represents an arbitrary norm. The Wasserstein distance essentially quantifies the “work” or “effort” required to transform one distribution into another.

One can construct the following divergence-constrained ambiguity set(7) $${\mathcal{A}}_{\mathrm{W}}=\{P\in \mathcal{P}|{\mathrm{d}}_w(P,Q)\le \rho \}.$$(7)

Note that the set ${\mathcal{A}}_{\mathrm{W}}$ encompasses all probability distributions that reside within a ball in the probability space, which is centered at the nominal distribution Q and has a radius of ρ.

The application of Wasserstein ambiguity set in the newsvendor problem has been widely investigated in recent years. Chen and Xie (2021) investigated a stochastic newsvendor model, addressing distributional ambiguity with a data-driven distributionally robust optimization approach. This method hedges against distributions close to a uniform, discrete empirical data set, measured by the type-$\infty$ Wasserstein distance. Numerical comparisons highlighted the data-driven minimax regret model’s superiority over models using the Hurwicz criterion and those based on partial statistical information.

Li and Lu (2023) examined the pricing newsvendor problem, tackling demand ambiguity and optimizing both price and order quantity for perishable products in a single selling period. Using the Wasserstein distance, their model identified worst-case distributions and maximum regret for given prices and quantities, demonstrating the minimax regret approach’s effectiveness over the more conservative max-min robust optimization.

Wasserstein ambiguity sets have also been applied in inventory routing (Liu et al., 2021), dual channel inventory management (Sun et al., 2022), and feature-based newsvendor problems (Zhang et al., 2024).

3.3 Summary and Comparisons of Uncertainty/Ambiguity sets

The importance of uncertainty and ambiguity sets is crucial in RO and DRO. Computational tractability largely depends on the characteristics of these sets, while the achievement of objective values and the robustness of solutions are significantly influenced by their dimensions/sizes. In Tables 3 and 4, we present a summary of computational tractability for uncertain linear optimization problems across different uncertainty or ambiguity sets, highlighting key inventory-related studies.

For detailed guidance on constructing appropriate uncertainty or ambiguity sets, readers are referred to Bertsimas and Brown (2009), Gorissen et al. (2015), Bertsimas et al. (2018), and Mohajerin Esfahani and Kuhn (2018)

The fundamental divergence between RO and DRO lies in their distinct paradigms for handling uncertainty. As previously noted, this difference is succinctly encapsulated by the use of the “uncertainty set” in RO and the “ambiguity set” in DRO. For both academic researchers and real-world inventory managers, the choice between these two approaches often hinges on the specific challenges posed by the problem at hand, the nature of the uncertainties involved, and the trade-offs between computational complexity and model performance.

In practice, inventory managers may choose RO for its computational efficiency and straightforward application of the uncertainty set, especially in complex inventory systems involving multi-period inventory management and multiple inventory nodes. Evidence from industry case studies, such as those referenced by Lim and Wang (2017) and Bandi et al. (2019), suggests that RO is well-suited for multi-period or multi-node inventory systems. On the other hand, DRO, with its ambiguity set, typically outperforms RO by employing a more sophisticated mechanism for addressing both parameter and distributional uncertainty. This approach is particularly advantageous in relatively simple decision settings, such as the newsvendor model. To date, real-world case studies have mainly focused on newsvendor problems, as seen in Natarajan et al. (2018) and Zhang et al. (2024).

4 Decision Criteria

In RO and DRO, parameter uncertainty or distribution ambiguity leads to two types of uncertainties in robust models’ outcomes, namely solution feasibility and objective value (Gabrel et al., 2014). By feasibility, we mean the ability of the derived solutions to keep the model’s constraints valid across different realizations of uncertain parameters or the underlying probability distribution.

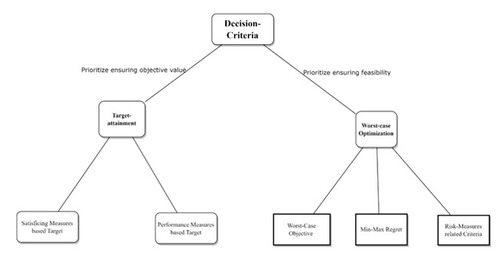
Decision-makers often face the challenge of prioritizing either feasibility or optimality. This dichotomy results in two main decision criteria: worst-case optimization and target attainment. Figure 1 presents a detailed categorization.

Worst-case optimization seeks a solution that remains optimal regardless of the actual coefficients or probability distributions within a given uncertainty or ambiguity set. It ensures a certain level of feasibility, dependent on the set’s size, but leaves the optimal objective value unknown until resolution. This approach is crucial when maintaining solution feasibility is critical.

Target attainment, on the other hand, sets a predefined performance target based on the optimal objective value from the worst-case optimization. It aims to maximize the probability of achieving this target by expanding the uncertainty/ambiguity sets (Chen and Sim, 2009; Lim and Wang, 2017; Zhu et al., 2022). While the objective value is fixed, the robustness/feasibility level, influenced by the set’s size, is determined after solving the model. This criterion focuses on achieving a specific objective value.

4.1 Worst-Case Optimization

Within the RO and DRO framework, worst-case analysis is utilized to manage the influence of uncertainty on the feasibility of the solution. By evaluating a solution under the most unfavorable realization of the uncertainty or ambiguity, it is possible to secure a robust feasible solution that maintains feasibility, irrespective of the realization assumed by the uncertain parameters or ambiguous distribution. Subsequently, the worst-case objective value can be optimized by selecting the optimal solution from a pool of robust feasible solutions. This approach ensures that the chosen solution not only withstands the most unfavorable conditions but also optimizes the worst-case performance. For a comprehensive overview of worst-case analysis, readers are directed to Ben-Tal et al. (2009).

Worst-Case Objective: Much of the existing work within the RO and DRO paradigm addresses worst-case optimization by directly optimizing the objective value under the most unfavorable outcome. To facilitate the introduction of these concepts, we utilize the newsvendor problem as an illustrative example. This problem serves as the cornerstone of numerous operational management models, spanning areas from inventory control to revenue management.

Consider a retailer managing an inventory of n distinct items. For each item $i=1,2,\dots ,n$, let ${\tilde{d}}_i$, p_i , and c_i represent the random demand, unit selling price, and unit cost, respectively. For simplicity, we assume the salvage value of unsold items to be zero. The decision-makers’ objective is to determine an optimal order quantity vector $\mathbf{q}=(q_1,q_2,\dots ,q_n)$ before the actual realization of demand, aiming to maximize profit. Given the known joint probability distribution $\mathcal{F}$ of the multivariate random demand $\tilde{\mathbf{d}}=({\tilde{d}}_1,{\tilde{d}}_2,\dots ,{\tilde{d}}_n)$, the classical newsvendor model can be formulated as follows:(8) $$\underset{\mathbf{q}}{\max }{\mathbb{E}}_{\mathcal{F}}[\sum _{i=1}^n{p}_i\min ({\tilde{d}}_i,q_i)-\sum _{i=1}^n{c}_i{q}_i].$$(8)

Regrettably, eliciting the precise distribution of random demand is challenging in most practical scenarios. To address this issue, the robust newsvendor model posits that the random demand belongs to a predefined uncertainty set. The objective then becomes the selection of order quantities that perform optimally under any possible realization of the uncertain demand $\tilde{\mathbf{d}}$. Consequently, the robust newsvendor model can be formulated as follows:(9) $$\underset{\mathbf{q}}{\max }\underset{\tilde{\mathbf{d}}\in \Omega }{\min }\{\sum _{i=1}^n{p}_i\min ({\tilde{d}}_i,q_i)-\sum _{i=1}^n{c}_i{q}_i\},$$(9) where the uncertainty set Ω can adopt any form, as discussed in Section 3.1.

Note that Eq.(9) seeks to optimize the objective value (profit): ${\max }_{\mathbf{q}}$ under the worst realization of the uncertainty: ${\min }_{\tilde{\mathbf{d}}\in \Omega }$. This worst-case objective criterion is often referred to as the “min-max” for a minimization problem or “max-min” for a maximization problem.

In RO models that include constraints, the pursuit of the worst-case objective typically aligns with ensuring robust feasibility. This concept can be illustrated using an example from Lu and Shen (2021). In the robust newsvendor model, suppose there is an additional constraint stipulating that for each item i, the inventory shortage cannot exceed a threshold k. This implies that the order quantities q_i for $i=(1,2,\dots n)$ must satisfy this requirement for all possible demand realizations from the uncertainty set Ω; that is:(10) $${\tilde{d}}_i-q_i\le k\hspace{1em}\forall {\tilde{d}}_i\in \Omega \hspace{1em}\forall i.$$(10)

Eq.(10) in its current form is computationally intractable as it encompasses an infinite number of constraints due to the universal quantifier ( $\forall$). To illustrate this, consider the following scenario:

Suppose the demand ${\tilde{d}}_i$ for item i can take any value within a continuous range, say $\Omega =[d_{\min },d_{\max }]$. If we need to ensure that the shortage ${\tilde{d}}_i-q_i\le k$ holds for every possible value of ${\tilde{d}}_i$ within this range, it would imply checking this inequality for an infinite number of points between $d_{\min }$ and $d_{\max }$. This is clearly impractical to compute directly because it would require evaluating the constraint for an uncountably infinite set of demand scenarios.

The intractable constraint Eq.(10) can be reformulated into a more tractable form using worst-case analysis. Instead of checking the inequality for every possible value of ${\tilde{d}}_i$, we can focus on the worst-case scenario, which simplifies the problem. The reformulated constraint is:(11) $$\underset{{\tilde{d}}_i\in \Omega }{\max }\{{\tilde{d}}_i-q_i\le k\},$$(11)

This reformulation reduces the infinite set of constraints into a single constraint that considers only the worst-case demand scenario. Note that any $q_i$ satisfying constraint (11) also satisfies constraint (10). The equivalent deterministic form of constraint (10) can thus be derived by solving the optimization problem (11). A model with both a worst-case objective and robust feasibility constraints is referred to as absolute robustness by Kouvelis and Yu (2013) and Lu and Shen (2021).

In a manner analogous to RO, the worst-case objective is also widely used in DRO. For instance, in his seminal paper, Scarf (1958) studied the distributionally robust newsvendor problem as follows:(12) $$\underset{\mathbf{q}}{\max }\underset{\mathcal{F}\in \mathcal{A}}{\min }\mathbb{E}[\sum _{i=1}^n{p}_i\min ({\tilde{d}}_i,q_i)-\sum _{i=1}^n{c}_i{q}_i],$$(12) where $\mathcal{A}$ is an ambiguity set containing all possible probability distributions of random demand $\tilde{\mathbf{d}}$. The joint distribution $\mathcal{F}$ is assumed to be ambiguous and resides within the set $\mathcal{A}$, which can take any form, as discussed in Section 3.2. Consequently, Eq. (12) seeks to maximize profit, assuming that the most unfavorable distribution from the ambiguity set is realized. Due to its distribution-free nature, Eq. (12) and its variants have been widely studied by Gallego and Moon (1993), Gallego et al. (2001), Hanasusanto et al. (2015), Natarajan et al. (2018), Das et al. (2021), Wang and Chen (2020), Singh and Zhang (2020), and Gao and Kleywegt (2023) in the inventory management literature.

The worst-case objective is RO and DRO’s most widely used decision criterion, due to its modeling tractability. Many min-max or max-min (distributionally) robust formulations can be solved analytically or efficiently using the reformulation techniques listed in Tables 3and 4. This decision criterion is also employed in most of the works reviewed in Section 2.1.

Min-Max Regret: In addition to optimizing the objective value, there are alternative approaches that aim to achieve solution optimality while ensuring robust feasibility. The min-max (max-min) criterion yields a solution that is optimal under the worst-case scenario but may prove highly suboptimal under other realizations of uncertainty or ambiguity. This approach, while providing a safeguard against the most unfavorable outcomes, may lead to overly conservative decisions in less extreme scenarios. To mitigate this, the min-max regret approach was introduced to control the level of suboptimality under all possible outcomes. The suboptimality is typically measured by regret, a concept first introduced by Savage (1951), which is defined as the difference between the objective value and the optimal hindsight objective value, given the exact probability distribution.

The min-max regret robust newsvendor problem with uncertainty set Ω is formulated as follows:(13) $$\underset{\mathbf{q}}{\min }\underset{\tilde{\mathbf{d}}\in \Omega }{\max }\{\pi (\mathbf{q},\mathbf{d})-\pi (\overline{\mathbf{q}},\tilde{\mathbf{d}})\},$$(13) where $\pi (\mathbf{q},\mathbf{d})={\sum }_{i=1}^n{p}_i\min (d_i,q_i)-{\sum }_{i=1}^n{c}_i{q}_i$, represents the profit of newsvendor model with exact demand d. $\pi (\overline{\mathbf{q}},\tilde{\mathbf{d}})$ represents the profit with random demand $\tilde{\mathbf{d}}\in \Omega$.

The application of the min-max regret criterion to inventory management was first pioneered by Kasugai and Kasegai (1961). This development emerged in response to critiques that their previous work Kasugai and Kasegai (1960), which relied on a worst-case objective, was excessively conservative. Leveraging an absolute regret minimization approach, Jiang et al. (2011) derived closed-form solutions for the robust Nash equilibrium in a multi-player newsvendor competition. They uniquely assumed that the bounds of random demand span two distinct intervals, thereby introducing asymmetric demand information. Their results indicate that the competitive solution under this asymmetry naturally extends the robust solution from the monopolistic newsvendor context. Using uncertainty intervals, a similar minimax regret objective within the newsvendor problem was also explored by Lin and Ng (2011).

In a recent study, He and Lu (2021) tackled the price-setting newsvendor problem where demand knowledge is limited and sourced from a handful of exercised price points combined with random noise distribution. By employing both additive and multiplicative demand models, the authors aim to minimize the maximum regret, which measures the difference between expected profits based on limited versus complete demand information. Its numerical studies validate the superior performance of this method compared to regression-based approaches.

With the recent advancements in DRO, the min-max regret decision criterion has garnered increased attention within the inventory management community. The distributionally robust newsvendor model utilizing min-max regret criteria is given by(14) $$\underset{\mathbf{q}}{\min }\underset{\mathcal{F}\in \mathcal{A}}{\max }\left\{{\mathbb{E}}_f\right[\pi (\mathbf{q},\mathbf{d})]-{\mathbb{E}}_{\mathcal{F}}[\pi (\overline{\mathbf{q}},\tilde{\mathbf{d}})\left]\right\},$$(14) where ${\mathbb{E}}_f[\pi (\mathbf{q},\mathbf{d})]$, represents the expected profit of the newsvendor model with exact probability distribution of random demand f. ${\mathbb{E}}_{\mathcal{F}}[\pi (\overline{\mathbf{q}},\tilde{\mathbf{d}})]$ represents the expected profit with ambiguous probability distribution of random demand $\mathcal{F}\in \mathcal{A}$.

Early research on the distribution-free newsvendor problem often assumed only partial information, like mean and standard deviation, without requiring distributions to be within predefined ambiguity sets. For instance, Yue et al. (2006) proposed an optimization method for determining order quantities that minimize maximum regret based on these parameters. They provided evidence for the tightness of the cost function’s lower bound and outlined the optimal solution range using two-point distributions. Similarly, Perakis and Roels (2008) investigated the newsvendor problem with limited demand distribution information, focusing on characteristics like mean, variance, symmetry, and unimodality. Their goal was to identify order quantities minimizing maximum regret from suboptimal decisions. A significant finding was that demand distributions with maximized entropy performed well under the regret criterion.

Leveraging ambiguity sets has notably improved the tractability and applicability of DRO. Chen and Xie (2021) investigated the stochastic newsvendor model under demand and yield fluctuations, adopting a data-driven DRO approach. They utilized a type-$\infty$ Wasserstein distance-based ambiguity set to hedge against distributions close to empirical data, focusing on the min-max regret criterion for optimal order quantity. The study also delved into optimality conditions, regret bounds, and extended to the Hurwicz criterion model.

Li and Lu (2023) addressed the pricing newsvendor problem, optimizing price and order quantity for perishable items under demand ambiguity using the Wasserstein distance. Their approach, based on the mini-max regret criterion, demonstrated advantages over conventional models, particularly in scenarios with limited data and significant demand fluctuations. Numerical analyses highlighted the benefits of integrating partial distributional data.

The Min-Max regret decision criterion’s application in distribution-free inventory management is further studied in works by Jammernegg and Kischka (2009), Wang et al. (2014), Rodrigues et al. (2021), and Yang and Shi (2023), showcasing its relevance in various contexts.

Risk-related Performance Criteria: RO’s and DRO’s inherent risk aversion aligns well with risk measures. Bertsimas and Brown (2009) detailed the link between uncertainty sets and coherent risk measures like Conditional-Value-at-Risk (CVaR), particularly emphasizing the connection between polyhedral uncertainty sets and a subset of coherent risk measures known as distortion risk measures. On the other hand, Natarajan et al. (2009) investigated how uncertainty sets in RO correspond to risk measures in finance, proposing a method to derive coherent risk measures from specific uncertainty sets.

DRO techniques have also been combined with CVaR and other risk measures. Zymler et al. (2013) developed semidefinite programming-based approximations for distributionally robust individual and joint chance constraints, utilizing only the first two moments and the support of uncertain parameters. Their research shows that worst-case CVaR constraints are effective approximations for robust individual chance constraints in concave or quadratic functions.

Over recent decades, the field of inventory management has incorporated various risk measures, refer to Table 5 for more details. Prominent examples include mean-variance (Tekin and Özekici, 2015), Value-at-Risk (VaR) (Lin et al., 2022), CVaR (Shi et al., 2019), mean-CVaR (Chen et al., 2009), and mean-VaR (Kouvelis and Li, 2019). Specifically, CVaR, defined as the weighted average of VaR and losses exceeding VaR, has gained considerable attraction in inventory management due to its inherent convexity (Qiu et al., 2014; Hanasusanto et al., 2015).

CVaR, as proposed by Rockafellar and Uryasev (2000), was initially designed to evaluate the downside risk inherent in unpredictable cash flows. When applied to the newsvendor problem, the CVaR of the profit can be delineated through the following procedure.

Let $\pi (q,\tilde{d})$ denote the profit of a single-item newsvendor model. The probability of the stochastic profit, $\pi (q,\tilde{d})$, does not exceed a threshold, γ, is given by$$\begin{array}{c}\Phi (q,\gamma )=\text{Pr}\{\pi (q,\tilde{d})\le \gamma \}={\int }_{ℝ:\pi (q,d)\le \gamma }{f}_d(x)dx\hfill \end{array}$$where f_d is the probability density function of random demand $\tilde{d}$.

Then we can find the $\alpha -$ quantile of $\pi (q,\tilde{d})$ as follows:(15) $${\Phi }_{\alpha }(q):=\text{Inf}\{\gamma \in ℝ|\text{Pr}\{\pi (q,\tilde{d}\}\le \gamma )\ge \alpha \}.$$(15)

The metric ${\Phi }_{\alpha }(q)$ represents the VaR ${}_{\alpha }$ of an inventory manager’s profit, indicating the threshold below which the profit falls with a probability of at least $\alpha \times 100\%$. For instance, with $\alpha =0.05$ the actual profit is expected to be below ${\Phi }_{0.05}(q)$ with a 5% likelihood.

VaR ${}_{\alpha }$ indicates the likelihood that the actual profit will fall at or below the $\alpha$-quantile. However, it does not capture the magnitude or severity of potential losses in the tail region below this quantile. To this end, Rockafellar and Uryasev (2002) introduced the $\alpha$-tail distribution function, specifically designed to emphasize the upper tail portion of the distribution(16) $${\Pi }_{\alpha }(q,\gamma ):=\{\begin{array}{cc}0\hfill & \text{if}\mathrm{ }\gamma <{\Phi }_{\alpha }(q)\hfill \\ \frac{{\Phi }_{\alpha }(q,\gamma )-\alpha }{1-\alpha }\hfill & \text{if}\mathrm{ }\gamma \ge {\Phi }_{\alpha }(q).\hfill \end{array}$$(16)

Using the expection operator ${\mathbb{E}}_{\alpha }[·]$ under the $\alpha -$ tail distribution ${\Pi }_{\alpha }(q,\gamma )$, α-CVaR is given by(17) $${\text{CVaR}}_{\alpha }:={\mathbb{E}}_{\alpha }[\pi (q,\tilde{d})].$$(17)

It’s noteworthy that ${\text{CVaR}}_{\alpha }$ can be conceptualized as a weighted average of ${\text{VaR}}_{\alpha }$ and ${\text{CVaR}}_{\alpha }^{+}=\mathbb{E}[\pi (q,\tilde{d})|\pi (q,\tilde{d})<{\text{VaR}}_{\alpha }]$. This relationship is captured by:(18) $${\text{CVaR}}_{\alpha }=\chi {\text{VaR}}_{\alpha }+(1-\chi ){\text{CVaR}}_{\alpha }^{+},$$(18) where $\chi =\frac{\Phi (q,\gamma )-1+\alpha }{\alpha }\in [0,1]$. Here, ${\text{CVaR}}_{\alpha }^{+}$ signifies the expected profit, $\pi (q,\tilde{d})$, falling below ${\text{VaR}}_{\alpha }$, effectively capturing the lower tail profit. As such, ${\text{CVaR}}_{\alpha }$ adeptly gauges both the likelihood and magnitude of tail-region profits.

For tractability, Rockafellar and Uryasev (2002) proved that CVaR ${}_{\alpha }$ has an equivalent definition as(19) $${\text{CVaR}}_{\alpha }:=\underset{\gamma }{\min }\left\{\gamma +\frac{1}{1-\alpha }\mathbb{E}\left[\max (\pi (q,\tilde{d})-\gamma ,0)\right]\right\}.$$(19)

Also, they show that equation (19) is convex with respect to γ, and(20) $$\underset{q}{\min }{\mathbb{E}}_{\alpha }[\pi (q,\tilde{d})]=\underset{q,\gamma }{\min }\left\{\gamma +\frac{1}{1-\alpha }\mathbb{E}\left[\max (\pi (q,\tilde{d})-\gamma ,0)\right]\right\}.$$(20)

The optimal order quantity $q^{*}$ under the CVaR ${}_{\alpha }$ measure can be obtained from the right-hand side of Equation (20) by jointly optimizing $q$ and $\gamma$.

Qiu and Shang (2014) investigated robust multi-period inventory strategies for risk-averse managers handling products with short life cycles and unpredictable demand. The study introduced three innovative inventory models aimed at different objectives: maximizing profit expectation, enhancing profit based on CVaR, and a combined approach. Empirical analyses demonstrated the models’ effectiveness in managing uncertain demands and their applicability to decision-makers with varying risk preferences. Notably, these models proved robust within both ellipsoidal and box-shaped uncertainty sets. Similarly, Qiu et al. (2014) presented three models within the newsvendor framework: one for expected profit maximization, another for CVaR-based profit, and a hybrid model. These models, suitable for both ellipsoidal and box discrete distributions, focus on the uncertainty in the probability of discrete random demand values, rather than the demand itself.

Risk measures integration in inventory management has also been explored using the DRO approach. For example, Sun et al. (2022) examined a retailer distributing various products through physical and online channels, aiming to optimize expected profit. They constructed Wasserstein ambiguity sets from historical data, leading to a distributionally robust joint chance-constrained model. This model, featuring a conservative CVaR approximation for joint chance constraints, was transformed into a tractable bilinear program through mathematical manipulations.

Similarly, Lotfi et al. (2022) highlighted the effectiveness of vendor-managed inventory policies in reducing medical supply chain costs during the COVID-19 crisis, using Wasserstein ambiguity sets. The study introduced three hybrid models: one focusing on average and mean absolute function, another on CVaR, and a third employing the minimax model, compared to a traditional inventory model. Sensitivity analyses revealed that increasing parameters like fuzzy cut, confidence level, and CVaR confidence level lead to higher costs, with the mini-max function being preferable for more conservative decision-makers.

4.2 Target-Attainment

In conventional RO and DRO frameworks, random variables are viewed as uncertain parameters restricted to a given set, with subsequent application of worst-case analysis. Conversely,target-oriented RO/DRO adopts an inverse procedure. It initially designates a particular objective value as the target, then endeavors to identify solutions maximizing the likelihood of reaching this set objective. The rationale for integrating target-attainment decision criteria into the RO and DRO paradigms is rooted in specific practical necessities, particularly evident in the dynamic landscape of business and operations where decision-makers frequently encounter scenarios such as:

1. Focus on Target-Attainment Decision Criteria: Decision-makers aim to maximize the likelihood of achieving a predefined performance target (cost or profit) rather than solely optimizing the objective value (Brown and Tang, 2006; Chen and Sim, 2009; Chen et al., 2015; Chen and Tang, 2022).

2. Adaptable Uncertainty/Ambiguity Level: Classical RO/DRO solutions, robust to data perturbations, depend on well-defined deterministic support sets (Qiu et al., 2017). The challenge lies in predetermining the uncertainty/ambiguity level to ensure the objective value meets the performance target under all data/distribution realizations (Zhu et al., 2022; Long et al., 2023).

3. Difficulty in Specifying Compact Support Sets: Accurately sizing support sets is often impractical (Zhu et al., 2022), especially when knowledge is limited to nominal values, bounds, or the first and second moments of probability distributions. This complicates the task of setting an uncertainty/ambiguity level that aligns the post-decision objective value with the desired performance target.

To overcome these limitations, Chen and Sim (2009) and Lim and Wang (2017) introduced target-driven robust optimization methodologies, effectively applied to inventory management.

Satisficing-Measures based Target: Drawing from satisficing theory Simon (1959), Chen and Sim (2009) proposed a shortfall-aware aspiration-level criterion using the CVaR measure. This approach robustly approximates the likelihood of reaching a performance target and quantifies the expected underperformance magnitude.

Assuming the random parameters $\tilde{\mathbf{d}}$ lie in the uncertainty set, the Goal-driven Robust Optimization (GRO) model can be articulated as follows:(21) $$\begin{array}{ccc}\underset{\mathbf{x}}{\max }\hspace{1em}\hfill & \rho (\mathrm{F}(\mathbf{x},\tilde{\mathbf{d}})-\tau (\tilde{\mathbf{d}}))\hfill & \tilde{\mathbf{d}}\in \Omega \hfill \\ \mathrm{s}.\mathrm{t}.\hspace{1em}\hfill & \mathbf{A}(\tilde{\mathbf{d}})\mathbf{x}=\mathbf{b}(\tilde{\mathbf{d}})\hfill & \tilde{\mathbf{d}}\in \Omega \hfill \\ \hfill & \mathbf{x}\ge 0,\hfill & \hfill \end{array}$$(21) where $\mathrm{F}(\mathbf{x},\tilde{\mathbf{d}})$ is the objective function to maximize, and $\tau (\tilde{\mathbf{d}})$ is the specified target for the objective function value.

The function $\rho (·)$ acts as the satisficing measure, assessing the probability of achieving the designated performance target, $\tau (\tilde{\mathbf{d}})$. Readers are directed to Brown and Sim (2009) for an in-depth understanding of the satisficing measure. The difference $\mathrm{F}(\mathbf{x},\tilde{\mathbf{d}})-\tau (\tilde{\mathbf{d}})$, referred to as the target premium in Chen and Sim (2009), signifies the excess relative to the predetermined target. In contrast, the gap $\tau (\tilde{\mathbf{d}})-\mathrm{F}(\mathbf{x},\tilde{\mathbf{d}})$ is denoted as the target shortfall.

Noticing that the choice of satisficing measure, $\rho (·)$, plays a pivotal role in determining the computational tractability of the GRO model in Eq.(21). Commonly, probability measures are employed as satisficing measures (Castagnoli and Calzi, 1996; Bordley and LiCalzi, 2000). When considering a specified target premium $\tilde{v}:=\mathrm{F}(\mathbf{x},\tilde{\mathbf{d}})-\tau (\tilde{\mathbf{d}})$, the probability measure can be defined as:(22) $$\rho (\tilde{v}):=\text{Pr}\{\tilde{v}\ge 0\}$$(22)

Employing the probability measure, as defined in Eq.(22), the GRO model seeks the robust optimal solution that maximizes the likelihood of achieving the prescribed target $\tau (\tilde{\mathbf{d}})$. While conceptually straightforward, the probability measure in Eq.(22) is computationally challenging and neglects to account for the target shortfall. To address these limitations, Chen and Sim (2009) proposed a satisficing measure, termed the shortfall-aware aspiration-level criteria, as follows(23) $$\beta (\tilde{v}):={\text{sup}}_{\mathrm{a}>0}(\mathbb{E}[\min \{\tilde{v}/a,1\}]),$$(23)

where $\mathbb{E}[\tilde{v}]>0$ and $\text{Pr}\{\tilde{v}<0\}>0.$

Crucially, Chen and Sim (2009) established a connection between the duality form of (23) and the CVaR measure, as detailed below:(24) $$\beta (\tilde{v}):={\text{sup}}_{\alpha }\{1-\alpha :{\text{CVaR}}_{1-\alpha }(-\tilde{v})\le 0,\alpha \in (0,1)\},$$(24) where(25) $${\text{CVaR}}_{1-\alpha }(\tilde{v})={\min }_{\gamma }\left\{\gamma +\frac{1}{\alpha }\mathbb{E}\left[\max (\tilde{v}-\gamma ,0)\right]\right\}.$$(25)

Observe that the expression in Eq. (24) represents the dual of the satisficing measure in Eq.(23). As a result, the GRO model in Eq.(21) employing the shortfall-aware aspiration-level criteria and can be equivalently reformulated as an RO model with CVaR measures, as follows:(26) $$\begin{array}{ccc}\underset{\mathbf{\alpha },\mathbf{x}}{\max }\hspace{1em}\hfill & 1-\alpha \hfill & \hfill \\ \mathrm{s}.\mathrm{t}.\hspace{1em}\hfill & {\text{CVaR}}_{1-\alpha }(\tau (\tilde{\mathbf{d}})-\mathrm{F}(\mathbf{x},\tilde{\mathbf{d}}))\le 0\hfill & \tilde{\mathbf{d}}\in \Omega \hfill \\ \hfill & \mathbf{A}(\tilde{\mathbf{d}})\mathbf{x}=\mathbf{b}(\tilde{\mathbf{d}})\hfill & \tilde{\mathbf{d}}\in \Omega \hfill \\ \hfill & \mathbf{x}\ge 0,\hspace{1em}\alpha \in (0,1)\hfill & \hfill \end{array}$$(26)

For a given α, the initial constraint in model (26) exhibits convexity for its decision variable x. This allows model (26) to be addressed using standard RO techniques. Chen and Sim (2009) introduced a binary search algorithm to closely approximate the optimal α value, facilitating the derivation of a near-optimal solution for model (26) in polynomial time.

Echoing Chen and Sim (2009), Brown and Sim (2009) advanced the concept of satisficing measures, establishing their duality with risk measures like VaR and CVaR. These measures, when quasiconcave, function as an ’ambiguity level,’ ensuring expected performance despite variations between assumed and actual probability distributions, thereby linking goal-driven optimization with DRO methodologies.

Modifying the GRO model to assume that the probability distribution of $\tilde{\mathbf{d}}$ lies within the ambiguity set $\mathcal{A}$, instead of the uncertainty set Ω, evolves into a Goal-driven Distributionally Robust Optimization (GDRO) model. Long et al. (2023) introduced a robust satisficing framework, emphasizing solutions that meet risk-aware objectives under varying probability distributions. This GDRO model allows decision-makers to set feasible targets, balancing optimality with uncertainty resilience. The study focuses on the Wasserstein distance measure, offering robust satisficing models for various optimization problems, including risk-based linear, combinatorial, and linear optimization with recourse. It also suggests methods for approximating complex SO problems. Numerical studies validate the enhanced out-of-sample performance of these models.

In inventory management, Ng et al. (2012) applied the GRO methodology to improve demand service levels in a co-production newsvendor model, involving a two-tiered system producing various grades from a single input. With only average values and constraints of uncertain demands and grading fractions known, the goal was to enhance demand service levels within resource or budget limits. In the traditional newsvendor problem, Chen et al. (2015) examined the impact of a predetermined target on profit and associated risks. Using GRO and a box uncertainty set for demand, they investigated two satisficing measures: (i) the CVaR satisficing measure, assessing the highest confidence level at which CVaR meets the target, and (ii) the entropic satisficing measure, identifying the minimum risk tolerance for the exponential utility function’s certainty equivalent to reach the target. They found that increasing target levels for both measures leads to higher optimal order quantities.

Performance-Measures based Target: Addressing decision-makers focused on target attainment, Chen and Sim (2009) developed a satisficing measure to determine the upper threshold of the aversion parameter (notably, the confidence level α for CVaR) to ensure a tolerable risk level for achieving a given target. Conversely, Lim and Wang (2017) charted a distinct path by introducing the Target-Oriented Robust Optimization (TRO) framework. This framework modulates the risk associated with target attainment by fine-tuning the dimensions of the uncertainty set.

Departing from the traditional approach of using uncertainty sets with fixed sizes, Lim and Wang (2017) introduced the innovative concept of uncertainty sets that have adjustable sizes.(27) $${\Omega }_{\mathrm{A}}(\nu )=\{{\tilde{\mathbf{d}}}_{\mathbf{t}}\in {ℝ}_{+}^T|{\tilde{d}}_t\in \left[{\overline{d}}_t-\nu {\underset{¯}{z}}_t,{\overline{d}}_t+\nu {\overline{z}}_t\right],\forall t\},$$(27)

where ${\underset{¯}{z}}_t={\overline{d}}_t-{\underset{¯}{d}}_t$, ${\overline{z}}_t={\overline{d}}_t-{\overline{d}}_t$. $\nu \in [0,1]$ is referred to as uncertainty set parameter. ${\underset{¯}{d}}_t,{\overline{d}}_t$ represent the lower and upper bound of ${\tilde{d}}_t$, respectively.

Given a predefined target τ on objective function value $\mathrm{F}(\mathbf{x},\tilde{\mathbf{d}})$, the TRO model is formulated as follows:(28) $$\begin{array}{cc}\hfill & \max \hspace{1em}\nu \hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\hspace{1em}\mathrm{F}(\mathbf{x},\tilde{\mathbf{d}})\le \tau ,\hspace{1em}\tilde{\mathbf{d}}\in {\Omega }_{\mathrm{A}}(\nu )\hfill \\ \hfill & \hspace{1em}\mathbf{A}(\tilde{\mathbf{d}})\mathbf{x}=\mathbf{b}(\tilde{\mathbf{d}}),\hspace{1em}\tilde{\mathbf{d}}\in {\Omega }_{\mathrm{A}}(\nu )\hfill \\ \hfill & \hspace{1em}\mathbf{x}\ge 0,\hspace{1em}0\le \tau \le 1\hfill \end{array}$$(28)

TRO model (28) seeks a solution ${\mathbf{x}}^{*}$ that maximizes the size of the adjustable uncertainty set ${\Omega }_{\mathrm{A}}(\nu )$. The resulting objective value should not exceed τ for all demand realizations within this set. By employing the target constraint $\mathrm{F}(\mathbf{x},\tilde{\mathbf{d}})\le \tau$, a flexible trade-off can be achieved between the worst-case objective value τ and the protection level against uncertainty, as dictated by ν. In classical RO, this balance is typically achieved by first setting a protection level with a fixed-size uncertainty, followed by obtaining the worst-case objective value $\mathrm{F}({\mathbf{x}}^{*},\tilde{\mathbf{d}})$ upon model resolution. In contrast, the TRO framework enables decision-makers to ensure a worst-case objective value, even before the model is resolved.

In Lim and Wang (2017), the authors applied the TRO method (28) to address a multi-period, multi-item inventory management problem. Their goal was to formulate an ordering policy that expands all uncertainty sets, guaranteeing that each demand realization from these sets yields a total cost beneath a set cost target. Numerical analyses indicate that the TRO model possesses a notable trait by adjusting the cost target. The resulting policy can effectively balance the expected cost against its variance.

5 Decision Rules

Inventory management often necessitates decisions across multiple periods or stages. As such, robust multistage optimization techniques have become instrumental in addressing these challenges. Adjustable/Adaptive Robust Optimization (ARO) is specifically designed for multistage uncertain optimization scenarios. In ARO, certain decision variables, termed “wait-and-see” decisions, can be modified once a subset of uncertain parameters establishes their actual values. Due to its inherent flexibility, ARO typically achieves a more favorable objective value compared to static RO, where decisions are made upfront without the benefit of adapting to realized data (Yan ikoğlu et al., 2019).

ARO advances the static RO methodology by incorporating decision rules. In this framework, “wait-and-see” decision variables are parameterized based on actualized uncertainties. To illustrate decision rules, we consider the single installation, single product, multi-period inventory management problem, while closely following Solyal i et al. (2016). We define the following terms for periods $t\in \mathcal{T}=1,2,\dots ,T$: I_t as the stock available at the beginning of period t, x_t as the stock ordered at the beginning of period t, ${\tilde{d}}_t$ as the demand during period t, c_t as the variable ordering cost per unit at period t, h_t as the holding cost per unit at period t, l_t as the backlogging cost per unit for period t, and f_t as the fixed ordering cost for period t.

The lead time is zero. Let z_t be the holding/backlogging cost at the end of period t, and let y_t be 1 if an order is placed in period t and 0 otherwise. Then, the multi-period robust inventory management model is as follows:(29) $$\begin{array}{ccc}\min \hspace{1em}\hfill & \sum _{t=1}^T(f_t{y}_t+c_t{x}_t+z_t)\hfill & \hfill \\ \mathrm{s}.\mathrm{t}.\hspace{1em}\hfill & z_t\ge h_t(I_1+\sum _{i=1}^t(x_i-\widetilde{d_i})),\hfill & {\tilde{d}}_t\in \Omega ,t\in \mathcal{T}\hfill \\ \hfill & z_t\ge -l_t(I_1+\sum _{i=1}^t(x_i-\widetilde{d_i})),\hfill & {\tilde{d}}_t\in \Omega ,t\in \mathcal{T}\hfill \\ \hfill & 0\le x_t\le M{y}_t,\hspace{1em}{y}_t\in \{0,1\},\hfill & t\in \mathcal{T}\hfill \end{array}$$(29) where M is a large positive number.

Problem (29) entails multi-stage decision-making. At the onset of time period $t$, only $x_t$ and $y_t$ are immediate decisions made before the uncertain demand ${\tilde{d}}_t$ materializes. Conversely, the subsequent “wait-and-see” decisions, $x_{t+1},x_{t+2},\dots ,x_T$ and $y_{t+1},y_{t+2},\dots ,y_T$, can be deferred until the demand ${\tilde{d}}_t$ becomes known. Specifically, in each period $t$, the decisions $x_t$ and $y_t$ can leverage the information from the previously realized uncertain demands ${\tilde{\mathbf{d}}}_{t-1}=({\tilde{d}}_1,{\tilde{d}}_2,\dots ,{\tilde{d}}_{t-1})$. This characteristic allows for the parameterization of decision variables based on the actualized demands ${\mathbf{d}}_{t-1}=(d_1,d_2,\dots ,d_{t-1})$ realized by period t.

Decision rules, mapping realized demands ${\mathbf{d}}_{t-1}$ to decision variables $x_t$ and $y_t$, were initially introduced in stochastic programming (Garstka and Wets, 1974). The concept gained renewed attention with the adjustable robust counterpart in Ben-Tal et al. (2004), where functionalizing decision variables based on realized uncertainties was shown to enhance robust formulations’ performance. However, only a few decision rules lead to computationally tractable robust formulations. For an extensive review of tractable decision rules, see Yan ikoğlu et al. (2019).

This survey focuses on three key decision rules: static, linear, and piece-wise linear. These are known for their effectiveness in inventory problems (Ben-Tal et al., 2004; Bertsimas et al., 2010; See and Sim, 2010). Notably, DRO, even with static rules, is computationally demanding. Integrating more dynamic rules, like linear or piece-wise linear, into DRO models poses significant challenges. Therefore, our discussion and application of these dynamic rules are confined to classical RO.

Static Decision Rule: Most early work on RO focuses on static decision-making. In this case, the Static Decision Rule (SDR) is used where decision variables can be deemed as a static function of the uncertain factors. Take problem (29) as an example, under SDR, we have: $x_t({\mathbf{d}}_{t-1})=x_t,\hspace{1em}{y}_t({\mathbf{d}}_{t-1})=y_t\hspace{1em}t\in \mathcal{T},$ where $x(·),y(·)$ here, are static functions that map ${\tilde{\mathbf{d}}}_{t-1}$ to x_t , y_t , respectively.

Static models typically offer superior computational tractability. Existing literature has demonstrated that under certain specific conditions, the worst-case objective values of a static RO problem and its corresponding adjustable variant can be identical (Ben-Tal et al., 2004; Bertsimas et al., 2015). Therefore, SDR emerges as the optimal choice under these conditions.

Ben-Tal et al. (2004) demonstrated that SDR is optimal for a linear optimization problem with constraintwise uncertainty and a compact uncertainty set. Constraintwise uncertainty refers to a scenario where each constraint is linked to its own independent uncertainty set, and these sets are mutually independent across different constraints. Building on constraintwise uncertainty, the optimality of SDR is generalized to fixed recourse nonlinear optimization problems by Marandi and Den Hertog (2018). Additionally, Bertsimas et al. (2015) relaxed the constraintwise uncertainty condition, demonstrating that SDR is optimal for robust linear optimization problems if and only if a certain transformation of the uncertainty set is convex.

Due to its computational tractability and robust performance in diverse settings, static RO methodology has emerged as a leading approach in the field of robust inventory management. Notably, many static robust inventory models offer analytical results for optimal solutions or provide insights into the structure of optimal policies, as evidenced by works such as Yu (1997), Bertsimas and Thiele (2006), Mamani et al. (2017), Lim and Wang (2017), and Sun and Van Mieghem (2019).

Linear Decision Rule: While static RO methods may be optimal under certain specialized conditions, it’s worth noting that RO models employing dynamic decision rules, such as linear or piece-wise linear rules, can often yield solutions that significantly outperform those obtained through static RO, as highlighted by Ben-Tal et al. (2004). The introduction of the Linear Decision Rule (LDR) in RO, initially inspired by the same authors, serves a dual purpose: first it mitigates the over-conservatism often associated with static RO and second maintains a level of computational tractability.

In the context of LDR, take model (29) as an example, the ordering quantity $x_t({\mathbf{d}}_{t-1})$ can be parameterized as follows:$$x_t({\mathbf{d}}_{t-1})=q_{t,0}+\sum _{j=1}^{t-1}{q}_{t,j}{\tilde{d}}_j\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}t\in \mathcal{T}$$

The adjustable variables $q_{t,j},j=0,\dots ,T-1$ will be realized sequentially. At period t, the factors $q_{t,j},j=0,\dots ,t-1$ have already been unveiled. When transitioning to period t + 1, the new factors $q_{t+1,j},j=0,\dots ,t$ become accessible. In contrast, binary variables $y_t({\mathbf{d}}_{t-1})$ $t\in \mathcal{T}$ are not amenable to linear parameterization. One could employ a SDR or turn to more intricate dynamic decision rules, such as piece-wise linear ones. An alternative approach involves partitioning the uncertainty set into subsets, each associated with different decisions. This stratification allows for a more nuanced adaptation of the “wait-and-see” integer variables in response to realized uncertainties (Bertsimas and Georghiou, 2015; Postek and Hertog, 2016).

Bertsimas et al. (2010) established the optimality of LDR for one-dimensional robust optimization problems with convex state costs and linear control costs. Expanding on this, Bertsimas and Goyal (2012) showed that LDR remains optimal in linear ARO problems with right-hand side uncertainty and simplex uncertainty sets. Iancu et al. (2013) further demonstrated LDR’s optimality in unconstrained multistage ARO problems, particularly when uncertainty sets are integer sublattices of the unit hypercube and the objective function is convex and supermodular.

Additional research exploring LDR’s efficacy includes Kuhn et al. (2011), Bertsimas and Bidkhori (2015), Georghiou et al. (2015), and El Housni and Goyal (2017). These studies contribute to a deeper understanding of LDR’s applicability and performance in optimization problems.

LDRs offer significant flexibility in complex, multi-stage inventory management scenarios with fluctuating demand and supply. Building on their foundational work in RO, including the Affinely Adjustable Robust Counterpart (AARC) by Ben-Tal et al. (2004) and the Globalized Robust Counterpart (GRC) by Ben-Tal et al. (2006), Ben-Tal et al. (2009) explored inventory management in serial supply chains over extended periods. They introduced an advanced version of AARC, GRC, which allows for controlled infeasibility. Simulation studies demonstrated that this approach effectively minimizes operational costs and mitigates the bullwhip effect in supply chains.de Ruiter et al. (2017) further investigated ARO’s limitations in production-inventory systems under demand uncertainty, particularly with unreliable historical data. They proposed an augmented ARO model that treated past data as uncertain, thereby enhancing robustness. The computational feasibility and effectiveness of this model were validated through numerical experiments, indicating its potential in various production-inventory scenarios.

In addition to the conventional LDRs, such as AARC and GRC, alternative variants have been explored in the context of inventory problems. Specifically, Bandi et al. (2019) introduces periodic-affine policies, a novel class of adaptive, data-driven strategies engineered for optimally managing large-scale newsvendor networks under demand uncertainty. The authors established that these policies outperform traditional base-stock, affine, and approximative methods in terms of profitability, sensitivity to parameter changes, and computational scalability.

The efficacy of LDRs can be further enhanced through more accurate approximations of the cost functions. Ardestani-Jaafari and Delage (2016) introduced an innovative mixed-integer linear programming-based approximation scheme designed to construct conservative approximations for sums of piecewise linear functions over polyhedral uncertainty sets. This results in two computationally tractable models: linear and semidefinite programs. The authors establish that this new approximation scheme can elevate the quality of solutions derived from any AARC approximations in robust multistage problems. Furthermore, this study delineates conditions under which these approximations yield exact solutions and presents the first exact reformulations for robust multi-item newsvendor problems with budgeted uncertainty sets and robust multi-period inventory problems.

Piece-wise Linear Decision Rule: In the seminar work of Chen et al. (2008) a rigorous analysis of the limitations associated with LDRs is presented, particularly highlighting the issues that arise when the uncertainty set $\Omega$ of ${\tilde{\mathbf{d}}}_t$ is unbounded in both directions ( ${\widehat{d}}_t\to \infty$). They noted that under such conditions, LDRs could become infeasible or degenerate into constant functions, compromising their utility. To illustrate, consider the nonnegative constraint of ordering quantity when using an LDR, which can be expressed as follows:(30) $$q_{t,0}+\sum _{j=1}^{t-1}{q}_{t,j}{\tilde{d}}_j\ge 0\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\tilde{d}\in (-\infty ,+\infty )\hspace{1em}t\in \mathcal{T}.$$(30)

Constraints (30) holds if and only if $x_t({\mathbf{d}}_{t-1})=q_{t,0}\hspace{1em}t\in \mathcal{T}.$ Two types of Piece-wise Linear Decision Rules (PLDRs)—Deflected Linear Decision Rule (DLDR) and Segregated Linear Decision Rule (SLDR)—are introduced to tackle this limitation.

Using DLDR, the ordering quantity $x_t({\mathbf{d}}_{t-1})$ can be parameterized as follows:(31) $$x_t({\mathit{d}}_{t-1})=\max \{q_{t,0}+\sum _{j=1}^{t-1}{q}_{t,j}{\tilde{d}}_j,0\}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\forall t\in \mathcal{T}$$(31)

Note that the functional $\max \{·,0\}$ serves to relax the nonnegative constraint $q_{t,0}+{\sum }_{j=1}^{t-1}{q}_{t,j}{\tilde{d}}_j\ge 0$. This relaxation effectively expands the feasible solution space for the decision variables $q_{t,0},q_{t,j}$ where $j\le t,t\in \mathcal{T}$, thereby improving upon the LDR.

To effectively implement the SLDR methodology, it is essential to partition primitive uncertainties, such as uncertain demand $\tilde{\mathbf{d}}$, into their positive and negative components. Chen and Zhang (2009) made a seminal contribution by introducing the concept of the Extended Affinely Adjustable Robust Counterpart (EAARC), an enhancement over the original AARC.

Chen and Zhang (2009) introduced the concept of the lifted or extended uncertainty set as follows:$${\Omega }^l=\left\{(w_t,w_t^{+},w_t^{-})|\begin{array}{cccc}\hfill & w_t^{+}=\max (0,w_t),\hfill & \hfill & \hfill \\ \hfill & w_t^{-}=\max (0,-w_t),\hfill & \hfill & \hspace{1em}t\in \mathcal{T}\hfill \\ \hfill & w_t=w_t^{+}-w_t^{-},\hfill & \hfill & \hfill \\ \hfill & -1\le w_t\le 1,\hfill & \hfill & \hfill \end{array}\right\}$$where $w_t=({\tilde{d}}_t-{\overline{d}}_t)/{\widehat{d}}_t,{\tilde{d}}_t\in [{\overline{d}}_t-{\widehat{d}}_t,{\overline{d}}_t+{\widehat{d}}_t]\forall t\in \mathcal{T}$.

Here, $w_t^{+}$ and $w_t^{-}$ represent the positive and negative parts of w_t , respectively. The ordering quantity using SLDR is as follows:(32) $$x_t({\overrightarrow{\mathbf{d}}}_{\mathbf{t}-\mathbf{1}})=q_{t,0}+\sum _{j=1}^{t-1}{q}_{t,j}^{+}{w}_j^{+}+\sum _{j=1}^{t-1}{q}_{t,j}^{-}{w}_j^{-}.$$(32)

Note that when $q_{t,j}^{+}=-q_{t,j}^{-}$ for $2\le t\le T$ and $j\le t-1$, SLDR simplifies to an LDR. Thus, LDR can be viewed as a special case of SLDR. Chen and Zhang (2009) both theoretically and empirically showed that SLDR can offer significant improvements over LDR. Furthermore, Ben-Tal et al. (2020) established that PLDR is optimal for linear ARO problems that contain only right-hand side uncertainty.

In See and Sim (2010), DLDR was used to approximate the optimal replenishment policy in a multi-period stochastic inventory management model. The resulting policy is a piecewise linear one regarding demand history and outperforms static and linear decision rules.

Note that SDR is a special case of LDR, which itself is a specific version of PLDR. A summary of decision rules comparisons and applications in robust inventory models is provided in Table 6.

6 Findings and Framework for Comparative Analysis

The preceding sections have meticulously delineated various prevalent uncertainty/ambiguity sets, decision criteria, and decision rules, elucidating their practicality in inventory management. The salient findings are encapsulated as follows:

1. Effectiveness in Varied Scenarios: Our analysis underscores:

• DRO vs. RO: DRO offers less conservative, less nuanced solutions than RO, considering both uncertain parameters and probability distribution elements (see Tables 3 and 4), at the cost of higher computational complexity.

• Decision Criteria Selection: As documented in Section 4, the choice of decision criteria, from worst-case objectives to min-max regret, varies based on managerial preferences, with each offering different balances of analytical complexity and risk management.

• Dynamic vs. Static Rules: In multi-stage settings, dynamic rules often surpass static ones in performance, albeit with increased computational demands (see Table 6).

2. Navigating Key Trade-offs: Key trade-offs include:

• Optimal Value vs. Solution Robustness: Balancing inventory cost minimization with solution robustness, is often achieved through tunable uncertainty sets (e.g., budget or CLT type sets) or target-attainment criteria (refer to Eqs. (3) and (4)).

• Model Performance vs. Complexity: Striking a balance between model performance, such as objective function value, solution robustness, and associated model complexity, including the number of decision variables and constraints, is influenced by the selection of decision rules and methods for representing uncertainty (see Tables, 3, 4, and 6).

3. Emerging Trends and Innovations: Notable trends include:

• Dynamic Decision Rules: A shift towards dynamic rules in multi-stage inventory management for adaptability (See and Sim, 2010; Qiu and Shang, 2014; Bandi et al., 2019).

• Innovative Uncertainty Representation: Development of hybrid, CLT-inspired, and Strong Law of Large Numbers-based uncertainty sets, and adaptive robust models (Hanasusanto et al., 2015; Mamani et al., 2017; Wagner, 2018; See and Sim, 2010; Zhang et al., 2024).

• Balancing Robustness and Performance: Focused efforts on balancing robustness with cost-efficiency and computational tractability (Bertsimas and Thiele, 2006; Lim and Wang, 2017; Bandi et al., 2019).

Insights from Part A’s extensive survey are instrumental in guiding Part B’s comparative study. They inform both the literature selection and the development of comparative criteria and metrics. For practical recommendations and future research directions, a detailed analysis incorporating structural results and numerical evidence is essential. Key questions emerging from Part A’s findings will be thoroughly explored in Part B. These questions include:

1. Optimal Uncertainty Representation: What are the most effective methods for depicting uncertainty in robust inventory management models?

2. Optimizing Decision Criteria: Which decision criteria are most suitable for enhancing performance in specific robust inventory management contexts?

3. Influence of Decision Rules: How do different decision rules affect the efficiency of robust inventory management systems?

1. Addressing Computational Hurdles: What are the primary computational challenges in robust inventory management, and how can they be effectively tackled?

2. Future-Readiness and Adaptability: How can certain RO approaches be tailored to accommodate future technological and market shifts?

Data availability statement

Data sharing is not applicable to this article as no new data were created or analyzed in this study.

Acknowledgments

The authors gratefully acknowledge Prof. Dr. Michael R. Wagner for his generous support and the Editor-in-Chief, Prof. Dr. Yu Ding, and anonymous referees for their contributions in improving the quality of the paper, which substantially contributed to the accomplishment of this work.

Table 1 Representative papers from the considered three streams of inventory systems.

References		Problem Setting	Modeling Method	Theoretical Contribution	Solution Approach	Practical Implication
Distribution System	Clark and Scarf (1960)	Multi-echelon inventory system with stochastic demand and constant lead times	DP	Proved that optimal policies are base-stock policies, computed recursively	Proposed the Clark-Scarf decomposition making the model polynomially solvable.	Provided a practical method for designing inventory policies across multiple echelons.
	Shen et al. (2022)	Multi-echelon inventory system considering expediting and service time target for customer orders.	DP	Proved that optimal policies are echelon base-stock policies depending on the vector of backlog classes in each period.	Proposed a polynomial-time algorithm by extending the Clark-Scarf decomposition.	Provided an efficient tool for managing serial supply chains with service time targets and expediting.
	Angelus (2011)	Multi-echelon inventory system with the addition of secondary market sales.	DP	Extended inventory theory by including secondary market sales, showing conditions for their benefit.	Identified disposal policies makes the objective function Clark-Scarf decomposable and the model solvable.	Offered insights for optimizing inventory and leveraging secondary markets to reduce costs and enhance profitability.
	Angelus and Özer (2021)	Multi-echelon inventory system with multiple flows including forward and reverse logistics.	DP	Demonstrated the value of managing variability in product returns and offers optimal echelon base-stock policies.	Make the model polynomially solvable by using Clark-Scarf decomposition.	Offered insights for optimizing inventory control, managing product returns, and improving supply chain performance.
	Bertsimas and Thiele (2006)	Multi-echelon inventory system with uncertain demand characterized by polyhedral set.	RO	Extended inventory theory with robust optimization, proving robust optimal (s,S) policy.	Equivalently reformulated the robust inventory model as a mixed-integer linear program.	Provided resilient inventory policies for industries facing high uncertainty, improving stability and reducing costs
ATO System	Lu and Song (2005)	One-period multi-item ATO system with stochastic demand and lead times	SP	Offered insights into optimal policies: item complementarity and increasing base-stock levels with lead times.	Applied newsvendor decomposition for approximations, followed by a greedy algorithm for optimal solutions.	Offered strategies for achieving cost savings and improving order fulfillment efficiency in ATO systems.
	DeValve et al. (2020)	One-period ATO system, later extended to a multi-period setting with constant lead times.	SP	Introduced a primal-dual framework for analyzing ATO systems, providing fresh insights into optimal policies.	Developed a linear programming rounding algorithm that achieves asymptotic optimality as demand increases.	Offered strategies for optimizing inventory and assembly processes in general ATO systems.
	Doğru et al. (2017)	One-period ATO system with demand following the Compound Poisson process and constant lead times.	SP	Defined a new type of “chained-BOM“ ATO structures that can be efficiently solved via SPs.	Transformed the two-stage SPs into one-stage optimization problems via the property of $L^{\mathrm{♮}}$-convexity.	Offered efficient solution procedures for ATO systems with particular structures.
	Song et al. (1999)	Multi-item continuous-review dynamic ATO system with stochastic lead times	${\text{SO}}^1$	Provided analytical expressions for key performance measures, offered insights into the impact of lead time variability.	Developed a matrix-geometric solution based on the special structure of the multivariate Poisson demand process.	Offered strategies for managing lead time variability, improving order fulfillment in ATO systems
	Song and Yao (2002)	Single-item continuous-review dynamic ATO system with stochastic lead times.	${\text{SO}}^2$	Provided bounds as surrogates for calculating performance measures and optimizing inventory policies.	Used performance bounds as surrogates in the optimization problem, then solved by a greedy-type algorithm.	Provided effective strategies to trade-off order fulfillment and inventory costs for ATO systems with random lead times.
	Song and Zhao (2009)	Two-product continuous-review dynamic ATO system with constant positive lead times	SP	Quantified the value of component commonality, provided analytical results on its effects on inventory-service tradeoffs.	Derived closed-form performance expressions under a base-stock policy and first-in-first-out allocation rule.	Offers strategies to make use of component commonality in inventory management.
	Reiman et al. (2023)	Multi-item continuous-review dynamic ATO system with nonidentical, constant lead times.	SP	Provided asymptotically optimal policy that converges to optimal one when lead time grows infinitely.	Relaxed some feasibility constraints of the system to formulate a proxy model to derive asymptotically optimal policy.	Offered effective strategies for achieving cost savings and improving order fulfillment efficiency in general ATO systems
	Long et al. (2024)	Periodic-review dynamic ATO system with supermodular objective function.	RO	Provided conditions to check for supermodularity and a procedure to solve the model if it exists.	Transform the robust ATO model where the objective function has supermodularity property to a linear program.	Provided effective strategies to address the ATO systems where the objective function has supermodularity property.
Dual-Sourcing System	Fukuda (1964)	Dual-sourcing inventory system with lead-time difference equal to one	DP	Proved that the optimal policy is a Single-Index Dual-Base-Stock policy.	Extended the optimal single-sourcing base-stock policy (Scarf et al., 1960) to the dual-sourcing case.	Provided the optimal policy for the dual-sourcing inventory system where the lead-time difference is equal to one.
	Li and Yu (2014)	Dual-sourcing periodic-review inventory system with a general lead-time difference.	DP	Established monotone optimal polices (Dual-Index) with bounded sensitivity by using the multimodularity.	Derived analytical expressions for the inequalities that optimal policies must satisfy.	Provides insights for dual-sourcing inventory model in which the objective function is of multimodularity.
	Hua et al. (2015)	Dual-sourcing periodic-review inventory system with a general lead-time difference.	DP	Explored the structural properties of the optimal policy (Dual-Index) by using the notion of $L^{\mathrm{♮}}$-convexity	Characterized structural properties of the optimal orders, designed effective heuristic policy.	Offers insights and effective tools for optimizing general dual-sourcing inventory systems.
	Allon and Van Mieghem (2010)	Dual-sourcing continuous-review inventory system with a general supply rate difference.	DP	Introduced the TBS policy framework in the context of global dual-sourcing, providing conditions for optimal allocation.	Established analytical expressions for TBS policy, including its allocation, base-stock level, and expected costs.	Offers strategies for optimizing global sourcing, and leveraging strengths of nearshore and offshore production.
	Janakiraman et al. (2015)	Dual-sourcing periodoc-review inventory system with a general lead time difference	DP	Established that the TBS policy is optimal when demand follows a two-point distribution.	Derived analytical expressions for the TBS policy.	Identified conditions where the TBS policy performs well, such as large lead time differences.
	Sun and Van Mieghem (2019)	Dual-sourcing periodic-review inventory system with a general lead time difference	RO	Established the optimal Capped Dual-Index policy with a limit on slow order quantities.	Derived closed-form expressions for the Capped Dual-Index policy.	Presented closed-form expressions for the optimal policy of robust dual-sourcing inventory model.

Note. ${\text{SO}}^1$ modeled the occupancy in the supply system as a quasi-birth-death process; ${\text{SO}}^2$ is based on probabilistic methods and queuing theory.

Table 2 Comparisons of RO with DP and SP

Method	Promises	Pitfalls	Seminar works
RO	Computational tractability Provides solutions resilient to data perturbation Does not necessitate full distribution information	Can be overly conservative Difficulties in specifying appropriate uncertainty sets	Ben-Tal et al. (2009) Bertsimas et al. (2011) Delage and Ye (2010) Ben-Tal et al. (2013) Mohajerin Esfahani and Kuhn (2018)
SP	Incorporates uncertainty directly Provides probabilistic guarantees	Requires precise distribution information Computationally intensive for large scenarios	Birge and Louveaux (2011) Ruszczyński and Shapiro (2003) Prékopa (2013)
DP	Solves complex problems efficiently Provides optimal solution at each stage	Suffers from the “curse of dimensionality” Requires perfect state (distribution) information	Bellman (1966) Bellman and Dreyfus (2015)

Table 3 Tractability and application of various classes of uncertainty sets

Uncertainty Set	Reformulation Technique	Tractability	Representative Literature
Box	Consider the maximum absolute values within the box (Ben-Tal et al., 2009)	Linear Program	Qiu et al. (2014), Qiu and Shang (2014), Qiu et al. (2017), Lim and Wang (2017), Lotfi et al. (2022)
Ellipsoidal	Karush-Kuhn-Tucker conditions (Ben-Tal and Nemirovski, 1998; Ben-Tal et al., 2005)	Conic Quadratic Program	Ben-Tal et al. (2005), Zhu et al. (2012), Dorofieiev et al. (2014), Qiu et al. (2017), Lim (2019), Ohmori and Yoshimoto (2020)
Budget	Strong duality theorem (Bertsimas and Sim, 2004; Bertsimas and Thiele, 2006)	Linear Program	Bertsimas and Thiele (2006), Adida and Perakis (2006), Bienstock and Özbay (2008), Solyal i et al. (2012), Bandi et al. (2019)
CLT	Consider the maximum permissible deviation of uncertain parameters from their nominal value (Mamani et al., 2017).	Linear Program	Mamani et al. (2017), Thorsen and Yao (2017), Sun and Van Mieghem (2019), Xie et al. (2021)

Table 4 Tractability and application of various classes of ambiguity sets

Ambiguity Set	Reformulation Technique	Tractability	Representative Literature
Moment Information	Strong duality theorem (Delage and Ye, 2010; Wiesemann et al., 2014)	Convex Optimization	Hanasusanto et al. (2015), Natarajan et al. (2018), Qiu et al. (2021), Das et al. (2021), Qiu et al. (2022), Xue et al. (2022), Li et al. (2023)
Divergence Distance ${}^{*}$	Strong duality theorem (Ben-Tal et al., 2013; Jiang and Guan, 2016)	Linear Program/Conic quadratic Program/ Self-concordant barrier	Rahimian et al. (2019), van der Laan et al. (2022), Yang and Shi (2023)
Wasserstein Metric	Strong duality theorem (Mohajerin Esfahani and Kuhn, 2018; Gao and Kleywegt, 2023)	Convex Optimization	Chen and Xie (2021), Liu et al. (2021), Lee et al. (2021), Sun et al. (2022), Li and Lu (2023), Zhang et al. (2024)

Note. The tractability of divergence-based ambiguity sets depends on the specific divergence functional.

Table 5 Promises and Pitfalls of Risk Measures

Risk Measure	Promises	Pitfalls
VaR	Intuitive interpretation Widely accepted in finance Allows specification of confidence level	Lacks sub-additivity Does not focus on tail risk Not always coherent
CVaR	Coherent risk measure Focuses on tail risk Convex and suitable for optimization	Computationally intensive for some distributions Less intuitive than VaR
Mean-Variance	Simple and intuitive Widely used in portfolio optimization Provides a trade-off between risk and return	Requires concave quadratic utility function Equally penalizes upside and downside outcomes
Mean-VaR	Combines mean and VaR Provides a balance between expected return and risk	Inherits some limitations of VaR May not be coherent
Mean-CVaR	Combines mean and CVaR Focuses on expected return and tail risk	Computationally more intensive than Mean-VaR Less intuitive than Mean-VaR

Table 6 Comparisons of Decision Rules

Decision Rules	Characteristics	Optimality Conditions	Representative Literature
SDR	Advantages: Simplicity: Easy to understand and implement Quick Decisions: No need for real-time re-optimization Limitations: Inflexibility: Fixed decisions, not adaptive	Constraintwise Uncertainty (Ben-Tal et al., 2004; Marandi and Den Hertog, 2018) Convex transformation of the uncertainty set (Bertsimas et al., 2015)	Yu (1997) Bertsimas and Thiele (2006) Lim and Wang (2017)
LDR	Advantages: Flexibility: Adapts to new information Analytical Tractability: Mathematically tractable Good Approximation: Often close to the optimal Limitations: Complexity: Can be computational resource intensive Linearity : Less effective if the system is non-linear	One-dimensional problems with convex state costs and linear control costs (Bertsimas et al., 2010) Right-hand side uncertainty and a simplex uncertainty set (Bertsimas and Goyal, 2012) Uncertainty sets are integer sublattices of the unit hypercube (Iancu et al., 2013).	Ben-Tal et al. (2009) de Ruiter et al. (2017) Bandi et al. (2019) Ben-Tal et al. (2005) Qiu et al. (2014)
PLDR	Advantages: Higher Flexibility: Models non-linear behaviors Better Performance: Excels in complex scenarios Limitations: Complexity: Computationally demanding Overfitting: May tailor too closely to data	Right-hand side uncertainty alone (Ben-Tal et al., 2020).	See and Sim (2010) Ardestani-Jaafari and Delage (2016) Rodrigues et al. (2021)

Figure 1 Decision Criteria

Additional information

Notes on contributors

Daoheng Zhang

Daoheng Zhang: Daoheng Zhang is currently a Ph.D. student in Computer Science at the School of Systems and Computing, UNSW Canberra, Australia. He received an MS degree in Management Science and Engineering from Nanjing University in 2017. His research areas are robust optimization and its application to supply chain management.

Hasan Hüseyin Turan

Hasan Hüseyin Turan: Hasan H. Turan is a Senior Lecturer and the Research Lead at Capability Systems Centre, University of New South Wales (UNSW Canberra). He obtained his Ph.D. and master’s degrees both in Industrial and Systems Engineering from Istanbul Technical University and North Carolina State University, respectively. Dr. Turan's research interests revolve around the development and application of data-driven optimization algorithms and simulation models arising in different domains including service and maintenance logistics, defense applications, energy capacity expansion, and telecommunications networks.

Ruhul Sarker

Ruhul Sarker: Ruhul Sarker received his Ph.D. in 1992 from Dalhousie University, Halifax, Canada. He is currently a Professor in the School of Systems and Computing, UNSW Canberra, Australia. His main research interests are Evolutionary Optimization, and Applied Operations Research. He is the lead author of the book Optimization Modelling: A Practical Approach.

Daryl Essam

Daryl Essam: Daryl Essam received his B.Sc. degree in computer science from University of New England, Australia in 1990 and Ph.D. degree from University of New South Wales, Australia, in 2000. Since 1994, he has been with the UNSW Canberra campus, where he is currently a Senior Lecturer and Deputy Head of School (Research) in the School of Systems and Computing. His research interests include genetic algorithms, with a focus on both evolutionary optimisation and large-scale problems.