Variation of sediment grain size parameters, fish diversity, and phytoplankton richness in relation to sand and silt fractions in estuaries

ABSTRACT

Estuaries are highly dynamic zones. They are confluence of sea, river, tributaries, effluents, and runoff water that modify constantly their physical conditions and affect growth, productivity, and survival of inhabiting biota. In the current study, we investigated the extent to which estuarine sediment fractions explain variation of grain size parameters (mean size: Mz, standard deviation: σI, skewness: Ski and kurtosis: KG), fish diversity, and phytoplankton richness in estuaries. We applied series of multivariate regression models and controlled for the effect of sediment origin, season, and measurement method. The models output showed that sand fraction explained consistently variation of all the four grain size parameters. However, silt fraction was significantly associated with Mz, Ski, and KG but not σI. We couldn’t detect any significant relationship between sand or silt fraction with fish diversity. In contrast, we found that high richness in phytoplankton species was associated with low sand and low silt conditions. We therefore conclude that it is possible to reliably estimate Mz, σI, Ski, KG, and phytoplankton richness from sand and silt fractions. Moreover, managing sand and silt fractions ejected in estuaries may be an alternative of protecting and restoring estuarine biodiversity.

KEYWORDS:

• Grain size
• sediment
• estuary
• texture
• plankton

1. Introduction

Estuaries are highly dynamic zones (Day et al., 2012). They are confluence of river, sea, and effluents water that modify constantly their physico-chemical conditions and affect their ecosystems (Rice et al., 2008). More importantly, estuaries are gradually fragilized by polluted water discharged from surrounding human activities and settlement (Nemerow, 1991; Reeves & Patton, 2005; Solai et al., 2013). Estuaries are also subject to natural events including extreme levels of tides, currents, inundation and erosion; which affect their sediment shape, composition and quantity (Macpherson & Ivan Haigh, 2011; Yin et al., 2018). In the current study, we examine the extent to which sediment fractions affect sediment grain size parameters, fish diversity, and phytoplankton richness; and we suggest the output models for research and estuary conservation applications.

Sediment grain size parameters are usually described into four measures: mean size (Mz), standard deviation (σ_I), skewness (Ski) and kurtosis (K_G; Folk, 1966; Friedman & Sanders, 1978; McLaren, 1981). They are calculated by plotting cumulative weight percentage in relation to phi value (ϕ), which is the negative logarithm to the base 2 of the sieve diameter (Folk & Ward, 1957). Mz, σ_I, Ski and K_G are respectively obtained by applying the following Folk and Ward formulae: (ϕ16 + ϕ50 + ϕ84) /3, (ϕ84 – ϕ16 /4) + (ϕ95 – ϕ5/6.6), [(ϕ16 + ϕ84 – 2 ϕ50) /2(ϕ84 – ϕ16)] + [(ϕ5 + ϕ95 – 2 ϕ50)/2(ϕ95 – ϕ5)], and (ϕ95 – ϕ5)/2.44(ϕ75 – ϕ25); whereby ϕn is the phi value at n^th percentile (ibid.). Because this process can be arduous, time consuming and error-prone, the use of linear models and computer-based applications has been long preferred (Bartholdy et al., 2007; Blott & Pye, 2001; Poppe & Eliason, 2008). Moreover, values of each of the above-described grain size parameters in estuaries are not static but constantly changing with inflowing and circulating sediments (Blott & Pye, 2001; Shiozawa & Campbell, 1991). Furthermore, strong energetic conditions such as tides and currents shape constantly the sediments’ texture, especially by removing fine-grained fraction, and reducing consequently sediment particles size (Schoellhamer, 2002; Sondy & Pravdic, 2002; Tattersall et al., 2003; Van Leussen, 1991). Therefore, the sediment fractions influence values of grain size parameters; however, the extent of this influence is not documented.

Sediment characteristics are also expected to influence estuarine ecosystems. First, sediment fractions constitute the physical habitat of estuarine biota and any change in their gradient may disrupt or create optimal conditions for estuarine ecosystems, especially, the life cycle of marine fishes, which are known to come to estuaries to breed, refuge, or nurse (Julien & Bergeron, 2006; Kondolf, 2000; Meynecke et al., 2006). Second, sediment fractions bind and circulate essential nutrients for estuarine species. Documented nutrients include Phosphorus, which is adsorbed by sediment fine-grained fractions (silt and clay), released in reducing conditions, and up taken by phytoplankton to incorporate the biosynthesis of nucleic acids, phosphoproteins, phospholipids, sugar phosphates, enzymes, and energy-rich phosphate compounds like adenosine triphosphate; which plays an indispensable role in energy transfer during photosynthesis (Hossain et al., 2014; Lin et al., 2016; Y. Wang et al., 2021). Nevertheless, sediment fine-grained fractions tend also to trap a wide spectrum of heavy metals such as Cd, Co, Cr, Ni, Cu, Zn, Rb, Ba, Pb, Fe, V, and Mg (Ali et al., 2018; Huu Hieu et al., 2002; Shilla & Shilla, 2020; Yavar Ashayeri & Keshavarzi, 2019; W. Zhang et al., 2009). Heavy metals occur naturally in living organisms at a concentration of less than 10 ppm. They are constituents of important metalloenzymes and catalyze several oxidation-reduction reactions. However, the concentrations exceeding normal range inflict toxic and carcinogenic effects on cells by, for example, damaging cellular organelles, damaging DNA, inhibiting DNA repair, inducing chromosomal aberrations, activating protein degradation, impairing cellular respiration, and blocking calcium channels (Tchounwou et al., 2012; Yi et al., 2008). Hence, starting monitoring connection between sediment fractions and biota is of paramount importance in this era whereby compiling researches demonstrate increasing discharge of heavy metals into estuaries via sediments.

The aim of this study is three-fold. First, it evaluates the extent to which sediment fractions explain variation of grain size parameters. Second, it evaluates the relationship between sediment fractions and fish diversity and phytoplankton richness. Third, it generates linear formulae modeling sediment grain size parameters, fish diversity and phytoplankton in relation to sediment fractions for research and conservation applications.

2. Methods

2.1. Sediment data

We obtained sediment data from scientific literature on Google Scholar database. We used the following search terms: estuary*or sediment* and grain size or sand or silt or skewness or kurtosis. We obtained 62 publications that had raw data on either season of sample collection, grain size parameters and/or texture of estuary sediments. However, we only retained nine of them that had simultaneous data on each of those characteristics (see Table 1). We then recorded the estuary name, seasons, laboratory analytical method, Mz, σ_I, Ski, K_G, sand percent, silt percent, clay percent and organic matter percent. Since data on organic matter were present for only 71 out of total 500 data lines, we constituted a corresponding dataset, and referred it as “Sub” in contrast to the full dataset referred as “Main.”

Table 1. Data source.

Nr	Country	Estuary/Site	Sediment	Phytoplankton	Fish Diversity
1	India	Arasalar	Ramesh G et al.(2015)	Annalakshmi G and Amsath A, (2012)	Mogalekar HS et al. (2017)
2	India	Coleroon	Anithamary I et al. (2011a)	Rajasekar KT et al.(2005)	Balakrishnan T et al(2015)
3	India	Kayamkulam	Reji S (2002)	Nandan (2008)	Remya R and Amina S (2017)
4	India	Pichavaram	Krishna M and Ramanathan AL (2008)	Rajkumar M et al.(2009)	Mogalekar HS et al. (2017)
5	India	Tirumalairajan	Venkatramanan S et al. (2010)
6	India	Uppanar	Sheeba SJ (2016)	Periyanayagi R et al. (2007)	Veerasingam S et al., (2011)
7	China	Pearl	Wang S et al.(2008)	Huang L et al.(2004)	Zhang X et al (2020)
8	South Korea	Nakdong	Yoon EC and Lee JS (2008)
9	South America	Rio de la Plata	Moreira D et al. (2016)		Jaureguizar AJ et al (2016)
10	India	West Coast of India	(2017)^(a)
11	India	Eastern Indian Ocean	Thayer PA et al.(1974)^(a)
12	India	Tropical River-Estuary	Prasad MB et al.(2020)^(a)
13	India	Bengal	Adhikari SK et al.(2018)^(a)

^(a)Used for testing formulae.

For formulae testing, we constituted a verification dataset by performing a similar search as above but dropped “estuary” and “season” as compulsory criteria. We retained four publications that 1) were not indeed part of the above-mentioned datasets, 2) and contained raw data of both texture and grain size parameters. This verification dataset had 336 samples.

2.2. Fish diversity and phytoplankton data

We obtained fish diversity and phytoplankton data from referred literature (see, Table 1). For each of these two variables, we captured the number of reported species and created a corresponding categorical variable comprising the following levels: above average, below average, and average. These levels corresponded respectively to values above 84^th, below 16^th, and in-between percentiles.

2.3. Data analysis

For descriptive statistics, we calculated and report mean ± standard deviation for all numeric variables and applied Kruskal-Wallis test to tell apart significant difference grain size and texture of sediments across levels of seasons, methods, phytoplankton, and fish diversity variables. We conducted Bonferroni-corrected pairwise comparison between levels every time Kruskal-Wallis test results indicated significant difference (Benjamini & Hochberg, 2000; Hochberg, 1988; Holm, 1979; Hommel, 1988).

To evaluate the relationship between grain size parameters and texture of sediments, we used linear regression models. We first checked the distribution of all numeric variables and made logarithmic, cube rooted, or square rooted transformation wherever data appeared skewed. We then constructed a model for each of grain size parameter, fitted the latter as the response, texture of sediments and locality variables as predictors, and seasons together with laboratory analytical methods as controls (See, Table 2). We further checked stability of every model by plotting residuals against their frequency, fitted and leverage data to respectively check if residuals are normally distributed, do not show a pattern left over by the model, and detect any influential cases. Moreover, we checked collinearity between predictors and kept in the actual full model the predictors with variance inflation factor below 2.5 (Field, 2005; Quinn & Keough, 2002). We compared the full model with a null model lacking predictor but comprising controls by using ANOVA test (Dobson, 2002; Forstmeier & Schielzeth, 2011).

Table 2. Specification of generalized linear models terms used in the analysis of sediment texture in relation to sediment grain size.

Model	Dataset	Response Variable	Initial Full Model		Actual Full Model
			Predictors	Controls	Predictors	Controls
1	Main	Square rooted Mean Size	Cube rooted Sand %, Cube rooted Silt %, Cube rooted Clay % Locality	Seasons Methods	Cube rooted Sand %, Cube rooted Silt % Locality	Seasons
2		Logarithmic Standard Deviation
3		Cube rooted Skewness
4		Logarithmic Kurtosis
5	Sub	Mean Size	Cube rooted Sand %, Square rooted Silt %, Cube rooted Clay %, Square rooted Organic Matter % Locality		Cube rooted Sand %, Square rooted Organic Matter %
6		Logarithmic Standard Deviation
7		Cube rooted Skewness
8		Logarithmic Kurtosis

We used R statistical software version 3.6.3 using the function kruskal.test () for Kruskal-Wallis test, pairwise.t.test () for pairwise comparison, lm () for regression model and formulae output, plot () for diagnostic plots, vif () for variance inflation factor and anova () for ANOVA test. Ratio, assumptions and procedures of all above functions and tests are detailed in Wilcox (2016) and Faraway (2016).

To test the effect of sediment texture on fish diversity and phytoplankton in estuaries, we used two ordinal logistic regression models. For the first model, we fitted fish diversity as response variable. For the second model, we fitted phytoplankton as response variable. In each model, we used sand, silt and clay variables as predictors. We performed ordinal logistic regression model by using polr () function of MASS package in R software.

2.4. Linear formulae extraction

We extracted linear formulae from above-mentioned models in the following form:

(1) $\mathit{Y}=b_0+b_1{X}_1+b_2{X}_2+\mathit{E}.$(1)

Whereby Y is the response, b₀ is the intercept, b₁ is the first fraction slope, X₁ is the first fraction, b₂ is the second fraction slope, X₂ is the second fraction, and E is the error term (Tranmer & Elliot, 2008). For grain size parameters, we tested the obtained formulae by fitting them with the verification dataset and evaluating predicted against real grain size data. Error term was estimated to the mean of differences between real and predicted values (ibid.).

3. Results

3.1. Descriptive statistics

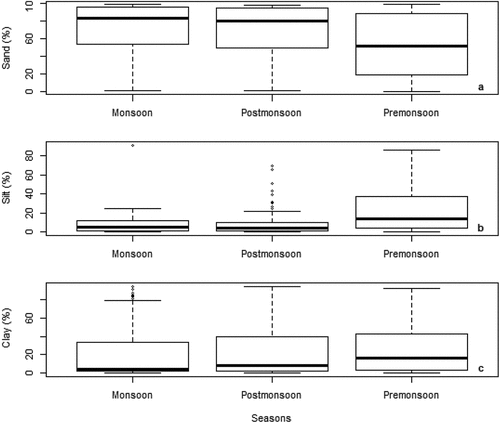
The analysis involved eight numeric variables: Mz (N = 500), σ_I(N = 500), Ski (N = 500), K_G (N = 474), sand percent (N = 500), silt percent (N = 492), clay percent (N = 496), and organic matter (N = 76). They respectively averaged 4.87 ± 3.0 ϕ, 2.16 ± 1.69 ϕ, 0.44 ± 1.50 ϕ, 1.30 ± 0.81 ϕ, 60.44 ± 33.76%, 15.86 ± 19.17%, 23.90 ± 26.41%, and 4.29 ± 2.54%. They showed significant variance across estuaries, types of analytical methods, fish diversity and phytoplankton (Table 3). Premonsoon had higher levels of Mz and σ_I than monsoon and postmonsoon (Figure 1). Monsoon tended to have higher Ski and K_G levels than postmonsoon and premonsoon while the latter seasons had comparable levels. Premonsoon sediments had lower proportions of sand and higher proportions of silt and clay than monsoon and postmonsoon sediments (Figure 2).

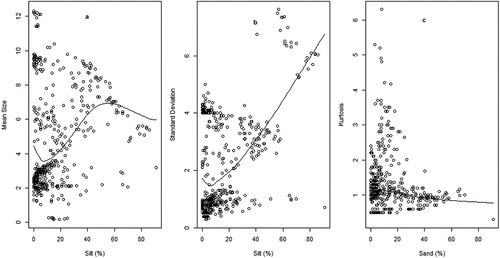
Figure 1. Variation of sediment mean size (a & b) and standard deviation (c & d) in relation to sand and silt fractions.

Figure 2. Variation of sand (a), silt (b), and clay (c) fractions across seasons.

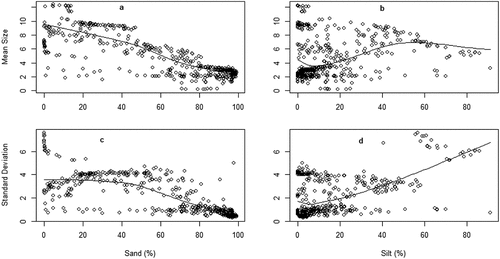
Table 3. Variation of sediment grain size parameters across the study variables.

Variable	Group Level	Kruskal-Wallis chi-squared	Degree of Freedom	P-Value
Mz	Estuaries	227.07	8	<0.001
	Analytical Methods	206.2	6	<0.001
	Seasons	21.61	2	<0.001
	Fish diversity	126.18	2	<0.001
	Phytoplankton	126.18	2	<0.001
σI	Estuaries	120.08	8	<0.001
	Analytical Methods	117.61	6	<0.001
	Seasons	16.48	2	<0.001
	Fish diversity	31.56	2	<0.001
	Phytoplankton	31.56	2	<0.001
Ski	Estuaries	111.02	8	<0.001
	Analytical Methods	110.4	6	<0.001
	Seasons	17.65	2	<0.001
	Fish diversity	21.75	2	<0.001
	Phytoplankton	21.75	2	<0.001
KG	Estuaries	14.5	7	<0.05
	Analytical Methods	14.1	5	<0.05
	Seasons	6.41	2	<0.05
	Fish diversity	0.09	2	0.96
	Phytoplankton	0.09	2	0.96

3.2. Prediction of sediment grain size parameters from texture

Full models, except model 8, fitted data better than their corresponding null models (Table 4). Adjusted R-squared values indicated that predictors (texture) in model 1 to 7 explained variation of response variable (grain size parameters) at respective rate of 0.78 (F = 257.1 on 7 and 484 DF), 0.52 (F = 78.13 on 7 and 484 DF), 0.67 (F = 95.86 on 7 and 323 DF), 0.10 (F = 9.833 on 6 and 459 DF), 0.77 (F = 65.06 on 4 and 71), 0.86 (F = 118.4 on 4 and 71), and 0.75 (F = 56.8 on 4 and 71 DF), all with p-values below 0.05. Specifically, sand fraction predicted significantly Mz (estimate ± SE: −0.577 ± 0.019, t = −30.488, p < 0.001), σI (estimate ±SE: −0.554 ± 0.036, t = −15.380, p < 0.001), Ski (estimate ± SE: 0.062 ± 0.026, t = 2.384, p < 0.05), and K_G (estimate ± SE: 0.226 ± 0.031, t = 7.255, p < 0.001; Figure 3).

Figure 3. Variation of sediment skewness (a & b) and kurtosis (c & d) in relation to sand and silt fractions.

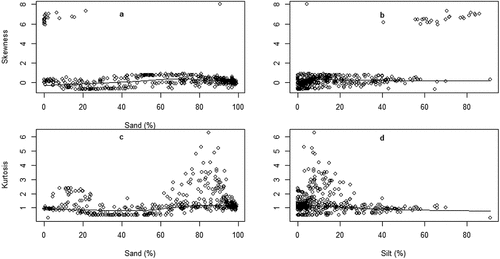
Table 4. Comparison of null to full models estimating grain size parameters from texture.

Model	Type	Degree of freedom in the denominator	Residual Sum of Squares	Degree of freedom in the numerator	Sum of Squares	F -ratio	P-value
1	Null Model	489	212.834
	Full Model	484	87.515	5	165.47	338.13	<0.001
2	Null Model	489	346.03
	Full Model	484	171.48	5	174.56	98.54	<0.001
3	Null Model	323	19.869
	Full Model	328	57.599	-5	-37.73	122.67	<0.001
4	Null Model	459	110.64
	Full Model	463	123.48	-4	-12.842	13.318	<0.001
	Null Model	72	76.038
5	Full Model	71	66.061	1	9.9766	10.723	<0.01
6	Null Model	72	36.603
	Full Model	71	8.041	1	28.562	252.18	<0.001
7	Null Model	72	8.721
	Full Model	71	3.517	1	5.204	105.07	<0.001
8	Null Model	46	1.145
	Full Model	45	1.113	1	0.0326	1.317	0.257

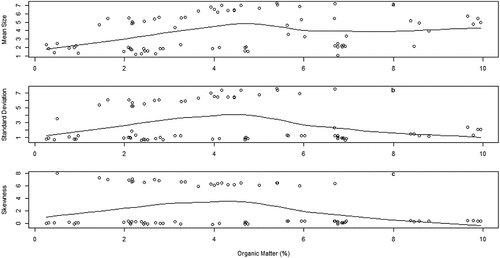
India sediments influenced significantly Mz (estimate ± SE: −0.197 ± 0.071, t = −2.778, p < 0.05) and K_G (estimate ± SE: −0.345 ± 0.113, t = −3.064, p < 0.05) but did not affect σ_I (estimate ±SE: 0.124 ± 0.135, t = 0.917, p = 0.360) and Ski (estimate ± SE: −0.089 ± 0.071, t = −1.253, p = 0.211; Figure 4). Silt texture influenced Mz (estimate ± SE: −0.169 ± 0.019, t = −8.977, p < 0.001), Ski (estimate ± SE: 0.132 ± 0.024, t = 5.395, p < 0.01), and K_G (estimate ± SE: 0.079 ± 0.030, t = 2.658, p < 0.05) but not σ_I (estimate ± SE: 0.015 ± 0.035, t = 0.422, p = 0.673) (Figure 5). Organic matter variable predicted Mz (estimate ± SE: 0.583 ± 0.1781, t = 3.275, p < 0.01), σ_I (estimate ± SE: −0.171 ± 0.06215, t = −2.757, p < 0.01), and Ski (estimate ± SE: 0.24420 ± 0.04110, t = 5.942, p < 0.001; Figure 6).

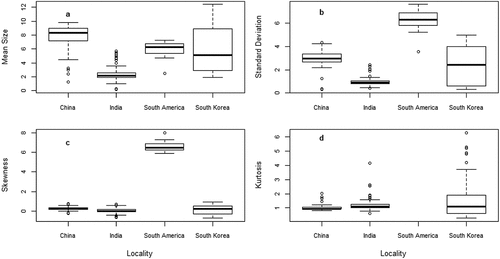
Figure 4. Variation of sediments mean size (a), standard deviation (b), skewness (c) and kurtosis (d) in relation to locality.

Figure 5. Variation of sediments mean size (a), skewness (b), and kurtosis (c) versus silt percentage.

Figure 6. Variation of sediments mean size (a), standard deviation (b), and skewness (c) versus organic matter percentage.

3.3. Prediction of fish diversity and phytoplankton from texture

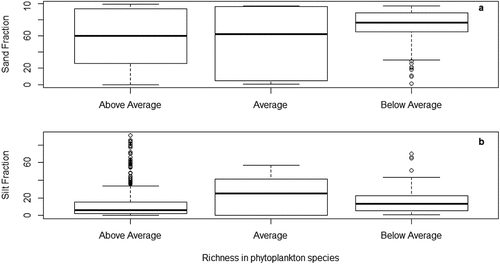
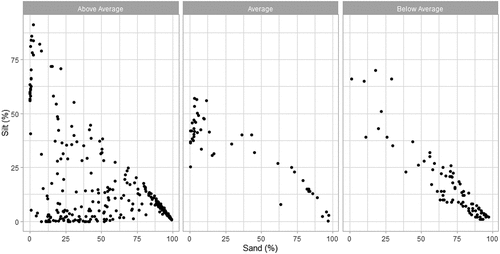
We found that sand (estimate ± SE: 0.045 ± 0.029, t = 1.536, p = 0.124), silt (estimate ± SE: 0.037 ± 0.030, t = 1.214, p = 0.225), and clay (estimate ± SE: 0.031 ± 0.029, t = 1.050, p = 0.294) fractions were not associated with fish diversity. In contrast, we found that silt fraction was a significant predictor of phytoplankton richness (estimate ± SE: 0.123 ± 0.062, t = 2.004, p = 0.045). Sand tended to be a significant predictor of phytoplankton (estimate ± SE: 0.108 ± 0.061, t = 1.773, p = 0.076). More specifically, high richness in phytoplankton species appeared to be associated with low sand and low silt conditions (Figure 7). Moreover, sand and silt data points appeared linear when phytoplankton richness is in the average or below average (Figure 8). Clay was not a predictor of phytoplankton richness (estimate ± SE: 0.087 ± 0.061, t = 1.425, p = 0.154).

Figure 7. Phytoplankton richness in relation to silt and sand fractions.

Figure 8. Phytoplankton richness in relation to linearity of silt and sand.

3.4. Formulae output

As reported hitherto, silt and sand variables were found to be the main predictors of phytoplankton richness and grain size parameters.

For phytoplankton richness; we wrote the linear formulae as follows:

(2) $\mathrm{logit}\left(\mathrm{P}\left(\mathrm{Y}\le \mathrm{average}\right)\right)=11.932-0.108X_1-0.123X_2+\mathit{E}.$(2)

(3) $\mathrm{logit}\left(\mathrm{P}\left(\mathrm{Y}\ge \mathrm{average}\right)\right)=11.196-0.108X_1-0.123X_2+\mathit{E}.$(3)

Whereby X₁ is the sand fraction, X₂ is the silt fraction, and E, the model error.

For grain size parameters; we drew linear formulae as follows:

(4) $Y_{\mathit{Mz}}=12.74143-0.10584X_1-0.09371X_2+\mathit{E}.$(4)

Whereby X₁ is the sand fraction, X₂ is the silt fraction, E, which is estimated to the mean of differences between predicted and real values, is equal to 0.1880007. Mz values were slightly higher than predicted values (t = 2.5061, df = 335, p-value = 0.01268; Figure 9), but were comparable to predicted values added with the error term (t = −4.9988e-07, df = 335, p-value = 1). The second reduced model included only sand fraction as the predictor of σ_I since the influence of silt fraction was not significant in the full model. The output formula is

(5) $Y_{\mathit{\sigma I}}=4.50580-0.03872X_1+\mathit{E}.$(5)

Figure 9. Predicted values of mean size (a), standard deviation (b), skewness (c) and kurtosis (d).

Whereby X₁ is the sand fraction, and E equated to −1.068359. σ_I values were lower than predicted values (t = −15.07, df = 335, p-value < 2.2e-16), but were comparable to predicted values added with the error term (t = −5.2394e-06, df = 335, p-value = 1)

The third reduced model comprised Ski as dependent variable, and sand and silt as independent variables. The proposed formula is

(6) $Y_{\mathit{Ski}}=-1.038798+0.008941X_1+0.060113X_2+\mathit{E}.$(6)

Whereby X₁ is the sand fraction, X₂ is the silt fraction; E was calculated to −1.194697. Ski values were lower than predicted values (t = −19.821, df = 335, p-value < 2.2e-16), but were comparable to predicted values added with the error term (t = −3.4302e-06, df = 335, p-value = 1).

The last reduced model included both sand and silt fractions since they were significant predictors of K_G. The established formula was

(7) $Y_{\mathit{KG}}=0.832936+0.007082X_1+0.001156X_2+\mathit{E}.$(7)

Whereby X₁ is the sand fraction, X₂ is the silt fraction, E equated to −0.2954181. K_G values were lower than predicted values (t = −14.86, df = 321, p-value < 2.2e-16), but were comparable to predicted values added with the error term (t = 3.8429e-07, df = 321, p-value = 1).

4. Discussion

We demonstrated that it is possible to reliably estimate grain size parameters from linear formulae incorporating sand and silt fractions as input variables. The precision of these formulae is tested and proven by the fact they are apt to produce an accurate prediction when fitted with a different dataset (see, also Borovicka et al., 2012; Lionard et al., 2008). Thus, these formulae might be incorporated in routine laboratory worksheets and/or customized in existing softwares for the calculation sediment grain size parameters (Bartholdy et al., 2007; Blott & Pye, 2001). The use of these formulae entails advantage of saving time and preventing errors incurred when using traditional procedures of graphing and extracting different percentiles of phi values required in Folk and Ward formulae to obtain grain size parameters.

We have also found an effect of silt fraction on phytoplankton richness. Specifically, the lowest silt average corresponded to highest richness in phytoplankton, corroborating previous studies showing that when the quantity of fine-grained sediments is low, solar light penetration is deep and extended on large surface of water column, and phytoplankton can capture enough energy to perform photosynthesis and grow (Aguilera et al., 1999; Carstensen et al., 2011; Lancelot & Muylaert, 2012; Ryther, 1956; Schallenberg & Burns, 2004). Low silt content may suggest also that surface cells of phytoplankton on the sides of the water column are less clotted and can perform respiration at the highest (Muylaert et al., 2005). Low silt content may also suggest that the big amount of silt is settled and become de facto fertile grounds for phytoplankton species (Lancelot & Muylaert, 2012; Muylaert et al., 2005). Additionally, low silt concentration may indicate that energetic condition of water column of highest richness of phytoplankton is on average low, and circulating phytoplankton that arrive from effluents have time and opportunity to settle and grow (Howarth et al., 2000; Lionard et al., 2008). Lastly, low silt fraction may indicate that the estuarine environment is less disturbed; thus, a favorable habitat for phytoplankton species (Hossain et al., 2014; Lancelot & Muylaert, 2012).

We could detect neither positive nor negative connection between fish diversity and sediment fractions. First, this may point out that concentrations of nutrients affixed on fine-grained fractions are not alone sufficient to determine fish diversity and welfare in estuaries. Actually, more influent factors including water salinity, temperature, dissolved oxygen, and turbidity are reported elsewhere (Harrison & Whitfield, 2006; Marshall & Elliott, 1998). Second, this result may suggest that fine-grained fractions are in the natural range. Otherwise, excessive amounts would be interfering with fish fitness by hindering respiration, causing gills damage, depleting water oxygen, impairing visual communication, impeding migration, and disrupting spawn habitat (Kemp et al., 2011). Third, this result may suggest that toxic pollutants affixed on fine-grained fractions haven’t yet attained lethal concentrations for fishes. Though, estuarine fishes are increasingly diagnosed with pollutants in their tissues (Kwok et al., 2014; Y. Liu et al., 2018; Vicente-Martorell et al., 2009). Additionally, it may be that pollutants are progressively loading in trophic levels of fish food chain (Kemp et al., 2011). Therefore, stringent conservation measures and further studies are still to be undertaken.

Furthermore, our descriptive data show that the levels of MZ, Ski, and KG varied across estuaries. This might be attributed to variation in the amplitude of length, drainage area, water discharge, tides and waves, influencing sediment input, content and shape in the study estuaries (C. Wang et al., 2020). Some of the study estuaries like Rio de la Plata and Coleroon are long-sized with more than 200 Km of length while others such as Uppanar and Arasalar are ten times smaller than the former (Anithamary, Ramkumar, Venkatramanan et al., 2011b; Mianzan et al., 2001; Ramesh et al., 2015; Sheeba et al., 2016). Long estuaries as opposed to small estuaries are characterized by massive drainage area and water discharge, reaching respectively 3,100, 000 Km² and 22,000 m³/s at Rio de la Plata, and receive consequently a very large and diversified amount of sediments (Uncles et al., 2002). Specifically, when water discharge is high, estuaries are likely to carry a great amount of fine-grained sediments (Oyedotun, 2016). This effect of water discharge is synergized with the tidal range energy which erode sand from shore faces and transport it via longshore towards estuarine mouth, and its amplitude influences the size and kurtosis of suspended sediments (Anthony & Héquette, 2007). Moreover, the tidal range is variable across the study estuaries with 0.7–1.2 m at Coleroon, 0.15–1 m at Pichavaram, 1–2 m at Tirumalairajan, 0.9 m at Uppanar, 2 m at Pearl, 1.5 m at Nakdong, and 0.60–0.79 m at Rio de la Plata, pointing out that the tidal range was likely the key cause of the study estuaries difference in sediment size parameters (Pousa et al., 2012; Prasad & Ramanathan, 2008; Sheeba et al., 2016; Venkatramanan et al., 2014; Woo et al., 2017).

Moreover, the analysis output shows a season effect on sediment size parameters. Premonsoon was associated with high levels of MZ and σI than Monsoon and Postmonsoon. Premonsoon is generally characterized by a low fluvial flow, which favors the fine-grained sediments deposition and sorts sediments from moderately to poorly sorted nature (Singh et al., 2007). Consequently, MZ and σI are elevated. After Premonsoon, MZ and σI begin to decrease and reaches the minimum in Monsoon (Sharma et al., 2017). The level of σI is further controlled by the distance of sediment transport from the source area to depositing area (Ian, 2020). A lower σI level indicates that granule of the sediments is in the same range, whereas higher σI level indicates that granule of the sediments is in different ranges, and infer that sediments have not transported far from the source area (Solai et al., 2013). This seasonal effect on sediment size parameters can be used to investigate and/or detect alterations of rain patterns, which threaten to degrade estuaries.

We have also found that Monsoon tend to have higher Ski and KG levels than Postmonsoon and Premonsoon. During Monsoon, estuaries receive large amount of river run-off and supply of fine sediments (Milliman et al., 1985; Selvaraj et al., 2017). The addition of fine-grained sediments into estuaries increases KG levels (Ramesh et al., 2015). Similarly, the high value of Ski in Moonson is due to high amount of finer sediments such as silt and clay into estuarine system (Venkatesan & Singarasubramanian, 2016). Comparable pattern was found in shore sediments along east coast of India (Pradhan et al., 2020; Sathasivam et al., 2015).

Premonsoon was associated with lower levels of Sand % and higher levels of Silt % and clay % than Monsoon and Postmonsoon. Silt and clay are expected to accumulate during Premonsoon and removed in the estuary during high river runoff seasons (Chang et al., 2006; Sheeba et al., 2016). Moreover, these results might infer that the sand are deposited close to its sources, and silt and clay has probably traveled a long distance. The lower levels of sand percentage during Premonsoon may be attributed to low energy condition and calm nature in the estuarine environment.

We found also across-methods difference in MZ, σI, Ski, KG, Sand, Silt, Clay and Organic Matter levels. Sediment analysis methods are usually chosen based on whether they fit for a specific range of sediment size fraction (Celia Magno et al., 2018). However, measurements of the same sample or the same sediment fraction might yield different results due to different working principles and technical features of the instrument (ibid). This is the case of Laser Granulometer and X-ray Sedigraph, when used to measure sand composition of sediment, might report results that are different by 15 to 25% (Ramaswamy & Rao, 2006). Other potential reasons of difference in measurements results might be the origin, composition and nature of the sediment sample (Sperazza et al., 2004). For example, the presence of phyllosilicates may interfere with sonification and intercept large amount of the optical laser (ibid.). Considering all these together with the findings of the current research, we recommend that all future research has to control for methods variable in any statistical analysis involving data coming from different methods.

Our data show that sand fraction has a significant effect on sediments MZ, σI, Ski and KG (Martins, 1965). Sand fraction has an inverse relation with the Mz and Ski, and direct relation with σI, and KG. This inverse and direct relation can be explained by energy of wave regime and tidal currents energy that move sediments in and out of estuary (Yan et al., 2009). Sand fraction is typically deposited literally close to the source area because they are too heavy to be transported far (Venkatramanan et al., 2014). However, silt fraction varied with MZ, Ski and KG but not σI. Other studies found silt fraction has direct relation with the Mz and Ski, an inverse relation with the KG (Moreira et al., 2016). This might be explained by the fact that river discharge carries in estuary finer sediments. However, silt fraction has not influenced σI because the degree of sorting much depends upon how long transport sediment has undergone (H. Liu et al., 2010; Wang & Ke, 1997). This significant effect of sand fraction on grain size parameters can be used to predict and/or detect alteration of wave’s regime and tidal currents, which can threaten estuarine ecosystem.

Location was also significantly associated with sediment grain size parameters. Specifically, India sediments were associated with lower levels of MZ and KG but did not affect σI and Ski. Indian estuaries had perhaps experienced high interaction of freshwater flow, wave and tide comparing to China, South America, South Korea (Selvaraj et al., 2017). The leptokurtic behavior of the India sediments reflects a coarsely skewed character indicating the concentration of coarse-grained materials, and exhibiting the impact of fluctuation of energy conditions in the deposition of sediments (Venkatramanan et al., 2014a). The coarse-grained implies the influence of higher energy conditions (Folk & Ward, 1957). Yet, India sediments but did not affect σI and Ski perhaps the velocity of the depositing agent operated at a higher value than the average velocity for a greater length of time than normal (Sahu, 1964). Location can be applied to detect country-specific alteration of freshwater flow patterns, wave and tide in estuaries.

We also found that organic matter fraction predicted MZ, σI, and Ski but not KG. The percentage of organic matter predicted MZ, σI, and Ski which favor the deposition of finer particles and the sorting nature. Bordovskiy (1965) found that about a quarter of the organic matter in sediments contains of humic acids. Organic content typically increases as the particle size of sediments reduces, the quantity of humic acids rises from sandy fraction to clay fraction (Zhu et al., 2011). Organic matter concentrations tend to be associated with the finer grained sediments, which are usually deposited at low energy condition.

5. Conclusion

We conclude that there is a robust linear relationship between sand fraction and grain size parameters; thus, deduce linear formulae that can be easily customized by sedimentology laboratories to fast deliver results of sediment grain size parameters analysis. We also show that phytoplankton richness is associated with low silt and low sand fractions, and suggest that sand and silt fractions may be respectively maintained below the observed medians of 60% and 6% to ensure maximum phytoplankton richness in estuary. We further note that no sediment fraction could predict fish diversity but caution a near-future negative connection as pollutants discharge in estuaries continues. Lastly, we demonstrate that future studies investigating sediment texture and grain size parameters should control for, whenever possible, sediment source, seasons and measurement methods.

Acknowledgments

Authors acknowledge technical support from the research group led by T.Ramkumar, Professor and Director i/c Centre for International Relations at Annamalai University, India; G.Gnanachandrasamy, Associate Researcher at Sun Yat-Sen University, China; and S.R. Singara Subramanian, Professor and Member of the Governing Council of Indian Association of Sedimentologists. R. Rumuri is grateful to his family for their constant prayer and untiring support during this work period.

Disclosure statement

No potential conflict of interest was reported by the author(s).