Quasi-Monte Carlo simulation of Brownian sheet with application to option pricing

ABSTRACT

Monte Carlo and quasi-Monte Carlo methods are widely used in scientific studies. As quasi-Monte Carlo simulations have advantage over ordinary Monte Carlo methods, this paper proposes a new quasi-Monte Carlo method to simulate Brownian sheet via its Karhunen–Loéve expansion. The proposed new approach allocates quasi-random sequences for the simulation of random components of the Karhunen–Loéve expansion by maximum reducing its variability. We apply the quasi-Monte Carlo approach to an option pricing problem for a class of interest rate models whose instantaneous forward rate driven by a different stochastic shock through Brownian sheet and we demonstrate the application with an empirical problem.

KEYWORDS:

• Brownian sheet
• Karhunen–Loéve expansion
• Monte Carlo
• option pricing
• Quasi-Monte Carlo

1. Introduction

Monte Carlo (MC) methods are widely used in modern complex scientific studies. One such application is to price complex financial instruments in finance. Since asset price can be expressed as the discounted expected value of its future pay-off under a martingale measure in the absence of arbitrage, the pricing problem can be reduced to computation of an expectation, and MC methods are natural choices especially in the case of evaluating expectation for complicated stochastic process numerically. For estimating the expectation by MC simulation, we may obtain unbiased MC estimators of the expectation with variability σn^{− 1/2}, where n is sample size of the simulation and σ is a constant depending on the underlying problem. Variance reduction techniques such as antithetic method, control variates and importance sampling can reduce the constant σ but not the n^{− 1/2} dependence on the sample size. Quasi-Monte Carlo (QMC) methods adopt deterministic low-discrepancy sequences, which are more uniformly distributed compared to the random sequences in MC simulation. These quasi-random sequences are usually generated in the unit d-dimensional hypercube, C^d = [0, 1)^d, and attempt to fill the hypercube as evenly distributed as is mathematically possible. Among them, the Halton sequence (Halton, 1960), the Sobol’ sequence (Sobol', 1967) and the Faure sequence (Faure, 1982) are well-known ones. The major advantage of QMC methods is that the QMC approach can achieve a much faster convergence rate than the order of n^{− 1/2}, which makes it very attractive in applications like asset pricing where problems involve high dimensions and require efficient simulation.

This paper investigates the QMC simulation of Brownian sheet and then studies its application to an option pricing problem. We consider a class of interest rate models proposed by Santa-Clara and Sornette (2001) whose instantaneous forward rate driven by a different stochastic shock through Brownian sheet. Compared with the traditional HJM model by Heath, Jarrow and Morton (1992), the new model has a much richer class of term structure dynamics of interest rates that allows capturing a larger volatility in modelling of pricing contingent claims. As forward interest rate curve simulation requires a simulation scheme of Brownian sheet, we introduce a new QMC method to simulate Brownian sheet via its Karhounen–Loéve expansion. The proposed QMC approach allocates quasi-random sequences for the simulation of random components of the Karhounen–Loéve expansion by maximum reducing its variability. We show that the QMC simulations of Brownian sheet and the option price have a great performance.

The rest of the paper is organised as follows. Section 2 provides a review of quasi-random sequences with their properties and applications in MC simulation. Section 3 describes the interest rate models and proposes QMC simulation of Brownian sheet. We also present empirical applications considering valuation of long bond futures contract traded on the Chicago Board of Trade (CBOT) in this section. Section 4 concludes the paper.

2. Quasi-Monte Carlo method

Consider the problem of numerically computing a high-dimensional integral, where x = (x₁, …, x_d) and C^d = [0, 1)^d. MC methods, as a useful tool, try to solve the integration problem by computing the sample mean where x₁, …, x_n are independent and identically distributed random vectors drawn from the uniform distribution over C^d. We focus on the simulation problem for uniformly distributed random vectors since non-uniformly distributed random vectors can be sampled by applying the inverse cumulative distribution function or via other transformation algorithms, such as acceptance–rejection method. MC methods are simple to implement, and in many practical problems are the only known computational method of solution. Despite the advantages of MC methods, their slow convergence rate, σ(f)n^{− 1/2}, is a problem, where σ(f) depends on f. Even with the help of variance reduction techniques such as antithetic method, control variates and importance sampling, only the constant term, σ(f), can be lowered. One alternative approach to improve the convergence rate of MC methods is QMC methods. QMC methods adopt low-discrepancy sequences (or quasi-random numbers), instead of randomly distributed sequences for x₁, …, x_n. 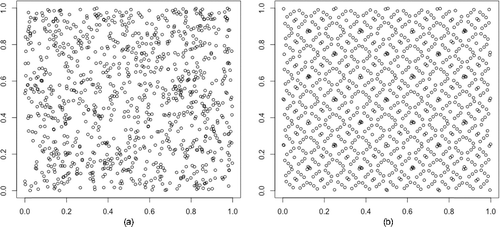These quasi-random sequences are usually generated in the d-dimensional unit hypercube, C^d = [0.1)^d, and attempt to fill the hypercube as evenly distributed as is mathematically possible. Figure 1 offers a visual comparison of pseudo-random numbers and quasi-random numbers. It demonstrates that pseudo-random numbers tend to cluster whereas quasi-random numbers are more uniformly distributed.

Figure 1. (a) Scatter plot of 1000 pseudorandom numbers; (b) scatter plot of 1000 Sobol’ numbers (one example of quasi-random numbers).

2.1 Low-discrepancy sequence

First we define discrepancy (Morokoff & Caisch, 1995), a measure for lack of uniformity given a set of points and low-discrepancy sequences (Niederreiter, 1988).

Definition 2.1:

For the sequence x_i of N points, let Q be a cuboid contained in [0, 1)^d and let m(Q) denote the volume of the cuboid. Discrepancy D_N of the sequence is then defined as

where N is the number of points in the sequence. This is the common definition of discrepancy for studying low-discrepancy sequences and intuitively, it compares the difference between the ratio of generated points lie within a selected rectangle Q to total generated points N, with the ratio of volume for cuboid Q to [0, 1)^d.

Definition 2.2:

Given any N > 1, if the first N points of a sequence x_i satisfies

where c_d is a constant depending only on the dimension d, then the sequence x_i is a low-discrepancy sequence. In this paper, we denote by c_d a generic constant depending only on the dimension d whose value may change from appearance to appearance. The three basic quasi-random (low-discrepancy) sequences that have been often used in literature are Halton, Sobol’ and Faure sequences (Morokoff & Caisch, 1995; Niederreiter, 1973; Niederreiter, 1988; Niederreiter, 1992). They are low-discrepancy sequences with good asymptotic behaviours, i.e. smaller c_d, and are easy for implementation.

2.1.1 Halton sequence

The one-dimensional Halton sequence (Halton, 1960; Morokoff & Caisch, 1995 is generated by using a prime p and expanding integers 0, 1, 2, …, into base p notation. Specifically, nth term of the sequence is defined as where the a_is are integers from the base p expansion of n − 1, with 0 ⩽ a_i < p. For example, assume the base p = 2, the one-dimensional Halton sequence follows to be

For the generation of d-dimensional Halton sequence, the d one-dimensional Halton sequences with d different primes are generated and paired. In a normal case, first d primes are selected to be the d different primes.

2.1.2 Sobol’ sequence

Sobol’ sequence only uses p = 2. It is generated with the first 2^m (m = 0, 1, 2, …) terms for each dimension, representing a permutation of the Halton sequence's corresponding terms with prime base of 2.

2.1.3 Faure sequence

Faure sequence uses the smallest prime greater than or equal to the dimension as the prime base p. The Faure sequence is then generated with the first p^m (m = 0, 1, 2, …) terms for each dimension, representing a permutation of the corresponding terms from the Halton sequence with prime base p.

2.2 Convergence rate

It has been shown in Niederreiter (1978 , 1988) that discrepancy D_N for Halton, Sobol’ and Faure satisfies the following property: where c_d is a constant depending on dimension d only. It is important to state the upper bound for integration error when quasi-random sequence is applied to multi-dimensional integral computation problem. Set (1) where C^d = [0, 1)^d, the following Koksma–Hlawka inequality gives the bounds of integration error.

2.2.1 Koksma–Hlawka inequality

For any sequence x_i and any function f with variation in the sense of Hardy–Krause, V(f), bounded, there exists an upper bound,(2) where D_N is the discrepancy for a given set of points x₁, …, x_N. With the application of quasi-random sequences, one can expect to achieve an upper bound for integration error as where points x₁, …, x_N belong to a quasi-random sequence (Niederreiter, 1992). Therefore, asymptotically, QMC provides a faster convergence rate than that of MC methods, σ(f)N^{− 1/2}. However, when d is large, (logN)^d/N is considerably larger than N^{− 1/2} unless N is large. Therefore, it is widely believed that QMC performs better than MC when dimension d ⩽ 15 (Wang & Fang, 2003). Besides the theoretical upper bound, many numerical examples and experiments have shown that QMC methods converge much faster than MC methods in real applications (Acworth, Broadie & Glasserman, 1996; Morokoff & Caisch, 1995). Numerical experiments in Morokoff and Caisch (1995)) show that in one-dimensional integration problems, error is bounded by c₁N^{− 1} for QMC methods and is bounded by c₂N^{− 1/2} for MC methods. For multi-dimensional integration problems or with less smooth functions f, QMC methods perform at a convergence rate of c₁N^{− λ}, where , still better than that of MC methods.

Moreover, it is straightforward to combine variance reduction techniques with QMC methods in order to increase computation efficiency. Acworth, Broadie and Glasserman (1996) present an example of using principal components construction technique along with Sobol’ sequences to generate far more accurate results compared with other popular MC methods.

3. Interest rate model with stochastic string shocks

In this section, we demonstrate valuation of financial assets, such as options, through QMC methods. As option pricing requires a stochastic model for underlying asset, e.g., bond, in Section 3.1, we introduce a bond pricing model to describe the dynamic evolution of bond price over time. The key factor in bond pricing model is instantaneous forward rate, the interest rate at a future time. Traditional bond pricing models such as HJM model proposed by Heath, et al. (1992) have term structures sharing the same set of shocks that affects all forward interest rates. Our introduced model, interest rate model with stochastic strings (Santa-Clara & Sornette, 2001), is capable of generating much richer class of term structure dynamics of interest rates, by driving each instantaneous forward rate with a distinct stochastic shock and therefore, is capable of capturing a larger volatility in the modelling of pricing contingent claims. In Section 3.2, we discuss simulation for forward interest rate curves based on model introduced in Section 3.1 via QMC method. In Section 3.3, we apply QMC simulation method for interest rate model with stochastic string shocks to an empirical option valuation problem.

3.1 Interest rate model with stochastic string shocks

First we give a brief description for the interest rate model with stochastic string shocks. Assume at any time t, riskless discount bonds of all maturity dates s trade in an economy and let P(t, s) denote the time t price of the s maturity bond. Assume and instantaneous forward rates at time t for all times to maturity x > 0, f(t, x) is the rate that can be contracted at time t for instantaneous borrowing or lending at time t + x. The initial forward rate f(0, x) is assumed to be continuous in x. The spot interest rate r(t) at time t is the instantaneous forward rate at time t with time to maturity 0, that is, r(t) = f(t, 0). Forward rates fully represent the information in the price of all zero coupon bonds. In fact, with the instantaneous forward rates for all times to maturity between 0 and time s − t, the price at time t of a bond with maturity s can be obtained by

Thus we can naturally model forward rates given a fixed time to maturity (Santa-Clara & Sornette, 2001) with stochastic string shock model where Z(t, x) is a stochastic string that is assumed to be continuous in x for all t and in t for all x, which further satisfies φ(t, y) is the market price of risk which could in principle be different for each shock to curve (for simplicity, we may take φ(t, y) = φ(t)). Define

Then, f(t, x) can be solved as

This is a forward rate model driven by the stochastic string Z(t, x), which is a two-dimensional stochastic process depending on time t and time to maturity x. d_tZ(t, x) denotes a stochastic perturbation to the forward rate curve at time t, with different magnitudes for forward rates with different times to maturity. d_t means that the increment is taken with respect to time.

3.1.1 Stochastic strings constructed from Brownian sheet

Denote by W(t, x) a standard Brownian sheet, and define the corresponding white noise It follows that Given any continuous function h(x), we define the first kind of stochastic string as with

We define the second kind of stochastic string for any g(u, v) with ∫^∞₀[g(u, v)]²dv = 1 as and

Important examples belonging to the two kinds of stochastic string defined are summarised below:

Example 1.

Brownian sheet Z(t, x) = W(t, x) with

Example 2.

Modified Brownian sheet. Take h(x) = x, we have

and

Example 3.

The Ornstein–Uhlenbeck (O–U) sheet U(t, x).

with and

Example 4.

Integrated O–U sheet.

and

Example 5.

String with term structure of correlations. Take to produce a stochastic string of the first kind with

and

Example 6.

Take [g(x, ·)]² to be the density of N(x, 1) and obtain a stochastic string of the second kind with

and

Similarly, take [g(x, ·)]² to be the density of N(0, x²) and obtain a stochastic string with.

3.2 QMC simulations of Brownian sheet and forward curve

In Section 3.1, we have reviewed a bond pricing model, the interest rate model with stochastic string shocks, which is a continuous stochastic diffusion process driven by a two-dimensional stochastic process depending both on time and time to maturity that is constructed from Brownian sheet. Simulation of bond price based on introduced model therefore requires discretisation of the continuous stochastic process and extension of QMC method for two-dimensional applications. In Section 3.2.1, we present discretised version for forward interest rate curves and in Section 3.2.2, we propose a new QMC method to simulate Brownian sheet via Karhunen–Loéve expansion (Mallat, 2008).

3.2.1 Forward curve simulation

To simulate the evolution of the forward curves, we need to discretise the process both in time and time to maturity. Let ▵t be the length of discretised time interval and ▵x be the length of the discretised time-to-maturity interval. (3)

Suppose that we have simulated W(t, x) at (t, x) = (i/n, j/n) for i, j = 1, …, n. Given we simulate Z(t, x) by (4)

On the other hand, given

Z(t, x) can be simulated via

3.2.2 QMC simulation by Karhunen–Loéve expansion

As the forward curve simulation requires a simulation scheme of Brownian sheet, we propose a new QMC method to simulate Brownian sheet via its Karhunen–Loéve expansion (Mallat, 2008). As the Karhunen–Loéve expansion decomposes Brownian sheet into random components, which may be considered as an analog of an infinite dimensional principal components analysis. In Acworth, Broadie and Glasserman (1996), the principal components QMC method is introduced to allocate maximum variability to each initial portion of driving sequence, and is argued to be the optimal method when applied together with Sobol’ sequence. Our proposal is to allocate maximum variability to each initial portion of the random components in the Karhounen–Loéve expansion in order to have a better performance for the QMC approach than usual MC methods.

The eigenvalues and eigenfunctions for the covariance kernel of Brownian sheet are where i, j = 1, 2, …. Thus, W_{t, x} has the Karhounen–Loéve expansion where Z_ij are i.i.d. standard normal random variables. We rank λ_ij from the largest to the smallest. First, since λ_ij = λ_ji, (i, j) and (j, i) have the same rank; second, λ_ij decreases in both i and j. Given i ⩽ j, we find k = k(i, j) = (2i − 1)j − i + 1 such that λ_1k = λ_ij. Note k (i, i) = (2i − 1) i − i + 1 = 2i² − 2i + 1 = 5, 13, 25, 41 for i = 2, 3, 4, 5. Our next step is to insert (i, i) in (1, k, k, 1) right after k(i, i) and then after every 2i − 1 number of (1, k, k, 1)′s, insert (i, i + 1, i + 1, i), (i, i + 2, i + 2, i), etc.

More specifically, value for k has been obtained given a set of i, j values as below:

Now for k = 1, 2, 3, …, line up all (1, k, k, 1): (1, 1), (1, 2, 2, 1), (1, 3, 3, 1), …. Right after k(i, i) = 2i² − 2i + 1 for i = 2, 3, …, insert (i, i) and once (i, i) is inserted, after every 2i − 1 positions, insert (i, i + 1, i + 1, i), (i, i + 2, i + 2, i), etc. The 99 largest λ_ij are listed in Table 1 and approximation to Brownian sheet with top 99 terms can be expressed as (5)

Table 1. (i, j) pairs for 99 largest λ_ij in Karhunen–Loéve expansion.

k	(i, j) pairs	k	(i, j) pairs
k  =  1	(1, 1)	k  =  19	(1, 19,  19, 1)
k  =  2	(1, 2,  2, 1)	k  =  20	(1, 20,  20, 1,  2, 7,  7, 2)
k  =  3	(1, 3,  3, 1)	k  =  21	(1, 21,  21, 1)
k  =  4	(1, 4,  4, 1)	k  =  22	(1, 22,  22, 1)
k  =  5	(1, 5,  5, 1,  2, 2)	k  =  23	(1, 23,  23, 1,  2, 8,  8, 2,  3, 5,  5, 3)
k  =  6	(1, 6,  6, 1)	k  =  24	(1, 24,  24, 1)
k  =  7	(1, 7,  7, 1)	k  =  25	(1, 25,  25, 1,  4, 4)
k  =  8	(1, 8,  8, 1,  2, 3,  3, 2)	k  =  26	(1, 26,  26, 1,  2, 9,  9, 2)
k  =  9	(1, 9,  9, 1)	k  =  27	(1, 27,  27, 1)
k  =  10	(1, 10,  10, 1)	k  =  28	(1, 28,  28, 1,  3, 6,  6, 3)
k  =  11	(1, 11,  11, 1,  2, 4,  4, 2)	k  =  29	(1, 29,  29, 1,  2, 10,  10, 2)
k  =  12	(1, 12,  12, 1)	k  =  30	(1, 30,  30, 1)
k  =  13	(1, 13,  13, 1,  3, 3)	k  =  31	(1, 31,  31, 1)
k  =  14	(1, 14,  14, 1,  2, 5,  5, 2)	k  =  32	(1, 32,  32, 1,  2, 11,  11, 2,  4, 5,  5, 4)
k  =  15	(1, 15,  15, 1)	k  =  33	(1, 33,  33, 1,  3, 7,  7, 3)
k  =  16	(1, 16,  16, 1)	k  =  34	(1, 34,  34, 1)
k  =  17	(1, 17,  17, 1,  2, 6,  6, 2)	k  =  35	(1, 35)⋅⋅⋅⋅⋅⋅
k  =  18	(1, 18,  18, 1,  3, 4,  4, 3)

We use quasi-random sequences to simulate Z_ij in an order according to the decreasing order of λ_ij listed above and in Table 1 and then compute .

3.3 Pricing the long bond futures delivery option

This section provides an empirical application of proposed QMC method to introduced forward interest rate model with stochastic string shocks. We consider the problem of pricing the delivery option of long bond futures contract traded on the CBOT (Santa-Clara & Sornette, 2001). The underlying asset for long bond contract is 20-year Treasury bond with 8% coupon. This Treasury bond is hypothetical and in reality, on the delivery day, seller of the contract can choose from the Treasury bond with either at least 15 years to maturity or first call date to delivery, which is referred to as the delivery option (Santa-Clara & Sornette, 2001). It is clear that deliverable bonds circulated in the market are not worth the same. To ensure that sellers of futures contract will be indifferent about which bond to deliver, CBOT publishes conversion factors so that all bonds are worth the same to sellers. More specifically, if a seller would like to deliver a bond trading at a lower price, the seller will have to deliver a greater par value, which is determined by the conversion factor. The method of adopting conversion method, however, do not work perfectly and the bonds price will not be exactly the same. As a result, there is usually one bond that is cheapest to deliver (CTD), which will be the one bond that a seller will choose to deliver. Therefore, valuation of delivery option embedded in futures contract becomes crucial. Besides delivery option, seller of the futures contract has the right to choose the exact delivery date during the delivery month, which is referred to as timing option (Santa-Clara & Sornette, 2001). As our purpose in this section is to demonstrate the implementation of QMC method with proposed model in Section 3, the timing option is ignored.

The data set studied in Santa-Clara and Sornette (2001) are long bond futures from March 1999, delivery option as of 15 October 1998 was the focus. Since the timing option is ignored, we fix the delivery date as 15 March 1999. The volatility function is assumed to be and three forward interest rate models are selected for comparison: the simple Brownian motion the O–U sheet and string with term structure of correlations

Several additional inputs are required for implementation of proposed QMC methods for long bond futures contract valuation. Input values are provided in Tables 2–4. More specifically, the initial forward rates as of 15 October 1998 are listed in Table 2; parameter values used in the volatility and correlation functions are provided in Table 3; specifics for 33 deliverable bonds, e.g., maturity date, coupon value, are presented in Table 4.

Table 2. Implied forward interest rates.

Date	Forward	Date	Forward	Date	Forward	Date	Forward
15 October 1998	5.1572%	15 October 2006	5.9618%	15 October 2014	5.7862%	15 October 2022	5.7862%
15 April 1999	4.5420%	15 April 2007	5.9858%	15 April 2015	5.7862%	15 April 2023	5.7862%
15 October 1999	4.4722%	15 October 2007	6.2611%	15 October 2015	5.7862%	15 October 2023	5.7862%
15 April 2000	4.2391%	15 April 2008	6.2820%	15 April 2016	5.7862%	15 April 2024	5.7862%
15 October 2000	5.0690%	15 October 2008	5.9657%	15 October 2016	5.7862%	15 October 2024	5.7862%
15 April 2001	5.2236%	15 April 2009	5.9615%	15 April 2017	5.7862%	15 April 2025	5.7862%
15 October 2001	4.9391%	15 October 2009	5.9516%	15 October 2017	5.7862%	15 October 2025	5.7862%
15 April 2002	4.9687%	15 April 2010	5.9384%	15 April 2018	5.7862%	15 April 2026	5.7862%
15 October 2002	5.6378%	15 October 2010	5.9203%	15 October 2018	5.7862%	15 October 2026	5.7862%
15 April 2003	5.7631%	15 April 2011	5.9005%	15 April 2019	5.7862%	15 April 2027	5.7862%
15 October 2003	5.4199%	15 October 2011	5.8746%	15 October 2019	5.7862%	15 October 2027	5.7862%
15 April 2004	5.4611%	15 April 2012	5.8474%	15 April 2020	5.7862%	15 April 2028	5.7862%
15 October 2004	5.5992%	15 October 2012	5.8177%	15 October 2020	5.7862%	15 October 2028	5.7862%
15 April 2005	5.6378%	15 April 2013	5.7862%	15 April 2021	5.7862%	15 April 2029	5.7862%
15 October 2005	5.7792%	15 October 2013	5.7862%	15 October 2021	5.7862%	15 October 2029	5.7862%
15 April 2006	5.8102%	15 April 2014	5.7862%	15 April 2022	5.7862%	15 April 2030	5.7862%

Table 3. Parameter estimates of volatility and correlation functions.

Parameter	Brownian motion	O–U Sheet	Subexponential correlation
σ	0.0316	0.0396	0.0485
γ	0.0359	0.0046	0.0228
λ		0.1782	1.0888

Table 4. Deliverable bonds.

Bond no.	Maturity	Coupon	Conversion factor	Market price
1	15 February 2015	11.25	1.2879	167.9688
2	15 November 2015	9.875	1.1701	152.5000
3	15 August 2015	10.625	1.2361	161.1563
4	15 February 2016	9.25	1.114	145.2188
5	15 May 2017	8.75	1.0709	140.3125
6	15 August 2017	8.875	1.083	141.9688
7	15 May 2016	7.25	0.931	122.1563
8	15 November 2016	7.5	0.9533	125.2500
9	15 May 2018	9.125	1.1089	145.9063
10	15 November 2018	9	1.0979	144.9688
11	15 February 2019	8.875	1.0859	143.8125
12	15 August 2019	8.125	1.0122	134.6875
13	15 May 2020	8.75	1.0757	143.3438
14	15 February 2020	8.5	1.05	139.9063
15	15 August 2020	8.75	1.0758	143.5938
16	15 May 2021	8.125	1.0128	136.1563
17	15 February 2021	7.875	0.987	132.7813
18	15 August 2021	8.125	1.0127	136.3750
19	15 November 2021	8	1	135.0000
20	15 November 2022	7.625	0.9605	130.6875
21	15 August 2022	7.25	0.9212	125.6875
22	15 February 2023	7.125	0.9074	124.1563
23	15 August 2023	6.25	0.8137	111.8750
24	15 November 2024	7.5	0.946	130.7188
25	15 February 2025	7.625	0.9592	132.5938
26	15 August 2025	6.875	0.8771	122.2188
27	15 August 2026	6.75	0.862	121.0625
28	15 November 2026	6.5	0.8342	117.6250
29	15 February 2026	6	0.7805	110.2188
30	15 February 2027	6.625	0.8475	119.9063
31	15 August 2027	6.375	0.8189	116.6250
32	15 November 2027	6.125	0.7907	115.0000
33	15 August 2028	5.5	0.7189	108.1250

Given all inputs values, the forward rate curve was simulated based on discretised version of proposed model seen in Equation (3)(3) . We chose ▵t to be 1 day and ▵x to be 6 months, i.e., x = 0, 0.5, 1, 1.5, …, 30. Z(t, x) were simulated according to Equation (4)(4) . Sobol’ sequence was chosen to be the low-discrepancy sequence for implementation of QMC method. For each simulation, a set of 99 dimensional Sobol’ points were generated according to functions in Press, Teukolsky, Vetterling and Flannery (Numerical Recipes in C). Sobol’ points were transformed to normal distribution by applying inverse of cumulative distribution function for normal distribution. Equation (5)(5) was used to compute Brownian sheet W(t, x) for (t, x) = (i/64, j/64), i, j = 1, …, 64. With obtained Brownian sheet W(t, x), Equations (3)(3) and (4(4) ) together were used to compute f(t, x), the forward rate at time t and with time to maturity x. Fifty thousand simulations were repeated for each of the three interest rate models to capture the evolution of forward rate curve on a daily basis from 15 October 1998 to 15 March 1999. Under risk-neutral probability measure and for each simulation, values for all 33 deliverable bonds were computed using simulated forward interest rate on 15 March 1999. The bond that is cheapest-to-deliver was also recorded and corresponding futures price at maturity was computed. Table 5 summarises simulation results for three different correlation functions where futures price is the average of all simulated futures prices at maturity for cheapest-to-deliver bonds. We note that the current cheapest-to-deliver bond is the bond with maturity in February 2015. To evaluate the delivery option, we compute the futures price for the bond with maturity in February 2015 and subtract the futures price that includes the delivery option from it. Table 5 presents the value of the delivery option based on three different correlation functions. We demonstrate the ease of implementation for proposed QMC method with proposed model and simulation results suggest that delivery option is around five times more valuable in the interest rate model constructed based on O–U sheet compared to model driven by Brownian sheet; around six times more valuable in the interest rate model constructed based on subexponential correlation compared to model driven by Brownian sheet. We understand this observation as the interest rate models with stochastic strings are capable of generating much richer class of term structure dynamics of interest rates and therefore result in larger variability in the forward rates at maturity. Therefore, the delivery option becomes more valuable due to greater variety at maturity.

Table 5. Simulation results of the option prices.

Model	Futures price of today's CTD	Futures price	Delivery option value
Brownian motion	124.4917	124.4083	0.0833
O–U sheet	123.9798	123.4682	0.5116
Subexp. corr.	124.5605	124.1593	0.4012

4. Conclusion

In this paper, we review QMC simulations and discuss its advantages over ordinary MC simulations. We focus on the application of QMC simulations for valuation of financial assets such as options. Under the assumption of no arbitrage and based on risk-neutral valuation, option value can be expressed as the discounted expected pay-off of the underlying asset at maturity. When the underlying asset is a bond, pay-off of the bond at maturity requires a stochastic model on the dynamic evolution of bond price over time. We introduce a bond pricing model, the interest rate model with stochastic strings, which is a continuous stochastic diffusion process driven by two-dimensional stochastic strings constructed based on Brownian sheet. For simulation, we investigate discretised version of introduced model and propose a new QMC method for simulating Brownian sheet via its Karhunen–Loéve expansion. Karhunen–Loéve expansion, which can be considered as principal components decomposition in infinite dimensions, decomposes Brownian sheet into random components and allocates maximum variability to each initial portion of the random components. We demonstrate proposed QMC simulation method for introduced interest rate model via an empirical application. In the empirical study, we investigate delivery option in long bond futures contract and show that delivery option is more valuable in stochastic string models compared to model driven by simple Brownian sheet. This observation from empirical study is consistent with the fact that introduced model has a much richer class of term structure dynamics of interest rates that allows capturing a larger volatility in modelling and pricing contingent claims. We demonstrate the ease of implementation with the proposed QMC method and believe that it can be easily extended or modified for studying valuation of other contingent claims.

Acknowledgements

The research of Yazhen Wang was supported in part by NSF [grant number DMS-12-65203], [grant number DMS-15-28375].

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

The research of Yazhen Wang was supported in part by NSF [grant number DMS-12-65203], [grant number DMS-15-28375]

Notes on contributors

Xinyu Song

Xinyu Song is a graduate student in the Department of Statistics at University of Wisconsin-Madison. Her research interests are in modelling financial instruments, particularly based on high frequency data.

Yazhen Wang

Yazhen Wang is professor of statistics at the University of Wisconsin-Madison and also serves as Chair for the Department of Statistics at University of Wisconsin-Madison. His major research interests are in financial statistics and financial data science (both high frequency and low frequency), quantum computing as well as high dimensional statistics and statistics learning. He holds fellowship at Institute of Mathematical Statistics (IMS) and at American Statistical Association (ASA).