Power analysis for stratified cluster randomisation trials with cluster size being the stratifying factor

ABSTRACT

Stratified cluster randomisation trial design is widely employed in biomedical research and cluster size has been frequently used as the stratifying factor. Conventional sample size calculation methods have assumed the cluster sizes to be constant within each stratum, which is rarely true in practice. Ignoring the random variability in cluster size leads to underestimated sample sizes and underpowered clinical trials. In this study, we proposed to directly incorporate the variability in cluster size (represented by coefficient of variability) into sample size calculation. This approach provides closed-form sample size formulas, and is flexible to accommodate arbitrary randomisation ratio and varying numbers of clusters across strata. Simulation study shows that the proposed approach achieves desired power and type I error over a wide spectrum of design configurations, including different distributions of cluster sizes. An application example is presented.

KEYWORDS:

• Clinical trials
• power
• sample size
• cluster size
• stratified
• cluster randomisation trial

1. Introduction

Cluster randomisation trials are widely employed in biomedical research (Bland, 2004), where groups of subjects (denoted as clusters) instead of individuals serve as randomisation units. The advantages of cluster randomisation trials include the ability to study interventions that are delivered in a grouped fashion (such as a radio campaign) and the ability to control for ‘contamination’ across individuals within a group. One issue frequently encountered by practitioners is that naturally occurring clusters are varying in size. Cluster size may be associated with important cluster-level factors, and it has been recognised as a surrogate for within-cluster dynamics that predicts outcome in cluster randomisation trials (Donner & Klar, 2000). The conventional randomisation procedure might fail to achieve balance in cluster size between intervention arms when the number of clusters is moderate, which in turn might lead to biased estimation of intervention effect. One possible solution is to adopt the stratified cluster randomisation design where clusters are first grouped into strata based on size (e.g., small, medium and large), and then randomised within each stratum to intervention arms. In the following, this design is denoted as size-stratified cluster randomisation design.

To the best of our knowledge, there are only two published papers that investigate sample size requirement for size-stratified cluster randomisation trials. In the context of binary outcomes, Donner and Klar (1996) presented a sample-size approach for size-stratified cluster randomisation trials. The null hypothesis tested is that the odds ratio equals to one. This approach is an extension of the sample-size formula developed by Woolson, Bean, and Rojas (1986), based on the Cochran–Mantel–Haenszel statistic (Mantel, 1963). In the context of continuous outcomes, Lewsey (2004) conducted a simulation study to assess the benefit of stratified randomisation by cluster size when the cluster size is associated with an important cluster-level factor which is otherwise unaccounted for in the analysis. Both Donner and Klar (1996) and Lewsey (2004) assume cluster sizes to be equal within, but different across, strata. This assumption might be unrealistic because clusters are naturally formed with random sizes. Practitioners are rarely able to construct strata that consist of equal-sized clusters. A more likely scenario is that each stratum contains clusters with sizes of similar magnitude. It is hence more appropriate to characterise the cluster sizes within a stratum by a distribution (e.g., with specific mean and variance) instead of a single value (Lauer, Kleinman, & Reich, 2015). Currently, the common practice is to plug the average cluster size within each stratum into formula to assess sample-size requirement. This approach, however, ignores the additional variability caused by random cluster sizes, which leads to underestimated sample sizes and underpowered studies. Manatunga, Hudgens, & Chen (2001) proposed a method that incorporates the random variability in cluster size into sample-size calculation for cluster randomisation trials. Specifically, their approach modifies the conventional sample-size formula by a correction term that involves the coefficient of variation of cluster sizes.

In this study, we propose to extend Manatunga's method to size-stratified cluster randomisation trials where the outcome evaluated is continuous. This extension allows researchers to directly take random variability in cluster size into consideration at the design stage. Furthermore, the derived sample-size formula has a closed form which is easy to use in practice. The rest of the paper is organised as follows. In Section 2, derivation of sample-size formulas for size-stratified cluster randomisation trials under two assumptions, constant or random cluster size within stratum, are presented. We also investigate how random variability in cluster size affects sample-size requirement and what other designing factors are involved. In Section 3, we conduct simulation studies to assess the performance of the proposed approach under a wide range of design configurations. An application example is presented in Section 4. Finally, we discuss the pros and cons of the proposed approach and potential future development in Section 5.

2. Methods

We assume that in a cluster randomisation trial, the clusters are grouped into L strata based on their sizes. The number of clusters within each stratum is denoted by  J_l (l = 1,… , L). We assume the cluster sizes within the lth stratum, denoted by n_lj (j = 1,… ,  J_l), to be independent samples from a certain discrete distribution with mean θ_l and variance τ²_l. The total sample size of a stratified cluster randomisation trial is , which depends on the number of strata (L), the number of clusters in each stratum ( J_l), and cluster sizes (n_lj).

We use Y_lji to denote the continuous outcome measured on the ith (i = 1,… , n_lj) subject from the jth cluster of the lth stratum, and x_lj = 0/1 to indicate that all patients in the (l, j)th cluster are assigned to the control/treatment arm. We use randomisation probability r ≡ P(x_lj = 1) to generally accommodate balanced (r = 0.5) and unbalanced randomisation. We employ the generalised estimating equation (GEE) approach (Liang & Zeger, 1986), which only requires specifying models for the first two moments of Y_lji. The mean model is specified as (1) where β₀ is the intercept representing the baseline mean response under control, and β₁ represents the treatment effect. The null hypothesis of interest is H₀ : β₁ = 0. The covariance of , defined as , is assumed to be an n_lj × n_lj matrix with the diagonal elements being σ² and off-diagonal elements being ρσ². Here σ² is the variance of random error and ρ is the intracluster correlation coefficient quantifying the similarity of subjects within the same cluster (Rutterford, Copas, & Eldridge, 2015; Zou & Donner, 2004). The observations are assumed to be independent across clusters.

Define , and . Here denotes a vector with all elements being 1. Then we have . Using an independent working correlation structure, it is easy to show that the GEE estimator of is According to Liang and Zeger (1986), as n → ∞, approximately follows a normal distribution with mean and variance , which is consistently estimated by Here is the residual term. We reject H₀: β₁ = 0, if , where is the (2,2)th element of , α is the level of two-sided type I error, and z_{1 − α/2} is the 100(1 − α/2)th percentile of the standard normal distribution.

After algebraical simplification, it can be shown that with Using the fact that E(n_lj) = θ_l and Var(n_lj) = τ²_l, for large  J_l, we have Here ξ_l = τ_l/θ_l is the coefficient of variation (CV) within stratum l. Similarly, v₂ can be approximated by It is obvious that v₁ = v₂ under balanced randomisation (r = 0.5).

The power analysis of a stratified cluster randomisation trial requires the specification of the following parameters: the type I error α, true treatment effect b₁, randomisation probability r, variance σ², intracluster correlation coefficient ρ, the number of strata L, the numbers of clusters within strata , the stratum-specific mean cluster sizes , and the stratum-specific CVs . The testing power under sample size can be evaluated by (2) where Φ(·) is the standard normal cumulative distribution function. This power analysis approach (2(2) ) is flexible to accommodate a wide spectrum of realistic trial scenarios, including unbalanced randomisation (through r), different numbers of clusters across strata (through ), arbitrary averaged cluster sizes within strata (through ), and different variability in cluster size within each stratum (through .

Sample-size calculation is more complicated because the total sample size involves many variables: L and {( J_l, θ_l) : l = 1,… ,  J}. We explore a relatively simpler scenario of balanced randomisation (r = 0.5) and equal number of clusters across strata ( J₁ = ⋅⋅⋅ =  J_L =  J), to help understand the impact of various parameters on sample-size requirement in a size-stratified cluster randomisation trial. By setting Expression (2(2) ) to the target power 1 − γ, we can solve the required number of clusters per stratum ( J) given L, , and other parameters: (3) When L = 1, the second term in (3(3) ) simplifies to , which is identical to the correction term derived by Manatunga et al. (2001) for conventional cluster randomisation trials with varying cluster sizes.

When there is no variability in cluster size ξ_l = 0 for l = 1,… , L, and hence n_lj = θ_l, the number of clusters per stratum required is We define the relative change in sample size due to varying cluster size by (4) To investigate the impact of different factors on sample size, we equivalently write R as (5)

We have several observations:

• In real cluster randomisation trials, we usually have 0 < ρ < 1. Under this assumption, (5(5) ) shows that R is always positive. That is, variability in cluster size always leads to increased sample-size requirement. The common practice of using the average cluster size in each stratum for sample-size computation will lead to underpowered clinical trials.

• More specifically, (5(5) ) shows a linear relationship between 1/R and 1/ρ. The same variability in cluster size would lead to a greater increase in sample size when the intracluster correlation is stronger.

• Under the extreme case of ρ = 0, a cluster randomised trial is equivalent to an individual randomisation trial. The variability in cluster size has no impact on sample size (R = 0).

• Equation (4(4) ) shows that R is a linear function of ξ²_l for every l = 1,… , L. That is, increased variability of cluster size within any stratum would lead to increase in the total sample size.

• When the CVs are equal across strata, ξ_l = ξ for l = 1,… , L, we can further simplify (5(5) ) as (6) where and . is the overall mean of cluster sizes across strata. As for s²_θ, we borrow the concept of between-group variability from ANOVA and consider s²_θ a measurement of between-stratum variability in cluster size. Recall that within-stratum variability in cluster size is measured by τ²_l or ξ_l (l = 1,… , L). Hence (6(6) ) shows that a greater between-stratum variability in cluster size is associated with a larger sample size requirement, even if the overall mean of cluster sizes () remains the same.

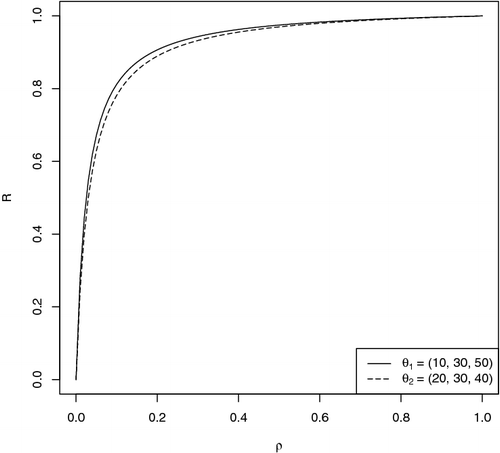
For illustration, in Figure 1, we plot R versus ρ in a simple scenario where the numbers of clusters and CVs are equal across strata. Without loss of generality, we set ξ = 1. Two sets of are explored: and . We can see that the curve corresponding to is always higher than that corresponding to , because has a greater between-stratum variability in cluster size than although their overall mean cluster sizes are the same. It is noteworthy that the assumed value of ξ only affects the range of the vertical axis. The shape and relative position of the two curves remain unchanged.

Figure 1. Percentage increase in sample size (R) versus intraclass correlation coefficient (ρ). The vertical axis corresponds to R and the horizontal axis corresponds to ρ. We assume the numbers of clusters and CVs to be equal across strata. The common CV is set at ξ = 1.

3. Simulation

We conduct simulation studies to assess the performance of the proposed sample-size approach. We assume that in a size-stratified cluster randomisation trial, the clusters are stratified into L = 3 groups according to their sizes: small, medium and large. We consider two types of within-stratum distributions for the cluster sizes: discrete uniform (DU) and zero-truncated negative binomial (tNB) distribution (Ahn, 1997; Speigel, 1975). Let m be an integer random variable, and the probability mass function of DU() is Here integers a and b (b ≥ a) are the lower and upper limits, respectively. The mean and variance of DU(a, b) are The probability mass function of tNB() is The mean and variance are (7) (8) In Scenario D₁ we assume the distributions of cluster sizes in the small, medium and large strata to be DU(1, 8), DU(9, 24) and DU(25, 100), respectively. In Scenario D₂, the distributions of cluster sizes are assumed to be tNB, with parameters (s, P) solved to have matching means and variances (and hence CV) to those under Scenario D₁. For example, DU(25, 100) corresponds to mean θ_l = 62.5, variance τ²_l = 481.25 and CV ξ_l = 0.35. Using Equations (7(7) ) and (8(8) ), we can solve for tNB parameters s = 9.33 and P = 6.70. Details of D₁ and D₂ are presented in Table 1. Considering D₁ and D₂ in the simulation study allows us to assess the robustness of the proposed sample-size approach to different distributions of cluster sizes.

Table 1. Specification of scenarios D₁ and D₂.

	Scenarios		Mean	Variance	CV
Stratum	D1	D2	(θl)	(τ^2l)	(ξl)
1	DU(1, 8)	tNB(17.29, 0.26)	4.5	5.25	0.509
2	DU(9, 24)	tNB(57.31, 0.29)	16.5	21.25	0.279
3	DU(25, 100)	tNB(9.33, 6.70)	62.5	481.25	0.351

We set the levels of type I error at α = 0.05, power at 1 − γ = 0.9. We assume 1:1 randomisation (r = 0.5), and consider five levels of intracluster correlation (ρ): 0.01, 0.02, 0.03, 0.05, 0.1, as well as three levels of true treatment effect (b₁): 0.2, 0.25, 0.3. Without loss of generality, we specify the true value of intercept β₀ = 0 and variance σ² = 1. We use D to indicate Scenarios D₁ and D₂, which implicitly specifies the mean (θ_l) and CV (ξ_l) of cluster sizes in each stratum. We assume an equal number of clusters across strata, and compute the number of clusters per stratum with and without accounting for variability in cluster size ( J and J^*) under each combination of design parameters (α, γ, r, L, σ², β₀, b₁, ρ, D). For each computed J, we assess the empirical power according to the following algorithm: at iteration k, (k = 1,… , K):

(1)	Based on the distributions specified in D, generate sets of cluster sizes within each stratum , l = 1,… , L. The total sample size is n(k) = ∑Ll = 1∑j = 1Jn(k)lj.
(2)	For the (l, j)th (l = 1,… , L; j = 1,… , J) cluster, generate treatment indicator x(k)lj from the Bernoulli distribution with probability r, and the vector of observations from a multivariate normal distribution with mean 1(β0 + x(k)ljb1) and n(k)lj × n(k)lj covariance matrix . Here indicates the identity matrix.
(3)	Obtain estimates and .

The empirical power is estimated by . Here I{·} is an indicator function. The total number of iterations is set at K = 10000. The same algorithm can be used to compute the empirical type I error by setting the true treatment effect b₁ = 0. The empirical power and type I error for J^* can be evaluated similarly, where we simulate the situation that sample size is calculated assuming constant cluster size but the cluster sizes are actually random.

In Table 2, we present the estimated numbers of clusters per stratum ( J and J^*) and empirical powers under different design configurations. The empirical powers corresponding to J are all close to their nominal levels, suggesting that the proposed method allows size-stratified cluster randomisation trials to be adequately powered in the presence of random cluster sizes. Furthermore, the performance of J is similar under D₁ and D₂, indicating the general applicability of the proposed method to different distributions of cluster sizes. On the other hand, if the variability in cluster size is ignored, the sample sizes ( J^*) is underestimated, resulting in underpowered clinical trials. Note that due to the integer constraint, J and J^* are rounded to the same values under certain configurations (such as when b₁ = 0.3 and ρ = 0.01 and 0.02). In such cases, the powers of J and J^* are identical. Table 2 also confirms our theoretical conclusion that intracluster correlation (ρ) has a great impact on sample-size requirement. With all other design parameters fixed, stronger intracluster correlation is associated with larger sample sizes. For example, under b₁ = 0.2, the numbers of clusters ( J) under ρ=0.01, 0.02, 0.03, 0.05 and 0.1 are 20, 27, 34, 48 and 83, respectively. Finally, in Table 2, we have explored a wide range of sample sizes ( J from 9 to 83), suggesting that, although developed based on the large sample theory, the proposed method can maintain the desired power and type I error in scenarios where the sample size is relatively small.

Table 2. Empirical power from 10,000 simulations for the fixed cluster size method and proposed method.

			b1
ρ	Method	D	0.20	0.25	0.30
0.01	J^*	D1	89.66% (19)	91.38% (13)	91.67% (9)
		D2	89.12% (19)	91.03% (13)	91.56% (9)
	J	D1	90.64% (20)	91.74% (13)	91.28% (9)
		D2	90.27% (20)	91.29% (13)	91.27% (9)
0.02	J^*	D1	88.20% (25)	88.90% (16)	91.05% (12)
		D2	88.68% (25)	89.05% (16)	91.26% (12)
	J	D1	90.55% (27)	90.27% (17)	91.22% (12)
		D2	90.71% (27)	90.56% (17)	91.12% (12)
0.03	J^*	D1	88.80% (32)	88.70% (20)	89.39% (14)
		D2	88.48% (32)	88.33% (20)	89.00% (14)
	J	D1	90.71% (34)	91.03% (22)	91.04% (15)
		D2	90.72% (34)	91.08% (22)	91.34% (15)
0.05	J^*	D1	87.79% (44)	87.92% (28)	89.11% (20)
		D2	88.09% (44)	87.63% (28)	89.28% (20)
	J	D1	90.37% (48)	90.61% (31)	91.69% (22)
		D2	91.10% (48)	91.14% (31)	91.51% (22)
0.10	J^*	D1	87.71% (75)	87.70% (48)	88.03% (34)
		D2	87.85% (75)	87.26% (48)	88.46% (34)
	J	D1	91.16% (83)	90.70% (53)	90.56% (37)
		D2	90.39% (83)	90.22% (53)	90.36% (37)

Note: In each cell, we present empirical power (number of clusters per stratum) under a combination of trial parameters.

4. An application example

An investigator is interested in assessing the effect of an information technology (IT)-based novel intervention platform on the well-being of patients with a triad of chronic kidney disease, diabetes and hypertension. The size-stratified cluster randomisation design will be employed. Patients are clustered by clinics, which are stratified by the size of clinic and randomly allocated at a 1:1 ratio to either the IT-based intervention group or the control group (standard medical care) within each stratum. Here, clinics are stratified to three groups – small, medium and large – based on their sizes. Based on the assignment of his or her clinic, each patient will receive either the intervention or control treatment. The primary outcome of well-being will be measured using the instrument of Bradley (1994) after three-month intervention. We estimate the sample size based on the comparison of well-being scores between the control and IT-based intervention groups. From preliminary data, we observe that the mean of the well-being score at three months was 30 with a standard deviation of 12 across all three strata in the control group. We hypothesise that the mean well-being scores in the IT-based intervention group will be 10% higher than that in the standard medical care group. We assumed an equal standard deviation between two groups, From a preliminary data-set, we obtained an intracluster correlation coefficient (ρ) of 0.03. To be conservative, we assume ρ = 0.05 for sample-size calculation. The average cluster sizes (i.e. the average numbers of patients in a clinic) are 5, 17 and 65 in the small, medium and large strata, respectively, with variances 6, 25 and 500. With an equal number of 30 clinics for small, medium and large strata, the power of the study is 90.13% at a two-sided 5% significance level. When the number of clinics is unequal with 40, 30 and 20 clinics in small, medium and large strata, the power of the study becomes 84.32%.

5. Discussion

In this study, we proposed a sample-size calculation method for size-stratified cluster randomisation trials which no longer requires the unrealistic assumption of constant cluster size within each stratum. Furthermore, this method is flexible to accommodate arbitrary randomisation ratio and arbitrary numbers of clusters within each stratum. The random variability in cluster size is incorporated into sample-size formula through CV, which only requires information about the first two moments instead of the specific distribution, improving the applicability of the proposed method in practice. The simulation studies demonstrate robust performance of this approach under different types of distributions.

The proposed sample-size formula was derived using the independent working correlation structure, which greatly simplifies computation (allowing us to obtain a closed-form sample size formula) and the parameter estimators remain consistent (Crowder, 1995; McDonald, 1993). It has been shown that the estimators under the independent working correlation are highly efficient compared with those under the true correlation structure (Liang & Zeger, 1986). The slight loss in efficiency due to not using the true correlation structure means that the proposed approach provides a conservative estimation of sample size.

We have theoretically shown that random variability in cluster sizes always leads to increased sample-size requirement in realistic scenarios (intracluster correlation 1 > ρ > 0). The common practice of assuming equal cluster size (ignoring variability) within each stratum for sample-size calculation underestimates sample size and results in underpowered clinical trials. We further show that the impact of varying cluster sizes depends on intracluster correlation. Stronger intracluster correlation is associated with greater increase in sample size given the same variability in cluster size (measured by CV).

The proposed sample-size method is developed for size-stratified cluster randomisation trials with continuous outcomes. In many cluster randomisation trials, patients are followed longitudinally, contributing multiple measurements. Extending this approach to trials with binary or ordinal outcomes, or longitudinal measurements, will be the topic of our future research.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

The work was supported in part by NIH grant [1UL1TR001105], AHRQ grant [R24HS22418], CPRIT grants [RP110562-C1] and [RP120670-C1], and NSF grant [IIS-1302497-04].

Notes on contributors

Jijia Wang

Jijia Wang is a PhD student in the joint biostatistic program of Southern Methodist University and the University of Texas Southwestern Medical Center (UTSW).

Song Zhang

Song Zhang is an associate professor of biostatistics in the Clinical Sciences Department at UTSW.

Chul Ahn

Chul Ahn is a professor of biostatistics in the Clinical Sciences Department at UTSW.