Sequential profile Lasso for ultra-high-dimensional partially linear models

ABSTRACT

In this paper, we study ultra-high-dimensional partially linear models when the dimension of the linear predictors grows exponentially with the sample size. For the variable screening, we propose a sequential profile Lasso method (SPLasso) and show that it possesses the screening property. SPLasso can also detect all relevant predictors with probability tending to one, no matter whether the ultra-high models involve both parametric and nonparametric parts. To select the best subset among the models generated by SPLasso, we propose an extended Bayesian information criterion (EBIC) for choosing the final model. We also conduct simulation studies and apply a real data example to assess the performance of the proposed method and compare with the existing method.

Keywords:

• Sequential profile Lasso
• partially linear model
• extended Bayesian information criterion
• screening property
• ultra-high-dimensional data

1. Introduction

High-dimensional data are becoming increasingly popular in the past two decades, and they have wide applications in various fields such as genomics, economics, finance and epidemiology. As one example, genome-wide association studies usually encompass hundreds of thousands, or millions, of single nucleotide polymorphism (SNP) at the same time, and that pose new computational and statistical challenges. To analyse ultra-high-dimensional data, Fan and Lv (2008) proposed the sure independence screening (SIS) method to ultra-high-dimensional linear models. Owing to its great success, the SIS method was further extended to more general models in the recent literature. To name a few, Fan, Feng, and Song (2011) proposed the nonparametric independence screening for ultra-high-dimensional additive models. Fan, Ma, and Dai (2014) extended the nonparametric independence screening to ultra-high-dimensional varying coefficient models. Li, Peng, Zhang, and Zhu (2012) developed a robust rank correlation screening based on Kendall's rank correlation. Li, Zhong, and Zhu (2012) proposed a sure independence screening method based on the distance correlation for general parametric models. Zhu, Li, Li, and Zhu (2011) proposed the variable screening method under a unified model framework. Cui, Li, and Zhong (2015) proposed a model free variable screening method for categorical response variable. Note also that Wang (2009) applied the forward regression (FR) in Weisberg (1980) to ultra-high-dimensional linear regression models. Cheng, Honda, and Zhang (2016) further extended the FR method to ultra-high-dimensional varying coefficient models.

Partially linear models are important semiparametric models and are widely used in practice, which possess both the flexibility of nonparametric models and the ease of interpretation of linear regression models. Partially linear models have been extensively studied in the literature (see for example Härdle, Liang, and Gao (2000) and Li, Zhang, and Feng (2016)). In this paper, we propose to analyse partially linear models when the dimension of the linear predictors grows exponentially with the sample size. Specifically, letting Y be the response variable, we consider the partially linear model as follows: (1) where is a p-dimensional vector of unknown regression coefficients, U is a univariate variable, g( · ) is an unknown smooth function, and ϵ follows a distribution with mean 0 and variance σ². We assume that ϵ is independent of the associated covariates , and that the predictor variable has a ultra-high-dimensionality or a nonpolynomial dimensionality such that ln p = O(n^κ) for some κ > 0, where p is the dimension and n is the sample size.

Variable selection for model (1(1) ) is very challenging because it involves both parametric and nonparametric parts. When p is fixed, variable selection and parameter shrinkage are conventional and there are many related methods in the literature such as Bunea (2004), Liang and Li (2009), Liu, Wang, and Liang (2011), Mammen and van de Geer (1997) and Wang, Liu, Liang, and Carroll (2011). When p grows with n, Xie and Huang (2009) applied the SCAD penalty to partially linear models and studied the asymptotic properties of the proposed estimators. Sherwood and Wang (2016) considered partially linear additive quantile regression models and studied the oracle property for a general class of nonconvex penalty functions. We note however that, due to the challenges in computational expediency, statistical accuracy and algorithm stability, the aforementioned penalised variable selection methods may not work well for model (1(1) ). To overcome the challenges, Liang, Wang, and Tsai (2012) proposed the profile forward regression (PFR) algorithm to perform the variable screening for model (1(1) ). Li, Li, Lian, and Tong (2017) extended the PFR algorithm to ultra-high-dimensional varying coefficient partially linear models.

The L₁ penalty or Lasso proposed by Tibshirani (1996) is a popular variable selection method. When p diverges to infinity faster than n but not too fast, under the irrepresentability condition, Zhao and Yu (2006) established the selection consistency for the fixed design, and Meinshausen and Bühlmann (2006) established the selection consistency for the random design. To alleviate the irrepresentability condition, Zou (2006) proposed the adaptive Lasso and showed that the adaptive Lasso has the oracle property when p is fixed. Luo (2012) and Luo and Chen (2014) proposed the sequential Lasso which chooses the largest tuning parameter in the sequentially partially penalised least squares objective function to assure at least one (mostly just one) of the regression coefficients being estimated as nonzero. Furthermore, under the partial positive cone condition, they proved the set of the predictors which maximise the correlation with the current residual, i.e., the response vector projected onto the orthogonal complement of the space spanned by the currently selected predictors, is the set of nonzero elements of the solution. This means that the next predictors being selected by the sequential Lasso can be chosen from the set of the predictors which maximise the correlation with the current residual. Such a method enjoys the expected theoretical properties including the screening property, meanwhile, it has some advantages from the numerical aspects.

Inspired by the above advantages, in this paper, we also apply the profile technique to convert model (1(1) ) to a linear model, and apply the sequential Lasso to develop a sequential profile Lasso (SPLasso) procedure. To select the best subset among the models generated by SPLasso, we propose an extended Bayesian information criterion (EBIC) for choosing the final model. We further show that our proposed SPLasso method can identify all relevant predictors with probability tending to one, and that the resulting model determined by EBIC possesses the screening property.

The rest of this paper is organised as follows. In Section 2, the SPLasso procedure is introduced for model (1(1) ). In Section 3, the asymptotic properties are derived under some regularity conditions. In Section 4, simulation studies are carried out to evaluate the finite sample performance of our proposed method and to compare it with existing method. Section 5 presents the application of our proposed method to a real data set. The technical proofs of the two theorems, together with some lemmas, are given in the Appendix.

2. Sequential profile Lasso

To avoid confusion, we specify in the beginning that the boldface roman B represents a matrix, and the boldface italics represents a vector. Throughout this paper, we denote and as the smallest and largest eigenvalues of an arbitrary matrix , respectively. Suppose that are independent and identically distributed copies of that are generated from model (1(1) ). For ease of notation, we denote as the response vector, as the matrix of explanatory variables, where is the predictor vector, and as the vector of random errors. We write and as the index sets of the full and true predictors, respectively. Let also denote the number of the elements of a candidate model , where is the index set of the predictors in the corresponding candidate model. Thus, and , where p₀ is the size of the true model or the number of relevant predictors in the true model. For any candidate model , we use to represent the subvector of corresponding to , and to denote the matrix consisting of the column of X with indices in . Similarly, let denote the vector consisting of the corresponding components of . For any candidate model , let be the complement of in the full model .

By model (1(1) ) and the fact that , we have (2) For simplicity, we define the profile response as Y*_i = Y_i − E(Y_i|U_i) and the profile predictor vector as , where X*_ij = X_ij − E(X_ij|U_i) for i = 1,… , n and j = 1,… , p. By (2(2) ), model (1(1) ) reduces to the following linear regression model: (3)

Note that model (3(3) ) contains the unknown functions E(Y_i|U_i) and and they need to be estimated in practice. In this paper, we approximate E(Y_i|U_i) locally by a linear function, and consider the following objective function (Fan & Gijbels, 1996): where K_h( · ) = K( · /h)/h with K( · ) a kernel function and h a bandwidth. By minimising the above weighted least squares objective function, we can obtain the local linear regression estimator of E(Y_i|U_i = u) as follows: where and S_nℓ = ∑ⁿ_{i = 1}K_h(U_i − u)(U_i − u)^ℓ for ℓ = 0, 1, 2. We note that the above method can also be applied to estimate E(X_ij|U_i = u) for 1 ≤ j ≤ p. To facilitate the notation, we write the estimator of the profile response as with , and the estimators of the profile predictors as with . This gives rise to the following linear model: (4)

In what follows, we introduce our SPLasso procedure. At the initial step, the SPLasso method minimises the following penalised least squares objective function: (5) where λ₁ is the largest value such that at least one (mostly just one) β_j will be estimated as nonzero. The index set of the selected predictors with nonzero estimated coefficient is labelled as . Let be the index set of the predictors being selected until step k. At the (k + 1)th step, we consider the following partially penalised objective function: (6) where λ_{k + 1} is the largest value such that at least one (mostly just one) , will be estimated as nonzero. According to the Karush–Kuhn–Tucker (KKT) condition (see Proposition 3.3.1 in Bertsekas, 1999), the solution of is equivalent to the minimisation of where , , I_n is an n × n identity matrix, and . Let also . Following Luo and Chen (2014), we consider the new predictors selected by the (k + 1)th step are from the set . For this, we consider the following objective function: (7) If has only one element, then the jth predictor with is the predictor with nonzero estimated coefficient in the minimisation of . If has more than one element, we need to minimise the objective function (7(7) ) by applying the R function ‘glmpath’ developed by Park and Hastie (2007). Our proposed SPLasso is as follows:

[S1]	Let . If has only one element, we update . Otherwise, use ‘glmpath’ to and and obtain the solution path. Let be the index of the first predictor with nonzero estimated coefficient in the solution path.
[S2]	At the (k + 1)th step, let , where and . If has only one element, we update . Otherwise, use ‘glmpath’ to and , where , and obtain the solution path. We add the index of the first predictor with nonzero estimated coefficient in the solution path in the current model , and write the new model as .
[S3]	Iterate the S2 step for n times to obtain a total of n nested candidate models by the solution path .

Note that we can update from . Suppose the predictors with indices {j_k: k = 1,… , M} are added to the current model at the (k + 1)th step, and denote the index set as for m ≥ 1 and let . The recursive formula is given by By the above discussion, it is evident that our proposed SPLasso procedure has the advantage of reducing the computational burden by avoiding the computation of the inverse matrices.

3. Asymptotic properties

In this section, we establish the screening property of SPLasso. We use an EBIC to obtain the best model in the solution path and show that this model contains the true model with probability tending to one. To derive the theoretical results, we need some regularity conditions.

(C1)	There exist two positive constants τmin  and τmax , such that 2τmin  < γmin (Σ) ≤ γmax (Σ) < 2−1τmax , where Σ is the covariance matrix of the profile predictor .
(C2)	Assume that for some positive constant and for some positive constants ξmin  and , where .
(C3)	There exist positive constants ξ, ξ0 and ν, such that ln p ≤ min (νnξ, n3/10), , and ξ + 3ξ0 + 6ξmin  < 1.
(C4)	and E(Y|U = u) are uniformly Lipschitz continuous of order one.
(C5)	The weight functions wk( · ) satisfy, with probability tending to one, max 1 ⩽ k ⩽ n∑ni = 1wk(Ui) = O(1), max 1 ≤ i, k ≤ n wk(Ui) = O(bn) with bn = n−4/5, and max 1 ⩽ i ⩽ n∑nk = 1wk(Ui)I(|Ui − Uk| > cn) = O(cn) with cn = n−2/5ln n.
(C6)	Assume that max {Eexp (u|Y*i|), max 1 ⩽ j ⩽ pEexp (u|X*ij|)} < ∞ for all 0 ≤ u ≤ t0/σv, where t0 and σv are positive constants, and that the moment generating functions Mj(u) of X*ij for j = 1,… , p and M0(u) of Y*i satisfy Furthermore, assume that max {E|Y*i|2k, max 1 ⩽ j ⩽ pE|X*ij|2k} ⩽ σ2v for some k > 2, and that ϵ follows a normal distribution.

Conditions (C1)–(C3) are technical requirements for model selection (see Li et al., 2017; Liang et al., 2012; Wang, 2009). Conditions (C4) and (C5) are commonly used in the semiparametric regression and can be easily verified (see Härdle et al., 2000). Condition (C6) follows from Liang et al. (2012) to obtain an exponential inequality of a sum of random variables. It is worth noting that we do not pose any restriction on the distribution on , whereas the SIS method in Fan and Lv (2008) requires it to be the spherically symmetric distribution, and the FR method in Wang (2009) and Lasso in Zhang and Huang (2008) require it to be the normal distribution. In addition, we replace the L₂ norm with the maximum norm of that is slightly different from Li et al. (2017), Liang et al. (2012) and Wang (2009).

Theorem 3.1:

Suppose that regularity conditions (C1)–(C6) hold, and let where [t] denotes the largest integer less than t and λ₀ is a constant larger than 1. Then, (8) where denotes the selected K_nth model in the solution path .

Theorem 3.1 shows that the proposed SPLasso procedure can identify all relevant predictors within steps with probability tending to one, which is better than the order of derived in Theorem 2 of Liang et al. (2012). Since the models generated by SPLasso are nested, we need to determine which model should be used for further statistical inference. To this end, we consider the EBIC as follows: (9) where η is a fixed positive constant, is any candidate model with , and where . Note that for ζ = 1, EBIC has been used in Chen and Chen (2008), Liang et al. (2012) and Wang (2009). Let , then the resulting model is . In the following, we show that contains the true model with probability tending to one.

Theorem 3.2:

Under regularity conditions (C1)–(C6), as n → ∞, we have (10)

4. Simulation study

In this section, we present the results of Monte Carlo simulations to evaluate the finite sample performance of the proposed SPLasso procedure. We employ the Epanechnikov kernel K(u) = 0.75(1 − u²)₊ and the bandwidth , where is the sample standard deviation of U. In all examples, the variable U is generated from the uniform distribution on [0, 1]. We consider n =100, 150 and 200, p =500, 1000 and 2000, and compare SPLasso with the PFR method in Liang et al. (2012).

Let be the estimator obtained from the kth simulation, and the resulting model be . We consider the following eight performance measures to evaluate the performance of SPLasso: (1) AMS: the average model size of the resulting model based on 200 simulations; (2) CP: the average coverage probability that all relevant predictors are detected among 200 simulations; (3) CZ: the proportion of correct identified zeros among 200 simulations; (4) IZ: the proportion of incorrect identified zeros among 200 simulations; (5) CF: the average of correctly fitted that all relevant predictors are detected and no irrelevant predictors are contained in the resulting model among 200 simulations; (6) AEE: the average estimation error is computed as ; (7) PDR: the average positive discovery rate is computed as ; and (8) FDR: the average false discovery rate is computed as .

Example 4.1:

In this example, we consider that the relevant predictors are independent and are generated from the standard normal distribution. The regression coefficient vector of relevant predictors is (3, 3.75, 4.5, 5.25, 6, 6.75, 7.5, 8.25, 9, 9.75). The irrelevant predictors are generated as where Z_j are independent standard normal random variables, and are independent of the relevant predictors. The nonlinear function is g(U) = 4sin (2πU), a non-monotonic function. The noises ϵ are generated from the standard normal distribution. The simulation results are reported in Table 1.

Table 1. Simulation results for Example 4.1.

p	n	AMS	PDR	FDR	AEE	CP	CZ	IZ	CF
				Method:	PFR
	100	13.810	0.848	0.378	1.926	0.025	0.989	0.152	0.000
500	150	14.225	0.916	0.350	1.170	0.325	0.989	0.084	0.000
	200	13.930	0.974	0.293	0.498	0.770	0.991	0.026	0.000
	100	12.315	0.812	0.337	2.804	0.015	0.996	0.188	0.000
1000	150	13.200	0.880	0.330	1.817	0.150	0.996	0.120	0.000
	200	13.530	0.953	0.290	0.881	0.590	0.996	0.047	0.000
	100	12.295	0.803	0.343	3.159	0.000	0.998	0.198	0.000
2000	150	13.240	0.860	0.347	2.348	0.065	0.998	0.141	0.000
	200	13.450	0.927	0.305	1.295	0.385	0.998	0.073	0.000
				Method:	SPLasso
	100	11.490	1.000	0.124	0.274	1.000	0.997	0.000	0.000
500	150	11.285	1.000	0.111	0.137	1.000	0.997	0.000	0.000
	200	11.155	1.000	0.103	0.064	1.000	0.998	0.000	0.000
	100	11.060	0.990	0.096	0.121	0.995	0.999	0.001	0.000
1000	150	11.035	1.000	0.094	0.060	1.000	0.999	0.000	0.000
	200	11.015	1.000	0.092	0.037	1.000	0.999	0.000	0.000
	100	11.085	0.970	0.097	0.123	0.990	0.999	0.008	0.000
2000	150	11.015	1.000	0.092	0.067	1.000	0.999	0.000	0.000
	200	11.030	1.000	0.093	0.045	1.000	0.999	0.000	0.000

Example 4.2:

In this simulation, we consider a compound symmetry structure for the covariance of the relevant predictors. Specially, the relevant predictors follow the p₀-dimensional multivariate normal distribution . The size of the true model is set to p₀ = 8. The covariance matrix Σ₀ has σ_ii = 1 and σ_ij = 0.5 for 1 ≤ i ≠ j ≤ p₀. The irrelevant predictors X_j are generated as where ε_j are independent and identically distributed with . The nonzero coefficients are generated as (− 1)^V(4n^−0.15 + |T|), where V is a binary random variable with and T is a normal random variable with mean 0 and satisfies . Let the nonlinear component g(U) = exp (3U), a monotone function. The noises ϵ are independent and identically distributed with . The variance σ² is chosen such that is approximately 80%. The simulation results are reported in Table 2.

Table 2. Simulation results for Example 4.2.

p	n	AMS	PDR	FDR	AEE	CP	CZ	IZ	CF
				Method:	PFR
	100	6.875	0.467	0.490	111.060	0.050	0.994	0.533	0.025
500	150	7.255	0.638	0.354	80.577	0.385	0.996	0.363	0.290
	200	7.490	0.658	0.335	55.135	0.540	0.995	0.340	0.500
	100	7.375	0.464	0.516	144.029	0.055	0.996	0.536	0.050
1000	150	6.980	0.523	0.455	114.385	0.230	0.997	0.478	0.180
	200	7.230	0.603	0.380	90.892	0.435	0.998	0.397	0.345
	100	9.150	0.426	0.608	205.817	0.010	0.997	0.574	0.005
2000	150	7.500	0.557	0.452	126.259	0.265	0.998	0.443	0.155
	200	7.475	0.591	0.406	95.332	0.370	0.999	0.409	0.280
				Method:	SPLasso
	100	5.865	0.570	0.281	98.091	0.345	0.997	0.430	0.195
500	150	7.205	0.757	0.218	62.354	0.615	0.998	0.243	0.410
	200	7.760	0.840	0.165	34.328	0.730	0.998	0.160	0.500
	100	6.145	0.561	0.315	116.950	0.355	0.998	0.439	0.155
1000	150	6.580	0.623	0.306	100.934	0.425	0.998	0.378	0.270
	200	7.410	0.741	0.239	70.525	0.590	0.999	0.259	0.380
	100	6.250	0.486	0.375	144.353	0.220	0.999	0.514	0.085
2000	150	7.08	0.666	0.305	106.756	0.500	0.999	0.334	0.250
	200	7.295	0.726	0.250	72.007	0.570	0.999	0.274	0.355

From Tables 1 and 2, we have the comparison results in what follows.

(1)	The irrelevant predictors are equally and almost highly correlated with the relevant predictors in both examples, and SPLasso is always better than PFR. For example, when n = 200, PFR has the CP values at 0.770, 0.590 and 0.385, while SPLasso has the CP values all at 1, for p = 500, 1000 and 2000, respectively, in Table 1.
(2)	Note that the larger PDR values and the smaller FDR values are, the better the associated procedure performs. From this point of view, SPLasso also behaves better than PFR.
(3)	For the fixed p, SPLasso performs better as the sample size increases. It is clear that the coverage probability changes substantially as the sample size increases. In addition, the coverage probability approaches 1 as long as the sample size is enough large. For the fixed n, the finite sample performance of SPLasso becomes worse as the dimension of predictors increases. However, from the variation rate, we note that the performance does not deteriorate rapidly as the dimension p increases. This means that the sample size is more important than the dimension of predictors in ultra-high-dimensional variable screening.
(4)	Note that the proportion of correctly zeros is almost 1. As a result, the average model size is small, and is close to the true model size when the sample size increases. Consequently, the average estimation error decreases as the sample size increases.

In conclusion, the numerical results are in line with the theoretical results that SPLasso contains the true model with probability tending to one. These results demonstrate that SPLasso is one of the best variable screening methods and it can be useful in real data analysis.

5. Real data analysis

We demonstrate the effectiveness of SPLasso by an application to a breast cancer data. As reported in Stewart and Wild (2014), breast cancer is one of the leading causes of cancer death among women, and there were about 1.7 million new cases (25% of all cancers in women) and 0.5 million cancer deaths (15% of all cancer deaths in women) in 2012. Breast cancer is the most common cancer diagnosis in women in 140 countries and is the most frequent cause of cancer mortality in 101 countries. van't Veer et al. (2002) collected the samples from a total of 97 lymph node-negative breast cancer patients under 55 years old. The collected dataset consists of expression levels for 24,481 gene probes and seven clinical risk factors including age, tumour size, histological grade, angioinvasion, lymphocytic infiltration, estrogen receptor (ER) and progesterone receptor status for the 97 participators in this study. Among the 97 participators, 46 developed distant metastases within 5 years and 51 remained metastases free for more than 5 years. Yu, Li, and Ma (2012) proposed a receiver operating characteristic approach to rank the genes by adjusting the clinical risk factors. In addition, they removed the severe missing genes, and obtained an effective number of 24,188 genes. Each data vector is normalised to have sample mean 0 and standard deviation 1.

Knight, Livingston, Gregory, and McGuire (1977) found the absence of estrogen receptor in primary breast tumours is associated with the early recurrence. We are interested in finding genes that are related to the estrogen receptor. We consider the following partially linear model to fit the data: (11) where U is the age of the patients, GE_j is the jth gene.

As in Section 4, the Epanechnikov kernel K(u) = 0.75(1 − u²)₊ and the bandwidth are adopted to fit the nonlinear function, where denotes the sample standard deviation of U. We first compare SPLasso with PFR in terms of the prediction mean squared errors (PMSE) based on 100 random partitions. For each partition, we randomly select 90 observations as the training set and the remaining seven observations as the test set. Based on the training set, we fit the data with the partially linear model (11(11) ) via SPLasso and PFR. The resulting models are used to predict the value of the seven observations in the test set. The five-number summary of the prediction mean squared errors is listed in Table 3. From Table 3, we know that SPLasso is better than PFR in terms of the PMSE.

Table 3. Five-number summary of PMSEs for PFR and SPLasso.

Method	Minimum	First quartile	Median	Third quartile	Maximum
PFR	0.139	0.403	0.602	1.839	3.494
SPLasso	0.130	0.305	0.368	0.478	1.906

We observe that different models are often selected for different random partitions. Table 4 shows the top five genes selected by SPLasso and PFR in the 100 random partitions. Gene 15835 is detected as important at each time among the 100 random partitions by both methods. We note that gene 15835 was also identified in Cheng et al. (2016). In addition, gene 1279 is also identified by both methods. From all these findings, we conclude that gene 15835 is associated with the estrogen receptor.

Table 4. Top five genes selected among 100 random partitions.

PFR	1279	1690	5985	15835	23134
SPLasso	1279	6257	9918	14117	15835

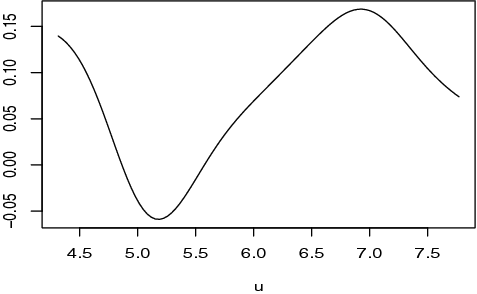
To investigate the estimated nonlinear effects of the patient's age based on one random split in which SPLasso identified two genes 15835 and 14117, we present the estimated nonparametric function in Figure 1. It shows that the patient's age almost has a positive impact on the estrogen receptor. We note that the value of effect first decreases (up to about 5.2), then increases (up to about 7), and then decreases again. Hence, from a practical point of view, we have demonstrated that our proposed SPLasso method can be an efficient method for analysing partially linear models.

Figure 1. The fitted nonlinear function .

6. Conclusion and discussion

In this paper, we propose a SPLasso procedure to screen predictors for ultra-high-dimensional partially linear models, and we further show that SPLasso can identify all relevant predictors with probability tending to one, and that it provides a satisfactory performance in finite samples.

SPLasso selects the next predictor which has the highest correlation with the current residual. It is interesting to point out that LARS proposed by Efron, Hastie, Johnstone, and Tibshirani (2004) also selects the next predictor like SPLasso. However, the current residual of LARS is based on a shrunken estimation of the regression coefficients. The effect of the selected predictors on response variable is not fully used in this estimation. Consequently, this gives a chance for the predictors that have high spurious correlation with predictors in the current model. Simulation studies in Wang (2009) also show that the finite sample performance of LARS is worse than FR. Fitting the response by adding one predictor to the current model, FR selects the next predictor which minimises the residual sum of squares. This amounts to select the next predictor with the largest partial correlation with . It is clear that the difference between SPLasso and PFR is the factor . As a result, if has a higher correlation with the predictors in , it will have priority to be selected by PFR. Therefore, we expect that SPLasso will perform better than the profile LARS (or its variants) and the profile FR.

Finally, we note that the errors are assumed to be homogeneous in the current paper. However, as the heterogeneity is often presented in ultra-high-dimensional data, we will investigate the heterogeneity in our future study by combining the quantile regression with the sequential Lasso. Another interesting direction is to extend SPLasso to other semiparametric models including generalised semiparametric models, varying coefficient models and semi-varying coefficient models.

Acknowledgments

The authors thank the editor, the associate editor and two reviewers for their constructive comments that have led to a substantial improvement of the paper.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

Gaorong Li's research was supported in part by the National Natural Science Foundation of China [number 11471029]. Tiejun Tong's research was supported in part by the National Natural Science Foundation of China [number 11671338] and the Hong Kong Baptist University grants [grant number FRG2/15-16/019], [grant number FRG1/16-17/018].

Notes on contributors

Yujie Li

Yujie Li is a Ph.D. candidate in College of Applied Sciences at Beijing University of Technology. Her research interests are high-dimensional statistics and nonparametric statistics.

Gaorong Li

Gaorong Li is Professor of Statistics, Beijing Institute for Scientific and Engineering Computing at Beijing University of Technology. His major research interests are high-dimensional statistics, nonparametric statistics, statistics learning, empirical likelihood, longitudinal data analysis and measurement error models.

Tiejun Tong

Tiejun Tong is Associate Professor of Statistics in the Department of Mathematics at Hong Kong Baptist University. His major research interests are medical statistics and meta-analysis, high-dimensional data analysis, and nonparametric and semiparametric regression.

Appendices

We introduce the following notation to simplify our presentation. Let ∂|x| be r if x = 0, where r is an arbitrary number with |r| ≤ 1, otherwise be sgn(x). For any set , let , and . For any n-dimensional vectors and , define and . Furthermore, define , and for any candidate model .

Appendix 1. Some lemmas

Lemma A.1:

Suppose that regularity conditions (C3)–(C6) hold. We have (A.1) where is the estimator of E(X_j|U_i), is the estimator of E(Y|U_i) for 1 ≤ i ≤ n and 1 ≤ j ≤ p, and c_n = n^−1/4ln ⁻¹n.

Lemma A.2:

Suppose that regularity conditions (C1) and (C3)–(C6) hold, and let with probability tending to one. Then, (A.2)

The proofs of Lemmas A.1 and A.2 can be found in Liang et al. (2012), and hence we omit the details.

Lemma A.3:

Suppose that regularity conditions (C1) and (C3)–(C6) hold. Then, we have, for 1 ≤ k ≤ K_n,

(1)	, uniformly for all .
(2)	with Dn → ∞.

Proof:

By Lemma A.2, it is easy to obtain that . Hence, we have By the Bonferroni inequality, This leads to the result of (1). Next we prove (2). By some simple calculations, we have (A.3) and (A.4) with . Inequality (A.4(A.4) ) follows the fact that is a sub-matrix of by the inverse of the block matrix. Combining (A.3(A.3) ) and (A.4(A.4) ), we have where . By conditions (C2)–(C3) along with Lemma A.2, we have D_n → ∞. Hence, the proof of (2) is completed.

Lemma A.4:

Let be the index set of the variables being added at the (k + 1)th step of the SPLasso method. There exists a vector with componentwise nonzero elements such that for , where and .

Proof:

Differentiating the objective function with respect to , we have Let the above derivative equal to zero, we can get the following solution: (A.5) Substituting (A.5(A.5) ) into , we obtain is equivalent to solve the following objective function: (A.6) By the KKT condition, (A.6(A.6) ) can reach its minimum at if and only if (A.7) Noting that , we have (A.8) Plugging (A.8(A.8) ) into (A.7(A.7) ), we have (A.9) As is the set of variables being added at the (k + 1)th step, (A.7(A.7) ) holds for some which satisfies and for any . Let λ*_{k + 1} be the corresponding λ in (A.8(A.8) ) for this estimator . Noting that this particular also satisfies (A.7(A.7) ) and (A.9(A.9) ), we have (A.10) (A.11) By (A.10(A.10) ) and the definition of ∂( · ), it is easy to see that . Furthermore, plugging (A.10(A.10) ) into (A.11(A.11) ), it can be shown that is equal to (A.12) where . By some algebraic operations, we have . Plugging this result into (A.12(A.12) ), the proof of Lemma A.4 is completed.

Lemma A.5:

Suppose that regularity conditions (C1)–(C6) hold. If , for 1 ≤ k ≤ K_n − 1, we have

Proof:

We prove this conclusion by contradiction. Assume that there exists k such that . Let . If a_{k + 1} is not unique, we choose one of them. Note that a_{k + 1} may be the index of the predictor being selected at the (k + 2)th step. Let the two terms of in Lemma A.4 as I₁ and I₂, respectively. By Lemma A.3, we have (A.13) By Lemma A.1, it is easy to see that, with probability tending to one, (A.14) For the last two terms of (A.14(A.14) ), if , we have, for any t > 0, with some positive constants c₁ and c₂. Letting t = 4ln n, the right-hand side of the above inequality converges to 0 as n → ∞. Since follows the standard normal distribution, we have This leads to . By the fact that we have

On the other hand, multiplying on both sides of (A.10(A.10) ), by the last equation of Lemma A.4 along with the positivity of the left-hand side, we have (A.15) Noting that and have the same order, by (A.13(A.13) )–(A.15(A.15) ), we have (A.16) Note that (A.17) Hence, . By the above results, we have Therefore, we have , which contradicts with Lemma A.4, that is, the assumption is false. This completes the proof of Lemma A.5.

Appendix 2. Proof of Theorem 3.1

To prove Theorem 3.1, we consider what happens if , that is, there still exist relevant variables, which are not identified after K_n steps. For simplicity, we assume that the variables enter the model one by one. We first focus on the two terms in as in Lemma A.5. Note that (A.18) On the other hand, by Lemma A.5, we have (A.19) Therefore, by (A.3(A.3) ), (A.18(A.18) ), (A.19(A.19) ), with probability tending to one, (A.20)

By some simple calculations, we have (A.21) where the last inequality is obtained by (A.17(A.17) ) and (A.18(A.18) ). Let By (A.20(A.20) ) and (A.21(A.21) ), we have If t_{k, n} → ∞, we have , which contradicts with Lemma A.4. This means that t_{k, n} < ∞. Then, we have . Together with Lemma A.4, we have By this result, we have 0 < t_{k, n} < λ₀ + 1. Using the definition of t_{k, n} in (A.20(A.20) ), we have (A.22) If for 0 ≤ k ≤ K_n − 1, by the Cauchy–Schwarz inequality and (A.4(A.4) ), we can further get Then, (A.23) where . On the other hand, we have (A.24) Under regular conditions (C1)–(C3), and by the definition of K_n, we have It contradicts with the results (A.23(A.23) ) and (A.24(A.24) ), and this means that with probability tending to one. Hence, the proof of Theorem 3.1 is completed.

Appendix 3. Proof of Theorem 3.2

Define . By Theorem 3.1, k_min is well defined and satisfies . For any 1 ≤ k ≤ k_min, are underfitted models such that and are nested. Therefore, if we can prove , the conclusion (10(10) ) will follow. According to Theorem 3.1, with probability tending to one, (A.25)

Next, we study (A.25(A.25) ) under the following two cases. First, if , then by (A.4(A.4) ) and (A.22(A.22) ), with probability tending to one, the right-hand side of (A.25(A.25) ) is bounded below by (A.26) According to the inequality ln (1 + x) ≥ min (ln 2, x/2) and Lemma A.2, the right-hand side of (A.26(A.26) ) is bounded below by, with probability tending to one, (A.27) Under condition (C3), the right-hand side of (A.27(A.27) ) is positive with probability tending to one uniformly for k ≤ k_min.

Second, if , by the fact along with (A.4(A.4) ) and (A.22(A.22) ), with probability tending to one, the right-hand side of (A.25(A.25) ) is bounded below by (A.28) By Lemma A.2, with probability tending to one, the right-hand side of (A.26(A.26) ) is further bounded below by (A.29) Under condition (C3), the right-hand side of (A.25(A.25) ) is positive with probability tending to one uniformly for k ≤ k_min. This finishes the proof of Theorem 3.2.