Statistical analysis of dependent competing risks model in constant stress accelerated life testing with progressive censoring based on copula function

ABSTRACT

In this paper, we consider the statistical analysis for the dependent competing risks model in the constant stress accelerated life testing with Type-II progressive censoring. It is focused on two competing risks from Lomax distribution. The maximum likelihood estimators of the unknown parameters, the acceleration coefficients and the reliability of unit are obtained by using the Bivariate Pareto Copula function and the measure of dependence known as Kendall's tau. In addition, the 95% confidence intervals as well as the coverage percentages are obtained by using Bootstrap-p and Bootstrap-t method. Then, a simulation study is carried out by the Monte Carlo method for different measures of Kendall's tau and different testing schemes. Finally, a real competing risks data is analysed for illustrative purposes. The results indicate that using copula function to deal with the dependent competing risks problems is effective and feasible.

KEYWORDS:

• Dependent competing risks
• Bivariate Pareto Copula
• Kendall's tau
• Bootstrap method
• constant stress accelerated life testing
• maximum likelihood estimators

1. Introduction

In reliability life testing, it is quite common that various competing failure causes may be present at the same time. This problem is known as the competing risks/failure model, which involves multiple failure modes, while only the smallest failure time and the associated failure mode are observed. In practice, competing risks data appears in engineering, biological, social science, medical statistics and other fields; see Beyersmann, Schumacher, and Allignol (2012). Recently years, the statistical inference of competing risks model has been widely studied. Sarhan, Hamilton, and Smith (2010) considered the statistical inference for the unknown parameters in the competing risks models. Mazucheli and Achcar (2011) applied the Lindley distribution to competing risks lifetime data. Wu and Shi (2016) discussed the Bayes estimation for the competing risks model under progressively hybrid censoring with binomial removals. Xu and Zhou (2017) considered the Bayesian analysis of series system whose failure time is assumed to follow a Marshall–Olkin bivariate Weibull distribution. In accelerated life testing (ALT), Balakrishnan and Han (2008), Han and Balakrishnan (2010) combined simple step-stress ALT and competing risks model. The inference for a simple step-stress model with progressively censored competing risks data from Weibull distribution was considered by Liu and Shi (2017).

It can be seen that previous studies have usually considered the causes of failure to be independent, even when the interpretation of the causes implies dependency. Naturally, once independence between risks has been established, it is reasonable to consider a univariate distribution for the lifetimes. However, in fact, the competing risk modes are usually dependent. Thus, the univariate distribution model is not applicable yet. The copula function provides a means to examine the dependence structure between multiple random variables, so it attracts more and more attentions from scientists and technicians engaged in the study of reliability. Muliere and Scarsini (1987) discussed some characterisations of a class of Marshall–Olkin type distributions and introduced the copula of the bivariate distributions functions. Yi and Wei (2007) studied on the reliability of dependent parts vote unit based on copula functions. The reliability of k-out-of-n:G supply chain unit and dependent failure units based on copula were discussed by Jia and colleagues (Jia & Cui, 2012; Jia, Wang, & Wei, 2014). Dimitrova, Haberman, and Kaishev (2013) expressed the dependence of lifetimes using multivariate copula function and studied the dependent competing risks model of human mortality. Many papers about copulas can be referred, such as Aristidis (2013), Cheng, Zhou, Chen, and Zhuang (2014), Grothe and Hofert (2015) and so on.

Recently, the copula theory has become a hot topic in ALT to research the characters of products with dependent competing risks model, but related literatures are very few. Xu and Tang (2012) researched the statistical analysis of competing failure modes in ALT base on copulas. The statistical inference of ALT with dependent competing failures based on copula theory can refer to Zhang, Shang, Chen, Zhang, and Wang (2014). Wu, Shi, and Zhang (2017) discussed the statistical analysis of dependent competing risks model in ALT using copula function based on progressively hybrid censored data. Although some papers have discussed the statistical inference for estimating parameters from different lifetime distributions based on dependent competing risks model, the dependent competing risks model about Pareto type distribution in ALT has not been considered yet.

The Pareto type distribution was proposed by Pareto (1987), which was used to model the unequal distribution of personal income and wealth. Many scholars have discussed the applications of Pareto type distribution in reliability. Sarhan and El-Gohary (2003) developed the maximum likelihood and Bayes estimators for the parameters in Pareto reliability model with masked data. The latest papers can refer to Bourguignon, Saulo, and Fernandez (2016), Dixit and Nooghabi (2010), Fernández (2014) and so on. There is a hierarchy of Pareto distributions known as Pareto Type I, II, III and IV, where the Lomax distribution is a special case of Pareto Type II distribution and its support begins at zero. The Lomax distribution has a long heavy tail and a wide application in economics, business, insurance, reliability, engineering, finance and related fields. The Lomax distribution has been studied by many scholars, such as Cramer and Schmiedt (2011), Helu, Samawi, and Raqab (2015), Yang, Wei, and Fan (2014), etc.

Considering the above-mentioned papers, in this paper, we analyse the lifetime data with dependent competing risks model in CSALT under Type-II progressive censoring based on copula theory. The failure time of the unit due to one of the failure modes follows to a Lomax distribution. The joint distribution function is expressed by marginal functions and Bivariate Pareto Copula. The rest of this paper is organised as follows. In Section 2, the copula theory and their characters are introduced. The dependent competing risks model under CSALT Type-II censoring is constructed, and the basic assumptions and the maximum likelihood estimators (MLEs) of the model parameters are presented in Section 3. Bootstrap-p and Bootstrap-t methods are used to construct the confidence intervals (CIs) for model parameters in Section 4. We carry out several numerical simulations for illustrative purposes in Section 5. An analysis about competing risks data using the proposed model is shown in Section 6. Some conclusions appear in Section 7.

2. Copula theory

2.1. Bivariate copula function

Theorem 2.1

(Sklar's theorem) (Nelsen, 2006): Let H be a joint distribution function with marginal functions F and G. Then there exists a copula function C such that for all x, y in , (2.1)

If F and G are continuous, then C is unique; otherwise, C is unique on RanF × RanG, where RanF(x) is the domain of function F(x). Conversely, if C is a copula, F and G are distribution functions, then the function H defined by Equation (2.1(2.1) ) is a joint distribution with marginal functions F and G.

Let C(u, v) be a bivariate copula for u, v in , if replace C, u, v, the function is called survival copula and meets the following formulas:(2.2)

Let be the joint survival function of C, then we have(2.3)

More properties about copula please refer to Balakrishnan and Lai (2009) and Nelsen (2006).

2.2. Archimedean copula

In some situations, there is a function ϕ satisfiesthen the copula function with the above expression is called Archimedean copula. To solve C, we need to find an appropriately defined ‘inverse’ function ϕ^{[ − 1]}, such that

If ϕ(t) = t^{− 1/θ} − 1, θ ⩾ 1, then(2.4) Equation (2.4)(2.4) is called Bivariate Pareto Copula (BPC).

2.3. Measure of association

There are many kinds of copulas, and different copulas have different parameters; hence, these copulas are not comparable. In order to compare them, the Kendall's tau can be considered. In the meaning of copula, Kendall's tau can be written as follows:(2.5)

If C is an Archimedean copula, then Equation (2.5(2.5) ) is rewritten as(2.6)

Thus, the Kendall's tau of BPC is τ = 1/(2θ + 1).

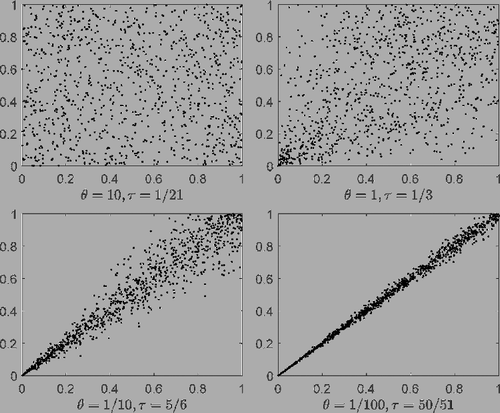
To illustrate the dependent relationship of BPC, the scatter plots of BPC with different Kendall's tau are shown in Figure 1. From Figure 1, we conclude that the dependency becomes higher when theta tends to be zero.

Figure 1. Scatter plots of BMP with different Kendall's tau.

3. Maximum likelihood estimations

In this section, we analyse the data with dependent competing risks by using an assumed copula function in CSALT under Type-II progressive censoring scheme (PCS). Under a k constant stress levels ALT, s₁ < s₂ < ⋅⋅⋅ < s_k are accelerated stress levels and s₀ is the normal stress level. The Type-II PCS can be described as: at each stress level s_i, i = 1, 2, …, k, suppose there are n_i identical units are put into the life test with PCS. When the first failure time t_i1 is observed, R_i1 survivals are randomly removed from the remaining n_i − 1 units. At the second failure time t_i2 is observed, R_i2 survivals are randomly removed from the remaining n_i − R_i1 − 2 units. And so on, until the r_ith failure time is observed, all of the remaining units are removed and the testing is terminated. Then we obtain the failure data , where and c_il take any number in the set of {1, 2}, and c_il = j, j = 1, 2 indicates that the failure is caused by failure mode j.

3.1. Basic assumptions

A1. Only one of the two competing risk modes causes the unit failure. The dependence of two competing risk modes and their survival copula function are given in Equation (2.4(2.4) ), and their lifetimes are T₁andT₂, respectively. So the lifetime of a unit is T = min (T₁, T₂).

A2. Under stress level s_i, the failure time of the unit due to risk mode j, denoted by T_ij, which follows a Lomax distribution Lo(m_ij, τ_ij) with shape parameter m_ij and scale parameter τ_ij. The probability density function and survival function are given as follows:

A3. The failure mechanisms are the same under different stress levels. Because the shape parameters reflect the failure mechanism, that is, they have the same shape parameter m_ij = m_j(i = 0, 1, …, k; j = 1, 2). In practical tests, to ensure the failure mechanism is constant, the highest stress level s_k should be less than the extreme stress level s_max which cannot change the failure mechanism of the units.

According to A1–A3, we can obtain the survival function of the unit under stress s_i as follows:(3.1)

A4. Under stress level s_i, the accelerated life equation of the jth failure mechanism(3.2) where a_j, b_j are unknown coefficients and ϕ(s) is a given function of the stress level s.

3.2. Maximum likelihood estimation

Under stress level s_i, let q_ij denote the failure number caused by jth failure mode, namely(3.3) when δ₁(c_il) = 1, t_il is the failure time caused by failure mode 1, and when δ₂(c_il) = 1, t_il is the failure time due to failure mode 2. Thus, the likelihood function under stress level s_i is (3.4)

Based on Equations (2.4)(2.4) , (3.1(3.1) ) and (3.3(3.3) ), L_i can be written as

The full likelihood function is , and the log-likelihood function is

By setting the first partial derivative of log L with respect to the parameters m_j, τ_ij, θ to zero, the likelihood equations are derived as(3.5) (3.6) (3.7)

As the MLEs are hard to be solved analytically from Equations (3.5)(3.5) –(3.7(3.7) ), numerical methods can be considered, such as Newton–Raphson iteration method or other iteration methods.

4. Confidence intervals and reliability estimation of unit

From the above analysis, the exact CIs of m_j, τ_ij, θ(i = 1, 2, 3; j = 1, 2) are hard to get, so we can consider the Bootstrap method.

4.1. Bootstrap-p method

• Step 1: Given n_i, r_i, i = 1, 2, …, k and progressive censored sample , compute the MLEs of unknown parameters m_j, τ_ij, θ based on the Type-II progressive censored data .

• Step 2: Generate a bootstrap sample by using and . Obtain the bootstrap estimators of m_j, τ_ij, θ, say , by using the bootstrap sample.

• Step 3: Repeat Step 2 N times, N estimators can be obtained.

• Step 4: Arrange in ascending order to obtain

• Step 5: The approximate 100(1 − α)% CIs of m_j, τ_ij, θ are given by

4.2. Bootstrap-t method

• Step 1: Given n_i, r_i, i = 1, 2, …, k and progressive censored sample , compute the MLEs of unknown parameters m_j, τ_ij, θ based on the Type-II progressive censored data .

• Step 2:Generate a bootstrap sample by using and . Obtain the bootstrap estimators of m_j, τ_ij, θ, say , by using the bootstrap sample.

• Step 3:Compute , where D*_ij represents the totally observed failure numbers due to failure cause j under the stress level s_i, and .

• Step 4:Let . Repeat Steps 2 and 3 N times, and we can get N values .

• Step 5:Arrange in ascending order, then

• Step 6:The two-sided 100(1 − α)% CIs for parameters m_j, τ_ij, θ are given by

4.3. Reliability estimation of unit

According to A4, the least squares estimators of a_j, b_j from the Gauss–Markov theorem are(4.1) where .

Hence, under the normal stress level s₀, the shape parameter under failure mode j is

Thus, the reliability estimator of unit is

5. Numerical simulation

Consider a three-level constant stress ALT with two dependent competing risks modes under Type-II PCS. Select the temperature as the stress level, and suppose the normal stress level and the accelerated stress levels are 25, 60, 90 and 120 °C, respectively, namely s₀ = 298.15 K, s₁ = 333.15 K, s₂ = 363.15 K, s₃ = 393.15 K, and the accelerated function is ϕ(s) = 1/s. Given the values of parameters a₁ = −3, b₁ = 1640, a₂ = −4, b₂ = 2000, m₁ = 2, m₂ = 1.8, then we can obtain that the true values of shape parameters under three stress levels are τ₁₁ = 6.8395, τ₁₂ = 7.4135, τ₂₁ = 4.5542, τ₂₂ = 4.5148, τ₃₁ = 3.2266, τ₃₂ = 2.9657.

Take the sample sizes under each stress level s_i(i = 1, 2, 3) as n₁ = 20, n₂ = 40, n₃ = 80; the numbers of failure are (r₁, r₂, r₃) = (6, 12, 24) and (r₁, r₂, r₃) = (12, 24, 48). The pre-fixed sampling schemes are given in Table 1.

Table 1. The pre-fixed sampling scheme.

Case	n1	r1		n2	r2		n3	r3
I	20	6	(3,2,2,3,2,2)	40	12	(3,2,2,…, 3,2,2)	80	24	(3,2,2,…, 3,2,2)
II	20	12	(1,1,0,…1,1,0)	40	24	(1,1,0,…1,1,0)	80	48	(1,1,0,…1,1,0)

Considering two competing risks modes and the dependence structure is determined by BPC. Thus, the accelerated function under the stress level s_i based on Arrhenius formula is

5.1. Data generation and results analysis

The copula function of (U_i1, V_i2) is BPC C(u, v); let c_u(v) = ∂C(u, v)/∂u. Under stress level s_i, the failure data can be generated as follows:

• Step 1: Generate n_i independent uniform (0,1) vectors (U^(k)_i1, Z_i2^(k)), k = 1, 2, …, n_i;

• Step 2: Calculate V^(k)_i2 = c_u^{− 1}(Z^(k)_i2), then (U^(k)_i1, V_i2^(k)) is the data of C(u, v), where c^{− 1}_u( · ) is the pseudo-inverse of c_u( · );

• Step 3: Let ;

• Step 4: Obtain (t_ij, δ_ij) = (min (x^(k)_i1, x^(k)_i2), I(x^(k)_i1 < x_i2^(k))), j = 1, 2, …, n_i;

• Step 5: Sort the data (t_ij, δ_ij) by their times t_ij in an increasing order. Choose r_i data according to the characteristic of the Type-II PCS. Then we can obtain the needed data (t_il, δ_il), l = 1, 2, …, r_i under the stress level s_i.

The Kendall's tau τ = 1/3, 1/5 when given different relation coefficients θ = 1, 2. Based on the generated competing failure data, the MLEs of the unknown parameters, the mean square errors (MSEs), the 95% confidence intervals of Bootstrap-p (BPCIs) and Bootstrap-t (BTCIs), as well as the coverage percentages (CPs) are computed through 1000 times simulations. The numerical simulation results are shown in Tables 2–5.

Table 2. Average MLEs, MSEs, BPCIs, BTCIs and CPs under different stress levels in two cases when (τ₁₁, τ₁₂, τ₂₁, τ₂₂, τ₃₁, τ₃₂) = (6.8395, 7.4135, 4.5542, 4.5148, 3.2266, 2.9657), (m₁, m₂) = (2, 1.8), θ = 1.

Testing plan	Case I			Case II
Parameters	MLEs (MSEs)	BPCIs CPs	BTCIs CPs	MLEs (MSEs)	BPCIs CPs	BTCIs CPs
τ11	7.2510 (1.1125)	(4.5621, 9.5124) 0.9270	(3.9894, 9.2511) 0.9350	6.9211 (1.1054)	(4.6785, 9.5211) 0.9520	(3.9032, 8.4577) 0.9460
τ12	7.3589 (1.1547)	(4.4325, 9.8014) 0.9370	(3.7854, 8.9602) 0.9420	7.4874 (1.0201)	(4.6987,9.0003) 0.9580	(3.1245, 8.3211) 0.9610
τ21	4.6720 (0.8965)	(2.9685, 6.1714) 0.9250	(1.4214, 6.2387) 0.9460	4.5966 (0.8108)	(2.8857, 6.0032) 0.9600	(1.7754, 5.2018) 0.9440
τ22	4.4547 (0.8487)	(2.6598, 6.1469) 0.9350	(2.0521, 5.8715) 0.9340	4.4987 (0.7856)	(2.6098, 6.0122) 0.9550	(1.5987, 5.2705) 0.9450
τ31	3.4369 (0.7544)	(1.4102, 4.5368) 0.9310	(0.8547, 3.9874) 0.9260	3.3022 (0.7091)	(1.6987, 4.0789) 0.9520	(0.8074, 4.0221) 0.9460
τ32	3.3897 (0.8217)	(1.1478, 4.3698) 0.9340	(0.8854, 3.6597) 0.9400	3.1986 (0.6855)	(1.2587, 4.0538) 0.9320	(0.0024, 3.9608) 0.9480
m1	2.2147 (0.3698)	(1.3864, 3.1153) 0.9380	(0.5960, 2.4712) 0.9490	1.9849 (0.2098)	(1.5584, 2.4001) 0.9510	(0.9806, 2.2644) 0.9450
m2	1.9025 (0.3001)	(1.1054, 2.4987) 0.9460	(0.7785, 2.0956) 0.9440	1.8547 (0.1935)	(1.2547, 2.3365) 0.9340	(0.8857, 2.2579) 0.9590
θ	1.1125 (0.4035)	(0.5986,1.4335) 0.9120	(0.6784,1.5698) 0.9200	1.0986 (0.3051)	(0.4725,1.1989) 0.9350	(0.0035,1.2966) 0.9410

Table 3. Estimators of acceleration coefficients in two cases when (a₁, a₂, b₁, b₂) = ( − 3, −4, 1640, 2000), θ = 1.

Testing plan	Parameters	a1	a2	b1	b2
Case I	MLE	−3.5687	−4.6520	1877	2204
	MSE	1.5406	1.8744	502	621
Case II	MLE	−3.4322	−4.1279	1774	2078
	MSE	1.1254	1.4511	442	549

Table 4. Average MLEs, MSEs, BPCIs, BTCIs and CPs under different stress levels in two cases when (τ₁₁, τ₁₂, τ₂₁, τ₂₂, τ₃₁, τ₃₂) = (6.8395, 7.4135, 4.5542, 4.5148, 3.2266, 2.9657), (m₁, m₂) = (2, 1.8), θ = 2.

Testing plan	Case I			Case II
Parameters	MLEs (MSEs)	BPCIs CPs	BTCIs CPs	MLEs (MSEs)	BPCIs CPs	BTCIs CPs
τ11	7.1145 (1.4571)	(4.2510, 9.7225) 0.9350	(1.7985, 8.3328) 0.9270	7.0504 (1.2589)	(4.3396, 9.0957) 0.9410	(1.8500, 8.7336) 0.9500
τ12	7.6637 (1.6987)	(4.0327, 10.8998) 0.9400	(1.7985, 8.5698) 0.9430	7.4478 (1.1250)	(4.6587, 9.9965) 0.9360	(2.3321,8.9633) 0.9420
τ21	4.7666 (0.9718)	(2.9605, 6.7854) 0.9290	(1.4533, 5.9632) 0.9410	4.6547 (0.9411)	(3.0958, 6.1579) 0.9570	(1.9658, 5.3366) 0.9600
τ22	4.8041 (0.8741)	(2.9687, 6.7441) 0.9490	(1.5784, 5.7789) 0.9300	4.5987 (0.7985)	(3.0052,5.6985) 0.9480	(1.2258, 5.4369) 0.9620
τ31	3.5625 (0.7554)	(1.4874, 4.9052) 0.9340	(0.5698, 3.8471) 0.9260	3.2987 (0.6985)	(1.6548, 4.7752) 0.9440	(0.8890, 3.9961) 0.9350
τ32	3.2598 (0.7114)	(1.1784, 4.3598) 0.9360	(0.4747, 3.9652) 0.9380	2.8741 (0.6621)	(1.1056, 3.8714) 0.9540	(0.5269, 3.2458) 0.9470
m1	2.2544 (0.4521)	(1.0537, 3.2210) 0.9420	(0.3524, 2.6754) 0.9370	1.8896 (0.3002)	(1.1025, 2.6524) 0.9550	(1.0024, 2.1108) 0.9480
m2	1.9587 (0.3002)	(1.1574, 2.3305) 0.9430	(0.8451, 2.2732) 0.9320	1.7099 (0.2457)	(0.9762, 2.2487) 0.9470	(0.6785, 2.1017) 0.9510
θ	2.1132 (0.4322)	(1.2587,2.9645) 0.9250	(0.9352,2.6147) 0.9330	1.9365 (0.2874)	(1.4520,2.7855) 0.9420	(0.8695,2.3369) 0.9380

Table 5. Estimators of acceleration coefficients in two cases when (a₁, a₂, b₁, b₂) = ( − 3, −4, 1640, 2000), θ = 2.

Testing plan	Parameters	a1	a2	b1	b2
Case I	MLE	−3.5471	−4.6300	1799	2214
	MSE	1.4578	1.8957	549	633
Case II	MLE	−3.3369	−4.4722	1687	2143
	MSE	1.2547	1.5897	451	578

From the tables, some conclusions can be obtained as follows:

(1)	The MLEs of the unknown parameters are better when the effective sample size is larger.
(2)	The MSEs of the unknown parameters are close to zero when the sample size becomes larger.
(3)	The CPs of the unknown parameters are close to 0.95 when the effective sample size gets larger.

5.2. Reliability analysis of unit

Given the parameters of lifetime distribution functions and the coefficients of accelerated functions, the true values and the estimators of reliability function of the unit at any time t are the reliability function of unit when the failure causes are independent is

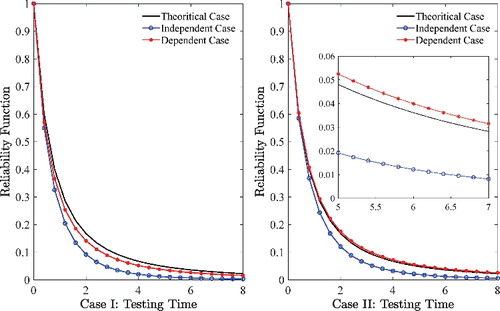
Figures 2 and 3 give the trends of three reliability functions over time in Case I and Case II when θ = 1, respectively.

Figure 2. Comparison of three reliability functions when θ = 1.

Figure 3. Comparison of three reliability functions when θ = 2.

From Case I of Figure 2, we can find that the estimators of reliability are close to the true values, while the values in independent case are far away from the true values. According to Case II, the curves of three reliability functions are very close, as time goes on, the estimators of dependent case close to the true values, but the values in independent case are far away from the true values. In this example, the independent case is lower than the dependent case.

From Figure 3, we can get the same conclusions like Figure 2. Due to the different correlation coefficients, it may estimate lower when considering the dependent competing risks modes as independent in our simulation cases.

6. Illustrative example

In this section, an example is presented to support the proposed model and methods. The data-set includes the accelerated failure times and failure causes in bivariate dependent competing risks model, which was presented in Wu et al. (2017), and Zhang, Shi, Bai, and Fu (2017) also analysed this data-set. In the data-set, the accelerated stress is the temperature; there are three accelerated stress levels, namely, s₁ = 303 K, s₂ = 333 K and s₃ = 363 K. The normal stress level is s₀ = 278 K. At each stress level s_i, n_i = 20 units are put into the life testing for i = 1, 2, 3. The numbers of failures and removals are and . The accelerated function with ϕ(s_i) = 1/s_i is used to extrapolate the estimators of unknown parameters at normal stress level s₀. From Equations (3.5)(3.5) –(3.7(3.7) ), the MLEs, BPCIs and BTCIs of unknown parameters are obtained, and the dependent coefficient and the results are presented in Table 6.

Table 6. MLEs, BPCIs and BTCIs of unknown parameters.

Parameters	MLEs	BPCIs	BTCIs
τ11	1437	(896, 2033)	(678, 1901)
τ12	2549	(1344, 3908)	(1058, 3569)
τ21	1278	(960, 1672)	(804, 1578)
τ22	1931	(1158, 2930)	(908, 2631)
τ31	783	(502, 1116)	(433, 1027)
τ32	872	(638, 1305)	(529, 1192)
m1	89.04	(61.77, 115.69)	(58.74, 104.13)
m2	116.90	(78.52, 160.24)	(69.88, 148.71)
θ	1.4320	(1.2580, 1.6323)	(1.1982, 1.5411)

Then we can calculate the estimators of the acceleration coefficients a₁, a₂, b₁ and b₂ by using Equation (4.1)(4.1) , . And the estimators of unknown parameters under stress level s₀ can be obtained as .

7. Conclusions

ALT is an important testing scheme to obtain the lifetime data of units. Since the failure causes of the unit are manifold and it is not completely independent among these failure causes. Thus, it is very meaningful to consider the dependent competing risks modes in ALT. In this paper, we consider the dependent competing risks model with two failure modes, and some simulations are given under the Type-II censoring ALT. According to the results, we find it advantageous to analyse the failure data of dependent competing risks modes by using copula theory, which avoids the reliability estimators of unit too high or too low. The copula theory provides an effective and feasible basis in theory to analyse the reliability of components and units in the future and has some theoretic meaning and applied values.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work is supported by the National Natural Science Foundation of China [grant number 71571144], [grant number 71401134], [grant number 71171164], [grant number 11701406]; Natural Science Basic Research Program of Shaanxi Province [grant number 2015JM1003]; Program of International Cooperation and Exchanges in Science and Technology Funded by Shaanxi Province [grant number 2016KW-033].