Step-stress accelerated degradation test planning based on Wiener process with correlation

ABSTRACT

To assess the lifetime distribution of highly reliable or expensive product, one of the most commonly used strategies is to construct step-stress accelerated degradation test (SSADT) which can curtail the test duration and reduce the test cost. In reality, it is not unusual for a unit with a higher degradation rate which exhibits a more volatile degradation path. Recently, Ye, Chen, and Shen [(2015). A new class of Wiener process models for degradation analysis. Reliability Engineering and System Safety, 139, 58–67] proposed a Wiener process to capture the positive correlation between the drift rate and the volatility. In this paper, an optimal SSADT plan is developed under the assumption that the underlying degradation path follows the Wiener process with correlation. Firstly, the stochastic diffusion process is introduced to model a typical SSADT problem. Then the design variables, including the sample size, the measurement frequency and the numbers of measurements under each stress level, are optimised by minimising the asymptotic variance of the estimated p-percentile of the product's lifetime distribution subject to the total experimental cost not exceeding a pre-specified budget. Finally, a numerical example is presented to illustrate the proposed method.

KEYWORDS:

• Step-stress accelerated degradation test
• Wiener process
• correlation
• optimal test plan

1. Introduction

With the rapid development of modern technology, the reliability of newly designed products has been greatly improved. Accordingly, reliability assessment has become a critical and challenging task for such highly reliable products. The traditional accelerated life test is a commonly used approach that records only time-to-failure data under harsher conditions (such as higher temperature, voltage, pressure and vibration). For highly reliable products, however, a failure phenomenon is difficult to appear during a short period of time. In such restraints, if there are some quality characteristics of the product, which can reflect the variety of product properties and can be easily observed within the product degradation process. Then collecting these degradation data at higher stress level is an alternative approach to predict the product's lifetime information under normal operating conditions. Such an experiment is called as an accelerated degradation test (ADT). In this respect, it is worth mentioning the monographs by Nelson (1990) and Meeker and Escobar (1998).

Research on statistical inference for data from ADT or the optimal design of an ADT experiment has been done by numerous authors. Among these, a famous degradation model is the Wiener process with positive drifts, which means the degradation increment is independent and normally distributed due to the law of large numbers. Doksum and Normand (1995) used the Wiener process to describe a biomarker series, and they assumed that the drifts are the function of stress levels (also called covariates). Similar assumptions to incorporate covariates in the Wiener process can be found in Park and Padgett (2006), Pan and Balakrishnan (2010), Lim and Yum (2011), Lim (2012) and Guan et al. (2015). In addition, it is to be remarked that the Gamma process and the inverse Gaussian process have also wide applications in degradation data analysis. See Ye and Chen (2014), Ye et al. (2014), Guida et al. (2018) and among others, for some recent references.

According to different stress loadings, ADTs can be classified into constant-stress ADT (CSADT), step-stress ADT (SSADT) and progressive-stress ADT . Here, CSADT is the most popular method in practical applications. However, it usually needs a number of products to proceed the experiment. For instance, we consider a 3-level CSADT with 25 test units allocated at each stress level, then 3 accelerated loading devices and 75 test units are needed to complete the experiment. In general, it may not be possible to obtain so many test units because of the constraint of the manufacturing costs. To overcome this problem, Tseng and Wen (2000) proposed the SSADT, which is a special type of stress loading in which all units are tested together and the stress level is increased step by step until the experiment is completed. Clearly, the advantage of the SSADT is that only a few test units are needed to collect degradation data.

It is well known that a careful choice of design can improve the quality of statistical analysis substantially, and therefore, the optimal design problem of an SSADT experiment received considerable attention in the literature. For example, Liao and Tseng (2006) designed an optimal SSADT by minimising the variance of the estimated p-percentile subject to constraint on the total cost. Tseng et al. (2009) provided an optimal SSADT plan by minimising the asymptotic variance of the estimated mean-time-to-failure (MTTF) under the same cost constraint. A Bayesian methodology for designing SSADT has been presented by Li et al. (2015) using Kullback–Leibler divergence as the optimality criterion. For more recent developments on this topic, one may refer to Pan and Sun (2014), Hamada (2015), Hu et al. (2015), Sung and Yum (2016), Wang et al. (2016) and Kim and Sung (2017).

For many products, it is not uncommon to see that a unit with a higher degradation rate would possess a larger degradation variation (see, e.g. Ye et al., 2015). In general, the Gamma process model and the inverse Gaussian process model can be used to show the positive correlation between the drift rate and the volatility. However, the existing Wiener process models fail to capture such an important relation. In order to fill the gap, Ye et al. (2015) proposed a new class of Wiener process to describe the degradation path. The degradation characteristic with at time t can be expressed as (1) where η is the drift parameter reflecting the effect of stress level in the ADT model, which determines the degradation rate of the products, is a monotone increasing function with , σ is an unknown parameter and is a standard Brownian motion. It is easily seen that model (1(1) ) is slightly different from the typical Wiener process (see Whitmore and Schenkelberg, 1997) given by (2) and implies the positive correlation by setting the volatility parameter as .

To the best of our knowledge, no research focuses on the modelling and design problems of the SSADT for the Wiener process with correlation. The purpose of the present paper is to extend the recent result of Ye et al. (2015) to model a typical SSADT problem using the Wiener process model (1(1) ), and an optimal SSADT plan for the degradation data based on Wiener process model (1(1) ) is developed. Several design variables, including the sample size, the measurement frequency and the numbers of measurements under each stress level, are to be determined by minimising the asymptotic variance of the estimated p-percentile of the product's lifetime distribution under the total cost constraints.

The rest of this paper is structured as follows. In Section 2, the SSADT model based on the Wiener process with correlation is described and several assumptions are given. In Section 3, the optimisation problem for the SSADT is constructed and the detailed algorithm is developed to solve this problem. In Section 4, a pilot study is carried out to show the performance of the proposed method. Some concluding remarks are given in Section 5.

2. The stochastic SSADT model

Suppose that the degradation follows Wiener process model (1(1) ), and the time-to-failure is defined as the moment that the corresponding degradation process first reaches a pre-specified failure threshold , say τ, then It is readily shown that conforms to the inverse Gaussian distribution. But the p-quantile of the inverse Gaussian distribution does not have an analytic form. By Padgett and Tomlinson (2004) and Ye et al. (2015), when the lifetime is large enough the approximate form of the p-quantile of τ can be expressed as (3) To assess the reliability of the product, we want to design an efficient SSADT experiment under some constraints, so that the p-quantile of the lifetime distribution of the product can be predicted as precisely as possible. Let denote m higher accelerating stress levels such that where denotes the normal usage stress level. Then an SSADT experiment can be expressed as follows: firstly, we assume that there are n units available for a degradation test that uses stress level , and the measurement frequency and the number of measurements under the stress are f and , respectively. Thus, the duration time under the stress is . Then we increase the stress level to , and the duration time is up to . Continue the process until the stress is up to , and the experiment is terminated at . Consequently, the testing stress S of an SSADT experiment can be described as It is well known that the accelerating stress S can affect the degradation process of the product. Given , then we have (4) Furthermore, the following assumptions and will be considered in this paper.

A1: The degradation under each stress follows a normal distribution with mean and variance . For simplicity, it is assumed that , where is a constant.

A2: The relationship between and the stress level is log-linear. Then, after standardising the stress levels, we have (5) where a and b>0 are unknown parameters to be estimated, and . Usually, the typical inverse power law relation, the Arrhenius relation and the exponential relation are included in the assumption . For more details, see Xu and Tang (2015) and Ye et al. (2014).

Let be the degradation path of an SSADT based on Wiener process model (1(1) ), and , the equivalent starting time of the degradation process under stress level with . Then, the relationship between and , , can be expressed as It is easy to see that the equivalent degradation time under stress contains the accumulated amount of degradation from t=0 to the end of degradation test under stress , which satisfies According to Equations (4(4) ) and (5(5) ), we have (6) which yields (7) It follows from Equation (7(7) ) that (8) Thus, the distribution of the degradation at time can be written in the following unified form: (9) where (10)

3. Optimal test plan

Based on the SSADT modelling above, we now consider the optimisation problem of determining the sample size n, the measurement frequency f and the measurement times within the stress level , , by minimising the asymptotic variance of the estimated under the usage stress subject to a pre-specified total cost. Therefore, the framework for accomplishing the optimisation problem includes the following three main parts: (i) the estimation of the model parameters by using the maximum-likelihood estimator (MLE) method; (ii) the computation of the asymptotic variance of under the usage stress and (iii) the definition of the total cost function.

3.1. Parameters estimation

Let be a set of observed SSADT paths from Wiener process model (1(1) ), where , , , and with . According to Equation (9(9) ), we obtain that where (11) Because the degradation of the product follows Wiener process model (1(1) ) under the different stress , then each independent increment conforms to the normal distribution, which is where , Moreover, 's are mutually independent. Thus, the likelihood function of θ is given by (12) Then, the MLE of θ can be obtained by a numerical optimisation approach after logarithm transformation. Substituting the MLE into Equations (3(3) ) and (5(5) ), we can obtain the estimator of under the normal operating stress .

3.2. Computation of AVar

Based on the assumption in Section 2, the approximated p-quantile of the lifetime distribution of the product under the usage stress can be readily obtained, i.e., (13) By the delta method, the asymptotic variance of can be expressed as where is the gradient vector of with respect to , i.e., (14) and is the Fisher information matrix of θ, i.e., where denotes the log-likelihood function of θ, up to a constant, which is given by The detailed expressions for all the elements of and are listed in the appendix.

3.3. The cost function

Similar to Liao and Tseng (2006), we define the total cost of conducting the SSADT experiment as (15) which includes three principal forms of the experimental cost as follows: (i) the cost of conducting the experiment , where denotes the unit cost of operation per time; (ii) the cost of measurement , where denotes the unit cost of measurement and (iii) the cost of testing the devices , where denotes the unit cost for each test device.

3.4. Optimisation model and algorithm

Let denotes the total experimental budget, then the constraint in the SSADT plan is that the total experimental cost TC does not exceed the pre-specified budget . Therefore, the optimisation problem can be written as

Minimise: AVar,

Subject to: where .

In fact, due to the complexity of the objective function, the solution of the above optimisation problem does not have an analytic expression. However, with the simplicity in the structure of the constraint, and the integer restriction on the decision variables, the optimal solution can be obtained easily by using the following algorithm.

Step 1: Set , where is the largest integer that is not greater than x, and is the largest possible number for n when f=1, and for .

Step 2: Let n=1.

Step 3: Set , where is the largest possible number for f when for , under fixed n.

Step 4: Let f=1.

Step 5: Find such that

Step 6: Compute AVar by .

Step 7: Set f=f+1, and repeat steps 5 and 6 until .

Step 8: Set n=n+1, and repeat steps 3 and 7 until .

Step 9: The optimal solution can then be obtained by minimising AVar.

It should be pointed out that the asymptotic variance AVar is the function of the parameters θ given the design variables . Therefore, it is necessary to give an initial value of the parameter in order to determine the optimal plan. In practical applications, initial values could be obtained from the previous experience or engineering judgement. For illustrative purpose, we adopt a pilot study to evaluate the performance of the proposed SSADT optimal plan in the next section.

4. Illustrative examples

In this section, we illustrate the proposed procedure with the degradation data of light-emitting diodes (LEDs) in Hamada et al. (2008, p. 290). In the experiment, 25 LEDs were observed at , and , respectively, and the luminosity data of each LED product were collected at 29 inspection times. It was assumed that the standard operating temperature was . An LED fails when the LED relative luminosity drops to 0.5, i.e., 50% of initial luminosity. In order to capture the degradation path of the LED products by the Wiener process with correlation, a logarithm transformation for degradation data is considered, then the threshold value ω is equivalent to . Furthermore, let , and the Arrhenius relationship is assumed between the parameter η and the temperature.

To assess the goodness of fit between the Wiener process with correlation and the general Wiener process for the data from the CSADT, the AIC is employed, where the AIC is defined to be with k the number of parameters and ℓ the maximised value of the likelihood function of the model. Then the MLEs of the model parameters and the corresponding values of the AIC are calculated and given in Table 1. From Table 1, we can see that the degradation model based on the Wiener process with correlation fits the data better.

Table 1. MLEs and AIC of two different Wiener process models for the LEDs' data.

	a	b			β		AIC
		1.3035	12,819.21	–	1.4916	1594.93
		2.3262	–		1.4445	1502.81

In the following, we use the MLEs of the parameters in model as the true values, then a pilot study is developed, and a corresponding SSADT experiment is arranged to estimate the model parameters. By applying the Monte Carlo method, a set of SSADT data are generated based on two stress levels and . Also we set , , unit time is 4 (in hours), and the numbers of measurements for and are and , respectively. Then, the MLE of θ can be obtained directly from Equation (12(12) ), which is It can be observed that the estimation and the true values are nearly the same. Now, we use the estimation to compute the asymptotic variance of in the optimisation problem accordingly.

For illustrative purposes, we assume that the cost configurations of , and are respectively. Under a pre-specified budget , an optimal SSADT plan with m higher stress levels can be determined by using the algorithm given in Section 3. In the following, we will mainly discuss the optimal design for the cases of m=2 and m=3.

4.1. Optimal SSADT plan for m=2

Suppose that two higher stress levels are set as and . Then the design variables are , which can be determined under different budget constraint . The results are summarized in Table 2. For instance, the optimal test plan is when , which means that the optimal sample size is 6, and the optimal measurement frequency is hours. The corresponding optimal numbers of measurements for and are 25 and 19, respectively. Under such a test plan, the total cost is $1495.6, and the corresponding approximate standard deviation of is 435.58.

Table 2. Optimal two-level SSADT plans under different .

						Total cost
1000	4	10	19	15	699.49	992.8
1500	6	11	25	19	435.58	1495.6
2000	8	11	31	24	324.72	2000.0
2500	10	13	32	25	261.53	2491.6
3000	12	13	36	29	219.20	2996.0

According to Table 2, it can be seen that the optimal sample size, the optimal measurement frequency and the total measurement times are increasing when the budget increases. However, the approximate standard deviation of is gradually decreasing with the budget . The results indicate that the precision of the estimated becomes higher with the increase of the total budget .

4.2. Optimal SSADT plan for m=3

In this subsection, we consider a three-level SSADT plan and set the three levels as , , , where is the highest allowable stress condition. Also suppose that the true value of the model parameters is , and . Then, the optimal design variables , under various constraints of pre-fixed budget , can be determined by solving the optimisation problem addressed in Section 3. The optimal test plans are shown in Table 3.

Table 3. Optimal three-level SSADT plans under different .

							Total cost
1000	4	10	21	1	12	648.63	992.8
1500	6	12	26	1	14	417.92	1494
2000	8	11	34	1	14	310.55	2000
2500	10	16	30	1	18	246.76	2496.4
3000	11	16	37	1	22	205.86	2999

In this case, we also find that the optimal sample size, the optimal measurement frequency and the total measurement times increase with the budget , and the approximate standard deviation of decreases with . However, it should be noted that only one measurement time is assigned to the second stress level for each budget constraint. That is, the optimal experiment is mainly determined by the lowest and highest stress level. Comparing the results in Tables 2 and 3, we can see that the test plans with m=2 and m=3 are nearly the same in terms of the sample size, the measurement frequency and the total experiment cost, while the standard deviation of in the test plans with m=2 is slightly larger than the case of m=3. Under the allowed loss of the estimated precision of the parameters, we recommend using the SSADT plans with m=2 in practical application, since it is convenient and effective compared with the three-stress SSADT plans.

4.3. Sensitive analysis for the parameters and stress levels

In practice, the unknown parameters could not be estimated precisely in the pilot study. Thus, it is of great importance to investigate the effect of the estimated error on the optimal test plan. Let , , and denote the predicted errors of the parameters a, b, and β, respectively. Then, by setting the same cost configuration , the optimal plan, the corresponding approximate standard deviation and the estimated can be obtained under various combinations of , which are listed in Table 4. From these results, it is easy to see that the optimal test plan tends to be robust when the bias is not too large.

Table 4. Optimal plans under various combination of .

4%	2%	8%	2%	6	11	26	18	510.42	4674.32
4%	0	0	0	6	11	26	18	653.51	5565.53
4%				6	12	24	17	842.74	6675.59
0	2%	0		6	11	24	20	568.85	4467.13
0	0		2%	6	11	25	19	331.53	3236.26
0		8%	0	6	11	24	20	442.69	3749.21
	2%		0	6	8	29	27	282.59	2555.69
	0	8%		6	11	22	22	372.93	2942.87
		0	2%	6	8	30	26	224.02	2170.88
0	0	0	0	6	11	25	19	435.58	3775.96

On the other hand, we find that the optimal design problem is also dependent on the choice of the stress levels. Hence, it is equally vital to investigate the sensitivity of the stress level selection for the test plan. Taking the same constraint settings above, the results of the optimal test plans under various combinations of stress levels can be obtained by solving the optimisation problem in Section 3. Then, some of the points are quite clear from Table 5:

• For the fixed , the estimated precision of becomes lower when the stress level increases, since the approximate standard deviation of gets the maximal value at . Instead, the estimated precision of increases with when the stress level is pre-fixed, since the approximate standard deviation of is decreasing.

• The approximate standard deviation of is larger in the case of increasing when the range of – is fixed. But if the range of – is flexible, the approximate standard deviation of decreases with the various cases of .

Table 5. Optimal plans under various combination of and with .

		6	11	25	19	435.58
		4	1	16	225	1302.41
		5	1	8	183	2976.79
		14	1	3	21	5649.51
		6	11	23	21	450.32
		4	1	13	228	1618.30
		7	1	5	120	4464.34
		6	8	24	32	482.67
		5	1	9	182	2530.13
		5	6	27	52	692.90

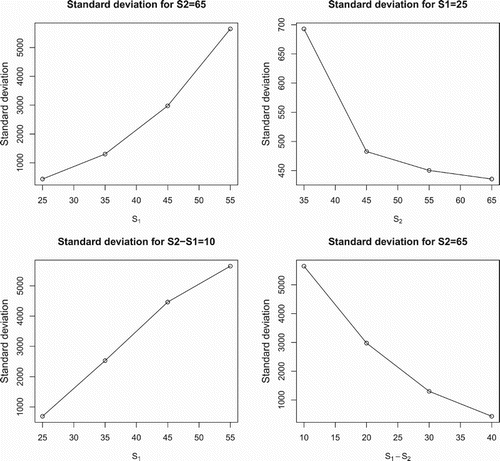
Note that these two findings can also be displayed clearly in Figure 1. Based on the sensitivity analysis for the stress levels and , it can be seen that the reasonable choice of stress level is of critical importance for the optimal test plan. Since the stress level selection has substantial effect on the estimated precision of . So in order to make the test more effective, we recommend extending the difference between the stress levels and in practice.

Figure 1. Plots of the trends revealed by Tabel 5.

4.4. Stability of the SSADT plan

To assess the stability of the optimal test plan (such as, ) under the cost configuration , a simulation experiment is constructed to compare the case of varying in terms of the average of the MLEs and the root-mean-squared errors (RMSE). Set as the true parameters of the SSADT model. By pre-fixing , 1000 sets of SSADT degradation data are generated for each combination under the restriction . The simulated results are listed in Table 6. From Table 6, it is seen that the proposed optimal test plan yields the smallest RMSE of that is near to the theoretical result by altering the test plan.

Table 6. A stability analysis for the optimal SSADT plan with .

	12.9266	1.3080	123.04	1.4915	3804.08
	(0.5194)^b	(0.1208)	(37.19)	(0.0697)	(300.66)	224.28
	12.9571	1.3073	120.40	1.4958	3793.05
	(0.5237)	(0.1187)	(38.20)	(0.0702)	(295.78)	220.58
	12.9367	1.3065	118.57	1.4916	3795.13
	(0.4810)	(0.1125)	(33.34)	(0.0637)	(263.50)	219.20
	12.9507	1.3103	118.67	1.4951	3793.89
	(0.4617)	(0.1079)	(32.24)	(0.0605)	(259.48)	222.90
	12.9534	1.3089	120.20	1.4953	3800.73
	(0.4668)	(0.1112)	(36.43)	(0.0601)	(259.36)	223.39
True value	12.9156	1.3097	112.98	1.4906	3775.96

^aTS denotes the theoretical standard deviation of .

^bThe value in parentheses is the corresponding RMSE of the estimated parameter.

5. Concluding remarks

In this paper, we propose an optimal SSADT plan for the Wiener degradation process with correlation. By using the criterion of minimising the asymptotic variance of the estimated p-quantile of the product's lifetime distribution under the usage stress subject to the total cost not exceeding a pre-specified budget, several decision variables, including the sample size, the measurement frequency and the numbers of measurements under each stress level, are determined. An optimisation algorithm is proposed to derive the optimal test plan. Finally, a pilot study is conducted to evaluate the performance of the proposed SSADT optimal plan. Optimal two-level SSADT plans and optimal three-level SSADT plans are discussed under the same cost configuration. Two sensitivity analyses for the estimated parameters and stress levels are also considered respectively. And a Monte Carlo simulation method is employed to study the stability of the proposed optimal test plan. From the numerical results, some concluding remarks are addressed as follows:

• A two-level SSADT plan is recommended in practical applications, since it is easy to implement and has similar efficiency compared with the three-level SSADT plan.

• The sensitivity analysis for the parameters reveals that the optimal test plan is quite robust to moderate departures of the real values of the model parameters.

• The sensitivity analysis for the stress levels shows that extending the difference between the low stress and the high stress in the allowable range can improve the effectiveness of the test.

• The simulation study indicates that the optimal test plan is stable, since most of the simulation results are close to the theoretical results.

This study has considered taking the asymptotic variance of the estimated p-percentile of the product's lifetime distribution as the objective function of the optimisation problem. In fact, other objective functions, such as minimising the approximate variance of the estimated MTTF, can also be considered. And similar results can be obtained by using the same optimisation algorithm.

Acknowledgements

The authors thank the associate editor and the referees for their constructive suggestions that greatly improved the article.

Disclosure statement

No potential conflict of interest was reported by the authors.

Notes on contributors

Lei He is a Ph.D candidate in the Department of Mathematics at Shanghai Normal University.

Rong-Xian Yue is a professor in Shanghai Normal University.

Daojiang He is a professor in Anhui Normal University.

Additional information

Funding

Rong-Xian Yue's research was supported by the National Natural Science Foundation of China [grant number 11471216]. Daojiang He's research was supported by the National Natural Science Foundation of China [grant number 11201005].

Appendix

The elements of the Fisher information matrix are given by where and is defined in Equation (11(11) ). Furthermore, the detailed expressions of in Equation (14(14) ) are derived as follows.