Abstract
This paper considers the problem of jointly estimating marginal quantiles of a multivariate distribution. A sufficient condition for an estimator that converges in probability under a multivariate version of Robbins–Monro procedure is provided. We propose an efficient procedure which incorporates the correlation structure of the multivariate distribution to improve the estimation especially for cases involving extreme marginal quantiles. Estimation efficiency of the proposed method is demonstrated by simulation in comparison with a general multivariate Robbins–Monro procedure and an efficient Robbins–Monro procedure that estimates the marginal quantiles separately.
1. Introduction
Let be the distribution function of a random variable X. Robbins and Monro (Citation1951) introduced a stochastic approximation method to find the α-quantile
(assuming it is unique) through a sequential search given by
(1) where
is an arbitrary initial guess of θ,
is the binary response with expected value
and
is a prespecified sequence of positive constants. They showed that when
satisfies
and
,
converges to θ in probability. Applications of this procedure include quantal response curve estimation in sensitivity experiments, dose-finding in clinical trials and sequential learning, to just name a few (Cheung, Citation2010; Duflo, Citation1997; Wu, Citation1985).
It is known that the procedure is asymptotically efficient when , where
is the first derivative of M (Chung, Citation1954; Sacks, Citation1958). Various variants of Robbins–Monro procedure of (Equation1
(1) ) and other model-based approaches were proposed to improve the finite sample performance (Chaloner & Larntz, Citation1989; Chaudhuri & Mykland, Citation1993; Dror & Steinberg, Citation2006, Citation2008; Hung & Joseph, Citation2014; Lai & Robbins, Citation1979; Neyer, Citation1994; Ruppert, Citation1988; Wu, Citation1985, Citation1986; Wu & Tian, Citation2014). It is also known that the Robbins–Monro procedure does not perform well for extreme values of α (Wetherill, Citation1963; Young & Easterling, Citation1994). To improve the convergence performance in this case, Joseph (Citation2004) proposed an efficient Robbins–Monro procedure which modifies (Equation1
(1) ) by
(2) where
is a sequence of constants in
converging to α. The sequences
and
are chosen in a way such that the conditional mean square error is minimised under a Bayesian framework. The explicit forms of
and
under normal approximation are derived and showed to work for general M as well.
In this paper, we consider a multivariate extension of this estimation problem. Let be the distribution function of a p-dimensional random vector
with finite second moments. Denote its jth marginal distribution by
. Given a constant vector
in
, we are interested in jointly estimating the marginal quantiles
, assuming that
is unique for each j. We also assume that
for all
. Suppose that given each factor
, we observe an independent binary response
with
. Such situation arises in different fields of researches. For instance, in sensitivity experiment study, several sensitivity experiments are conducted in parallel. In each experiment, stimulus level of one factor is tested with dichotomous outcome, response or non-response, and the factors considered across experiments are highly correlated. It is of interest to coordinate the designs for individual factor for more efficiency. In oncology dose-finding clinical trials, several agents are considered at the same time. For each agent, a trial is conducted to search for the level of maximum tolerated dose, which corresponds to the 25% or 30% quantile of a unknown distribution. Across the agents, various binary responses representing different types of adverse events are observed. The joint marginal dose levels are used for evaluation of possible combination agent trials. Apparently,
can be estimated by applying the Robbins–Monro procedure or the efficient version to each component of
. However since
are correlated, these methods may lose efficiency when estimating the marginal quantiles separately. This motivates us to seek a sequential procedure that estimates
jointly.
Multivariate Robbins–Monro procedures that aim to find the root of a multivariate continuous function through a regression
have been studied (Duflo, Citation1997). For example, Ruppert (Citation1985) proposed a multivariate Newton–Raphson version which is in a way similar to multivariate Kiefer–Wolfowitz procedure to minimise
. Wei (Citation1987) proposed a multivariate Robbins–Monro procedure which employs a Venter-type estimate of the Jacobian of
. The method we propose here is primarily for binary responses.
The remainder of the paper is organised as follows. In Section 2, we first present a general multivariate Robbins–Monro procedure under which the sequential estimator converges in probability. Second, we develop an efficient version which is optimal under a criterion that is naturally extended from the univariate case. Section 3 contains simulation studies to demonstrate the superiority of the proposed method over a general multivariate Robbins–Monro procedure and an efficient Robbins–Monro procedure that estimates the marginal quantiles separately. All proofs are gathered in Appendix.
2. Main results
First, we extend (Equation1(1) ) to a multivariate version as follows:
(3) where
contains p binary responses observed at
and each
has the expected value
,
is a sequence of
constant matrices whose
th element is denoted by
. The following theorem gives a sufficient condition for
to converge to
in probability.
Theorem 2.1
Suppose that satisfies the following conditions:
(4) Then,
in (Equation3
(3) ) converges to
in probability as
.
When for all
, Theorem 2.1 reduces to p univariate Robbins–Monro procedures. It indicates that when the diagonal elements of
are of
and dominate the off-diagonal elements in magnitude, the sequential estimator converges regardless of the exact values of
. Clearly, this arbitrariness of
can lead to inefficiency in estimation as showed by simulation in Section 3.
In light of Joseph (Citation2004) to improve the convergence in case of extreme quantile, we propose an efficient version of (Equation3(3) ) by replacing
by a vector sequence
in
, i.e.
(5) Additional condition on
to guarantee the convergence is provided in the following theorem.
Theorem 2.2
Suppose that satisfies (Equation4
(4) ) and
satisfies
(6) where
is a
vector of ones,
stands for the operator that takes element-wise absolute value of a vector or a matrix. Then,
in (Equation5
(5) ) converges to
in probability as
.
Here the idea of introducing a varying sequence is to create a balanced step length in early stage when
contains extreme values. As n gets large,
converges to
and its effect diminishes. Again, there are many sequences of
and
satisfying the conditions of Theorem 2.2. We now seek a pair of them that is optimal in a way that is naturally extended from the univariate case.
Assume that M is from a location family with parameter . Hereafter, we denote
by
. Suppose the initial guess
is obtained with some prior information of
, to be specific, a prior distribution of
with
and
.
Let . Then, (Equation5
(5) ) becomes
(7) where
is a binary variable with expected value
. Denote
and
. As a natural extension of the univariate case in Joseph (Citation2004), we propose to choose
and
such that
is minimised subject to the condition that
. By (Equation7
(7) ), this condition implies
Since
are chosen such that
, we have
, which, together with (Equation7
(7) ), leads to
Minimising
with respect to
by solving
, we obtain
and
(8) The components of
can be expressed as
(9) The expectations of
,
and
in (Equation8
(8) ) and (Equation9
(9) ) depend on the unknown distribution M and the distribution of
. (Note that
is invertible unless some
and
are identical.)
To facilitate the evaluation of these expectations, we first approximate by
(10) where
is the distribution function of p-dimensional normal vector with mean
and covariance Σ,
,
with
, Φ and φ are respectively the distribution function and density of the standard normal variable,
with
. Then, the marginal distribution of G, given by
, coincides with
in both the value and the derivative at 0, i.e.
and
. In this way, G captures the local behaviour of M at the point of interest. Further let
.
Second, denote the density of by
. Observe that
can be obtained recursively by
which is rather complicated. Again, we choose to approximate the distribution of
by another multivariate normal distribution
as their first two moments agree.
It is worth pointing out that neither the first-order approximation by G nor the moment agreement by guarantees the overall closeness to the distribution. Such approximations are not unique or optimal. The main advantages of using multivariate normal approximations are computational ease and sufficiency for the desired convergence, as we show next.
Now, based on these two approximations, we can estimate ,
and
respectively by
,
and
, where the expectations are taken with respect to
. Their expressions are obtained as follows:
(11)
(12)
(13) where
At last, we obtain the sequences of
and
in the efficient procedure of (Equation5
(5) ) or (Equation7
(7) ) as
(14) with
(15) where the components of
,
and
are given in (Equation11
(11) )–(Equation13
(13) ). Note that
and
are sequences that can be specified before the experiment once
is provided. When
is diagonal, i.e. the components of
are uncorrelated, the component-wise coefficients of
and
in (Equation14
(14) ) reduce to
and
respectively in (Equation2
(2) ) given by Joseph (Citation2004).
The following theorem gives the convergence property of the proposed sequential design when M is multivariate normal.
Theorem 2.3
Suppose that the distribution of is given by (Equation10
(10) ). Then, for the procedure in (Equation7
(7) ) with coefficient sequences in (Equation14
(14) ),
as
.
Theorem 2.3 implies that converges to
and hence
converges to
in probability. The next theorem shows that the result in fact holds for general M.
Theorem 2.4
For the procedure in (Equation7(7) ) with coefficient sequences in (Equation14
(14) ),
in probability, as
.
We call the sequential design in (Equation5(5) ) with coefficients in (Equation14
(14) ) efficient multivariate Robbins–Monro procedure. A couple of points are worthy to be noted. (i) The most important impact of the procedure lies on the sequence
for which each of its component is between
and 0.5 for the early stage to avoid unnecessary large-scale oscillation of the search steps as pointed out by Joseph (Citation2004). (ii) The contribution of the correlation structure of
is implemented through the procedure in (Equation14
(14) ) to minimise
.
In the end, we would like to comment on two practical issues in carrying out the procedure. First, as seen from (Equation5(5) ), the starting value of
plays a key role in the construction of
and
. In reality it is usually unknown to the experimenter. A plausible solution is to estimate it from a moderate sample of
. It is possible and less expensive since no response of
is needed. Second, for the unknown coefficients
which also depends on the unknown
, it can be estimated adaptively from the data by fitting a parametric model like in Anbar (Citation1978) and Lai and Robbins (Citation1979). We will demonstrate the effect of these approximations through simulation in the next section.
3. Simulations
In this section, we conduct simulations to compare the performance of the following four procedures for jointly estimating the marginal quantiles: (i) the multivariate Robbins–Monro procedure in (Equation3(3) ), denoted by MRM; (ii) the proposed efficient version in (Equation5
(5) ), denoted by eMRM; (iii) the procedure that estimates the marginal quantiles separately by (Equation1
(1) ), denoted by RM; (iv) the efficient procedure that estimates the marginal quantiles separately by (Equation2
(2) ), denoted by eRM.
3.1. Set up
Consider three bivariate distributions given in the first column of Table , where (i) is bivariate normal distribution with mean
and
, (ii)
is bivariate t distribution with location parameter
, scale matrix Σ and degrees of freedom four (Kotz & Nadarajah, Citation2004), (iii)
is a bivariate skew-normal distribution with location parameter
, scale matrix Σ, shape parameter
(Azzalini, Citation1998). The covariance matrices of these three distributions are respectively
(16) where
, all indicating a strong positive correlation. The marginal distribution of
under these models are given in the second column of Table , where (i)
,
and
are respectively the distribution function, quantile and density of a t random variable with degrees of freedom f, (ii)
,
and
are the distribution function, quantile and density of a (univariate) skew-normal random variable with location parameter μ, scale parameter ω and shape parameter s. In addition, the corresponding
under these models are given in the third column of Table , where
,
(Azzalini, Citation2014).
Table 1. Three bivariate distributions and their marginal distributions.
Since we are mainly concerned with the estimation performance under moderate sample size, we compare the efficiency of these estimations by the sum of marginal square root of the mean square error (RMSE) of after 20, 30 and 50 iterations, respectively.
3.2. Comparison with true 
First, we consider the comparison with to be the true value or equivalently
and
to be its corresponding true value given in (Equation16
(16) ).
For MRM, we let
(17) which satisfies the conditions in (Equation4
(4) ). For eMRM,
is given in (Equation14
(14) ) with
to be the true value. For RM, we set
to be the optimal value
for the jth margin. And for eRM, the sequences
and
are obtained by (Equation5
(5) ) with
replaced by
. Then, we use (Equation3
(3) ) and (Equation5
(5) ) to obtain sequences for MRM and eMRM respectively and use (Equation1
(1) ) and (Equation2
(2) ) to obtain RM and eRM respectively. For all procedures, the binary responses
, are obtained as Bernoulli variables with success probabilities
, respectively.
Tables respectively report the sum of marginal RMSEs of ,
and
obtained by the four procedures under various values of
and
and the three models in Table . (The simulation size is 1000 throughout.) The sequential design of
corresponds to simultaneous estimates of two (
and
) marginal quantiles of an unknown bivariate distribution. For example, one wants to simultaneously estimate the 30th percentiles of two dose response curves based on two possibly correlated agents.
Table 2. Sum of marginal RMSEs of  obtained by the four procedures.
obtained by the four procedures.
Table 3. Sum of marginal RMSEs of  obtained by the four procedures.
obtained by the four procedures.
Table 4. Sum of marginal RMSEs of  obtained by the four procedures.
obtained by the four procedures.
We summarise the finding as follows. (i) The proposed efficient multivariate Robbins–Monro procedure (Equation5(5) ) has significant improvement over the general multivariate version of (Equation3
(3) ). The reduction in terms of the sum of marginal RMSEs is ∼78.7% when the joint estimators are concern with extreme marginal quantile (the first three cases in Tables ). The reduction is still remarkable (by ∼15.5%) for the median. The averaged reduction is
across all 18 cases. This type of improvement is also seen in comparison between eRM and RM, as reported by Joseph (Citation2004). (ii) The proposed eMRM procedure uniformly outperforms the eRM in terms of reduction in the sum of marginal RMSEs by an average (over 18 cases) of
for
,
for
and
for
. This exactly shows the efficiency gained by the joint estimation with incorporation of the correlation. (The reduction percentage gets smaller as n increases since both procedures converge.) (iii) The results of MRM and RM are comparable since the
we chose in (Equation17
(17) ) only guarantees the convergence in large sample. This also reflects the importance of an appropriate selection of coefficient matrix
in the sequential design when the sample size is limited.
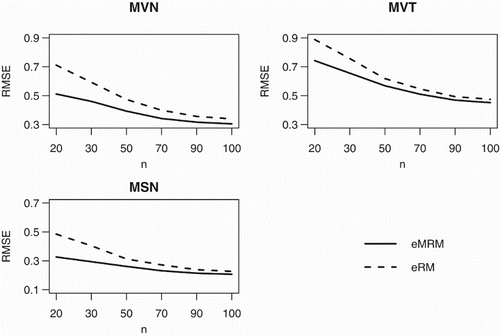
We continue the sequential experiments up to 100 steps to examine the convergence behaviour of the procedures. We use the first combination of as an example to illustrate. Figure shows the declining trend of the sum of marginal RMSEs by eMRM and eRM under the three models. (Those by MRM and RM are significantly larger, thus not included.) It is seen that the superiority of the joint estimation prevails with a remarkable difference.
3.3. Comparison with estimated 
The previous simulations are carried out under the perfect initial guess and the true M. Now we consider the situation that these values are unknown. We propose using a pilot sample of to estimate them. To be specific, we (i) estimate the initial value of
by the sample
-quantile; (ii) estimate
based on a bootstrap sample (of size 500) of
; and (iii) approximate
by its normal counterpart, i.e.
, hence
. The size of the pilot sample depends on the dimension of
. For the bivariate models considered in Section 3.1, we set the size to be 20. Noted that this pilot sample does not need responses of ys so that in reality it is feasible, as observing responses
can be expensive or time consuming. When the dimension increases, the size of the pilot sample should increase as well. After obtaining
and
, we proceed the four competing procedures in the same way as outlined in Section 3.2.
We carry out the similar comparison under the same models and obtain results in the last four columns of Tables . It is seen that the reduction in the sum of marginal RMSEs are even larger for eMRM both from MRM (by for
, by
for
and by
for
) and from eRM (by
for
, by
for
and by
for
) in average across all 18 cases.
Certainly larger sample size of the pilot study can yield more accurate estimation of and hence better result in sequential estimation. Here our simulation shows that a pilot study of a moderate sample (without responses) serves the purpose for providing initial information of
and
in practice. On the other hand, if
is mis-specified, e.g. use negative values for positive correlations, we found the performance of the sequential estimation of eMRM is worse than those of the separate eRM procedures, though the sequence still converges (result not shown). This indicates that correct estimation of the sign of the correlation is important.
Disclosure statement
No potential conflict of interest was reported by the authors.
Additional information
Funding
Notes on contributors
Cui Xiong
Cui XIong is a PhD student at the school of statistics, East China Normal University. She is currently a biostatistician at GlaxoSmithKline.
Jin Xu
Jin Xu is a professor at the school of statistics, East China Normal University.
References
- Anbar, D. (1978). A stochastic Newton–Raphson method. Journal of Statistical Planning and Inference, 2, 153–163. doi: 10.1016/0378-3758(78)90004-6
- Azzalini, A. (2014). The skew-normal and related families. Cambridge: Cambridge University Press.
- Azzalini, A., & Capitanio, A. (1999). Statistical applications of the multivariate skew normal distribution. Journal of the Royal Statistical Society, Series B, 61, 579–602. doi: 10.1111/1467-9868.00194
- Chaloner, K., & Larntz, K. (1989). Optimal Bayesian design applied to logistic regression experiments. Journal of Statistical Planning and Inference, 21, 191–208. doi: 10.1016/0378-3758(89)90004-9
- Chaudhuri, P., & Mykland, P. A. (1993). Nonlinear experiments: Optimal design and inference based on likelihood. Journal of the American Statistical Association, 88, 538–546. doi: 10.1080/01621459.1993.10476305
- Cheung, Y. K. (2010). Stochastic approximation and modern model-based designs for dose-finding clinical trials. Statistical Science, 25, 191–201. doi: 10.1214/10-STS334
- Chung, K. L. (1954). On a stochastic approximation method. Annals of Mathematical Statistics, 25, 463–483. doi: 10.1214/aoms/1177728716
- Dror, H. A., & Steinberg, D. M. (2006). Robust experimental design for multivariate generalized linear models. Technometrics, 48, 520–529. doi: 10.1198/004017006000000318
- Dror, H. A., & Steinberg, D. M. (2008). Sequential experimental designs for generalized linear models. Journal of the American Statistical Association, 103, 288–298. doi: 10.1198/016214507000001346
- Duflo, M. (1997). Random iterative models. Berlin: Springer-Verlag.
- Hung, Y., & Joseph, V. R. (2014). Discussion of “Three-phase optimal design of sensitivity experiments” by Wu and Tian. Journal of Statistical Planning and Inference, 149, 16–19. doi: 10.1016/j.jspi.2013.12.011
- Joseph, V. R. (2004). Efficient Robbins–Monro procedure for binary data. Biometrika, 91, 461–470. doi: 10.1093/biomet/91.2.461
- Kotz, S., & Nadarajah, S. (2004). Multivariate t distributions and their applications. Cambridge: Cambridge University Press.
- Lai, T. L., & Robbins, H. (1979). Adaptive design and stochastic approximation. Annals of Statistics, 7, 1196–1221. doi: 10.1214/aos/1176344840
- Neyer, B. T. (1994). A D-optimality-based sensitivity test. Technometrics, 36, 61–70. doi: 10.2307/1269199
- Robbins, H., & Monro, S. (1951). A stochastic approximation method. Annals of Mathematical Statistics, 22, 400–407. doi: 10.1214/aoms/1177729586
- Ruppert, D. (1985). A Newton-Raphson version of the multivariate Robbins-Monro procedure. Annals of Statistics, 13, 236–245. doi: 10.1214/aos/1176346589
- Ruppert, D. (1988). Efficient estimators from a slowly convergent Robbins–Monro process. School of Operations Research and Industrial Engineering Technical Report, 781. Cornell University, Ithaca, NY.
- Sacks, J. (1958). Asymptotic distribution of stochastic approximation procedures. Annals of Mathematical Statistics, 29, 373–405. doi: 10.1214/aoms/1177706619
- Wei, C. Z. (1987). Multivariate adaptive stochastic approximation. Annals of Statistics, 15, 1115–1130. doi: 10.1214/aos/1176350496
- Wetherill, G. B. (1963). Sequential estimation of quantal response curves. Journal of the Royal Statistical Society, Series B, 25, 1–48.
- Wu, C. F. J. (1985). Efficient sequential designs with binary data. Journal of the American Statistical Association, 80, 974–984. doi: 10.1080/01621459.1985.10478213
- Wu, C. F. J. (1986). Maximum likelihood recursion and stochastic approximation in sequential designs. In J. V. Ryzin (Ed.), IMS monograph series: Vol. 8. Adaptive statistical procedures and related topics (pp. 298–314). Hayward, CA: Institute of Mathematical Statistics.
- Wu, C. F. J., & Tian, Y. (2014). Three-phase optimal design of sensitivity experiments. Journal of Statistical Planning and Inference, 149, 1–15. doi: 10.1016/j.jspi.2013.10.007
- Young, L. J., & Easterling, R. G. (1994). Estimation of extreme quantiles based on sensitivity tests: A comparative study. Technometrics, 36, 48–60. doi: 10.1080/00401706.1994.10485400
Appendices
Appendix 1. Proof of Theorem 2.1
First, by (Equation3(3) ), we have
where the expectations are taken with respect to
,
. Let
. Clearly,
is bounded. Observe that
can be expressed as
By assumption (Equation4
(4) ), both series
and
converge absolutely and hence converge. Thus, the series
converges (to a non-negative value). Therefore,
.
Second, for , since
is a distribution function and
, there exist positive constants
and
such that
for all
. Let
and
. Let
be the jth column of
. Then,
where
with
(A1) Then, we have
. Since this quantity can be expressed as
(A2) Observe that the second term of (EquationA2
(A2) ) is no greater than
The assumptions
when
for
and
imply that there exists an integer N such that for n>N,
for all
, where c is some constant great than
and u and ℓ are defined in (EquationA1
(A1) ). Hence, for fixed j
Then, the infinite sum
which is positive by the choice of c. This implies that (EquationA2
(A2) ) is also bounded from below. Thus, the first term of (EquationA2
(A2) ) is finite. And by (Equation4
(4) ),
must converge to 0 for all
, which implies
converges to
in probability.
Appendix 2. Proof of Theorem 2.2
The proof is similar to the proof of Theorem 2.1. First, by (Equation3(3) ), we have
where
is as defined before. The finiteness of
(showed by the same way as for the case
in the proof of Theorem 2.1) implies that
.
Second, similar to the proof in Theorem 2.1, we can show that
where
and
are some positive constants depending on
. Then,
Since
and
(by assumption), we have
which is finite by the assumption in (Equation6
(6) ). Thus,
. Finally, using the same argument in the proof of Theorem 2.1,
converges to
in probability.
Appendix 3. Proof of Theorem 2.3
First, under the assumption that M is given by (Equation10(10) ), (Equation15
(15) ) is the covariance of
. We have
Recall that the expectations are taken with respect to
with distribution
.
Let
,
. Let
(A3) be a function of
. Since
as its jth element is not zero, we have
and
Thus,
is strictly decreasing to a limit
. Since
satisfies the equation
where q is a non-negative function of
. The unique solution is
for all
. This implies
and by (Equation11
(11) )
.
Appendix 4. Proof of Theorem 2.4
(i) First, we show that for
. By Theorem 2.3, we have
and
hence
. Then, for sufficiently large n, there exist positive constants
such that
where
is defined in (EquationA3
(A3) ). It is clear that
(A4)
Now, treat
as a function of
given
. Observe that
when
. Then, we get
where the last inequality is obtained from (A4). By mathematical induction,
is
.
Further, by (Equation15(15) ) and (EquationA3
(A3) ), we have for
Using the fact that
, we express
which is
from the previous result. Thus, if
is
,
is
. This can be achieved by properly choosing the starting value of
.
(ii) Second, we show that in (Equation14
(14) ) satisfies (Equation4
(4) ). By the construction in (Equation14
(14) ), we have
Then, the results in (i) imply that
is
for j=k and
for
.
(iii) Third, we show together with
in (Equation14
(14) ) satisfies (Equation6
(6) ). By (Equation14
(14) ) and the results in (i), we have each component of
is
and each component of
is
. Observe that
which is
after the result in (ii). Then (Equation6
(6) ) follows.
Combining (ii) and (iii), the result follows after Theorem 2.2.