Some results on quantile-based Shannon doubly truncated entropy

ABSTRACT

Sunoj et al. [(2009). Characterization of life distributions using conditional expectations of doubly (Intervel)truncated random variables. Communications in Statistics – Theory and Methods, 38(9), 1441–1452] introduced the concept of Shannon doubly truncated entropy in the literature. Quantile functions are equivalent alternatives to distribution functions in modelling and analysis of statistical data. In this paper, we introduce quantile version of Shannon interval entropy for doubly truncated random variable and investigate it for various types of univariate distribution functions. We have characterised certain specific lifetime distributions using the measure proposed. Also we discuss one fascinating practical example based on the quantile data analysis.

KEYWORDS:

• Quantile function
• interval entropy
• geometric vitality function
• characterisation

1. Introduction

Let X be a non-negative absolutely continuous random variable representing the lifetime of a component with cumulative distribution function (CDF) $F\left(t\right)=P(X\le t)$ and survival function $\overline{F}\left(t\right)=P(X>t)=1-F\left(t\right)$. In modelling and analysis of lifetime data, the average amount of uncertainty associated with a non-negative continuous random variable X is given in the differential entropy function $H\left(X\right)=-{\int }_0^{\mathrm{\infty }}f\left(x\right)\log f\left(x\right)\mathrm{d}x,$ a continuous counterpart of the Shannon (1948) entropy in the discrete case and $f\left(x\right)$ is the probability density function (pdf) of the random variable X. While the concept of entropy has found increased application, little attention has yet been given to the practical problems of estimating entropy. Gong, Yang, Gupta, and Nearing (2014) discussed a method for computing robust and accurate estimates of entropy that accounts for several important characteristics of hydrological data sets. Since this entropy is not applicable to a system which has survived for some unit of time or for used item. The residual lifetime of the system when it is still operating at time t is $X_t=(X-t|X>t);$ which has the probability density $f(x;t)=f\left(x\right)/\overline{F}\left(t\right)$, $x\ge t>0$. Ebrahimi (1996) proposed the entropy of the residual lifetime $X_t$ as (1) $H(X;t)=-{\int }_t^{\mathrm{\infty }}\frac{f\left(x\right)}{\overline{F}\left(t\right)}\log \frac{f\left(x\right)}{\overline{F}\left(t\right)}\mathrm{d}x,t>0.$(1) In some practical situations, uncertainty is related to past life time rather than future. In this situation, the random variable $X_t^{\ast }=(t-X|X\le t),$ which is known as inactivity time is suitable to describe the time elapsed between the failure of a system and the time when it is found to be ‘down’. Based on this idea, Di Crescenzo and Longobardi (2002, 2004) have considered the entropy of the inactivity time $X_t^{\ast }$ given as (2) $\overline{H}(X;t)=-{\int }_0^t\frac{f\left(x\right)}{F\left(t\right)}\log \frac{f\left(x\right)}{F\left(t\right)}\mathrm{d}x.$(2) In many situations, we only have information between two points, and in this case statistical measures are studied under the condition of doubly truncated random variables. The doubly truncated measures are applicable to engineering systems when the observations are measured after it starts operating and before it fails. If the random variable X denotes the lifetime of a unit, then the random variable $X_{t_1,t_2}=(X-t_1|t_1\le X\le t_2)$ is called the doubly truncated (interval) residual lifetime, which in special case $t_2\to \mathrm{\infty }$ tends to residual lifetime random variable $X_t$. Also, we can use the doubly truncated past lifetime random variable $X_{t_1,t_2}^{\ast }=(t_2-X|t_1\le X\le t_2)$, which in special case $t_1=0$, it tends to past lifetime random variable $X_t^{\ast }$. Another extension of Shannon entropy is based on a doubly truncated (interval) random variable, which is as follows, (3) $\begin{array}{rl}& H(X;t_1,t_2)\\ & =-{\int }_{t_1}^{t_2}\frac{f\left(x\right)}{F\left(t_2\right)-F\left(t_1\right)}\log \frac{f\left(x\right)}{F\left(t_2\right)-F\left(t_1\right)}\mathrm{d}x.\end{array}$(3) Given that a system has survived up to time $t_1$ and has been found to be down at time $t_2$, then $H(X;t_1,t_2)$ measure the uncertainty about its lifetimes between $t_1$ and $t_2$. Different aspects and properties of $H(X;t_1,t_2)$ have been studied by Sunoj, Sankaran, and Maya (2009) and Misagh and Yari (2011, 2012). For various results on doubly truncated random variable, we refer to Sankaran and Sunoj (2004)), Khorashadizadeh, Rezaei Roknabadi, and Mohtashami Borzadaran (2013), Kayal and Moharana (2016), and Kundu (2017).

All the theoretical investigations and applications using these information measures are based on the distribution function. A probability distribution can be specified either in terms of its distribution function or by the quantile function. Although both convey the same information about the distribution with different interpretations, the concepts and methodologies based on distribution functions are traditional. When traditional approach are either difficult or fails to obtain desired results then quantile-based study were carried out. However, as Gilchrist (2000) discussed, there are many distinct properties for quantile functions that are not shared by the distribution functions, which makes the former attractive in certain practical situations. For inference purposes, quantile-based statistics are often more robust than those based on moments in the distribution function approach. Furthermore, there exist many simple quantile functions, that serve very well in empirical model building, for which distribution function are not in tractable forms, refer to van Staden and Loots (2009), Hankin and Lee (2006) and Nair, Sankaran, and Vinesh Kumar (2012). In many cases, QF is more convenient as it is less influenced by extreme observations and thus provides a straightforward analysis with a limited amount of information. In such cases, conventional tools of analysis using distribution functions are difficult to apply. An alternative approach to the study is to use the quantile functions (QFs), defined by (4) $Q\left(u\right)=F^{-1}\left(u\right)=inf\left\{x|F\right(x)\ge u\},0\le u\le 1.$(4) When F is continuous, we have from (4(4) $Q\left(u\right)=F^{-1}\left(u\right)=inf\left\{x|F\right(x)\ge u\},0\le u\le 1.$(4) ), $FQ\left(u\right)=u$, where $FQ\left(u\right)$ represents the composite function $F\left(Q\right(u\left)\right)$. Defining the density quantile function by $fQ\left(u\right)=f\left(Q\right(u\left)\right)$ and quantile density function by $q\left(u\right)=Q^{\prime }\left(u\right)$, where prime denotes the differentiation, we have $q\left(u\right)fQ\left(u\right)=1,$ refer to Nair, Sankaran, and Balkrishanan (2013). Several researchers have studied information theoretic measures based on quantile function. Sunoj and Sankaran (2012) have considered the quantile version of Shannnon entropy and its residuals form, defined as (5) $\text{̧}H={\int }_0^1\log q\left(p\right)\mathrm{d}p$(5) and (6) $\text{̧}H\left(u\right)=\log (1-u)+(1-u{)}^{-1}{\int }_u^1\log q(p)\mathrm{d}p$(6) respectively. Sunoj, Sankaran, and Nanda (2013) have considered the quantile past entropy, which is defined as (8) $\overline{\text{̧}H}\left(u\right)=\log u+u^{-1}{\int }_0^u\log q\left(p\right)\mathrm{d}p.$(8) Readers can refer to Nanda, Sankaran, and Sunoj (2014), Baratpour and Khammar (2018), Sankaran and Sunoj (2017), Guoxin (2018), and Kumar (2018) for more works on this line.

Motivated with the usefulness of the quantile function and the interval entropy, in the present note, we introduced a quantile version of Shannon interval entropy and derived some new characterisations to certain probability distributions as well as study its important properties. The proposed measure has several advantage. The measure proposed for doubly truncated random variable appears in quasar survey, where an investigator assumes that the apparent magnitude is doubly truncated. Also, the times to progression for patients with certain disease who received chemotherapy, experienced tumour progression and subsequently died, are doubly truncated. Secondly, quantile functions (QFs) have several properties that are not shared by distribution functions. Application of these properties give some new results and better insight into the properties of the measure that are difficult to obtain in the conventional approach. However, the use of QFs in the place of F provides new models, alternative methodology, easier algebraic manipulations, and methods of analysis in certain cases and some new results that are difficult to derive by using distribution function.

The paper is organised as follows. In Section 2, we consider the quantile version of Shannon interval entropy. In Section 3, the quantile interval entropy has been derived in case of some specific distributions. In Section 4, we study characterisation results concerning Quantile Interval Entropy (QIE) and also characterise a few specific lifetime distributions. Finally, conclusions have been given along with comments.

2. Quantile interval entropy

Defining a doubly truncated random variable $(X|u_1\le X\le u_2)$ which represents the lifetime of a unit between $u_1$ and $u_2$, where $(u_1,u_2)\in D=\left\{\right(u_1,u_2);Q(u_1)<Q(u_2\left)\right\}$. Corresponding to (4(4) $Q\left(u\right)=F^{-1}\left(u\right)=inf\left\{x|F\right(x)\ge u\},0\le u\le 1.$(4) ), a measure of uncertainty for the doubly truncated random variable in term of quantile function (4(4) $Q\left(u\right)=F^{-1}\left(u\right)=inf\left\{x|F\right(x)\ge u\},0\le u\le 1.$(4) ) is defined as (8) $\begin{array}{rl}\text{̧}H(u_1,u_2)& =-{\int }_{u_1}^{u_2}\frac{f\left(Q\right(p\left)\right)}{(u_2-u_1)}\log \frac{f\left(Q\right(p\left)\right)}{u_2-u_1}\mathrm{d}Q\left(p\right)\\ & =\log (u_2-u_1)\\ & +\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\log \left(q\right(p\left)\right)\mathrm{d}p.\end{array}$(8) The important quantile measures useful in reliability analysis are hazard quantile function and reversed hazard quantile, defined as $A\left(u\right)=\left(\right(1-u\left)q\right(u){)}^{-1}$ and $\overline{A}\left(u\right)=\left(uq\right(u){)}^{-1}$, respectively, corresponding to the hazared rate $a\left(x\right)=f\left(x\right)/\overline{F}\left(x\right)$ and reversed hazared rate $\overline{a}\left(x\right)=f\left(x\right)/F\left(x\right)$ of X. In doubly truncation, Ruiz and Navarro (1996) defined the generalised hazard function (GHF) given by $h_1(t_1,t_2)=f\left(t_1\right)/\left(F\left(t_2\right)-F\left(t_1\right)\right)$ and $h_2(t_1,t_2)=f\left(t_2\right)/\left(F\right(t_2)-F(t_1\left)\right)$, respectively. Thus, generalised quantile hazard functions (GQHF) are defined as (9) $\begin{array}{rl}\text{̧}{h}_1(u_1,u_2)& =\frac{1}{(u_2-u_1)q\left(u_1\right)}\mathrm{and}\\ \text{̧}{h}_2(u_1,u_2)& =\frac{1}{(u_2-u_1)q\left(u_2\right)},\end{array}$(9) respectively. Equation (8(8) $\begin{array}{rl}\text{̧}H(u_1,u_2)& =-{\int }_{u_1}^{u_2}\frac{f\left(Q\right(p\left)\right)}{(u_2-u_1)}\log \frac{f\left(Q\right(p\left)\right)}{u_2-u_1}\mathrm{d}Q\left(p\right)\\ & =\log (u_2-u_1)\\ & +\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\log \left(q\right(p\left)\right)\mathrm{d}p.\end{array}$(8) ) can be rewritten as (10) $\begin{array}{rl}\text{̧}H(u_1,u_2)& =1-\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\log A\left(p\right)\mathrm{d}p\\ & +\frac{1}{(u_2-u_1)}\left[\right(1-u_2)\log (1-u_2)\\ & -(1-u_1)\log (1-u_1)+\log (u_2-u_1)],\end{array}$(10) (11) $\begin{array}{rl}\text{̧}H(u_1,u_2)& =1-\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\log \overline{A}\left(p\right)\mathrm{d}p\\ & +\frac{1}{(u_2-u_1)}[u_2\log (u_2-u_1)\log u_1\\ & +\log (u_2-u_1)]\end{array}$(11) where (10(10) $\begin{array}{rl}\text{̧}H(u_1,u_2)& =1-\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\log A\left(p\right)\mathrm{d}p\\ & +\frac{1}{(u_2-u_1)}\left[\right(1-u_2)\log (1-u_2)\\ & -(1-u_1)\log (1-u_1)+\log (u_2-u_1)],\end{array}$(10) ) and (11(11) $\begin{array}{rl}\text{̧}H(u_1,u_2)& =1-\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\log \overline{A}\left(p\right)\mathrm{d}p\\ & +\frac{1}{(u_2-u_1)}[u_2\log (u_2-u_1)\log u_1\\ & +\log (u_2-u_1)]\end{array}$(11) ) are the expression of quantile entropy in terms of hazard quantile function and reversed hazard quantile function, respectively. Using (6(6) $\text{̧}H\left(u\right)=\log (1-u)+(1-u{)}^{-1}{\int }_u^1\log q(p)\mathrm{d}p$(6) ), (7(8) $\overline{\text{̧}H}\left(u\right)=\log u+u^{-1}{\int }_0^u\log q\left(p\right)\mathrm{d}p.$(8) ) and (8(8) $\begin{array}{rl}\text{̧}H(u_1,u_2)& =-{\int }_{u_1}^{u_2}\frac{f\left(Q\right(p\left)\right)}{(u_2-u_1)}\log \frac{f\left(Q\right(p\left)\right)}{u_2-u_1}\mathrm{d}Q\left(p\right)\\ & =\log (u_2-u_1)\\ & +\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\log \left(q\right(p\left)\right)\mathrm{d}p.\end{array}$(8) ), the quantile entropy (5(5) $\text{̧}H={\int }_0^1\log q\left(p\right)\mathrm{d}p$(5) ) can be decomposed as (12) $\begin{array}{rl}\text{̧}H& =u_1\overline{\text{̧}H}\left(u_1\right)+(u_2-u_1)\text{̧}H(u_1,u_2)+(1-u_2)\text{̧}H\left(u_2\right)\\ & -[u_1\log u_1+(u_2-u_1)\log (u_2-u_1)\\ & +(1-u_2)\log (1-u_2)].\end{array}$(12) The identity (12(12) $\begin{array}{rl}\text{̧}H& =u_1\overline{\text{̧}H}\left(u_1\right)+(u_2-u_1)\text{̧}H(u_1,u_2)+(1-u_2)\text{̧}H\left(u_2\right)\\ & -[u_1\log u_1+(u_2-u_1)\log (u_2-u_1)\\ & +(1-u_2)\log (1-u_2)].\end{array}$(12) ) can be interpreted by decomposing the uncertainty about the failure of item into in the following way. into four parts:

1. The uncertainty about the failure time in $(0,u_1)$ given that the item has failed before $u_1$,

2. The uncertainty about the failure time in the interval $(u_1,u_2)$ given that the item has failed after $u_1$ but before $u_2$,

3. The uncertainty about the failure time in $(u_2,\mathrm{\infty })$ given that it has failed after $u_2$,

4. The uncertainty of the item that has failed before $u_1$ or in between $u_1$ and $u_2$ or after $u_2$,

   Differentiating $\text{̧}H(u_1,u_2)$ with respect to $u_1$ and $u_2$, we have (13) $\begin{array}{rl}\frac{\mathrm{\partial }\text{̧}H(u_1,u_2)}{\mathrm{\partial }{u}_1}& =\text{̧}{h}_1(u_1,u_2)\left(\log \text{̧}{h}_1(u_1,u_2)\right.\\ & \left.+\text{̧}H(u_1,u_2)-1\right)\end{array}$(13) and (14) $\begin{array}{rl}\frac{\mathrm{\partial }\text{̧}H(u_1,u_2)}{\mathrm{\partial }{u}_2}& =-\text{̧}{h}_2(u_1,u_2)\left(\log \text{̧}{h}_2(u_1,u_2)\right.\\ & \left.+\text{̧}H(u_1,u_2)-1\right).\end{array}$(14)

When $\text{̧}H(u_1,u_2)$ is increasing in $u_1$ and $u_2$, then, (13(13) $\begin{array}{rl}\frac{\mathrm{\partial }\text{̧}H(u_1,u_2)}{\mathrm{\partial }{u}_1}& =\text{̧}{h}_1(u_1,u_2)\left(\log \text{̧}{h}_1(u_1,u_2)\right.\\ & \left.+\text{̧}H(u_1,u_2)-1\right)\end{array}$(13) ) and (14(14) $\begin{array}{rl}\frac{\mathrm{\partial }\text{̧}H(u_1,u_2)}{\mathrm{\partial }{u}_2}& =-\text{̧}{h}_2(u_1,u_2)\left(\log \text{̧}{h}_2(u_1,u_2)\right.\\ & \left.+\text{̧}H(u_1,u_2)-1\right).\end{array}$(14) ) together imply $\begin{array}{rl}& (1-\log \text{̧}{h}_1(u_1,u_2\left)\right)\\ & \le \text{̧}H(u_1,u_2)\le \left(1-\log \text{̧}{h}_2(u_1,u_2)\right).\end{array}$

Nair and Rajesh (2000) gave some applications of geometric vitality function. Sunoj et al. (2009) discussed few properties of this measure and showed that it determines the distribution function uniquely. Next, we define the quantile-based geometric vitality function.

Definition 2.1

Let X be a non-negative random variable then geometric vitality quantile function (GVQF) for a doubly truncated random variable is defined by (15) $\begin{array}{rl}G(u_1,u_2)& =E(\log X|u_1<X<u_2)\\ & =\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}fQ\left(p\right)q\left(p\right)\log Q\left(p\right)\mathrm{d}p\\ & =\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\log Q\left(p\right)\mathrm{d}p.\end{array}$(15)

This gives the geometric mean life of a doubly truncated random variable between the points $u_1$ and $u_2$. Relationships between geometric vitality quantile function (15(15) $\begin{array}{rl}G(u_1,u_2)& =E(\log X|u_1<X<u_2)\\ & =\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}fQ\left(p\right)q\left(p\right)\log Q\left(p\right)\mathrm{d}p\\ & =\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\log Q\left(p\right)\mathrm{d}p.\end{array}$(15) ) for doubly truncated random variables and generalised hazard quantile function (9(9) $\begin{array}{rl}\text{̧}{h}_1(u_1,u_2)& =\frac{1}{(u_2-u_1)q\left(u_1\right)}\mathrm{and}\\ \text{̧}{h}_2(u_1,u_2)& =\frac{1}{(u_2-u_1)q\left(u_2\right)},\end{array}$(9) ) are given in Table 1.

Table 1. Relationship between GVQF and GHQF.

Distribution	Quantile Functions	$G(u_1,u_2)$
Exponential	$-{\lambda }^{-1}\log (1-u)$	$\frac{1}{\lambda }\left[\text{̧}{h}_1\right(u_1,u_2)\log Q(u_1)-\text{̧}{h}_2(u_1,u_2)\log Q(u_2)+R(u_1,u_2\left)\right]$
Finite Range	$\frac{1}{a}(1-(1-u{)}^{1/b})$	$\frac{1}{\left(ab\right)}\left[\right(1-aQ\left(u_1\right)\left)\text{̧}{h}_1\right(u_1,u_2)\log Q(u_1)-(1-aQ\left(u_2\right)\left)\text{̧}{h}_2\right(u_1,u_2)\log Q(u_2)+R(u_1,u_2)-a]$
Pareto-II	$\frac{1}{p}\left(\right(1-u{)}^{1/q}-1)$	$\frac{1}{\left(pq\right)}\left[\right(1+pQ\left(u_1\right)\left)\text{̧}{h}_1\right(u_1,u_2)\log Q(u_1)-(1+pQ\left(u_2\right)\left)\text{̧}{h}_2\right(u_1,u_2)\log Q(u_2)+R(u_1,u_2)+p]$
Power	$a{u}^{{}^{1/b}}$	$\log a+\frac{1}{b}\left[Q\left(u_2\right)\text{̧}{h}_2(u_1,u_2)\log \left(\frac{Q\left(u_2\right)}{a}\right)-Q\left(u_1\right)\text{̧}{h}_1(u_1,u_2)\log \left(\frac{Q\left(u_1\right)}{a}\right)-1\right]$
Pareto-1	$a(1-u{)}^{-1/b}$	$\log a+\frac{1}{b}\left[Q\left(u_2\right)\text{̧}{h}_2(u_1,u_2)\log \left(\frac{a}{Q\left(u_2\right)}\right)-Q\left(u_1\right)\text{̧}{h}_1(u_1,u_2)\log \left(\frac{a}{Q\left(u_1\right)}\right)+1\right]$

where (16) $\begin{array}{rl}R(u_1,u_2)& =E\left(\frac{1}{X}|u_1<X<u_2\right)\\ & =\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\frac{1}{Q\left(p\right)}\mathrm{d}p.\end{array}$(16)

2.1. Relationship between $H(u_1,u_2)$ and quantile condition measure of uncertainty

Based on residual life distribution, Sankaran and Gupta (1999) have introduced a new measure of uncertainty known as conditional measure of uncertainty, which is defined as $M(X;t)=-E(\log f(X)|X>t)=-\left(1/\overline{F}\left(t\right)\right){\int }_t^{\mathrm{\infty }}f\left(x\right)\log f\left(x\right)\mathrm{d}x.$ The doubly truncated situation was considered in Sunoj et al. (2009) given as follows $M(X;t_1,t_2)=-E(\log f(X)|t_1<X<t_2)=\left(\right(-1\left)/\left(F\right(t_2)-F(t_1\left)\right)\right){\int }_{t_1}^{t_2}f\left(x\right)\log f\left(x\right)\mathrm{d}x.$ Using (4(4) $Q\left(u\right)=F^{-1}\left(u\right)=inf\left\{x|F\right(x)\ge u\},0\le u\le 1.$(4) ), the quantile-based condition measure of uncertainty for the doubly truncated random variable defined as (17) $\begin{array}{rl}& \text{̧}M(u_1,u_2)\\ & =-\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}f\left(Q\right(u\left)\right)\log f\left(Q\right(u\left)\right)\mathrm{d}Q\left(u\right)\\ & =\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\log q\left(u\right)\mathrm{d}u.\end{array}$(17) Using (17(17) $\begin{array}{rl}& \text{̧}M(u_1,u_2)\\ & =-\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}f\left(Q\right(u\left)\right)\log f\left(Q\right(u\left)\right)\mathrm{d}Q\left(u\right)\\ & =\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\log q\left(u\right)\mathrm{d}u.\end{array}$(17) ) in (8(8) $\begin{array}{rl}\text{̧}H(u_1,u_2)& =-{\int }_{u_1}^{u_2}\frac{f\left(Q\right(p\left)\right)}{(u_2-u_1)}\log \frac{f\left(Q\right(p\left)\right)}{u_2-u_1}\mathrm{d}Q\left(p\right)\\ & =\log (u_2-u_1)\\ & +\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\log \left(q\right(p\left)\right)\mathrm{d}p.\end{array}$(8) ), we obtain (18) $\text{̧}M(u_1,u_2)=\text{̧}H(u_2-u_1)-\log (u_2-u_1).$(18) Differentiation of (18(18) $\text{̧}M(u_1,u_2)=\text{̧}H(u_2-u_1)-\log (u_2-u_1).$(18) ) with respect to $u_1$ and $u_2,$ respectively, provides the relationships with GHQF, which is given as $\mathrm{\partial }\text{̧}M(u_1,u_2)/\mathrm{\partial }{u}_1=\mathrm{\partial }\text{̧}H(u_1,u_2)/\mathrm{\partial }{u}_1+\text{̧}{h}_1(u_1,u_2),$ and $\mathrm{\partial }\text{̧}M(u_1,u_2)/\mathrm{\partial }{u}_2=\mathrm{\partial }\text{̧}H(u_1,u_2)/\mathrm{\partial }{u}_2-\text{̧}{h}_2(u_1,u_2).$ The various relationships between the quantile condition measure of uncertainty (17(17) $\begin{array}{rl}& \text{̧}M(u_1,u_2)\\ & =-\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}f\left(Q\right(u\left)\right)\log f\left(Q\right(u\left)\right)\mathrm{d}Q\left(u\right)\\ & =\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\log q\left(u\right)\mathrm{d}u.\end{array}$(17) ) and GHQF (9(9) $\begin{array}{rl}\text{̧}{h}_1(u_1,u_2)& =\frac{1}{(u_2-u_1)q\left(u_1\right)}\mathrm{and}\\ \text{̧}{h}_2(u_1,u_2)& =\frac{1}{(u_2-u_1)q\left(u_2\right)},\end{array}$(9) ) for some commonly used probability models are given in Table 2.

Table 2. Relation between $\text{̧}M(u_1,u_2)$ and GHQF for various distributions.

Distribution	$\text{Quantile Functions}$	$\text{̧}M(u_1,u_2)$
Exponential	$-{\lambda }^{-1}\log (1-u)$	$\lambda m(u_1,u_2)-\log \lambda$
Finite range	$\frac{1}{a}(1-(1-u{)}^{1/b})$	$-\log ab+(-b+1)E[\log (1-aX\left)\right|u_1<X<u_2]$
Pareto -II	$\frac{1}{p}\left(\right(1-u{)}^{1/q}-1)$	$(q+1)E[\log (1+pQ\left(u\right)\left)\right|u_1<X<u_2]-\log pq$
Power	$a{u}^{{}^{1/b}}$	$\left(\frac{b-1}{b}\right)\left[1+Q\left(u_1\right)\text{̧}{h}_1(u_1,u_2)\log \left(\frac{Q\left(u_1\right)}{a}\right)-Q\left(u_2\right)\text{̧}{h}_2(u_1,u_2)\log \left(\frac{Q\left(u_2\right)}{a}\right)\right]+\log \left(\frac{a}{b}\right)$
Pareto -I	$a(1-u{)}^{-1/b}$	$\left(\frac{b+1}{b}\right)\left[1-Q\left(u_1\right)\text{̧}{h}_1(u_1,u_2)\log \left(\frac{a}{Q\left(u_1\right)}\right)+Q\left(u_2\right)\text{̧}{h}_2(u_1,u_2)\log \left(\frac{a}{Q\left(u_2\right)}\right)\right]+\log \left(\frac{a}{b}\right)$
Weibull	$(-\log (1-u){)}^{1/p}$	$-\log p-(p-1)G(u_1,u_2)+E\left[\right(X{)}^p|u_1<X<u_2]$
Rayleigh	$(-\log (1-u){)}^{1/2}$	$-\log 2-\log G(u_1,u_2)+E\left[\right(X{)}^2|u_1<X<u_2]$

3. Quantile interval entropy for various univariate distributions

In reliability theory, while studying the lifetime of a component or a system, a flexible model which is used in the literature is that of a generalised Pareto distribution (GPD) with survival function $\overline{F}\left(x\right)={\left(\frac{b}{ax+b}\right)}^{1/a+1},x>0b>0,a>-1.$ It plays an important role in extreme value theory and other branches of statistics. The GPD, as a family of distributions, includes the exponential distribution when $a\to 0,$ the Pareto type-II distribution or Lomax distribution for $a>0,$ which is used in the investigation of city population, occurrence of natural resources, insurance risk, size of human settlements, reliability modelling and business failure. It has been an important model in many socio-economic studies. The GPD becomes power distribution for $-1<a<0$. Next, let us discuss some examples on expression for quantile interval entropy function for some commonly used univariate distribution.

Example 3.1

If X is a random variable following the GPD with quantile function and quantile density function are given, respectively, by $Q\left(p\right)=\left(b/a\right)\left(\right(1-p{)}^{-a/\left(a+1\right)}-1)$ and $q\left(p\right)=\left(b/\right(a+1\left)\right)(1-p{)}^{-\left(\right(2a+1\left)/\right(a+1\left)\right)}$. Hence quantile interval entropy (8(8) $\begin{array}{rl}\text{̧}H(u_1,u_2)& =-{\int }_{u_1}^{u_2}\frac{f\left(Q\right(p\left)\right)}{(u_2-u_1)}\log \frac{f\left(Q\right(p\left)\right)}{u_2-u_1}\mathrm{d}Q\left(p\right)\\ & =\log (u_2-u_1)\\ & +\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\log \left(q\right(p\left)\right)\mathrm{d}p.\end{array}$(8) ) for GPD is given by $\begin{array}{rl}& \text{̧}H(u_1,u_2)\\ & =\log (u_2-u_1)+\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\log q\left(p\right)\mathrm{d}p\\ & =\log (u_2-u_1)+\frac{1}{(u_2-u_1)}\\ & {\int }_{u_1}^{u_2}\log \left[\left(\frac{b}{a+1}\right){\left(1-p\right)}^{-}\left(\frac{2a+1}{a+1}\right)\right]\mathrm{d}p,\\ & =\log (u_2-u_1)+\frac{\log \left(\frac{b}{a+1}\right)}{(u_2-u_1)}{\int }_{u_1}^{u_2}\mathrm{d}p\\ & -\left(\frac{2a+1}{(a+1)(u_2-u_1)}\right){\int }_{u_1}^{u_2}\log (1-p)\mathrm{d}p,\end{array}$ which gives, (19) $\begin{array}{rl}\text{̧}H(u_1,u_2)& =\log (u_2-u_1)+\log \left(\frac{b}{a+1}\right)\\ & -\left(\frac{2a+1}{a+1}\right)\frac{1}{(u_2-u_1)}\left[(1-u_2)\right.\\ & \left(1-\log (1-u_2)\right)-(1-u_1)\\ & \left.\left(1-\log (1-u_1)\right)\right].\end{array}$(19) When $u_1=u$ and $u_2=1,$ then (19(19) $\begin{array}{rl}\text{̧}H(u_1,u_2)& =\log (u_2-u_1)+\log \left(\frac{b}{a+1}\right)\\ & -\left(\frac{2a+1}{a+1}\right)\frac{1}{(u_2-u_1)}\left[(1-u_2)\right.\\ & \left(1-\log (1-u_2)\right)-(1-u_1)\\ & \left.\left(1-\log (1-u_1)\right)\right].\end{array}$(19) ) reduces to $\text{̧}H\left(u\right)=\log \left(b/\right(a+1\left)\right)+\left(\right(2a+1\left)/\right(a+1\left)\right)-\left(a/\right(a+1\left)\right)\log (1-u),$ the quantile residual entropy (6(6) $\text{̧}H\left(u\right)=\log (1-u)+(1-u{)}^{-1}{\int }_u^1\log q(p)\mathrm{d}p$(6) ) for GPD. Also when $u_1=0$ and $u_2=u$, then (19(19) $\begin{array}{rl}\text{̧}H(u_1,u_2)& =\log (u_2-u_1)+\log \left(\frac{b}{a+1}\right)\\ & -\left(\frac{2a+1}{a+1}\right)\frac{1}{(u_2-u_1)}\left[(1-u_2)\right.\\ & \left(1-\log (1-u_2)\right)-(1-u_1)\\ & \left.\left(1-\log (1-u_1)\right)\right].\end{array}$(19) ) reduces to $\overline{\text{̧}H}\left(u\right)=\log \left(b/\right(a+1\left)\right)+\left(\right(2a+1\left)/\right(a+1\left)\right)+\log u+\left(\right(2a+1\left)/\right(a+1\left)\right)\left[\right(\left(1-u\right)/u)\log (1-u)+1],$ the quantile past entropy (7(8) $\overline{\text{̧}H}\left(u\right)=\log u+u^{-1}{\int }_0^u\log q\left(p\right)\mathrm{d}p.$(8) ) for GPD.

Example 3.2

If random variable X having the Pareto-II distribution with quantile function and quantile density function are given, respectively, by $Q\left(p\right)=a\left(\right(1-p{)}^{-1/b}-1)$ and $q\left(p\right)=\left(a/b\right)(1-p{)}^{-(1+b)/b}$. Then quantile interval entropy (8(8) $\begin{array}{rl}\text{̧}H(u_1,u_2)& =-{\int }_{u_1}^{u_2}\frac{f\left(Q\right(p\left)\right)}{(u_2-u_1)}\log \frac{f\left(Q\right(p\left)\right)}{u_2-u_1}\mathrm{d}Q\left(p\right)\\ & =\log (u_2-u_1)\\ & +\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\log \left(q\right(p\left)\right)\mathrm{d}p.\end{array}$(8) ) becomes $\begin{array}{rl}\text{̧}H(u_1,u_2)& =\log (u_2-u_1)+\frac{1}{(u_2-u_1)}\\ & {\int }_{u_1}^{u_2}\log \left(\frac{a}{b}(1-p{)}^{\left(-(1+b)\right)/b}\right)\mathrm{d}p\\ & =\log (u_2-u_1)+\frac{\log \left(\frac{a}{b}\right)}{(u_2-u_1)}{\int }_{u_1}^{u_2}\mathrm{d}p\\ & -\frac{(1+b)}{b(u_2-u_1)}{\int }_{u_1}^{u_2}\log (1-p)\mathrm{d}p\\ & =\log (u_2-u_1)+\log \left(\frac{a}{b}\right)\\ & -\frac{(1+b)}{b(u_2-u_1)}[\left(1-u_2)\left(1-\log (1-u_2)\right)\right.\\ & \left.-(1-u_1)(1-\log (1-u_1)\right)].\end{array}$

Example 3.3

If a random variable X follows the rescaled beta distribution distribution with quantile and quantile density functions are given, respectively, by $Q\left(p\right)=R(1-(1-p{)}^{1/c})$ and $q\left(p\right)=\left(R/c\right)(1-p{)}^{(1-c)/c}$. Then quantile interval entropy for the rescaled beta distribution is given as $\begin{array}{rl}\text{̧}H(u_1,u_2)& =\log (u_2-u_1)+\frac{1}{(u_2-u_1)}\\ & {\int }_{u_1}^{u_2}\log \left(\frac{R}{c}(1-p{)}^{(1-c)/c}\right)\mathrm{d}p,\\ & =\log (u_2-u_1)+\frac{\log \left(\frac{R}{c}\right)}{(u_2-u_1)}{\int }_{u_1}^{u_2}\mathrm{d}p\\ & +\frac{(1-c)}{c(u_2-u_1)}{\int }_{u_1}^{u_2}\log (1-p)\mathrm{d}p\end{array}$ which gives, $\begin{array}{rl}\text{̧}H(u_1,u_2)& =\log (u_2-u_1)+\log \left(\frac{R}{c}\right)\\ & +\left(\frac{1-c}{c}\right)\left(\frac{1}{u_2-u_1}\right)\\ & \left[\right(1-u_2\left)\right(1-\log (1-u_2))\\ & -(1-u_1)(1-\log (1-u_1\left)\right)].\end{array}$

Example 3.4

If a random variable X having half logistic distribution with quantile and quantile density functions as $Q\left(p\right)=\sigma \log \left(\right(1+p\left)/\right(1-p\left)\right)$ and $q\left(p\right)=2\sigma /(1-p)(1+p)$, respectively. Then quantile interval entropy (8(8) $\begin{array}{rl}\text{̧}H(u_1,u_2)& =-{\int }_{u_1}^{u_2}\frac{f\left(Q\right(p\left)\right)}{(u_2-u_1)}\log \frac{f\left(Q\right(p\left)\right)}{u_2-u_1}\mathrm{d}Q\left(p\right)\\ & =\log (u_2-u_1)\\ & +\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\log \left(q\right(p\left)\right)\mathrm{d}p.\end{array}$(8) ) for half logistic distribution is given as $\begin{array}{rl}\text{̧}H(u_1,u_2)& =\log (u_2-u_1)+\frac{1}{(u_2-u_1)}\\ & {\int }_{u_1}^{u_2}\log \left(\frac{2\sigma }{(1-p)(1+p)}\right)\mathrm{d}p,\\ & =\log (u_2-u_1)+\log 2\sigma \\ & -\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\log (1-p)(1+p)\mathrm{d}p.\end{array}$ after some algebraic simplifications, we obtain (20) $\begin{array}{rl}\text{̧}H(u_1,u_2)& =\log (u_2-u_1)+\log \left(2\sigma \right)\\ & -\frac{1}{(u_2-u_1)}(1-u_2)(1-\log (1-u_2\left)\right)\\ & +\frac{1}{(u_2-u_1)}(1-u_1)(1-\log (1-u_1\left)\right)\\ & -\frac{1}{(u_2-u_1)}(1+u_2)(\log (1+u_2)-1)\\ & +\frac{1}{(u_2-u_1)}(1+u_1)(\log (1+u_1)-1).\end{array}$(20) Put $u_1=u$ and $u_2=1,$ in (20(20) $\begin{array}{rl}\text{̧}H(u_1,u_2)& =\log (u_2-u_1)+\log \left(2\sigma \right)\\ & -\frac{1}{(u_2-u_1)}(1-u_2)(1-\log (1-u_2\left)\right)\\ & +\frac{1}{(u_2-u_1)}(1-u_1)(1-\log (1-u_1\left)\right)\\ & -\frac{1}{(u_2-u_1)}(1+u_2)(\log (1+u_2)-1)\\ & +\frac{1}{(u_2-u_1)}(1+u_1)(\log (1+u_1)-1).\end{array}$(20) ), we have the quantile residual entropy for the half logistic distribution which is given by $\begin{array}{rl}& \text{̧}H\left(u\right)=3+\log 2\sigma -\frac{2}{(1-u)}\log 2\\ & +\log (1-u)+\frac{2}{(1-u)}\log (1+u),\end{array}$ and for $u_1=0$ and $u_2=u$ then we get quantile past entropy for the half logistic distribution as $\begin{array}{rl}\overline{\text{̧}H}\left(u\right)& =2+\log u+\log 2\sigma -\left(\frac{1+u}{u}\right)\log (1+u)\\ & +\left(\frac{1-u}{u}\right)\log (1-u).\end{array}$

Example 3.5

If a random variable X having log logistic distribution with quantile function and quantile density function are respectively given as $Q\left(p\right)=\left(1/a\right)\left(\right(p/\left(1-p\right){)}^{1/b})$ and $q\left(p\right)=\left(1/ab\right)\left(p/\right(1-p\left){)}^{1/b}\right(\left(p\right(1-p){)}^{-1}$. Then quantile interval entropy for log logistic distribution is given as $\begin{array}{rl}& \text{̧}H(u_1,u_2)\\ & =\log (u_2-u_1)+\frac{1}{(u_2-u_1)}\\ & {\int }_{u_1}^{u_2}\log \left(\frac{1}{ab}{\left(\frac{p}{1-p}\right)}^{1/b}{\left(p(1-p)\right)}^{-1}\right)\mathrm{d}p,\\ & =\log (u_2-u_1)+\log \left(\frac{1}{ab}\right)+\frac{1}{(u_2-u_1)}\\ & {\int }_{u_1}^{u_2}\log \left({\left(\frac{p}{1-p}\right)}^{1/b}{\left(p(1-p)\right)}^{-1}\right)\mathrm{d}p,\\ & =\log (u_2-u_1)+\log \left(\frac{1}{ab}\right)+\frac{(1-b)}{b(u_2-u_1)}\\ & {\int }_{u_1}^{u_2}\log p\mathrm{d}p-\frac{(1+b)}{b(u_2-u_1)}{\int }_{u_1}^{u_2}\log (1-p)\mathrm{d}p.\end{array}$ which gives, (21) $\begin{array}{rl}& \text{̧}H(u_1,u_2)\\ & =\log (u_2-u_1)+\log \left(\frac{1}{ab}\right)\\ & +\left(\frac{1-b}{b}\right)\frac{1}{(u_2-u_1)}\\ & [u_2\left(\log u_2-1\right)-u_1(\log u_1-1\left)\right]\\ & -\left(\frac{1+b}{b}\right)\frac{1}{(u_2-u_1)}\left[\right(1-u_2)\left(1-\log (1-u_2)\right)\\ & -(1-u_1)\left(1-\log (1-u_1)\right)].\end{array}$(21) Substituting $u_1=u$ and $u_2=1$ in (21(21) $\begin{array}{rl}& \text{̧}H(u_1,u_2)\\ & =\log (u_2-u_1)+\log \left(\frac{1}{ab}\right)\\ & +\left(\frac{1-b}{b}\right)\frac{1}{(u_2-u_1)}\\ & [u_2\left(\log u_2-1\right)-u_1(\log u_1-1\left)\right]\\ & -\left(\frac{1+b}{b}\right)\frac{1}{(u_2-u_1)}\left[\right(1-u_2)\left(1-\log (1-u_2)\right)\\ & -(1-u_1)\left(1-\log (1-u_1)\right)].\end{array}$(21) ), then we get quantile residual entropy for log logistic distribution given as $\begin{array}{rl}\text{̧}H\left(u\right)& =2+\log \left(\frac{1}{ab}\right)+\left(\frac{b-1}{b}\right)\left(\frac{u}{1-u}\right)\log u\\ & -\left(\frac{1}{b}\right)\log (1-u),\end{array}$ whereas the quantile past entropy for log logistic distribution is obtain, when we take $u_1=0$ and $u_2=u$ is given as $\begin{array}{rl}\overline{\text{̧}H}\left(u\right)& =2-\log \left(\frac{1}{ab}\right)+\frac{1}{b}\log u\\ & +\left(\frac{1+b}{b}\right)\left(\frac{1-u}{u}\right)\log (1-u).\end{array}$

Example 3.6

Let X be a random variable having the exponential geometric distribution with quantile and quantile density functions are given, respectively, by $Q\left(p\right)=\left(1/\lambda \right)(\log (\left(1-qp\right)/\left(1-p\right)\left)\right)$ and $q\left(p\right)=\left(1/\lambda \right)\left(\right(1-q\left)/\right(1-qp\left)\right)(1-p{)}^{-1}$. Then quantile interval entropy for the exponential geometric distribution is given as $\begin{array}{rl}\text{̧}H(u_1,u_2)& =\log (u_2-u_1)+\frac{1}{(u_2-u_1)}\\ & {\int }_{u_1}^{u_2}\log \left[\frac{1}{\lambda }\left(\frac{1-q}{1-qp}\right)(1-p{)}^{-1}\right]\mathrm{d}p,\\ & =\log (u_2-u_1)+\log \left(\frac{1-q}{\lambda }\right)\\ & -\frac{1}{(u_2-u_1)}\\ & {\int }_{u_1}^{u_2}\log \left[\left(1-qp\right)(1-p)\right]\mathrm{d}p,\end{array}$ which gives (22) $\begin{array}{rl}& \text{̧}H(u_1,u_2)\\ & =\log (u_2-u_1)+\log \left(\frac{1-q}{\lambda }\right)\\ & -\frac{1}{q(u_2-u_1)}\left[\right(1-q{u}_2\left)\right(1-\log (1-u_2))\\ & -(1-q{u}_1)(1-\log (1-u_1\left)\right)]\\ & -\frac{1}{(u_2-u_1)}\left[\right(1-u_2)\left(1-\log (1-u_2)\right)\\ & -(1-u_1)(1-\log (1-u_1\left)\right)].\end{array}$(22) Particularly, if we put $u_1=u$ and $u_2=1$ in (22(22) $\begin{array}{rl}& \text{̧}H(u_1,u_2)\\ & =\log (u_2-u_1)+\log \left(\frac{1-q}{\lambda }\right)\\ & -\frac{1}{q(u_2-u_1)}\left[\right(1-q{u}_2\left)\right(1-\log (1-u_2))\\ & -(1-q{u}_1)(1-\log (1-u_1\left)\right)]\\ & -\frac{1}{(u_2-u_1)}\left[\right(1-u_2)\left(1-\log (1-u_2)\right)\\ & -(1-u_1)(1-\log (1-u_1\left)\right)].\end{array}$(22) ), then we get quantile residual entropy for the exponential geometric distribution as $\begin{array}{rl}\text{̧}H\left(u\right)& =\log 2+\log (1-u)+\log \left(\frac{1-q}{\lambda }\right)\\ & +\frac{1}{q}\left[(1-q)\log (1-q)\right.\\ & \left.-(1-qu)\log (1-qu)\right],\end{array}$ and if we take $u_1=0$ and $u_2=u,$ we get quantile past entropy for the exponential geometric distribution as $\begin{array}{rl}\overline{\text{̧}H}\left(u\right)& =\log u+\log \left(\frac{1-q}{\lambda }\right)+\left(\frac{1+q}{q}\right)\left(\frac{1}{u}\right)\\ & +\log \left(\frac{1-u}{1-qu}\right).\end{array}$

Example 3.7

If X is a random variable following the quantile function and quantile density functions of linear hazard rate distribution are given, respectively, by $Q\left(p\right)=\left(1/(a+b)\right)\log \left(\right(a+bp\left)/a(1+p)\right)$ and $q\left(p\right)=\left(\right(a+b\left)/\right(b-a\left)\right)\left(1/(a+bp)(1+p)\right)$. Hence quantile interval entropy $\text{̧}H(u_1,u_2)$ is given as $\begin{array}{rl}\text{̧}H(u_1,u_2)& =\log (u_2-u_1)\\ & +\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\log q\left(p\right)\mathrm{d}p,\\ & =\log (u_2-u_1)+\frac{1}{(u_2-u_1)}\\ & {\int }_{u_1}^{u_2}\log \left(\left(\frac{a+b}{b-a}\right)\frac{1}{(a+bp)(1+p)}\right)\mathrm{d}p,\\ & =\log (u_2-u_1)+\log \left(\frac{b+a}{b-a}\right)\\ & -\frac{1}{(u_2-u_1)}\left[{\int }_{u_1}^{u_2}\log (1+p)\mathrm{d}p\right.\\ & \left.+{\int }_{u_1}^{u_2}\log (a+bp)\mathrm{d}p\right].\end{array}$ After some algebraic simplifications, we have $\begin{array}{rl}\text{̧}H(u_1,u_2)& =2+\log (u_2-u_1)+\log \left(\frac{b+a}{b-a}\right)\\ & +\left(\frac{1+u_1}{u_2-u_1}\right)\log (1+u_1)\\ & -\left(\frac{1+u_2}{u_2-u_1}\right)\log (1+u_2)\\ & +\frac{1}{b(u_2-u_1)}\left[\right(a+b{u}_1)\log (1+b{u}_1)\\ & -(1+b{u}_2)\log (1+b{u}_2)].\end{array}$

Example 3.8

If X be a random variable following the Davies distribution (2006), that do not have any closed form expressions for distribution and density function, then QFs and quantile density functions are given, respectively, by $Q\left(p\right)=c{p}^{{\lambda }_1}(1-p{)}^{-{\lambda }_2}$ and $q\left(p\right)=c{p}^{({\lambda }_1-1)}(1-p{)}^{(-{\lambda }_2-1)}({\lambda }_{2}p+{\lambda }_1(1-p))$. Hence quantile interval entropy (8(8) $\begin{array}{rl}\text{̧}H(u_1,u_2)& =-{\int }_{u_1}^{u_2}\frac{f\left(Q\right(p\left)\right)}{(u_2-u_1)}\log \frac{f\left(Q\right(p\left)\right)}{u_2-u_1}\mathrm{d}Q\left(p\right)\\ & =\log (u_2-u_1)\\ & +\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\log \left(q\right(p\left)\right)\mathrm{d}p.\end{array}$(8) ) for Davies distribution is given by $\begin{array}{rl}\text{̧}H(u_1,u_2)& =\log (u_2-u_1)\\ & +\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\log q\left(p\right)\mathrm{d}p,\\ & =\log (u_2-u_1)+\frac{1}{(u_2-u_1)}\\ & {\int }_{u_1}^{u_2}\log \left[c{p}^{({\lambda }_1-1)}\right(1-p{)}^{(-{\lambda }_2-1)}\\ & \left({\lambda }_{2}p+{\lambda }_1(1-p)\right)]\mathrm{d}p,\\ & =\log (u_2-u_1)+\log c+\frac{1}{(u_2-u_1)}\\ & \left[({\lambda }_1-1){\int }_{u_1}^{u_2}\log p\mathrm{d}p-({\lambda }_2+1)\right.\\ & \left.{\int }_{u_1}^{u_2}\log (1-p)\mathrm{d}p\right]+\frac{1}{(u_2-u_1)}\\ & {\int }_{u_1}^{u_2}\log \left({\lambda }_{2}p+{\lambda }_1(1-p)\right)\mathrm{d}p,\end{array}$ We get, after some algebraic calculations, (23) $\begin{array}{rl}\text{̧}H(u_1,u_2)& =({\lambda }_2-{\lambda }_1+1)+\log c+\log (u_2-u_1)\\ & +\frac{({\lambda }_1-1)u_2}{(u_2-u_1)}\log u_2\\ & -\frac{u_1({\lambda }_1-1)}{(u_2-u_1)}\log u_1+\frac{({\lambda }_2+1)(1-u_2)}{(u_2-u_1)}\\ & \log (1-u_2)+({\lambda }_2+1)\\ & \frac{(1-u_1)}{(u_2-u_1)}\log (1-u_1)\\ & +\frac{({\lambda }_2{u}_2+(1-u_2\left){\lambda }_1\right)}{({\lambda }_2-{\lambda }_1)(u_2-u_1)}\log ({\lambda }_2{u}_2\\ & +(1-u_2){\lambda }_1)-\frac{({\lambda }_2{u}_1+(1-u_1\left){\lambda }_1\right)}{({\lambda }_2-{\lambda }_1)(u_2-u_1)}\\ & \log \left({\lambda }_2{u}_1+(1-u_1\right){\lambda }_1).\end{array}$(23) If we substitute $u_1=u$ and $u_2=1$, then (23(23) $\begin{array}{rl}\text{̧}H(u_1,u_2)& =({\lambda }_2-{\lambda }_1+1)+\log c+\log (u_2-u_1)\\ & +\frac{({\lambda }_1-1)u_2}{(u_2-u_1)}\log u_2\\ & -\frac{u_1({\lambda }_1-1)}{(u_2-u_1)}\log u_1+\frac{({\lambda }_2+1)(1-u_2)}{(u_2-u_1)}\\ & \log (1-u_2)+({\lambda }_2+1)\\ & \frac{(1-u_1)}{(u_2-u_1)}\log (1-u_1)\\ & +\frac{({\lambda }_2{u}_2+(1-u_2\left){\lambda }_1\right)}{({\lambda }_2-{\lambda }_1)(u_2-u_1)}\log ({\lambda }_2{u}_2\\ & +(1-u_2){\lambda }_1)-\frac{({\lambda }_2{u}_1+(1-u_1\left){\lambda }_1\right)}{({\lambda }_2-{\lambda }_1)(u_2-u_1)}\\ & \log \left({\lambda }_2{u}_1+(1-u_1\right){\lambda }_1).\end{array}$(23) ) reduces to $\begin{array}{rl}\text{̧}H\left(u\right)& =({\lambda }_2-{\lambda }_1+1)+\log c\\ & -\frac{1}{(1-u)({\lambda }_2-{\lambda }_1){\lambda }_2\log {\lambda }_2}-{\lambda }_2\log (1-u)\\ & -\frac{1}{(1-u)({\lambda }_1-1)u}\log u\\ & -\frac{\left({\lambda }_1\right(1-u)+{\lambda }_{2}u)}{(1-u)({\lambda }_2-{\lambda }_1)}\log \left({\lambda }_1\right(1-u)+{\lambda }_{2}u),\end{array}$ the quantile residual entropy (6(6) $\text{̧}H\left(u\right)=\log (1-u)+(1-u{)}^{-1}{\int }_u^1\log q(p)\mathrm{d}p$(6) ) for Davies distribution. When we put $u_1=0$ and $u_2=u$, then (23(23) $\begin{array}{rl}\text{̧}H(u_1,u_2)& =({\lambda }_2-{\lambda }_1+1)+\log c+\log (u_2-u_1)\\ & +\frac{({\lambda }_1-1)u_2}{(u_2-u_1)}\log u_2\\ & -\frac{u_1({\lambda }_1-1)}{(u_2-u_1)}\log u_1+\frac{({\lambda }_2+1)(1-u_2)}{(u_2-u_1)}\\ & \log (1-u_2)+({\lambda }_2+1)\\ & \frac{(1-u_1)}{(u_2-u_1)}\log (1-u_1)\\ & +\frac{({\lambda }_2{u}_2+(1-u_2\left){\lambda }_1\right)}{({\lambda }_2-{\lambda }_1)(u_2-u_1)}\log ({\lambda }_2{u}_2\\ & +(1-u_2){\lambda }_1)-\frac{({\lambda }_2{u}_1+(1-u_1\left){\lambda }_1\right)}{({\lambda }_2-{\lambda }_1)(u_2-u_1)}\\ & \log \left({\lambda }_2{u}_1+(1-u_1\right){\lambda }_1).\end{array}$(23) ) reduces to $\begin{array}{rl}\overline{\text{̧}H}\left(u\right)& =({\lambda }_2-{\lambda }_1+1)+\log c+{\lambda }_1\log u\\ & +\frac{({\lambda }_2+1)(1-u)}{u}\log (1-u)\\ & +\frac{({\lambda }_{2}u+(1-u\left){\lambda }_1\right)}{({\lambda }_2-{\lambda }_1)u}\log ({\lambda }_{2}u+(1-u\left){\lambda }_1\right)\\ & -\frac{{\lambda }_1}{({\lambda }_2-{\lambda }_1)u}\log {\lambda }_1,\end{array}$ the quantile past entropy (7(8) $\overline{\text{̧}H}\left(u\right)=\log u+u^{-1}{\int }_0^u\log q\left(p\right)\mathrm{d}p.$(8) ) for Davies Distribution.

Example 3.9

If X be a random variable following the Govindarajulu's distribution that do not have any closed form expressions for distribution and density function, then QFs and quantile density functions are given, respectively, by $\begin{array}{rl}Q\left(u\right)& =a\left\{\right(b+1)u^b-b{u}^{b+1}\}\mathrm{and}\\ q\left(u\right)& =ab(b+1)(1-u)u^{b-1};0\le u\le 1;a,b>0.\end{array}$ Thus quantile-based interval entropy (8(8) $\begin{array}{rl}\text{̧}H(u_1,u_2)& =-{\int }_{u_1}^{u_2}\frac{f\left(Q\right(p\left)\right)}{(u_2-u_1)}\log \frac{f\left(Q\right(p\left)\right)}{u_2-u_1}\mathrm{d}Q\left(p\right)\\ & =\log (u_2-u_1)\\ & +\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\log \left(q\right(p\left)\right)\mathrm{d}p.\end{array}$(8) ) for Govindarajulu's distribution is given as (24) $\begin{array}{rl}\text{̧}H(u_1,u_2)& =\log (u_2-u_1)+\frac{1}{(u_2-u_1)}\\ & {\int }_{u_1}^{u_2}\log ab(b+1)(1-p)p^{b-1}\mathrm{d}p,\\ & =\log (u_2-u_1)+\log ab(b+1)\\ & +\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\log (1-p)\mathrm{d}p\\ & +\frac{(b-1)}{(u_2-u_1)}{\int }_{u_1}^{u_2}\log p\mathrm{d}p\end{array}$(24) which gives $\begin{array}{rl}\text{̧}H(u_1,u_2)& =\log (u_2-u_1)+\log ab(b+1)\\ & -\left(\frac{1-u_2}{u_2-u_1}\right)\log (1-u_2)\\ & +\left(\frac{1-u_1}{u_2-u_1}\right)\log (1-u_1)\\ & +\frac{(b-1)}{u_2-u_1}\left(u_2\log u_2-u_1\log u_1\right).\end{array}$

Table 3 provides the relationships between the quantile interval entropy $\text{̧}H(u_1,u_2)$, quantile conditional expectation (25) $\begin{array}{rl}m(u_2,u_1)& =E(X|u_1<X<u_2)\\ & =\frac{1}{(u_1-u_2)}{\int }_{u_1}^{u_2}Q\left(u\right)\mathrm{d}u,\end{array}$(25) and generalised hazard quantile function $\text{̧}{h}_i(u_1,u_2);i=1,2$ for some commonly used distribution.

Table 3. Relationships between $\text{̧}{h}_i(u_1,u_2);i=1,2$ and $\text{̧}H(u_1,u_2)$.

Distribution	$\text{Quantile Functions}$	$\text{̧}H(u_1,u_2)$
Exponential	$-{\lambda }^{-1}\log (1-u)$	$\lambda m(u_1,u_2)-\lambda Q\left(u_2\right))-\log \text{̧}{h}_2(u_1,u_2)$
Finite Range	$\frac{1}{a}(1-(1-u{)}^{1/b})$	$(-b+1)E[\log (1-aQ\left(u\right)|u_1<X<u_1]-\log \frac{ab}{\left(\right(1-aQ(u_1{)}^b-((1-aQ(u_2{)}^b}$
Pareto-II	$\frac{1}{p}\left(\right(1-u{)}^{1/q}-1)$	$(q+1)E[\log (1+pQ\left(u\right)\left)\right|u_1<X<u_1]-\log \frac{pq}{\left(\right(1+pQ(u_1{)}^{-q}-((1+pQ(u_2{)}^{-q}}$
Power	$a{u}^{{}^{1/b}}$	$1+G(u_1,u_2)+Q\left(u_1\right)\text{̧}{h}_1(u_1,u_2)\log \left(\frac{Q(u_1}{a}\right)-Q\left(u_2\right)\text{̧}{h}_2(u_1,u_2)\log \left(\frac{Q(u_2}{a}\right)-\log \left[\frac{b}{{\left(\frac{Q\left(u_2\right)}{a}\right)}^b-{\left(\frac{Q\left(u_1\right)}{a}\right)}^b}\right]$
Pareto-1	$a(1-u{)}^{-1/b}$	$1+G(u_1,u_2)-Q\left(u_1\right)\text{̧}{h}_1(u_1,u_2)\log \left(\frac{a}{Q\left(u_1\right)}\right)+Q\left(u_2\right)\text{̧}{h}_2(u_1,u_2)\log \left(\frac{a}{Q\left(u_2\right)}\right)-\log \left[\frac{b}{{\left(\frac{a}{Q\left(u_1\right)}\right)}^b-{\left(\frac{a}{Q\left(u_1\right)}\right)}^b}\right]$

4. Characterisation results

In the literature, the problem of characterising probability distributions has been investigated by many researchers. The standard practice in modelling statistical data is either to derive the appropriate model based on the physical properties of the system or to choose a flexible family of distributions and then find a member of the family that is appropriate to the data. In both the situations, it would be of more use if we find characterisation theorems that explain the distribution using important measures of indices as. In this section, we discussed some characterisation theorems for lifetime distribution taking some important concepts like GHQF, GVQF and quantile-based condition Shannon's measures of uncertainty.

Theorem 4.1

Let X be a random variable defined on $(0,\mathrm{\infty })$ having the quantile function $Q\left(u\right),$ then the relationship (26) $\begin{array}{rl}G(u_1,u_2)& =\frac{1}{k}\left[\right(1+CQ\left(u_1\right)\left)\text{̧}{h}_1\right(u_1,u_2)\log Q(u_1)\\ & -(1+CQ(u_2\left)\right)\text{̧}{h}_2(u_1,u_2)\log Q\left(u_2\right)\\ & +R(u_1,u_2)+C]\end{array}$(26) where k, C are constants holds for all $(u_1,u_2)\in D$. If and only if for

1. C=0, X has exponential distribution with quantile function $Q\left(u\right)=-\left(1/\lambda \right)\log (1-u)$,

2. $C>0,$ X has Pareto distribution with quantile function $Q\left(u\right)=\left(1/a\right)(1-u{)}^{1/b},$ and

3. $C<0,$ X has finite range distribution with quantile function $Q\left(u\right)=a(1-(1-u{)}^{1/b}$.

Proof.

The if part is straightforward from the Table 1. To prove the converse, let us assume that (26(26) $\begin{array}{rl}G(u_1,u_2)& =\frac{1}{k}\left[\right(1+CQ\left(u_1\right)\left)\text{̧}{h}_1\right(u_1,u_2)\log Q(u_1)\\ & -(1+CQ(u_2\left)\right)\text{̧}{h}_2(u_1,u_2)\log Q\left(u_2\right)\\ & +R(u_1,u_2)+C]\end{array}$(26) ) holds. Using (15(15) $\begin{array}{rl}G(u_1,u_2)& =E(\log X|u_1<X<u_2)\\ & =\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}fQ\left(p\right)q\left(p\right)\log Q\left(p\right)\mathrm{d}p\\ & =\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\log Q\left(p\right)\mathrm{d}p.\end{array}$(15) ), (9(9) $\begin{array}{rl}\text{̧}{h}_1(u_1,u_2)& =\frac{1}{(u_2-u_1)q\left(u_1\right)}\mathrm{and}\\ \text{̧}{h}_2(u_1,u_2)& =\frac{1}{(u_2-u_1)q\left(u_2\right)},\end{array}$(9) ) and (16(16) $\begin{array}{rl}R(u_1,u_2)& =E\left(\frac{1}{X}|u_1<X<u_2\right)\\ & =\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\frac{1}{Q\left(p\right)}\mathrm{d}p.\end{array}$(16) ) in (26(26) $\begin{array}{rl}G(u_1,u_2)& =\frac{1}{k}\left[\right(1+CQ\left(u_1\right)\left)\text{̧}{h}_1\right(u_1,u_2)\log Q(u_1)\\ & -(1+CQ(u_2\left)\right)\text{̧}{h}_2(u_1,u_2)\log Q\left(u_2\right)\\ & +R(u_1,u_2)+C]\end{array}$(26) ), we obtain (27) $\begin{array}{rl}& {\int }_{u_1}^{u_2}fQ\left(p\right)q\left(p\right)\log Q\left(p\right)\mathrm{d}p\\ & =\frac{1}{k}\left\{\log Q\left(u_1\right)\left(1+CQ\left(u_1\right)\right)fQ\left(u_1\right)\right.\\ & \left.-\left(1+CQ\left(u_2\right)\right)fQ\left(u_2\right)\log Q\left(u_2\right)\right\}\\ & +{\int }_{u_1}^{u_2}\frac{1}{Q\left(p\right)}\mathrm{d}p\\ & +C(u_2-u_1).\end{array}$(27) Differentiating (27(27) $\begin{array}{rl}& {\int }_{u_1}^{u_2}fQ\left(p\right)q\left(p\right)\log Q\left(p\right)\mathrm{d}p\\ & =\frac{1}{k}\left\{\log Q\left(u_1\right)\left(1+CQ\left(u_1\right)\right)fQ\left(u_1\right)\right.\\ & \left.-\left(1+CQ\left(u_2\right)\right)fQ\left(u_2\right)\log Q\left(u_2\right)\right\}\\ & +{\int }_{u_1}^{u_2}\frac{1}{Q\left(p\right)}\mathrm{d}p\\ & +C(u_2-u_1).\end{array}$(27) ) with respect to $u_i,$ i=1,2 we get, after some algebraic calculations, $\frac{f^{\prime }\left(Q\right(u_i\left)\right)}{f\left(Q\right(u_i\left)\right)}=\frac{(k+C)}{(1+CQ(u_i\left)\right)},i=1,2$ or $f^{\prime }\left(Q\right(u\left)\right)/f\left(Q\right(u\left)\right)=(k+C)/(1+CQ(u\left)\right)$, which gives the required result.

Theorem 4.2

For a non-negative random variable X, the relation (28) $\text{̧}M(u_1,u_2)-\lambda m(u_1,u_2)=k,(k>0,a\mathrm{constant})$(28) holds for all $(u_1,u_2)\in D$ if and only if X follows exponential distribution with quantile function $Q\left(u\right)=-\left(1/\lambda \right)\log (1-u)$.

Proof.

The if part is straightforward from the Table 2. To prove the converse, let us assume that (28(28) $\text{̧}M(u_1,u_2)-\lambda m(u_1,u_2)=k,(k>0,a\mathrm{constant})$(28) ) holds. Then using (16(16) $\begin{array}{rl}R(u_1,u_2)& =E\left(\frac{1}{X}|u_1<X<u_2\right)\\ & =\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\frac{1}{Q\left(p\right)}\mathrm{d}p.\end{array}$(16) ) and (25(25) $\begin{array}{rl}m(u_2,u_1)& =E(X|u_1<X<u_2)\\ & =\frac{1}{(u_1-u_2)}{\int }_{u_1}^{u_2}Q\left(u\right)\mathrm{d}u,\end{array}$(25) ), (28(28) $\text{̧}M(u_1,u_2)-\lambda m(u_1,u_2)=k,(k>0,a\mathrm{constant})$(28) ) becomes (29) ${\int }_{u_1}^{u_2}\log q\left(p\right)\mathrm{d}p-\lambda {\int }_{u_1}^{u_2}Q\left(p\right)\mathrm{d}p=k(u_2-u_1).$(29) Differentiating (29(29) ${\int }_{u_1}^{u_2}\log q\left(p\right)\mathrm{d}p-\lambda {\int }_{u_1}^{u_2}Q\left(p\right)\mathrm{d}p=k(u_2-u_1).$(29) ) with respect to $u_i$, $i=1,2,$ we get, after some algebraic calculations, $f\left(Q\right(u_i\left)\right)=K{e}^{-\lambda Q\left(u_i\right)},i=1,2\mathrm{and}K>0\left(\mathrm{constant}\right)$ or $f\left(Q\right(u\left)\right)=K{e}^{-\lambda Q\left(u\right)},$ which characterise the exponential distribution.

Theorem 4.3

If X be a non-negative random variable with quantile function $Q\left(u\right),$ and constants k>0 and c>0. A relationship of the form (30) $\text{̧}M(u_1,u_2)-(c+1)G(u_1,u_2)=k,$(30) holds for $a<u_1<u_2$ with $Q\left(u_2\right)<Q\left(u_2\right)$ if and only if X follows Pareto-1 distribution with quantile function $Q\left(u\right)=\left(a/(1-u{)}^{1/c}\right)$; $a>0.$

Proof.

The if part is straightforward. To prove the converse, let us assume that (30(30) $\text{̧}M(u_1,u_2)-(c+1)G(u_1,u_2)=k,$(30) ) holds. Then using (15(15) $\begin{array}{rl}G(u_1,u_2)& =E(\log X|u_1<X<u_2)\\ & =\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}fQ\left(p\right)q\left(p\right)\log Q\left(p\right)\mathrm{d}p\\ & =\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\log Q\left(p\right)\mathrm{d}p.\end{array}$(15) ) and (16(16) $\begin{array}{rl}R(u_1,u_2)& =E\left(\frac{1}{X}|u_1<X<u_2\right)\\ & =\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\frac{1}{Q\left(p\right)}\mathrm{d}p.\end{array}$(16) ), we have (31) $\begin{array}{rl}& {\int }_{u_1}^{u_2}\log q\left(p\right)\mathrm{d}p-(c+1)\\ & {\int }_{u_1}^{u_2}\log Q\left(p\right)\mathrm{d}p=k(u_2-u_1).\end{array}$(31) Differentiating (31(31) $\begin{array}{rl}& {\int }_{u_1}^{u_2}\log q\left(p\right)\mathrm{d}p-(c+1)\\ & {\int }_{u_1}^{u_2}\log Q\left(p\right)\mathrm{d}p=k(u_2-u_1).\end{array}$(31) ) with respect to $u_i$, $i=1,2,$ we get, after some algebraic calculations $\begin{array}{rl}f\left(Q\right(u_i\left)\right)& =k_1\left(Q\right(u_i){)}^{-(c+1)},\\ & i=1,2\mathrm{and}{k}_1\left(\mathrm{constant}\right)\end{array}$ or $f\left(Q\right(u\left)\right)=k_1\left(Q\right(u){)}^{-(c+1)},$ which gives the required result.

Next, we state the characterisation of power distribution. The proof is similar to that of Theorem 4.3 and hence omitted.

Theorem 4.4

If X is a non-negative random variable with quantile function $Q\left(u\right),$ and $K>0,$ C>1 be constants. A relationship of the form $\text{̧}M(u_1,u_2)+(c-1)G(u_1,u_2)=k,$ is holds for $0<u_1<u_2<b$ with $Q\left(u_1\right)<Q\left(u_1\right)$ if and only if X follows power distribution with quantile function $Q\left(u\right)=a{u}^{1/b}$.

Theorem 4.5

Let X be a random variable defined on $(0,\mathrm{\infty })$ with quantile function $Q\left(u\right)$. Then X follows one- parameter log exponential distribution if and only if (32) $\text{̧}M(u_1,u_2)=\log A\left(\theta \right)-\theta G(u_1,u_2)-m_c(u_1,u_2),$(32) where $m_c(u_1,u_2)=E[\log C(X)|u_1<X<u_2]$ for all $(u_1,u_1)\in D.$

Proof.

The if part is straightforward from the Table 1. To prove the converse, let us assume that (32(32) $\text{̧}M(u_1,u_2)=\log A\left(\theta \right)-\theta G(u_1,u_2)-m_c(u_1,u_2),$(32) ) holds. Using (15(15) $\begin{array}{rl}G(u_1,u_2)& =E(\log X|u_1<X<u_2)\\ & =\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}fQ\left(p\right)q\left(p\right)\log Q\left(p\right)\mathrm{d}p\\ & =\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\log Q\left(p\right)\mathrm{d}p.\end{array}$(15) ) and (16(16) $\begin{array}{rl}R(u_1,u_2)& =E\left(\frac{1}{X}|u_1<X<u_2\right)\\ & =\frac{1}{(u_2-u_1)}{\int }_{u_1}^{u_2}\frac{1}{Q\left(p\right)}\mathrm{d}p.\end{array}$(16) ) in (32(32) $\text{̧}M(u_1,u_2)=\log A\left(\theta \right)-\theta G(u_1,u_2)-m_c(u_1,u_2),$(32) ), we have (33) $\begin{array}{rl}& {\int }_{u_1}^{u_2}\log f\left(Q\right(p\left)\right)\mathrm{d}p=(u_2-u_1)\log A\left(\theta \right)\\ & -\theta {\int }_{u_1}^{u_2}\log Q\left(p\right)\mathrm{d}p-{\int }_{u_1}^{u_2}\log C\left(Q\right(p\left)\right)\mathrm{d}p.\end{array}$(33) Differentiating (33(33) $\begin{array}{rl}& {\int }_{u_1}^{u_2}\log f\left(Q\right(p\left)\right)\mathrm{d}p=(u_2-u_1)\log A\left(\theta \right)\\ & -\theta {\int }_{u_1}^{u_2}\log Q\left(p\right)\mathrm{d}p-{\int }_{u_1}^{u_2}\log C\left(Q\right(p\left)\right)\mathrm{d}p.\end{array}$(33) ) with respect to $u_i,i=1,2$ we get, after some algebraic calculations, $f\left(Q\right(u_i\left)\right)=\frac{{\left(Q\left(u_i\right)\right)}^{\theta }C\left(Q\right(u_i\left)\right)}{A\left(\theta \right)},i=1,2$ or $f\left(Q\right(u\left)\right)=\left(Q\right(u\left){)}^{\theta }C\right(Q\left(u\right))/A\left(\theta \right)$, which gives the required result.

We conclude this section by characterising exponential distribution. The proof is similar to that of Theorem 4.5 and hence omitted.

Theorem 4.6

Let $X\in (0,\mathrm{\infty })$ be a random variable having absolutely continuous quantile function $Q\left(u\right)$. Then the relationship of the form $M(u_1,u_2)=\log b\left(\theta \right)-m(u_1,u_2)\log \theta -m_a(u_1,u_2),$ where $m_a(u_1,u_2)=E[\log a(X)|u_1<X<u_2]$ holds for all $(u_1,u_2)\in D$ if and only if X follows one-parameter exponential distribution.

4.1. Exploratory data analysis using Q-Q Plot

Quantile-quantile (Q-Q) plot is a diagnostic tool, which is widely used to assess the distributional similarities and differences between two independent univariate samples. It is also a popular device for checking the appropriateness of a specified probability distribution for a given univariate data. The advantages of the Q-Q plot are: The sample sizes do not need to be equal. Many distributional aspects can be simultaneously tested. For example, shifts in location, shifts in scale, changes in symmetry, and the presence of outliers can all be detected from this plot. The Q-Q plot is similar to a probability plot. For a probability plot, the quantiles for one of the data samples are replaced with the quantiles of a theoretical distribution.

Example 4.1

Consider the Rainfall data from seeded clouds and non-seeded clouds are given below: (numbers in paratheses indicate the number of repetitions of the values)

Rainfall from control clouds: 1, 4.9(2), 11.5, 17.3, 21.7, 24.4, 26.1, 26.3, 28.6, 29,36.6,41.1, 47.3, 68.5, 81.2, 87.0, 95, 147.8, 163, 243.3, 321.2, 345.5,372.4, 830.1, 1202.6.

Rainfall from seeded clouds: 4.1, 7.7, 17.5, 31.4, 32.7, 40.6, 92.4, 115.3, 118.3, 119, 129.6, 198.6, 200.7, 242.5, 255.0, 274.7(2),302.8,334.1, 430.0, 489.1, 703.4, 978, 1656, 1697.8, 2745.6. (Source: Simpson, Olsen, & Eden, 1975)

The conclusions of our data analysis are as follows:

Compare the location of the data sample (mean, median): Seeded rainfall has greater location parameter than non-seeded rainfall.

Compare scale: The interquartile range indicates the variability of seeded rainfall is greater than non-seeded rainfall.

Side by side box plots: These plot reader can draw using Table 4; non-seeded rainfall has a skew distribution,whereas seeded rainfall is symmetric.

Table 4. Numerical summary of rainfall for seeded clouds and non- seeded clouds.

	Rainfall from non-seeded clouds	Rainfall from seeded clouds
Sample size	26	26
Number of different values	25	25
Sample mean	601.8	1374.85
Sample standard deviation	849.66	1938.533
$S/\sqrt{n}$	166.63	380.18
sample min	1	4.1
Sample max	1202.6	2745.6
Next to min	4.9	7.7
Next to max	830.1	1697.8
$Q_1$	24.4	92.4
$Q_2$	44.2	221.25
$Q_3$	163	430
MQ	93.7	261.2
IQR2	277.2	675.2
$\frac{Q_2-MQ}{IQR2}$	−0.18	−0.06
Upper fence	370.9	936.4
Upper outliers	830.1,1202.6	1656,1697.8,2745.6
$\frac{MIN-MQ}{IQR2}$	−0.33	−0.38
Conclusion	Skew	symmetric

Identification of probability laws: Seeded rainfall and non-seeded data both indicates fit by exponential distribution.

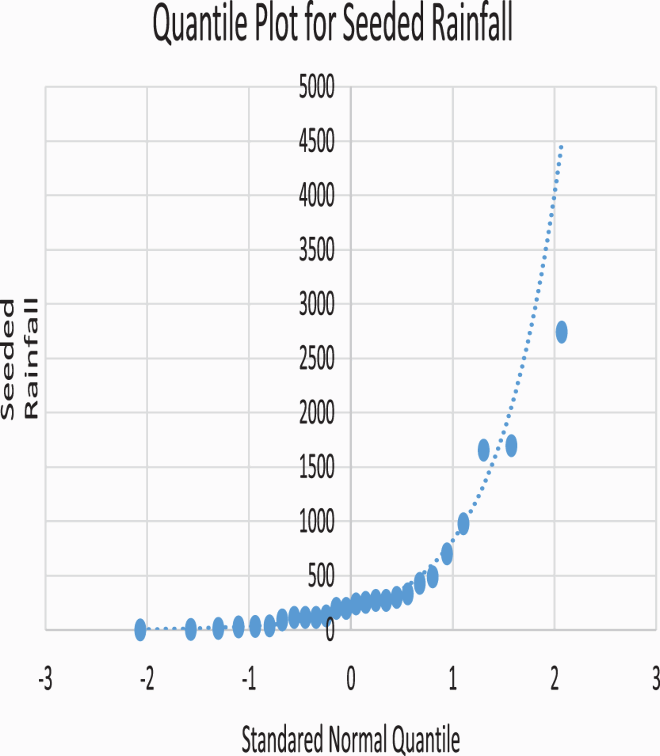
The Q-Q plot is a graphical technique for determining if two data sets come from populations with a common distribution. A Q-Q plot is a plot of the quantiles of the first data set against the quantiles of the second data set. In general for computing a normal probability plot,the standard normal table could be used to approximate the normal quantile. We look up the Z value corresponding to the $p_i$ for $i=1,2,3\cdots n$ and then plot the ordered data against the corresponding Z value. Table 5 displays the quantiles for rainfall data from seeded clouds as well as the corresponding normal quantile approximated from a standard normal table (Table 6).

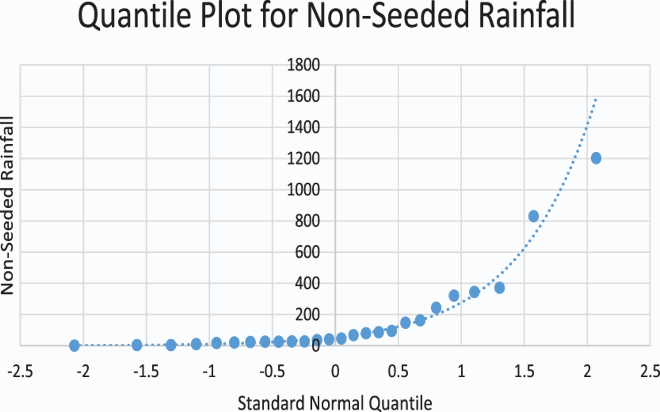
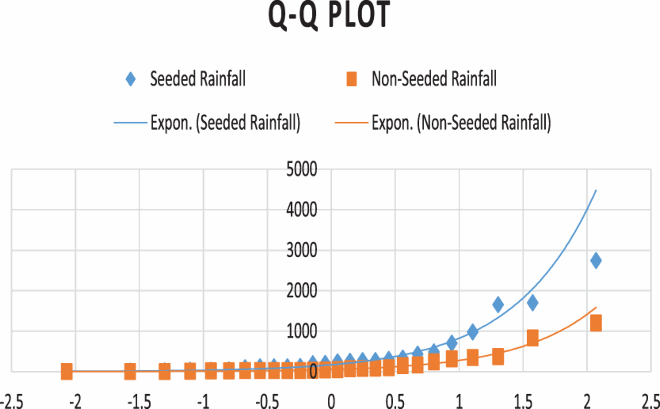
Table 5. Quantile plot table of seeded rainfall.

Rank	$Q\left(u_i\right)$	$u_i$	$Z_i$
1	4.1	.01923	−2.070
2	7.7	.076923	−1.425
3	17.5	.096154	−1.304
.	.	.	.
.	.	.	.
.	.	.	.
24	1656	.90385	1.304
25	1697	.94231	1.425
26	2745.6	.98077	2.069

Table 6. Quantile plot table of non-seeded rainfall.

Rank	$Q\left(u_i\right)$	$u_i$	$Z_i$
1	1.0	.01923	−2.070
2	4.9	.076923	−1.425
3	4.9	.096154	−1.304
4	11.5	.13462	−1.108
.	.	.	.
.	.	.	.
.	.	.	.
24	372.4	.90385	1.304
25	830.1	.94231	1.425
26	1202.6	.98077	2.070

5. Conclusion

Recently, there has been a great interest in the study of information measures based on quantile functions, namely quantile entropy. When a system has lifetime between two time points $(t_1,t_2),$ the interval entropy plays an important role, in the field of reliability theory and survival analysis. The present work introduced an alternative approach to interval entropy measure using quantile functions. The proposed measures may help information theorists and reliability analysts to study the various characteristics of a system when it fails between two time instants. The results presented here generalise the related existing results in context with quantile entropy for residual and past lifetime random variables.

Acknowledgments

The authors would like to express their gratitude to the reviewers and the editor-in-chief for their valuable comments, which have considerably improved the earlier version of the article.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

The first author wishes to acknowledge the Science and Engineering Research Board (SERB), Government of India, for the financial assistance (Ref. No. ECR/2017/001987) for carrying out this research work.

Notes on contributors

Vikas Kumar

Vikas Kumar has obtained his M.Sc and M.Phil degree in Applied Mathematics from IIT Roorkee and ISM University, Dhanbad in 2005 and 2007 respectively. He received the Ph.D. degree in Mathematics from University of Delhi, Delhi. Currently, he is a Assistant Professor in Mathematics, UIET, M. D. University, Rohtak, India. His research interests are information theory and its applications and mathematical modeling. He has published research articles in reputed international journals of Mathematics and Statistical sciences.

Gulshan Taneja

Dr. Gulshan Taneja is working as Professor in Mathematics at M. D. University, Rohtak. He has vast experience of about 25 years of teaching in mathematics and statistics both at UG and PG levels. Dr. Taneja has published more than sixty research papers in the field of Information Theory & Reliability Theory in journals of international repute and is a member of various national and international societies.

Samsher Chhoker

Samsher Chokker has obtained his M.Sc and M.Phil degree in Mathematics from M. D. University, Rohtak in 2015 and 2017 respectively. He pursuing his Ph.D. degree in Mathematics from M. D. University, Rohtak . Currently, he is a Assistant Professor in Mathematics, Government PG Nehru College Jhajjar, India. His research interests are information theory and and mathematical modeling.