Small area prediction of quantiles for zero-inflated data and an informative sample design

ABSTRACT

The Conservation Effects Assessment Project (CEAP) is a survey intended to quantify soil and nutrient loss on cropland. Estimates of the quantiles of CEAP response variables are published. Previous work develops a procedure for predicting small area quantiles based on a mixed effects quantile regression model. The conditional density function of the response given covariates and area random effects is approximated with the linearly interpolated generalised Pareto distribution (LIGPD). Empirical Bayes is used for prediction and a parametric bootstrap procedure is developed for mean squared error estimation. In this work, we develop two extensions of the LIGPD-based small area quantile prediction procedure. One extension allows for zero-inflated data. The second extension accounts for an informative sample design. We apply the procedures to predict quantiles of the distribution of percolation (a CEAP response variable) in Kansas counties.

KEYWORDS:

• Quantile regression
• mixed effects models
• bootstrap

1. Introduction

Small area estimation procedures traditionally make use of fully parametric models (Battese, Harter, & Fuller,1988). When analyzing data, evidence of nonlinearity, nonconstant variances, or outliers can make the problem of specifying an appropriate parametric form a challenging task. To address challenges in parametric modelling, several semiparametric small area estimation procedures have been proposed. Opsomer, Claeskens, Ranalli, Kauermann, and Breidt (2008) use penalised spline regression for small area estimation. Sinha and Rao (2009) consider outlier-robust estimation. Chambers and Tzavidis (2006) use M-quantile regression. See Rao and Molina (2015) for further background on the wide range of models used for small area estimation.

Berg and Lee (2019a) develop a small area procedure for estimating quantiles based on the semiparametric mixed effects quantile regression model of Jang and Wang (2015). The model of Jang and Wang (2015) approximates the conditional distribution of the response given a covariate and a random effect using a distribution that they term the linearly interpolated generalised Pareto dentisy (LIGPD). The name for the approximate density function (LIGPD) refers to the two main aspects of the approach. First, for a fine grid of interior quantiles, the LIGPD approximates the quantile function corresponding to the distribution of the response given a covariate using linear interpolation (LI). Second, an extreme value distribution, namely the generalised Pareto distribution (GPD), is used to model the distribution of the response for quantile levels that exceed the lower and upper bounds of the interior grid. We define these two aspects of the LIGPD of Jang and Wang (2015) more precisely in Section 1.2. Jang and Wang (2015) use Bayesian methods to conduct inference for the parameters of the LIGPD model. Berg and Lee(2019a) adopt the LIGPD model for small area estimation. Their interest in using the LIGPD for small area estimation stems from a survey called the Convservation Effects Assessment Project (CEAP), which is intended to measure different types of erosion. A preliminary analysis of the CEAP data indicated that finding a single parametric form to describe the distributions of all CEAP response variables of interest is difficult. As a consequence, semi-parametric procedures are of interst. Further, the CEAP survey publishes estimates of the quantiles of distributions of erosion variables, which makes an estimation procedure based on quantile regression attractive. While Jang and Wang (2015) use Bayesian methods for inference and focus on estimating the quantile regression coefficients, Berg and Lee (2019a) define a frequentist estimation procedure, an empirical Bayes predictor, and a parametric bootstrap MSE estimator. Section 1.2 defines the Berg and Lee (2019a) procedure in more detail. Berg and Lee (2019a) restrict attention to a continuous response variable and assume that the sample design is noninformative for the specified model.

We consider two extensions of the LIGPD SAE procedure developed in Berg and Lee (2019a). The first is an extension to zero-inflated data. The second is an extension to an informative sample design.

Existing small area estimation procedures for zero-inflated data utilise fully parametric models. Pfeffermann, Terryn, and Moura (2008) and Chandra and Sud (2012) consider linear mixed effects models for the non-zero component of the zero-inflated distribution. To ensure that the support of the distribution for the nonzero component is positive, Dreassi, Petrucci, and Rocco (2014) and Lyu (2018) consider gamma and lognormal distributions, respectively, for the positive component. Outside the context of small area estimation, quantile regression procedures for zero-inflated data build on the concept underlying Tobit regression. Such quantile regression procedures for zero-inflated data typically assume that the observed response variable is a truncated version of a partially observed variable with support on the real line (Buchinsky & Hahn, 1998; Powell, 1986). The partially observed variable is assumed to satisfy a standard quantile regression model. We specify a zero-inflated quantile regression model for small area estimation in the spirit of Dreassi et al. (2014) and Lyu (2018). We assume that the positive component of the model satisfies a modification of the quantile regression model of Berg and Lee (2019a). We assume a logistic mixed effects model for the probability of observing a zero.

Numerous small area procedures for an informative sample design have been developed. You and Rao (2002) use inverse selection probabilities as weights. Verret, Rao, and Hidiroglou (2015) propose an augmented model. Pfeffermann and Sverchkov (2007) exploit relationships between the sample distribution, the sample complement distribution, and the survey weights. We adapt the approach of Pfeffermann and Sverchkov (2007) to the quantile regression framework. To our knowledge, this is the first work to consider estimation of small area quantiles when the sample design is informative for the small area model.

1.1. Overview of CEAP survey data

Our interest in small area estimation for zero-inflated data under a complex sample design stems partly from a survey called the Conservation Effects Assessment Project (CEAP). The CEAP survey uses a multi-phase design. The first phase is a longitudinal survey called the National Resources Inventory (NRI) that collects information on agriculture and natural resources through visual interpretation of aerial photographs of sampled segments. The CEAP survey collects more detailed information for a subset of NRI locations through farmer interviews. Primary response variables in CEAP are measures of soil and nutrient loss that result from processing farmer interview data through a computer model called the Agricultural Policy Environmental Extender (APEX). Berg and Lee (2019a) analyze several CEAP response variables for Wisconsin. The model of Berg and Lee (2019a) is not appropriate for data with a large proportion of zeros. Their model, for example, would not be well suited to the percolation variable for Kansas, where approximately 12% of the sampled values are equal to zero. Berg and Lee (2019a) also assume that the sample design is noninformative for the specified model, an assumption that we examine more rigorously in this paper.

1.2. Overview of LIGPD small area procedure

We provide an overview of the LIGPD model and estimation procedure used in Berg and Lee (2019a). Further detail is provided in Berg and Lee (2019a) and in the supplementary document (Berg & Lee, 2019b). A sample of $n_i$ elements is selected from the population of $N_i$ elements for area i, where $i=1,\dots ,D$. Let $y_{ij}$ denote the variable of interest for unit j in area i, and assume $y_{ij}$ is observed only for sampled elements. We assume that a vector of covariates ${\mathit{x}}_{ij}$ is available for all $N_i$ elements in the population. Parameters of interest are quantiles of $\{y_{ij}:j=1,\dots ,N_i\}$.

The LIGPD model and estimator of Berg and Lee (2019a) begins with specification of a mixed effects quantile regression model. Let $b_i\sim N(0,{\sigma }_b^2)$ denote a normally distributed random effect for area i with mean 0 and variance ${\sigma }_b^2$. Assume the conditional distribution of $y_{ij}$ given $b_i$ is absolutely continuous. Denote the τth quantile of the conditional distribution of $y_{ij}$ given ${\mathit{x}}_{ij}$ and $b_i$ by $q_{ij}\left(\tau \right)$. Specifically, $q_{ij}\left(\tau \right)$ satisfies $P(y_{ij}\le q_{ij}(\tau )\mid b_i,{\mathit{x}}_{ij})=\tau$. The model underlying the LIGPD is a mixed effects quantile regression model. The model assumes that $q_{ij}\left(\tau \right)$ satisfies (1) $q_{ij}\left(\tau \right)={\mathit{x}}_{ij}^{\prime }\text{β}\left(\tau \right)+b_i,$(1) and that ${\mathit{x}}_{ij}^{\prime }\text{β}\left(\tau \right)\le {\mathit{x}}_{ij}^{\prime }\text{β}(\tau +\delta )$ for $\delta \ge 0$. The critical assumption in (1(1) $q_{ij}\left(\tau \right)={\mathit{x}}_{ij}^{\prime }\text{β}\left(\tau \right)+b_i,$(1) ) is that the area random effect $b_i$ is constant across quantile levels. Because the area random effect is fixed across quantile levels, $q_{ij}\left(\tau \right)$ is nondecreasing in τ for fixed $(i,j)$ as long as ${\mathit{x}}_{ij}^{\prime }\text{β}\left(\tau \right)\le {\mathit{x}}_{ij}^{\prime }\text{β}(\tau +\delta )$ for $\delta \ge 0$.

The LIGPD of Jang and Wang (2015) defines an approximation to the density of the conditional distribution of $y_{ij}$ given ${\mathit{x}}_{ij}$ and $b_i$, denoted as $f_Y(y\mid {\mathit{x}}_{ij},b_i,\mathit{\theta })$. The approximation for the density derives from the assumed quantile regression model (1(1) $q_{ij}\left(\tau \right)={\mathit{x}}_{ij}^{\prime }\text{β}\left(\tau \right)+b_i,$(1) ). The quantile function and the density function are related by (2) $f_Y\left(q_{ij}\right(\tau )\mid {\mathit{x}}_{ij},b_i,\mathit{\theta })=\underset{h\to 0}{lim}\frac{h}{q_{ij}(\tau +h)-q_{ij}\left(\tau \right)}.$(2) As explained in Jang and Wang (2015), the relationship (2(2) $f_Y\left(q_{ij}\right(\tau )\mid {\mathit{x}}_{ij},b_i,\mathit{\theta })=\underset{h\to 0}{lim}\frac{h}{q_{ij}(\tau +h)-q_{ij}\left(\tau \right)}.$(2) ) motivates the LIGPD approximation for $f_Y(y\mid {\mathit{x}}_{ij},b_i)$ for a grid of interior quantiles. For extreme values, the conditional distribution of $y_{ij}$ given ${\mathit{x}}_{ij}$ and $b_i$ is assumed to have a generalised Pareto distribution. We now define the LIGPD approximation precisely. Let $0<{\tau }_1<\cdots <{\tau }_K<1$ partition $(0,1)$ into K+1 evenly spaced subintervals. We use as our basis for inference the approximate density function defined in Jang and Wang (2015) by (3) $\begin{array}{rl}& f_Y(y|{\mathit{x}}_{ij},b_i,\mathit{\theta })\\ & =I[y<q_{ij}({\tau }_1\left)\right]{\tau }_1{f}_{\ell }(y|{\rho }_{\ell },{\xi }_{\ell })\\ & +I[y\ge q_{ij}({\tau }_K\left)\right](1-{\tau }_K)f_u(y|{\rho }_u,{\xi }_u)\\ & +\sum _{k=1}^{K-1}I\left[q_{ij}\right({\tau }_k)\le y<q_{ij}({\tau }_{k+1}\left)\right]\frac{{\tau }_{k+1}-{\tau }_k}{q_{ij}\left({\tau }_{k+1}\right)-q_{ij}\left({\tau }_k\right)},\end{array}$(3) where the vector of fixed parameters to be estimated is $\mathit{\theta }=({\text{β}}_K^{\prime },{\sigma }_b^{\prime },{\rho }_{\ell },{\xi }_{\ell },{\rho }_u,{\xi }_u{)}^{\prime }$, ${\text{β}}_K=\left(\text{β}\right({\tau }_1{)}^{\prime },\dots ,\text{β}({\tau }_K{)}^{\prime }{)}^{\prime }$, and $f_s(y|{\rho }_s,{\xi }_s)$ for $s=\ell ,u$ are densities of generalised Pareto distributions defined as in Jang and Wang (2015) and in Berg and Lee (2019a). For interior quantiles, the LIGPD approximates the density function as a piecewise constant function on the intervals $\left[{\mathit{x}}_{ij}^{\prime }\text{β}\right({\tau }_j),{\mathit{x}}_{ij}^{\prime }\text{β}({\tau }_{j+1}\left)\right]$ for $j=1,\dots ,J-1$. By the relationship (2(2) $f_Y\left(q_{ij}\right(\tau )\mid {\mathit{x}}_{ij},b_i,\mathit{\theta })=\underset{h\to 0}{lim}\frac{h}{q_{ij}(\tau +h)-q_{ij}\left(\tau \right)}.$(2) ), the approximation for the density function as a piece-wise constant function corresponds to an approximation for the CDF using linear interpolation. The approximation for the quantile function through linear interpolation is the inverse of the approximation for the CDF.

Using the LIGPD for small area estimation requires predicting the area random effect $b_i$. An approximation for the conditional distribution of $b_i$ given the data corresponding to (3(3) $\begin{array}{rl}& f_Y(y|{\mathit{x}}_{ij},b_i,\mathit{\theta })\\ & =I[y<q_{ij}({\tau }_1\left)\right]{\tau }_1{f}_{\ell }(y|{\rho }_{\ell },{\xi }_{\ell })\\ & +I[y\ge q_{ij}({\tau }_K\left)\right](1-{\tau }_K)f_u(y|{\rho }_u,{\xi }_u)\\ & +\sum _{k=1}^{K-1}I\left[q_{ij}\right({\tau }_k)\le y<q_{ij}({\tau }_{k+1}\left)\right]\frac{{\tau }_{k+1}-{\tau }_k}{q_{ij}\left({\tau }_{k+1}\right)-q_{ij}\left({\tau }_k\right)},\end{array}$(3) ) is given by (4) $\begin{array}{rl}& f_{b\mid y}(b_i\mid y_{i1},\dots ,y_{i{n}_i};\mathit{\theta })\\ & =\frac{\prod _{j=1}^{n_i}f(y_{ij}|{\mathit{x}}_{ij},b_i,\mathit{\theta })f_b(b_i\mid {\sigma }_b^2)}{{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\prod _{j=1}^{n_i}f(y_{ij}|{\mathit{x}}_{ij},b_i,\mathit{\theta })f_b(b_i\mid {\sigma }_b^2)\mathrm{d}{b}_i},\end{array}$(4) where $f_b(b_i\mid {\sigma }_b^2)$ is the density function of a normal distribution with mean zero and variance ${\sigma }_b^2$, and ${\mathit{y}}_i=(y_{i1},\dots ,y_{i{n}_i}{)}^{\prime }$. The density function (4(4) $\begin{array}{rl}& f_{b\mid y}(b_i\mid y_{i1},\dots ,y_{i{n}_i};\mathit{\theta })\\ & =\frac{\prod _{j=1}^{n_i}f(y_{ij}|{\mathit{x}}_{ij},b_i,\mathit{\theta })f_b(b_i\mid {\sigma }_b^2)}{{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\prod _{j=1}^{n_i}f(y_{ij}|{\mathit{x}}_{ij},b_i,\mathit{\theta })f_b(b_i\mid {\sigma }_b^2)\mathrm{d}{b}_i},\end{array}$(4) ) allows defining a Bayes (minimum MSE) predictor of the area random effect $b_i$. Specifically, the Bayes predictor of $b_i$ (for squared error loss) is given by (5) $\begin{array}{rl}& E[b_i\mid {\mathit{y}}_i;\mathit{\theta }]\\ & =\frac{{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\prod _{j=1}^{n_i}{b}_{i}f(y_{ij}|{\mathit{x}}_{ij},b_i,\mathit{\theta })f_b(b_i\mid {\sigma }_b^2)\mathrm{d}{b}_i}{{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\prod _{j=1}^{n_i}f(y_{ij}|{\mathit{x}}_{ij},b_i,\mathit{\theta })f_b(b_i\mid {\sigma }_b^2)\mathrm{d}{b}_i}.\end{array}$(5) With the predictor (5(5) $\begin{array}{rl}& E[b_i\mid {\mathit{y}}_i;\mathit{\theta }]\\ & =\frac{{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\prod _{j=1}^{n_i}{b}_{i}f(y_{ij}|{\mathit{x}}_{ij},b_i,\mathit{\theta })f_b(b_i\mid {\sigma }_b^2)\mathrm{d}{b}_i}{{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\prod _{j=1}^{n_i}f(y_{ij}|{\mathit{x}}_{ij},b_i,\mathit{\theta })f_b(b_i\mid {\sigma }_b^2)\mathrm{d}{b}_i}.\end{array}$(5) ) of $b_i$, a predictor of $q_{ij}\left(\tau \right)$ is ${\tilde{q}}_{ij}\left(\tau \right)={\mathit{x}}_{ij}^{\prime }\text{β}\left({\tau }_i\right)+E[b_i\mid {\mathit{y}}_i;\mathit{\theta }].$ The set of $\left\{{\tilde{q}}_{ij}\right({\tau }_k):k=1,\dots ,K;j=1,\dots ,N_i\}$ defines an approximation for the distribution of the population of $y_{ij}$ for $j=1,\dots ,N_i$. The predictor ${\tilde{q}}_{ij}\left(\tau \right)$ requires an estimate of the unknown $\text{β}\left({\tau }_k\right)$ for $k=1,\dots ,K$.

Berg and Lee (2019a) define an iterative procedure to estimate $\text{β}\left({\tau }_k\right)$. We summarise the critical aspects of the estimation procedure and refer the reader to Berg and Lee (2019a) and to the supplementary material (Berg & Lee, 2019b) for details. The two critical components of the estimation procedure involve (1) the use of Koenker's check function to estimate the quantile regression coefficients and (2) the use of the distribution (4(4) $\begin{array}{rl}& f_{b\mid y}(b_i\mid y_{i1},\dots ,y_{i{n}_i};\mathit{\theta })\\ & =\frac{\prod _{j=1}^{n_i}f(y_{ij}|{\mathit{x}}_{ij},b_i,\mathit{\theta })f_b(b_i\mid {\sigma }_b^2)}{{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\prod _{j=1}^{n_i}f(y_{ij}|{\mathit{x}}_{ij},b_i,\mathit{\theta })f_b(b_i\mid {\sigma }_b^2)\mathrm{d}{b}_i},\end{array}$(4) ) to estimate ${\sigma }_b^2$ and to predict $b_i$. Koenker's check function (Koenker, 2005) is defined as (6) ${\rho }_{\tau }\left(u\right)=u(\tau -I[u<0\left]\right).$(6) Koenker's check function is a standard objective function for estimating quantiles because $q_{ij}\left(\tau \right)={\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}_{a}E\left[{\rho }_{\tau }\right(y_{ij}-a)\mid {\mathit{x}}_{ij},b_i]$. The estimation procedure of Berg and Lee (2019a) alternates between optimisation of Koenker's check function to estimate ${\text{β}}_K$ and use of the distribution (4(4) $\begin{array}{rl}& f_{b\mid y}(b_i\mid y_{i1},\dots ,y_{i{n}_i};\mathit{\theta })\\ & =\frac{\prod _{j=1}^{n_i}f(y_{ij}|{\mathit{x}}_{ij},b_i,\mathit{\theta })f_b(b_i\mid {\sigma }_b^2)}{{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\prod _{j=1}^{n_i}f(y_{ij}|{\mathit{x}}_{ij},b_i,\mathit{\theta })f_b(b_i\mid {\sigma }_b^2)\mathrm{d}{b}_i},\end{array}$(4) ) to estimate ${\sigma }_b^2$ and to predict $b_i$. The estimates of the parameters of the extreme value distribution are obtained using a procedure recommended in Jang and Wang (2015). Note that the estimates of the parameters of the extreme value distribution are required for the LIGPD approximation but are not explicitly part of the specified quantile regression model (1(1) $q_{ij}\left(\tau \right)={\mathit{x}}_{ij}^{\prime }\text{β}\left(\tau \right)+b_i,$(1) ). In this sense, the estimates of the extreme value distribution are less central than the estimates of ${\text{β}}_K$ and ${\sigma }_b^2$. We define the estimator of the extreme value distribution that we use for zero-inflated data precisely in Section 2.

Given estimates $\widehat{\text{β}}\left({\tau }_k\right)$ and ${\hat{\sigma }}_b^2$, one can construct predictors of small area parameters. A predictor of $q_{ij}\left({\tau }_k\right)$ is given by ${\hat{q}}_{ij}\left({\tau }_k\right)={\mathit{x}}_{ij}^{\prime }\widehat{\text{β}}\left({\tau }_k\right)+E[b_i\mid {\mathit{y}}_i,\hat{\mathit{\theta }}],$ where $\widehat{\text{β}}\left({\tau }_k\right)$ is the estimator of $\text{β}\left({\tau }_k\right)$. The $\left\{{\hat{q}}_{ij}\right({\tau }_k):j=1,\dots ,N_i;k=1,\dots ,K\}$ approximates the distribution of $\{y_{ij}:j=1,\dots ,N_i\}$. We use $\left\{{\hat{q}}_{ij}\right({\tau }_k):j=1,\dots ,N_i;k=1,\dots ,K\}$ to define small area predictors, as in Berg and Lee (2019a). Define a predictor of the τth population quantile for area i by (7) $\begin{array}{rl}{\hat{q}}_i\left(\tau \right)& =min\left\{{\hat{q}}_{ij}\right({\tau }_k):{\hat{F}}_{y_i}({\hat{q}}_{ij}\left({\tau }_k\right))\ge \tau ;\\ j& =1,\dots ,N_i;k=1,\dots ,K\},\end{array}$(7) where ${\hat{F}}_{y_i}\left(t\right)=\left(N_{i}K{)}^{-1}\sum _{j=1}^{N_i}\sum _{k=1}^{K}I\right[{\hat{q}}_{ij}\left({\tau }_k\right)\le t]$.

1.3. Outline

We extend the LIGPD model and estimation procedure outlined in Section 1.2 to zero-inflated data and an informative sample design. In Section 2, we describe the extension to zero-inflated data. In Section 3, we describe the extension to the informative sample design. In Section 4, we illustrate the procedures using the variable percolation for Kansas.

2. Zero-Inflated model and estimation procedure

We modify the LIGPD model and estimation procedure of Section 1.2 for a case in which the support of $y_{ij}$ is $[0,\mathrm{\infty })$. As discussed in Section 1, several examples in which small area estimates of a zero-inflated variable are of interest exist in small area estimaton (SAE) literature. For instance, $y_{ij}$ may be grape production as in Dreassi et al. (2014) or $y_{ij}$ may be sheet and rill erosion as in Lyu (2018). In Section 2.1, we describe the extension of the LIGPD model to accommodate zero-inflated data. In Section 2.2, we describe the procedure to estimate the parameters of the zero-inflated model. Section 2.3 proposes a bootstrap MSE estimator. The procedures are modifications of the estimation and bootstrap MSE estimation methods defined in Berg and Lee (2019a).

Before describing the procedures in detail, we note that the method described in Section 2 is one of many possible ways to accommodate zero-inflated, positive data. We adopt the approach described below for two main reasons. First, the approach allows us to remain within the framework of modelling quantiles. Second, the estimation procedures require only minor modifications to the procedures in Berg and Lee (2019a)Berg and Lee (2019a).

2.1. Zero-Inflated mixed effects quantile regression model

Assume the support of the response variable $y_{ij}$ is $[0,\mathrm{\infty })$. As for Section 1.2, assume $y_{ij}$ is observed for a sample $A_i$ of $n_i$ elements in area i. Assume a vector of covariates $({\mathit{x}}_{ij}^{\prime },{\mathit{z}}_{ij}^{\prime }{)}^{\prime }$ is available for the full population of $N_i$ elements in area i. The parameters of interest are quantiles of $\{y_{ij}:j=1,\dots ,N_i\}$.

We specify a model with two components. One component is for the probability that $y_{ij}$ is zero. We refer to this component as the binary component. The second component is a model for the quantile of the conditional distribution given that $y_{ij}>0$. We first define the model for the binary component and then define the model for the positive component. Finally, we explain how these two models combine to form a model for the quantile of the conditional distribution of $y_{ij}$ given the covariates and area random effects.

First, we define the model for the binary component. Assume (8) $\begin{array}{rl}P(y_{ij}& =0\mid u_i,{\mathit{z}}_{ij})=(1+\exp ({\mathit{z}}_{ij}^{\prime }\mathit{\gamma }+u_i){)}^{-1}\\ & \times \exp ({\mathit{z}}_{ij}^{\prime }\mathit{\gamma }+u_i),\end{array}$(8) where $u_i\sim N(0,{\sigma }_u^2)$. The model (8(8) $\begin{array}{rl}P(y_{ij}& =0\mid u_i,{\mathit{z}}_{ij})=(1+\exp ({\mathit{z}}_{ij}^{\prime }\mathit{\gamma }+u_i){)}^{-1}\\ & \times \exp ({\mathit{z}}_{ij}^{\prime }\mathit{\gamma }+u_i),\end{array}$(8) ) is a standard mixed effects logistic regression model for $I[y_{ij}=0]$. We advise the reader to make note that the model (8(8) $\begin{array}{rl}P(y_{ij}& =0\mid u_i,{\mathit{z}}_{ij})=(1+\exp ({\mathit{z}}_{ij}^{\prime }\mathit{\gamma }+u_i){)}^{-1}\\ & \times \exp ({\mathit{z}}_{ij}^{\prime }\mathit{\gamma }+u_i),\end{array}$(8) ) is a model for the probability of observing a zero, and $P(y_{ij}>0\mid u_i,{\mathit{z}}_{ij})=1-P(y_{ij}=0\mid u_i,{\mathit{z}}_{ij})$.

Next, we define the model for the positive component. Define $q_{posij}\left(\tau \right)$ to be the τth quantile of the conditional distribution of $y_{ij}$ given $y_{ij}>0$. Specifically, $q_{posij}\left(\tau \right)$ satisfies $P(y_{ij}\le q_{posij}(\tau )\mid y_{ij}>0,b_i,{\mathit{x}}_{ij})=\tau$. We define a quantile regression model for $q_{posij}$ that is a modification of the model (1(1) $q_{ij}\left(\tau \right)={\mathit{x}}_{ij}^{\prime }\text{β}\left(\tau \right)+b_i,$(1) ) to respect the restricted sample space for $y_{ij}>0$. Define a model for $q_{posij}\left(\tau \right)$ by (9) $q_{posij}\left(\tau \right)={\mathit{x}}_{ij}^{\prime }\text{β}\left(\tau \right)\exp \left(b_i\right),$(9) where ${\mathit{x}}_{ij}^{\prime }\text{β}(\tau +\delta )\ge {\mathit{x}}_{ij}\text{β}\left(\tau \right)$ for $\delta >0$, ${\mathit{x}}_{ij}^{\prime }\text{β}\left(\tau \right)>0$ for all $\tau \in (0,1)$, and $b_i\sim \text{N}(0,{\sigma }_b^2)$.

Finally, we combine (8(8) $\begin{array}{rl}P(y_{ij}& =0\mid u_i,{\mathit{z}}_{ij})=(1+\exp ({\mathit{z}}_{ij}^{\prime }\mathit{\gamma }+u_i){)}^{-1}\\ & \times \exp ({\mathit{z}}_{ij}^{\prime }\mathit{\gamma }+u_i),\end{array}$(8) ) and (9(9) $q_{posij}\left(\tau \right)={\mathit{x}}_{ij}^{\prime }\text{β}\left(\tau \right)\exp \left(b_i\right),$(9) ) to define a model the τth quantile of the conditional distribution of $y_{ij}$ given ${\mathit{x}}_{ij},b_i,{\mathit{z}}_{ij},$ and $u_i$. Precisely, the τth quantile of the conditional distribution of $y_{ij}$, denoted $q_{ij}\left(\tau \right)$, satisfies $P(y_{ij}\le q_{ij}(\tau )\mid {\mathit{x}}_{ij},b_i,{\mathit{z}}_{ij},u_i)=\tau$. The models (8(8) $\begin{array}{rl}P(y_{ij}& =0\mid u_i,{\mathit{z}}_{ij})=(1+\exp ({\mathit{z}}_{ij}^{\prime }\mathit{\gamma }+u_i){)}^{-1}\\ & \times \exp ({\mathit{z}}_{ij}^{\prime }\mathit{\gamma }+u_i),\end{array}$(8) ) and (9(9) $q_{posij}\left(\tau \right)={\mathit{x}}_{ij}^{\prime }\text{β}\left(\tau \right)\exp \left(b_i\right),$(9) ) induce a model for $q_{ij}\left(\tau \right)$. It is the induced model for $q_{ij}\left(\tau \right)$ that we would like to use for small area prediction. The key idea to deriving the induced model for $q_{ij}\left(\tau \right)$ is the observation that for $\tau >P(y_{ij}=0\mid u_i,{\mathit{z}}_{ij})$, $q_{ij}\left(\tau \right)$ has the same functional form as $q_{posij}\left(\tau \right)$ but with shifted quantile levels. To derive the model for $q_{ij}\left(\tau \right)$, let t>0 satisfy $P(y_{ij}\le t\mid b_i,u_i,{\mathit{x}}_{ij},{\mathit{z}}_{ij})=\tau$. Observe that $\begin{array}{rl}\tau & =P(y_{ij}=0\mid b_i,u_i,{\mathit{x}}_{ij},{\mathit{z}}_{ij})\\ & +P(y_{ij}\le t\mid y_{ij}>0,b_i,u_i,{\mathit{x}}_{ij},{\mathit{z}}_{ij})P(y_{ij}\\ & >0\mid b_i,u_i,{\mathit{x}}_{ij},{\mathit{z}}_{ij}),\\ & =P(y_{ij}=0\mid u_i,{\mathit{z}}_{ij})+{\tau }^{\ast }P(y_{ij}>0\mid u_i,{\mathit{z}}_{ij}),\end{array}$ where $q_{posij}\left({\tau }^{\ast }\right)=t$. Solving for ${\tau }^{\ast }$ gives (10) $\begin{array}{r}{\tau }^{\ast }=\frac{\tau -P(y_{ij}=0\mid u_i,{\mathit{z}}_{ij})}{1-P(y_{ij}=0\mid u_i,{\mathit{z}}_{ij})}.\end{array}$(10) Then, (11) $q_{ij}\left(\tau \right)=\left\{\begin{array}{ll}0& \\ \text{if }\tau \le P(y_{ij}=0\mid u_i,{\mathit{z}}_{ij})\\ q_{posij}\left(\frac{\tau -P(y_{ij}=0\mid u_i,{\mathit{z}}_{ij})}{1-P(y_{ij}=0\mid u_i,{\mathit{z}}_{ij})}\right)& \\ \text{if }\tau >P(y_{ij}=0\mid u_i,{\mathit{z}}_{ij}).\end{array}\right.$(11) As a remark on the model for the positive component, one can consider alternatives to the model (9(9) $q_{posij}\left(\tau \right)={\mathit{x}}_{ij}^{\prime }\text{β}\left(\tau \right)\exp \left(b_i\right),$(9) ) for the quantile of the conditional distribution given that $y_{ij}$ is positive. For instance, a different approach is to use a transformation of $y_{ij}$ for $y_{ij}>0$, as in Berg and Lee (2019a). The relationship (11(11) $q_{ij}\left(\tau \right)=\left\{\begin{array}{ll}0& \\ \text{if }\tau \le P(y_{ij}=0\mid u_i,{\mathit{z}}_{ij})\\ q_{posij}\left(\frac{\tau -P(y_{ij}=0\mid u_i,{\mathit{z}}_{ij})}{1-P(y_{ij}=0\mid u_i,{\mathit{z}}_{ij})}\right)& \\ \text{if }\tau >P(y_{ij}=0\mid u_i,{\mathit{z}}_{ij}).\end{array}\right.$(11) ) holds for any $q_{posij}\left(\tau \right)>0$. In the data analysis of Section 4, we consider an expansion of the model (9(9) $q_{posij}\left(\tau \right)={\mathit{x}}_{ij}^{\prime }\text{β}\left(\tau \right)\exp \left(b_i\right),$(9) ).

To construct small area predictors according to the distribution (11(11) $q_{ij}\left(\tau \right)=\left\{\begin{array}{ll}0& \\ \text{if }\tau \le P(y_{ij}=0\mid u_i,{\mathit{z}}_{ij})\\ q_{posij}\left(\frac{\tau -P(y_{ij}=0\mid u_i,{\mathit{z}}_{ij})}{1-P(y_{ij}=0\mid u_i,{\mathit{z}}_{ij})}\right)& \\ \text{if }\tau >P(y_{ij}=0\mid u_i,{\mathit{z}}_{ij}).\end{array}\right.$(11) ), we require estimates of the model parameters. In the estimation procedure defined below, we first estimate $q_{posij}\left(\tau \right)$ and $P(y_{ij}=0\mid u_i,{\mathit{z}}_{ij})$. We then predict finite population quantiles of $y_{ij}$ according to (11(11) $q_{ij}\left(\tau \right)=\left\{\begin{array}{ll}0& \\ \text{if }\tau \le P(y_{ij}=0\mid u_i,{\mathit{z}}_{ij})\\ q_{posij}\left(\frac{\tau -P(y_{ij}=0\mid u_i,{\mathit{z}}_{ij})}{1-P(y_{ij}=0\mid u_i,{\mathit{z}}_{ij})}\right)& \\ \text{if }\tau >P(y_{ij}=0\mid u_i,{\mathit{z}}_{ij}).\end{array}\right.$(11) ). Details of the estimation and prediction procedures are defined in Section 2.2.

2.2. Estimation procedure for zero-inflated model

The estimation procedure consists of three main steps. We first estimate the parameters of the model for $q_{posij}\left(\tau \right)$. We then estimate the probability of a zero. Finally, we combine the predictor of $q_{posij}\left(\tau \right)$ with the predictor of the probability of a zero to obtain predictors of population quantiles.

2.2.1. Estimator of positive component

We use the LIGPD of (Jang & Wang, 2015) to approximate the conditional density function for $y_{ij}$ given that $y_{ij}>0$. The approximation is analogous to the approach outlined in Section 1.2, except that we use the LIGPD to approximate the conditional density of $y_{ij}$ given that $y_{ij}>0$. Define a sequence of quantile levels by ${\tau }_k=k(K+1{)}^{-1}$ for $k=1,\dots ,K$, where $K\to \mathrm{\infty }$ as $D\to \mathrm{\infty }$. The approximate density function for the conditional distribution of $y_{ij}$ given $y_{ij}>0$ and $b_i$ is defined by (12) $\begin{array}{rl}& f_Y(y|y_{ij}>0,{\mathit{x}}_{ij},b_i,\mathit{\theta })=I[y<q_{posij}({\tau }_1\left)\right]{\tau }_1{f}_{\ell }(y|{\rho }_{\ell },{\xi }_{\ell })\\ & +I[y\ge q_{posij}({\tau }_K\left)\right](1-{\tau }_K)f_u(y|{\rho }_u,{\xi }_u)\\ & +\sum _{k=1}^{K-1}I\left[q_{posij}\right({\tau }_k)\le y<q_{posij}({\tau }_{k+1}\left)\right]\\ & \times \frac{{\tau }_{k+1}-{\tau }_k}{q_{posij}\left({\tau }_{k+1}\right)-q_{posij}\left({\tau }_k\right)},\end{array}$(12) where $\mathit{\theta }=({\text{β}}_K^{\prime },{\sigma }_b^2,{\rho }_{\ell },{\xi }_{\ell },{\rho }_u,{\xi }_u{)}^{\prime }$, ${\text{β}}_K=\left(\text{β}\right({\tau }_1{)}^{\prime },\dots ,\text{β}({\tau }_K{)}^{\prime }{)}^{\prime }$ is the vector of fixed parameters to be estimated, $I[\cdot ]$ is the indicator function that is equal to 1 if the argument is true and zero otherwise, and $f_s(y|{\rho }_s,{\xi }_s)$ for $s=\ell ,u$ are densities of generalised Pareto distributions defined as follows. Letting $u_{ij}=0.5\left({\mathit{x}}_{ij}^{\prime }\text{β}\right({\tau }_K)+{\mathit{x}}_{ij}^{\prime }\text{β}({\tau }_{K-1}\left)\right)$ and ${\ell }_{ij}=0.5\left({\mathit{x}}_{ij}^{\prime }\text{β}\right({\tau }_1)+{\mathit{x}}_{ij}^{\prime }\text{β}({\tau }_2\left)\right)$, (13) $f_u(y|{\rho }_u,{\xi }_u)=\frac{1-0.5({\tau }_{K-1}+{\tau }_K)}{1-{\tau }_K}g(y-u_{ij}\mid {\rho }_u,{\xi }_u),$(13) and (14) $f_{\ell }(y|{\rho }_{\ell },{\xi }_{\ell })=\frac{0.5({\tau }_1+{\tau }_2)}{{\tau }_1}g(-y+{\ell }_{ij}\mid {\rho }_{\ell },{\xi }_{\ell }),$(14) where (15) $g(y\mid {\rho }_s,{\xi }_s)=\left\{\begin{array}{ll}{\rho }_s^{-1}(1+{\xi }_{s}y/{\rho }_s{)}^{-(1+1/{\xi }_s)},& {\xi }_s\ne 0\\ {\rho }_s^{-1}\exp (-y/{\rho }_s),& {\xi }_s=0,\end{array}\right.$(15) for $s=\ell ,u$ with y>0 for $\xi \ge 0$, and $0\le y<-\rho /\xi$ for $\xi <0$. The function (15(15) $g(y\mid {\rho }_s,{\xi }_s)=\left\{\begin{array}{ll}{\rho }_s^{-1}(1+{\xi }_{s}y/{\rho }_s{)}^{-(1+1/{\xi }_s)},& {\xi }_s\ne 0\\ {\rho }_s^{-1}\exp (-y/{\rho }_s),& {\xi }_s=0,\end{array}\right.$(15) ) is a density function of a generalised Pareto distribution. The multipliers defining (13(13) $f_u(y|{\rho }_u,{\xi }_u)=\frac{1-0.5({\tau }_{K-1}+{\tau }_K)}{1-{\tau }_K}g(y-u_{ij}\mid {\rho }_u,{\xi }_u),$(13) ) and (14(14) $f_{\ell }(y|{\rho }_{\ell },{\xi }_{\ell })=\frac{0.5({\tau }_1+{\tau }_2)}{{\tau }_1}g(-y+{\ell }_{ij}\mid {\rho }_{\ell },{\xi }_{\ell }),$(14) ) are derived in Jang and Wang (2015), and we summarise the motivation in Jang and Wang (2015) for these multipliers for internal consistency. We consider the density for the upper extreme value distribution, $f_u$, recognising that the motivation for $f_{\ell }$ is completely analogous. By the definition of $u_{ij}$, (16) $\begin{array}{rl}& P(Y>y\mid Y>u_{ij},{\mathit{x}}_{ij},b_i,u_{ij}>0)\\ & =\frac{F_Y(y\mid {\mathit{x}}_{ij},b_i,y>0)-0.5({\tau }_{K-1}+\tau K)}{1-0.5({\tau }_{K-1}+{\tau }_K)}.\end{array}$(16) Taking derivatives of both sides with respect to y gives $(1-{\tau }_K)f_u(y|{\rho }_u,{\xi }_u)=[1-0.5({\tau }_{K-1}+{\tau }_K\left){]}^{-1}{f}_Y\right(y\mid x_{ij},b_i,y>0)$. Under the assumption that the generalised Pareto distribution describes the conditional distribution of $y_{ij}$ for $y_{ij}>u_{ij}$, $g(y-u_{ij}\mid {\rho }_u,{\xi }_u)=f_Y(y\mid {\mathit{x}}_{ij},b_i,y>0)[1-({\tau }_{K-1}+{\tau }_K)/2{]}^{-1}$. The form for $f_u$ follows from setting $(1-{\tau }_K)f_u(y_{ij}\mid {\mathit{x}}_{ij},b_i,y>0)=[1-({\tau }_{K-1}+{\tau }_K\left)/2\right]g(y-u_{ij}\mid {\rho }_u,{\xi }_u)$.

Before proceeding with the prediction and estimation procedure, we add a brief comment on the relationship between the model and the LIGPD approximation, particularly the role of the generalised Pareto distribution. The assumed model for the positive component is defined in (9(9) $q_{posij}\left(\tau \right)={\mathit{x}}_{ij}^{\prime }\text{β}\left(\tau \right)\exp \left(b_i\right),$(9) ). The density function (12(12) $\begin{array}{rl}& f_Y(y|y_{ij}>0,{\mathit{x}}_{ij},b_i,\mathit{\theta })=I[y<q_{posij}({\tau }_1\left)\right]{\tau }_1{f}_{\ell }(y|{\rho }_{\ell },{\xi }_{\ell })\\ & +I[y\ge q_{posij}({\tau }_K\left)\right](1-{\tau }_K)f_u(y|{\rho }_u,{\xi }_u)\\ & +\sum _{k=1}^{K-1}I\left[q_{posij}\right({\tau }_k)\le y<q_{posij}({\tau }_{k+1}\left)\right]\\ & \times \frac{{\tau }_{k+1}-{\tau }_k}{q_{posij}\left({\tau }_{k+1}\right)-q_{posij}\left({\tau }_k\right)},\end{array}$(12) ) is an approximation that provides a tool for defining predictors and estimators. The extreme value distributions are adapted from Berg and Lee (2019a) and from Jang and Wang (2015). Conceptually, the extreme value distribution for the lower tail can be improved for the case of zero-inflated data. We retain the estimator defined in step 3 of Section 2.2.1 largely for simplicity. Based on past experiments with different estimators of the extreme value distribution, we expect the choice of the extreme value distribution to have little impact on the efficiency of the predictors.

We recognise that the use of the same notation for $\mathit{\theta }$ in the model for the zero-inflated response that we use in Section 1.2 is a slight abuse of notation. We use the same notation $\mathit{\theta }$ in defining the model for $q_{posij}\left({\tau }_k\right)$ that we use in defining the general LIGPD in Section 1.2 for simplicity. We recognise that the $\mathit{\theta }$ in (12(12) $\begin{array}{rl}& f_Y(y|y_{ij}>0,{\mathit{x}}_{ij},b_i,\mathit{\theta })=I[y<q_{posij}({\tau }_1\left)\right]{\tau }_1{f}_{\ell }(y|{\rho }_{\ell },{\xi }_{\ell })\\ & +I[y\ge q_{posij}({\tau }_K\left)\right](1-{\tau }_K)f_u(y|{\rho }_u,{\xi }_u)\\ & +\sum _{k=1}^{K-1}I\left[q_{posij}\right({\tau }_k)\le y<q_{posij}({\tau }_{k+1}\left)\right]\\ & \times \frac{{\tau }_{k+1}-{\tau }_k}{q_{posij}\left({\tau }_{k+1}\right)-q_{posij}\left({\tau }_k\right)},\end{array}$(12) ) is different from the $\mathit{\theta }$ for the unconditional distribution of Section 1.2.

An important distribution used to define estimators and predictors is the conditional distribution of $b_i$ given the data. An expression for the conditional distribution of $b_i$ given the data corresponding to the LIGPD is (17) $\begin{array}{rl}& f_{b\mid y_{pos}}(b_i\mid {\mathit{y}}_{posi};\mathit{\theta })\\ & =\frac{\begin{array}{c}\prod _{\{j\in A_i:y_{ij}>0\}}{f}_Y(y_{ij}|y_{ij}\\ >0,{\mathit{x}}_{ij},b_i,\mathit{\theta }\left)\phi \right(b_i/{\sigma }_b)\mathrm{d}{b}_i\end{array}}{\begin{array}{c}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\prod _{\{j\in A_i:y_{ij}>0\}}{f}_Y(y_{ij}|y_{ij}\\ >0,{\mathit{x}}_{ij},b_i,\mathit{\theta }\left)\phi \right(b_i/{\sigma }_b)\mathrm{d}{b}_i\end{array}},\end{array}$(17) where φ is the density function of a standard normal distribution, and ${\mathit{y}}_{posi}=\{y_{ij}:j\in A_i,y_{ij}>0\}$. If the area has no sampled units, then the conditional density of $b_i$ is that of a normal distribution with mean zero and variance ${\sigma }_b^2$. One can calculate expectations with respect to (17(17) $\begin{array}{rl}& f_{b\mid y_{pos}}(b_i\mid {\mathit{y}}_{posi};\mathit{\theta })\\ & =\frac{\begin{array}{c}\prod _{\{j\in A_i:y_{ij}>0\}}{f}_Y(y_{ij}|y_{ij}\\ >0,{\mathit{x}}_{ij},b_i,\mathit{\theta }\left)\phi \right(b_i/{\sigma }_b)\mathrm{d}{b}_i\end{array}}{\begin{array}{c}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\prod _{\{j\in A_i:y_{ij}>0\}}{f}_Y(y_{ij}|y_{ij}\\ >0,{\mathit{x}}_{ij},b_i,\mathit{\theta }\left)\phi \right(b_i/{\sigma }_b)\mathrm{d}{b}_i\end{array}},\end{array}$(17) ) to obtain Bayes predictors under squared error loss. For an integrable function $h(\cdot )$, the Bayes preditor of $h\left(b_i\right)$ for squared error loss is defined as (18) $\begin{array}{rl}& E\left[h\right(b_i)\mid {\mathit{y}}_{posi};\mathit{\theta }]\\ & =\frac{\begin{array}{c}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\prod _{\{j\in A_i:y_{ij}>0\}}h\left(b_i\right)f_Y(y_{ij}|y_{ij}\\ >0,{\mathit{x}}_{ij},b_i,\mathit{\theta }\left)\phi \right(b_i/{\sigma }_b)\mathrm{d}{b}_i\end{array}}{\begin{array}{c}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\prod _{\{j\in A_i:y_{ij}>0\}}{f}_Y(y_{ij}|y_{ij}\\ >0,{\mathit{x}}_{ij},b_i,\mathit{\theta }\left)\phi \right(b_i/{\sigma }_b)\mathrm{d}{b}_i\end{array}}.\end{array}$(18) In particular, for $h\left(b\right)=\exp \left(b\right)$, we obtain the Bayes predictor of $\exp \left(b_i\right)$. The Bayes predictor of $q_{posij}\left(\tau \right)$ for squared error loss corresponding to the approximate density function (12(12) $\begin{array}{rl}& f_Y(y|y_{ij}>0,{\mathit{x}}_{ij},b_i,\mathit{\theta })=I[y<q_{posij}({\tau }_1\left)\right]{\tau }_1{f}_{\ell }(y|{\rho }_{\ell },{\xi }_{\ell })\\ & +I[y\ge q_{posij}({\tau }_K\left)\right](1-{\tau }_K)f_u(y|{\rho }_u,{\xi }_u)\\ & +\sum _{k=1}^{K-1}I\left[q_{posij}\right({\tau }_k)\le y<q_{posij}({\tau }_{k+1}\left)\right]\\ & \times \frac{{\tau }_{k+1}-{\tau }_k}{q_{posij}\left({\tau }_{k+1}\right)-q_{posij}\left({\tau }_k\right)},\end{array}$(12) ) and the model (9(9) $q_{posij}\left(\tau \right)={\mathit{x}}_{ij}^{\prime }\text{β}\left(\tau \right)\exp \left(b_i\right),$(9) ) is (19) $q_{ij}^B\left(\tau \right)={\mathit{x}}_{ij}^{\prime }\text{β}\left(\tau \right)E[\exp (b_i)\mid {\mathit{y}}_{posi};\mathit{\theta }].$(19) A predictor of the form (19(19) $q_{ij}^B\left(\tau \right)={\mathit{x}}_{ij}^{\prime }\text{β}\left(\tau \right)E[\exp (b_i)\mid {\mathit{y}}_{posi};\mathit{\theta }].$(19) ) will provide the basis of the small area predictors for zero-inflated data. However, the predictor (19(19) $q_{ij}^B\left(\tau \right)={\mathit{x}}_{ij}^{\prime }\text{β}\left(\tau \right)E[\exp (b_i)\mid {\mathit{y}}_{posi};\mathit{\theta }].$(19) ) is unattainable because (19(19) $q_{ij}^B\left(\tau \right)={\mathit{x}}_{ij}^{\prime }\text{β}\left(\tau \right)E[\exp (b_i)\mid {\mathit{y}}_{posi};\mathit{\theta }].$(19) ) is a function of the unknown $\mathit{\theta }$.

We next define an estimator of $\mathit{\theta }$. The estimator is a modification of the iterative estimation procedure used in Berg and Lee (2019a) to account for the zero-inflated nature of the data. The iteration involves optimisation of Koenker's check function (6(6) ${\rho }_{\tau }\left(u\right)=u(\tau -I[u<0\left]\right).$(6) ) and calculation of conditional moments according to (17(17) $\begin{array}{rl}& f_{b\mid y_{pos}}(b_i\mid {\mathit{y}}_{posi};\mathit{\theta })\\ & =\frac{\begin{array}{c}\prod _{\{j\in A_i:y_{ij}>0\}}{f}_Y(y_{ij}|y_{ij}\\ >0,{\mathit{x}}_{ij},b_i,\mathit{\theta }\left)\phi \right(b_i/{\sigma }_b)\mathrm{d}{b}_i\end{array}}{\begin{array}{c}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\prod _{\{j\in A_i:y_{ij}>0\}}{f}_Y(y_{ij}|y_{ij}\\ >0,{\mathit{x}}_{ij},b_i,\mathit{\theta }\left)\phi \right(b_i/{\sigma }_b)\mathrm{d}{b}_i\end{array}},\end{array}$(17) ).

Begin with the initial estimator ${\hat{\mathit{\theta }}}^{\left(0\right)}$ defined in Appendix 1. For $m=1,2,\dots ,M$, alternate between the following steps.

1. Define the updated estimator of ${\sigma }_b^2$ by (20) $\begin{array}{r}{\hat{\sigma }}_b^{2\left(m\right)}=(D-p{)}^{-1}\sum _{i=1}^{D}E[b_i^2\mid {\mathit{y}}_{posi};{\hat{\mathit{\theta }}}^{(m-1)}],\end{array}$(20) where p is the dimension of ${\mathit{x}}_{ij}$. Define predictors of $b_i$ and $\exp \left(b_i\right)$ in the mth step by $\begin{array}{rl}{\hat{b}}_i^{\left(m\right)}& =E[b_i\mid {\mathit{y}}_{posi};{\hat{\mathit{\theta }}}^{(m-1)}],\text{and}\\ {\hat{e}}_{bi}^{\left(m\right)}& =E[\exp (b_i)\mid {\mathit{y}}_{posi},{\hat{\mathit{\theta }}}^{(m-1)}].\end{array}$ To approximate the integrals defining the conditional expectations, we use a Riemann sum, as described in Berg and Lee (2019a). The motivation for the estimator ${\hat{\sigma }}_b^{2\left(m\right)}$ is from the EM algorithm for a linear mixed effects model with normally distributed random terms (Searle, Casella, & McCulloch, 1992, p. 300).

2. We use the method of Koenker and Ng (2005) to update the estimator of ${\text{β}}_K$ to maintain the monotonicity restriction. The motivation for the estimator of $\text{β}\left({\tau }_k\right)$ is that for known $b_i$, ${\mathit{x}}_{ij}^{\prime }\text{β}\left(\tau \right)={\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}_{a}E\left[{\rho }_{\tau }\right(y_{ij}\exp (-b_i)-a)\mid y_{ij}>0,b_i]$, where ${\rho }_{\tau }\left(u\right)$ is the check function defined in (6(6) ${\rho }_{\tau }\left(u\right)=u(\tau -I[u<0\left]\right).$(6) ). The estimates of $\text{β}\left({\tau }_j\right)$ are obtained sequentially to enforce the monotonicity condition. First, define (21) $\begin{array}{rl}{\widehat{\text{β}}}^{\left(m\right)}\left({\tau }_1\right)& ={\text{argmin}}_{\text{β}}\sum _{i=1}^D\sum _{\{j\in A_i:y_{ij}>0\}}\\ & {\rho }_{{\tau }_1}(y_{ij}\exp (-{\hat{b}}_i^{\left(m\right)})-{\mathit{x}}_{ij}^{\prime }\text{β}),\end{array}$(21) subject to the restriction that ${\mathit{x}}_{ij}^{\prime }{\widehat{\text{β}}}^{\left(m\right)}\left({\tau }_1\right)>c_0$, where $c_0$ is a specified constant. For $k=2,\dots ,K$, define (22) $\begin{array}{rl}{\widehat{\text{β}}}^{\left(m\right)}\left({\tau }_k\right)& ={\text{argmin}}_{\text{β}}\sum _{i=1}^D\sum _{\{j\in A_i:y_{ij}>0\}}\\ & {\rho }_{{\tau }_k}(y_{ij}\exp (-{\hat{b}}_i^{\left(m\right)})-{\mathit{x}}_{ij}^{\prime }\text{β})\end{array}$(22) subject to the restriction that ${\mathit{x}}_{ij}^{\prime }{\widehat{\text{β}}}^{\left(m\right)}\left({\tau }_k\right)\ge {\mathit{x}}_{ij}^{\prime }{\widehat{\text{β}}}^{\left(m\right)}\left({\tau }_{k-1}\right)$ for $j=1,\dots ,N_i$ and $i=1,\dots ,D$. To enforce the monotonicity restrictions, we implement the constrained optimisation method of Koenker and Ng (2005) using the method fn in the R function rq.

3. Next, we estimate ${\rho }_s$ and ${\xi }_s$ for $s=\ell ,u$, the parameters of the generalised Pareto density. The estimators are minor modifications of the procedures used in Jang and Wang (2015) to account for the zero-inflated nature of the data. Specifically, (23) $\begin{array}{rl}{\hat{\rho }}_{\ell }^{\left(m\right)}& =0.5({\tau }_1+{\tau }_2)\sum _{i=1}^D\sum _{\{j\in A_i:y_{ij}>0\}}\\ & \times \frac{{\hat{q}}_{ij}^{\left(m\right)}\left({\tau }_2\right)-{\hat{q}}_{ij}^{\left(m\right)}\left({\tau }_1\right)}{n({\tau }_2-{\tau }_1)},\\ {\hat{\rho }}_u^{\left(m\right)}& =[1-0.5({\tau }_K+{\tau }_{K-1}\left)\right]\sum _{i=1}^D\sum _{\{j\in A_i:y_{ij}>0\}}\\ & \times \frac{{\hat{q}}_{ij}^{\left(m\right)}\left({\tau }_K\right)-{\hat{q}}_{ij}^{\left(m\right)}\left({\tau }_{K-1}\right)}{n({\tau }_K-{\tau }_{K-1})},\end{array}$(23) where ${\hat{q}}_{ij}^{\left(m\right)}\left({\tau }_k\right)={\mathit{x}}_{ij}^{\prime }{\widehat{\text{β}}}^{\left(m\right)}\left({\tau }_k\right){\hat{e}}_{bi}^{\left(m\right)}$, and $n=\sum _{i=1}^D\sum _{j=1}^{n_i}I[y_{ij}>0]$. Holding ${\hat{\rho }}_{\ell }^{\left(m\right)}$ and ${\hat{\rho }}_u^{\left(m\right)}$ fixed, the estimator of ${\xi }_s$ is the maximum likelihood estimator using only $\{y_{ij}<{\hat{\ell }}_{ij}^{\left(m\right)}\}$ for $s=\ell$ and $\{y_{ij}>{\hat{u}}_{ij}^{\left(m\right)}\}$ for s=u, where ${\hat{\ell }}_{ij}^{\left(m\right)}=0.5\left({\mathit{x}}_{ij}^{\prime }{\widehat{\text{β}}}^{\left(m\right)}\right({\tau }_1)+{\mathit{x}}_{ij}^{\prime }{\widehat{\text{β}}}^{\left(m\right)}({\tau }_2\left)\right){\hat{e}}_{bi}^{\left(m\right)}$ and ${\hat{u}}_{ij}^{\left(m\right)}=0.5\left({\mathit{x}}_{ij}^{\prime }{\widehat{\text{β}}}^{\left(m\right)}\right({\tau }_K)+{\mathit{x}}_{ij}^{\prime }{\widehat{\text{β}}}^{\left(m\right)}({\tau }_{K-1}\left)\right){\hat{e}}_{bi}^{\left(m\right)}$. Precisely, (24) $\begin{array}{rl}{\hat{\xi }}_{\ell }^{\left(m\right)}& ={\text{argmax}}_{\xi }\prod _{\left\{\right(ij):0<y_{ij}<{\hat{\ell }}_{ij}^{\left(m\right)}\}}g(-(y_{ij}-{\hat{\ell }}_{ij}^{\left(m\right)}\left)\right)\mid \\ & \times {\hat{\rho }}_{\ell }^{\left(m\right)},\xi ),\end{array}$(24) and (25) $\begin{array}{rl}{\hat{\xi }}_u^{\left(m\right)}& ={\text{argmax}}_{\xi }\prod _{\left\{\right(ij):y_{ij}>{\hat{u}}_{ij}^{\left(m\right)}>0\}}\\ & g(y_{ij}-{\hat{u}}_{ij}^{\left(m\right)}\mid {\hat{\rho }}_u^{\left(m\right)},\xi ).\end{array}$(25)

Let $\hat{\mathit{\theta }}=\left(\right({\widehat{\text{β}}}_K{)}^{\prime },{\hat{\sigma }}_b^2,{\hat{\rho }}_{\ell },{\hat{\xi }}_{\ell },{\hat{\rho }}_u,{\hat{\xi }}_u{)}^{\prime }$ denote the estimator of $\mathit{\theta }$ obtained in the final step of the iteration.

2.2.2. Estimator of Binary component

One can use standard software to estimate the parameters of the logistic mixed effects model (8(8) $\begin{array}{rl}P(y_{ij}& =0\mid u_i,{\mathit{z}}_{ij})=(1+\exp ({\mathit{z}}_{ij}^{\prime }\mathit{\gamma }+u_i){)}^{-1}\\ & \times \exp ({\mathit{z}}_{ij}^{\prime }\mathit{\gamma }+u_i),\end{array}$(8) ). To estimate ${\sigma }_u^2$ and $\mathit{\gamma }$, we use a Laplace approximation, as implemented in the R function glmer. Let ${\hat{\sigma }}_u^2$ and $\hat{\mathit{\gamma }}$ be the resulting estimates of ${\sigma }_u^2$ and $\mathit{\gamma }$. We use penalised quasi-likelihood (Breslow & Clayton, 1993), as implemented with the predict method for glmer objects to predict $u_i$, and we let ${\hat{u}}_i$ be the resulting predictor. We then define a predictor of the probability that $y_{ij}$ is zero by (26) ${\hat{p}}_z({\hat{u}}_i,{\mathit{z}}_{ij})=(1+\exp ({\mathit{z}}_{ij}^{\prime }\hat{\mathit{\gamma }}+{\hat{u}}_i){)}^{-1}\exp ({\mathit{z}}_{ij}^{\prime }\hat{\mathit{\gamma }}+{\hat{u}}_i).$(26)

2.2.3. Predictors of quantiles

Given estimates of parameters $\mathit{\theta }$, $\mathit{\gamma }$, and ${\sigma }_u^2$, as well as predictors of $u_i$ and $\exp \left(b_i\right)$, the next step is to construct small area predictors. The small area prediction procedure involves two main steps. First, we define an approximation for the population. The approximation for the population is similar in structure to the method of Berg and Lee (2019a), except that the unconditional distribution (11(11) $q_{ij}\left(\tau \right)=\left\{\begin{array}{ll}0& \\ \text{if }\tau \le P(y_{ij}=0\mid u_i,{\mathit{z}}_{ij})\\ q_{posij}\left(\frac{\tau -P(y_{ij}=0\mid u_i,{\mathit{z}}_{ij})}{1-P(y_{ij}=0\mid u_i,{\mathit{z}}_{ij})}\right)& \\ \text{if }\tau >P(y_{ij}=0\mid u_i,{\mathit{z}}_{ij}).\end{array}\right.$(11) ) is used to accommodate the zero-inflated nature of the data. The second step is to use the approximation for the population to define estimates of small area quantiles.

The details of the two steps of the small area prediction procedure are as follows. For $i=1,\dots ,D$, $j=1,\dots ,N_i$, and $k=1,\dots ,K$, define a predictor of the ${\tau }_k$th conditional quantile for $y_{ij}>0$ by ${\hat{q}}_{posij}\left({\tau }_k\right)=E[\exp (b_i)\mid {\mathit{y}}_{posi},\hat{\mathit{\theta }}]{\mathit{x}}_{ij}^{\prime }\widehat{\text{β}}\left({\tau }_k\right),$ where the expectation is approximated using the Riemann sum defined in Berg and Lee (2019a). Then, define a predictor of the unconditional quantile by (27) ${\hat{q}}_{ij}\left(\tau \right)=\left\{\begin{array}{ll}0& \text{if }\tau \le {\hat{p}}_z({\hat{u}}_i,{\mathit{z}}_{ij})\\ {\hat{q}}_{posij}\left(\frac{\tau -{\hat{p}}_z({\hat{u}}_i,{\mathit{z}}_{ij})}{1-{\hat{p}}_z({\hat{u}}_i,{\mathit{z}}_{ij})}\right)& \text{if }\tau >{\hat{p}}_z({\hat{u}}_i,{\mathit{z}}_{ij}).\end{array}\right.$(27) The $\left\{{\hat{q}}_{ij}\right({\tau }_k):i=1,\dots ,D;j=1,\dots ,N_i;k=1,\dots ,K\}$ defines an approximation for the population. We define a predictor of the τth population quantile by (28) $\begin{array}{rl}{\hat{q}}_i\left(\tau \right)& =min\left\{{\hat{q}}_{ij}\right({\tau }_k):{\hat{F}}_{y_i}({\hat{q}}_{ij}\left({\tau }_k\right))\\ & \ge \tau ;j=1,\dots ,N_i;k=1,\dots ,K\},\end{array}$(28) where ${\hat{F}}_{y_i}\left(t\right)=\left(N_{i}K{)}^{-1}\sum _{j=1}^{N_i}\sum _{k=1}^{K}I\right[{\hat{q}}_{ij}\left({\tau }_k\right)\le t]$.

2.3. Bootstrap MSE estimation

We modify the parametric bootstrap MSE estimator of Berg and Lee (2019a) to account for the zero-inflated nature of the data. The main idea of the bootstrap simulation procedure is to use the probability integral transform to simulate from the conditional distribution of $y_{ij}$ given ${\mathit{x}}_{ij}$ and $b_i$. First, a $b_i^{\ast }$ is generated from the estimated marginal distribution of $b_i$. Then, linear interpolation is used to approximate the quantile function corresponding to the conditional distribution of $y_{ij}$ given ${\mathit{x}}_{ij}$ and $b_i^{\ast }$. The probability integral transform is then used to simulate a new variable, $y_{ij}^{\ast }$ from this linear approximation to the conditional quantile function. Finally, the estimation procedure is repeated using the original sample and the new simulated $y_{ij}^{\ast }$.

To define a bootstrap MSE estimator, repeat the following steps for $t=1,\dots ,T$.

1. First, generate a bootstrap approximation for the population. Generate $b_i^{\ast \left(t\right)}\sim N(0,{\hat{\sigma }}_b^2)$, and define $q_{posij}^{\ast \left(t\right)}\left({\tau }_k\right)={\mathit{x}}_{ij}^{\prime }\widehat{\text{β}}\left({\tau }_k\right)\exp \left(b_i^{\ast \left(t\right)}\right)$ . Generate $u_i^{\ast \left(t\right)}\sim N(0,{\hat{\sigma }}_u^2)$, and define ${\hat{p}}_{zij}^{\ast \left(t\right)}=\exp ({\mathit{z}}_{ij}^{\prime }\hat{\mathit{\gamma }}+u_i^{\ast \left(t\right)})(\exp ({\mathit{z}}_{ij}^{\prime }\hat{\mathit{\gamma }}+u_i^{\ast \left(t\right)})+1{)}^{-1}$. Define (29) $q_{ij}^{\ast \left(t\right)}\left({\tau }_k\right)=\left\{\begin{array}{ll}0& \text{if }\tau \le {\hat{p}}_{zij}^{\ast \left(t\right)}\\ {\hat{q}}_{posij}\left(\frac{\tau -{\hat{p}}_{zij}^{\ast \left(t\right)}}{1-{\hat{p}}_{zij}^{\ast \left(t\right)}}\right)& \text{if }\tau >{\hat{p}}_{zij}^{\ast \left(t\right)}.\end{array}\right.$(29) Define a bootstrap version of the τth population quantile by (30) $\begin{array}{rl}{q}_i^{\ast \left(t\right)}\left(\tau \right)& =min\left\{q_{ij}^{\ast \left(t\right)}\right({\tau }_k):{\hat{F}}_{y_i}^{\ast \left(t\right)}(q_{ij}^{\ast \left(t\right)}\left({\tau }_k\right))\\ & \ge \tau ;j=1,\dots ,N_i;k=1,\dots ,K\},\end{array}$(30) where ${\hat{F}}_{y_i}^{\ast \left(t\right)}\left(t\right)=\left(N_{i}K{)}^{-1}\sum _{j=1}^{N_i}\sum _{k=1}^{K}I\right[q_{ij}^{\ast \left(t\right)}\left({\tau }_k\right)\le t]$.

2. Generate a bootstrap sample as follows. Generate $v_{ij}^{\ast \left(t\right)}\stackrel{iid}{\sim }\text{Unif}(0,1)$ for $i=1,\dots ,D$, and $j=1,\dots ,N_i$. Define $y_{ij}^{\ast \left(t\right)}=y_{ij}^{\ast }(\hat{\mathit{\theta }},b_i^{\ast \left(t\right)},v_{ij}^{\ast \left(t\right)})$ by (31) $\begin{array}{rl}{y}_{ij}^{\ast \left(t\right)}& =\left\{\begin{array}{l}{q}_{ij}^{\ast \left(t\right)}\left({\tau }_{k_{ij}^{\ast \left(t\right)}}\right)\\ +(v_{ij}^{\ast \left(t\right)}-{\tau }_{k_{ij}^{\ast \left(t\right)}})\\ \times \left(\frac{\begin{array}{c}{q}_{ij}^{\ast \left(t\right)}\left({\tau }_{k_{ij}^{\ast \left(t\right)}+1}\right)\\ -q_{ij}^{\ast \left(t\right)}\left({\tau }_{k_{ij}^{\ast \left(t\right)}}\right)\end{array}}{{\tau }_{k_{ij}^{\ast \left(t\right)}+1}-{\tau }_{k_{ij}^{\ast \left(t\right)}}}\right),\\ {\hat{p}}_{zij}^{\ast \left(t\right)}<v_{ij}^{\ast \left(t\right)}<{\tau }_K\\ 0,& v_{ij}^{\ast \left(t\right)}\le {\hat{p}}_{zij}^{\ast \left(t\right)}\\ q_{ij}^{\ast \left(t\right)}\left({\tau }_K\right),& v_{ij}^{\ast \left(t\right)}\ge {\tau }_K,\end{array}\right.\end{array}$(31) where $k_{ij}^{\ast \left(t\right)}=max\{k:{\tau }_k\le v_{ij}^{\ast \left(t\right)}\}$. Define the bootstrap sample to be $\{y_{ij}^{\ast \left(t\right)}:(i,j)\in A\}$, where A denotes the original sample. Note that the operation in the first line of (31(31) $\begin{array}{rl}{y}_{ij}^{\ast \left(t\right)}& =\left\{\begin{array}{l}{q}_{ij}^{\ast \left(t\right)}\left({\tau }_{k_{ij}^{\ast \left(t\right)}}\right)\\ +(v_{ij}^{\ast \left(t\right)}-{\tau }_{k_{ij}^{\ast \left(t\right)}})\\ \times \left(\frac{\begin{array}{c}{q}_{ij}^{\ast \left(t\right)}\left({\tau }_{k_{ij}^{\ast \left(t\right)}+1}\right)\\ -q_{ij}^{\ast \left(t\right)}\left({\tau }_{k_{ij}^{\ast \left(t\right)}}\right)\end{array}}{{\tau }_{k_{ij}^{\ast \left(t\right)}+1}-{\tau }_{k_{ij}^{\ast \left(t\right)}}}\right),\\ {\hat{p}}_{zij}^{\ast \left(t\right)}<v_{ij}^{\ast \left(t\right)}<{\tau }_K\\ 0,& v_{ij}^{\ast \left(t\right)}\le {\hat{p}}_{zij}^{\ast \left(t\right)}\\ q_{ij}^{\ast \left(t\right)}\left({\tau }_K\right),& v_{ij}^{\ast \left(t\right)}\ge {\tau }_K,\end{array}\right.\end{array}$(31) ) defines a linear interpolation of the estimated quantile function.

3. Repeat the estimation procedure of Section 2 using $\{y_{ij}^{\ast \left(t\right)}:(i,j)\in A\}$ to obtain ${\hat{q}}_i^{\ast \left(t\right)}\left(\tau \right)$. As in Berg and Lee (2019a), we simplify the estimation procedure to reduce the computational burden. Rather than estimate the quantile regression coefficients sequentially to enforce the monotonicity constraint, as in (A6(A6) $\begin{array}{rl}{\widehat{\text{β}}}^{\left(m\right)}\left({\tau }_1\right)& ={\text{argmin}}_{\text{β}}\sum _{i=1}^D\sum _{\{j\in A_i:y_{ij}>0\}}{\rho }_{{\tau }_{\left[1\right]}}(y_{ij}\exp (-{\hat{b}}_i^{\left(m\right)})\\ & -x_{ij}^{{\hat{\eta }}^{(m-1)}}\text{β}),\end{array}$(A6) )-(A7(A7) $\begin{array}{rl}{\widehat{\text{β}}}^{\left(m\right)}\left({\tau }_k\right)& ={\text{argmin}}_{\text{β}}\sum _{i=1}^D\sum _{\{j\in A_i:y_{ij}>0\}}{\rho }_{{\tau }_k}(y_{ij}\exp (-{\hat{b}}_i^{\left(m\right)})\\ & -x_{ij}^{{\hat{\eta }}^{(m-1)}}\text{β})\end{array}$(A7) ), we simultaneously minimise Koenker's check function for all quantile levels and then sort the estimates of the quantiles to obtain a nondecreasing quantile function (Chernozhukov, Fernandez-Val, & Galichon, 2009) for element $(i,j)$. A more specific definition of the rearrangement operation is defined following (A3(A3) ${\widehat{\text{β}}}^{\left(0\right)}\left({\tau }_k\right)={\text{argmin}}_{\text{β}}\sum _{i=1}^D\sum _{\{j\in A_i:y_{ij}>0\}}{\rho }_{{\tau }_k}(y_{ij}/\exp ({\hat{b}}_i^{\left(0\right)})-{\mathit{x}}_{ij}^{\prime }\text{β}).$(A3) ) of Appendix 2.

Define the bootstrap MSE estimator for ${\hat{q}}_i\left(\tau \right)$ by (32) ${\widehat{MSE}}_i\left(\tau \right)=\frac{1}{T}\sum _{t=1}^T\left({\hat{q}}_i^{\ast \left(t\right)}\right(\tau )-q_i^{\ast \left(t\right)}(\tau ){)}^2.$(32) The bootstrap MSE estimator is similar to bootstrap MSE estimators for small area predictors for parametric models developed in Lahiri, Maiti, Katzoff, and Parsons (2007) and in Hall and Maiti (2006). The MSE estimator (32(32) ${\widehat{MSE}}_i\left(\tau \right)=\frac{1}{T}\sum _{t=1}^T\left({\hat{q}}_i^{\ast \left(t\right)}\right(\tau )-q_i^{\ast \left(t\right)}(\tau ){)}^2.$(32) ) is an estimator of $E\left[\right({\hat{q}}_i^{\ast \left(t\right)}\left(\tau \right)-q_i^{\ast \left(t\right)}\left(\tau \right){)}^2]$ and does not account for a possible bias of the estimator of the leading term due to estimating $\mathit{\theta }$. In a simulation study, Berg and Lee (2019a) evaluate the quality of an MSE estimator similar to (32(32) ${\widehat{MSE}}_i\left(\tau \right)=\frac{1}{T}\sum _{t=1}^T\left({\hat{q}}_i^{\ast \left(t\right)}\right(\tau )-q_i^{\ast \left(t\right)}(\tau ){)}^2.$(32) ) for the quantile regression model with no modification for zero-inflated data. Because the MSE estimator (32(32) ${\widehat{MSE}}_i\left(\tau \right)=\frac{1}{T}\sum _{t=1}^T\left({\hat{q}}_i^{\ast \left(t\right)}\right(\tau )-q_i^{\ast \left(t\right)}(\tau ){)}^2.$(32) ) is similar in structure to the MSE estimator of Berg and Lee (2019a), we do not present further simulation results here. Instead, we focus on an application of (32(32) ${\widehat{MSE}}_i\left(\tau \right)=\frac{1}{T}\sum _{t=1}^T\left({\hat{q}}_i^{\ast \left(t\right)}\right(\tau )-q_i^{\ast \left(t\right)}(\tau ){)}^2.$(32) ) to the data presented in Section 4 in this manuscript.

3. Modification for an informative design

The development of Section 2 assumes that the sample design is noninformative for the quantile regression model. In this section, we consider an informative sample design. Assume all areas are included in the sample, and assume that a subset of elements is selected from area i. Let ${\pi }_{ij}=P(I_{ij}=1\mid y_{ij},{\mathit{x}}_{ij},{\mathit{z}}_{ij},b_i,u_i)$, where $I_{ij}$ is the sample inclusion indicator for element $(i,j)$. We adapt the approach of Pfeffermann and Sverchkov (2007) to the quantile regression setting in order to modify the predictors to account for unequal selection probabilities. Pfeffermann and Sverchkov (2007) develop small area predictors for a fully parametric model under an informative sample design. Their approach exploits relationships between the sample distribution and the sample complement distribution. They construct predictors relative to the population distribution using estimates of the parameters of the sample distribution. For the fully parametric model considered in Pfeffermann and Sverchkov (2007), a closed form expression for the small area predictor is available. For the quantile regression model, a closed-form expression relating the sample distribution to the sample complement distribution is not available. Nonetheless, the basic idea of the Pfeffermann and Sverchkov (2007) approach applies easily to the quantile regression framework. Below, we use importance sampling to simulate from the sample complement distribution.

3.1. Procedure to account for informative design

First, we introduce the definitions of the population, sample, and sample complement distributions more formally. Let $f_p(y_{ij}\mid b_i,{\mathit{x}}_{ij},u_i,{\mathit{z}}_{ij})$ be the density/mass function corresponding to the population distribution of $y_{ij}$. Let $f_s(y_{ij}\mid b_i,{\mathit{x}}_{ij},u_i,{\mathit{z}}_{ij})=f_p(y_{ij}\mid b_i,{\mathit{x}}_{ij},u_i,{\mathit{z}}_{ij},I_{ij}=1)$ denote the corresponding sample distribution. From Pfeffermann and Sverchkov (2007; also see Kim & Yu, 2011 for a related result in the context of nonignorable nonresponse), the sample complement distribution is of the form (33) $\begin{array}{rl}& f_c(y_{ij}\mid b_i,u_i,{\mathit{x}}_{ij},{\mathit{z}}_{ij})\propto E_s\left[{\pi }_{ij}^{-1}\right(1-{\pi }_{ij})\mid \\ & y_{ij},{\mathit{x}}_{ij},{\mathit{z}}_{ij},b_i,u_i\left]f_s\right(y_{ij}\mid b_i,{\mathit{x}}_{ij},u_i,{\mathit{z}}_{ij}),\end{array}$(33) where $E_s[\cdot ]$ denotes expectation with respect to the sample distribution, and $f_c(y_{ij}\mid b_i,u_i,{\mathit{x}}_{ij},{\mathit{z}}_{ij})=f_p(y_{ij}\mid b_i,{\mathit{x}}_{ij},u_i,{\mathit{z}}_{ij},I_{ij}=0)$. (We refer the reader to Pfeffermann & Sverchkov, 2007 for further background on the concepts of the sample distribution and the sample complement distribution.)

We obtain estimates of $f_s(y_{ij}\mid b_i,{\mathit{x}}_{ij},u_i,{\mathit{z}}_{ij})$ and of $E_s\left[{\pi }_{ij}^{-1}\right(1-{\pi }_{ij})\mid y_{ij},{\mathit{x}}_{ij},{\mathit{z}}_{ij},b_i,u_i]$ using the sample data. We use the quantile regression procedure defined in Section 2 to obtain an estimate of the quantiles of the distribution of $f_s(y_{ij}\mid b_i,{\mathit{x}}_{ij},u_i,{\mathit{z}}_{ij})$. Let ${\hat{q}}_{ij}\left({\tau }_k\right)$ for $k=1,\dots ,K$ be the estimated quantiles based on the sample for evenly spaced quantile levels, obtained using the procedure of Section 2. Denote the estimate of $E_s\left[{\pi }_{ij}^{-1}\right(1-{\pi }_{ij})\mid y_{ij},{\mathit{x}}_{ij},{\mathit{z}}_{ij},b_i,u_i]$ based on the sample by (34) ${\hat{\omega }}_{ij}\left(y_{ij}\right)=E_s\left[{\pi }_{ij}^{-1}\right(1-{\pi }_{ij})\mid y_{ij},{\mathit{x}}_{ij},{\mathit{z}}_{ij},b_i,u_i].$(34) A variety of models and procedures may be used to obtain the estimates ${\hat{\omega }}_{ij}\left(y_{ij}\right)$. We use a weight model similar to that of Pfeffermann and Sverchkov (2007). In this section, we first define the method to simulate from the population distribution for an arbitrary definition of ${\hat{\omega }}_{ij}\left(y_{ij}\right)$. We then define the procedure that we use to estimate $E_s\left[{\pi }_{ij}^{-1}\right(1-{\pi }_{ij})\mid y_{ij},{\mathit{x}}_{ij},{\mathit{z}}_{ij},b_i,u_i]$.

We simulate from the population distribution using the relationship (33(33) $\begin{array}{rl}& f_c(y_{ij}\mid b_i,u_i,{\mathit{x}}_{ij},{\mathit{z}}_{ij})\propto E_s\left[{\pi }_{ij}^{-1}\right(1-{\pi }_{ij})\mid \\ & y_{ij},{\mathit{x}}_{ij},{\mathit{z}}_{ij},b_i,u_i\left]f_s\right(y_{ij}\mid b_i,{\mathit{x}}_{ij},u_i,{\mathit{z}}_{ij}),\end{array}$(33) ). Let ${\hat{q}}_{ij}\left({\tau }_k\right)$ for $k=1,\dots ,K$ be the estimated quantiles based on the sample for evenly spaced quantile levels, obtained using the procedure of Section 2. Let ${\hat{\omega }}_{ij}\left(y_{ij}\right)$ be an estimate of $E_s\left[{\pi }_{ij}^{-1}\right(1-{\pi }_{ij})\mid y_{ij},{\mathit{x}}_{ij},{\mathit{z}}_{ij},b_i,u_i]$ based on the sample. Define a simulated population by sampling from $\left\{{\hat{q}}_{ij}\right({\tau }_k):k=1\dots ,K\}$ with probabilities proportional to ${\hat{\omega }}_{ij}\left({\hat{q}}_{ij}\right({\tau }_k\left)\right)$. For $r=1,\dots ,R$, let (35) $\begin{array}{rl}{\tilde{q}}_{ij}^{\left(r\right)}& =\left\{\begin{array}{l}{\hat{q}}_{ij}\left({\tau }_k\right)\text{ with probability }\\ \frac{{\hat{\omega }}_{ij}\left({\hat{q}}_{ij}\right({\tau }_k\left)\right)}{\sum _{k=1}^K{\hat{\omega }}_{ij}\left({\hat{q}}_{ij}\right({\tau }_k\left)\right)}& \text{if }(i,j)\notin A\\ {\hat{q}}_{ij}\left({\tau }_k\right)\text{ with probability }{K}^{-1}& \text{if }(i,j)\in A.\end{array}\right.\end{array}$(35) The $\{{\tilde{q}}_{ij}^{\left(r\right)}:i=1,\dots ,D;j=1,\dots ,N_i;r=1,\dots ,R\}$ defines an approximation for the population. We define a predictor of the τth population quantile by (36) $\begin{array}{rl}{\hat{q}}_i\left(\tau \right)& =min\left\{{\hat{q}}_{ij}\right({\tau }_k):{\hat{F}}_{y_i}^{\left(R\right)}({\hat{q}}_{ij}\left({\tau }_k\right))\\ & \ge \tau ;j=1,\dots ,N_i;r=1,\dots ,R\},\end{array}$(36) where ${\hat{F}}_{y_i}^{\left(R\right)}\left({\hat{q}}_{ij}\right({\tau }_k\left)\right)=\left(N_{i}R{)}^{-1}\sum _{j=1}^{N_i}\sum _{r=1}^{R}I\right[{\tilde{q}}_{ij}^{\left(r\right)}\le t]$. This simulation procedure is essentially the ‘weighted bootstrap method’ defined in Section 3.2 of Smith and Gelfand (1992). The quantile regression model lends itself naturally to a procedure such as (35(35) $\begin{array}{rl}{\tilde{q}}_{ij}^{\left(r\right)}& =\left\{\begin{array}{l}{\hat{q}}_{ij}\left({\tau }_k\right)\text{ with probability }\\ \frac{{\hat{\omega }}_{ij}\left({\hat{q}}_{ij}\right({\tau }_k\left)\right)}{\sum _{k=1}^K{\hat{\omega }}_{ij}\left({\hat{q}}_{ij}\right({\tau }_k\left)\right)}& \text{if }(i,j)\notin A\\ {\hat{q}}_{ij}\left({\tau }_k\right)\text{ with probability }{K}^{-1}& \text{if }(i,j)\in A.\end{array}\right.\end{array}$(35) ) to simulate from the sample complement distribution. Because the quantile estimates are already computed, one only needs to obtain the importance weight ${\hat{\omega }}_{ij}\left({\hat{q}}_{ij}\right({\tau }_k\left)\right)$.

Implementation of (35(35) $\begin{array}{rl}{\tilde{q}}_{ij}^{\left(r\right)}& =\left\{\begin{array}{l}{\hat{q}}_{ij}\left({\tau }_k\right)\text{ with probability }\\ \frac{{\hat{\omega }}_{ij}\left({\hat{q}}_{ij}\right({\tau }_k\left)\right)}{\sum _{k=1}^K{\hat{\omega }}_{ij}\left({\hat{q}}_{ij}\right({\tau }_k\left)\right)}& \text{if }(i,j)\notin A\\ {\hat{q}}_{ij}\left({\tau }_k\right)\text{ with probability }{K}^{-1}& \text{if }(i,j)\in A.\end{array}\right.\end{array}$(35) ) and (36(36) $\begin{array}{rl}{\hat{q}}_i\left(\tau \right)& =min\left\{{\hat{q}}_{ij}\right({\tau }_k):{\hat{F}}_{y_i}^{\left(R\right)}({\hat{q}}_{ij}\left({\tau }_k\right))\\ & \ge \tau ;j=1,\dots ,N_i;r=1,\dots ,R\},\end{array}$(36) ) requires a model for $E_s\left[{\pi }_{ij}^{-1}\right(1-{\pi }_{ij})\mid {\mathit{x}}_{ij},{\mathit{z}}_{ij},y_{ij},b_i,u_i]$. We assume (37) $\begin{array}{rl}& E_s\left[{\pi }_{ij}^{-1}\right(1-{\pi }_{ij})\mid {\mathit{x}}_{ij},{\mathit{z}}_{ij},y_{ij},b_i,u_i]\\ & =\exp ({\alpha }_0+{\tilde{\mathit{x}}}_{ij}^{\prime }{\mathit{\alpha }}_1+y_{ij}{\alpha }_2+{\delta }_i),\end{array}$(37) where ${\delta }_i\sim \text{N}(0,{\sigma }_{\delta }^2)$, and ${\tilde{\mathit{x}}}_{ij}$ may contain elements of ${\mathit{x}}_{ij}$ or ${\mathit{z}}_{ij}$. To estimate $E_s\left[{\pi }_{ij}^{-1}\right(1-{\pi }_{ij})\mid {\mathit{x}}_{ij},{\mathit{z}}_{ij},y_{ij},b_i,u_i]$ we use a working model defined by (38) $\begin{array}{rl}\log \left({\pi }_{ij}^{-1}\right(1-{\pi }_{ij}\left)\right)& ={\alpha }_0+{\tilde{\mathit{x}}}_{ij}^{\prime }{\mathit{\alpha }}_1+y_{ij}{\alpha }_2+{\delta }_i+r_{ij},\\ & i=1,\dots ,D;j\in A_i,\end{array}$(38) where ${\delta }_i\sim \text{N}(0,{\sigma }_{\delta }^2)$, and $r_{ij}\sim \text{N}(0,{\sigma }_r^2)$. The model (38(38) $\begin{array}{rl}\log \left({\pi }_{ij}^{-1}\right(1-{\pi }_{ij}\left)\right)& ={\alpha }_0+{\tilde{\mathit{x}}}_{ij}^{\prime }{\mathit{\alpha }}_1+y_{ij}{\alpha }_2+{\delta }_i+r_{ij},\\ & i=1,\dots ,D;j\in A_i,\end{array}$(38) ) is implicitly specified conditional on $I_{ij}=1$ (i.e., a sample distribution model) and is defined only for sampled elements. Because we require an estimate of the mean of ${\pi }_{ij}^{-1}(1-{\pi }_{ij})$ with respect to the sample distribution as defined in (37(37) $\begin{array}{rl}& E_s\left[{\pi }_{ij}^{-1}\right(1-{\pi }_{ij})\mid {\mathit{x}}_{ij},{\mathit{z}}_{ij},y_{ij},b_i,u_i]\\ & =\exp ({\alpha }_0+{\tilde{\mathit{x}}}_{ij}^{\prime }{\mathit{\alpha }}_1+y_{ij}{\alpha }_2+{\delta }_i),\end{array}$(37) ), we can estimate the parameters of the model (38(38) $\begin{array}{rl}\log \left({\pi }_{ij}^{-1}\right(1-{\pi }_{ij}\left)\right)& ={\alpha }_0+{\tilde{\mathit{x}}}_{ij}^{\prime }{\mathit{\alpha }}_1+y_{ij}{\alpha }_2+{\delta }_i+r_{ij},\\ & i=1,\dots ,D;j\in A_i,\end{array}$(38) ) using only the sample data, as in Pfeffermann and Sverchkov (2007). We estimate ${\alpha }_0$, ${\mathit{\alpha }}_1$, ${\alpha }_2$, and ${\sigma }_{\delta }^2$ using restricted maximum likelihood (REML) applied to the sample data. We denote the REML estimates by ${\hat{\alpha }}_0$, ${\hat{\mathit{\alpha }}}_1$, ${\hat{\alpha }}_2$, and ${\hat{\sigma }}_{\delta }^2$. We define the estimator of $E_s\left[{\pi }_{ij}^{-1}\right(1-{\pi }_{ij})\mid {\mathit{x}}_{ij},{\mathit{z}}_{ij},y,b_i,u_i]$ by ${\hat{\omega }}_{ij}\left(y\right)=\exp ({\hat{\alpha }}_0+{\tilde{\mathit{x}}}_{ij}{\hat{\mathit{\alpha }}}_1+y{\hat{\alpha }}_2+{\hat{\delta }}_i),$ where ${\hat{\delta }}_i$ is the EBLUP of ${\delta }_i$. As mentioned above, other possible models for ${\pi }_{ij}$ are possible. We use the model (38(38) $\begin{array}{rl}\log \left({\pi }_{ij}^{-1}\right(1-{\pi }_{ij}\left)\right)& ={\alpha }_0+{\tilde{\mathit{x}}}_{ij}^{\prime }{\mathit{\alpha }}_1+y_{ij}{\alpha }_2+{\delta }_i+r_{ij},\\ & i=1,\dots ,D;j\in A_i,\end{array}$(38) ) primarily for mathematical simplicity. The model (38(38) $\begin{array}{rl}\log \left({\pi }_{ij}^{-1}\right(1-{\pi }_{ij}\left)\right)& ={\alpha }_0+{\tilde{\mathit{x}}}_{ij}^{\prime }{\mathit{\alpha }}_1+y_{ij}{\alpha }_2+{\delta }_i+r_{ij},\\ & i=1,\dots ,D;j\in A_i,\end{array}$(38) ) is similar to that of Pfeffermann and Sverchkov (2007), which has been vetted in the literature, and permits a computationally simple estimation procedure.

3.2. Simulation study for informative sampling modification

We conduct a limited simulation study to vet the modification for the informative sample design. The aim of the simulation is to verify that the modification for informative sampling reduces a bias in the predictor that ignores the survey weights when the sample design is informative for the specified model.

To focus attention on the informative sampling procedure, we do not use a zero-inflated model for the simulation. We use one of the simulation models from Berg and Lee (2019a). The simulation model is defined by (39) $y_{ij}={\text{β}}_0+{\text{β}}_1{x}_{ij}+b_i+e_{ij},$(39) where $x_{ij}\stackrel{iid}{\sim }N(0,1)$, ${\text{β}}_0=-1.5$, ${\text{β}}_1=0.5$, $b_i\sim N(0,0.5)$, and $e_{ij}=(1+0.1x_{ij})(e_{ij}^{\ast }-2)/2$, and $e_{ij}^{\ast }\sim {\chi }_{\left(2\right)}^2$. We generate D=60 areas with $(N_i,n_i)=(143,5)$ for 20 areas, $(N_i,n_i)=(286,10)$ for 20 areas, and $(N_i,n_i)=(571,20)$ for 20 areas. The MC sample size for each simulation is 200. The population quantile is $q_i\left(\tau \right)=min\{y_{ij}:F_{y_i}(y_{ij})\ge \tau :j=1,\dots ,N_i\}$, where $F_{y_i}\left(y\right)=N_i^{-1}\sum _{j=1}^{N_i}I[y_{ij}\le y]$.

A sample is selected using systematic probability proportional to size sampling. The inclusion probability for element j in area i is (40) ${\pi }_{ij}=\frac{n_i{z}_{ij}}{\sum _{j=1}^{N_i}{z}_{ij}},$(40) where (41) $\log \left(z_{ij}\right)=-y_{ij}/3+{\text{β}}_0/3+{\text{β}}_1{x}_{ij}/3+u_i/15.$(41) Table 1 contains the average Monte Carlo (MC) MSE and average MC bias of two predictors, where the average is across areas of the same sample size. The predictor denoted ‘SRS’ is the predictor of Berg and Lee (2019a), which ignores the unequal selection probabilities. The predictor denoted ‘Inf’ uses the modification (35(35) $\begin{array}{rl}{\tilde{q}}_{ij}^{\left(r\right)}& =\left\{\begin{array}{l}{\hat{q}}_{ij}\left({\tau }_k\right)\text{ with probability }\\ \frac{{\hat{\omega }}_{ij}\left({\hat{q}}_{ij}\right({\tau }_k\left)\right)}{\sum _{k=1}^K{\hat{\omega }}_{ij}\left({\hat{q}}_{ij}\right({\tau }_k\left)\right)}& \text{if }(i,j)\notin A\\ {\hat{q}}_{ij}\left({\tau }_k\right)\text{ with probability }{K}^{-1}& \text{if }(i,j)\in A.\end{array}\right.\end{array}$(35) ) to account for the informative design. The bias for the SRS procedure that ignores the weights is negative because the probability of selection increases as $y_{ij}$ decreases. Incorporating the survey weights through the procedure of Section 3.1 reduces the average MC MSE and absolute average MC bias of the predictor.

Table 1. Comparison of MC bias and MC MSE for LIGPD predictors.

τ	Criterion	Predictor	$n_i=5$	$n_i=10$	$n_i=20$
0.25	MSE	SRS	0.0403	0.0229	0.0166
0.25	MSE	Inf	0.0316	0.0146	0.0077
0.25	Bias	SRS	−0.0954	−0.0935	−0.0965
0.25	Bias	Inf	−0.0166	−0.0145	−0.0174
0.50	MSE	SRS	0.0636	0.0453	0.0387
0.50	MSE	Inf	0.0349	0.0173	0.0095
0.50	Bias	SRS	−0.1740	−0.1720	−0.1756
0.50	Bias	Inf	−0.0322	−0.0301	−0.0338
0.75	MSE	SRS	0.1656	0.1446	0.1352
0.75	MSE	Inf	0.0546	0.0316	0.0204
0.75	Bias	SRS	−0.3442	−0.3472	−0.3508
0.75	Bias	Inf	−0.0654	−0.0686	−0.0725

Notes: SRS: predictors ignoring sampling weights. Inf: predictors that incorporate the modification for informative sampling defined in Section 3.1.

4. Illustration for Kansas CEAP data

We illustrate the procedures using data collected from the 2003–2006 CEAP surveys in Kansas. We consider the response variable, percolation. Approximately 12% of the sampled values of percolation are zero for Kansas. A preliminary analysis shows that the conditional distribution of the percolation variable given the covariates that we considered violates the assumptions of simple parametric models, such as the linear mixed effects model (Battese et al., 1988) and the lognormal mixed effects model (Berg & Chandra, 2014). Therefore, the percolation variable provides a realistic candidate for demonstrating the quantile regression procedures.

We apply the procedures of Sections 2 and 3 above to obtain county level predictors of the quantiles of the percolation variable for Kansas. We use M=2 steps of the iterative estimation procedure and T=100 bootstrap samples. For the informative sampling modification, we use $R=100$ to obtain a simulated approximation for the population. As a covariate, we use a rainfall erosion index (RFACT). The covariate RFACT is defined geographically, as in Wischmeier and Smith (1978, p. 11), for the full population. We obtain the RFACT from the NRI survey data. For this illustration, we treat the NRI as a population.

4.1. Model and estimators for CEAP data analysis

The rainfall factor is used as the univariate covariate in all components of the model. We consider an extension of the model (9(9) $q_{posij}\left(\tau \right)={\mathit{x}}_{ij}^{\prime }\text{β}\left(\tau \right)\exp \left(b_i\right),$(9) ) for the CEAP data analysis. The extended model for the conditional quantile of $y_{ij}$ given that $y_{ij}>0$ is (42) $q_{posij}\left(\tau \right)=x_{ij}^{\eta }\text{β}\left(\tau \right)\exp \left(b_i\right),$(42) where $x_{ij}$ is the rainfall factor, and the power η is constant across quantile levels. We chose to expand the model to include the power η after exploratory work indicated a nonlinear association between $x_{ij}$ and $y_{ij}$ for $y_{ij}>0$. We provide an overview of the estimator of η in this section and relegate details to Appendix 2.

To estimate η, we add a step to the iterative estimation procedure defined in Section 2.2.1. After step 3 of Section 2.2.1, we implement the following step 4:

Define $\begin{array}{rl}{\tilde{L}}^{\left(m\right)}\left(\eta \right)& ={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\prod _{\{j\in A_i:y_{ij}>0\}}{f}_Y(y_{ij}\mid y_{ij}>0,x_{ij}^{\eta },b_i,{\hat{\mathit{\theta }}}^{\left(m\right)})\\ & \phi \left(b_i/{\hat{\sigma }}_b^{\left(m\right)}\right)\mathrm{d}{b}_i,\end{array}$ and define ${\hat{\eta }}^{\left(m\right)}={\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}}_{\eta }{\tilde{L}}^{\left(m\right)}\left(\eta \right)$.

The objective function, ${\tilde{L}}^{\left(m\right)}$, has an interpretation similar to a profile likelihood. We replace $x_{ij}$ with $x_{ij}^{{\hat{\eta }}^{(m-1)}}$ when implementing steps 1-3 of the procedure with estimated η. In each step m of the iteration, we restrict $x_{ij}^{{\hat{\eta }}^{(m-1)}}{\widehat{\text{β}}}^{\left(m\right)}\left(\tau \right)$ such that $x_{ij}^{{\hat{\eta }}^{(m-1)}}{\widehat{\text{β}}}^{\left(m\right)}\left(\tau \right)$ is nondecreasing in τ and $x_{ij}^{{\hat{\eta }}^{(m-1)}}{\widehat{\text{β}}}^{\left(m\right)}\left(\tau \right)>0.001$. We use 0.001 as the lower bound because 0.001 is the smallest possible nonzero value for percolation. In the model for the probability of a zero, $z_{ij}=(1,x_{ij}{)}^{\prime }$. In the model for the survey weights, ${\tilde{\mathit{x}}}_{ij}=(1,x_{ij}{)}^{\prime }$. For the bootstrap, we use the simulation procedure defined in Section 2.2 with $q_{posij}^{\ast \left(t\right)}\left({\tau }_k\right)=x_{ij}^{\hat{\eta }}\widehat{\text{β}}\left(\tau \right)$, where $\hat{\eta }$ is the final estimator of η. We estimate η for each bootstrap sample, and define a bootstrap standard error for $\hat{\eta }$ as $\sqrt{(B-1{)}^{-1}\sum _{b=1}^B({\hat{\eta }}^{\left(b\right)}-\overline{\eta }{)}^2}$, where ${\hat{\eta }}^{\left(b\right)}$ is the estimate of η obtained in bootstrap sample b, and $\overline{\eta }=B^{-1}\sum _{b=1}^B{\hat{\eta }}^{\left(b\right)}$.

4.2. Results for CEAP data analysis

The rainfall factor is positively correlated with percolation. Among units with a positive value for percolation, the correlation between the rainfall factor and percolation is 0.49, and the variance of percolation tends to increase with the rainfall factor. The estimate of the slope for the rainfall factor in the model for the probability that percolation is zero is $\hat{\gamma }=-0.0139$, with a standard error of 0.0035. The estimate of η is $\hat{\eta }=1.075$, and the bootstrap standard error is 0.014. An approximate $t-$statistic for the null hypothesis that $\eta =1$ is given by (43) $t=\frac{\hat{\eta }-1}{\sqrt{(B-1{)}^{-1}\sum _{b=1}^B({\hat{\eta }}^{\left(b\right)}-\overline{\eta }{)}^2}}=5.4,$(43) suggesting that η differs significantly from 1.

In Figure 1, county level estimates of the quartiles and the median are plotted along with normal theory 95% prediction intervals. The prediction intervals are calculated for the predictors that ignore the sampling weights. The intervals are defined as ${\hat{q}}_i\left(\tau \right)\pm 1.96\sqrt{{\widehat{MSE}}_i\left(\tau \right)}$, where ${\widehat{MSE}}_i\left(\tau \right)$ is defined in (32(32) ${\widehat{MSE}}_i\left(\tau \right)=\frac{1}{T}\sum _{t=1}^T\left({\hat{q}}_i^{\ast \left(t\right)}\right(\tau )-q_i^{\ast \left(t\right)}(\tau ){)}^2.$(32) ), and the lower interval endpoint is truncated at zero. The solid lines correspond to the procedure that ignores the sampling weights. The estimates that account for the sample design, as described in Section 3, are depicted with a dashed line.

Figure 1. Black: predictors of quartiles and the median based on the zero-inflated quantile regression model. Top left: 25 percentile. Top right: median. Bottom: 75 percentile. Solid black line: predictors do not use sampling weights. Dashed black line: predictors incorporate the sampling weights through the preocedure of Section 3.1. Green and red: upper and lower endpoints of 95% prediction intervals.

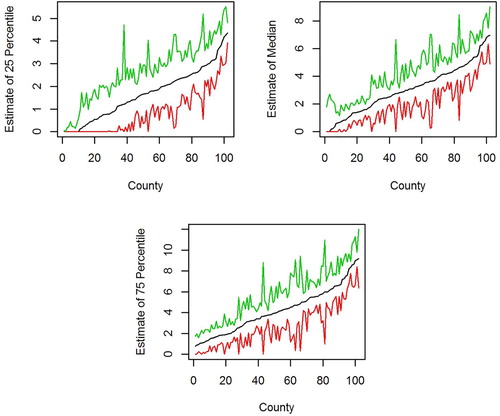
For this data set, the estimates that account for the informative sample design are nearly indistinguishable from the estimates that ignore the survey weights. Figure 2 shows the estimates for the informative design plotted on the horizontal axis with the corresponding estimates that ignore the sampling weights plotted on the vertical axis. The two sets of estimates nearly lie on the 45 degree line through the origin.

Figure 2. Comparison of predictors that incorporate the modification for informative sampling (x-axis) to predictors that do not use the sampling weights (y-axis). Top left: 25 percentiles. Top right: median. Bottom: 75 percentile.

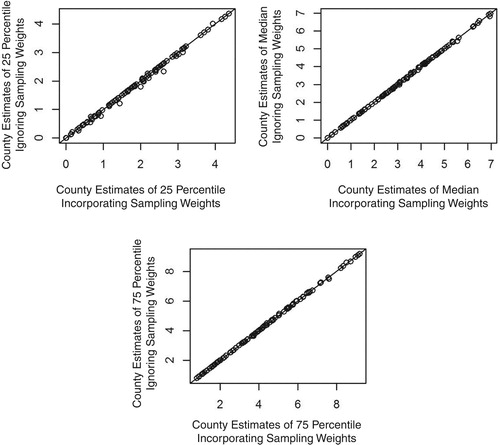
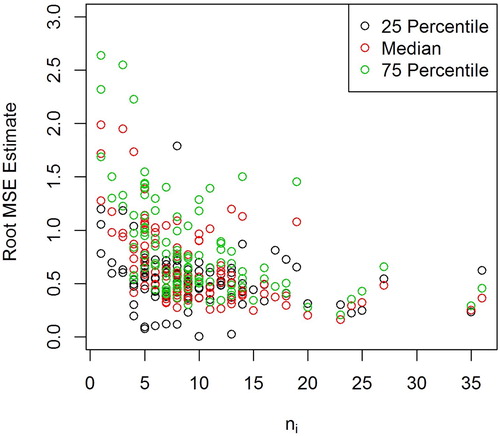
Figure 3 contains square roots of the estimated MSEs plotted against the sample sizes for the areas. The variation in the widths of the intervals is due partly to variation in the sample sizes. The use of the multiplicative lognormal distribution for $b_i$ in (42(42) $q_{posij}\left(\tau \right)=x_{ij}^{\eta }\text{β}\left(\tau \right)\exp \left(b_i\right),$(42) ) also contributes to the variation in the estimated root MSEs. The estimated MSEs from a model with an additive normal random effect show less variation than the estimated MSEs in Figure 3. Because the additive normal model does not preserve the parameter space for the zero-inflated data, we prefer the multiplicative model (42(42) $q_{posij}\left(\tau \right)=x_{ij}^{\eta }\text{β}\left(\tau \right)\exp \left(b_i\right),$(42) ).

Figure 3. Estimated root mean squared errors plotted against county sample sizes. Estimated mean squared errors are defined in (32(32) ${\widehat{MSE}}_i\left(\tau \right)=\frac{1}{T}\sum _{t=1}^T\left({\hat{q}}_i^{\ast \left(t\right)}\right(\tau )-q_i^{\ast \left(t\right)}(\tau ){)}^2.$(32) ).

We also compare the estimates with estimated η to the estimates with $\eta =1$. The absolute differences between the predictions obtained from the model with estimated η and the predictions from the model with $\eta =1$ are less than the estimated standard errors of the predictors with $\eta =1$ for all but one area. We present results for estimated η because the $t-$statistic defined in (43(43) $t=\frac{\hat{\eta }-1}{\sqrt{(B-1{)}^{-1}\sum _{b=1}^B({\hat{\eta }}^{\left(b\right)}-\overline{\eta }{)}^2}}=5.4,$(43) ) indicates that $\eta \ne 1$. For this data set, estimating η is of little practical significance.

5. Summary and future work

We develop two extensions to the mixed effects quantile regression small area procedure outlined in Section 1.2. One extension accommodates zero-inflated data. The second extension accounts for an informative sample design. To illustrate the procedures, we obtain predictors of quantiles of percolation for Kansas counties, using data from CEAP.

For this data analysis, incorporating the survey weights has only a minor effect on the estimates and estimated root mean squared errors. For this reason, we prefer the simpler predictors that do not use the sampling weights. In other applications, the effects of the sampling weights on the predictors may be important. For such situations, a mean squared error estimator that accounts for the modification for informative sampling would be desirable. Extending the bootstrap procedure of Pfeffermann and Sverchkov (2007) to estimation of quantiles is an area for future work.

For several counties, the estimated root mean squared errors are undesirably large. Expanding the model to incorporate additional covariates or spatial dependence is a possible future direction. A different approach for modelling the zero-inflated data would be to use a censored quantile regression model, as discussed in Section 1.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by National Science Foundation [MMS-000716934].

Notes on contributors

Emily Berg

Emily Berg is an assistant professor in statistics, Iowa State University.

Danhyang Lee

Danhyang Lee is an assistant professor in statistics, University of Alabama.

Appendices

Appendix 1: Initial Estimators

We define an initial estimator of $\mathit{b}=(b_1,\dots ,b_D{)}^{\prime }$ by (A1) ${\hat{\mathit{b}}}^{\left(0\right)}={\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}_{\mathit{b}}\sum _{i=1}^D\sum _{\{j\in A_i:y_{ij}>0\}}{\rho }_{0.5}(\log (y_{ij})-b_i),$(A1) where $-\sum _{i=1}^{D-1}{\hat{b}}_i^{\left(0\right)}={\hat{b}}_D^{\left(0\right)}$ . Let ${\hat{V}}_1\left({\hat{b}}_1^{\left(0\right)}\right),\dots ,{\hat{V}}_{D-1}\left({\hat{b}}_{D-1}^{\left(0\right)}\right)$ be estimates of the variance of the asymptotic distribution of $({\hat{b}}_1^{\left(0\right)},\dots ,{\hat{b}}_{D-1}^{\left(0\right)})$, estimated with the option se = "ker" in the R function summary.rq. To define an initial estimator of ${\sigma }_b^2$, define the area-level Fay-Herriot model, (A2) ${\hat{b}}_i^{\left(0\right)}=b_i+a_i,$(A2) where $a_i$ has a distribution with mean 0 and variance ${\hat{V}}_i\left\{{\hat{b}}_i^{\left(0\right)}\right\}$, and $b_i$ has a distribution with mean 0 and variance ${\sigma }_b^2$ for $i=1,\dots ,D-1$. The initial estimate of ${\sigma }_b^2$, denoted by ${\hat{\sigma }}_b^{2\left(0\right)}$, is obtained by applying the estimation procedure of Wang, Fuller, and Qu (2008) to the area level model (A2(A2) ${\hat{b}}_i^{\left(0\right)}=b_i+a_i,$(A2) ). The preliminary estimate of $\text{β}\left({\tau }_k\right)$ for $k=1,\dots ,K$ is defined by (A3) ${\widehat{\text{β}}}^{\left(0\right)}\left({\tau }_k\right)={\text{argmin}}_{\text{β}}\sum _{i=1}^D\sum _{\{j\in A_i:y_{ij}>0\}}{\rho }_{{\tau }_k}(y_{ij}/\exp ({\hat{b}}_i^{\left(0\right)})-{\mathit{x}}_{ij}^{\prime }\text{β}).$(A3) We rearrange $\left\{{\mathit{x}}_{ij}^{\prime }{\widehat{\text{β}}}^{\left(0\right)}\right({\tau }_k):k=1,\dots ,K\}$ for every $(i,j)$ to obtain a nondecreasing quantile function (Chernozhukov et al., 2009). The estimate ${\hat{q}}_{ij}^{\left(0\right)}\left({\tau }_k\right)$ is the kth order statistic of $\left\{{\mathit{x}}_{ij}^{\prime }{\widehat{\text{β}}}^{\left(0\right)}\right({\tau }_k)\exp ({\hat{b}}_i^{\left(0\right)}):k=1,\dots ,K\}$. Given the initial estimates of the quantile function, we use the procedure in Step 3 of Section 2.2 to obtain estimates ${\hat{\rho }}_s^{\left(0\right)}$ and ${\hat{\xi }}_s^{\left(0\right)}$ for $s=\ell ,u$.

Appendix 2: Details on Estimation of the Power η for the CEAP Data Analysis

Define an initial estimator of $\mathit{\theta }$ as in Appendix 2. Define an initial estimator of η as ${\hat{\eta }}^{\left(0\right)}={\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}}_{\eta }{\tilde{L}}^{\left(0\right)}\left(\eta \right),$ where $\begin{array}{rl}{\tilde{L}}^{\left(0\right)}\left(\eta \right)& ={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\prod _{\{j\in A_i:y_{ij}>0\}}{f}_Y(y_{ij}\mid y_{ij}>0,x_{ij}^{\eta },b_i,{\hat{\mathit{\theta }}}^{\left(0\right)})\\ & \phi \left(b_i/{\hat{\sigma }}_b^{\left(0\right)}\right)\mathrm{d}{b}_i.\end{array}$ For $m=1,\dots ,M$, repeat the following:

1. Define the updated estimator of ${\sigma }_b^2$ by (A4) ${\hat{\sigma }}_b^{2\left(m\right)}=(D-1{)}^{-1}\sum _{i=1}^{D}E[b_i^2\mid {\mathit{y}}_{posi};{\hat{\mathit{\theta }}}^{(m-1)}].$(A4) Define a predictor of $b_i$ in the mth step by ${\hat{b}}_i^{\left(m\right)}=E[b_i\mid {\mathit{y}}_{posi};{\hat{\mathit{\theta }}}^{(m-1)}].$ Also, define ${\hat{e}}_{bi}^{\left(m\right)}=E[\exp (b_i)\mid {\mathit{y}}_{posi},{\hat{\mathit{\theta }}}^{(m-1)}]$. The conditional expectation for estimated η is defined as (A5) $\begin{array}{rl}& E\left[h\right(b_i)\mid {\mathit{y}}_{posi};\mathit{\theta }]\\ & =\frac{\begin{array}{c}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\prod _{\{j\in A_i:y_{ij}>0\}}h\left(b_i\right)f_Y(y_{ij}|y_{ij}>0,\\ x_{ij}^{{\hat{\eta }}^{(m-1)}},b_i,{\hat{\mathit{\theta }}}^{(m-1)}\left)\phi \right(b_i/{\hat{\sigma }}_b^{(m-1)})\mathrm{d}{b}_i\end{array}}{\begin{array}{c}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\prod _{\{j\in A_i:y_{ij}>0\}}{f}_Y(y_{ij}|y_{ij}>0,\\ x_{ij}^{{\hat{\eta }}^{(m-1)}},b_i,{\hat{\mathit{\theta }}}^{(m-1)}\left)\phi \right(b_i/{\hat{\sigma }}_b^{(m-1)})\mathrm{d}{b}_i\end{array}}.\end{array}$(A5) To approximate the integrals defining the conditional expectations, we use the Riemann sum described in Appendix 1.

2. We use the method of Koenker and Ng (2005) to update the estimator of ${\text{β}}_K$ to maintain the monotonicity restriction. First, define (A6) $\begin{array}{rl}{\widehat{\text{β}}}^{\left(m\right)}\left({\tau }_1\right)& ={\text{argmin}}_{\text{β}}\sum _{i=1}^D\sum _{\{j\in A_i:y_{ij}>0\}}{\rho }_{{\tau }_{\left[1\right]}}(y_{ij}\exp (-{\hat{b}}_i^{\left(m\right)})\\ & -x_{ij}^{{\hat{\eta }}^{(m-1)}}\text{β}),\end{array}$(A6) subject to the restriction that $x_{ij}^{{\hat{\eta }}^{(m-1)}}{\widehat{\text{β}}}^{\left(m\right)}\left({\tau }_1\right)>c_0$, where $c_0$ is a specified constant. For $k=2,\dots ,K$, define (A7) $\begin{array}{rl}{\widehat{\text{β}}}^{\left(m\right)}\left({\tau }_k\right)& ={\text{argmin}}_{\text{β}}\sum _{i=1}^D\sum _{\{j\in A_i:y_{ij}>0\}}{\rho }_{{\tau }_k}(y_{ij}\exp (-{\hat{b}}_i^{\left(m\right)})\\ & -x_{ij}^{{\hat{\eta }}^{(m-1)}}\text{β})\end{array}$(A7) subject to the restriction that $x_{ij}^{{\hat{\eta }}^{(m-1)}}{\widehat{\text{β}}}^{\left(m\right)}\left({\tau }_k\right)\ge x_{ij}^{{\hat{\eta }}^{(m-1)}}{\widehat{\text{β}}}^{\left(m\right)}\left({\tau }_{k-1}\right)$ for $j=1,\dots ,N_i$ and $i=1,\dots ,D$. To enforce the monotonicity restrictions, we implement the constrained optimisation method of Koenker and Ng (2005) using the method fn in the R function rq.

3. We modify the method of Jang and Wang (2015) to estimate ${\rho }_s$ and ${\xi }_s$ for $s=\ell ,u$. Specifically, (A8) $\begin{array}{rl}{\hat{\rho }}_{\ell }^{\left(m\right)}& =0.5({\tau }_1+{\tau }_2)\sum _{i=1}^D\sum _{\{j\in A_i:y_{ij}>0\}}\\ & \times \frac{{\hat{q}}_{ij}^{\left(m\right)}\left({\tau }_2\right)-{\hat{q}}_{ij}^{\left(m\right)}\left({\tau }_1\right)}{n({\tau }_2-{\tau }_1)},\\ {\hat{\rho }}_u^{\left(m\right)}& =[1-0.5({\tau }_K+{\tau }_{K-1}\left)\right]\sum _{i=1}^D\sum _{\{j\in A_i:y_{ij}>0\}}\\ & \times \frac{{\hat{q}}_{ij}^{\left(m\right)}\left({\tau }_K\right)-{\hat{q}}_{ij}^{\left(m\right)}\left({\tau }_{K-1}\right)}{n({\tau }_K-{\tau }_{K-1})},\end{array}$(A8) where ${\hat{q}}_{ij}^{\left(m\right)}\left({\tau }_k\right)=x_{ij}^{{\hat{\eta }}^{(m-1)}}{\widehat{\text{β}}}^{\left(m\right)}\left({\tau }_k\right){\hat{e}}_{bi}^{\left(m\right)}$, and $n=\sum _{i=1}^D\sum _{j=1}^{n_i}I[y_{ij}>0]$. Holding ${\hat{\rho }}_{\ell }^{\left(m\right)}$ and ${\hat{\rho }}_u^{\left(m\right)}$ fixed, the estimator of ${\xi }_s$ is the maximum likelihood estimator using only $\{y_{ij}<{\hat{\ell }}_{ij}^{\left(m\right)}\}$ for $s=\ell$ and $\{y_{ij}>{\hat{u}}_{ij}^{\left(m\right)}\}$ for s=u, where ${\hat{\ell }}_{ij}^{\left(m\right)}=0.5\left(x_{ij}^{{\hat{\eta }}^{(m-1)}}{\widehat{\text{β}}}^{\left(m\right)}\right({\tau }_1)+x_{ij}^{{\hat{\eta }}^{(m-1)}}{\widehat{\text{β}}}^{\left(m\right)}({\tau }_2\left)\right){\hat{e}}_{bi}^{\left(m\right)}$ and ${\hat{u}}_{ij}^{\left(m\right)}=0.5\left(x_{ij}^{{\hat{\eta }}^{(m-1)}}{\widehat{\text{β}}}^{\left(m\right)}\right({\tau }_K)+x_{ij}^{{\hat{\eta }}^{(m-1)}}{\widehat{\text{β}}}^{\left(m\right)}({\tau }_{K-1}\left)\right){\hat{e}}_{bi}^{\left(m\right)}$. Precisely, (A9) $\begin{array}{rl}{\hat{\xi }}_{\ell }^{\left(m\right)}& ={\text{argmax}}_{\xi }\prod _{\left\{\right(ij):0<y_{ij}<{\hat{\ell }}_{ij}^{\left(m\right)}\}}\\ & \times g(-(y_{ij}-{\hat{\ell }}_{ij}^{\left(m\right)}\left)\right)\mid {\hat{\rho }}_{\ell }^{\left(m\right)},\xi ),\end{array}$(A9)

   and (A10) $\begin{array}{rl}{\hat{\xi }}_u^{\left(m\right)}& ={\text{argmax}}_{\xi }\prod _{\left\{\right(ij):y_{ij}>{\hat{u}}_{ij}^{\left(m\right)}>0\}}g(y_{ij}-{\hat{u}}_{ij}^{\left(m\right)}\mid {\hat{\rho }}_u^{\left(m\right)},\xi ).\end{array}$(A10)

4. Define an updated estimator of η as ${\hat{\eta }}^{\left(m\right)}={\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}}_{\eta }{\tilde{L}}^{\left(m\right)}\left(\eta \right),$ where $\begin{array}{rl}{\tilde{L}}^{\left(m\right)}\left(\eta \right)& ={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\prod _{\{j\in A_i:y_{ij}>0\}}{f}_Y(y_{ij}\mid y_{ij}>0,x_{ij}^{\eta },b_i,{\hat{\mathit{\theta }}}^{\left(m\right)})\\ & \times \phi \left(b_i/{\hat{\sigma }}_b^{\left(m\right)}\right)\mathrm{d}{b}_i.\end{array}$