?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.Abstract
In this paper, we study the derangement of 2n persons sitting 2 rows and n columns. In how many ways can the persons rearrange their seating in accordance with the following condition. Each seat is located by one person and reoccupied by another person and each person moves to a horizontal or a vertical or a diagonal neighboring seat. We establish the system of recurrence relations for the solution of this problem and provide the solution of the system of recurrence relations.
Keywords:
PUBLIC INTEREST STATEMENT
A 2 x n seating derangement is any movement of persons among the 2n seats, arranged in 2 rows and n columns, so that each seat is located by one person and reoccupied by another person and each person moves to a horizontal or a vertical or a diagonal neighboring seat. How many ways can the directive in a 2 x n seating derangement be carried out? What is the number of ways that this can be done? The objective of this paper is to solve a 2 x n seating derangement. The system of recurrence relations for the solution of this problem is established and the solution of the system of recurrence relations is obtained.
1. Introduction
Kennedy and Cooper (Citation1993) are interested in the following problem.
“A classroom has
rows of
desks per row. The teacher requests each pupil to change his seat by going either to the seat in front, the one behind, the one to his left, on to the one on his right (of course not all these options are possible for all students). How many ways can this direcitve be carried out?” (p. 60)
The answer to the classroom is
where
is the
th Fibonacci number (Honsberger, Citation1997; Kennedy & Cooper, Citation1993; Otake, Kennedy, & Cooper, Citation1996). The following problem, which were raised in Kennedy and Cooper (Citation1993) and still remain open, as follows:
“A classroom has
rows of
desks per row. The teacher requests each pupil to change his seat by going either to the seat in front or behind, the one to the left or the right, or to one of the diagonal seats (of course, not all these options are possible for all students). How may ways can this directive be carried out?”
The purpose of this paper is to study derangement for the classroom problem. We can restate the
classroom problem as follows: Consider
person seated at the 2 rows of n seats per row; in how many ways, the
person can be derangement such that each seat can located by one person and reoccupied by another person and each person moves to a horizontal or a vertical or a diagonal neighboring seat.
2. Main results
For any positive integer , suppose that
persons are seated at the 2 rows of
seats per row.
Definition 1. Let be a positive integer.
A seating derangement is any movement of person among the
seats, arranged in 2 rows and
columns, so that each seat is located by one person and reoccupied by another person and each person moves to a horizontal or a vertical or a diagonal neighboring seat.
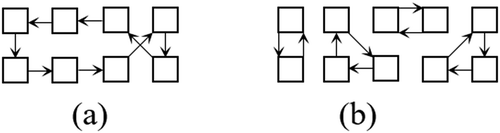
For example, the figure of seating derangement and
seating derangement are shown in Figure (a) and (b), respectively.
In Figure , Ↄ denotes a seat and denotes the movement of a person from one seat to another.
Next, we are interested in the problem of a seating derangement, in how many ways the seats can be derangement? What is the number of ways that this can be done?
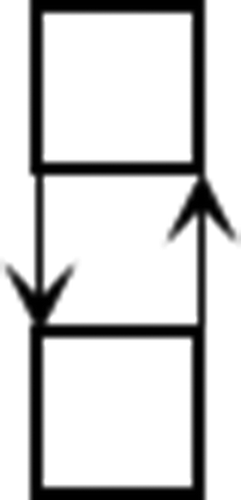
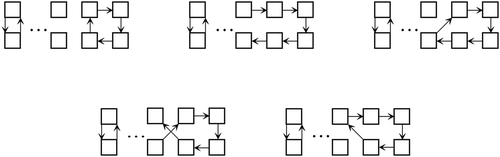
We may find that it is not easy to get a direct answer to the problem. Let us consider some special cases. When , it is clear that there is one and only one way to interchange the two seats in a
seating derangement as shown in Figure .
When there are exactly 9 ways to rearrange the 4 seats in a
seating derangement as shown in Figure .
When there are 33 different ways to rearrange the 6 seats on a
seating derangement as shown in Figure .
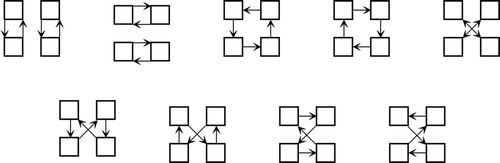
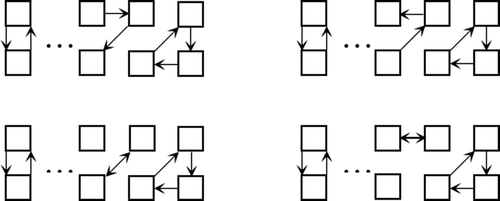
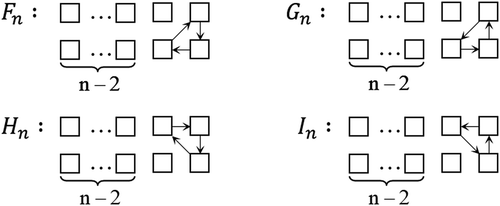
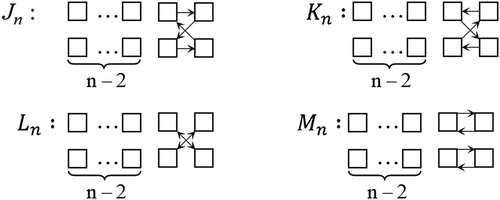
We observed that each figure in the seating derangement(Figure ) are ended by
and the
seating derangements. These exhibit endings that may be classified into 13 types, call type
, type
, type
, type
, type
, type
, type
, type
, type
, type
, type
, type
, type
as shown in Figure .
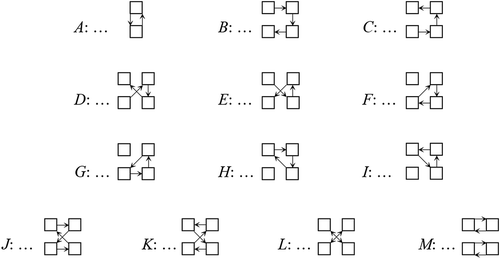
Type may be further subdivided into five kinds shown in Figure ; similarly for type
, type
and type
.
There are 4 kinds of type shown in the Figure , similarly for type
, type
and type
. It is easy to see that there is only one kind of type
and
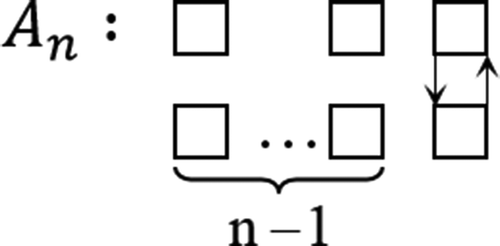
For convenience, let be the set of all
seating derangements and
denote the number of the set
. As shown before, we have
Next, we will find
The set may be partitioned into 13 subsets
and
according to the 41 endings (Figure –1).
Let and
be the cardinalities of
and
respectively.
Then, the number of the seating derangement is
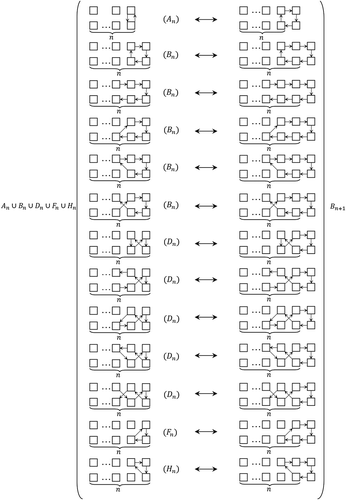
Theorem 2. The number of the seating derangement is
where satisfy the recurrence matrix
and
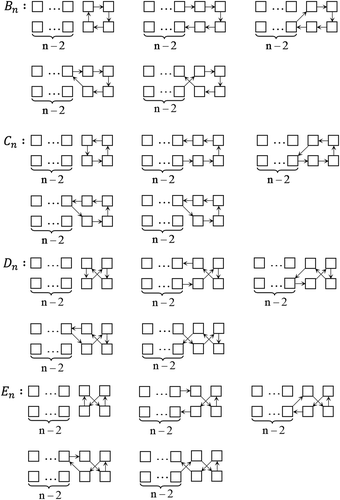
Proof. It is clear that any member of becomes a member of
when an extra column (Figure ) is attached to the end, and conversely. Then,
Next, there is a 1–1 correspondences between and
, shown in Figure . Then,
Since is a one-to-one correspondence to
we have
Similarly, we have
From the seating derangement, we obtain that
and
For we derive
and
form the following recurrence relation.
We notice that
and
It follows that
Since and
we have
and
Set and
Therefore, the number of the
seating derangement is
where
and
These results are summarized in the matrix equation:
where
Ↄ
The following table shows the values of and
in Theorem 2. when
Theorem 3. Let be a positive integer.
The number of the seating derangement is
where
and
Proof. By Theorem 2, the number of the seating derangement is
(1)
where
(*)
for positive integer and
The system of equations in (*) are reduced to a single equation:
(2)
The characteristic equation is
The zeros of this polynomial are
The general solution of Equation (2) is
(3)
and using the initial conditions, and
we obtain
We substitute Equation (3) into which yields
Since (by Theorem 2), we have
This completes the proof.
Additional information
Funding
Notes on contributors
Monrudee Sirivoravit
Monrudee Sirivoravit is a lecturer in the Department of Mathematics at Kasetsart University. She obtained her M.Sc. degree in Mathematics from Chulalongkorn University, Thailand, in 2004. Her research interests are Algebra, Number Theory and Combinatorics.
Utsanee Leerawat
Utsanee Leerawat is an associate professor in the Department of Mathematics at Kasetsart University. She received her Ph.D. degree in Mathematics in 1994 at Chulalongkorn University, Thailand. Her research interests are Ring Theory (derivations, commutativity conditions in rings), Universal algebra and Combinatorics.
References
- Honsberger, R. (1997). In Polya’s footsteps: Miscellaneous problems and essays, Dolciani mathematical exposition number 19. MAA, New york, USA.
- Kennedy, R. E., & Cooper, C. (1993). Variation on a five - by - five seating rearrangement problem (pp. 59–67). Mathematics in College. Fall-Winter, New York.
- Otake, T., Kennedy, R. E., & Cooper, C. (1996). On a seating rearrangement problem. Mathematics and informatics quarterly, 52, 63–71.