Soret and Dufour effects on transient free convention heat and mass transfer flow in a vertical channel with ramped wall temperature and specie concentration: an analytical approach

Abstract

This work investigates unsteady free convection heat and mass transfer flow in a vertical channel in the presence of Soret and Dufour effects. The bounding walls and the specie are considered to have ramped temperature and ramped concentration respectively. Perturbation method is first used to decouple the governing equations that arise from the model due to the presence of combined Soret and Dufour effects. Laplace transform technique is then used to obtain an analytical solutions for the temperature, concentration and velocity. In order to cross check the accuracy of the proposed analytical method, numerical solutions are obtained using PDEPE in MATLAB. The influences of the two effects as well as the ramped boundary conditions on the fluid flow are graphically presented and discussed. The results show that these two effects and the imposed boundary conditions affect the fluid temperature, concentration, velocity, rate of heat transfer, rate of mass transfer and wall Skin friction. Moreover, it is found that the solutions obtained by the authors Jha and Gambo correspond to the results of the present work when Soret effect is absent.

Keywords:

• Dufour effect
• free convection
• mass transfer
• perturbation method
• ramped concentration
• ramped temperature
• Soret effect

1. Introduction

Studies on Soret and Dufour effects on free convection heat and mass transfer flow continue to attract the attention of several scholars recently due to their applications in many engineering and scientific systems. Soret effect is the mass transfer generated by temperature gradients while Dufour effect is the transfer of heat generated by concentration gradients. Although the magnitudes of the two effects are small, however, they have been seen to have direct relevance in systems where density differences in the flow region exist such as in petrology, isotopes separation, hydrology, chemical processing, geoscience among others (Ashyralyev & Gambo, 2016; Isah, Jha, & Jeng-Eng, 2016; Jha & Gambo, 2019; Omowaye, Fagbade, & Ajayi, 2015; Tippa, Narahari, & Rajashekhar, 2014; Uwanta & Usman, 2014). Several studies reveal that free convection heat and mass transfer flow can be affected by Soret effect, Dufour effect or the combination of the two (Bourich, Hasnaoui, Mamou, & Amahmid, 2004; Isah et al., 2016; Jha & Gambo, 2019; Kafoussias & Williams, 1995; Lagra, Bourich, Hasnaoui, Amahmid, & Er-Raki, 2018; Mortimer & Eyring, 1980; Omowaye et al., 2015; Raju, Narahari, & Rajashekhar, 2014; Reddy, 2016; Soret, 1979; Tippa et al., 2014; Uwanta & Usman, 2014). However, when the two effects are combined, the resulting system of governing equations becomes highly complicated and its analytical solution has been an outstanding challenge in heat and mass transfer process. In fact, all analytical studies on the combined Soret and Dufour effects that exist in literatures are so far limited to steady-state case. On the other hand, in all investigations concerning combined effects of Soret and Dufour, numerical, experimental or steady-state analytical solutions are obtained by assuming the boundary conditions on velocity, temperature and concentration to be continuous. However, real-life problems involve non-uniform boundary conditions.

Makinde (2011) presented a numerical investigation on combined Soret and Dufour effects for mixed convection flow of an incompressible fluid using shooting technique. His work was done on a single porous plate and he also analyzed the effects of other parameters including buoyancy ratio and transverse magnetic field. The author showed that Soret and Dufour effects influenced the local skin friction. Srinivas, Sreedhar, and Govardhan (2015) carried out numerical investigation on Soret and Dufour effects on a steady 2D free convection flow through a vertical porous surface with viscous dissipation. They adopted implicit finite difference scheme to solve the resulting governing PDEs by first transforming them in to a system of ODEs. Dufour and Soret effects on steady mass transfer flow on a boundary layer with mixed free-forced convection are studied in Gbadeyan, Idowu, Ogunsola, Agboola, and Olanrewaju (2011). The observation they made was that the occurrence of heat transfer and mass transfer concurrently in non-static fluids made the relationship between the driving force and the fluxes to be more complex. They concluded that it is possible to produce an energy flux by concentration gradients too. Jha and Ajibade Alam (2010) clearly indicated the elusiveness in finding analytical solutions of the resulting system of equations by combining Soret and Dufour effects, and so they avoided combining the two effects. Instead, they employed Laplace transform technique (LTT) and solved the resulting governing system of PDEs from free convection and mass transfer flow in a vertical channel with Dufour effect only under the influence of asymmetric temperature and concentration on the plates. Their results showed that for large value of time, the transient solution matched the steady-state solution. They also observed that for small Prandtl numbers, the Dufour effect produced an unusual situation in the fluid temperature and velocity. Jha and Ajibade (2010) analytically investigated the free-convection and mass transfer flow in a vertical channel formed by two vertical parallel plates. Fully developed laminar flow was considered with uniform temperature and concentration on the plates. The Dufour effect was taken into consideration. The analytical solutions for velocity, temperature, and concentration were obtained using LTT and were used to compute the shear stress, Nusselt number, and mass flux. Chamkha (2002) considered unsteady, laminar, double-diffusive, free convection flow inside a rectangular enclosure filled with a uniform porous medium with cooperating temperature and concentration gradients.

Real-life problems often require non-uniform or arbitrary boundary conditions. This makes it very useful to study problems which are subjected to step change in wall temperature. Quite a lot of work in this aspect were carried out by various authors. In Chandran, Sacheti, and Singh (2005), the influence of ramped wall temperature on free convection flow over a vertical single plate was studied. The authors presented and discussed the effect of ramped boundary conditions on the fluid velocity, temperature, skin friction and coefficient of heat transfer. Neither Soret nor Dufour effects was considered in the article. Marneni, Tippa, and Pendyala (2015) analytically investigated the influence of Dufour effect, magnetic field, heat absorption or generation, thermal radiation and chemical reaction on unsteady free convection flow over a vertical plate contained in a porous medium with ramped wall temperature. They observed that increase in Dufour parameter, heat source number and permeability parameter accelerated the fluid flow whereas the flow slowed down when Schmidt parameter, radiation parameter and magnetic field number increased. Narahari and Raghavan (2009) obtained an analytical solution to the free convective flow of an incompressible fluid through a channel as a result of ramped heating at one boundary using LTT. Narahari, Sowmya, and Rajashekhar (2015) investigated Dufour effect on free convective flow with heat absorption, thermal radiation, chemical reaction, and magnetic field with ramped wall temperature over a single vertical plate contained in a permeable medium. By applying LTT and including ramped wall temperature condition, Asma, Ilyas, and Sharidan (2015) carried out research on free convective flow of nanofluids past an oscillating wall. The ramped and isothermal cases were compared. More works on the influence of ramped boundary conditions are discussed in Das (2012); Kataria and Mittal (2017); Narahari (2012); Narahari et al. (2013). Ahmad, Asghar, and Afzal (2016) studied the mixed convection boundary layer flow of a nanofluid past a vertical Riga plate in the presence of strong suction. The mathematical model incorporated the Brownian motion and thermophoresis effects due to nanofluid and the Grinberg-term for the wall parallel Lorentz force due to Riga plate. The analytical solution of the problem is presented using the perturbation method for small Brownian and thermophoresis diffusion parameters. The numerical solution is also presented to ensure the reliability of the asymptotic method. The comparison of the two solutions shows an excellent agreement.

Combining Soret and Dufour effects helps in understanding some important phenomena such as chemical processing, thermoconvective currents and so on. However, the governing system of partial differential equations that result from the model is highly complicated and thus difficult to solve analytically. For this reason, all studies involving coupling the two effects are so far limited to numerical, experimental or analytical for only steady-state case. The objective and novelty of this research is to present an analytical solutions to the coupled system of governing equations that arise from combining Soret and Dufour effects on unsteady free convection flow in a vertical channel. The work becomes even more complicated as the bounding walls and the specie are considered to have ramped temperature and concentration profiles, respectively. The analytical solutions are obtained by first decoupling the system using perturbation method as proposed in Ahmad et al. (2016) and then solved by applying LTT. It is important to note that although parameter expanding method was used in He (2000, 2006), however, in the present research work, the analytical solution of the problem is derived using the perturbation method for small Soret and Dufour parameter. To ensure accuracy in the results, comparison is made with numerical results obtained using PDEPE in MATLAB. Moreover, the results presented here are related with existing literature in the absence of Soret effect. In fact, the solutions obtained by Jha and Gambo (2019) can be derived as a particular case. This is one of the validity checks for our results.

2. Governing equations

The unsteady flow of a viscous incompressible fluid between two infinite parallel vertical plates of width $l$ is considered. The $x$ axis is chosen alongside the plates going upward while the $y$ axis is the one perpendicular to it going along the channel width (Figure 1).

Figure 1. Physical configuration.

Originally, at time $t\mathrm{\text{'}}\le \mathrm{}0,$ the two bounding walls and the fluid are considered to have the same constant temperature $T_l^{\mathrm{\text{'}}}$ and concentration $C_l^{\mathrm{\text{'}}},$ respectively. At $t^{\mathrm{\text{'}}}>0,$ the temperature and concentration at the wall $y^{\mathrm{\text{'}}}=0$ have, respectively, a temporally ramped function given by $T_l^{\mathrm{\text{'}}}+\left(T_0^{\mathrm{\text{'}}}-T_l^{\mathrm{\text{'}}}\right)t^{\mathrm{\text{'}}}\nu /l^2$ and $C_l^{\mathrm{\text{'}}}+\left(C_0^{\mathrm{\text{'}}}-C_l^{\mathrm{\text{'}}}\right)t^{\mathrm{\text{'}}}\nu /l^2$ at $t\mathrm{\text{'}}\le \mathrm{}{l}^2/\nu ,$ and then, at $t^{\mathrm{\text{'}}}>\mathrm{}{l}^2/\nu ,$ the temperature and concentration are maintained at $T_0^{\mathrm{\text{'}}}$ and $C_0^{\mathrm{\text{'}}},$ respectively, while at the other wall $y^{\mathrm{\text{'}}}=l,$ the temperature and concentration remain the same as the initial temperature $T_l^{\mathrm{\text{'}}}$ and concentration $C_l^{\mathrm{\text{'}}},$ giving raise to free convection currents. The temperature, concentration and velocity solely become functions of $y^{\mathrm{\text{'}}}$ and $t^{\mathrm{\text{'}}}$ because we assume infinite lengths for the both walls. Using Boussinesq’s approximations, the mathematical model for the present physical situation in dimensional form are: (1) $$\frac{\partial u^{\mathrm{\text{'}}}}{\partial t^{\mathrm{\text{'}}}}=\nu \frac{{\partial }^2{u}^{\mathrm{\text{'}}}}{\partial y^{\mathrm{\text{'}}2}}+g\beta \left(T^{\mathrm{\text{'}}}-T_l^{\mathrm{\text{'}}}\right)+g{\beta }^{\mathrm{*}}\left(C^{\mathrm{\text{'}}}-{C\mathrm{\text{'}}}_l\right)$$(1) (2) $$\frac{\partial T^{\mathrm{\text{'}}}}{\partial t^{\mathrm{\text{'}}}}=\alpha \frac{{\partial }^2{T}^{\mathrm{\text{'}}}}{\partial y^{\mathrm{\text{'}}2}}+D^{\mathrm{*}}\frac{{\partial }^2{C}^{\mathrm{\text{'}}}}{\partial y^{\mathrm{\text{'}}2}}$$(2) (3) $$\frac{\partial C^{\mathrm{\text{'}}}}{\partial t\mathrm{\text{'}}}=D\frac{{\partial }^2{C}^{\mathrm{\text{'}}}}{\partial y^{\mathrm{\text{'}}2}}+S^{\mathrm{*}}\frac{{\partial }^2{T}^{\mathrm{\text{'}}}}{\partial y^{\mathrm{\text{'}}2}}$$(3)

The initial and the ramped wall boundary conditions are (4) $$\{\begin{array}{l}{t}^{\mathrm{\prime }}\le 0:{\mathrm{}u}^{\mathrm{\prime }}=0,T^{\mathrm{\prime }}=T_l^{\mathrm{\prime }},C^{\mathrm{\prime }}=C_l^{\mathrm{\prime }}\mathit{for}0\le y^{\mathrm{\prime }}\le l\\ t^{\mathrm{\prime }}>0:\{\begin{array}{l}at{y}^{\mathrm{\prime }}=0:\{\begin{array}{l}\begin{array}{l}{u}^{\mathrm{\prime }}=0\\ \\ \{\begin{array}{l}{T}^{\mathrm{\prime }}=T_l^{\mathrm{\prime }}+\frac{(T_0^{\mathrm{\prime }}-T_l^{\mathrm{\prime }})t^{\mathrm{\prime }}\nu }{l^2},0<t^{\mathrm{\prime }}<\frac{l^2}{\nu }\\ \\ T^{\mathrm{\prime }}=T_0^{\mathrm{\prime }},t^{\mathrm{\prime }}\ge \frac{l^2}{\nu }\end{array}\\ \\ \{\begin{array}{l}\begin{array}{l}{C}^{\mathrm{\prime }}=C_l^{\mathrm{\prime }}+\frac{(C_0^{\mathrm{\prime }}-C_l^{\mathrm{\prime }})t^{\mathrm{\prime }}\nu }{l^2},0<t^{\mathrm{\prime }}<\frac{l^2}{\nu }\\ \\ C^{\mathrm{\prime }}=C_0^{\mathrm{\prime }},t^{\mathrm{\prime }}\ge \frac{l^2}{\nu }\end{array}\\ \end{array}\end{array}\\ \end{array}\\ at{y}^{\mathrm{\prime }}=l:\{\begin{array}{l}\begin{array}{l}{u}^{\mathrm{\prime }}=0\\ T^{\mathrm{\prime }}=T_l^{\mathrm{\prime }}\\ C^{\mathrm{\prime }}=C_l^{\mathrm{\prime }}\end{array}\\ \end{array}{t}^{\mathrm{\prime }}>\frac{l^2}{\nu }\end{array}\end{array}$$(4)

The following substitutions change Equations (1)–(3) into non-dimensional forms: (5) $$\begin{array}{l}t=\frac{t^{\mathrm{\prime }}\nu }{l^2},y=\frac{y^{\mathrm{\prime }}}{l},Pr=\frac{\nu }{\alpha },\\ \\ \theta =\frac{T^{\mathrm{\prime }}-{T\mathrm{\prime }}_l}{T_0-{T\mathrm{\prime }}_l},\varphi =\frac{C^{\mathrm{\prime }}-{C\mathrm{\prime }}_l}{C_0-{C\mathrm{\prime }}_l},u=\frac{u^{\mathrm{\prime }}\nu }{g\beta \left({T^{\mathrm{\prime }}}_0-{T^{\mathrm{\prime }}}_l\right)l^2},\\ S_r=\frac{S^{\mathrm{*}}\left({T\mathrm{\prime }}_0-{T\mathrm{\prime }}_l\right)}{D(C_0^{\mathrm{\prime }}-C_l^{\mathrm{\prime }})},D_f=\frac{D^{\mathrm{*}}\left({C\mathrm{\prime }}_0-{C\mathrm{\prime }}_l\right)}{\alpha (T_0^{\mathrm{\prime }}-T_l^{\mathrm{\prime }})},Sc=\frac{\nu }{D},N=\frac{{\beta }^{\mathrm{*}}\left(C_0^{\mathrm{\prime }}-C_l^{\mathrm{\prime }}\right)}{\beta \left({T^{\mathrm{\prime }}}_0-{T^{\mathrm{\prime }}}_l\right)}.\end{array}\}$$(5)

Thus, Equations (1)–(3) becomes (6) $$\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u}{\partial y^2}+\theta +N\varphi$$(6) (7) $$\frac{\partial \theta }{\partial t}=\frac{1}{Pr}\frac{{\partial }^2\theta }{\partial y^2}+\frac{D_f}{Pr}\frac{{\partial }^2\varphi }{\partial y^2}$$(7) (8) $$\frac{\partial \varphi }{\partial t}=\frac{1}{Sc}\frac{{\partial }^2\varphi }{\partial y^2}+\frac{S_r}{Sc}\frac{{\partial }^2\theta }{\partial y^2}$$(8)

The initial and boundary conditions given in Equation (4)(4) $$\{\begin{array}{l}{t}^{\mathrm{\prime }}\le 0:{\mathrm{}u}^{\mathrm{\prime }}=0,T^{\mathrm{\prime }}=T_l^{\mathrm{\prime }},C^{\mathrm{\prime }}=C_l^{\mathrm{\prime }}\mathit{for}0\le y^{\mathrm{\prime }}\le l\\ t^{\mathrm{\prime }}>0:\{\begin{array}{l}at{y}^{\mathrm{\prime }}=0:\{\begin{array}{l}\begin{array}{l}{u}^{\mathrm{\prime }}=0\\ \\ \{\begin{array}{l}{T}^{\mathrm{\prime }}=T_l^{\mathrm{\prime }}+\frac{(T_0^{\mathrm{\prime }}-T_l^{\mathrm{\prime }})t^{\mathrm{\prime }}\nu }{l^2},0<t^{\mathrm{\prime }}<\frac{l^2}{\nu }\\ \\ T^{\mathrm{\prime }}=T_0^{\mathrm{\prime }},t^{\mathrm{\prime }}\ge \frac{l^2}{\nu }\end{array}\\ \\ \{\begin{array}{l}\begin{array}{l}{C}^{\mathrm{\prime }}=C_l^{\mathrm{\prime }}+\frac{(C_0^{\mathrm{\prime }}-C_l^{\mathrm{\prime }})t^{\mathrm{\prime }}\nu }{l^2},0<t^{\mathrm{\prime }}<\frac{l^2}{\nu }\\ \\ C^{\mathrm{\prime }}=C_0^{\mathrm{\prime }},t^{\mathrm{\prime }}\ge \frac{l^2}{\nu }\end{array}\\ \end{array}\end{array}\\ \end{array}\\ at{y}^{\mathrm{\prime }}=l:\{\begin{array}{l}\begin{array}{l}{u}^{\mathrm{\prime }}=0\\ T^{\mathrm{\prime }}=T_l^{\mathrm{\prime }}\\ C^{\mathrm{\prime }}=C_l^{\mathrm{\prime }}\end{array}\\ \end{array}{t}^{\mathrm{\prime }}>\frac{l^2}{\nu }\end{array}\end{array}$$(4) becomes (9) $$\begin{array}{c}\\ t\le 0:u\left(y,t\right)=0,\theta \left(y,t\right)=0,\varphi \left(y,t\right)=0\mathit{for}0\le y\le 1\\ \\ t>0:\{\begin{array}{c}u\left(0,t\right)=0,u\left(1,t\right)=0\\ \\ \{\begin{array}{c}\theta \left(0,t\right)=t,\varphi \left(0,t\right)=t0<t<1\\ \\ \theta \left(0,t\right)=1,\varphi \left(0,t\right)=1,t\ge 1\end{array}\\ \\ \theta \left(1,t\right)=\varphi \left(1,t\right)=0\end{array}\end{array}$$(9)

The heat transfer coefficient ($Nu$), mass transfer coefficient ($Sh$) and Skin friction $\left(C_f\right)$ are defined, respectively, as (10) $${\tau }_{0,1}=-{\left(\frac{\partial u}{\partial y}\right)}_{y=0,1}$$(10) (11) $$N{u}_{0,1}=-{\left(\frac{\partial \theta }{\partial y}\right)}_{y=0,1}$$(11) (12) $$S{h}_{0,1}=-{\left(\frac{\partial \varphi }{\partial y}\right)}_{y=0,1}$$(12)

3. Analytical solutions

In order to decouple the system of Equations (6)–(8), a small non-zero parameter $\epsilon$ is used such that the Soret and Dufour parameters are of order $O(\epsilon )$ (Ahmad et al., 2016). Perturbation method has been used to write the analytical solution of the problem utilizing the fact that Soret and Dufour parameters are small (Isah et al., 2016; Lagra et al., 2018; Makinde, 2011; Reddy, 2016; Uwanta & Usman, 2014).

Thus, (13) $$\theta ={\theta }_0+\epsilon {\theta }_1+\dots$$(13) (14) $$\varphi ={\varphi }_0+\epsilon {\varphi }_1+\dots$$(14) (15) $$u=u_0+\epsilon u_1+\dots$$(15) where (16) $$D_f=a\epsilon ,\mathrm{}{S}_r=b\epsilon$$(16) and $a$ and $b$ are constants of order $O(1).$ Then substituting Equations (13)(13) $$\theta ={\theta }_0+\epsilon {\theta }_1+\dots$$(13) and (14)(14) $$\varphi ={\varphi }_0+\epsilon {\varphi }_1+\dots$$(14) in (7) and (8), respectively, gives:

Order ${\mathit{\epsilon }}^0:$ (17) $$\frac{\partial u_0}{\partial t}=\frac{{\partial }^2{u}_0}{\partial y^2}+{\theta }_0+N{\varphi }_0$$(17) (18) $$\frac{\partial {\theta }_0}{\partial t}=\frac{1}{Pr}\frac{{\partial }^2{\theta }_0}{\partial y^2}$$(18) (19) $$\frac{\partial {\varphi }_0}{\partial t}=\frac{1}{Sc}\frac{{\partial }^2{\varphi }_0}{\partial y^2}$$(19) (20) $$\left.\begin{array}{c}\\ u_0\left(y,0\right)=0,{\theta }_0\left(y,0\right)=0,{\varphi }_0\left(y,0\right)=0;0\le y\le 1\\ \\ \begin{array}{c}{u}_0\left(0,t\right)=0,u_0\left(1,t\right)=0\\ \\ \begin{array}{c}{\theta }_0\left(0,t\right)=t,{\varphi }_0\left(0,t\right)=t,0<t<1\\ \\ {\theta }_0\left(0,t\right)=1,{\varphi }_0\left(0,t\right)=1,t\ge 1\end{array}\\ \\ {\theta }_0\left(1,t\right)={\varphi }_0\left(1,t\right)=0\end{array}\end{array}\right\}$$(20)

Using the Heaviside step function $H(t),$ we write the ramped boundary conditions for the temperature and concentration given in (Bourich et al., 2004) as (21) $${\theta }_0\left(0,t\right)={\varphi }_0\left(0,t\right)=tH\left(t\right)-(t-1)H(t-1)$$(21)

Then applying LTT (Abramowitz & Stegun, 1965; Carslaw & Jaeger, 1959, 1963) to Equations (17)(17) $$\frac{\partial u_0}{\partial t}=\frac{{\partial }^2{u}_0}{\partial y^2}+{\theta }_0+N{\varphi }_0$$(17) and (18)(18) $$\frac{\partial {\theta }_0}{\partial t}=\frac{1}{Pr}\frac{{\partial }^2{\theta }_0}{\partial y^2}$$(18) with the initial and boundary conditions (Chandran et al., 2005) and taking (Marneni et al., 2015) into consideration we obtain (22) $${\theta }_0(y,t)=\sum _{k=0}^{\mathrm{\infty }}\{F_1(y,t)-F_2(y,t)-[F_1(y,t-1)-F_2(y,t-1)]H(t-1)\}$$(22) (23) $${\varphi }_0(y,t)=\sum _{k=0}^{\mathrm{\infty }}\{G_1(y,t)-G_2(y,t)-[G_1(y,t-1)-G_2(y,t-1)]H(t-1)\}$$(23) (24) $$u_0(y,t)=\sum _{k=0}^{\mathrm{\infty }}\{{\beta }_1[L_1(y,t)-L_2(y,t)-\{L_1(y,t-1)-L_2(y,t-1)\}H(t-1)]-{\beta }_2[L_3(y,t)-L_4(y,t)-\{L_3(y,t-1)-L_4(y,t-1)\}H(t-1)]-{\beta }_3[L_5(y,t)-L_6(y,t)-\{L_5(y,t-1)-L_6(y,t-1)\}H(t-1)]\}$$(24) where (25) $$F_1\left(y,t\right)=\left[t+\frac{Pr{\left(2k+y\right)}^2}{2}\right]\mathrm{erfc}\left(\frac{\sqrt{Pr}\left(2k+y\right)}{2\sqrt{t}}\right)-\sqrt{\frac{\mathit{tPr}}{\pi }}\left(2k+y\right)\exp \left(-\frac{Pr{\left(2k+y\right)}^2}{4t}\right)$$(25) (26) $$\begin{array}{c}{F}_2\left(y,t\right)=\left[t+\frac{Pr{\left(2k+2-y\right)}^2}{2}\right]\mathrm{erfc}\left(\frac{\sqrt{Pr}\left(2k+2-y\right)}{2\sqrt{t}}\right)\\ -\sqrt{\frac{\mathit{tPr}}{\pi }}\left(2k+2-y\right)\exp \left(-\frac{Pr{\left(2k+2-y\right)}^2}{4t}\right)\end{array}$$(26) (27) $$G_1\left(y,t\right)=\left[t+\frac{Sc{\left(2k+y\right)}^2}{2}\right]\mathrm{erfc}\left(\frac{\sqrt{Sc}\left(2k+y\right)}{2\sqrt{t}}\right)-\sqrt{\frac{\mathit{tSc}}{\pi }}\left(2k+y\right)\exp \left(-\frac{Sc{\left(2k+y\right)}^2}{4t}\right)$$(27) (28) $$G_2\left(y,t\right)=\left[t+\frac{Sc{\left(2k+2-y\right)}^2}{2}\right]\mathrm{erfc}\left(\frac{\sqrt{Sc}\left(2k+2-y\right)}{2\sqrt{t}}\right)-\sqrt{\frac{\mathit{tSc}}{\pi }}\left(2k+2-y\right)\exp \left(-\frac{Sc{\left(2k+2-y\right)}^2}{4t}\right)$$(28) (29) $$\begin{array}{c}{L}_1\left(y,t\right)=\frac{1}{2}\left[\frac{{\left(2k+y\right)}^4}{12}+{\left(2k+y\right)}^{2}t+t^2\right]\mathrm{erfc}\left(\frac{2k+y}{2\sqrt{t}}\right)\\ -\frac{1}{6}\sqrt{\frac{t}{\pi }}\left(2k+y\right)\left[\frac{{\left(2k+y\right)}^2}{2}+5t\right]\exp \left(-\frac{{\left(2k+y\right)}^2}{4t}\right)\end{array}$$(29) (30) $$\begin{array}{c}{L}_2\left(y,t\right)=\frac{1}{2}\left[\frac{{\left(2k+2-y\right)}^4}{12}+{\left(2k+2-y\right)}^{2}t+t^2\right]\mathrm{erfc}\left(\frac{2k+2-y}{2\sqrt{t}}\right)\\ -\frac{1}{6}\sqrt{\frac{t}{\pi }}\left(2k+2-y\right)\left[\frac{{\left(2k+2-y\right)}^2}{2}+5t\right]\exp \left(-\frac{{\left(2k+2-y\right)}^2}{4t}\right)\end{array}$$(30) (31) $$\begin{array}{c}{L}_3\left(y,t\right)=\frac{1}{2}\left[\frac{{{Pr}^2\left(2k+y\right)}^4}{12}+{Pr\left(2k+y\right)}^{2}t+t^2\right]\mathrm{erfc}\left(\frac{\sqrt{Pr}\left(2k+y\right)}{2\sqrt{t}}\right)\\ -\frac{1}{6}\sqrt{\frac{\mathit{tPr}}{\pi }}\left(2k+y\right)\left[\frac{{Pr\left(2k+y\right)}^2}{2}+5t\right]\exp \left(-\frac{{Pr\left(2k+y\right)}^2}{4t}\right)\end{array}$$(31) (32) $$L_4\left(y,t\right)=\frac{1}{2}\left[\frac{{{Pr}^2\left(2k+2-y\right)}^4}{12}+{Pr\left(2k+2-y\right)}^{2}t+t^2\right]\mathrm{erfc}\left(\frac{\sqrt{Pr}\left(2k+2-y\right)}{2\sqrt{t}}\right)$$(32) (33) $$\begin{array}{c}-\frac{1}{6}\sqrt{\frac{\mathit{tPr}}{\pi }}\left(2k+2-y\right)\left[\frac{{Pr\left(2k+2-y\right)}^2}{2}+5t\right]\exp \left(-\frac{{Pr\left(2k+2-y\right)}^2}{4t}\right)\\ L_5\left(y,t\right)=\frac{1}{2}\left[\frac{{{Sc}^2\left(2k+y\right)}^4}{12}+{Sc\left(2k+y\right)}^{2}t+t^2\right]\mathrm{erfc}\left(\frac{\sqrt{Sc}\left(2k+y\right)}{2\sqrt{t}}\right)\\ -\frac{1}{6}\sqrt{\frac{\mathit{tSc}}{\pi }}\left(2k+y\right)\left[\frac{{Sc\left(2k+y\right)}^2}{2}+5t\right]\exp \left(-\frac{{Sc\left(2k+y\right)}^2}{4t}\right)\end{array}$$(33) (34) $$\begin{array}{c}{L}_6\left(y,t\right)=\frac{1}{2}\left[\frac{{{Sc}^2\left(2k+2-y\right)}^4}{12}+{Sc\left(2k+2-y\right)}^{2}t+t^2\right]\mathrm{erfc}\left(\frac{\sqrt{Sc}\left(2k+2-y\right)}{2\sqrt{t}}\right)\\ -\frac{1}{6}\sqrt{\frac{\mathit{tSc}}{\pi }}\left(2k+2-y\right)\left[\frac{{Sc\left(2k+2-y\right)}^2}{2}+5t\right]\exp \left(-\frac{{Sc\left(2k+2-y\right)}^2}{4t}\right)\end{array}$$(34) (35) $${\beta }_1=\frac{1}{Pr-1}+\frac{N}{Sc-1};\mathrm{}{\beta }_2=\frac{1}{Pr-1};\mathrm{}{\beta }_3=\frac{N}{Sc-1};\mathrm{}Pr\ne 1\mathrm{}\ne Sc$$(35)

Order${\mathit{\epsilon }}^1:$ (36) $$\frac{\partial u_1}{\partial t}=\frac{{\partial }^2{u}_1}{\partial y^2}+{\theta }_1+N{\varphi }_1$$(36) (37) $$\frac{\partial {\theta }_1}{\partial t}=\frac{1}{Pr}\frac{{\partial }^2{\theta }_1}{\partial y^2}+\frac{a}{Pr}\frac{{\partial }^2{\varphi }_0}{\partial y^2}$$(37) (38) $$\frac{\partial {\varphi }_1}{\partial t}=\frac{1}{Sc}\frac{{\partial }^2{\varphi }_1}{\partial y^2}+\frac{b}{Sc}\frac{{\partial }^2{\theta }_0}{\partial y^2}$$(38) (39) $$\left.\begin{array}{c}\\ u_1\left(y,0\right)=0,{\theta }_1\left(y,0\right)=0,{\varphi }_1\left(y,0\right)=0;0\le y\le 1\\ \\ \begin{array}{c}{u}_1\left(0,t\right)=0,u_1\left(1,t\right)=0\\ \\ {\theta }_1\left(0,t\right)=0,{\varphi }_1\left(0,t\right)=0,t>0\\ \\ {\theta }_1\left(1,t\right)={\varphi }_1\left(1,t\right)=0\end{array}\end{array}\right\}$$(39)

Order ${\epsilon }^1$ solutions are given by (40) $${\theta }_1(y,t)=\frac{\mathit{aSc}}{Pr-Sc}\sum _{k=0}^{\mathrm{\infty }}\{F_2(y,t)-F_1(y,t)-[F_2(y,t-1)-F_1(y,t-1)]H(t-1)+G_1(y,t)-G_2(y,t)-[G_1(y,t-1)-G_2(y,t-1)]H(t-1)\}$$(40) (41) $${\varphi }_1\left(y,t\right)=\frac{\mathit{bPr}}{Pr-Sc}{\theta }_1\left(y,t\right)$$(41) (42) $$u_1(y,t)=\sum _{k=0}^{\mathrm{\infty }}\{{\sigma }_1[L_1(y,t)-L_2(y,t)-\{L_1(y,t-1)-L_2(y,t-1)\}H(t-1)]+{\sigma }_2[L_3(y,t)-L_4(y,t)-\{L_3(y,t-1)-L_4(y,t-1)\}H(t-1)]+{\sigma }_3[L_6(y,t)-L_5(y,t)-\{L_6(y,t-1)-L_5(y,t-1)\}H(t-1)]\}$$(42) where (43) $$\begin{array}{c}{\sigma }_1=\frac{\mathit{aSc}+\mathit{bNPr}}{\left(Pr-1\right)\left(Sc-1\right)};\mathrm{}{\sigma }_2=\frac{\mathit{aSc}+\mathit{bNPr}}{\left(Pr-1\right)\left(Pr-Sc\right)};\mathrm{}\\ {\sigma }_3=\frac{\mathit{aSc}+\mathit{bNPr}}{\left(Sc-1\right)\left(Pr-Sc\right)}\\ Pr\ne \mathrm{}Sc\ne 1\end{array}$$(43)

Using Equations (13)–(16), (22)–(24) and (40)–(42), the final analytical solutions for the temperature, concentration and velocity are, respectively, obtained below: (44) $$\theta (y,t)=\sum _{k=0}^{\mathrm{\infty }}[\left(1-\frac{D_{f}Sc}{Pr-Sc}\right)\{F_1(y,t)-{\mathrm{F}}_2(y,t)-[F_1(y,t-1)-F_2(y,t-1)]H(t-1)\}+\frac{D_{f}Sc}{Pr-Sc}\{G_1(y,t)-G_2(y,t)-[G_1(y,t-1)-G_2(y,t-1)]H(t-1)\}]$$(44) (45) $$\varphi (y,t)=\sum _{k=0}^{\mathrm{\infty }}[\left(1+\frac{S_{r}Pr}{Pr-Sc}\right)\{G_1(y,t)-G_2(y,t)-[G_1(y,t-1)-G_2(y,t-1)]H(t-1)\}-\frac{S_{r}Pr}{Pr-Sc}\{F_1(y,t)-F_2(y,t)-[F_1(y,t-1)-F_2(y,t-1)]H(t-1)\}]$$(45) (46) $$u(y,t)=\sum _{k=0}^{\mathrm{\infty }}\{\frac{Sc(D_f+1)+\mathit{NPr}(S_r+1)-(N+1)}{(Pr-1)(Sc-1)}\times [L_1(y,t)-L_2(y,t)-\{L_1(y,t-1)-L_2(y,t-1)\}H(t-1)]+\frac{Sc(D_f+1)+Pr({NS}_r-1)}{(Pr-1)(Pr-Sc)}\times [L_3(y,t)-L_4(y,t)-\{L_3(y,t-1)-L_4(y,t-1)\}H(t-1)]-\frac{Sc(D_f-N)+\mathit{NPr}(S_r+1)}{(Sc-1)(Pr-Sc)}\times [L_6(y,t)-L_5(y,t)-\{L_6(y,\mathrm{t}-1)-L_5(y,t-1)\}H(t-1)]\}$$(46)

It is important to note that in the absence of Soret effect (i.e. when $S_r=0$), the analytical solutions for temperature, concentration and velocity given by Equations (44)–(46) correspond with the solutions obtained in Jha and Gambo (2019). In other words, the result obtained in Jha and Gamb (2019) is a particular case of the results presented in this article.

3.1. Solutions for certain cases of $\mathit{Pr}$ and $\mathit{Sc}$

If $Pr=Sc,$ then Equations (44)(44) $$\theta (y,t)=\sum _{k=0}^{\mathrm{\infty }}[\left(1-\frac{D_{f}Sc}{Pr-Sc}\right)\{F_1(y,t)-{\mathrm{F}}_2(y,t)-[F_1(y,t-1)-F_2(y,t-1)]H(t-1)\}+\frac{D_{f}Sc}{Pr-Sc}\{G_1(y,t)-G_2(y,t)-[G_1(y,t-1)-G_2(y,t-1)]H(t-1)\}]$$(44) and (45)(45) $$\varphi (y,t)=\sum _{k=0}^{\mathrm{\infty }}[\left(1+\frac{S_{r}Pr}{Pr-Sc}\right)\{G_1(y,t)-G_2(y,t)-[G_1(y,t-1)-G_2(y,t-1)]H(t-1)\}-\frac{S_{r}Pr}{Pr-Sc}\{F_1(y,t)-F_2(y,t)-[F_1(y,t-1)-F_2(y,t-1)]H(t-1)\}]$$(45) do not hold. Moreover, Equation (46)(46) $$u(y,t)=\sum _{k=0}^{\mathrm{\infty }}\{\frac{Sc(D_f+1)+\mathit{NPr}(S_r+1)-(N+1)}{(Pr-1)(Sc-1)}\times [L_1(y,t)-L_2(y,t)-\{L_1(y,t-1)-L_2(y,t-1)\}H(t-1)]+\frac{Sc(D_f+1)+Pr({NS}_r-1)}{(Pr-1)(Pr-Sc)}\times [L_3(y,t)-L_4(y,t)-\{L_3(y,t-1)-L_4(y,t-1)\}H(t-1)]-\frac{Sc(D_f-N)+\mathit{NPr}(S_r+1)}{(Sc-1)(Pr-Sc)}\times [L_6(y,t)-L_5(y,t)-\{L_6(y,\mathrm{t}-1)-L_5(y,t-1)\}H(t-1)]\}$$(46) becomes invalid when $Pr=1$ or $Sc=1.$

To overcome this problem and obtain the analytical solutions in these cases, appropriate substitutions need to be made since from Equations (7)(7) $$\frac{\partial \theta }{\partial t}=\frac{1}{Pr}\frac{{\partial }^2\theta }{\partial y^2}+\frac{D_f}{Pr}\frac{{\partial }^2\varphi }{\partial y^2}$$(7) and (8)(8) $$\frac{\partial \varphi }{\partial t}=\frac{1}{Sc}\frac{{\partial }^2\varphi }{\partial y^2}+\frac{S_r}{Sc}\frac{{\partial }^2\theta }{\partial y^2}$$(8) and then applying the methods established in this work.

3.2. Steady-state solution

Setting $\partial /\partial t=0$ in Equations (6)(6) $$\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u}{\partial y^2}+\theta +N\varphi$$(6) and (8)(8) $$\frac{\partial \varphi }{\partial t}=\frac{1}{Sc}\frac{{\partial }^2\varphi }{\partial y^2}+\frac{S_r}{Sc}\frac{{\partial }^2\theta }{\partial y^2}$$(8) , we obtain the steady-state of the problem as the following set of ODEs: (47) $$\frac{d^{2}u}{d{y}^2}+\theta +N\varphi =0$$(47) (48) $$\frac{d^2\theta }{d{y}^2}+D_f\frac{d^2\varphi }{d{y}^2}=0$$(48) (49) $$\frac{d^2\varphi }{d{y}^2}+S_r\frac{d^2\theta }{d{y}^2}=0$$(49)

From Equation (48)(48) $$\frac{d^2\theta }{d{y}^2}+D_f\frac{d^2\varphi }{d{y}^2}=0$$(48) , (50) $$\frac{d^2\theta }{d{y}^2}=-D_f\frac{d^2\varphi }{d{y}^2}$$(50)

Substituting Equation (50)(50) $$\frac{d^2\theta }{d{y}^2}=-D_f\frac{d^2\varphi }{d{y}^2}$$(50) into Equation (49)(49) $$\frac{d^2\varphi }{d{y}^2}+S_r\frac{d^2\theta }{d{y}^2}=0$$(49) such that $D_f\ne 1\ne S_r$ gives (51) $$\frac{d^2\varphi }{d{y}^2}=0$$(51)

Thus, Equation (50)(50) $$\frac{d^2\theta }{d{y}^2}=-D_f\frac{d^2\varphi }{d{y}^2}$$(50) becomes (52) $$\frac{d^2\theta }{d{y}^2}=0$$(52)

Observe that Equations (51)(51) $$\frac{d^2\varphi }{d{y}^2}=0$$(51) and (52)(52) $$\frac{d^2\theta }{d{y}^2}=0$$(52) are free from Soret and Dufour effects. Moreover, if $D_f=S_r=1,$ then the substitutions above result in a trivial solution.

Therefore, using the initial and boundary conditions (9), we obtain the following steady-state solutions for the momentum, concentration and energy Equations (47)(47) $$\frac{d^{2}u}{d{y}^2}+\theta +N\varphi =0$$(47) , (51)(51) $$\frac{d^2\varphi }{d{y}^2}=0$$(51) and (52)(52) $$\frac{d^2\theta }{d{y}^2}=0$$(52) , respectively: (53) $$\theta =1-y$$(53) (54) $$\varphi =1-y$$(54) (55) $$u=\left(\frac{N+1}{6}\right)\left(y^3-3y^2+2y\right)$$(55)

4. Numerical solution

The influence of combined Soret and Dufour effects as well as ramped boundary conditions on the flow of a viscous fluid through a channel are analysed. The numerical solutions to the system of PDEs (6)–(8) with appropriate ICs and BCs given in Equation (9)(9) $$\begin{array}{c}\\ t\le 0:u\left(y,t\right)=0,\theta \left(y,t\right)=0,\varphi \left(y,t\right)=0\mathit{for}0\le y\le 1\\ \\ t>0:\{\begin{array}{c}u\left(0,t\right)=0,u\left(1,t\right)=0\\ \\ \{\begin{array}{c}\theta \left(0,t\right)=t,\varphi \left(0,t\right)=t0<t<1\\ \\ \theta \left(0,t\right)=1,\varphi \left(0,t\right)=1,t\ge 1\end{array}\\ \\ \theta \left(1,t\right)=\varphi \left(1,t\right)=0\end{array}\end{array}$$(9) are obtained using PDEPE in MATLAB. Results are presented for various values of the parameters embedded in the problem. The buoyancy ratio $(N),$ Soret parameter $\left(S_r\right)$ and Dufour parameter $\left(D_f\right)$ are arbitrarily taken. In all computations, we choose $Pr$ as 0.025 for mercury, 0.71 for air, 7.0 for water, 11.62 for water at $4°C,$ while $Sc$ values are chosen such that 0.22 is for hydrogen, 0.60 for water vapour, 0.66 for oxygen while 0.78 for ammonia (Gebhart & Pera, 1971; Jithender, Anand, & Srinivasa, 2015).

5. Results and discussions

In order to highlight the accuracy of the analytical and numerical results, comparison is made and presented in Table 1. From the table, it is clear that there is a good match between the analytical and numerical solutions.

Table 1. Comparison of numerical and analytical results for temperature $(\theta ),$ concentration $(\varphi )$ and velocity ($u$) profiles $N=2,\mathrm{}Pr=0.71,\mathrm{}Sc=0.78,\mathrm{}{S}_r=0.01,\mathrm{}{D}_f=0.01,\mathrm{}t=0.8.$

$y$	Numerical solution			Analytical solution
	$\theta$	$\varphi$	$u$	$\theta$	$\varphi$	$u$
0.00	0.80000	0.80000	0.00000	0.80000	0.80000	0.00000
0.25	0.56159	0.55773	0.10591	0.56160	0.55773	0.10586
0.50	0.35611	0.35169	0.11592	0.35611	0.35170	0.11586
0.75	0.17257	0.16981	0.07053	0.17257	0.16981	0.07049
1.00	0.00000	0.00000	0.00000	0.00000	0.00000	0.00000

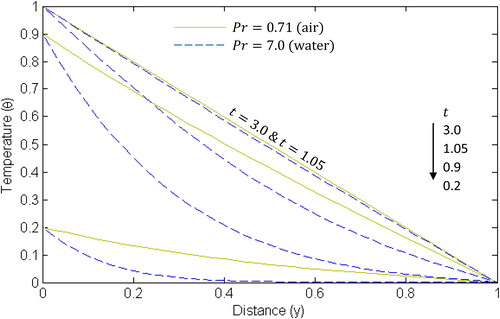
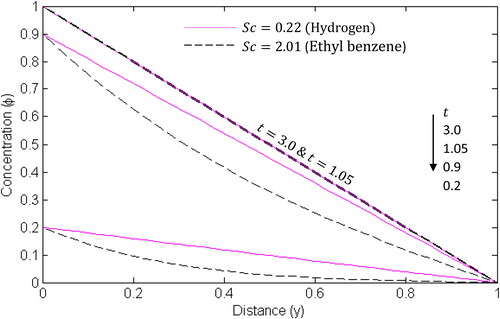
Figures 2 and 3 display results for the temperature and concentration for different values of Prandtl and Schmidt numbers respectively. In Figure 2, it can be seen that the temperature drops from its ramped value at the plate $y=0$ towards the plate $y=1.$ It is clear from the graph that the temperature increases as $t$ increases. Moreover, it can be observed that for all $t,$ the temperature of air is greater than that of water because $Pr<1$ of air signifies thermal diffusion rate is dominant over the momentum diffusion rate and therefore it will move with diffusion of thermal energy more rapidly than its flow. Similarly, the concentration is seen to increase with increasing $t$ but drops in value as the fluid flow towards the plate $y=1$ (Figure 3). On the other hand, higher values of Schmidt number makes the specie concentration lower.

Figure 2. Temperature profile for different values of $t$ for two cases of Prandtl numbers. $N=2,Sc=0.60,S_r=0.3,D_f=0.3.$

Figure 3. Concentration profile for different values of $t$ for two cases of Schmidt numbers. $N=2,Pr=0.71,S_r=0.3,D_f=0.3.$

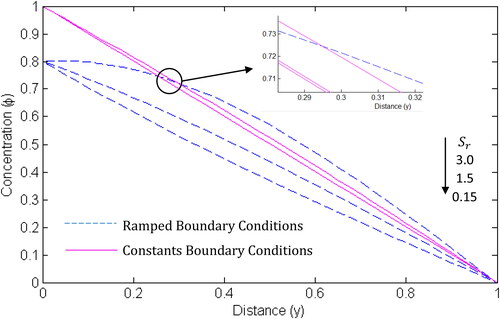
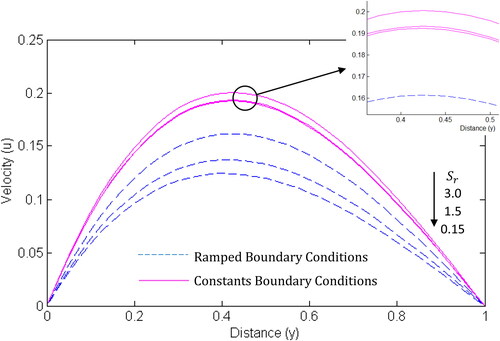
The influences of Soret and Dufour effects on the temperature, concentration and velocity are presented in Figures 4–12. It is clear from Figures 4–6 that increase in Soret number increases the concentration and velocity but decreases the fluid temperature. It can also be observed that the Soret number affects the velocity and concentration more than it affects the temperature.

Figure 4. Temperature profile for different values of $S_r.$

$N=2,Pr=0.71,\mathrm{}Sc=0.60,D_f=0.15.$

Figure 5. Concentration profile for different values of $S_r.$

$N=2,Pr=0.71,\mathrm{}Sc=0.60,D_f=0.15.$

Figure 6. Velocity profile for different values of $S_r.$

$N=2,Pr=0.71,\mathrm{}Sc=0.60,D_f=0.15.$

Figure 7. Temperature profile for different values of $D_f.$

$N=2,Pr=0.71,\mathrm{}Sc=0.60,S_r=0.15.$

Figure 8. Concentration profile for different values of $D_f.$

$N=2,Pr=0.71,\mathrm{}Sc=0.60,S_r=0.15.$

Figure 9. Velocity profile for different values of $D_f.$

$N=2,Pr=0.71,\mathrm{}Sc=0.60,S_r=0.15.$

Figure 10. Temperature profile for different values of $t$ for various cases of the Soret and Dufour numbers. $N=2,Pr=0.71,Sc=0.60.$

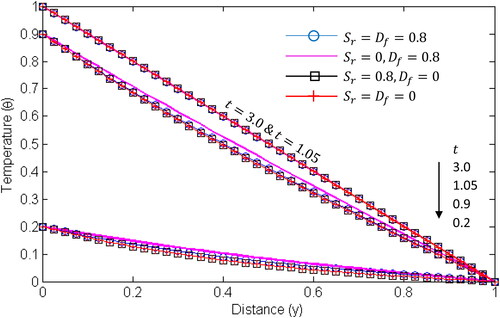
Figure 11. Concentration profile for different values of $t$ for various cases of the Soret and Dufour numbers. $N=2,Pr=0.71,Sc=0.60.$

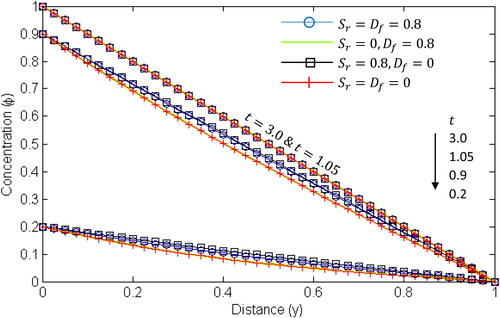
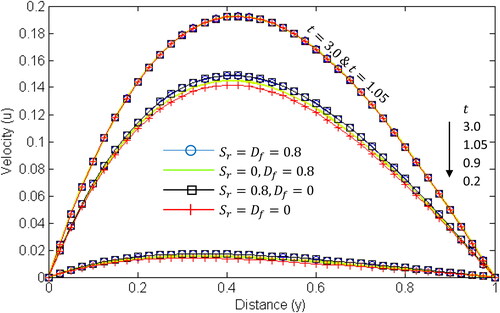
Figure 12. Velocity profile for different values of $t$ for various cases of the Soret and Dufour numbers. $N=2,Pr=0.71,Sc=0.60.$

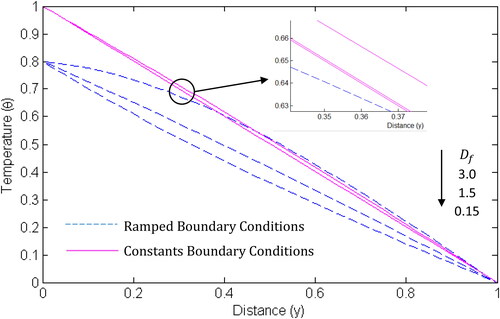
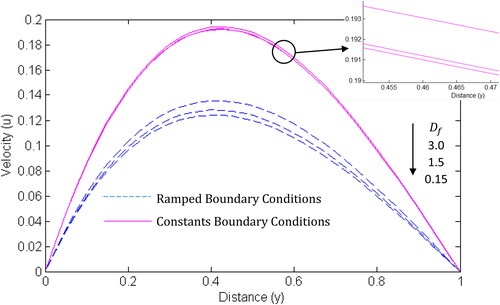
Similarly, the temperature and velocity increase with an increase in Dufour number while the concentration decreases as the Dufour number increases (Figures 7–9). The Dufour number affects the velocity and temperature significantly than it affects the concentration. This is in order considering the settings of Equations (6)(6) $$\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u}{\partial y^2}+\theta +N\varphi$$(6) and (8)(8) $$\frac{\partial \varphi }{\partial t}=\frac{1}{Sc}\frac{{\partial }^2\varphi }{\partial y^2}+\frac{S_r}{Sc}\frac{{\partial }^2\theta }{\partial y^2}$$(8) .

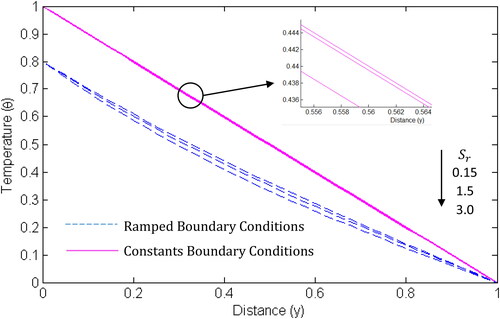
From Figures 10 and 12, $S_r=0$ shows that mass fluxes are not generated by temperature gradients while $D_f=0$ indicates that the energy flux is not caused by specie concentration gradient. It is important to observe that the influences of Soret and Dufour effects are more significant when ramped boundary conditions are imposed.

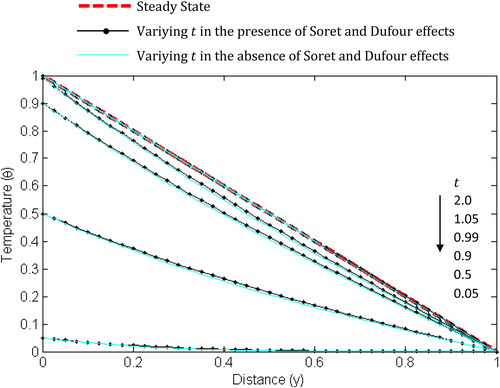
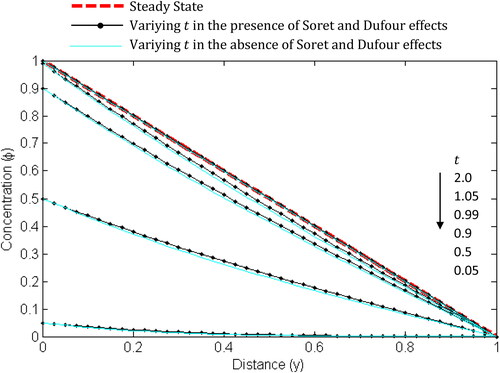
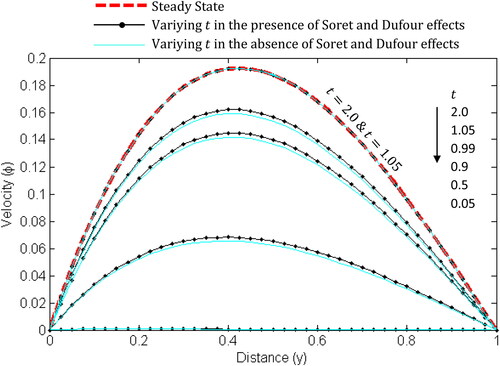
Figures 13 and 15 present the influence of time $t$ on the temperature, concentration and velocity with ramped boundary conditions. In Figure 13 and 14, it can be seen that the temperature and concentration increase with time rapidly at first and then gradually until their steady-state values are attained. From the graphs, it is clear that the rise in the fluid’s temperature and specie’s concentration is higher in the presence of Soret and Dufour effects. In Figure 15, it can be observed that there is no fluid movement at the very initial stage. On the other hand, the presence of Soret and Dufour effects cause the fluid’s velocity to be greater as time increases which consequently accelerates the attainment of steady-state velocity. Moreover, the velocity gradient near the heated plate is higher than near the other plate.

Figure 13. Temperature profile for different values of $t$ with ramped boundary conditions.

$N=2,Pr=0.71,\mathrm{}Sc=0.60,S_r=0.3,D_f=0.3.$

Figure 14. Concentration profile for different values of $t.$

$N=2,Pr=0.71,\mathrm{}Sc=0.60,S_r=0.3,D_f=0.3.$

Figure 15. Concentration profile for different values of $t.$

$N=2,Pr=0.71,\mathrm{}Sc=0.60,S_r=0.3,D_f=0.3.$

The Nusselt number $Nu,$ Sherwood number $Sh$ and the wall skin friction $C_f$ are presented in Tables 2 and 3 with constant boundary conditions at $\mathrm{y}=0$ and $y=1$ respectively. In Table 2, it is clear that $Nu$ decreases while $Sh$ and $C_f$ increase as the Dufour number increases. On the other hand, increase in the Soret number $S_r$ increases the Nusselt number and the Skin friction while the Sherwood number decreases. More so, the Nusselt and Sherwood numbers decrease quickly at the early time and then gradually reaching the steady-state values. However, the Skin friction increases steadily up to the steady-state as the time increases. The influences of Prandtl number, Schmidt number and buoyancy ratio parameter are also presented in the table. $Nu$ increase while $Sh$ and $C_f$ decrease as $Pr$ increases, but $Sh$ increase while $Nu$ and $C_f$ decrease as $Sc$ increases. However, all the behavior of Nuselt number, Sherwood number and Skin friction at $y=0$ described in Table 2 are precisely contrary when $y=1$ as shown in Table 3. From both tables, the buoyancy ratio is seen to have no influence on the temperature and concentration which is expected considering the settings of the governing equations.

Table 2. Variation of Skin coefficients with constant boundary conditions for different values of the embedded parameters at $y=0.$

$N$	$Pr$	$Sc$	$S_r$	$D_f$	$t$	$N{u}_0$	$S{h}_0$		${C_f}_0$
2.0	0.71	0.78	0.15	0.15	0.2	1.173370	1.233770		0.680452
2.0	0.71	0.78	0.15	0.15	0.0	40.065000	40.065000		0.000000
2.0	0.71	0.78	0.15	0.0	0.2	1.248900	1.221980		0.674729
2.0	0.71	0.78	0.0	0.15	0.2	1.162510	1.300410		0.668353
2.0	0.71	0.78	0.0	0.0	0.2	1.248900	1.300530		0.660565
2.0	0.71	0.78	0.15	1.5	0.2	0.351776	1.356640		0.736873
2.0	0.71	0.78	1.5	0.15	0.2	1.285340	0.506905		0.799734
2.0	0.71	2.01	0.15	0.15	0.2	1.066430	2.017230		0.580200
2.0	7.0	0.78	0.15	0.15	0.2	3.839480	0.871381		0.583814
4.0	0.71	0.78	0.15	0.15	0.2	1.173370	1.233770		1.130490
2.0	0.71	0.78	0.15	0.15	0.5	1.000260	1.004040		0.942929
Steady state						1.000000		1.000000	0.962812

The variations of the parameter values are indicated in bold.

Table 3. Variation of Skin coefficients with constant boundary conditions for different values of the embedded parameters at $y=1.$

$N$	$Pr$	$Sc$	$S_r$	$D_f$	$t$	$N{u}_1$	$S{h}_1$	${C_f}_1$
2.0	0.71	0.78	0.15	0.15	0.2	0.826183	0.767296	–0.219675
2.0	0.71	0.78	0.15	0.15	0.0	0.000000	0.000000	0.000000
2.0	0.71	0.78	0.15	0.0	0.2	0.752003	0.778376	–0.214041
2.0	0.71	0.78	0.0	0.15	0.2	0.836464	0.701323	–0.207884
2.0	0.71	0.78	0.0	0.0	0.2	0.751997	0.701414	–0.200408
2.0	0.71	0.78	0.15	1.5	0.2	1.574410	0.667723	–0.273676
2.0	0.71	0.78	1.5	0.15	0.2	0.732114	1.434410	–0.331576
2.0	0.71	2.01	0.15	0.15	0.2	0.886837	0.192777	–0.135948
2.0	7.0	0.78	0.15	0.15	0.2	0.015419	0.818671	–0.157012
4.0	0.71	0.78	0.15	0.15	0.2	0.826183	0.767296	–0.362673
2.0	0.71	0.78	0.15	0.15	0.5	0.999739	0.995949	–0.479795
Steady state						1.000000	1.000000	–0.499688

The variations of the parameter values are indicated in bold.

Nomenclature
$C\mathrm{\text{'}}$	=	fluid specie concentration
$C_0^{\mathrm{\text{'}}}$	=	fluid specie concentration near the wall $y^{\mathrm{\text{'}}}=0$
$C_l^{\mathrm{\text{'}}}$	=	fluid specie concentration near the wall $y^{\mathrm{\text{'}}}=\mathrm{l}$
$D$	=	mass diffusivity
$g$	=	gravitational acceleration
$N$	=	buoyancy ratio parameter
$l$	=	distance between the two walls
$Pr$	=	Prandtl parameter
$Sc$	=	Schmidt parameter
$D_f$	=	dimensionless Dufour number
$t\mathrm{\text{'}}$	=	dimensional time
$S_r$	=	dimensionless Soret number
$t$	=	dimensionless time
$T^{\mathrm{\text{'}}}$	=	fluid temperature
$T_0^{\mathrm{\text{'}}}$	=	wall temperature at $y^{\prime }=0$
$T_l^{\mathrm{\text{'}}}$	=	wall temperature at $y^{\prime }=\mathrm{l}$
$D^{\mathrm{*}}$	=	dimensional Dufour parameter
$u^{\mathrm{\text{'}}}$	=	fluid velocity
$u$	=	dimensionless fluid velocity
$x^{\mathrm{\text{'}}}$	=	axis along vertical direction
$y^{\mathrm{\text{'}}}$	=	axis perpendicular to the walls
$y$	=	dimensionless axis in $y^{\mathrm{\text{'}}}$ direction
${\tau }_0$	=	skin friction at $y=0$
${\tau }_1$	=	skin friction at $y=1$
$N{u}_0$	=	Nusselt number at $y=0$
$N{u}_1$	=	Nusselt number at $y=1$
$S{h}_0$	=	Sherwood number at $y=0$
$S{h}_1$	=	Sherwood number at $y=1$
$S^{\mathrm{*}}$	=	dimensional Soret parameter
$\omega$	=	Laplace transform parameter
erfc	=	complementary error function
exp	=	exponential function

Greek letters
$\beta$	=	coefficient of thermal expansion
${\beta }^{\mathrm{*}}$	=	coefficient of concentration expansion
$\alpha$	=	thermal diffusivity
$\theta$	=	dimensionless temperature
$\varphi$	=	dimensionless concentration
$\nu$	=	kinematic viscosity
$\rho$	=	density

Disclosure statement

No potential conflict of interest was reported by the authors.