Effect of heat source/sink on MHD start-up natural convective flow in an annulus with isothermal and isoflux boundaries

Abstract

This article examines the influence of isothermal and isoflux heating/cooling with heat source/sink on unsteady hydromagnetic-free convective flow of a viscous incompressible fluid in an annulus. The flow is induced by buoyancy forces due to temperature differences as a result of the isothermal heating and constant heat flux applied on the outer surface of the inner cylinder. Our treatment of the governing energy and momentum equation is based on a two-step approach. First, the nonlinear partial differential equations are transformed to the Laplace domain using the Laplace transform method and solved analytically in the Laplace domain. The Laplace domain solution is then inverted back to time domain using a numerical scheme known as Riemann-Sum Approximation (RSA). The derived numerical values by the method of RSA exhibit an excellent conformity with PDEPE and steady-state solutions at large time. The influence of the various dimensionless controlling parameters on the flow formation is depicted graphically and in tabular form.

Keywords:

• Transient
• heat source/sink
• MHD
• isothermal–isoflux
• Riemann-Sum Approximation (RSA)
• PDEPE

1. Introduction

Over the years, studies carried out by many researchers have shown that the relevance of magnetohydrodynamics (MHD) fluid flow cannot be overemphasized due to its wide range of applications in industrial-driven systems and bio-applications such as plasma studies, MHD power generators, liquid-metal cooling of nuclear reactors and electron infusion chambers. Considering recent and existing literatures, an extensive investigation has been carried out by scientist to have an insight into the magnetic behaviour of viscous incompressible fluid flow in the presence of heat source/sink for different geometries and physical situations (Baag, Mishra, & Nayak, 2017; Banerjee, Kumar, & Kumaran, 2011; Chamkha, Rashad, Mansour, Armaghani, & Ghalambaz, 2017; Das, Sarkar, & Jana, 2012; Kalita, 2012; Nagaraju, Garvandha, & Ramana Murthy, 2019).

Early study shows that Couette (1890) was the first who reported the analytical solution of viscous incompressible fluid flow in an annulus in order to ascertain the fluid viscosity. The attributes of steady flow of an electrically conducting viscous fluid driven by convective current have been scrutinized by Gupta (1960), Nayak, Dash, and Singh (2014) and Yusuf (2017). Due to the advancement in various fields of science and engineering, the need to efficiently model and design real-time systems propelled research into the behaviour of hydromagnetic fluid flow under transient condition. In the works of Kumar and Singh (2016), Ibrahim and Suneetha (2016), Baag, Mishra, and Samantray (2017), Makinde, Khan, Ahmad, Haq, and Khan (2019) and Yusuf and Gambo (2020), the analysis of unsteady flow of an electrically conducting viscous fluid with heat source/sink was carried out. It is closely observed that some generally agreed results were established, they reported that an increase in the heat source/sink parameter, in turn, prompts an increase in the fluid velocity, induced magnetic field and fluid temperature in case of heat source and the reverse trend is noticed with heat sink. Consequently, a lot of investigators have made effort to examine this flow phenomenon analytically (Gupta, Kumar, & Singh, 2020; Jha, Aina, & Isa, 2015; Modather, Rashad, & Chamkha, 2009; Raju, Ananda Reddy, & Varma, 2014), semi-analytically (Jha & Yusuf, 2016, 2017a, 2017b; Yusuf & Jha, 2018) and numerically (Ajibade & Gambo, 2019; Reddy, Suneetha, & Reddy, 2017; Son & Park, 2017).

Recently, MHD fluid flow has gained enormous attention by a lot of investigators. Several literatures on MHD fluid flow have been reviewed for various physical situations. Chamkha and Al-Rashidi (2010) and Yusuf and Oni (2018) vetted the exact solution to steady natural convective hydromagnetic fluid flow of particulate suspension and the effect of viscous dissipation with isothermal–isoflux boundaries. Recent research explored the combination of several methods with the Laplace transform to solve linear and nonlinear partial differential equations for arbitrary orders. Several research topics based on Fractional Calculus solution to nonlinear partial differential equations can be seen in previous studies (Alshabanat, Jleli, Kumar, & Samet, 2020; Baleanu, Jleli, Kumar, & Samet, 2020; Kumar, Ghosh, Lotayif, & Samet, 2020; Kumar, Ghosh, Samet, & Goufo, 2020; Kumar, Kumar, Abbas, Al Qurashi, & Baleanu, 2020; Kumar, Kumar, Agarwal, & Samet, 2020; Kumar, Kumar, Cattani, & Samet, 2020; Kumar, Kumar, Odibat, Aldhaifallah, & Nisar, 2020; Kumar, Nisar, Kumar, Cattani, & Samet, 2020; Odibat & Kumar, 2019; Veeresha, Prakasha, & Kumar, 2020). This phenomenon is beneficial in modelling real-time system and accuracy.

The articles (Jha & Odengle, 2015, 2016; Yusuf & Gambo, 2019) had an enormous impact on the studies of transient flow formations in different geometries. From their work, they adopted a two-way method of solution in solving nonlinear partial differential equations. This is due to the complexity of the Laplace domain solution arising from the nonlinear nature of the governing equations which makes the classical Laplace inversion method rudimentary. Hence, using the Laplace transform, a Laplace domain solution is derived and then inverted back to time domain. The inversion is done using a numerical inversion approach based on Riemann-Sum Approximation (RSA). The RSA technique has proven to be very effective when compared with the exact solution at large time.

The concept of heat source/sink controlling heat transfer is one to be worthy of attention in view of many real-world problems. The heat distribution in the whole domain can be altered when heat source or sink is introduced. Lately, advances in MHD fluid flow and heat transfer with Hall effect has been studied extensively and can be found in papers of Kumar and Singh (Kumar & Singh, 2015, 2018; Kumar, Singh, & Kumar, 2018, 2020; Kumar, Singh, & Sarveshanand, 2017; Yadav, Kumar, & Singh, 2019).

However, to the best of authors’ knowledge, no investigation has been carried out on MHD-free convective flow of a viscous incompressible fluid in an annulus with isothermal and isoflux boundaries in the presence of heat source/sink. Therefore, to fill this gap, a mathematical model is presented to understand the effect of heat source/sink on MHD-free convective flow in a vertical concentric cylinder with isothermal and isoflux boundaries. The exact solution of the partial differential equations has been obtained in the Laplace domain due to the complexity of the geometry and transformed to the time domain using a numerical technique known as the RSA.

2. Mathematical formulation

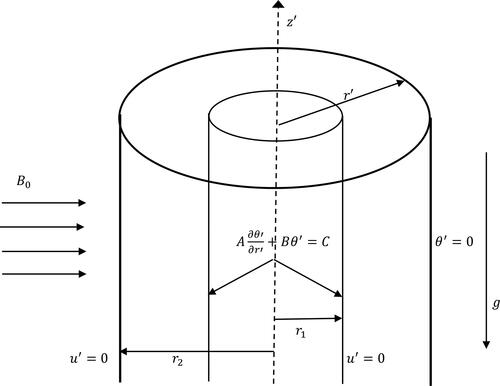
The flow of a fully developed transient natural convective flow of an incompressible and electrically conducting viscous fluid in a vertical annulus formed by two infinite and stationary concentric cylinders in the presence of heat source/sink is considered. The $z\prime$-axis is taken as the axis of the cylinder along the upward direction which is parallel to the gravitational force $(g)$ in the opposite direction while the radial direction is taken in the direction of the $r\prime$-axis as shown in Figure 1. $r_1$ and $r_2$ represent the radii of the inner and outer cylinder, respectively. The fluid and the cylinders are assumed to be at ambient temperature at time $t^{\prime }\le 0.$ At time $t^{\prime }>0$ the temperature of the inner cylinder is heated or cooled by either isothermally or at constant heat flux while maintaining the temperature of the outer cylinder $T_0.$ Due to the temperature gradient between the concentric cylinders, the transient natural convective current is triggered in the annular gap. Since the cylinders are of infinite length and the flow is fully developed, the flow is a function of time and the radial coordinates. Thus, under the usual Boussinesq approximation, the given dimensional partial differential equations responsible for the flow are: (1) $$\frac{\partial u^{\mathrm{\prime }}}{\partial t^{\mathrm{\prime }}}=v\left[\frac{{\partial }^2{u}^{\mathrm{\prime }}}{\partial r^{\mathrm{\prime }2}}+\frac{1}{r^{\mathrm{\prime }}}\frac{\partial u^{\mathrm{\prime }}}{\partial r^{\mathrm{\prime }}}\right]-\frac{\sigma B_0^2{u}^{\mathrm{\prime }}}{\rho }+g\beta \left(T^{\mathrm{\prime }}-T_0\right),$$(1) (2) $$\frac{\partial T^{\mathrm{\prime }}}{\partial t\mathrm{\prime }}=\frac{k}{\rho c_p}\left[\frac{{\partial }^2{T}^{\mathrm{\prime }}}{\partial r^{\mathrm{\prime }2}}+\frac{1}{r^{\mathrm{\prime }}}\frac{\partial T^{\mathrm{\prime }}}{\partial r^{\mathrm{\prime }}}\right]\pm \frac{Q_0}{\rho c_p}\left(T^{\mathrm{\prime }}-T_0\right).$$(2)

Figure 1. Geometry of annular system.

The initial and boundary conditions relevant to the present problem under consideration are $t^{\mathrm{\prime }}\le 0,\mathrm{}{u}^{\mathrm{\prime }}=0,\mathrm{}{T}^{\mathrm{\prime }}=T_0,$ for $r_1\le r^{\mathrm{\prime }}\le r_2.$ (3) $$t^{\mathrm{\prime }}>0\{\begin{array}{l}{u}^{\mathrm{\prime }}=0,\frac{\partial T^{\mathrm{\prime }}}{\partial r\mathrm{\prime }}=-\frac{q}{k}\text{or}{T}^{\mathrm{\prime }}=T_w\text{at}{r}^{\mathrm{\prime }}=r_1\\ u^{\mathrm{\prime }}=0,T^{\mathrm{\prime }}=T_0\text{at}{r}^{\mathrm{\prime }}=r_2.\end{array}$$(3)

The non-dimensional quantities used in the above equations are defined as: $$t=\frac{t^{\mathrm{\prime }}v}{r_1^2};\mathrm{}\theta =\frac{T^{\mathrm{\prime }}-T_0}{\Delta T};\mathrm{}R=\frac{r^{\mathrm{\prime }}}{r{}_1};\mathrm{}U=\frac{u^{\mathrm{\prime }}}{u_0};\mathrm{}{M}^2=\frac{\sigma B_0^2{r}_1^2}{\rho v};$$ (4) $$U_0=\frac{g\beta r_1^2\Delta T}{v};\mathrm{}Pr=\frac{\mu c_p}{k};H^2=\frac{Q_0{r}_1^2}{k};\mathrm{}\mu =\rho v;\mathrm{}\lambda =\frac{r_2}{r_1}.$$(4) where $\Delta T=T_w-T_0$ or $\frac{q^{\prime }r{}_1}{k}$ accordingly as the inner cylinder is maintained at constant temperature $T_w$ or constant heat flux $q^{\prime },$ respectively. Applying Equation (4)(4) $$U_0=\frac{g\beta r_1^2\Delta T}{v};\mathrm{}Pr=\frac{\mu c_p}{k};H^2=\frac{Q_0{r}_1^2}{k};\mathrm{}\mu =\rho v;\mathrm{}\lambda =\frac{r_2}{r_1}.$$(4) on Equations (1)–(3), the dimensionless forms of the momentum and energy equations are: (5) $$\frac{\partial U}{\partial t}=\frac{{\partial }^{2}U}{\partial R^2}+\frac{1}{R}\frac{\partial U}{\partial R}-M^{2}U+\theta ,$$(5) (6) $$Pr\frac{\partial \theta }{\partial t}=\frac{{\partial }^2\theta }{\partial R^2}+\frac{1}{R}\frac{\partial \theta }{\partial R}\pm H^2\theta .$$(6)

The initial and boundary conditions in the dimensionless form are $$t\le 0,\mathrm{}U=0,\mathrm{}\theta =0\text{for}1\le R\le \lambda ,$$ (7) $$t>0\{\begin{array}{l}U=0,\frac{\partial \theta }{\partial R}=-1\text{or θ}=1\text{at R}=1\\ U=0,\theta =0\text{at R}=\lambda .\end{array}$$(7)

Following Jha and Yusuf (2016), the unified form of isothermal and isoflux boundary condition in Equation (7)(7) $$t>0\{\begin{array}{l}U=0,\frac{\partial \theta }{\partial R}=-1\text{or θ}=1\text{at R}=1\\ U=0,\theta =0\text{at R}=\lambda .\end{array}$$(7) can be represented as: (8) $$A\frac{\partial \theta }{\partial R}+B\theta =C\mathrm{at}R=1.$$(8) where suitable values of $A,B$ and $C$ are chosen to match the isothermal and isoflux condition.

Using the Laplace transform technique, Equations (5)–(7) are transformed with the Laplace variable defined by $\overline{U}\left(R,s\right)={\int }_0^{\mathrm{\infty }}U\left(R,t\right)e^{-st}dt$ and $\overline{\theta }\left(R,s\right)={\int }_0^{\mathrm{\infty }}\theta \left(R,t\right)e^{-st}dt$ where $s$ is Laplace parameter and $s>0.$ (9) $$\frac{d^2\overline{U}}{d{R}^2}+\frac{1}{R}\frac{d\overline{U}}{dR}-\left(M^2+s\right)\overline{U}+\overline{\theta }=0,$$(9) (10) $$\frac{d^2\overline{\theta }}{d{R}^2}+\frac{1}{R}\frac{d\overline{\theta }}{dR}-\left(\mathit{sPr}\mp H^2\right)\overline{\theta }=0.$$(10) subject to (11) $$\overline{U}=0,\mathrm{}\frac{d\overline{\theta }}{dR}=-\frac{1}{s}\text{or}\overline{\theta }=\frac{1}{s}\text{at}R=1,$$(11) (12) $$\overline{U}=0,\mathrm{}\overline{\theta }=0\mathrm{at}R=\lambda .$$(12)

The solutions of Equations (9)(9) $$\frac{d^2\overline{U}}{d{R}^2}+\frac{1}{R}\frac{d\overline{U}}{dR}-\left(M^2+s\right)\overline{U}+\overline{\theta }=0,$$(9) and (10)(10) $$\frac{d^2\overline{\theta }}{d{R}^2}+\frac{1}{R}\frac{d\overline{\theta }}{dR}-\left(\mathit{sPr}\mp H^2\right)\overline{\theta }=0.$$(10) subject to the boundary conditions (11) and (12) in the Laplace domain are given in terms of modified Bessel functions, respectively (13) $$\overline{\theta }\left(R,s\right)=C_1{I}_0\left(R\delta \right)+C_2{K}_0\left(R\delta \right),$$(13) (14) $$\overline{U}\left(R,s\right)=C_3{I}_0\left(R\alpha \right)+C_4{K}_0\left(R\alpha \right)-\frac{\left[C_1{I}_0\left(R\delta \right)+C_2{K}_0\left(R\delta \right)\right]}{{\delta }^2-{\alpha }^2},$$(14) where $\delta =\sqrt{sPr\mp H^2},$ $\alpha =\sqrt{M^2+s},$ $C_1=-\frac{C{K}_0\left(\lambda \delta \right)}{s\left[I_0\right(\lambda \delta \left)\right\{B{K}_0\left(\delta \right)-A\delta K_1\left(\mathrm{\delta }\right)\}-K_0(\lambda \delta )\{B{I}_0\left(\delta \right)+A\delta I_1\left(\delta \right)\}},$ $C_2=\frac{C{I}_0(\lambda \delta )}{s\left[I_0\right(\lambda \delta \left)\right\{B{K}_0\left(\delta \right)-A\delta K_1\left(\delta \right)\}-K_0(\lambda \delta )\{B{I}_0\left(\delta \right)+A\delta I_1\left(\delta \right)\}},$ $C_3=-\frac{K_0\left(\lambda \alpha \right)\left[C_1{I}_0\left(\delta \right)+C_2{K}_0\left(\delta \right)\right]-K_0\left(\alpha \right)\left[C_1{I}_0\left(\lambda \delta \right)+C_2{K}_0\left(\lambda \delta \right)\right]}{\left[{\delta }^2-{\alpha }^2\right]\left[I_0\left(\lambda \alpha \right)K_0\left(\alpha \right)-I_0\left(\alpha \right)K_0\left(\lambda \alpha \right)\right]},$ $C_4=\frac{I_0\left(\lambda \alpha \right)\left[C_1{I}_0\left(\delta \right)+C_2{K}_0\left(\delta \right)\right]-I_0(\alpha )\left[C_1{I}_0\right(\lambda \delta )+C_2{K}_0(\lambda \mathrm{\delta }\left)\right]}{\left[{\delta }^2-{\alpha }^2\right]\left[I_0\left(\lambda \alpha \right)K_0\left(\alpha \right)-I_0\left(\alpha \right)K_0\left(\lambda \alpha \right)\right]}.$

2.1. Skin frictions, mass flow rate and Nusselt number

Using Equation (14)(14) $$\overline{U}\left(R,s\right)=C_3{I}_0\left(R\alpha \right)+C_4{K}_0\left(R\alpha \right)-\frac{\left[C_1{I}_0\left(R\delta \right)+C_2{K}_0\left(R\delta \right)\right]}{{\delta }^2-{\alpha }^2},$$(14) , the skin friction ${\overline{\tau }}_1(1,s)$ at $R=1$ and ${\overline{\tau }}_{\lambda }(\lambda ,s)$ at $R=\lambda$ in the Laplace domain is computed by differentiating Equation (14)(14) $$\overline{U}\left(R,s\right)=C_3{I}_0\left(R\alpha \right)+C_4{K}_0\left(R\alpha \right)-\frac{\left[C_1{I}_0\left(R\delta \right)+C_2{K}_0\left(R\delta \right)\right]}{{\delta }^2-{\alpha }^2},$$(14) and are given, respectively, as: (15) $${\overline{\tau }}_1\left(1,s\right)={\left.\frac{d\overline{U}}{dR}\right|}_{R=1}=\alpha \left[C_3{I}_1\left(\alpha \right)-C_4{K}_1\left(\alpha \right)\right]-\frac{\delta \left[C_1{I}_1\left(\delta \right)-C_2{K}_1\left(\delta \right)\right]}{\left[{\delta }^2-{\alpha }^2\right]},$$(15) (16) $${\overline{\tau }}_{\lambda }\left(\lambda ,s\right)={\left.\frac{d\overline{U}}{dR}\right|}_{R=\lambda }=\alpha \left[C_3{I}_1\left(\lambda \alpha \right)-C_4{K}_1\left(\lambda \alpha \right)\right]-\frac{\delta \left[C_1{I}_1\left(\lambda \delta \right)-C_2{K}_1\left(\lambda \delta \right)\right]}{\left[{\delta }^2-{\alpha }^2\right]}.$$(16)

The expression for mass flow rate in the annular gap in Laplace domain is given as: (17) $$\overline{Q}=2\pi {\int }_1^{\lambda }R\overline{U}\left(R,s\right)dR=2\pi [C_5-C_6].$$(17) where $C_5=\frac{C_3}{\alpha }\left\{\lambda I_1\left(\lambda \alpha \right)-I_1\left(\alpha \right)\right\}-\frac{C_4}{\alpha }\left\{\lambda K_1\left(\lambda \alpha \right)-K_1\left(\alpha \right)\right\},$ $$C_6=\frac{C_1\left\{\lambda I_1\left(\lambda \delta \right)-I_1\left(\delta \right)\right\}-C_2\left\{\right\{\lambda K_1\left(\lambda \delta \right)-K_1\left(\delta \right)\}}{\delta [{\delta }^2-{\alpha }^2]}.$$

The rate of heat transfer (Nusselt number) at the surfaces of the inner and outer cylinder, respectively, are derived by differentiating Equation (13)(13) $$\overline{\theta }\left(R,s\right)=C_1{I}_0\left(R\delta \right)+C_2{K}_0\left(R\delta \right),$$(13) at $R=1$ and $R=\lambda$ and are presented as: (18) $$\overline{Nu}\left(1,s\right)={\left.\frac{d\overline{\theta }}{dR}\right|}_{R=1}={\delta [C}_1{I}_1\left(\delta \right)-C_2{K}_1\left(\delta \right)],$$(18) (19) $$\overline{Nu}\left(\lambda ,s\right)={\left.\frac{d\overline{\theta }}{dR}\right|}_{R=\lambda }={\delta [C}_1{I}_1\left(\lambda \delta \right)-C_2{\mathrm{K}}_1\left(\lambda \delta \right)].$$(19)

The solutions of the temperature field, velocity field, skin frictions on the walls of the cylinders, mass flow rate and Nusselt number are presented in Equations (13)–(19) and are to be transformed to the time domain. Following the work of Jha and Yusuf (2016, 2017a, 2017b), a numerical procedure known as the RSA was employed, in this approach, functions of the Laplace domain can be inverted to the time domain as follows: (20) $$Z\left(R,t\right)=\frac{e^{\epsilon t}}{t}\left[\frac{1}{2}\overline{Z}\left(R,s\right)+Re\left(\sum _{n=1}^M\overline{Z}(R,\epsilon +\frac{in\pi }{t}\right){\left(-1\right)}^n\right],$$(20) where Re refers the real part of the summation, $i=\sqrt{-1}$ is the imaginary number, $M$ is the number of terms used in the RSA and $\epsilon$ is the real part of the Bromwich contour that is used in inverting Laplace transforms and the function $Z(R,t)$ represents $\theta \left(R,t\right),U\left(R,t\right),\tau \left(R,t\right),Q(R,t)$ or $Nu(R,t).$ The numerical method involves a single summation for the numerical process whose accuracy is dependent on the value ascribed to $\epsilon$ and the truncation error dictated by $M.$ According to Tzou (1997), taking a value of $\epsilon t$ to be 4.7 gives the most desired result.

2.2. Validation of the method

In order to establish the accuracy of the numerical scheme used in transforming Equations (13)–(19) to the time domain, the steady-state temperature and velocity is computed, this is obtained by setting $\frac{\partial ()}{\partial t}$ to zero in Equations (5)(5) $$\frac{\partial U}{\partial t}=\frac{{\partial }^{2}U}{\partial R^2}+\frac{1}{R}\frac{\partial U}{\partial R}-M^{2}U+\theta ,$$(5) and (6)(6) $$Pr\frac{\partial \theta }{\partial t}=\frac{{\partial }^2\theta }{\partial R^2}+\frac{1}{R}\frac{\partial \theta }{\partial R}\pm H^2\theta .$$(6) . The steady-state velocity distribution is computed analytically and is expected to sync with the transient state solution at large time. The following dimensionless Bessel ordinary differential equations are obtained: (21) $$\frac{d^{2}U}{d{R}^2}+\frac{1}{R}\frac{dU}{dR}-M^{2}U+\theta =0,$$(21) (22) $$\frac{d^2\theta }{d{R}^2}+\frac{1}{R}\frac{d\theta }{dR}\pm H^2\theta ,$$(22) with given boundary conditions (23) $$U=0,\mathrm{}\frac{d\theta }{dR}=-1\mathrm{\hspace{0.5em}or\hspace{0.5em}}\theta =1\mathrm{\hspace{0.5em}at\hspace{0.5em}}R=1,$$(23) (24) $$U=0,\theta =0\mathrm{\hspace{0.5em}at\hspace{0.5em}}R=\lambda .$$(24)

To ensure the accuracy of the numerical scheme employed, a numerical solution for the transient state momentum and energy equations in (5) and (6) under boundary conditions (7) and (8) has been computed using a MATLAB inbuilt program known as the parabolic and elliptic partial differential equations (PDEPE). A table of comparison (see Tables 1 and 2) between RSA approach and the PDEPE has been presented, the numerical values excellently agree at large time.

Table 1. Numerical comparison for the transient state velocity with heat source obtained using the Riemann-Sum Approximation (RSA), PDEPE and exact solution $(H=2.0,M=2.0,Pr=0.71,\mathrm{}\lambda =2).$

		Isothermal case			Constant heat flux case
$t$	R	RSA	PDEPE	Exact solution	RSA	PDEPE	Exact solution
0.1	1.2	0.0209	0.0208	0.0521	0.0060	0.0061	0.0205
	1.4	0.0200	0.0201	0.0663	0.0050	0.0051	0.0334
	1.6	0.0127	0.0128	0.0555	0.0028	0.0029	0.0189
	1.8	0.0056	0.0057	0.0303	0.0011	0.0012	0.0156
0.2	1.2	0.0354	0.0355	0.0521	0.0165	0.0165	0.0205
	1.4	0.0414	0.0415	0.0663	0.0173	0.0174	0.0334
	1.6	0.0322	0.0323	0.0555	0.0124	0.0126	0.0189
	1.8	0.0168	0.0169	0.0303	0.0061	0.0063	0.0156
3.0	1.2	0.0521	0.0521	0.0521	0.0205	0.0205	0.0205
	1.4	0.0663	0.0663	0.0663	0.0334	0.0334	0.0334
	1.6	0.0555	0.0555	0.0555	0.0189	0.0189	0.0189
	1.8	0.0303	0.0303	0.0303	0.0156	0.0156	0.0156

Table 2. Numerical comparison for the transient state velocity with heat sink obtained using the Riemann-Sum Approximation (RSA), PDEPE and exact solution $(H=2.0,M=2.0,Pr=0.71,\mathrm{}\lambda =2).$

		Isothermal case			Constant heat flux case
$t$	R	RSA	PDEPE	Exact solution	RSA	PDEPE	Exact solution
0.1	1.2	0.0162	0.0161	0.0257	0.0039	0.0038	0.0102
	1.4	0.0144	0.1143	0.0285	0.0032	0.0033	0.0112
	1.6	0.0086	0.0087	0.0215	0.0017	0.0019	0.0085
	1.8	0.0036	0.0035	0.0110	0.0007	0.0008	0.0043
0.2	1.2	0.0227	0.0226	0.0257	0.0072	0.0074	0.0102
	1.4	0.0239	0.0240	0.0285	0.0071	0.0073	0.0112
	1.6	0.0172	0.0171	0.0215	0.0050	0.0051	0.0085
	1.8	0.0085	0.0086	0.0110	0.0024	0.0023	0.0043
3.0	1.2	0.0257	0.0257	0.0257	0.0102	0.0102	0.0102
	1.4	0.0285	0.0285	0.0285	0.0112	0.0112	0.0112
	1.6	0.0215	0.0215	0.0215	0.0085	0.0085	0.0085
	1.8	0.0110	0.0110	0.0110	0.0043	0.0043	0.0043

3. Results and discussion

In order to have a good understanding of the effect of various controlling parameters on the flow formation, a MATLAB program is written to compute and generate line graphs and numerical values for the velocity field, temperature field, skin friction on both walls of the cylinders, the mass flux and Nusselt number. The present parametric study has been carried out over a reasonable scope of $1.0\le M\le 5.0,$ $1.0\le H\le 5.0,$ $0.71\le Pr\le 7.0$ with $Pr=0.71$ and $H=2$ taken as reference point. Throughout this work, figures labelled (a) and (b) denote heat source and heat sink, respectively, as shown in Figures 2–11.

Figure 2. Temperature profile for different values of time $(t)\mathrm{}(H=2.0,Pr=0.71,\lambda =2.0).$

Figure 3. Temperature profile for different values of Prandtl number $(Pr)\mathrm{}(H=2.0,t=0.1,\lambda =2.0).$

Figure 4. Velocity profile for different values of time $(t)\mathrm{}(Pr=0.71,M=3.0,H=3.0).$

Figure 5. Effect of Hartmann number on velocity profile $(Pr=0.71,t=0.1,H=2.0).$

Figure 6. Effect of Hartmann number on skin friction at $R=1\mathrm{}(Pr=0.71,H=1.0,\lambda =2.0).$

Figure 7. Effect of Prandtl number on skin friction at $R=1(M=2.0,H=1.0,\lambda =2.0).$

Figure 8. Effect of Hartmann number on skin friction at $R=\lambda (Pr=0.71,H=1.0,\lambda =2.0).$

Figure 9. Effect of Prandtl number on skin friction at $R=\lambda (M=2.0,H=1.0,\lambda =2.0).$

Figure 10. Distribution of mass flow rate for different values of Hartmann number $(H=1.0,Pr=0.71,\lambda =2.0).$

Figure 11. Distribution of mass flow rate for different values of Prandtl number $(H=1.0,M=2.01,\lambda =2.0).$

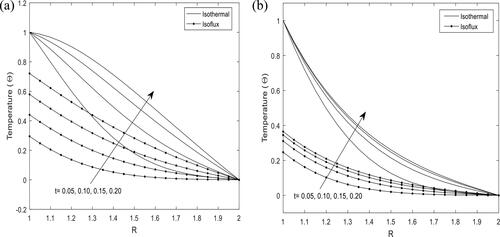
Figure 2 presents the effect of time $(t)$ on the temperature distribution at different points in the annular gap for heat source and sink. It is seen that fluid temperature increases with increase in time for isothermal heating and constant heat flux as it attains a steady state. Higher temperature profiles are perceived with isothermal heating at the walls. It is also noticed that the fluid temperature attains steady state faster with heat sink.

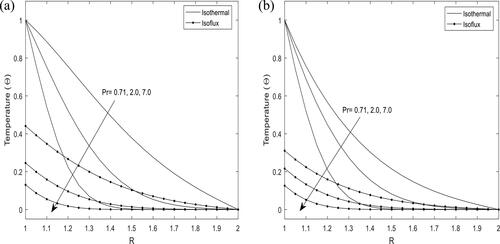
Figure 3 shows variations in temperature profiles for different values of Prandtl number $(Pr)$ at transient state. It is observed that as Prandtl number increases, there is a decrease in the fluid temperature as it approaches the cold wall for both cases of heat source and sink. In addition, the magnitude of the temperature is seen to be higher in the case of heat source.

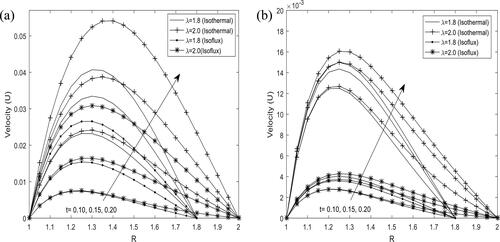
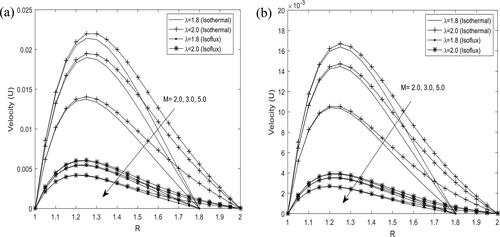
Figures 4 and 5 illustrate the combined effect of time $(t)$ and Hartmann number $(M)$ on the velocity distribution, respectively. It is evident from these figures that fluid velocity is enhanced with increase in time $(t)$ and the velocity is higher in case of isothermal heating when the annular gap is less than or equals the radius of the inner cylinder. This further confirms the finding of Jha and Yusuf (2016). On the other hand, the reverse trend is observed with increase in Hartmann number $(M)$ when the annular gap is less than or equals the radius of the inner cylinder. Moreover, the velocity distribution is seen to increase with increase in the annular gap and vice versa with increase in time $(t)$ and Hartmann number $(M),$ respectively.

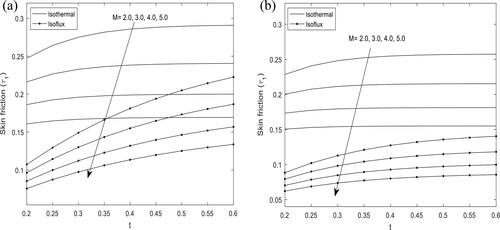
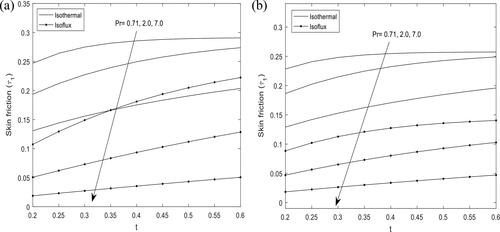
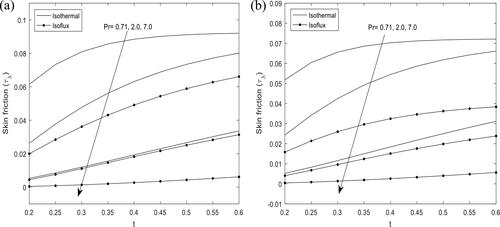
Figures 6 and 7 shows the influence of Hartmann number $(M)$ and Prandtl number $(Pr),$ respectively, on skin friction $({\tau }_1)$ at the outer surface of the inner cylinder $(R=1)$ for heat source and sink. It is interesting to note that skin friction $({\tau }_1)$ decreases for both cases of heat source and sink with increase in Hartmann number $(M)$ and Prandtl number $(Pr).$ In addition, the decrease is more evident in the case of constant heat flux for both heat source and sink.

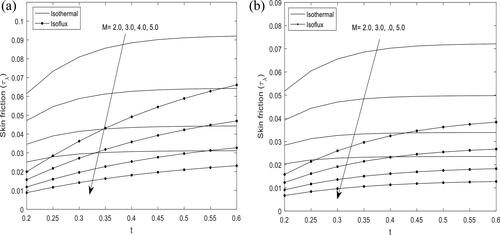
Variation of skin friction $({\tau }_{\lambda })$ at the inner surface of the outer cylinder $\left(R=\lambda \right)$ is presented in Figures 8 and 9. It is observed in Figure 8 that skin friction decreases with increase in Hartmann number $(M)$ but increases with time $(t)$ when the wall is heated isothermally and with constant heat flux until it attains a steady state. Similarly, it is found in Figure 9 that skin friction at the inner surface of the outer cylinder decreases with increase in Prandtl number $(Pr).$

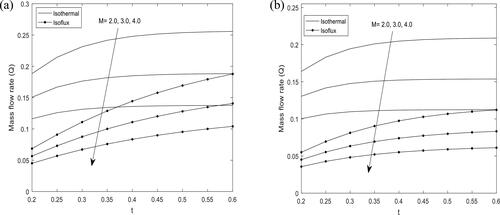
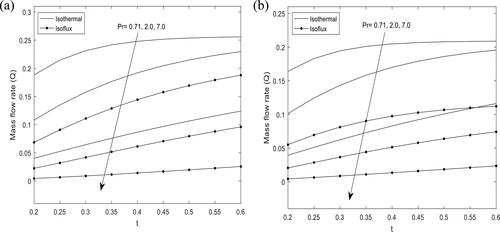
The variation of mass flow rate for different values of Hartmann number $(M)$ and Prandtl number $(Pr)$ is presented in Figures 10 and 11. It is obtained that the mass flow rate decreases as Hartmann number $(M)$ and Prandtl number $(Pr)$ increase for both cases of heat source and sink.

Furthermore, Tables 3 and 4 shows the rate of heat transfer at surfaces of the cylinder when the walls of the cylinder are subjected to both isothermal and constant heat flux heating. The increase in heat source parameter is seen to enhance the rate of heat transfer at both surfaces of the cylinder as time passes when the walls are heated isothermally as evident in Table 3. In a similar fashion, Table 4 shows that increasing heat sink parameter prompts an increase in the rate of heat transfer on both walls of the cylinder when heated isothermally and with constant heat flux. However, the magnitude of increase is less compared to when the heat source is applied.

Table 3. Numerical values for rate of heat transfer (Nusselt number) with heat source at the surfaces of the inner and outer cylinders for both isothermal and constant heat flux $(Pr=0.71,\lambda =2$).

		Isothermal case		Constant heat flux case
$t$	$H$	$N{u}_1$	$N{u}_{\lambda }$	$N{u}_1$	$N{u}_{\lambda }$
0.08	1.0	0.1182	0.2828	−1.0001	0.0505
	1.5	0.3720	0.3127	−1.0001	0.0562
	2.0	0.7496	0.3603	−1.0001	0.0654
	2.5	1.2784	0.4332	−1.0001	0.0796
0.1	1.0	0.1027	0.4001	−1.0001	0.0858
	1.5	0.3911	0.4501	−1.0001	0.0976
	2.0	0.8274	0.5318	−1.0001	0.1171
	2.5	1.4535	0.6612	−1.0001	0.1485
0.2	1.0	0.0381	0.7231	−1.0001	0.2674
	1.5	0.4601	0.8641	−1.0001	0.3339
	2.0	1.1522	1.1205	−1.0001	0.4603
	2.5	2.2803	1.5934	−1.0001	0.7071

Table 4. Numerical values for rate of heat transfer (Nusselt number) with heat sink at the surfaces of the inner and outer cylinders for both isothermal and constant heat flux $(Pr=0.71,\lambda =2$).

		Isothermal case		Constant heat flux case
$t$	$H$	$N{u}_1$	$N{u}_{\lambda }$	$N{u}_1$	$N{u}_{\lambda }$
0.08	1.0	0.2632	0.2411	−1.0001	0.0425
	1.5	0.4877	0.2184	−1.0001	0.0382
	2.0	0.7859	0.1904	−1.0001	0.0330
	2.5	1.1447	0.1599	−1.0001	0.0273
0.1	1.0	0.3239	0.3322	−1.0001	0.0699
	1.5	0.5713	0.2962	−1.0001	0.0616
	2.0	0.8962	0.2528	−1.0001	0.0517
	2.5	1.2816	0.2069	−1.0001	0.0414
0.2	1.0	0.5427	0.5503	−1.0001	0.1897
	1.5	0.8593	0.4674	−1.0001	0.1543
	2.0	1.2561	0.3752	−1.0001	0.1167
	2.5	1.7042	0.2869	−1.0001	0.0829

4. Conclusions

In this article, the flow of a fully developed transient natural convective flow of an incompressible and electrically conducting viscous fluid in a vertical annulus in the presence of heat source/sink is analysed. A semi-analytical solution responsible for the flow has been computed in terms of modified Bessel functions. The influence of Hartmann number $(M),$ Prandtl number $(Pr),$ heat source/sink parameter $(H)$ and time $(t)$ on the temperature field, velocity field, skin friction and mass flow rate has been illustrated with the aid of line graphs.

The following conclusion has been drawn:

1. Fluid temperature increases with time while the reverse trend is seen to occur with increase in Prandtl number.

2. Fluid velocity increase with time but decreases with increase in Hartmann number.

3. Both Hartmann number and Prandtl number are found to be inversely proportional to skin friction on the outer surface of the inner cylinder.

4. Skin friction on the inner surface of the outer cylinder decreases with increase in Hartmann number and Prandtl number.

5. increasing heat sink parameter prompts an increase in the rate of heat transfer on both walls for both isothermal and constant heat flux

Future research work that is still open for study include the study of the entropy generation caused as a result of heat and mass transfer, also the effect of viscous dissipation and axial conduction on the heat transfer are all available for study in relation to this present study.

Nomenclature
$B_0$	=	constant magnetic heat flux
$C_p$	=	specific heat at constant pressure (kJ/kg K)
$g$	=	gravitational acceleration (m/s2)
$k$	=	thermal conductivity of the fluid (W/mK)
$H$	=	dimensionless heat source/sink parameter
$M$	=	Hartmann number
$Nu$	=	Nusselt number
$Pr$	=	Prandtl number (µcp/k)
$Q_0$	=	dimensional heat source/sink parameter
$r_1$	=	radius of the inner cylinder (m)
$r_2$	=	radius of the outer cylinder (m)
$R$	=	dimensionless radial coordinate
$r^{\prime }$	=	dimensional radial coordinate
$t^{\prime }$	=	dimensional time (s)
$t$	=	dimensionless time
$T_0$	=	ambient temperature (K)
$T_w$	=	temperature of the hot cylinder (K)
$U$	=	dimensionless axial velocity
$u^{\prime }$	=	axial velocity (m/s)
$V$	=	dimensionless mass flow rate
$\theta$	=	dimensionless temperature

Greek letters
$\upsilon$	=	fluid kinematic viscosity
$\tau$	=	skin friction
$\sigma$	=	electrical conductivity of the fluid
$\rho$	=	density
$s$	=	Laplace parameter
$\lambda$	=	ratio of radii $(r_2/r_1)$
$\beta$	=	coefficient of thermal expansion

Disclosure statement

No potential conflict of interest was reported by the author(s).