Unstable novel and accurate soliton wave solutions of the nonlinear biological population model

Abstract

This paper investigates the soliton wave solution of the nonlinear biological population (NBP) model by employing a novel computational scheme. The selected model for this study describes the logistics of the population because of births and deaths. Some novel structures of the NBP model’s solutions, are obtained such as exponential, trigonometric, and hyperbolic. These solutions are clarified through some distinct graphs in contour three plot, three-dimensional, and two-dimensional plots. The Hamiltonian system’s characterizations are used to check the obtained solutions’ stability. The solutions’ accuracy is checked by handling the NBP model through the variational iteration (VI) method. The matching between analytical and semi-analytical solutions shows the accuracy of the obtained solutions. The method’s performance shows its effectiveness, power, and ability to apply to many nonlinear evolution equations.

Keywords:

• Nonlinear biological model
• Novel computational technique
• Approximate solutions
• Stability

AMS classification:

• 35E05
• 35Q51
• 35Q92

1. Introduction

In the last five decades, many complex phenomena have been being formulated through some nonlinear evolution equations (Khater, Akinyemi, et al., 2021; Khater & Alabdali, 2021). These equations describe the dynamical and physical behaviour of their phenomena for discovering their hidden characterizations (Khater, 2021a, 2021b; Khater, Alfalqi, Alzaidi, Salama, & Wang, 2022; Tariq, Khater, & Younis, 2021). These properties can be used in many applications in different areas such as engineering, chemistry, plasma, hydrodynamics, genetics, optics, and so on (Khater, Park, Lee, Mohamed, & Attia, 2021; Khater & Lu, 2021; Khater, Elagan, et al., 2021). Consequently, many researchers in different science branches have focusing on studying the nonlinear evolution equations’ analytical, semi-analytical, and numerical solutions (Khater & Attia, 2021; Khater, Mostafa, & Al-Ashkar, 2021; Khater, Lu, & Inc, 2021; Khater, 2021c; Khater & Salama, 2021a). The computer revolution helps in formulating some accurate techniques such as modified tanh-method, sech-tanh method, sine-Gorden method, direct algebraic technique, Adomian decomposition method, B-spline schemes, Khater methods, extended simplest equation method, and so on (Khater & Salama, 2021b; Khater, 2021d; Khater, Elagan, et al., 2021). Unfortunately, there is no unified computational techniques that can be applied to all nonlinear evolution equations (Attia et al., 2021; Khater, 2021e). Consequently, creating and formulating an accurate and stable technique is still going on, and recently Mostafa M. A. Khater has discovered a novel analytical approach and named with Khater II method (Khater et al., 2021f; Khater, 2021g).

This article studies the NBP model which is given by (Khater, Akinyemi, 2021a; Morris, Shertzer, & Rice, 2011; Rashid, Kubra, & Ullah, 2021; Sokal, Oden, & Thomson, 2010; Topaz & Bertozzi, 2004): (1) $${\mathcal{B}}_t={\mathcal{B}}_{x\mathrm{ }x}^2+{\mathcal{B}}_{y\mathrm{ }y}^2+\mathcal{V} ({\mathcal{B}}^2-\mathcal{S}),$$(1) where $\mathcal{B}, \mathcal{V} ({\mathcal{B}}^2-\mathcal{S})$ describe the population density, and population logistics dependent on deaths and births, respectively. Furthermore, $\mathcal{V}, \mathcal{S}$ are arbitrary constants. Handling Eq. (1)(1) $${\mathcal{B}}_t={\mathcal{B}}_{x\mathrm{ }x}^2+{\mathcal{B}}_{y\mathrm{ }y}^2+\mathcal{V} ({\mathcal{B}}^2-\mathcal{S}),$$(1) through the next wave transformation $\mathcal{B}(x,y,t)=\mathcal{Q}(\mathcal{T}), \mathcal{T}=x+i y+c t,$ where c is arbitrary constant and $i=\sqrt{-1},$ converts it into the following ordinary differential equation (ODE) (2) $$c \mathcal{Q}\prime -\mathcal{V} {\mathcal{Q}}^2+\mathcal{V} \mathcal{S}=0.$$(2)

Using the homogeneous balance method along with $\mathcal{F}\prime (\mathcal{T})=-\delta -\mathcal{F}{(\mathcal{T})}^2, \mathcal{H}\prime (\mathcal{T})=-\mathcal{F}(\mathcal{T})\mathcal{H}(\mathcal{T}),\mathcal{H}{(\mathcal{T})}^2=\alpha \left(\frac{1}{\delta } \mathcal{F}{(\mathcal{T})}^2+1\right),$ leads to $\left[n+1=2 n \to n=1\right].$ Thus, the general solution of the NBP model is ordered by the next format (3) $$\mathcal{Q}\left(\mathcal{T}\right)=\sum _{i=1}^n\left(a_i \mathcal{F}{(\mathcal{T})}^i+b_i \mathcal{H}(\mathcal{T}) \mathcal{F}{(\mathcal{T})}^{i-1}\right)+a_0=a_1 \mathcal{F}(\mathcal{T})+a_0+b_1 \mathcal{H}(\mathcal{T}),$$(3) where $a_0, a_1, b_1$ are arbitrary constants to be evaluated through the method’s steps.

The rest sections of this research paper are ordered as follows; Section 2 gets novel soliton wave solutions of the NBP model and explains them through some different graphs. Section 3 checks the solutions’ stability. Section 4 gets semi-analytical solutions of the considered model by applying the VI method. Section 5 shows the paper’s contributions and results’ novelty by comparing our obtained solutions with those that have been published recently. Section 6 gives the conclusion of the whole work.

2. Computational simulation

Implementing the Khater II method to find novel soliton wave solutions of the suggested model, get the following values of the above-mentioned parameters:

Set I$$a_0=0, a_1=\frac{i \sqrt{\mathcal{S}}}{\sqrt{\delta }}, b_1=\frac{i \sqrt{\mathcal{S}}}{\sqrt{\alpha }}, c=-\frac{2 i \sqrt{\mathcal{S}} \mathcal{V}}{\sqrt{\delta }}, \text{where} (\mathcal{S}<0).$$

Set II$$a_0=b_1=0, a_1=-\frac{i \sqrt{\mathcal{S}}}{\sqrt{\delta }}, c=\frac{i \sqrt{\mathcal{S}} \mathcal{V}}{\sqrt{\delta }}, \text{where} (\mathcal{S}>0).$$

Thus, the structures of the investigated model’s solutions are given by

For $\delta >0, \alpha =1,$ we get (4) $${\mathcal{B}}_{\mathrm{I},1}(x,y,t)=-\frac{\sqrt{\mathcal{S}} \left(e^{i\mathrm{ }\sqrt{\delta }\mathrm{ }(c\mathrm{ }t+x+i\mathrm{ }y)}-i\right)}{e^{i\mathrm{ }\sqrt{\delta }\mathrm{ }(c\mathrm{ }t+x+i\mathrm{ }y)}+i},$$(4) (5) $${\mathcal{B}}_{\mathrm{I},2}(x,y,t)=-\frac{\sqrt{\mathcal{S}} \left(1+e^{i\mathrm{ }\sqrt{\delta }\mathrm{ }(c\mathrm{ }t+x+i\mathrm{ }y)}\right)}{-1+e^{i\mathrm{ }\sqrt{\delta }(c\mathrm{ }t+x+i\mathrm{ }y)}}.$$(5)

For $\delta \ne 0, \alpha =1,$ we get (6) $${\mathcal{B}}_{\text{II},1}(x,y,t)=i \sqrt{\mathcal{S}} \hspace{0.17em}\text{tan}\hspace{0.17em}\left(\sqrt{\delta } (c t+x+i y)\right),$$(6) (7) $${\mathcal{B}}_{\text{II},2}(x,y,t)=-i \sqrt{\mathcal{S}} \text{cot}\left(\sqrt{\delta } (c t+x+i y)\right).$$(7)

3. Stability checking

This section studies the stability characterization of the above-obtained solutions based on the Hamiltonian system’s properties. The momentum of the Hamiltonian system based on Eq. (6)(6) $${\mathcal{B}}_{\text{II},1}(x,y,t)=i \sqrt{\mathcal{S}} \hspace{0.17em}\text{tan}\hspace{0.17em}\left(\sqrt{\delta } (c t+x+i y)\right),$$(6) is given by (8) $$\begin{array}{c}\mathcal{M}=\frac{1}{9c}[-6c({\tanh }^{-1}(\tanh (3(c+8)))-10{\tanh }^{-1}(\tanh (6(5c+4)))+{\tanh }^{-1}(\tanh (3-3c)))\\ +60c{\tanh }^{-1}(\tanh (3-30c))-\hspace{0.17em}\text{log}\hspace{0.17em}\left(1-{\tanh }^2(3(c+8))\right)+\hspace{0.17em}\text{log}\hspace{0.17em}\left(1-{\tanh }^2(6(5c+4))\right)\\ +\hspace{0.17em}\text{log}\hspace{0.17em}\left(1-{\tanh }^2(3-3c)\right)-\hspace{0.17em}\text{log}\hspace{0.17em}\left(1-{\tanh }^2(3-30c)\right)].\end{array}$$(8)

Consequently, we get (9) $$\frac{\partial \mathcal{M}}{\partial c}{|}_{c=-\frac{2}{3}}=-0.00642580424<0.$$(9)

Thus, this solution is not stable. Applying the same steps to the other solutions for investigating the stability property.

4. Numerical illustrations

This section checks the semi-analytical solutions of the NBP model by applying the VI method. This method’s framework is summarized as following:

Suppose the nonlinear PDE is given by (10) $$\mathcal{L} \mathcal{B}(x,y,t)+\mathcal{N} \mathcal{B}(x,y,t)=\mathcal{B}(x,t),$$(10) where $\mathcal{L}, \mathcal{N}$ represent linear and nonlinear operators respectively. While $\mathcal{B}(x,y,t)$ is unknown differential function. Thus, the semi-analytical solutions of the investigated PDE is given according to the VI method by the next formula (11) $${\mathcal{B}}_{n+1}(x,y,t)={\mathcal{B}}_n(x,y,t)+{\int }_0^t\lambda \{\mathcal{L} {\mathcal{B}}_n(x,y,s)+\mathcal{N}{\tilde{\mathcal{B}}}_n(x,y,s)-\mathcal{B}(x,y,s)\}\mathrm{d}s,$$(11) where $\lambda , {\mathcal{B}}_n(x,y,t), {\tilde{\mathcal{B}}}_n(x,y,t)$ are the general Lagrange multiplier, the n th approximate solution, and considered a restricted variation, respectively. On the other hand, this term ${\int }_0^t\lambda \{\mathcal{L} {\mathcal{B}}_n(x,y,s)+\mathcal{N}{\tilde{\mathcal{B}}}_n(x,y,s)-\mathcal{B}(x,y,s)\} \mathrm{d}s$ is called the correction.

Employing the VI method to the investigated model for constructing accurate semi–analytical solution, gets the following approximate solutions (12) $${\mathcal{B}}_0(x,y,t)=-2 \tanh (3(x+i y)),$$(12) (13) $${\mathcal{B}}_1(x,y,t)=-{\text{sech}}^2(3(x+i y)) (-4 t+\sinh (6(x+i y))),$$(13) (14) $$\begin{array}{cc}{\mathcal{B}}_2(x,y,t)=& \frac{4}{3} t^2 {\text{sech}}^4 (3 (x+i y)) (-4 t+3 \sinh (6 (x+i y)))\\ & -{\text{sech}}^2 (3 (x+i y)) (-4 t+\sinh (6 (x+i y))).\end{array}$$(14)

5. Results and discussion

Here, the scientific results of this article are explained by showing the main target of each of the above-section and if this target is achieved or not. Additionally, the paper’s novelty results are demonstrated by showing their similarity and difference with recently published articles investigating the NBP model. Our discussion is given by the next items

1. Employed Computational scheme:

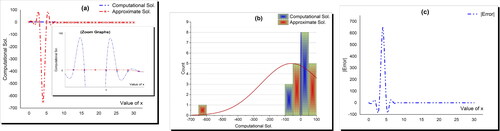
The Khater II method is applied to the NBP model for evaluating some novel soliton wave solutions that is already what has successfully happened. This novel technique is considered an undirect computational scheme that has been recently derived. Its performance shows its power, effective and ability to apply to so many nonlinear evolution equations. Additionally, the stability property of the obtained solutions is also investigated by using the Hamiltonian system’s characterizations. Furthermore, the solutions’ accuracy is checked by constructing the semi-analytical solution through the VI method. Table 1 explains the values of analytical, semi-analytical, and absolute error between both solutions. This table shows how the applied computational scheme is such an accurate scheme.

Table 1. Values of computational and approximate solutions for $x\in [0,30].$

Value of x	Computational sol.	Approximate sol.	|Error|
0	2	1.99999997266803	2.73319740173861E-08
1	2	1.9999889734929	0.0000110265071027182
2	2	1.99555130249855	0.00444869750140042
3	2	0.159088354811456	1.84091164516811
4	1.99999999175539	−646.666666666667	648.666666658422
5	1.99999667388789	0.105768212673022	1.89422846121487
6	1.99865859947813	−1.99456904594458	3.99322764542271
7	1.52318831191153	−1.99998653670116	3.52317484861269
8	−1.92805516015163	−1.99999996662781	0.0719448064761767
9	−1.99981840852519	−2	0.000181591392088176
10	−1.99999954985935	−2	4.50140443364333E-07
11	−1.99999999888421	−2	1.11578724037997E-09
12	−2	−2	2.76578759894619E-12
13	−2	−2	6.88338275267597E-15
14	−2	−2	−4.44089209850063E-16
15	−2	−2	4.44089209850063E-16
16	−2	−2	4.44089209850063E-16
17	−2	−2	0
18	−2	−2	0
19	−2	−2	−2.22044604925031E-16
20	−2	−2	0
21	−2	−2	−2.22044604925031E-16
22	−2	−2	0
23	−2	−2	0
24	−2	−2	−2.22044604925031E-16
25	−2	−2	0
26	−2	−2	−4.44089209850063E-16
27	−2	−2	0
28	−2	−2	0
29	−2	−2	4.44089209850063E-16
30	−2	−2	−6.66133814775094E-16

2. The obtained solutions:

Comparing our solutions with those that have been obtained in Abdel-Aty et al. (2020) by Mostafa M. A. Khater et al. shows the scientific values of our research paper. In this paper (Abdel-Aty et al., 2020), the extended exp-$(-\phi (\vartheta ))$-expansion and Jacobi elliptic function method have been applied, and some solutions have been constructed, but none of their solutions is similar to our obtained solutions which leads to the novelty of our paper and its results.

3. The figures interpretation:

This paper shows some distinct graphs of the obtained analytical and semi-analytical solutions. These figures show so many distinct properties of the NBP model such as Figures 1, 2, 3, 4 explain singular, kink, periodic, and cone respectively for $\alpha =1, c=5, \delta =9, s=4\& \alpha =1, a_0=0, \delta =-9, s=4, v=-1.$ While Figure 5 explains the matching between analytical and approximate solutions.

Figure 1. Distinct graphs of Eq. (4)(4) $${\mathcal{B}}_{\mathrm{I},1}(x,y,t)=-\frac{\sqrt{\mathcal{S}} \left(e^{i\mathrm{ }\sqrt{\delta }\mathrm{ }(c\mathrm{ }t+x+i\mathrm{ }y)}-i\right)}{e^{i\mathrm{ }\sqrt{\delta }\mathrm{ }(c\mathrm{ }t+x+i\mathrm{ }y)}+i},$$(4) in three different types (3 D, 2 D, contour) for its real, imaginary and absolute values.

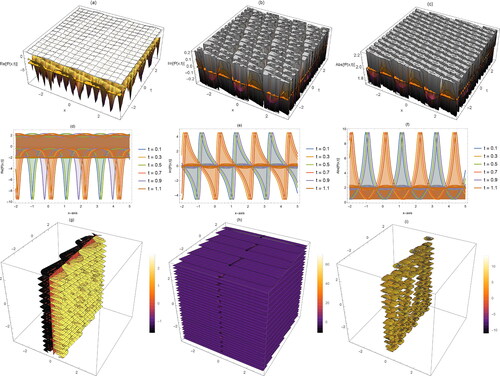
Figure 2. Distinct graphs of Eq. (5)(5) $${\mathcal{B}}_{\mathrm{I},2}(x,y,t)=-\frac{\sqrt{\mathcal{S}} \left(1+e^{i\mathrm{ }\sqrt{\delta }\mathrm{ }(c\mathrm{ }t+x+i\mathrm{ }y)}\right)}{-1+e^{i\mathrm{ }\sqrt{\delta }(c\mathrm{ }t+x+i\mathrm{ }y)}}.$$(5) in three different types (3 D, 2 D, contour) for its real, imaginary and absolute values.

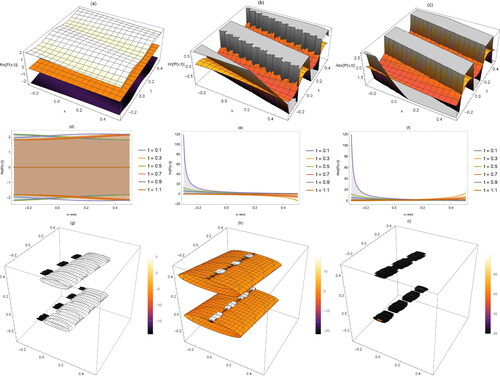
Figure 3. Distinct graphs of Eq. (6)(6) $${\mathcal{B}}_{\text{II},1}(x,y,t)=i \sqrt{\mathcal{S}} \hspace{0.17em}\text{tan}\hspace{0.17em}\left(\sqrt{\delta } (c t+x+i y)\right),$$(6) in three different types (3 D, 2 D, contour) for its real, imaginary and absolute values.

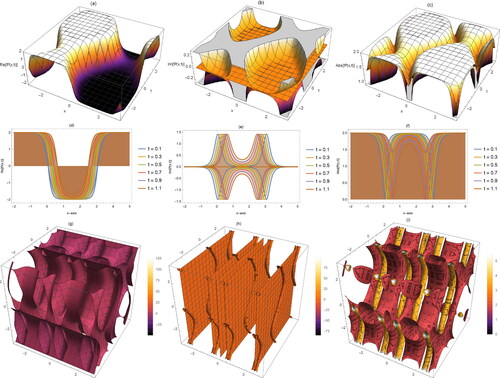
Figure 4. Distinct graphs of Eq. (7)(7) $${\mathcal{B}}_{\text{II},2}(x,y,t)=-i \sqrt{\mathcal{S}} \text{cot}\left(\sqrt{\delta } (c t+x+i y)\right).$$(7) in three different types (3 D, 2 D, contour) for its real, imaginary and absolute values.

Figure 5. Matching between computational and approximate solutions based on the calculated values in Table 1.

6. Conclusion

The paper has successfully applied novel computational (Khat II) and VI methods to the NBP model to obtain novel soliton wave solutions. Many novel solutions have been constructed and demonstrated in different graphs to explain more novel characterizations of the NBP model. The matching between both solutions (analytical and approximate) is explained to show the accuracy of both solutions. The stability of solutions is tested by employing the Hamiltonian system’s characterizations.

Acknowledgments

We thank the referee(s) for reading the manuscript very carefully and making a number of valuable and kind comments which improved the presentation.

Data availability statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of interest

This work does not have any conflicts of interest.