ANN-based methods for solving partial differential equations: a survey

Abstract

Traditionally, partial differential equation (PDE) problems are solved numerically through a discretization process. Iterative methods are then used to determine the algebraic system generated by this process. Recently, scientists have emerged artificial neural networks (ANNs), which solve PDE problems without a discretization process. Therefore, in view of the interest in developing ANN in solving PDEs, scientists investigated the variations of ANN which perform better than the classical discretization approaches. In this study, we discussed three methods for solving PDEs effectively, namely Pydens, NeuroDiffEq and Nangs methods. Pydens is the modified Deep Galerkin method (DGM) on the part of the approximate functions of PDEs. Then, NeuroDiffEq is the ANN model based on the trial analytical solution (TAS). Lastly, Nangs is the ANN-based method which uses the grid points for the training data. We compared the numerical results by solving the PDEs in terms of the accuracy and efficiency of the three methods. The results showed that NeuroDiffeq and Nangs have better performance in solving high-dimensional PDEs than the Pydens, while Pydens is only suitable for low-dimensional problems.

Keywords:

• Artificial neural networks
• discretization
• Pydens method
• Neuroiffeq method
• Nangs module
• partial differential equations

2010 MSC::

• 68-XX
• 68W25

1. Introduction

Many physical phenomena in modern sciences have been described by using Partial Differential Equations (PDEs) (Evans, Blackledge, & Yardley, 2012). Hence, the accuracy of PDE solutions is challenging among the scientists and becomes an interest field of research (LeVeque & Leveque, 1992). Traditionally, the PDEs are solved numerically through discretization process (Burden, Faires, & Burden, 2015),. For instance, the well-known finite difference method (FDM) and finite element method were utilized to solve many PDE linear and non-linear. Other methods, such as the variational iteration method (VIM) and its variations were used to solve the nonlinear PDE (He & Latifizadeh, 2020), and the finite difference-spectral method was investigated to solve the fractal mobile and immobile transport (Fardi & Khan, 2021). These methods typically end up with the algebraic systems that can be solved by using iterative methods (Hayati & Karami, 2007). The big issue in using the iterative solvers for solving the large scale of linear system of equations is that they potentially breakdown before getting a good approximate solution (Maharani & Salhi, 2015). In fact, their accuracy is not promising. To get rid of the breakdown problem, one has been done by using interpolation and extrapolation model (Bakar & Salhi, 2019; Maharani et al., 2018; Maharani, Larasati, Salhi, & Khan, 2019), and using prediction with support vector machine (Thalib, Bakar, & Ibrahim, 2021). However, the problem is still not fully addressed since computationally, they quite expensive. With no discretization process, artificial neural networks (ANNs) can be an alternative way.

ANN is well-known as one method under machine learning (ML) which is typically used for regressions and classification problems. The development of ANN for solving PDE problems has been investigated at the beginning of the 21st century. For instance (Malek & Beidokhti, 2006), combined ANN and Nelder–Mead simplex method to find the numerical solutions of the high-order of PDE. This hybrid method improved the ANN performances by approximating initial and boundary conditions. Moreover (Sirignano & Spiliopoulos, 2018), used the Deep-Galerkin method (DGM) embedded with ANN, for solving the high dimensional of PDE problems. While, modified DGM by introducing ansatz method for binding the initial and boundary conditions. This modification simplifies the DGM original algorithm. Furthermore, another ANN-based method for solving PDE, called Physics Informed Neural Network (PINN), was introduced by Raissi, Perdikaris, & Karniadakis (2017b), Raissi, Perdikaris, and Karniadakis (2019) and Raissi et al. (2017b). PINN considers the physical laws of PDE to be embedded in loss function as a regularization term. This method was improved by Guo, Cao, Liu, and Gao (2020), in terms of the training effect by using the residual-based adaptive refinement (RAR) method. This strategy will impact in increasing the number of residual points with the large residuals of PDE until the residuals are less than the threshold.

The ability of ANN in solving PDE problems gives some advantages, including continuous and differentiable of the approximate solutions, good interpolation characteristics and less memory (Chen et al., 2020). Other advantages of ANN are that it can utilize automatic differentiation tools, such as Tensorflow (Abadi et al., 2016) and PyTorch (Paszke et al., 2017; Rahaman et al., 2019), allow researchers make more simpler methods in solving PDE problems (Chen et al., 2020). In this study, we focus on three methods for solving PDEs based on ANN model, namely PyDEns which modifies the DGM, NeuroDiffEq which is the ANN approximator with TAS applied (Chen et al., 2020), and Nangs which based on the grid points for training data).

This article is structured by follows. Section 1 discusses introduction of ANN-based methods for solving PDEs. Section 2 describes the review of ANN to solve PDEs. In Section 3, the basic theory behind the three methods is also discussed. Section 4 illustrates the three methods solve the heat equation. The numerical results of the three methods in solving different types of PDEs are explained in Section 5. Lastly, we conclude our study in Section 6.

2. Artificial neural networks (ANN)

ANNs were introduced firstly in 1943 by McCulloch and Pitts (1943). It is inspired by biological neurons working to perform complex tasks (Schalkoff, 1997). At the beginning, ANN has been successful handling several data problems, which then becomes less popular since left out behind another ML techniques. In 1980s, with the tremendous increase in computing power and the amount of data used to training ANNs, this technique became more popular and was successfully applied in various practical applications (Goodfellow, Bengio, & Courville, 2016; Goldberg, 2016; Helbing & Ritter, 2018; LeCun, Bengio, & Hinton, 2015; Li et al., 2019; Mabbutt, Picton, Shaw, & Black, 2012; Nielsen, 2015; Shanmuganathan, 2016), including the differential equation problems discussed in this article.

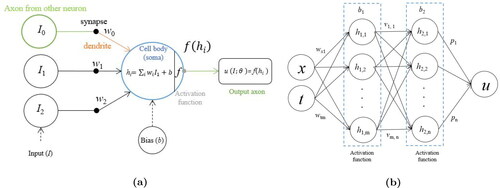
One of the most popular ANN architecture called Perceptron, as shown in Figures 1(a) (Haykin, 1999), consists of multiple hidden layers as visualized in Figure 1(b) (Khanna, 1990),. However, prior to the invention of the backpropagation algorithm (Rumelhart, Hinton, & Williams, 1985), it was not easy for training perceptron to make a better prediction. In short, backpropagation is a gradient descent method, which enables the perceptron to give a better approximation based on the gradient of the loss function. Furthermore, the backpropagation algorithm became the most popular ANN optimizer algorithm (Li, Cheng, Shi, & Huang, 2012; Nielsen, 2015).

Figure 1. ANN Perceptron 1 (a) and multi-layered perceptron (MLP) 1 (b) architectures.

2.1. Ann model for solving PDEs: overview

Consider the second-order PDE of the form (McFall, 2010), (1) $$\mathcal{F}\left(x,t,u,\frac{\partial u}{\partial x},\frac{\partial u}{\partial t},\frac{{\partial }^{2}u}{\partial x^2},\frac{{\partial }^{2}u}{\partial t^2}\right)=f(x,t),(x,t)\in \Omega ,$$(1) over the domain $\Omega \subset {\mathcal{R}}^2,$ with an initial condition (2) $$u(x,t_0)=u_0(x),x\in \sigma \Omega ,$$(2) and a boundary condition (3) $$u(x,t)=g(x,t),(x,t)\in \sigma \Omega .$$(3)

Generally, ANN to solve PDE (Equation (1)) is started by generating the weights to form a linear combination with the inputs x, t and the bias, b_i. This form is then used to compute the hidden layer as described in Equation (4)(4) $$h_1=\sum _{i=1}^m(w_{xi}x+w_{ti}t)+b_1,$$(4) as follows (4) $$h_1=\sum _{i=1}^m(w_{xi}x+w_{ti}t)+b_1,$$(4) where h₁ is the first hidden layer, w_xi and w_ti are the weights and b₁ is bias. The second hidden layer, as expressed in Equation (5), is computed by feeding h₁ into it and thus is processed to yield the output layer. (5) $$h_2=\sum _{j=1}^n\sum _{i=1}^m{v}_{ij}f(h_1)+b_2,$$(5) where v_ij are the weights, b₂ is the bias, and f is the activation function of the form (6) $$f(h_1)=\frac{e^{h_1}-e^{-h_1}}{e^{h_1}+e^{-h_1}}.$$(6)

The activation functions are commonly used to perform the diverse of computations between the layers. Several activation function, such as sigmoid or logistic, tanh, ReLU and Leaky-ReLU are often used (Haykin, 1999; Jagtap, Kawaguchi, & Karniadakis, 2020). Here, we take the hyperbolic tangent function (tanh) as it has been proved to provide the better results compared to other activation functions (Karlik & Olgac, 2011; Panghal & Kumar, 2021).

Our aim here is to obtain the approximate solution $u_{\mathit{net}}(x,t)$ which is written as follows, (7) $$u_{\mathit{net}}(x,t)=\sum _{j=1}^n{p}_{j}f(h_2),$$(7) where p_j are the weights of the output layers. To control the accuracy of the approximate solution, we compare it with the right-hand side of the PDE (Equation (1)), and this can be only done by differentiate partially $u_{\mathit{net}}(x,t)$ as follows (8) $$\frac{{\partial }^k{u}_{\mathit{net}}}{\partial x^k}(x,t)=\sum _{j=1}^n{p}_j\frac{{\partial }^{k}f(h_2)}{\partial x^k},$$(8) (9) $$\frac{{\partial }^k{u}_{\mathit{net}}}{\partial t^k}(x,t)=\sum _{j=1}^n{p}_j\frac{{\partial }^{k}f(h_2)}{\partial t^k},$$(9) where k = 1, 2.

3. Ann-based methods for solving PDEs

In this section, we discuss three methods and compare them in terms of accuracy and efficiency. They are Pyden, NeuroDiffeq and Nangs. They are differed by the way generating the training points and the loss functions.

3.1. Pydens method

All of ANN-based methods to solve the PDE problem used an optimizer in order to obtain the minimum error. The most common optimization method used is called Deep Galerkin Method (DGM), has been introduced by Sirignano and Spiliopoulos (2018). The name of Pydens was obtained from the python module with the DGM optimizer. Basically, to approximate u(t, x) in Equation (1) using $u_{\mathit{net}}(t,x),$ Pydens is modified by applying ansatz in binding the initial and boundary conditions. The procedure is explained as follows.

1. Bind the initial and boundary conditions using ansatz by setting up the equation (10) $$A_{\mathit{net}}(x,t)=\mathit{mult}(x,t)·u_{\mathit{net}}(x,t)+\mathit{add}(x,t).$$(10)

   Thus, the solution of PDE is approximated by transforming the ANN output rather than $u_{\mathit{net}}(x,t)$ itself. Equation (10)(10) $$A_{\mathit{net}}(x,t)=\mathit{mult}(x,t)·u_{\mathit{net}}(x,t)+\mathit{add}(x,t).$$(10) is to ensure the concatenation of the initial and boundary conditions in Equations (2)(2) $$u(x,t_0)=u_0(x),x\in \sigma \Omega ,$$(2) and (3)(3) $$u(x,t)=g(x,t),(x,t)\in \sigma \Omega .$$(3) , respectively, whenever the following is verified: (11) $$\mathit{mult}(x,t_0)=0,\hspace{1em}\mathit{add}(x,t_0)=u_0(x),$$(11) (12) $$\mathit{mult}{\prime }_t(x,t_0)=0,\hspace{1em}\mathit{add}{\prime }_t(x,t_0)=u{\prime }_{0}x,$$(12) (13) $$\mathit{mult}{(x,t)}_{x\in \sigma \Omega }=0,\hspace{1em}\mathit{add}{(x,t)}_{x\in \sigma \Omega }=g(x).$$(13)

2. Generate m points inside the batches of b₁ from the domain $(x,t)\times \Omega$ by using the uniform distribution v₁. Then, for each point (x, t), feed it to ANN architecture until the optimum output is obtained.

3. Build the loss function as follows (14) $$\mathcal{L}{(\theta )}_{DE}=\frac{1}{m}\sum _{i=1}^m{[\mathcal{F}(x_i,t_i,A_{\mathit{net}},\dots ,\frac{{\partial }^2{A}_{\mathit{net}}}{\partial x^2},\frac{{\partial }^2{A}_{\mathit{net}}}{\partial t^2})-f(x,t)]}^2(x_i,t_i)\in b_1,v_1,$$(14) where θ is a vector consists of the weights and biases.

4. Update the trainable parameter θ to minimize the loss function by using SGD optimizer.

3.2. Neurodiffeq method

NeuroDiffeq method applies the trial approximate solution (TAS) (Chen et al., 2020), that satisfies the initial and boundary conditions. Recall Equation (1)(1) $$\mathcal{F}\left(x,t,u,\frac{\partial u}{\partial x},\frac{\partial u}{\partial t},\frac{{\partial }^{2}u}{\partial x^2},\frac{{\partial }^{2}u}{\partial t^2}\right)=f(x,t),(x,t)\in \Omega ,$$(1) . The procedure of NeuroDiffeq method is explained as follows:

1. Generate m × n input points of $(x_i,t_j)\times \Omega ,$ where $i=1,2,\dots ,m$ and $j=1,2,\dots ,n,$ and divide the set points into training and validation points.

2. Build the TAS, u_T, as the form of McFall (2010). (15) $$u_T(x_i,t_j)=A(x_i,t_j)+F[u_{\mathit{net}}(x_i,t_j)],$$(15) where A(x) is a function that satisfies the initial and boundary conditions and $F[u_{\mathit{net}}(x_i,t_j)]$ is chosen to be zero for any (x_i, t_j) on the boundary. This approach is similar to the trial function discussed by Lagaris, Likas, and Fotiadis (1998).

3. Build the loss function (McFall, 2006). (16) $$\mathcal{L}(\theta )=\frac{1}{mn}\sum _{i=1}^m\sum _{j=1}^n\left[\mathcal{L}{(\theta )}_{DE}+\eta \mathcal{L}{(\theta )}_{BC}\right],$$(16) where θ is a vector consists of the weights and biases. Noted that the first term is (17) $$\mathcal{L}{(\theta )}_{DE}={[\mathcal{F}(x_i,t_i,u_{\mathit{net}},\dots ,\frac{{\partial }^2{u}_{\mathit{net}}}{\partial x^2},\frac{{\partial }^2{u}_{\mathit{net}}}{\partial t^2})-f(x,t)]}^2(x,t)\in \Omega ,$$(17) used as the approximate solutions of the PDE itself, while the second term is (18) $$\mathcal{L}{(\theta )}_{BC}={\left[u_T(x_i,t_j;\theta )-g(x,t)\right]}_{(x,t)\in \sigma \Omega }^2+{\left[u_T(x_i,t_0;\theta )-u_0(x)\right]}_{(x)\in \sigma \Omega }^2.$$(18)

used as the approximate for the boundary condition. Here, a weighting factor η is used to improve the performance of the loss function, as appeared in Equation (16)(16) $$\mathcal{L}(\theta )=\frac{1}{mn}\sum _{i=1}^m\sum _{j=1}^n\left[\mathcal{L}{(\theta )}_{DE}+\eta \mathcal{L}{(\theta )}_{BC}\right],$$(16) . In practice, it is arbitrary determined.

3.3. Nangs method

Different from both methods explained above, Nangs method is not required to create trial solution to minimize the loss functions, instead, it generates mesh points for the training data. The details of how Nangs method can approximate PDE are described as follows.

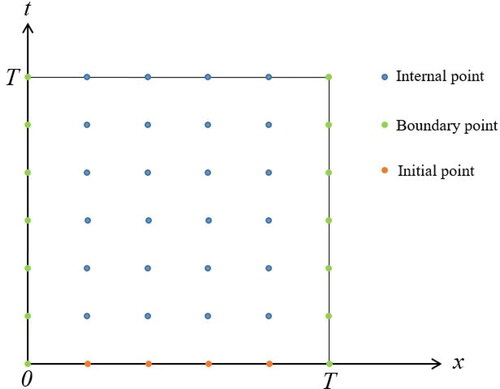
1. Set mesh points of $(x_i,t_j)\times \Omega$ for $i=1,2,\dots ,m$ and $j=1,2,\dots ,n$ inside the domain as visualized in Figure 2).

2. For each internal point, once feeding process has been done in ANN architecture, compare the output with the right side of the PDE using the following loss function: (19) $$\mathcal{L}{(\theta )}_{DE}=\frac{1}{{(mn)}_{\mathit{int}}}\sum _{i=1}^{m_{\mathit{int}}}\sum _{j=1}^{n_{\mathit{int}}}{[\mathcal{F}(x_i,t_i,u_{\mathit{net}},\dots ,\frac{{\partial }^2{u}_{\mathit{net}}}{\partial x^2},\frac{{\partial }^2{u}_{\mathit{net}}}{\partial t^2})-f(x,t)]}^2(x,t)\in {\Omega }_{in}.$$(19)

3. For all of the initial and boundary points, the outputs are compared with Equations (2)(2) $$u(x,t_0)=u_0(x),x\in \sigma \Omega ,$$(2) and (3)(3) $$u(x,t)=g(x,t),(x,t)\in \sigma \Omega .$$(3) , respectively, by using the following loss functions respectively: (20) $$\mathcal{L}{(\theta )}_{BC}=\frac{1}{n_{bc}}\sum _{j=1}^n{\left[u_{\mathit{net}}(x_{0,T},t_j;\theta )-g(x,t)\right]}^2(x,t)\in \sigma {\Omega }_{bc},$$(20) (21) $$\mathcal{L}{(\theta )}_{IC}=\frac{1}{m_{ic}}\sum _{i=1}^m{\left[u_{\mathit{net}}(x_i,t_0;\theta )-u_0(x)\right]}^{2}x\in \sigma {\Omega }_{ic}.$$(21)

Figure 2. Illustration of the internal, boundary and initial points of $m=6\times n=7.$

4. Simulation of the three ANN-based methods for solving heat equation

As an illustration of using ANN-based methods to solve PDEs, the following heat equation is considered (Burden et al., 2015), (22) $$\frac{\partial u}{\partial t}-\frac{{\partial }^{2}u}{\partial x^2}=0,\hspace{1em}0\le x\le 1,t\ge 0,$$(22) with the initial condition (23) $$u(x,0)=\hspace{0.17em}\text{sin}\hspace{0.17em}(\pi x),$$(23) and boundary conditions (24) $$u(0,t)=u(1,t)=0.$$(24)

The analytical solution for this PDE is given by (25) $$e^{-t{\pi }^2}\hspace{0.17em}\text{sin}\hspace{0.17em}(\pi x).$$(25)

To compare the three methods, we used the same architectures of ANN which are three hidden layers consisting 32 neurons each. The loss function is evaluated up to 100 × 100 points for the unit inputs (x, t). We also used various number of iterations because each method uses different python modules. Pydens is run under Tensorflow (Abadi et al., 2016), while NeuroDiffeq and Nangs are run under Pytorch (Paszke et al., 2017).

4.1. Pydens in solving PDE heat equation

To solve PDE heat in Equation (22)(22) $$\frac{\partial u}{\partial t}-\frac{{\partial }^{2}u}{\partial x^2}=0,\hspace{1em}0\le x\le 1,t\ge 0,$$(22) , firstly, we use ansatz function to bind the boundary and initial conditions. We then randomly generate up to 100 × 100 number of points inside the domain $[0,1].$ Finally, we compute the loss function as in Equation (11). The complete algorithm for this method is described in Algorithm 1.

Algorithm 1.

Pydens algorithm for solving PDE heat equation [14]

1. Approximate PDE (Equation (22)) by fitting u(x, t) with the following function $$A_{\mathit{net}}(x,t)=\mathit{mult}(x,t)·u_{\mathit{net}}(x,t)+\mathit{add}(x,t).$$

2. Generate up to $m=100\times 100$ points inside of the batches $b_1,b_2,b_3$ uniformly and inside of the $(x,t)\in [0,1].$

3. while $\mathit{iter}=0\le$ maxiteration do

4. for $(x,t)\in [0,1]$ do

5. Compute the output $$u_{\mathit{net}}(x,t)=\sum _{i=1}^{32}{p}_{i}f(h_3).$$

6. Substitute $u_{\mathit{net}}(x,t)$ into $A_{\mathit{net}}(x,t),$ then differentiate using the automatic differentiation to obtain the following functions $$\begin{array}{c}\frac{\partial A_{\mathit{net}}}{\partial t}(x,t)=\frac{\partial [\mathit{mult}(x,t)·u_{\mathit{net}}(x,t)+\mathit{add}(x,t)]}{\partial t},\\ \frac{{\partial }^2{A}_{\mathit{net}}}{\partial x^2}(x,t)=\frac{{\partial }^2[\mathit{mult}(x,t)·u_{\mathit{net}}(x,t)+\mathit{add}(x,t)]}{\partial x^2}.\end{array}$$

7. Compute the loss function by comparing the A_net with Equation (22)(22) $$\frac{\partial u}{\partial t}-\frac{{\partial }^{2}u}{\partial x^2}=0,\hspace{1em}0\le x\le 1,t\ge 0,$$(22) , as follows $$\mathcal{L}(\theta )=\frac{1}{m}\sum _{i=1}^m{\left[\frac{\partial A_{\mathit{net}}}{\partial t}(x_i,t_i;\theta )-\frac{\partial A_{\mathit{net}}^2}{\partial x^2}(x_i,t_i;\theta )\right]}^2,$$ where θ is a vector consists of the weights and biases.

8. end for

9. Apply the SGD to optimize the trainable parameter θ.

10. end while

4.2. Neurodiffeq in solving heat equation

Different from the PyDens method, NeuroDiffeq uses TAS (McFall, 2006), to approximate the initial and boundary conditions. Basically, once we set up the domain $[0,1]$ into 100 × 100 data points, we then construct TAS to satisfy the initial and boundary conditions 23 and 24. The details of solving the PDE heat in Equation (22)(22) $$\frac{\partial u}{\partial t}-\frac{{\partial }^{2}u}{\partial x^2}=0,\hspace{1em}0\le x\le 1,t\ge 0,$$(22) are described in Algorithm 2.

Algorithm 2.

NeuroDiffeq algorithm for solving PDE heat equation [19]

1. Generate $m=100\times 100$ points uniformly in the domain $[0,1],$ and then divide them into the training set and the validation set.

2. Construct a TAS which satisfies the initial and boundary conditions based on Equations (23) and (24) as follows $$u_T(x,t;\theta )=\hspace{0.17em}\text{sin}\hspace{0.17em}(\pi x)+xt(1-x)(1-t)u_{\mathit{net}}(x,t;\theta ).$$

   Noted here that we used θ to indicate that it consists of the weights and the biases.

3. while $\mathit{iter}=0\le$ maxiteration do

4. for each (x_i, t_i) do

5. Calculate the output of ANN $$u_{\mathit{net}}(x,t;\theta )=\sum _{i=1}^{32}{p}_{i}f(h_3).$$

6. Substitute u_net into u_T and differentiate it to obtain $$\begin{array}{c}\frac{\partial u_T}{\partial t}(x,t;\theta )=\frac{\partial [\text{sin}\hspace{0.17em}(\pi x)+xt(1-x)(1-t)u_{\mathit{net}}(x,t;\theta )]}{\partial t},\\ \frac{\partial u_T}{\partial x^2}(x,t;\theta )=\frac{\partial [\text{sin}\hspace{0.17em}(\pi x)+xt(1-x)(1-t)u_{\mathit{net}}(x,t;\theta )]}{\partial x^2}.\end{array}$$

7. Compute the loss function by comparing the output between Equations (22)–(24) as follows $$\mathcal{L}(\theta )=\frac{1}{m}\sum _{i=1}^m\left[{\mathcal{L}}_{DE}+\eta {\mathcal{L}}_{BC}\right],$$ with $${\mathcal{L}}_{DE}={\left[\frac{\partial u_T}{\partial t}(x_i,t_i;\theta )-\frac{\partial u_T^2}{\partial x^2}(x_i,t_i;\theta )\right]}^2,$$ and $${\mathcal{L}}_{BC}={\left[u_T(x_i,t_i;\theta )-0\right]}^2+{\left[u_T(x_i,0;\theta )-\hspace{0.17em}\text{sin}\hspace{0.17em}(\pi x_i)\right]}^2.$$

8. end for

9. Apply SGD optimizer to minimize the loss function.

10. end while

4.3. Nangs method in solving PDE heat equation

Nangs method adopts the grid points used in the discretization process as the training data. It is done by building mesh points from (x, t) in the entire domain. Then, split the mesh points into internal, initial, and boundary points (see Figure 2). The complete algorithm is shown in Algorithm 3.

Algorithm 3.

Nangs algorithm for solving PDE heat equation [23]

1. Set up $(x,t)\in [0,1]$ into $m=100\times n=100$ mesh points. Then, split them into internal and initial and boundary points.

2. while $\mathit{iter}=0\le$ maxiteration do

3. for each mesh point $(x,t)\in [0,1]$ do

4. Calculate the output as follows $$u_{\mathit{net}}(x,t;\theta )=\sum _{i=1}^{32}{p}_{i}f(h_3).$$

5. Differentiate the output to obtain the following functions $$\begin{array}{c}\frac{\partial u_{\mathit{net}}}{\partial t}(x,t;\theta )=\sum _{i=1}^{32}\frac{\partial p_{i}f(h_3)}{\partial t},\\ \frac{{\partial }^2{u}_{\mathit{net}}}{\partial x^2}(x,t;\theta )=\sum _{i=1}^{32}\frac{{\partial }^2{p}_{i}f(h_3)}{\partial x^2}.\end{array}$$

6. Calculate each internal point, then compare it with the original PDE of Equations (22) as follows $$\mathcal{L}{(\theta )}_{DE}=\frac{1}{(m-bc)\times (n-ic)}\sum _{i=1}^{m-bc}\sum _{j=1}^{n-ic}{\left[\frac{\partial u_{\mathit{net}}}{\partial t}(x_i,t_j;\theta )-\frac{\partial u_{\mathit{net}}^2}{\partial x^2}(x,t;\theta )\right]}^2.$$

7. Compute each initial and boundary points and compare them with the original initial and boundary condition of the PDE as in Equations (23) and (24) as follows $$\begin{array}{c}\mathcal{L}{(\theta )}_{\mathit{Left}}=\frac{1}{m-bc}\sum _{j=1}^{m-bc}{\left[u_{\mathit{net}}(0,t_j;\theta )-0\right]}^2,\\ \mathcal{L}{(\theta )}_{\mathit{Right}}=\frac{1}{m-bc}\sum _{j=1}^{m-bc}{\left[u_{\mathit{net}}(1,t_j;\theta )-0\right]}^2,\\ \mathcal{L}{(\theta )}_{\mathit{Initial}}=\frac{1}{n-ic}\sum _{i=1}^{n-ic}{\left[u_{\mathit{net}}(x_i,0;\theta )-\hspace{0.17em}\text{sin}\hspace{0.17em}(\pi x)\right]}^2.\end{array}$$

8. end for

9. Apply the SGD to optimize the weight and the biases.

10. end while

5. Results and discussion

In this section, the three methods, PyDens, NeuroDiffeq and Nangs, are compared in terms of the accuracy and efficiency by solving several three types of PDE, namely elliptic, parabolic and hyperbolic (Burden et al., 2015). We also compared all three methods performance with the classical method which is FDM. All of the results are shown in various tables and figures.

5.1. Simulation results in solving PDE heat equation

The comparison methods for solving PDE heat equation as in Equations (22)–(24) are recorded in Table 1.

Table 1. The performance of PyDens, NeuroDiffeq and Nangs methods for solving PDE heat equation.

Training data	FDM		Pydens		NeuroDiffeq		Nangs
	Time (s)	Loss	Time (s)	Loss	Time (s)	Loss	Time (s)	Loss
25 × 25	2.87	$3.04\times {10}^{-4}$	53	$2.6\times {10}^{-4}$	65	$1.52\times {10}^{-3}$	578	$2.41\times {10}^{-3}$
50 × 50	6.81	$2.67\times {10}^{-5}$	116	$7.59\times {10}^{-6}$	231	$2.97\times {10}^{-5}$	602	$5.49\times {10}^{-4}$
75 × 75	5.54	$2.31\times {10}^{-6}$	203	$8.52\times {10}^{-6}$	480	$2.25\times {10}^{-5}$	726	$4.61\times {10}^{-5}$
100 × 100	5.49	$5.56\times {10}^{-8}$	386	$7.91\times {10}^{-6}$	943	$7.02\times {10}^{-6}$	956	$8.74\times {10}^{-6}$

According to Table 1, Pydens was able to solve the problems most accurate between the other ANN-based methods. For instance, the loss values of Pydens when using 25 × 25, 50 × 50 and 75 × 75 training data are, respectively, $2.6\times {10}^{-4},7.59\times {10}^{-6}$ and $8.52\times {10}^{-6},$ or about 84, 87 and 72% more accurate compared with NeuroDiffeq and Nangs. In contrast, for 100 × 100 training data, the NeuroDiffeq gives the most accurate value of loss than the other methods, with the loss value $7.02\times {10}^{-6},$ compared with $7.91\times {10}^{-6}$ and $8.74\times {10}^{-6},$ or about 13 and 20%, respectively. While in comparison with the classical method, FDM give better loss value only in 75 × 75 and 100 × 100 training data, which is, respectively, given by $2.31\times {10}^{-6}$ and $5.56\times {10}^{-8}$ (Figure 3).

In terms of the computational times, Pydens also gives the shortest time compared with the other two ANN-based methods, it spent 53 seconds only when using 25 × 25 training data, whereas 65 and 578 s needed for NeuroDiffeq and Nangs, respectively, for using the same training data. The higher training data of the PDE problem, such as 50 × 50, 75 × 75 and 100 × 100, need more times for the three methods. However, Pydens is still the winner between them. While in comparison with classical method, FDM is still gives the shortest time compared to ANN-based method with less than 10 s in all problems. The results are more clearly seen when we visualized the analytical solution as in Figure 3 and the comparisons via Figures 4–6.

Figure 3. Analytical solution of heat equation.

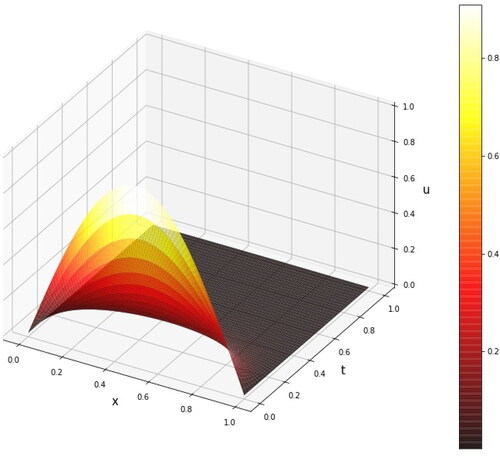
Figure 4. Comparison analytical and approximate solutions of PDE heat equation by using Pydens method.

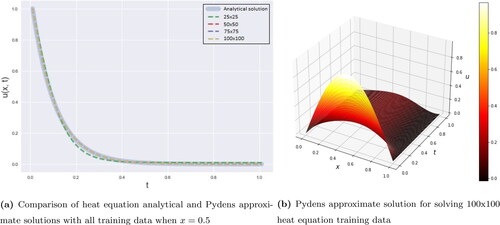
Figure 5. Comparison analytical and approximate solutions of PDE heat equation by using NeuroDiffeq method.

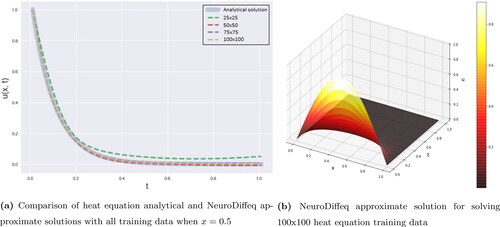
Figure 6. Comparison analytical and approximate solutions of PDE heat equation by using Nangs method.

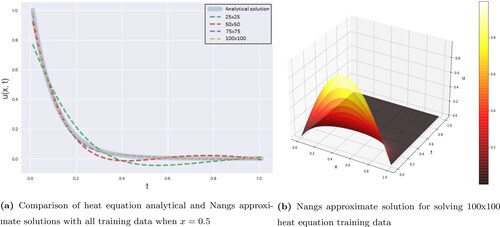
According to Figures 4(b)–6(b), all three methods almost give similar result from the analytical solution. However, from the other perspective as can be seen in Figures 4(a)–6(a) when all training data are shown, all methods show a little bit different from the analytical solution. Especially in lower training data, different results give in the 100 × 100 training data when all methods are closer to the analytical solution.

The comparison of all ANN-based methods in terms of the loss values and the computational times are shown in Figure 7. As we can see here that the higher numbers of training data used for solving the PDE heat would affect the performance of the methods. It is appeared in NeuroDiffEq and Nangs methods. For Pydens method, however, it just occurred when using the lower numbers of training data, namely 25 × 25 and 50 × 50, whereas greater than that, the Pydens performance slightly worse.

Figure 7. Comparisons of the loss values and the computational times between the ANN-based methods for solving heat equation at all training points.

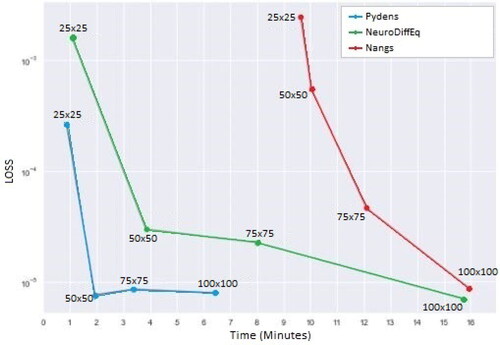
For further analysis of the performance of three methods, it is also shown in Table 2, where it illustrates all of the results of loss values of the variation number of hidden layers, and neurons per layer.

Table 2. The loss values of PDE Heat simulation for different number of layers and neurons.

Methods	Layers$\backslash$neurons	32	64	96
Pydens	3	$7.9\times {10}^{-6}$	$9.8\times {10}^{-3}$	$4.9\times {10}^{-5}$
	4	$1.1\times {10}^{-5}$	$9.4\times {10}^{-6}$	$8.1\times {10}^{-6}$
	5	$9.4\times {10}^{-6}$	$9.7\times {10}^{-3}$	$6.6\times {10}^{-6}$
NeuroDiffEq	3	$7.0\times {10}^{-6}$	$1.2\times {10}^{-6}$	$1.2\times {10}^{-6}$
	4	$8.5\times {10}^{-6}$	$3.6\times {10}^{-6}$	$4.9\times {10}^{-6}$
	5	$4.8\times {10}^{-6}$	$6.5\times {10}^{-7}$	$9.2\times {10}^{-7}$
Nangs	3	$8.7\times {10}^{-6}$	$2.8\times {10}^{-6}$	$2.0\times {10}^{-6}$
	4	$9.5\times {10}^{-7}$	$4.6\times {10}^{-7}$	$1.8\times {10}^{-6}$
	5	$2.4\times {10}^{-6}$	$1.4\times {10}^{-6}$	$2.1\times {10}^{-7}$

It can be seen from Table 2, in general, when the number of layers and neurons increased, the prediction accuracy also improved. However, more complex ANN architecture causes the computational time increased. Hence, determine the best ANN architecture is crucial.

5.1.1. Simulation results in solving PDE wave equation

Wave equation is one of the hyperbolic PDE and contains the second-order partial derivatives (Guo et al., 2020). Wave equation has been applied in many sciences fields, such as seismic wave propagation and acoustic wave propagations (Gu, Zhang, & Dong, 2018; Kim, 2019; Li, Feng, & Schuster, 2017). The wave equation is described as the following equations [3]: (26) $$\frac{{\partial }^{2}u}{\partial t^2}-4\frac{{\partial }^{2}u}{\partial x^2}=0,\hspace{1em}0\le x\le 1,t\ge 0,$$(26) with initial conditions (27) $$u(x,0)=\hspace{0.17em}\text{sin}\hspace{0.17em}(\pi x),$$(27) (28) $$\frac{\partial u}{\partial t}(x,0)=0,$$(28) and boundary conditions (29) $$u(0,t)=u(1,t)=0,$$(29)

The analytical solution is given as follows (30) $$u(x,t)=\hspace{0.17em}\text{sin}\hspace{0.17em}(\pi x)\hspace{0.17em}\text{cos}\hspace{0.17em}(2\pi t).,$$(30)

The simulation results of the three methods to solve the wave equation are shown in Table 3.

Table 3. The performance of the three methods for solving PDE wave equation.

Training data	FDM		Pydens		NeuroDiffeq		Nangs
	Time (s)	Loss	Time (s)	Loss	Time (s)	Loss	Time (s)	Loss
25 × 25	3.61	$1.01\times {10}^{-3}$	61	$2.82\times {10}^{-3}$	81	$4.33\times {10}^{-2}$	624	$1.84\times {10}^{-1}$
50 × 50	4.39	$2.50\times {10}^{-4}$	150	$2.43\times {10}^{-2}$	284	$1.21\times {10}^{-3}$	707	$7.38\times {10}^{-2}$
75 × 75	5.34	$1.11\times {10}^{-4}$	317	$7.84\times {10}^{-3}$	516	$2.38\times {10}^{-5}$	875	$1.85\times {10}^{-2}$
100 × 100	7.06	$6.21\times {10}^{-5}$	530	$3.42\times {10}^{-2}$	1274	$1.01\times {10}^{-5}$	1094	$1.63\times {10}^{-3}$

Similar to the previous results, in comparison with other ANN-based method, Pydens provides better performance in solving PDE wave for using 25 × 25 training data with a loss value of $2.80\times {10}^{-3},$ compared with $4.33\times {10}^{-2}$ and $1.84\times {10}^{-1}$ for, respectively, NeuroDiffeq and NAngs methods. It is more accurate about 94 and 98% than NeuroDiffEq and Nangs, respectively. Furthermore, for the remaining of using training data, NeuroDiffEq consistently performed well, as can be seen in Table 3, the loss values for NeuroDiffEq are $2.38\times {10}^{-5},$ and $1.01\times {10}^{-5}$ for 75 × 75 and 100 × 100 training data, respectively, or almost twice better than Pydens and Nangs. While compare to the classical method, FDM only performed better at 25 × 25 which is $2.50\times {10}^{-4}$ against $1.21\times {10}^{-2}$ that belongs to NeuroDiffEq. Figures 9–11 below support all performances of Pydens, NeuroDiffEq and Nangs methods for solving the PDE wave. It can be seen that Pydens curve get closer to the analytical curve for the lower dimension, whereas NeuroDiffEq curve gets closer to the analytical curve (Figure 8) in the higher dimensions.

Figure 8. Analytical solution of wave equation.

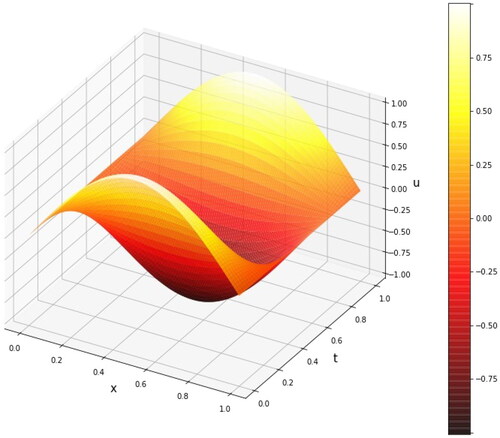
Figure 9. Comparison analytical and approximate solutions of PDE wave equation by using Pydens method.

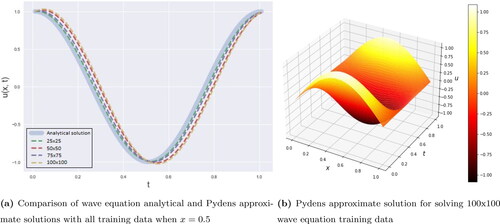
Figure 10. Comparison analytical and approximate solutions of PDE wave equation by using NeuroDiffeq method.

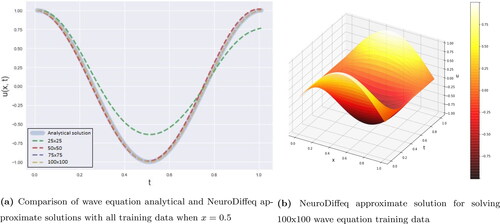
Figure 11. Comparison analytical and approximate solutions of PDE wave equation by using Nangs method.

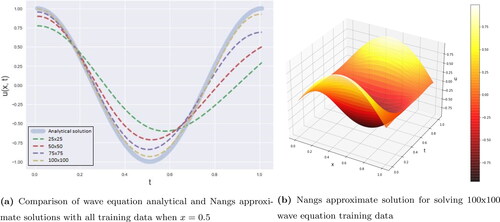
In Figures 9(a)–11(a), we can see that NeuroDiffEq closer to analytical solution from 50 × 50 to 100 × 100 training data compare to the other. Pydens in 25 × 25 training data is the best; however, the other training data gives no significant progress. Meanwhile for Nangs, all of the training data result is not close to the analytical solution.

Figure 12 above shows similar trends with the one in the previous section, where Pydens took the shortest time with about 61 s for 25 × 25 training data, compared with 81 and 1062 s for NeuroDiffeq and Nangs, respectively. However, NeuroDiffEq gives better results for using greater numbers of training data than the other two methods. The simulation results with different ANN architectures are shown in Table 4.

Figure 12. Comparisons of the loss values and the computational times between the ANN-based methods for solving wave equation at all training points.

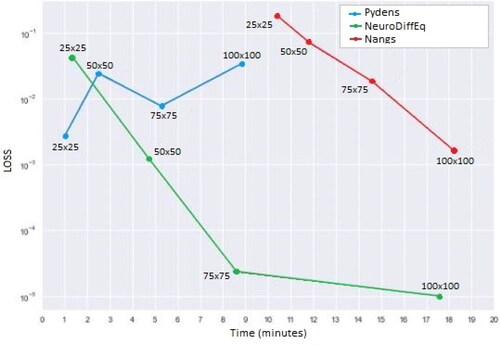
Table 4. Wave simulation results with different number of layers and neurons.

Methods	Layers$\backslash$neurons	32	64	96
Pydens method	3	$3.42\times {10}^{-2}$	$1.77\times {10}^{-2}$	$2.15\times {10}^{-2}$
	4	$2.46\times {10}^{-2}$	$5.9\times {10}^{-3}$	$3.92\times {10}^{-2}$
	5	$1.04\times {10}^{-1}$	$2.6\times {10}^{-2}$	$2.64\times {10}^{-2}$
NeuroDiffEq method	3	$1.0\times {10}^{-5}$	$1.9\times {10}^{-5}$	$5.0\times {10}^{-4}$
	4	$8.5\times {10}^{-6}$	$3.6\times {10}^{-6}$	$2.12\times {10}^{-4}$
	5	$1.9\times {10}^{-3}$	$8.1\times {10}^{-3}$	$2.8\times {10}^{-3}$
Nangs method	3	$1.6\times {10}^{-3}$	$2.1\times {10}^{-4}$	$2.3\times {10}^{-4}$
	4	$5.1\times {10}^{-3}$	$3.2\times {10}^{-4}$	$1.0\times {10}^{-4}$
	5	$1.18\times {10}^{-2}$	$7.0\times {10}^{-5}$	$2.7\times {10}^{-3}$

5.1.2. Simulation results in solving Poisson equation

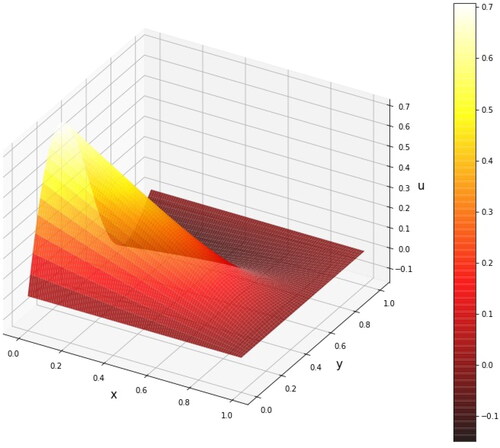
Poisson is applied in many modern technologies (Aggarwal & Ugail, 2019) and in a wide area of problems from simulating fluid flows (Xiao, Zhou, Wang, & Yang, 2020), modelling gravitational and electrostatic fields (Blakely, 1996), surface reconstruction (Kazhdan, Bolitho, & Hoppe, 2006), image processing (Pérez, Gangnet, & Blake, 2003), as well as other applications in geometric design (Arnal, Monterde, & Ugail, 2011; Ahmat, Castro, & Ugail, 2014; Chaudhry et al., 2015; Elmahmudi & Ugail, 2019; Jha, Ugail, Haron, & Iglesias, 2018; Shen, Sheng, Chen, Zhang, & Ugail, 2018; Ugail & Ismail, 2016). The PDE Poisson, as its anaytical solution is displayed in Figure 13, has the form of Elsherbeny, El-hassani, El-badry, and Abdallah (2018): (31) $$\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}=10(x-1)\hspace{0.17em}\text{cos}\hspace{0.17em}(5y)-25(x-1)(y-1)\hspace{0.17em}\text{sin}\hspace{0.17em}(5y),\hspace{1em}0\le (x,y)\le 1,$$(31) with boundary conditions (32) $$u(0,y)=(1-y)\hspace{0.17em}\text{sin}\hspace{0.17em}(5y),\hspace{1em}u(1,y)=u(y,0)=u(x,1)=1.$$(32)

Figure 13. Analytical solution of Poisson equation.

The analytical solution for this PDE is given as follows (33) $$u(x,y)=(1-x)(1-y)\hspace{0.17em}\text{sin}\hspace{0.17em}(5y)$$(33)

Table 5 shows detailed information of the three methods in solving Poisson equation above.

Table 5. The performance of the three methods for solving Poisson equation.

Training data	FDM		Pydens		NeuroDiffeq		Nangs
	Time (s)	Loss	Time (s)	Loss	Time (s)	Loss	Time (s)	Loss
25 × 25	3.41	$1.14\times {10}^{-6}$	53	$1.69\times {10}^{-4}$	105	$3.42\times {10}^{-7}$	544	$2.92\times {10}^{-3}$
50 × 50	4.34	$3.46\times {10}^{-7}$	126	$2.82\times {10}^{-4}$	391	$2.81\times {10}^{-8}$	653	$4.43\times {10}^{-4}$
75 × 75	11.14	$4.87\times {10}^{-6}$	250	$2.16\times {10}^{-4}$	656	$1.66\times {10}^{-9}$	760	$1.21\times {10}^{-4}$
100 × 100	12.26	$1.30\times {10}^{-4}$	423	$2.23\times {10}^{-4}$	1177	$4.17\times {10}^{-10}$	967	$5.83\times {10}^{-5}$

According to Table 5, all methods showed a good performance, NeuroDiffEq, however is still the most accurate with $3.42\times {10}^{-7},2.81\times {10}^{-7},1.66\times {10}^{-7}$ and $4.17\times {10}^{-10}$ for using 25 × 25 numbers of training data and above. This number is 99.8, 99, 100 and 100% more accurate than the other methods. This trend is clearly seen in Figures 11–13.

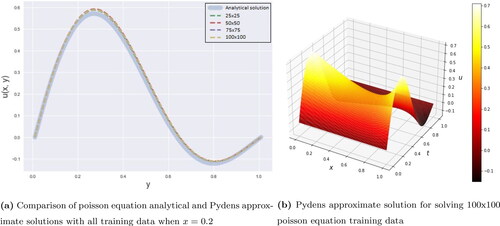
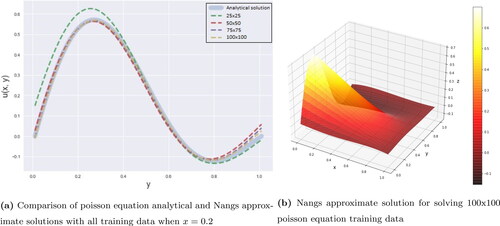
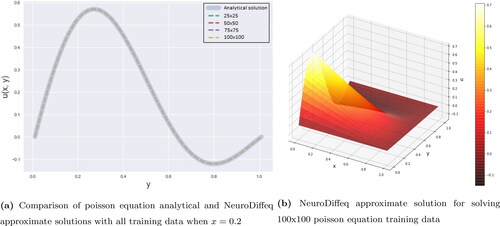
In Figure 14, when we see the overall result, Pydens failed to approximate the boundary condition well. That is the reason why even Pydens show a good results at x = 0.2, the overall error is not good enough. NeuroDiffEq in Figure 15 is the best in this case when all of the training data result is almost similar to the analytical solution. Meanwhile for Nangs in Figure 16, only 25 × 25 training data that not show a good result.

Figure 14. Comparison analytical and approximate solutions of PDE Poisson by using Pydens method.

Figure 15. Comparison analytical and approximate solutions of PDE Poisson by using NeuroDiffeq method.

Figure 16. Comparison analytical and approximate solutions of PDE Poisson by using Nangs method.

The performances of the three methods are summarized in Figure 17, when it can be seen that the NeuroDiffEq is the most accurate method to solve the Poisson Equation (31)(31) $$\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}=10(x-1)\hspace{0.17em}\text{cos}\hspace{0.17em}(5y)-25(x-1)(y-1)\hspace{0.17em}\text{sin}\hspace{0.17em}(5y),\hspace{1em}0\le (x,y)\le 1,$$(31) . However, this method is the slowest one compared with Pydens and Nangs methods, with 1177 s for using 100 × 100 training data. Pydens, in contrast, took the shortest time which only 53 s for 25 × 25 training data, compared with 105 and 544 s for NeuroDIffeq and Nangs methods, respectively. Similarly, when using 100 × 100 training data, Pydens needs 423 s only, compared with 1177 and 967 s for the other two methods, respectively. The simulation results for using different ANN architectures are recorded in Table 6.

Figure 17. Comparisons of the loss values and the computational times between the ANN-based methods for solving Poisson equation at all training points.

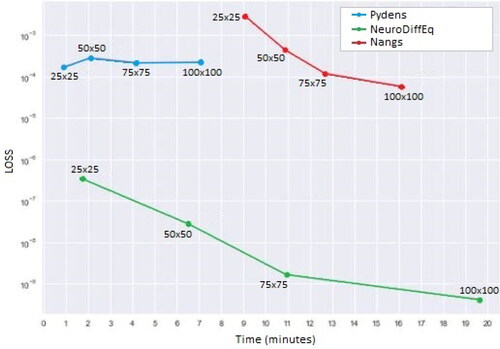
Table 6. Poisson simulation results with different number of layers and neurons.

Methods	Layers$\backslash$neurons	32	64	96
Pydens method	3	$2.2\times {10}^{-4}$	$2.4\times {10}^{-4}$	$1.8\times {10}^{-4}$
	4	$1.9\times {10}^{-4}$	$3.0\times {10}^{-4}$	$3.2\times {10}^{-4}$
	5	$3.1\times {10}^{-4}$	$2.7\times {10}^{-4}$	$1.4\times {10}^{-4}$
NeuroDiffEq method	3	$4.2\times {10}^{-10}$	$2.7\times {10}^{-10}$	$4.4\times {10}^{-10}$
	4	$4.4\times {10}^{-10}$	$3.3\times {10}^{-10}$	$1.3\times {10}^{-9}$
	5	$6.0\times {10}^{-10}$	$5.1\times {10}^{-10}$	$2.3\times {10}^{-9}$
Nangs method	3	$5.8\times {10}^{-5}$	$1.2\times {10}^{-5}$	$1.4\times {10}^{-5}$
	4	$1.8\times {10}^{-5}$	$1.1\times {10}^{-5}$	$6.1\times {10}^{-6}$
	5	$1.3\times {10}^{-5}$	$7.7\times {10}^{-6}$	$5.6\times {10}^{-6}$

5.2. Discussion

Overall, can be said the approximation solutions of PDE heat, PDE wave and PDE Poison equation using NeuroDiffEq give the better and stable accuracy than Pydens, Nangs, and even classical method FDM. This observation can be seen in Tables 1, 3 and 5, respectively. However, in the evaluation of the computational time, the FDM still give the shortest time compared to all ANN-based method. While comparing between the three ANN-based methods; this method took the longest when we added more training data. Furthermore, Pydens is the fastest method in solving all given problems. Unfortunately, the performance of this method is disappointing since more training data points do not affect its accuracy. Meanwhile, Nangs gives an unpredictable expectation results with its position is in the middle between the two methods. This method, in our point of view, can potentially give the better performance when solving the variety of PDE problems. The readers can see all the performances of the three methods through Figures 7, 12 and 17 which clearly indicate the conditions explained above.

To further investigation of the performances of these three methods, we also ran the simulations that can be seen in Tables 2, 4 and 6, respectively. The results showed that to improve the performance of the three methods, we can also change the ANN architectures by adding more numbers of layers and neurons. However, these options will increase the computational time. Another options are to increase iteration and change the optimizer.

6. Conclusion

We have discussed Pydens, NeuroDiffEq and Nangs methods to solve the heat, wave and Poisson equations of the second order of PDEs, and also compared with classical method. The training data used ranging from 25 × 25 to 100 × 100 points. We compared the accuracy as well as the time efficiency of each method. There are advantages and disadvantages of each method based on our experiments result. In term of the accuracy, NeuroDiffEq consistently produced the lowest loss values compared with Pydens, Nangs and FDM. To get better loss values, the training data points need to be increased though. However, it affected the longer computational time. On the other hand, the classical method FDM is still given the fastest method compared with the others. Interestingly, for Nangs method, although this method is not the fastest nor the lowest loss value, but it potentially produces the better loss values for solving high dimensional problems. It can be seen on Figures 6, 10 and 14 that the training data, the computation times, and the trend of loss values are potentially overtaken by NeuroDiffEq’s performance on high training data problems.

For future work, we recommend solving the smaller dimensional problems using the Pydens method because this method shows good performance. For higher dimensional problems, we recommend the NeuroDiffEq or Nangs methods. However, for NeuroDiffEq, we can see that this method is risky when using high amount of training data, affecting computation time. While for Nangs, although it does not perform very well, it is still capable of providing better performance and shorter computation time than NeuroDiffEq. Adjusting the ANN architecture, such as increasing the number of layers and neurons, can also improve the performance of ANN-based methods. However, the more complex the ANN architecture, the more expensive the method.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Data availability statement

Not applicable.