Analysis of plastically deformed functionally graded pressurized thick cylinder

Abstract

An analytical solution for stresses in a plastically deformed cylinder made of a functionally graded material (FGM) under internal pressure is provided. The cylindrical material is composed of two metal powder particles manufactured using centrifugal casting. While Poisson’s ratio is assumed constant, Young’s modulus is a power function of the radius. The von Mises yield criterion is used under the plane-strain condition. The constitutive material model obeys the Ludwik power law, with the yield strength and work-hardening coefficient as functions of the radius. The stress distributions along the radial direction for the elastic, elasto–plastic field and beyond plastic collapse cases were analyzed. To study the effect on the plastic zone in FGM, in addition to pressure, the gradient index was made to vary from −2 to 2 and different cylinder aspect ratios ranging from 1 up to 3 are considered. A finite-element simulation was run for comparison and validation of the analytical solution. The results showed a good agreement between the two methods.

Keywords:

• Functionally graded material
• internal pressure
• Ludwik hardening law
• plasticity solution
• stress analysis
• thick-walled cylinder

1. Introduction

Functionally graded materials (FGMs) are a new generation of advanced homogeneous composite materials and have recently been investigated in materials science and engineering. The mechanical properties of these materials are determined by continuously varying the volume fractions of their constituents. FGMs have been introduced in several industrial applications related to aerospace (Naik, Nazeer, Prasad, Laha, & Roy, 2022), nuclear (Heuer et al., 2019), automotive (Fracchia & Rosso, 2022; Srinivas, Ravindra Babu, & Balakrishna, 2020), biomedical (Fujii, Murakami, Kobayashi, Tohgo, & Shimamura, 2022) and oil and gas sectors, in general, and pressure vessel piping systems, in particular (Arslan, Mack, & Apatay, 2021; Yazhini & Chithra, 2022). A brief overview of the manufacturing methods, applications and future challenges of FGMs are presented in (Pasha & Rajaprakash, 2022; Saleh et al., 2020).

The behavior of a functionally graded pressurized hollow cylinder subjected to pressure is considered a classical problem in mechanical engineering and has been investigated by few researchers using different methods. A literature review dates back to 2012 (Sburlati, 2012), when a study on an FGM hollow cylinder subjected to pressure in the elastic domain was conducted, assuming a power function of the radius. The variation of the elastic modulus with geometry has also been investigated using different relationships, such as a linear function of the radius (Shi, Zhang, & Xiang, 2007), an exponential function of the radius (Benslimane, Bouzidi, & Methia, 2018; Chen & Lin, 2008; Nejad, Abedi, Lotfian, & Ghannad, 2016; Sondhi, Kumar, Sanyal, & Bhowmick, 2019) and in a more general form, some researchers have assumed that Young’s modulus varies according to a nonlinear function of the radius (Mognhod Bezzie & Engida Woldemichael, 2021, 2022). These studies on functionally graded materials cylinders are limited to the elastic range. With the ever-increasing pressures and temperatures due to higher efficiency demand, it is interesting to extend the analytical work employed in the elastic field (Sburlati, 2012) to the plastic range in order to investigate the integrity of these cylinders. The analytical development under such conditions and the prediction of stresses of interest to the pressure vessel industry.

Since the last decade, research in this field has evolved towards studying plastically deformed FGM cylinders using elastic–perfectly plastic analysis. Considering the Tresca yield criterion assumption, where the yield strength is either a constant (Eraslan & Akis, 2005; Xin, Dui, Yang, & Liu, 2016) or a power function of the radius (Sharma, Kaur, Sandhir, & Sharma, 2021); Eraslan & Akis (2005) studied the elasto–plastic response of a long functionally graded thick cylinder subjected to internal pressure. Xin et al. (2016) presented an analytical solution based on an elastic–perfectly plastic behavior under the Tresca yield criteria of a functionally graded thick-walled cylinder subjected to internal pressure. They considered the cylinder to be made of two functionally graded (FG) materials with a linear variation of the yield stress with radius. Sharma et al. (2021) presented stress and strain results of a finite element model of an FGM hollow cylinder subjected to steady-state temperature by considering both the elastic modulus and yield strength a power-law function of the radius. Similar stress analyses were conducted using FGM cylinders and discs subjected to thermomechanical loads (Alikarami & Parvizi, 2017; Ansari Sadrabadi et al., 2017; Benchallal, Benslimane, Bidgoli, & Hammiche, 2022; Benslimane, Benchallal, Mammeri, Methia, & Khadimallah, 2021).

In the previously mentioned papers, the analytical solutions of the stresses and radial displacements are based on an elastic–perfectly plastic FG material behavior. The modelling is based on Tresca’s yield criterion and ideal plastic material behavior. This approach does not give an accurate prediction of stresses and it is not suitable for different strain-hardening materials. The elastic-perfectly plastic material behavior is used for simplicity and is limited to certain homogeneous materials. FGMs are complex materials and are often made of two or more different material types. For the FGM cylinder fabricated with strain-hardened materials, the elastic modulus and the yield strength are not constant and are assumed to be a power function of the radius and so are the hardening parameters that define the plasticity behavior. In fact, the variation in these properties affects the distribution of stress and influences the plastic zone of the FMG cylinder.

For complex material behavior, exact analytical solutions are not easy to develop, and therefore, numerical methods become attractive. Numerical methods have been used to solve plastically deformed FGM cylinders (Heydari, 2019; Nayak, Bhowmick, & Saha, 2020; Saeedi, Kholdi, Loghman, Ashrafi, & Arefi, 2021). Nayak et al. (2020) conducted an elasto–plastic numerical analysis of thermo-mechanically loaded functionally graded discs using an iterative variational method. Heydari (2019) and Saeedi et al. (2021) analyzed the response of FGM discs with arbitrary material composition in the radial direction subjected to thermomechanical loads using differential transformation and successive approximation methods. While the first two researchers use Tresca criteria with an elastic perfectly plastic material, the last researcher investigates the effect of bilinear elasto–plastic behavior on ceramic/metal thick-walled FGM cylindrical vessels using Tresca yield criteria. Plastic analysis based on general nonlinear strain-hardening has rarely been investigated and analytical solutions are yet to be developed. The aim of this article is to provide an elasto–plastic analysis of an internally pressurized vessel made of a functionally graded material with nonlinear strain hardening material using a general constitutive model.

This article presents a new analytical model that is used to analyze the stresses and strains of plastically deformed FMG hollow cylinders manufactured using a metal matrix composite (Tayyebi & Alizadeh, 2022) the properties of which vary with the radius. In addition to the elastic modulus and yield stress, a more realistic nonlinear strain-hardening behavior that follows Ludwick power law (Khan & Huang, 1995) is used in the development of the analytical solution. In addition, the von Mises yield criteria under plane strain conditions are adopted as they are more representative of FGM cylinders. The proposed model is based on Hencky’s deformation theory under the von Mises yield criterion (Laghzale & Bouzid, 2016). In the optimum design of thick-walled cylinders used in the high-pressure technology industry, including artillery technology, internal pressure plays a key role. In this study, the pressures that start the yield and cause collapse were analyzed for different nonhomogeneity coefficients. The analytical model results are compared to their FEM counterparts in order to validate and verify the robustness of the exact solution.

2. Theoretical analysis

2.1. Material behavior and geometry characteristics

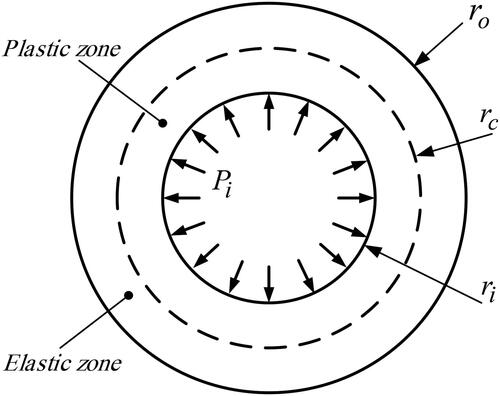
A thick hollow FGM cylinder with inner and outer radii, ${\mathrm{r}}_{\mathrm{i}}$ and ${\mathrm{r}}_{\mathrm{o}},$ respectively, is subjected to uniform internal pressure $P_{\mathrm{i}},$ as shown in Figure 1. It is assumed that the FGM cylinder has a constant Poisson’s ratio (Mognhod Bezzie & Engida Woldemichael, 2021). The plane strain state and small deformations are also assumed. The elastic modulus $\mathrm{E}$ and yield stress ${\mathrm{\sigma }}_{\mathrm{y}}$ are considered to vary with the radius according to the power-law expressed by Eqs. (1)(1) $$E(r)=E_a{\left(\frac{r}{r_i}\right)}^n$$(1) and (2)(2) $${\sigma }_y(r)={\sigma }_a{\left(\frac{r}{r_i}\right)}^s$$(2) , respectively: (1) $$E(r)=E_a{\left(\frac{r}{r_i}\right)}^n$$(1) (2) $${\sigma }_y(r)={\sigma }_a{\left(\frac{r}{r_i}\right)}^s$$(2) where ${\mathrm{E}}_{\mathrm{a}}$ and ${\sigma }_{\mathrm{a}}$ are the reference values for $\mathrm{E}$ and ${\mathrm{\sigma }}_{\mathrm{y}},$ respectively, at the inner radius, and $n$ and $s$ are gradient indices (Mognhod Bezzie & Engida Woldemichael, 2021). The material model behavior is described by an elastic–plastic relationship with a power law strain hardening expressed as follows: (3) $$\begin{array}{l}{\sigma }_{\text{eq}}(r)=E(r){\epsilon }_{\text{eq}}(if{\sigma }_{\text{eq}}\le {\sigma }_y)\\ {\sigma }_{\text{eq}}(r)=A(r)+B(r){\epsilon }_{\text{eq}}^m(if{\sigma }_{\text{eq}}\ge {\sigma }_y)\end{array}$$(3) where $A(r)$ and $B(r)$ are the Ludwik yield and work-hardening coefficients, respectively, and $m$ is a strain hardening exponent.

Figure 1. Schematic of elastic and plastic zones of FGM cylinder.

These coefficients are power functions of the radius expressed by Eq. (4)(4) $$\begin{array}{c}A(r)=A_a{\left(\frac{r}{r_i}\right)}^{\mathcal{l}}\\ B(r)=B_a{\left(\frac{r}{r_i}\right)}^q\end{array}$$(4) : (4) $$\begin{array}{c}A(r)=A_a{\left(\frac{r}{r_i}\right)}^{\mathcal{l}}\\ B(r)=B_a{\left(\frac{r}{r_i}\right)}^q\end{array}$$(4) where ${\mathrm{A}}_{\mathrm{a}}$ and $B_{\mathrm{a}}$ are the reference values of the Ludwik yield and work hardening coefficients $\text{A(r)}$ and $B(r),$ respectively, obtained at the inner radius, and $\mathcal{l}$ and $q$ are gradient parameters.

2.2. Phase I: elastic analysis

As the pressure increases, the deformation of the tube is purely elastic initially, and the stresses in the radial, tangential and longitudinal directions for a plane-strain case are expressed by Eq. (5)(5) $${\sigma }_r(r)=\frac{r_i^{-\frac{n}{2}+1}{r}^{\frac{n}{2}-1}}{\left(Y^{-\frac{k}{2}}-Y^{\frac{k}{2}}\right)}\left[{\left(\frac{r}{r_o}\right)}^{-\frac{k}{2}}-{\left(\frac{r}{r_o}\right)}^{\frac{k}{2}}\right]P_i$$(5) (Sburlati, 2012): (5) $${\sigma }_r(r)=\frac{r_i^{-\frac{n}{2}+1}{r}^{\frac{n}{2}-1}}{\left(Y^{-\frac{k}{2}}-Y^{\frac{k}{2}}\right)}\left[{\left(\frac{r}{r_o}\right)}^{-\frac{k}{2}}-{\left(\frac{r}{r_o}\right)}^{\frac{k}{2}}\right]P_i$$(5) (6) $${\sigma }_{\theta }(r)=\frac{r_i^{-\frac{n}{2}+1}{r}^{\frac{n}{2}-1}}{\left(Y^{-\frac{k}{2}}-Y^{\frac{k}{2}}\right)}\left[{\left(\frac{r}{r_o}\right)}^{-\frac{k}{2}}\left(\frac{n-k}{2}\right)-{\left(\frac{r}{r_o}\right)}^{\frac{k}{2}}\left(\frac{n+k}{2}\right)\right]P_i$$(6) (7) $${\sigma }_z(r)=\frac{\nu r_i^{-\frac{n}{2}+1}{r}^{\frac{n}{2}-1}}{\left(Y^{-\frac{k}{2}}-Y^{\frac{k}{2}}\right)}\left[{\left(\frac{r}{r_o}\right)}^{-\frac{k}{2}}\left(\frac{2+n-k}{2}\right)-{\left(\frac{r}{r_o}\right)}^{\frac{k}{2}}\left(\frac{2+n+k}{2}\right)\right]P_i$$(7) where $Y$ and $k$ is expressed as follows (Sburlati, 2012). (8) $$Y=\frac{r_o}{r_i}\hspace{1em}\text{and}\hspace{1em}k=-\sqrt{n²+4-\frac{4n\nu }{1-\nu }}$$(8)

For a hollow cylinder made of a homogeneous material, yielding starts at the inner surface as the pressure is increased (Huang, 2005). However, for functionally graded materials hollow cylinder yielding may start from the inner or outer surface depending on their geometrical and mechanical characteristics (Atai & Lak, 2017). In what follows, it is assumed that the yielding starts from the inner surface. Therefore, let us consider that at $r=r_i,$ when the internal pressure ${\mathrm{P}}_{\mathrm{i}}$ reaches the value of $P_{sy},$ yielding is initiated.

2.3. Phase II: elastoplastic analysis

As the internal pressure increases beyond $P_{sy},$ yielding, which starts at the inner surface, expands in the radial direction to reach a radius $r_c,$ which is the interface radius between the elastic and plastic regions (Figure 1).

The von Mises equivalent stress is expressed by Eq. (9)(9) $${\sigma }_{\text{eq}}=\frac{1}{\sqrt{2}}\sqrt{{\left({\sigma }_r-{\sigma }_{\theta }\right)}^2+{\left({\sigma }_{\theta }-{\sigma }_z\right)}^2+{\left({\sigma }_z-{\sigma }_r\right)}^2}$$(9) . (9) $${\sigma }_{\text{eq}}=\frac{1}{\sqrt{2}}\sqrt{{\left({\sigma }_r-{\sigma }_{\theta }\right)}^2+{\left({\sigma }_{\theta }-{\sigma }_z\right)}^2+{\left({\sigma }_z-{\sigma }_r\right)}^2}$$(9)

The mean stress is expressed by Eq. (10)(10) $$\overline{\sigma }=\frac{1}{3}\left({\sigma }_r+{\sigma }_{\theta }+{\sigma }_z\right)$$(10) . (10) $$\overline{\sigma }=\frac{1}{3}\left({\sigma }_r+{\sigma }_{\theta }+{\sigma }_z\right)$$(10)

In the plane-strain case and based on Hencky’s deformation theory, the strain–stress relationship in the z-direction can be expressed as follows: (11) $${\epsilon }_z=\frac{3{\epsilon }_{\text{eq}}}{4{\sigma }_{\text{eq}}}\left({\sigma }_z-\overline{\sigma }\right)=0$$(11)

In the plastic range, the longitudinal stress is given by (12) $${\sigma }_z=\frac{1}{2}\left({\sigma }_r+{\sigma }_{\theta }\right)$$(12)

Substituting Eq. (12)(12) $${\sigma }_z=\frac{1}{2}\left({\sigma }_r+{\sigma }_{\theta }\right)$$(12) into Eq. (9)(9) $${\sigma }_{\text{eq}}=\frac{1}{\sqrt{2}}\sqrt{{\left({\sigma }_r-{\sigma }_{\theta }\right)}^2+{\left({\sigma }_{\theta }-{\sigma }_z\right)}^2+{\left({\sigma }_z-{\sigma }_r\right)}^2}$$(9) gives the equivalent stress, as follows. (13) $${\sigma }_{\text{eq}}=\frac{\sqrt{3}}{2}\left({\sigma }_{\theta }-{\sigma }_r\right)$$(13)

Applying the von Mises yield criterion at $r=r_i,$ and noting that yield stress is given by Eq. (2)(2) $${\sigma }_y(r)={\sigma }_a{\left(\frac{r}{r_i}\right)}^s$$(2) , then: (14) $${{\sigma }_{\text{eq}}(r)|}_{r=r_i}^{}={\sigma }_y{(r)|}_{r=r_i}={\sigma }_a$$(14)

Substituting Eqs. (6)(6) $${\sigma }_{\theta }(r)=\frac{r_i^{-\frac{n}{2}+1}{r}^{\frac{n}{2}-1}}{\left(Y^{-\frac{k}{2}}-Y^{\frac{k}{2}}\right)}\left[{\left(\frac{r}{r_o}\right)}^{-\frac{k}{2}}\left(\frac{n-k}{2}\right)-{\left(\frac{r}{r_o}\right)}^{\frac{k}{2}}\left(\frac{n+k}{2}\right)\right]P_i$$(6) , (7)(7) $${\sigma }_z(r)=\frac{\nu r_i^{-\frac{n}{2}+1}{r}^{\frac{n}{2}-1}}{\left(Y^{-\frac{k}{2}}-Y^{\frac{k}{2}}\right)}\left[{\left(\frac{r}{r_o}\right)}^{-\frac{k}{2}}\left(\frac{2+n-k}{2}\right)-{\left(\frac{r}{r_o}\right)}^{\frac{k}{2}}\left(\frac{2+n+k}{2}\right)\right]P_i$$(7) and (14)(14) $${{\sigma }_{\text{eq}}(r)|}_{r=r_i}^{}={\sigma }_y{(r)|}_{r=r_i}={\sigma }_a$$(14) into Eq. (13)(13) $${\sigma }_{\text{eq}}=\frac{\sqrt{3}}{2}\left({\sigma }_{\theta }-{\sigma }_r\right)$$(13) , the pressure that causes yielding $P_{sy}$ is obtained as follows: (15) $$P_{sy}=\frac{4{\sigma }_a}{\sqrt{3}}.\frac{\left(Y^{-\frac{k}{2}}-Y^{\frac{k}{2}}\right)}{Y^{\frac{k}{2}}(n-k-2)+Y^{-\frac{k}{2}}(2-n-k)}$$(15)

With the assumed plane strain condition and considering material incompressibility in the plastic zone (Backhaus & Mendelson, 1969), the relationship between the radial and hoop strains is derived as follows: (16) $${\epsilon }_r=-{\epsilon }_{\theta }$$(16)

Therefore, the equivalent strain is expressed as follows: (17) $${\epsilon }_{\text{eq}}=\frac{2}{\sqrt{3}}{\epsilon }_{\theta }$$(17)

The compatibility equations are expressed by Eqs. (18)(18) $${\epsilon }_r=\frac{d{u}_r}{dr}$$(18) and (19)(19) $${\epsilon }_{\theta }=\frac{u_r}{r}$$(19) : (18) $${\epsilon }_r=\frac{d{u}_r}{dr}$$(18) (19) $${\epsilon }_{\theta }=\frac{u_r}{r}$$(19) where $u_r$ is the radial displacement. Substituting Eqs. (18)(18) $${\epsilon }_r=\frac{d{u}_r}{dr}$$(18) and (19)(19) $${\epsilon }_{\theta }=\frac{u_r}{r}$$(19) into Eq. (16)(16) $${\epsilon }_r=-{\epsilon }_{\theta }$$(16) and integrating $u_r$ with respect to r gives: (20) $$u_r=\frac{C}{r}$$(20) where $C$ is an integration constant. By neglecting the body forces, the equilibrium equation of an axisymmetric problem can be derived as follows. (21) $$\frac{d{\sigma }_r}{dr}+\frac{{\sigma }_r-{\sigma }_{\theta }}{r}=0$$(21)

Combining Eq. (13)(13) $${\sigma }_{\text{eq}}=\frac{\sqrt{3}}{2}\left({\sigma }_{\theta }-{\sigma }_r\right)$$(13) and Eq. (21)(21) $$\frac{d{\sigma }_r}{dr}+\frac{{\sigma }_r-{\sigma }_{\theta }}{r}=0$$(21) gives: (22) $$\frac{d{\sigma }_r}{dr}=\frac{2}{\sqrt{3}}\frac{{\sigma }_{eq}}{r}$$(22)

Substituting Eq. (3)(3) $$\begin{array}{l}{\sigma }_{\text{eq}}(r)=E(r){\epsilon }_{\text{eq}}(if{\sigma }_{\text{eq}}\le {\sigma }_y)\\ {\sigma }_{\text{eq}}(r)=A(r)+B(r){\epsilon }_{\text{eq}}^m(if{\sigma }_{\text{eq}}\ge {\sigma }_y)\end{array}$$(3) into Eq. (22)(22) $$\frac{d{\sigma }_r}{dr}=\frac{2}{\sqrt{3}}\frac{{\sigma }_{eq}}{r}$$(22) and integrating yields to: (23) $${\sigma }_r=\frac{2}{\sqrt{3}}\int \frac{1}{r}\left(A(r)+B(r){\epsilon }_{\text{eq}}^m\right)dr$$(23)

Combining Eqs. (17)(17) $${\epsilon }_{\text{eq}}=\frac{2}{\sqrt{3}}{\epsilon }_{\theta }$$(17) , (19)(19) $${\epsilon }_{\theta }=\frac{u_r}{r}$$(19) and (20)(20) $$u_r=\frac{C}{r}$$(20) gives (24) $${\epsilon }_{eq}=\frac{2}{\sqrt{3}}\frac{C}{r^2}$$(24)

In the plastic zone (Figure 1), the radial stress is determined by substituting Eqs. (4)(4) $$\begin{array}{c}A(r)=A_a{\left(\frac{r}{r_i}\right)}^{\mathcal{l}}\\ B(r)=B_a{\left(\frac{r}{r_i}\right)}^q\end{array}$$(4) and (24)(24) $${\epsilon }_{eq}=\frac{2}{\sqrt{3}}\frac{C}{r^2}$$(24) into Eq. (23)(23) $${\sigma }_r=\frac{2}{\sqrt{3}}\int \frac{1}{r}\left(A(r)+B(r){\epsilon }_{\text{eq}}^m\right)dr$$(23) and integrating between $r_i$ and $r_{}.$ (25) $${\sigma }_r(r)=\frac{2}{\sqrt{3}}\left[\frac{A_a}{\mathcal{l}}{\left(\frac{r}{r_i}\right)}^{\mathcal{l}}+\frac{B_{a}D}{\left(q-2m\right)}{\left(\frac{r}{r_i}\right)}^{(q-2m)}\right]+C_1$$(25)

The tangential stress is obtained by substituting Eq. (25)(25) $${\sigma }_r(r)=\frac{2}{\sqrt{3}}\left[\frac{A_a}{\mathcal{l}}{\left(\frac{r}{r_i}\right)}^{\mathcal{l}}+\frac{B_{a}D}{\left(q-2m\right)}{\left(\frac{r}{r_i}\right)}^{(q-2m)}\right]+C_1$$(25) into Eq. (21)(21) $$\frac{d{\sigma }_r}{dr}+\frac{{\sigma }_r-{\sigma }_{\theta }}{r}=0$$(21) such that: (26) $${\sigma }_{\theta }(r)=\frac{2}{\sqrt{3}}\left[A_a{\left(\frac{r}{r_i}\right)}^{\mathcal{l}}\left(1+\frac{1}{\mathcal{l}}\right)+B_{a}D\left[1+\frac{1}{\left(q-2m\right)}\right]{\left(\frac{r}{r_i}\right)}^{(q-2m)}\right]+C_1$$(26) where $C_1$ is an integration constant, and $D$ is defined as follows: (27) $$D={\left(\frac{2C_{}}{r_i²\sqrt{3}}\right)}^m$$(27)

The constants, $C_1$ and $D,$ are obtained in the case of stress-controlled boundary conditions expressed by Eq. (28)(28) $${{\sigma }_r|}_{r=r_i}^{}=-P_i,{{\sigma }_{\text{eq}}(r)|}_{r=r_c}^{}={\sigma }_y{(r)|}_{r=r_c}$$(28) . $C_1$ and $D$ are expressed by Eqs. (29)(29) $$C_1=-P_i-\frac{2}{\sqrt{3}}\left[\frac{A_a}{\mathcal{l}}+\frac{\left[{\sigma }_a{\left(\frac{r_c}{r_i}\right)}^s-A_a{\left(\frac{r_c}{r_i}\right)}^{\mathcal{l}}\right]{\left(\frac{r_c}{r_i}\right)}^{(2m-q)}}{(q-2m)}\right]$$(29) and (30)(30) $$D=\frac{\left[{\sigma }_a{\left(\frac{r_c}{r_i}\right)}^s-A_a{\left(\frac{r_c}{r_i}\right)}^{\mathcal{l}}\right]{\left(\frac{r_c}{r_i}\right)}^{(2m-q)}}{B_a}$$(30) , respectively. (28) $${{\sigma }_r|}_{r=r_i}^{}=-P_i,{{\sigma }_{\text{eq}}(r)|}_{r=r_c}^{}={\sigma }_y{(r)|}_{r=r_c}$$(28) (29) $$C_1=-P_i-\frac{2}{\sqrt{3}}\left[\frac{A_a}{\mathcal{l}}+\frac{\left[{\sigma }_a{\left(\frac{r_c}{r_i}\right)}^s-A_a{\left(\frac{r_c}{r_i}\right)}^{\mathcal{l}}\right]{\left(\frac{r_c}{r_i}\right)}^{(2m-q)}}{(q-2m)}\right]$$(29) (30) $$D=\frac{\left[{\sigma }_a{\left(\frac{r_c}{r_i}\right)}^s-A_a{\left(\frac{r_c}{r_i}\right)}^{\mathcal{l}}\right]{\left(\frac{r_c}{r_i}\right)}^{(2m-q)}}{B_a}$$(30)

At the elastic–plastic interface, $r_{}=r_c,$ the radial stress of the elastic zone expressed by Eq. (5)(5) $${\sigma }_r(r)=\frac{r_i^{-\frac{n}{2}+1}{r}^{\frac{n}{2}-1}}{\left(Y^{-\frac{k}{2}}-Y^{\frac{k}{2}}\right)}\left[{\left(\frac{r}{r_o}\right)}^{-\frac{k}{2}}-{\left(\frac{r}{r_o}\right)}^{\frac{k}{2}}\right]P_i$$(5) is equal to the radial stress of the plastic zone expressed by Eq. (25)(25) $${\sigma }_r(r)=\frac{2}{\sqrt{3}}\left[\frac{A_a}{\mathcal{l}}{\left(\frac{r}{r_i}\right)}^{\mathcal{l}}+\frac{B_{a}D}{\left(q-2m\right)}{\left(\frac{r}{r_i}\right)}^{(q-2m)}\right]+C_1$$(25) . Therefore, the elastic–plastic interface radius, $r_c,$ is obtained from the numerical solution of the following nonlinear equation: (31) $$\begin{array}{l}{A}_a{(\frac{r_c}{r_i})}^{\mathcal{l}}[\frac{1}{\mathcal{l}}-\frac{1}{(q-2m)}[1+{(\frac{r_c}{r_i})}^{2m-q}]]-\frac{A_a}{\mathcal{l}}-\frac{\sqrt{3}}{2}{P}_i+\\ {\sigma }_a{(\frac{r_c}{r_i})}^s[\frac{1}{(q-2m)}[1-{(\frac{r_c}{r_i})}^{2m-q}]-\frac{1}{2}\frac{({(\frac{r_c}{r_o})}^{\frac{k}{2}}-{(\frac{r_c}{r_o})}^{-\frac{k}{2}})}{{(\frac{r_c}{r_o})}^{-\frac{k}{2}}(n-k-2)+{(\frac{r_c}{r_o})}^{\frac{k}{2}}(2-n-k)}]=0\end{array}$$(31)

Substituting Eqs. (29)(29) $$C_1=-P_i-\frac{2}{\sqrt{3}}\left[\frac{A_a}{\mathcal{l}}+\frac{\left[{\sigma }_a{\left(\frac{r_c}{r_i}\right)}^s-A_a{\left(\frac{r_c}{r_i}\right)}^{\mathcal{l}}\right]{\left(\frac{r_c}{r_i}\right)}^{(2m-q)}}{(q-2m)}\right]$$(29) and (30)(30) $$D=\frac{\left[{\sigma }_a{\left(\frac{r_c}{r_i}\right)}^s-A_a{\left(\frac{r_c}{r_i}\right)}^{\mathcal{l}}\right]{\left(\frac{r_c}{r_i}\right)}^{(2m-q)}}{B_a}$$(30) into Eqs. (25)(25) $${\sigma }_r(r)=\frac{2}{\sqrt{3}}\left[\frac{A_a}{\mathcal{l}}{\left(\frac{r}{r_i}\right)}^{\mathcal{l}}+\frac{B_{a}D}{\left(q-2m\right)}{\left(\frac{r}{r_i}\right)}^{(q-2m)}\right]+C_1$$(25) and (26)(26) $${\sigma }_{\theta }(r)=\frac{2}{\sqrt{3}}\left[A_a{\left(\frac{r}{r_i}\right)}^{\mathcal{l}}\left(1+\frac{1}{\mathcal{l}}\right)+B_{a}D\left[1+\frac{1}{\left(q-2m\right)}\right]{\left(\frac{r}{r_i}\right)}^{(q-2m)}\right]+C_1$$(26) gives the radial and hoop stresses in the plastic zone $r_{}\le r_c$ as follows. (32) $${\sigma }_r(r)=\frac{2}{\sqrt{3}}\{\frac{A_a}{\mathcal{l}}[{(\frac{r}{r_i})}^{\mathcal{l}}-1]+\frac{1}{(q-2m)}.[{\sigma }_a{(\frac{r_c}{r_i})}^s-A_a{(\frac{r_c}{r_i})}^{\mathcal{l}}]{(\frac{r_c}{r_i})}^{(2m-q)}.[{(\frac{r}{r_i})}^{(q-2m)}-1]\}-P_i$$(32) (33) $${\sigma }_{\theta }(r)=\frac{2}{\sqrt{3}}\left[\begin{array}{l}{A}_a[{(\frac{r}{r_i})}^{\mathcal{l}}(1+\frac{1}{\mathcal{l}})-\frac{1}{\mathcal{l}}]+\\ [\{[1+\frac{1}{q-2m}]{(\frac{r}{r_i})}^{(q-2m)}\}-\frac{1}{q-2m}].[{\sigma }_a{(\frac{r_c}{r_i})}^s-A_a{(\frac{r_c}{r_i})}^{\mathcal{l}}]{(\frac{r_c}{r_i})}^{(2m-q)}\end{array}\right]-P_i$$(33)

2.4. Phase III: beyond plastic collapse analysis

As the internal pressure $P_i$ increases, the cylinder collapse when $r_c$ becomes equal to the outer radius $r_o.$ The elastic zone vanishes and the cylinder becomes fully plastic. In this case, the pressure required to cause the plastic collapse of the cylinder,$P_{\mathit{spc}},$ is determined by assuming the radial stress expressed by Eq. (32)(32) $${\sigma }_r(r)=\frac{2}{\sqrt{3}}\{\frac{A_a}{\mathcal{l}}[{(\frac{r}{r_i})}^{\mathcal{l}}-1]+\frac{1}{(q-2m)}.[{\sigma }_a{(\frac{r_c}{r_i})}^s-A_a{(\frac{r_c}{r_i})}^{\mathcal{l}}]{(\frac{r_c}{r_i})}^{(2m-q)}.[{(\frac{r}{r_i})}^{(q-2m)}-1]\}-P_i$$(32) at the outer radius to be equal to zero. (34) $${{\sigma }_r(r)|}_{r=r_o}^{}=0$$(34)

The collapse pressure is expressed as follows. (35) $$P_{\mathit{spc}}=\frac{2}{\sqrt{3}}\left[\frac{A_a}{\mathcal{l}}\left(Y^{\mathcal{l}}-1\right)+\frac{\left[{\sigma }_a{Y}^s-A_a{Y}^{\mathcal{l}}\right]}{q-2m}.\left(1-\frac{1}{Y^{(q-2m)}}\right)\right]$$(35)

The stresses beyond the plastic collapse are calculated using Eqs. (25)(25) $${\sigma }_r(r)=\frac{2}{\sqrt{3}}\left[\frac{A_a}{\mathcal{l}}{\left(\frac{r}{r_i}\right)}^{\mathcal{l}}+\frac{B_{a}D}{\left(q-2m\right)}{\left(\frac{r}{r_i}\right)}^{(q-2m)}\right]+C_1$$(25) and (26)(26) $${\sigma }_{\theta }(r)=\frac{2}{\sqrt{3}}\left[A_a{\left(\frac{r}{r_i}\right)}^{\mathcal{l}}\left(1+\frac{1}{\mathcal{l}}\right)+B_{a}D\left[1+\frac{1}{\left(q-2m\right)}\right]{\left(\frac{r}{r_i}\right)}^{(q-2m)}\right]+C_1$$(26) , with the constants obtained by considering that the radial stress equals the internal pressure $P_i>P_{\mathit{spc}}$ at the inner radius and zero at the outer radius. (36) $$\begin{array}{c}{\sigma }_r(r)=\frac{2}{\sqrt{3}}\frac{A_a}{\mathcal{l}}\left[{\left(\frac{r}{r_i}\right)}^{\mathcal{l}}-\frac{1}{\left(1-Y^{(q-2m)}\right)}.\left\{\left(1-Y^{\mathcal{l}}\right){\left(\frac{r}{r_i}\right)}^{\left(q-2m\right)}-\left(Y^{(q-2m)}-Y^{\mathcal{l}}\right)\right\}\right]\\ -\frac{P_i}{\left(1-Y^{(q-2m)}\right)}\left[{\left(\frac{r}{r_i}\right)}^{\left(q-2m\right)}+\left(2-Y^{\left(q-2m\right)}\right)\right]\end{array}$$(36) (37) $$\begin{array}{c}{\sigma }_{\theta }(r)=\frac{2}{\sqrt{3}}\frac{A_a}{l}\left[{\left(\frac{r}{r_i}\right)}^{\mathcal{l}}\left(1+\mathcal{l}\right)-\frac{1}{\left(1-Y^{(q-2m)}\right)}\left\{\left(1-Y^{\mathcal{l}}\right){\left(\frac{r}{r_i}\right)}^{\left(q-2m\right)}\left(q-2m+1\right)-\left(Y^{(q-2m)}-Y^{\mathcal{l}}\right)\right\}\right]\\ -\frac{P_i}{\left(1-Y^{(q-2m)}\right)}\left[{\left(\frac{r}{r_i}\right)}^{\left(q-2m\right)}\left(q-2m+1\right)+\left(2-Y^{\left(q-2m\right)}\right)\right]\end{array}$$(37)

3. Validation using numerical finite element model

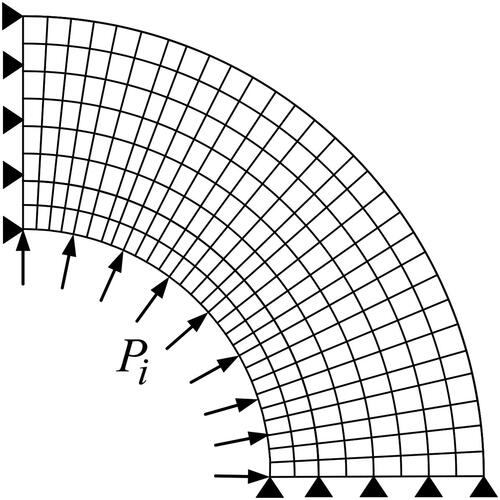
The proposed analytical approach was validated using a finite element model developed with ANSYS software (Figure 2). Although most finite element software programs do not have the option to model the variation of material properties with the coordinate position, some programs such as ANSYS offer the possibility to define temperature-dependent properties; in particular, temperature values can be assigned as a function of the position. By combining these two possibilities, material properties become position-dependent. In this study, the effect of temperature was ignored.

Figure 2. Finite element model in ANSYS.

Isoparametric eight-node plane-strain elements were used to model the hollow cylinder. The large-deformation option was considered. Because of the symmetry, only a quarter of the cylinder was modeled. A mesh convergence criterion based on a 1% difference in the maximum stress was used to validate the mesh refinement of the finite element model. The FGM cylinder is made of two metal powder particles. At the inner surface, the FGM exhibits properties similar to HB7 steel characteristics. There is a global interest in the HB7 material especially in the field of pressure vessels because of its high toughness and fatigue resistance (Maleki, Farrahi, Haghpanah Jahromi, & Hosseinian, 2010; Parker & Huang, 2007; Troiano, Parker, & Underwood 2004). The geometrical and mechanical characteristics of the FGM are listed in Table 1 (Parker & Huang, 2007).

Table 1. Geometrical and mechanical characteristics of FGM.

	$E_a$ (GPa)	$\nu$	${\sigma }_a\mathrm{}$ (MPa)	$n$	$s$	$\mathcal{l}$	$m$	$q$	$A_a$ (MPA)	$B_a$ (MPa)	$r_i\mathrm{}\mathrm{}$ (mm)	$r_o\mathrm{}$(mm)
FGM	202	0.3	1159.4	−2 to 2	$\frac{n}{4}$	$\frac{n}{4}$	–3.011	$l+{(n-s)}^m$	–1459.98	–5 E – 05	20	40

4. Result and discussion

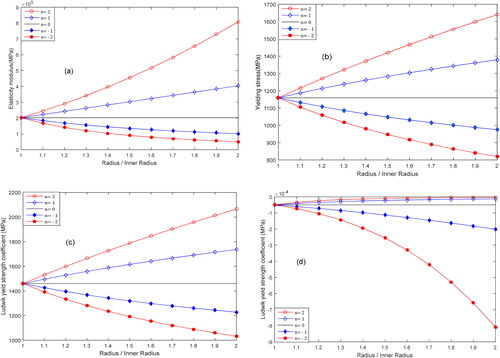
Figure 3 shows the variations in the elasticity modulus $E(r),$ yielding stress ${\sigma }_y(r),$ material yield coefficient $A(r)$ and work-hardening coefficient $B(r)$ as a function of the radial position in the cylinder for a nonhomogeneity coefficient $n$ varying between −2 and 2. Depending on the value of the latter, the rate of these properties can increase or decrease. For positive values of $n,$ the values of $E,$ ${\sigma }_y,$ $A$ and $B$ gradually increase from the inner surface to the outer surface. However, they decrease with the radius for negative values of $n.$ This trend is interesting because the value of $n$ can be adjusted according to the loading state and the highly stressed locations.

Figure 3. Variations in (a) elasticity modulus $E(r),$ (b) yielding stress ${\sigma }_y(r),$ Ludwik yield and work-hardening coefficients, (c)$A(r)$ and (d)$B(r)$ for different values of nonhomogeneity coefficient n.

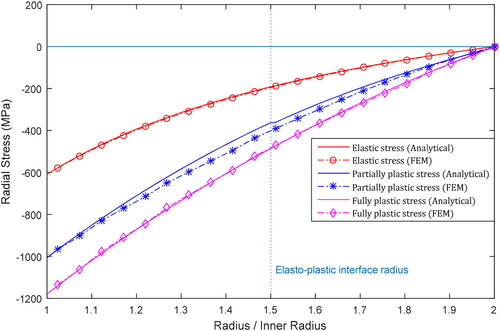
The distributions of the radial, tangential, longitudinal and equivalent stresses across the thickness of the cylinder are shown in Figures 4–7 for the three cases: elastic, partially plastic or 50% autofrettaged and fully plastic (100% autorettaged) cases. 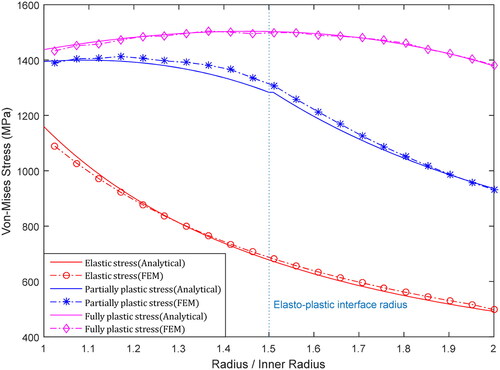The elastically deformed case is conducted with $P_i=609\text{MPa},$ the partially plastic deformed case is conducted with $P_i=1005\text{MPa},$ and the collapse case is run with $P_i=1179\text{MPa}.$ In all cases $n=1$ and $\nu =0.3.$ The radial stress a progressive increase from the value of the internal pressure inside the cylinder to zero outside the cylinder for all cases as shown in Figure 4. In addition, as the plastic zone increases, the rate of change in the radial stress increases because the internal pressure increases. The radial stress distributions of the analytical model fit precisely on top of the numerical ones.

Figure 4. Distribution of radial stress across thickness for elastic, elasto–plastic and beyond plastic collapse cases.

The distributions of the tangential and longitudinal stresses are shown in Figures 5 and 6, respectively. In the elastic phase, the tangential stress gradually decreases from the inner surface to the outer surface, with the maximum stress located at the inner radius. In the partially plastic case, the tangential and longitudinal stresses progressively increased until they reached their maximum values at the elasto–plastic interface radius, $r=r_c,$ and then, decrease in the former and reaches a plateau in the latter. However, beyond the plastic collapse, these stresses steadily increased throughout the cylinder thickness, with the maximum stress at the outer radius $r=r_o.$ For the elastic case, the equivalent stress decreases significantly, however with the two autofrettaged cases the stress increases slightly, and then, drops through the thickness while resulting in higher stress at the outside diameter depending on the level of autofrettage as observed in Figure 7. In the elastic phase, the equivalent stress decreases by 90% from the inner surface to the outer surface. In contrast, the decrease is 20% in the fully plastic case.

Figure 5. Distribution of tangential stress across thickness for elastic, elasto–plastic and beyond plastic collapse cases.

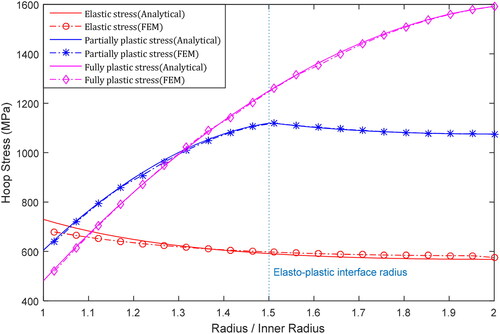
Figure 6. Distribution of longitudinal stress across thickness for elastic, partially plastic and beyond plastic collapse cases.

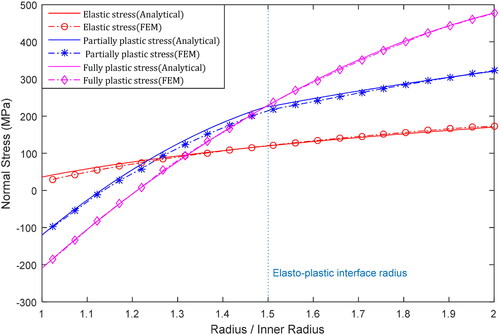
Figure 7. Distribution of equivalent stress in cylinder for elastic, partial autofrettage and beyond plastic collapse cases.

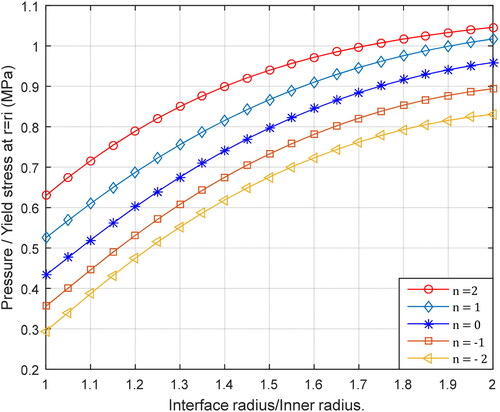
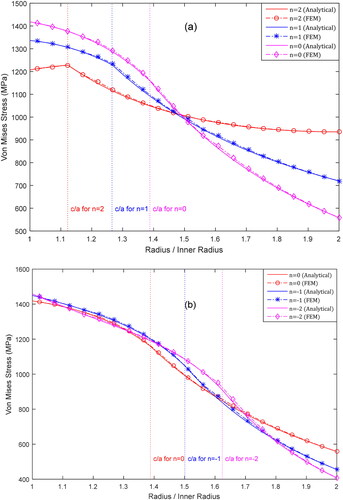
The effect of the nonhomogeneity parameter $n$ on the stresses in the FGM cylinders is evaluated. Figure 8 depicts the equivalent stress as a function of the radial position for $P_i=850\text{MPa},$ and different values of $n.$ The higher the value of $n,$ the lower the plastic zone. For positive values of $n,$ in comparison with the homogenous HB7 steel cylinder ($n=0$), the higher the value of $n,$ the lower the equivalent stress at the interface radius and the higher the equivalent stress at the outer radius. However, for negative $n$ values, there is no significant change in the equivalent stress distribution. In general, the von Mises stress rapidly decreases in the elastic zone and then slows down in the plastic zone. However, for $n=2,$ the von Mises stress slightly increases until it reached the maximum value at the elasto–plastic radius, and then, decreases. Yield starts from the inner surface and expands towards the outer surface. When $n$ decreases, the HB7 steel properties dominated the behavior, i.e., the behavior of the material becomes regular. The analytical results are consistent with those of the numerical finite element method.

Figure 8. Equivalent stress distributions for a partial autofrettage with (a) positive values of n and (b) negative values of n.

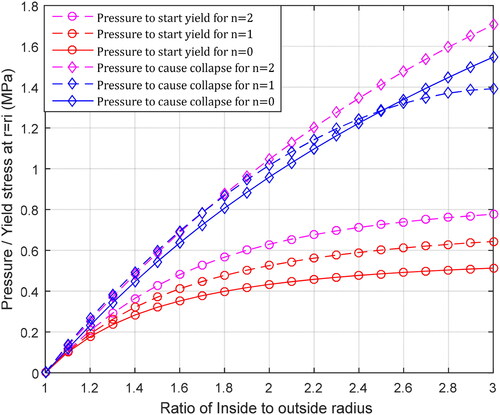
In a plastically deformed FGM cylinder, the plastic zone increased and the elastic zone decreased with the internal pressure increase. The values of the pressures that produced yielding and collapse of the hollow FGM cylinder for different $n$ values are listed in Table 2.

Table 2. Yield and collapse pressures of FGM cylinder for different values of the nonhomogeneity coefficient.

$n$	–2	–1	0	1	2
$\text{Yielding pressure}{P}_{sy}(\text{MPa}\mathrm{)}$	341.4035	412.7611	502.0349	609.2017	730.1822
$\text{Collapse pressure}{P}_{\mathit{spc}}(\text{MPa}\mathrm{)}$	963.1181	1036.7	1111.8	1179.4	1212.8

Figure 9 shows the internal pressure required to produce a plastic zone with a specific radius for a cylinder with Y = 2. The pressure graph is plotted as a function of the ratio of the elastoplastic interface radius. Although this study was on an FGM cylinder whose properties are listed in Table 1, the trend is representative of most FGM materials having properties as a function of the radius. As mentioned previously, the plastic deformation of the cylinder begins at the inner surface with $r_c=r_i$ when the internal pressure reaches $P_i=P_{sy}.$ In this case, the highest pressure is $P_{sy}=730\text{MPa}$ obtained with $n=2,$ whereas the lowest value is, $P_{sy}=413\text{MPa},$ obtained with $n=-2.$ The plastic region of the hollow cylinder increases with a pressure increase until the elasto–plastic interface radius reached the outer surface. At $r_c=r_o,$ the tube became fully plastic, and the internal pressure was $P_i=P_{\mathit{spc}}.$ The maximum pressure was $P_{\mathit{spc}}=1213\text{MPa}$ obtained with $n=2,$ whereas the minimum pressure was $P_{\mathit{spc}}=1037\text{MPa},$ with n = −2. Nevertheless, the pressure difference between the different n values is practically constant as the plastic zone increases.

Figure 9. Internal pressure as function of the radius of elasto–plastic interface.

The pressure to produce the start of yield, $P_{sy},$ and the pressure to cause collapse, $P_{\mathit{spc}},$ depend on the material behavior and geometry characteristics. Figure 10 shows the variations in these two limiting pressure values for different cylinder inner-to-outer ratios with $n=1$ and $n=0.$ The thicker the cylinder is, the higher the values of these two pressures are, and the more significant their difference is.

Figure 10. Pressure limit for different cylinder Y ratios and n = 0, n = 1 and n = 2.

5. Conclusion

A new analytical model of a plastically deformed thick-walled FGM cylinder subjected to internal pressure was developed in this study. The material constitutive model was based on the Ludwik law, with the strength and work-hardening coefficients as functions of the radius. The Hencky deformation theory under plane strain with the von Mises yield criterion was used in the model to obtain the stress distributions for elastic, partially plastic and fully plastic cases.

Different values of the material nonhomogeneity parameter, n, were used to determine the effect of nonhomogeneity on the stress distributions and elastic yield pressure. The influence of the material nonhomogeneity parameter on the radial stress distribution was negligible while it is significantly important on the tangential stress distribution and to a lesser extent on the pressure.

The analytical results for the stresses, including the von Mises stresses, were compared with those obtained using the numerical finite element model for different values of $n.$ As the pressure increased, the plastic zone expanded through the thickness. The plastic zone increased with a decrease in n. Moreover, the higher the plastic zone, the lower the equivalent stress at the interface radius. The load carrying capacity of the FGM cylinder increases with positive n values and so does the strength. The analytical model stress distributions of all the treated cases were consistent with the numerical finite element model distributions, which validate and show the robustness of the developed analytical solution.

Nomenclature
E	=	Young’s modulus at radius r (MPa)
${\mathrm{\sigma }}_y$	=	yield stress at radius r (MPa)
$E_a$	=	Young’s modulus at r = ri (MPa)
${\mathrm{\sigma }}_a$	=	yield stress at r = ri (MPa)
$A,B$	=	Ludwik plastic parameters at radius r (MPa)
$A_a,B_a$	=	Ludwik plastic parameters at r = ri (MPa)
$n,\mathcal{l},q,s$	=	FGM gradient indexes
$r_i,r_o$	=	inner and outer radii, respectively (mm)
$r_c$	=	elastic–plastic interface of cylinder (mm)
$Y=r_o/r_i$	=	inner-to-outer radius ratio of cylinder
m	=	strain hardening exponent
$\nu$	=	Poisson’s ratio
${\sigma }_{\text{eq}}$	=	equivalent stress (MPa)
${\epsilon }_{\text{eq}}$	=	equivalent strain (mm/mm)
${\sigma }_r,{\sigma }_{\theta },{\sigma }_z$	=	radial, tangential and longitudinal stresses, respectively (MPa)
${\epsilon }_r,{\epsilon }_{\theta },{\epsilon }_z$	=	radial, tangential and longitudinal strains, respectively (mm/mm)
$u_r$	=	radial displacement (mm)
$P_i$	=	internal pressure (MPa)
$P_{sy}$	=	pressure at which yielding starts
$P_{\mathit{spc}}$	=	pressure that causes plastic collapse
${\mathrm{C},\mathrm{C}}_1,D$	=	integration constants

Disclosure statement

No potential conflict of interest was reported by the authors.

Data availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author upon reasonable request.