Zero and nothing in medieval Arabic arithmetic

Abstract

Whether explaining calculations with decimal or sexagesimal notation, arithmetic books composed in Arabic beginning in the ninth century CE consistently describe the zero (ṣifr) as a sign indicating an empty place where there is no number. And yet we find that some arithmeticians explicitly performed operations on this zero. To understand how the zero was conceived and manipulated in medieval Arabic texts we first address the way that numbers themselves were conceived and how ‘nothing’ entered into arithmetical problem-solving. From there we examine arithmetic books for their treatment of zero. We find that there is no inconsistency in operating on what is literally nothing, and thus there was no motive for arithmeticians to regard zero as a number.

One fascinating characteristic of mathematics in medieval Islam is how authors brought together elements originating from different cultures. For instance, in the late seventh/thirteenth¹ century, the Moroccan polymath Ibn al-Bannāʾ was not unusual in incorporating techniques of Middle Eastern mental calculation and portions of Greek number theory into his book on Indian calculation. That book, titled Condensed book on calculation,² proved to be exceedingly popular and spawned many commentaries. Another example is Kūshyār ibn Labbān’s ca. early fifth/eleventh century Book on the principles of Indian calculation,³ which covers the rules for performing operations in both the Indian system and the sexagesimal (base 60) system of the astronomers.

This ‘Indian calculation’ (al-ḥisāb al-hindī), as it was frequently called in Arabic, is the same as calculation with what in English are called Arabic numerals. This system originated in India sometime in the first few centuries CE, and by the middle of the seventh century, knowledge of its use had reached westward as far as Syria. Writing in Nisibis in 662 CE, the bishop Severus Sebokht noted the superior Indian method of calculating, which ‘is done by means of nine signs’ (Ginsburg and Smith 1917, 368). However, it may be that Arabic calculators first learned the use of the nine figures 1, 2, 3, 4, 5, 6, 7, 8, 9 and the zero (0) later, in the second half of the eighth century through direct contact with Indian practitioners (Folkerts 2001; Kunitzsch 2003).

The treatment of the zero poses a dilemma. Reading through sample calculations made with Indian figures in medieval Arabic books, we sometimes find it added, subtracted, and multiplied with the other digits just as it is today, but at the same time, the author will state that the zero signifies an empty place where no number resides. So, on the one hand, zero seems to be treated as a number, but on the other, it is explicitly said to mean ‘nothing’. It is the purpose of the present article to make sense of the Arabic zero. To do so, we will need to first step back to consider how numbers were conceived by medieval Arabic authors and how ‘nothing’ was treated in arithmetical problem-solving. Because algebra enters into this story in different ways, we will also review key characteristics of premodern algebraic expressions. We will then at last be prepared to investigate the ways that zero, both decimal and sexagesimal, was treated in Arabic books, with an eye for any differences between authors. The discussion then passes to examples of zero and ‘nothing’ in the context of algebra in al-Samawʾal (d. 570/1174–75) and al-Hawārī (early eighth/fourteenth c.), after which we can summarize our findings on the meaning of zero (ṣifr) in medieval Arabic arithmetic.

1. The different arithmetics of medieval Islam

We begin with brief descriptions of the more important traditions in calculation that are presented in the books of Ibn al-Bannāʾ, Kūshyār ibn Labbān, and others.⁴ The first one we will cover requires no form of writing. The members of several professional groups in Islamicate societies, including merchants, surveyors, and government secretaries, traditionally performed calculations mentally in which intermediate results from 1 to 9999 were stored by positioning the fingers in particular ways. This method of calculating was called by various names, including ‘finger-reckoning’ and ‘mental reckoning’. Fractions in this system were spoken when possible in terms of the fractions ‘a half’, ‘a third’, up to ‘a tenth’, so that 5/12, for example, would be expressed as ‘two sixths and half a sixth’. Often, too, fractional approximations were formed with the aid of sexagesimal techniques. Algebra, the rule of three, double false position, and other problem-solving methods were initially associated with finger-reckoning, and by the early third/ninth century, when Muḥammad ibn Mūsā al-Khwārazmī (d. after 232H/847 CE) wrote his famous book on algebra, people were already calculating with irrational roots. The earliest extant book devoted to finger-reckoning is the Book of what is necessary for scribes, dealers, and others from the science of calculation by Abū l-Wafāʾ (328/940–388/998),⁵ which already imports many ideas from Euclid and Nicomachus.

It was mainly astronomers who performed sexagesimal calculations. In this base-60 system, the places 1 through 59 were traditionally written in what is called jummal or abjad notation, using the letters of the Arabic alphabet, together with a zero formed from a circle with a line over it that was copied from the Greek sexagesimal system. In some texts, Indian numerals took the place of jummal numerals. Degrees often play the role of units, so that the minutes, seconds, etc. that follow are fractional amounts. Because the techniques of performing operations in base 10 and base 60 are similar, many books describe them both.

Calculation with Indian numerals was sometimes called ‘dust arithmetic’ or ‘board arithmetic’, after the dust-board on which the calculations were commonly worked out. This was a board or other flat surface covered with fine sand on which one wrote with a stylus. One important feature of the dust-board for the rules of calculation is that digits can easily be erased and rewritten. The earliest known book on Indian calculation was aptly titled Book on Indian calculation,⁶ written in the first half of the third/ninth century in Baghdad by al-Khwārazmī. The Arabic original is lost, but we are fortunate that a reworking of a medieval Latin translation is extant. Al-Khwārazmī and later authors cover the shapes of the numerals and the rules for forming numbers, followed by rules for addition, subtraction, doubling, halving, multiplication, division for whole numbers and fractions, and root extraction. Fractions in this system were usually borrowed from finger reckoning. The earliest known author to describe decimal fractions, such as writing the equivalent of 12.75 instead of 12 ${\displaystyle \frac{3}{4}}$, is Ahmad ibn Ibrāhīm al-Uqlīdisī, in his Chapters on Indian calculation,⁷ completed in Damascus in 341/952–53. However, the fractions associated with finger-reckoning would remain in common use for several more centuries.

A system that became popular among accountants in the far western parts of the Islamic world used what were called rūmī signs. In this system 27 special characters designate the numbers 1, 2, 3, … , 9, 10, 20, 30, … , 90, 100, 200, … , 900. Al-Uqlīdisī gives the earliest known description of this way of calculating (al-Uqlīdisī 1978, 310). The name rūmī (‘Roman’) suggests that Arabic calculators acquired knowledge of this method from Byzantine sources.

Arabic mathematicians learned Greek number theory mainly from translations of the arithmetical Books VII–IX of Euclid’s Elements (ca. 300 BC) and Nicomachus of Gerasa’s Arithmetical Introduction (ca. 100 CE). The philosophical foundation of this theory stems from the writings of Aristotle and was elaborated by Muslim philosophers, most notably by Ibn Sīnā (Avicenna) in the early fifth/eleventh century. At the beginning of Book VII Euclid defines the unit as ‘that by virtue of which each of the things that exist is called one’, followed by ‘A number is a multitude composed of units’ (Euclid 1956 II, 277). These units were regarded as being indivisible, thus there could be no fractions. And because a single unit is not a multitude, numbers consist only of the positive integers 2, 3, 4, etc. The unit, 1, was not a number but was said to be the origin or cause of number. Rather than cover rules of calculation, these Greek authors investigated the classification of numbers into even, odd, and their sub-species; prime numbers and divisibility; amicable and perfect numbers; ratio and proportion; figurate numbers; and series summation. Several of these ideas are applicable to practical Arabic arithmetic, such as the sieve of Eratosthenes for determining prime numbers for working with the denominators of fractions.

The transmission of knowledge in medieval Islam was largely conducted orally. Written books were regarded as being transcriptions of lectures, and indeed textbooks were typically recited to students, and books were ‘published’ in public recitations.⁸ Authors wrote out the instructions for making dust-board calculations entirely in words, even spelling out the numbers, since notation serves no purpose to the listener. This was true for algebra as well, so that the polynomials and equations are presented rhetorically in the manuscripts. The Indian figures are shown in arithmetic books as occasional illustrations for what one should write on the board. A few books show some numbers in notation in the running text, but in a way that does not interfere with recitation. Arabic is read right to left, and when these Arabic books were translated into Latin, the figures showing the numerals were not reversed, causing us to read the numbers backwards. In both languages ‘one hundred fifty-four’ is written as 154, with the units on the right. In Arabic, it is the units that are read first. All figures reproduced in this article appear with the same orientation as shown in the manuscripts.

2. Theoretical and practical numbers in premodern arithmetic

The restriction of numbers to positive integers in Euclid and other Greek authors is at odds with the fractions and irrational roots of mental, sexagesimal, and Indian calculation. Although they disagree on the divisibility of the unit, these two ways of understanding numbers share the commitment that numbers must be amounts of something, or, as Ibn Sīnā argues, ‘it is impossible for number to exist except as an accident of something in existence’.⁹ Modern numbers, by contrast, have an existence independent of whatever units they may count or measure. When I teach the course Real Analysis to undergraduate mathematics majors, we work with the axioms for an ordered field. We define a real number to be any element of a set which, together with binary operations that we call addition and multiplication, satisfy those axioms. People without this formal training often think of numbers as points lying on some imagined number line, or they might think of numbers as the values that arise from counting without regard to anything counted. What these modern approaches have in common is that numbers are objects themselves, and because they are objects, each one is unique. There is only one ‘three’, for example.

Such was not the case in premodern mathematics. Whether one works with the discrete numbers of Euclid or the continuous numbers of the Arabic practitioners, numbers necessarily measure or count some divisible or indivisible unit. In Euclid’s number theory, a number is a multitude composed of intelligible, indivisible, and generic ‘units’. As Ian Mueller noted, ‘In Greek arithmetic there are indefinitely many units and indefinitely many ways of combining them into multitudes. Clearly, then, there is no unique 2 or 3; any pair of units is a 2, for example’ (Mueller 1981, 59). From the many examples in our extant Arabic texts, we know that numbers of practical arithmetic are either counted/measured in material units like men, mithqals (a unit of weight), hours, inches (aṣābiʿ), degrees, or dirhams (a silver coin), or they are stated in terms of intelligible, divisible, ‘units’. These units can be measured differently, too. By saying ‘five sevenths’ one is counting in sevenths of a unit, or by saying ‘eight thousands’ one is counting in thousands of units, and these eight thousands can in turn count another unit, like horses. Here, too, numbers are not unique. One can speak of five and a half silver dirhams, five and a half parasangs (a unit of distance), five and a half mithqals of grain from one merchant, the same amount from another merchant, or five and a half (intelligible) units.

We might think that we can gain a better understanding of the nature of the numbers of Arabic practitioners from the definitions given in their books. But the authors of books teaching practical calculation, whether finger-reckoning, sexagesimal, or decimal numerals, presume that students already know what a number is. Most books give no definition at all, including those of Abū l-Wafāʾ, al-Uqlīdisī, Kūshyār ibn Labbān, al-Samawʾal, and Jamshīd al-Kāshī (d. 832/1429)¹⁰ to name only a few, and begin straight away with how to work with them. Others, like al-Nīsābūrī (fourth/tenth c.), and Muḥammad al-Ḥaṣṣār (d. before 590/1194)¹¹ give their books a semblance of theoretical rigour by citing some of the characteristics of Greek numbers: that the unit is the origin of number, that a number is a collection of units, and that numbers begin with two. These characterizations, along with the implied indivisibility of the units, are then disregarded as the authors commence work with whole numbers and their fractions.

There were some authors with philosophical leanings who addressed the numbers of practical arithmetic, however. Taking their cue from the fact that Greek numbers are formed from indivisible units, these authors explain how the numbers of the arithmeticians are produced from divisible units. Kamāl al-Dīn al-Fārisī, a Persian contemporary of Ibn al-Bannāʾ, wrote his Foundation of rules on elements of benefits¹² to provide a foundation in Euclidean-style proofs for the rules of calculation in finger-reckoning. He first explains Euclid’s definition of number and then writes that for ‘the arithmeticians’ (ḥussāb) ‘the number is a quantity you obtain from one by repetition (takrīr) or partition (tajziʾa) or both, and it is clear by this meaning that the type is divided into whole numbers and their fractions’ (al-Fārisī 1994, 71.8). Ibn al-Bannāʾ gives different definitions in two of his books. In his Essays on Arithmetic¹³ he cites the Euclidean definition, but in his Condensed book on calculation he merges the Euclidean and practical definitions into one short statement: ‘A number is a collection of units, and it is divided according to how it is produced into two kinds: whole and fractional’ (Ibn al-Bannāʾ 1969, 39.6). Ibn al-Bannāʾ was well-versed in the works of Ibn Sīnā, and it is from that perspective, later in his 701/1301 commentary Lifting the veil from the face of the operations of arithmetic,¹⁴ that he defended fractional numbers by claiming that Euclid’s definition is not really a definition at all, but merely an expression of ‘what is in the soul’.¹⁵ Other writers, too, engaged in discussions of the nature of this divisible unit (Djebbar 2004, 13ff).

Al-Fārisī’s and Ibn al-Bannāʾ’s definitions of number, like many definitions in premodern arithmetic, were not intended to rigorously and definitively characterize the term. Rather, they served more to give the reader an intuitive sense of what the term intends, which Aristotle called its ‘cause’. This reflects a different understanding of the foundation of a science. Today we define numbers not by what they are but by their operational relations to each other via axioms. Just what kind of thing 17.2 or $\pi$ might be is not even a question we would think to ask. In premodern mathematics, it was up to philosophers to delineate the nature of the being of numbers and other objects like points and lines, from which mathematicians built up their theories. This accounts for why the definitions of al-Fārisī and Ibn al-Bannāʾ are imprecise by modern standards. So to gain a clear understanding of what constituted a number in medieval Arabic arithmetic we must forgo definitions and begin by reading through the arithmetic books to see what amounts were considered to be numbers. Judging by what they worked with in their books, numbers certainly include any positive quantity that can be obtained from a divisible unit through the operations of addition, subtraction, multiplication, division, and root extraction, including square, cube, and higher roots. Whether or not zero should be included will be investigated below, and negative numbers will be addressed when we look into al-Samawʾal’s algebra.

We can also learn a thing or two from some authors who relate these practical numbers to the theoretical numbers of Euclid and Nicomachus. In his Book of instruction in the elements of the art of astrology,¹⁶ which includes a rundown of the basic elements of arithmetic and calculation, the mathematician and astronomer Abū l-Rayḥān al-Bīrūnī (362/973–ca. 442/1050) contrasts the true, indivisible Greek unit with its practical counterpart in a way that agrees with Aristotle’s own distinction between noetic and sensible numbers from Physics 219b.5–9:

Although ‘one’ is in reality indivisible, nevertheless the unit, one by common consensus, employed in dealing with sense-objects, whether by weighing, measuring in bulk, or length or counting, or merely in thought, is obviously capable of sub-division, for by common consensus ‘one’ only means unity.¹⁷

It will be important to keep in mind that although the arithmeticians often worked with sensible units, they also dealt with intelligible divisible units that are apprehended ‘merely in thought’. The relation between practical and theoretical number is described again by the philosopher Abū Naṣr al-Fārābī (first half of the fourth/tenth c.) in the chapter on mathematics in his Enumeration of the Sciences:¹⁸

As for the science of number, there are two sciences known by this name, one of them the practical science of number, and the other the theoretical science of number. The practical investigates numbers insofar as they are the numbers of calculable objects that are needed to register the number of bodies and other [objects], like men or horses or dinars or dirhams or other things that can be numbered, which the public deals with in commercial and civil transactions.¹⁹

Here practical numbers are ‘the numbers of calculable objects’. In both the theoretical and the practical settings, then, a number has two principal aspects: its quantity and its species. For the number ‘five horses’, the quantity is five and the species is horses. The number is composed of horses which are seen from the perspective of ‘quantity’. Thus ‘five hours’, ‘five horses’, ‘five sevenths’, ‘five mithqals of grain’, ‘five degrees’, and ‘five other horses’ are all examples of fives.²⁰

This dual nature of premodern numbers becomes even clearer in remarks made in the arithmetic books themselves. One place where it becomes particularly apparent is in some definitions of division. Ibn al-Hāʾim, in his 1389 CE Guidebook for the science of mental reckoning,²¹ introduces the operation by distinguishing between two kinds of division:²²

Know that there are two kinds of division. In one of them the objective is to know what each one gets. This is dividing a species (jins) by another species, such as if [someone] says: divide ten dirhams by five men.²³ It is required to know how much each one gets. In the second [kind] the objective is the ratio of one of the two quantities to the other. Here you divide a species by the same species, such as if [someone] says, divide ten arādib²⁴ by five arādib. What is intended is to know the ratio of ten arādib to five arādib.

These are the two kinds, and even if [the process of] working them out and the amounts of the quotients are the same, their objectives are different. In the first meaning it is to decompose the dividend into equal parts of equal measure for each unit of the divisor. Can’t you see that the ten in the first example is divided into five equal parts by the amount of the divisor? In the second meaning it is to know what is in the dividend of copies of the divisor. Can’t you see that the outcome of dividing the ten by the five in the second example is two?

There are two kinds of division because numbers consist of a quantity–species pair, and not just a quantity as we regard them today. So the quotient in Ibn al-Hāʾim’s first example is two dirhams, while the quotient in the second example is the two copies of five arādib that are in the ten arādib. Ibn al-Bannāʾ also explains the two kinds of division in his Lifting the veil, where he gives these two examples:

Here is an example of division with the first meaning. Divide fifteen dirhams among three men. We decompose the fifteen into three equal parts, which is how many units are in the divisor. So each part consists of five dirhams, which is how many whole units there are of that three, the divisor.

Here is an example of the second meaning. Divide a piece of wood of fifteen spans by a piece of wood of three spans. The intention here is, how many copies of the divisor are in the dividend? So we cut up the dividend into copies of the divisor. There are five parts in the dividend of copies of the divisor, each part equal to the divisor. (Abdeljaouad and Oaks 2021, 70)

Ibn al-Bannāʾ also distinguished between two kinds of multiplication, again based on whether the species of the two numbers are the same or different. He calls the quantity and species of a number the ‘meaning’ (maʿnan) and the ‘term’ (lafẓ), respectively. For the number ‘three men’, the meaning is ‘three’ and the term is ‘men’ (Abdeljaouad and Oaks 2021, 56, 70). Ibn Ghāzī (841/1437–919/1513) and Sibṭ al-Māridīnī (826/1423–ca. 900/1495)²⁵ are two other authors who make this distinction in their definitions of division.

Because, as Ibn al-Hāʾim observes, ‘[the process of] working them out and the amounts of the quotients are the same’, taking note of this difference is not necessary for explaining how to perform divisions, whether mentally, in sexagesimal notation, or with Indian numerals. Most arithmetic books do not distinguish between the two kinds of division, and indeed they present the mechanics of the processes of operating on the quantities of numbers without regard to their species. When reading Arabic books on Indian calculation, then, it may seem that numbers are by nature independent of any species, but that is only a consequence of their focus on the rules for performing the operations. It is when an author reflects on the meanings of the operations, as Ibn al-Hāʾim did, that we are given some insight into how it is that they conceived of numbers.

Another feature of premodern numbers that will become relevant below is that they were sometimes expressed as sums or differences. Fractions were sometimes spoken this way for convenience, but it was necessary for binomials and apotomes. Where we write $6+\sqrt{28}$, Abū Bakr Muḥammad al-Karajī, writing in the early fifth/eleventh century, has ‘six and a root of twenty-eight’, and our $\sqrt{200}-20$ is al-Khwārazmī’s ‘a root of two hundred less twenty’ (al-Karajī 1964, 42.13; al-Khwārazmī 2009, 139.8). There were no words in Greek, Arabic, Latin, or medieval and Renaissance European vernaculars meaning ‘plus’ and ‘minus’. Those words function like prepositions to indicate the arithmetical operations, while the ‘and’ (wa) and ‘less’ (illā) in the Arabic are common conjunctions. Saying ‘six and a root of twenty-eight’ is like saying ‘three and a fourth’ for our $3{\displaystyle \frac{1}{4}}$. In English we do not make much use of ‘less’ or ‘lacking’, but one example could be: ‘Here is your fifty dollars, less the ten dollars for the cab ride’. The ‘less’ indicates that what follows it is lacking from what precedes it.²⁶

3. Algebraic polynomials as aggregations

Algebra enters into this discussion from several angles, beginning with the way that ‘nothing’ was treated in the algebraic solutions to some problems. To assess what was intended in these solutions, we need to review the nature of the expressions, which derive from the quantity–species nature of numbers.²⁷ As earlier in the algebra of Diophantus and later in medieval and Renaissance European algebra, the powers of the unknown in Arabic algebra constitute different species of number. The first power is called a ‘thing’ or a ‘root’. The second power is called a māl. This word ordinarily means an ‘amount of money’, and it is also found in many arithmetic questions with the meaning of a generic ‘quantity’ (Oaks and Alkhateeb 2005). Which meaning is intended is clear by the context. For the algebraic meaning, I will leave it untranslated, and for the plural, I give it the English suffix ‘s’: māls. The third power is called a ‘cube’, the fourth a ‘māl māl’, the fifth power a ‘māl cube’, etc. The constant term in an expression is based in an intelligible, divisible unit that is counted in ‘units’, ‘number’, or, more often, in (abstract) ‘dirhams’. Often, too, the unit was left off altogether. Thus ‘ten units’, ‘ten in number’, ‘ten dirhams’ and simply ‘ten’ all have the same meaning. In his [Book of] al-Fakhrī on the art of algebra,²⁸ henceforth al-Fakhrī, al-Karajī borrowed the idea of naming the reciprocal powers from Diophantus. He calls the reciprocal of a thing ‘a part of a thing’, the reciprocal of a māl ‘a part of a māl’, etc., and later algebraists adopted the same terms. As al-Khwārazmī indicated (2009, 97), the powers of the unknown behave like the powers of ten, so ‘eight things’ is like ‘eight tens’ (80), ‘five māls’ is like ‘five hundreds’ (500), etc. The powers assume the role of new units of measurement for intelligible, divisible numbers.

Consider this equation that al-Karajī sets up in the solution to a problem in al-Fakhrī: ‘four māls and nine dirhams less twelve things, and that equals nine less a māl’ (Saidan 1986, 234.3). We would write the equation in modern notation as $4x^2+9-12x=9-x^2$, but there are critical differences in the ways the two versions are conceived. Where our polynomials are constructed from the operations of exponentiation, scalar multiplication, addition, and subtraction, the two sides of the Arabic equation express aggregations of the different species with no operations intended. Al-Karajī’s ‘twelve things’ is a single number expressed as a quantity–species pair, in contrast to our $12x$, which is the product of two numbers unattached to any species, one of them known and the other unknown.²⁹ Further, the individual terms are joined with the same ‘and’ and ‘less’ that we saw above for binomials and apotomes. The ‘four māls and nine dirhams’ are spoken like one would say ‘four apples and nine pears’ and describe thirteen items of two different species. These are diminished by the twelve things, much like the deficient fifty dollars that are diminished by ten dollars in the example above. Arabic algebraic expressions are ways of stating unknown, intelligible numbers. In fact, al-Karajī and some other algebraists call monomials ‘simple numbers’ and polynomials ‘composite numbers’ in their rules for multiplying them. So just as one can count or measure hours, sevenths, mithqals, horses, and abstract units, one can also count or measure things, māls, cubes, and the higher powers.

Al-Karajī explains how he thought of expressions of the form ‘A less B’ in the context of a sample multiplication:

Multiply ten less a thing by ten. Then ten by ten is a hundred and less a thing by ten is ten things lacking (nāqiṣ). So the outcome is a hundred dirhams less ten things. Some people believe that this number is composite, because it is of two species (jinsān, the dual of jins). But this is not so, because in saying ‘ten less a thing’ you denote a single number of the rank of units. But if there were in its place ‘ten and a thing’, that would be composite. (al-Karajī MS, fol. 6r.1; Saidan 1986, 105.24)

The number ‘ten less a thing’ is a deficient ten units, with one thing missing from it. Thus it is composed only of units. In particular, the ‘less ten things’ in the calculation is not a negative number. Instead, the ‘less’ indicates that the (positive) amount ‘ten things’ is lacking from the hundred dirhams. This is also why, when simplifying an equation in which one side is of the form ‘A less B’, Arabic algebraists would ‘restore’ (from al-jabr) the A, which makes the deficient ‘A less B’ a complete ‘A’, and then add ‘B’ to the other side to balance the equation (Oaks and Alkhateeb 2007).

This word al-jabr, together with al-muqābala for the ‘confrontation’ of like terms on the two sides of an equation, formed the name given to algebra in medieval Arabic. Al-jabr wa-l-muqābala, literally ‘restoration and confrontation’, was a particular method of numerical problem-solving distinct from other problem-solving methods such as double false position and working backwards. Also, this ‘thing’ is an unknown and not a variable. Algebra was not used to state identities or formulas, or to express physical laws like it is today. Unless preceded by the word ‘modern’, the word ‘algebra’ in this article means algebra as it was understood by the medieval authors.

4. Worked-out problems in practical arithmetic leaving nothing

The problems posed and solved in Arabic arithmetic books are often stated in quotidian terms, such as asking how long it takes for two rivers to fill a reservoir, for the weights of gold and pearl in a piece of jewellery, how long it will take a courier to catch up with another, and how much money each man has who wants to buy a horse. Sometimes, in problems in which a man conducts business, he finds himself left with nothing. Abū Kāmil, an Egyptian author of the late ninth century, solves this problem in his Book on algebra:³⁰

A man has some money (māl).³¹ He does business with it and profits the same amount, and he gives ten dirhams in alms. Then he does business with it and profits the same as what remained, and gives ten dirhams in alms. Then he does business a third time with the remainder. He profits its same and gives ten dirhams in alms, after which he is left with nothing. (Abū Kāmil 2012, 717.12)

The problem is situated in the realm of everyday experience, and it is a common occurrence that people find themselves without any money. There is no need, then, for us to investigate the meaning of this ‘nothing’ (la shayʾ, literally ‘no thing’) from a philosophical perspective, or to identify it with our number zero. Abū Kāmil solves the problem by algebra by first naming the amount of money that the man started with as ‘a thing’ and calculating in turn the algebraic expressions that result from the transactions. At the end of the operations, he equates the final profited amount with the ten dirhams that the man last gave away, thus avoiding an equation with ‘nothing’ on one side. In the translation below, I insert modern algebraic expressions corresponding to those in the text in parentheses, even if the modern versions carry a different meaning:

Its rule is that you make his money a thing ($x$). He does business with it and profits its same, which is a thing, so it becomes two things. He gives ten dirhams in alms, leaving two things less ten dirhams ($2x-10$). Then he does business with it, profiting its same, so it becomes four things less twenty dirhams. He gives ten dirhams in alms, leaving four things less thirty dirhams ($4x-30$). He does business with it, profiting its same, so it becomes: eight things less sixty dirhams equal ten dirhams ($8x-60=10$), since he said, ‘he gives ten dirhams in alms, and he is left with nothing’, so what he had was necessarily ten dirhams. Simplify it, to get that the thing is eight dirhams and a half and a fourth ($8{\displaystyle \frac{3}{4}}$), which is his money.

This problem and most others like it that we encounter in the Arabic books are purely arithmetical problems framed in a real-world setting. More often, though, the quotidian dressing is dispensed with, such as in this problem, also from Abū Kāmil: ‘Ten: you divide it into two parts. You divide each of the parts by the other and you add them, so it gives a root of five dirhams’.³² Here one is asked to find intelligible numbers, where the units are now intelligible and not material dirhams. More common than problems of dividing ten (dirhams) into two parts are problems asking for a quantity (māl) that satisfies some condition, like this one from Ibn al-Yāsamīn’s (d. 601/1204) Grafting of opinions of the work on dust figures:³³ ‘A quantity (māl): you add its third and its fourth and two dirhams to get twice the quantity’.³⁴ This problem is ostensibly stated in terms of an amount of money (māl) that is counted in silver dirhams, but it, too, is a purely arithmetical problem. Many problems terminating in ‘nothing’ are also of this type. Al-Karajī solves the same problem as Abū Kāmil’s translated above but posed in these more abstract terms:

A quantity (māl): you double it and you subtract from it ten dirhams, then you double the outcome and you subtract from it ten dirhams, then you double the outcome and you subtract from it ten dirhams, leaving nothing. (Saidan 1986, 171.20)

His solution, also by algebra, follows Abū Kāmil’s, whose book he knew well.

Other problems resulting in nothing call for adding to the quantity fractions of itself and a dirham or more, then subtracting from the sum fractions of itself and a dirham or more. Ibn al-Hāʾim solves this problem in his Correct guide for the student to the highest aim in calculation, completed in 1381 CE:³⁵

A quantity (māl): adding to it its third and its fourth and a dirham, then subtracting from the sum its third and its fourth³⁶ and a dirham, leaves nothing. How much is it? (Ibn al-Hāʾim 1999, 186.3)

This time the solution is not worked out by algebra, but by a variation on what we call single false position. Ibn al-Hāʾim knows that applying 144 to the operations will result in a whole number, so he makes the calculations, working with the added dirhams separately. He then finds the answer from this guess and its error via a proportion:

The denominator is one hundred forty-four.³⁷ Add to it its third and its fourth and subtract from the outcome, which is two hundred twenty-eight, its third and its fourth, leaving ninety-five, which is the numerator. Then subtract from the added dirham its third and its fourth. The remainder from the subtracted dirham gives: the ratio of the numerator to the denominator is as the ratio of the remainder³⁸ to the unknown. So multiply the denominator by a third and a fourth and denominate³⁹ the outcome, which is eighty-four, from the numerator, to get sixteen parts of nineteen parts of a dirham, and four fifths of a part of it.

This is not an algebraic solution because no unknown is named, and no equation is set up. All calculations are made on known numbers. Of course, no one ever had in actual coins 84 95ths of a dirham, so this problem, too, is abstract. But even so, with the use of the word māl and with units counted in dirhams, the connection with money could not have been far from the thoughts of those working out the problems. The result of the operations stated in the enunciation is still ‘nothing’ in the sense that no amount is left at all. But now it is an intelligible, not a material, amount of dirhams that is reduced to nothing.

I have found in all 37 problems whose enunciations end with nothing—never ‘zero’—among the worked-out problems in 21 books by 19 different authors ranging in time from the late ninth century to the first half of the seventeenth century.⁴⁰ The problems stem from the finger-reckoning tradition, and in fact only six of these books also explain calculation with Indian numerals. Different methods are applied to solve the problems: algebra, single false position, double false position, working backwards, and in one problem Ibn al-Yāsamīn cleverly reasons through the operations of the enunciation to find the answer. Often, too, more than one method is applied to the same problem. Al-Fārisī, for instance, solves one problem three different ways: by algebra, working backwards, and double false position.

In all, 16 of those 37 problems, from the books of eleven authors, receive solutions by algebra, and in four of them the author takes the liberty to set up the equation with ‘nothing’ on one side. Here is problem II.5 from Ibn al-Bannāʾ’s Book on the fundamentals and preliminaries in algebra:⁴¹

A man has some money. He conducts some business from which he gains its same, and he gives a dirham in alms. Then he conducts business with the remainder, gaining its same and giving a dirham in alms. Then he conducts business with the remainder and earns its same and gives a dirham in alms, leaving nothing.

Make what he has a thing. Gaining its same and giving a dirham in alms leaves with him two things less a dirham. Then gaining its same and giving a dirham in alms leaves him with four things less three dirhams. Then gaining its same and giving a dirham in alms leaves him with eight things less seven dirhams, and this equals nothing. You restore and confront,⁴² resulting in eight things equal seven dirhams. The thing, or the money, which is what he had, is seven eighths of a dirham. So know that. (Saidan 1986, 572.1)

Reinterpreting the equation ‘eight things less seven dirhams, and this equals nothing’ in modern notation gives $8x-7=0$. It might be tempting to say that because the ‘nothing’ occupies a place in the equation where a number would ordinarily be, that this ‘nothing’ must be a number. For comparison, consider how we write intervals of real numbers: (0, 1) is the open unit interval, ($-10$, 10) consists of all numbers strictly between $-10$ and 10, etc. But we also write intervals like (0, $\mathrm{\infty }$) and ($-\mathrm{\infty }$, 1), where the signs $\mathrm{\infty }$ and $-\mathrm{\infty }$ occupy a place ordinarily reserved for a number. Of course, infinity is not a real number, but by a convenient abuse of notation it can take the place of a number when writing intervals. Similarly, we should consider that perhaps the ‘nothing’ on one side of the equations in these four problems was not regarded as a number, but conveniently expresses the ‘nothing’ that is left when an equal is removed from an equal. The prospect of writing such an equation must have made some algebraists feel uneasy, since most authors avoid it. Both the ‘nothing’ in Arabic and the ‘infinity’ in modern mathematics lie at a boundary of what was/is considered to be a number.

This nothing in an equation is shown in notation in one book. Ibn al-Qunfūdh (740/1339–810/1407) wrote a commentary on Ibn al-Bannāʾ’s Condensed book titled Removing the veil from the faces of arithmetical operations,⁴³ which he completed in 1370 CE. In it he solves many problems, among them the same problem just translated from Ibn al-Bannāʾ’s algebra book, with only some minor differences in wording. Unlike the other books that give algebraic solutions to problems that result in nothing, this one shows the algebraic notation that was practiced in the Western part of the Islamic world, beginning no later than the end of the sixth/twelfth century.⁴⁴ This is a notation that was written on the dust-board, and which was rendered into rhetorical form in the writing of books. We are fortunate that Ibn al-Qunfūdh took the pedagogical approach of showing what the student should write on the board at different stages of the solutions to problems.

In this notation, the quantity for each power is shown in Indian numerals underneath the first letter of the name of the power, a shīn (ش ) for shayʾ (‘thing’), a mīm (م ) for māl, etc. For ‘=’ the notation shows the letter lām (ل ), the last letter in taʿdil (‘equals’). In this problem Ibn al-Qunfūdh shows the notational version of the equation that he writes in the text as ‘eight things less seven equal nothing’ (Ibn al-Qunfūdh MS, 304.18). We reproduce it below in Figure 1 with some of the surrounding text together with a modern transcription. Here only the three dots of the letter shīn are shown.

Figure 1. A notational equation with zero from Ibn al-Qunfūdh.

Reading the middle line of the image beginning on the right, you see the ‘8’ with the three dots above it. To its left is the word illā (‘less’), which I write in the transcription as ‘$\ell$’ for ‘less’. Next there is a ‘7’, a large lām (ل ) for ‘=’, and ‘nothing’ is shown as a small circle, which is the Arabic zero. Ibn al-Qunfūdh needed a way to represent the ‘nothing’ that remains after subtracting the last dirham, and which we read in the rhetorical version of the equation. Since the notation employs Indian numerals, he chose to show this ‘nothing’ as a zero. Just what is meant by this zero will come into better focus in the next section, where we finally look into how zero was described and applied by various Arabic authors in Indian calculation.

5. Writing numbers with zeros in Indian arithmetic

I checked thirty-five books by thirty-two different authors that explain calculation with Indian numerals.⁴⁵ One of them is the Latin redaction of al-Khwārazmī’s book and the rest are in the original Arabic. They range in date across a span of nine centuries, from the first half of the third/ninth to the first half of the twelfth/eighteenth century, and in place from Morocco to central Asia. Some of them were written by prominent mathematicians and scientists such as al-Samawʾal, Naṣīr al-Dīn al-Ṭūsī, and Jamshīd al-Kāshī, while others were written by lesser known individuals. For the writing of the numerals, Ibn al-Bannāʾ’s Condensed book is an outlier. It is truly rhetorical in that it does not show the numerals at all, and no examples are given to illustrate the rules. All of the other 34 books begin by showing the nine figures for 1 through 9 and introduce the zero only later. The forms of the numerals vary across time and place and fall into two basic types. A manuscript of al-Nīsābūrī’s Attainment of students on truths in the science of calculation,⁴⁶ copied 843H/1443 CE, shows the eastern forms as , while a manuscript of Ibn al-Qunfūdh’s Removing the veil from the faces of arithmetical operations, copied in the fifteenth or sixteenth century CE, probably in Morocco, presents the western forms as ,⁴⁷ and both authors show several variations. The modern Arabic forms derive from the eastern versions, and the modern European forms derive from the western versions. In the translations below I write 1, 2, 3, etc., for whatever form an author used.

Here are some examples of the ways that zero is introduced in these books. The Latin redaction of al-Khwārazmī’s book begins by showing the nine numerals and explaining some variations. It is only later, as part of the description of the place value system, that the zero is brought up in the context of how to write the number ten using the numeral ‘1’:

So they put one space in front of it and put in it a little circle like the letter o, so that by means of this they might know that the place of the units was empty and that no number was in it beyond the little circle, which we have said occupied it … ⁴⁸

The earliest book on Indian calculation extant in Arabic is al-Uqlīdisī’s Chapters on Indian reckoning. He begins the first chapter with: ‘The beginner in this science should be first taught the nine letters. These are 1 2 3 4 5 6 7 8 9’. Then, after describing the place-value system along with several examples, he explains the zero:

Then he is informed that some of these places may be empty, with none of the nine letters falling in it. If this is the case, a circle is set in the empty place. This is what the people of this craft call a zero.⁴⁹

Later in the same century, ca. 367/977, the lexicographer Muḥammad ibn Aḥmad al-Khwārazmī wrote a guide for government secretaries in which he explained the zero in the brief section on calculation: ‘And these small circles, called zeros, are placed to keep the ranks in the places where there are no numbers’ (al-Khwārazmī 1895, 194.7). Around the same time, al-Nīsābūrī shows the forms of the nine numerals, covers the place-value system, and works through the operations of doubling and halving before he explains that in each rank, ‘if there is no number in it, place there a zero, which is a small circle’ (al-Nīsābūrī MS, 16.6).

Similarly, in the latter sixth/twelfth century in western North Africa, al-Ḥaṣṣār shows the nine figures and then explains zero in his instruction on how to write the number ten in his Book of demonstration and recollection in the art of dust-board calculation:⁵⁰

One needs to put something in the units rank to establish the rank, so that one will know that the units rank has nothing in it. Thus, the arithmeticians (ahl al-ḥisāb) put a zero in it, in the form of a small circle. (al-Ḥaṣṣār MS, fol. 5r)

A few decades later, at the other end of the Muslim world, the famous Persian astronomer, philosopher, and theologian Naṣīr al-Dīn al-Ṭūsī (597/1201–672/1274) wrote a textbook on Indian calculation titled Gathering of arithmetic by means of board and dust.⁵¹ About a page after showing the forms of the numerals, he writes: ‘and you put a zero, in the form of a small circle, in every rank devoid of a number’ (Saidan 1967, 115.1). Still later, in 830/1427, the Persian astronomer and mathematician Jamshīd al-Kāshī wrote in his Key to calculation⁵² after showing the nine figures: ‘A zero, in the form of a small circle, must be placed in every rank where there is no number, to avoid a gap in the ranks’.⁵³

And then there is an anonymous, untitled guide for government secretaries copied in 979/1571–72, which was put together from selections of the works of various authors. In the brief description of Indian calculation, we read: ‘And if you want a ten, you put it like this: 10. Since the units rank has no number in it, you put a zero in it to keep the place for you, and it will be clear to you that it is not a number’ (Anonymous MS, fol. 18r.1). Our last example is from Nūr al-Dīn al-Anṣārī’s Achievements of the giver in the pleasure of the arithmeticians,⁵⁴ completed in 1039/1629–30. Three pages after showing the nine figures he writes: ‘And the zero, spelled with an “ṣ”,⁵⁵ is a sign for an empty place, and this is its figure: o’ (al-Anṣārī MS, fol. 47r.24).

None of the thirty-five books diverge from the view that the zero is a sign for an empty place where there is no number. Thirty books assert this explicitly, three more were written by people who authored another text in which they made the assertion, and the remaining two, by al-Sakhāwī and al-ʿĀmilī, treat the writing of the numbers very concisely and left it to their commentators to explain the meaning of zero.⁵⁶

At this point, I should clarify what is intended by the word ‘zero’. The Arabic word for zero is ṣifr, which ordinarily means ‘empty, void, or vacant’ (Lane 1893, 1697). The sign for zero is described and shown in the manuscripts as a small circle, and as the texts repeat, it is a sign for an empty place. There are three parts to this relation that are better understood by comparison with an example from Greek arithmetic. Numbers in Greek were written using letters of the alphabet, beginning with ‘A’ for 1, ‘B’ for 2, and so on. So the Greek word beta is the name of the sign ‘B’, which means ‘two’. Similarly, the Arabic word ṣifr is the name of the sign ‘o’ which means ‘vacant’ or ‘empty’. Here the ṣifr is a technical term: the ‘o’ was never called by other words that mean ‘nothing’, ‘vacant’, or ‘empty’, like la shayʾ, khalāʾ, or ʿadam. When I write ‘zero’ I mean the name of the sign ‘o’ that is used in Arabic books on Indian arithmetic. So far, taking our authors at face value, the zero is a sign designating a place where there is no number. It is thus not a sign for a number, and the ‘nothing’ that resides in a place labelled with a zero should not be thought of as a number, either.

This practice of putting a special sign where there is no number is much like the modern practice of putting a dash (–) or an asterisk (*) or some other sign in a table where there is no data. Because we are accustomed to read 0 as a number, it might be helpful to replace it in the examples below with a different special sign, like •, at least for a while, to clear our heads of our modern reading. This way, for example, three thousand fifty-four looks like 3•54. The • indicates that there is no number in the hundreds place.

6. Operating on numbers with zeros in Indian arithmetic

The rules for operating on numbers expressed in Indian notation call for the addition, subtraction, multiplication, doubling, and halving of the individual places, and often one or both of these places is occupied by a zero. There were different approaches to working out operations involving a zero. Most authors took the view that because there is no number in that place, there is no operation to perform. A few others perform the operation with zero, and those who explain it either relate that this is done just to ‘keep the place’ or they say what it means to operate on ‘nothing’.

Below we cover in order addition, subtraction, multiplication, and halving. Like most Arabic rules for operating on the numerals, those described below were intended for the dust-board since they call for the erasing and rewriting of digits as the calculation progresses. In some rules, one of the two numbers is transformed, one digit at a time, into the answer, while in others, the answer is written on a separate line.

Ibn al-Yāsamīn writes in his explanation of addition with Indian numerals: ‘Then you add each digit of one of the addends to its counterpart in the other. If there is no counterpart, then the answer is the addend, as if it had a counterpart’ (Zemouli 1993, 131.11). By this rule, no addition is performed, but an answer is obtained anyway. We do this ourselves when we add, say, 351 and 18. There is nothing in the hundreds place of the second number, so the hundreds place of the sum is the 3 from 351. Al-Hawārī gives an example in his Essential commentary on the condensed [book] on the operations of arithmetic.⁵⁷ He begins the problem of adding 4•43 to 2685 by arranging the numbers one above the other like this: $\begin{array}{c}4\bullet 43\\ 2685\end{array}$. He begins the work from the units place, and after the tens place is finished and the 6 has been replaced with a 7 from carrying a 1, he writes: ‘Nothing in the upper line corresponds to the seven, so it is considered to be the sum of that rank and that of its counterpart as if it had something’ (Abdeljaouad and Oaks 2021, 45).

Most other authors similarly do not mention the operation of addition when there is a zero, like al-Baghdādī (d. 429/1037), who gives this instruction in his Completion of calculation⁵⁸ for a rule in which the top number will be replaced with the answer: ‘and if above the place of the added number there is a zero, then put the added number in place of the zero’ (al-Baghdādī 1985, 36.17). This is how al-Ḥaṣṣār adds 65•3 to 7•2•, in which the answer will be written on a separate line above. For the units, tens, and hundreds, he makes no mention of addition but simply puts the 3, 2, and 5 above the numbers, and then writes, ‘Then add the thousands, and that is seven and six, to get thirteen’ (al-Ḥaṣṣār MS, fol. 9r.10), which he then also puts above.

In rules for which the digits of one of the two numbers are replaced by digits of the answer, the zero is treated differently depending which row it is in. Al-Uqlīdisī performs this addition, $\begin{array}{c}27\bullet 36\\ 26\bullet 7\end{array}$, starting from the left in a scheme that calls for the replacement the upper digits with the digits of the sum. He writes: ‘Now we add the two to the seven, put the six in place of the zero, and add seven to the six. This becomes 29643’.⁵⁹ Here the 6 is not added to the zero, but replaces it, and the tens place is ignored altogether. The final figure would look like this: $\begin{array}{c}29643\\ 26\bullet 7\end{array}$. Al-Samawʾal works the operation similarly in his Book on insight in the science of calculation.⁶⁰ He arranges the numbers in his example one above the other like this: $\begin{array}{c}138\bullet 5\\ 17573\bullet \end{array}$, again adding the digits starting on the left, but this time replacing the lower digits with the sum. After adding the ten thousands, the thousands, and the hundreds, the figure becomes $\begin{array}{c}138\bullet 5\\ 18953\bullet \end{array}$. He does not mention the tens place at all and next writes: ‘Then add the upper five to what is below it, which is a zero, to get five’ (al-Samawʾal MS A, fol. 4v.7), which makes the final figure $\begin{array}{c}138\bullet 5\\ 189535\end{array}$, and the answer is the bottom line. He differs from the others in saying that he actually adds to the zero, but the fact that he omits any mention of adding zero to three in the tens place speaks for the same view of the operations as in al-Uqlīdisī and the others.

Al-Qalaṣādī states the rule in a way consistent with the rules and examples above. For each place, ‘if there is in one of them a zero and in the other a number, then the number which is in one of them is the answer. And if [instead] there is a zero there, then one of the two zeros is the answer’ (al-Qalaṣādī 1999, 45.13). But then, in his example of adding $\begin{array}{c}5\bullet 23\\ 25\bullet 2\end{array}$ he explicitly adds zero, without explaining what it means. Working from right to left, the answer will be written on a separate line above them. He writes: ‘Add the two to the three giving five. Put it in the units rank. Then add the zero to the two, giving two, which is the answer. Then add the five to the zero, giving five. Put it above that place … ’ (al-Qalaṣādī 1999, 46.2).

Addition was of course performed place by place outside the context of Indian calculation, too. The process is so simple that it is not explained in books on finger-reckoning. To add three hundred seven to fifty-two, for example, one easily arrives at the answer three hundred fifty-nine. The tens place of the answer retains the five of the ‘fifty-two’, since there is nothing in the tens rank of ‘three hundred seven’ to add to it. Seen this way, Ibn al-Yāsamīn’s rule that ‘If there is no counterpart, then the answer is the addend, as if it had a counterpart’ is intuitively clear. The rule does not require any actual addition with zero, and it certainly does not imply a shift to a formal way of reading the operation. And then, rarely an author like al-Qalaṣādī will state the operation anyway. It is plausible that he understood the addition of $\bullet$ to 2 like the addition of nothing to a purse containing two dirhams, which leaves its contents unchanged, or that the addition of 3 to $\bullet$ is like the addition of three dirhams to an empty purse, resulting in a purse with three dirhams.

Among the books I consulted, the subtraction of zero is routinely skipped. I found only one instance where the operation is explicitly performed, in al-Hawārī’s Essential commentary. He begins the subtraction of 4968 from 5•53 by stacking them as $\begin{array}{c}5\bullet 53\\ 4968\end{array}$, and the work begins with the thousands place: ‘We subtract the four which is in the thousands rank from its counterpart in the minuend, which is five. The remainder is one, so we put it above it’. The figure then becomes: $\begin{array}{c}1\\ 5\bullet 53\\ 4968\end{array}$. He continues:

Then we likewise subtract the nine that is in the hundreds rank from its counterpart. There is nothing but a zero there, and the zero is nothing. So we subtract this nothing of the minuend from the nine of the subtrahend, leaving nine. We subtract it from the one that is above the five, since it is ten with respect to the zero, as mentioned. This leaves one. We put it above the zero, and nothing is above the five. (Abdeljaouad and Oaks 2021, 50)

Now the figure becomes $\begin{array}{c}\bullet 1\\ 5\bullet 53\\ 4968\end{array}$, and he then proceeds with the tens and units places. Subtracting nothing means that nothing is taken away, so the nine remains unchanged. When a number is subtracted from its equal, we sometimes read, as in al-Qalaṣādī, ‘Then subtract the two from the two, which leaves nothing. Put a zero above the two subtrahends’ (al-Qalaṣādī 1988, 37).

Multiplication is more interesting. Most authors state the Euclidean definition in the beginnings of their chapters on multiplication, like Ibn al-Yāsamīn, who opens with: ‘Know that multiplying numbers, one of them by the other, is that you duplicate one of the numbers by the quantity of what is in the other number in units’.⁶¹ The most common dust-board technique of multiplying numbers in medieval Arabic books calls for shifting and erasing, which I explain now so that the quotations given below will make sense. Here is an example taken from al-Uqlīdisī (1978, 50) for multiplying 34 by 26. First, write the numbers with the units place of the multiplier under the highest place of the multiplicand, like this: $\begin{array}{c}34\\ 26\end{array}$. Then multiply the 3 by the 2 and put the 6 above the 2: $\begin{array}{c}634\\ 26\end{array}$. Then multiply the 3 by the 6 in the lower line and replace the 3 as you add the resulting 18 to the 6• above it: $\begin{array}{c}784\\ 26\end{array}$. Next, shift the 26 to the right one place: $\begin{array}{c}784\\ 26\end{array}$. Then multiply the 4 by the 2 and add the 8 to the 78 above the 2: $\begin{array}{c}864\\ 26\end{array}$. Last, multiply the 4 by the 6, and replace the 4 with the resulting 24, to get $\begin{array}{c}884\\ 26\end{array}$. The answer is 884.

As with addition and subtraction, many authors do not perform multiplication by zero. Naṣīr al-Dīn al-Ṭūsī writes this in his verbal explanation of the method just described:

And if there is a zero in the rank of the multiplicand, we do not need to shift to it, so we shift to what is on its right and calculate the remaining ranks. And if there is a zero in the rank of the multiplier, there is no need to multiply by it. (Saidan 1967, 122.18)

Then, in his first example, he multiplies 2•76 by 5•3, and after multiplying the 2 by the 5, writes: ‘and it is not necessary to multiply the two by the zero, so we place a zero above it’ (Saidan 1967, 123.2). He may not have performed the operation, but he nevertheless put a zero where it should be.

If we read these rules in light of the standard finger-reckoning rule for multiplying numbers with more than one rank, this practice of not performing multiplications with zero makes sense. Al-Karajī states this rule as: ‘you multiply each of the numbers [i.e., ranks] of the multiplicand by all numbers of the multiplier’ (al-Karajī 1986, 39.9). To multiply three hundred five by twenty-four, for example, only four products are necessary because there is literally nothing in the tens rank of the first number. Thus the zeros that are encountered in Indian notation can be disregarded since they designate places where there is no number.

Al-Uqlīdisī and Isḥāq Ibn-Yūsuf al-Ṣardafī omit multiplication by zero in some calculations and perform it in others. In his Condensed Indian [book] on the science of arithmetic⁶² al-Ṣardafī (d. ca. 500/1106) multiplies 2•2•2 by 22 by multiplying only the 2s in one number by the 2s in the other, but later, on the same page, he begins the multiplication of 2••••2 by 2•3••3 with: ‘Multiply two by two to get four. Then multiply the zero by the two to get zero, and put it above the zero … ’ (al-Ṣardafī MS, fol. 6v.27). Here, the reason for the difference may be that in the first problem, the answer 444444 has a number in each place, so there was no need to multiply by zero, but in the second problem if the zero is not placed next to the first calculated 4, and for other places as well, the answer 4•6•1••6••6 would have gaps in the ranks. This is what al-Uqlīdisī is referring to in his explanation of multiplication with zero:

If it is said: Why is zero by zero equal to zero and zero by any letter zero? We say that by multiplying zero by zero the aim is only to occupy the place; the same applies for multiplying the letter by zero. We multiply the letter by zero only once, the first time, by the first letter in the upper, to occupy the place, and tell that there is a place and that it is empty.⁶³

Four authors take the trouble to briefly explain, some better than others, what it means to multiply by zero. Al-Khwārazmī writes that ‘every circle [i.e., zero] that is multiplied by some number is nothing, that is to say, no number arises from it and whatever is multiplied by a circle is likewise nothing’.⁶⁴ Al-Nīsābūrī relates that the multiplication of one by zero is zero ‘because the zero, rather, takes the place of a number and there is no number in it. So if we multiply something by nothing, it gives nothing. So multiplying one by zero gives zero’ (al-Nīsābūrī MS, 33.7). The clearest accounts of multiplication by zero are given by two scholars from Marrakesh, Ibn Munʿim (d. 626/1228) and Ibn al-Bannāʾ, who both relate it to the duplication definition of multiplication. Ibn Munʿim explains it this way in his Understanding calculation,⁶⁵ written sometime 596/1199–610/1213: ‘And know that anything multiplied by zero is zero, since the zero is a sign for nothing (ʿadam), and nothing is gathered from duplicating it’ (Ibn Munʿim 2005, 33.21). Ibn al-Bannāʾ covered it even better close to a century later in his Lifting the veil: ‘Multiplying a number by a zero or a zero by a number is that you zero the number or you duplicate the zero, and neither of them gives a number. So its sign is always a zero’. Note the use of the related verb ‘to zero’, which can also be translated as ‘to empty’ or ‘to void’.

Other authors simply state that the product is zero, without any explanation. Al-Baghdādī writes in one calculation: ‘then we also multiply the five by the zero which is in the lower number to get zero, so we put a zero above the zero’ (al-Baghdādī 1985, 52.15), and al-Kāshī explains while working out one product, ‘ … since multiplying the zero by whatever number gives a zero’ (al-Kāshī 1969, 52.13, 2019, 48.18).

Zero makes its appearance also in doubling and halving, and the explanations there are similar. While taking half of a particular number, al-Kāshī writes ‘Since there is no half for zero, we put a zero underneath it’.⁶⁶

Taking into consideration the wording in all of the operations performed in these books, the authors do not waver from the position that zero means ‘nothing’ and that it is not a number. The fact that sometimes the operation with zero is omitted while in others it is performed are not signs of a difference in how the zero was conceived. If it seems irreconcilable that zero can mean ‘nothing’ and still be operated on, it may be because we are still thinking in terms of modern mathematics. Today mathematicians define numbers to be elements of a set on which binary operations we call addition and multiplication are defined. The operations exist only in the context of that set, so adding $a$ to $b$ only makes sense if both $a$ and $b$ are numbers. But premodern arithmetic has no foundation in axioms. Numbers consist of a quantity–species pair, like the material three mithqals of grain and nine apples, or the intelligible three and a third dirhams. Addition is simply the gathering together of two amounts, which is why even Euclid saw no reason to define it. To add three apples to five apples means simply to group them together into a collection of eight apples. Similarly, for subtraction, where one amount is removed from another. When the species are different, the conjunctions ‘and’ and ‘less’ are used. Adding three chickens to two starlings results in three chickens and two starlings, or in algebra, Sibṭ al-Māridīnī (826/1423–912/1506) writes: ‘if you add two dirhams to three things, the answer is two dirhams and three things’ (Sibṭ al-Māridīnī 1983, 59.8). Taking a bite from an apple leaves an apple less a bite, or, as al-Karajī writes after naming one amount ‘a māl’, ‘subtract ten dirhams from it, leaving a māl less ten dirhams’ (Saidan 1986, 194.18). The meaning of multiplication is less immediate, so Euclid gives a definition in this case. But even there the operation only consists of a repeated duplication. Abū l-Wafāʾ explains it in terms of an example: ‘And for example nine, if we want to multiply it by seven, we duplicate the nine seven times to get sixty-three, or we duplicate the seven nine times to again get sixty-three’ (Saidan 1971, 124.20). Multiplication is governed not by axioms, but by the intuitive notion of accumulating together copies of a number.

Adding, subtracting, and multiplying ‘nothing’ make sense with this material way of conceiving the operations. It is commonplace in the physical world to add nothing to something or to take away nothing from something, and duplicating nothing makes sense as well. And just as calculation with intelligible numbers remained somehow connected to the world of finance through repeated use of māl for ‘quantity’ and dirhams for units, the way people conceived of operations on these numbers would have likewise remained conceptually like the operations in the material world. So it is no contradiction for an Arabic arithmetician to regard zero as signifying nothing and at the same time to operate on it. There is no evidence in any of these texts on Indian calculation, even those by prominent mathematicians, that an author thought of zero as anything other than a sign for a place devoid of a number.

At this point, we can say a little more about how to read the zero in the notational version of Ibn al-Qunfūdh’s algebraic equation shown above in Figure 1. There the zero is not a sign for an empty place. It designates the ‘nothing’ that the businessman was left with as well as the same ‘nothing’ stated in the rhetorical version of the equation. This is a different use of the zero, one that reflects the meaning of the word ṣifr, and which, at the same time, is consistent with the meaning of the sign in Indian arithmetic. The algebraic notation uses Indian numerals for the quantities of the powers, and rather than write the words ‘no thing’, Ibn al-Qunfūdh, and probably many others whose dust-board calculations are irretrievably lost, chose to borrow the zero for this purpose. This innovation might have had the potential to lead to a more formal view of zero. But with the majority of algebraists avoiding equations with ‘nothing’ and with only this one notational example, we have no evidence that this happened.

7. The zero in Arabic sexagesimal arithmetic

It should not be a surprise that the zero in base sixty is described in Arabic texts in the same way as the zero in base ten. In most books, jummal figures were used for the sexagesimal places 1 to 59, though it is not uncommon to find Indian numerals instead. When jummal figures are used, the zero takes the form of a circle with a bar that was borrowed from the Greek: ō. The bar is important because without it, the sign could be read as the letter ha, which signifies the number 5. In texts that show Indian numerals, the zero is the usual small circle, and two digits are usually shown for each place even if the entry is less than ten. To perform calculations, the places are arranged vertically on the dust-board. For example, Naṣīr al-Dīn al-Ṭūsī sets up the subtraction of ‘three signs, eleven degrees, twenty-five minutes, and fifty seconds from two signs, eight degrees, and ten seconds’ using Indian notation on the dust-board as:⁶⁷ $\begin{array}{cc}02& 03\\ 08& 11\\ 00& 25\\ 10& 50\end{array}$

Here are some passages that explain zero in sexagesimal arithmetic. For calculation using jummal numerals, al-Bīrūnī explains: ‘When zero has to be written in places lacking a number, its circle must have a line over it … ’.⁶⁸ For calculation in which the places are written in Indian notation, al-Uqlīdisī writes in the context of addition: ‘if a place is empty, having nothing, we put two zeros in it to indicate that there is nothing in it’, and for subtraction he writes: ‘whenever a place becomes empty, we insert a zero in it’.⁶⁹ Al-Baghdādī writes in one subtraction problem: ‘Then we subtract the two degrees from the two degrees, and we put in place of the two degrees two zeros, so there is nothing in its place’ (al-Baghdādī 1985, 148.6). And al-Kāshī gives this instruction for writing the numbers in jummal notation: ‘At each position where there is no number, a zero is put to clarify any confusion’.⁷⁰

Three tables in Ptolemy’s Almagest (Greek, 2nd c. CE) are of particular interest because some entries are zero. Two medieval Arabic translations of this book are extant. One is the version of al-Ḥajjāj ibn Yūsuf ibn Maṭar (d. ca. 220/835), completed in 212/827–28, and the other is the revision by Thābit ibn Qurra (d. 288/901) of the translation made in the period 265/878-278-891 by Isḥāq ibn Ḥunayn (d. 298/910–11).

Ptolemy covers solar and lunar eclipses in Chapter 7 of Book VI, where he and the Arabic translators each give two tables: one for solar eclipses and one for lunar eclipses (Ptolemy 1998, 306–307). Each table is divided into two sub-tables, one for the moon at the greatest distance from the earth, and the other for the moon at least distance. Let us consider the case of a solar eclipse, partial or total, at the greatest distance, when the discs of the sun and the moon are the same apparent size. The lunar disc will pass in front of a certain portion of the solar disc, and Ptolemy measures this ‘magnitude of the obscuration’ in a linear fashion, in twelfths of the diameter of the solar disc. So for the ‘digit’ 6, for example, the moon sweeps across exactly half of the solar disc, and a ‘12’ corresponds to a total eclipse. These digits are entered in the third column of the table, which begin and end with 0, as he explains (here translated from the Greek): ‘The third column will contain the magnitude of the obscuration. On the two lines at top and bottom we put the 0 0 representing the touching positions, on the two lines next to those (i.e., in the second and penultimate lines) 1 digit, and so forth for the rest’.⁷¹ Here the ‘0’ is the Greek sign ‘ō’, familiar as the sexagesimal placeholder. Indeed, the column labelled ‘digits’ in the table shows a ‘0’ in the first line, a ‘1’ (‘A’, the Greek alphabetic numeral) in the second line, up to ‘12’ (‘IB’) in the thirteenth line, then descending back down to ‘0’ in the last line (Ptolemy 1898, 519). For these first and last lines, no eclipse takes place because the disc of the moon only comes to ‘touch’ the disc of the sun in one instant. Ptolemy’s fourth column shows the ‘minutes of immersion’, which is the angular distance in minutes travelled by the moon relative to the sun from the moment of tangency to the peak of the eclipse. For the first and last lines, then, the table shows ‘0 0’ (0 minutes, 0 seconds) in this column.

All four sub-tables are constructed in this same way. In all of them the first and last lines show a 0 in the third column and 0 0 in the fourth column. Al-Ḥajjāj translated Ptolemy’s instruction to put zeros in the first and last lines of the third column literally, which we translate as: ‘in the ends (i.e. top and bottom lines) we put the touching position as zero zero’ (Ptolemy (web A), f. 95v.21). But in the Isḥāq-Thābit translation, the passage reads: ‘we made the two lines at the two ends for the touching position, so we do not put a number in them’ (Ptolemy (web B), fol. 99v.1).⁷² For Thābit, these zeros in the tables are not numbers. They are signs indicating the absence of a number, like the dash or asterisk that we sometimes put in tables today in places where there are no numbers. Here the zero is not a placeholder in the sexagesimal representation of a number but plays an analogous role in the construction of the tables.

The third table with a zero entry is the table of stations in Book XII.8 (Ptolemy 1998, 588). I have found no instances in sexagesimal calculations or in astronomical tables in which zero was treated differently than it is in base ten calculations.

8. Nothing, zero, and lacking amounts in al-Samawʾal’s algebra

We might have suspected that some authors, through repeated calculations with Indian numerals in one problem after another, could have come to take a more formal view of the operations on individual places, so that the signs, including the zero, would be manipulated without an immediate regard to their meanings. This may have occurred to some extent in some people, but with the majority of authors not performing operations on zero at all, and with others taking the trouble to explain the meaning, such a perspective seems to have remained in the backs of the minds of anyone who might have adopted it. But there is one setting in which the development of such a formal perspective might seem more likely: in al-Karajī’s and especially al-Samawʾal’s rules for calculating with polynomials.

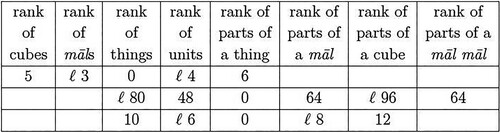
Because the powers of the unknown in algebra behave like the powers of ten in arithmetic, al-Karajī saw that he could adapt the rules for operating on numbers in Indian notation to polynomials that have no lacking terms (we would say ‘subtracted terms’). In the mid-sixth/twelfth century, al-Samawʾal studied these operations as described in al-Karajī’s Marvelous [Book] on calculation,⁷³ and he devised a way to make them work for polynomials in general. He shows tables for dividing and taking the square roots of polynomials by these rules in Dazzling [book] on the science of calculation.⁷⁴ In these tables, the names of the ranks are written above the columns of the respective quantities. For example, to take the square root of the expression that we write as $25x^6-30x^5+9x^4-40x^3+84x^2-116x+64-48{\displaystyle \frac{1}{x}+100{\displaystyle \frac{1}{x^2}-96{\displaystyle \frac{1}{x^3}+64{\displaystyle \frac{1}{x^4}}}}}$, he sets up the table in Figure 2.⁷⁵

Figure 2. Taking the square root of a polynomial in al-Samawʾal.

Then, working through the operations, the last table shown in the manuscript translates as in Figure 3.⁷⁶

Figure 3. The same table at a later stage of the solution.

The answer will be in the top row, and so far, it is the expression that we write as $5x^3-3x^2-4+6{\displaystyle \frac{1}{x}}$. All that needs to be done is to calculate the last term, which he finds to be a lacking $8{\displaystyle \frac{1}{x^2}}$. Just as 2, 6, 0, and 7 are the entries of different ranks in the representation of the number 2607, the 5, $\ell$ 3, 0, $\ell$ 4, 6, and $\ell$ 8 are the entries in the representation of the (algebraic) number ‘five cubes and six parts of a thing less three māls and 4 units and eight parts of a māl’ (Rashed 2021, 62.1).

Of the ten possible entries for the places of numbers written in Indian notation, all are valid as quantities of numbers except the zero, whose meaning as a sign for an empty place is repeatedly explained in the arithmetic books. But in al-Samawʾal’s tables, the entries can be any (positive) quantity, zero, and any quantity preceded by ‘less’, like ‘$\ell 3$’ and ‘$\ell 80$’ for ‘less three māls’ and ‘less eighty things’ in the first row of the table above. Because the rules call for operations on the entries and these entries can be appended (zāʾid), lacking (nāqiṣ), or zero, al-Samawʾal summarizes the rules for operating on them. These are remarkably close to our rules for operating on positive numbers, negative numbers, and zero:

The principle for taking the roots of quantities which have an exclusion [i.e. a lacking term] are: the product of the lacking (nāqiṣ) by the appended (zāʾid) is lacking, and by the lacking is appended; and if we subtract an appended number from a lacking number, it leaves the sum of the numbers lacking; and if we subtract a lacking number from a lacking number greater than it, it leaves their difference lacking; and if the lacking is less than the decreased [number], it leaves their difference appended; and if we subtract the lacking from the appended, it leaves their sum appended; and if we subtract an appended from an empty rank, it leaves in it that same number lacking; and if we subtract the lacking from an empty rank, it leaves in it that number appended. (Rashed 2021, 62.3)

Note that in these rules al-Samawʾal does not refer to ‘zero’, but to ‘an empty (khāliya) rank’. The zero in the rank of things in the table above indicates that there is no first-degree term, just as the zero indicates an empty place in the writing of a number. The one place in this book where zero appears in an operation occurs in the calculation of this square root. He writes ‘Then we search for that which, if we multiply it by the ten, gives nothing. We find it is zero, so we place it before the three … ’ (Rashed 2021, 60.4). This operation is in agreement with the multiplications involving zero quoted above for calculation with Indian numerals. In fact, al-Samawʾal introduces zero in his book on Indian calculation with: ‘[what] you write in an empty rank to take the place of its emptiness is called a zero, and it is this: o’ (al-Samawʾal MS A, fol. 3v.14).

For the ‘less 3’ in the rank of māls, the 3 is a positive quantity of māls and the ‘less’ indicates that that term will be lacking in the final answer. It is not necessary to think in terms of negative numbers to know that a lacking term multiplied by another lacking term is appended. Already in the first part of the third/ninth century al-Khwārazmī gave the example of multiplying ‘ten less a thing by ten less a thing’, in which he wrote ‘ … and less a thing by less a thing is an appended māl’ (al-Khwārazmī 2009, 125.17). The general rule was then stated by ʿAlī al-Sulamī in a tenth-century practical algebra book devoid of proofs:⁷⁷ ‘Know that the appended by the appended is appended, and the appended by the lacking is lacking, and the lacking by the lacking is appended’ (ʿAlī al-Sulamī MS, fol. 23v.8). And in arithmetic it was known that subtracting a lacking term is the same as adding it, as Ibn al-Bannāʾ noted when he wrote that ‘when subtracting the lacking from another lacking, it is appended’ in the context of evaluating $10\ell (8\ell (7\ell (5\ell 2)))$. Here the lacking 7 is removed from the lacking 8, so it is really appended.⁷⁸ It is also worth mentioning that in every example in al-Samawʾal, and for that matter in every other premodern algebraist as well, lacking terms are never admitted as stand-alone amounts. The answer to a question is never a value like ‘less ten dirhams’, and for a number like ‘ten less a thing’ the ten is presumed to be greater than the thing. The ‘less three māls’ in al-Samawʾal’s table is not a number but is an entry in a number that is expressed as an aggregation of two species that is diminished by three more, one of the latter being these ‘three māls’.

In a formal sense, al-Samawʾal’s rules are equivalent to our rules for operating on signed numbers, but we know from the ways he described them and worked with them that he did not conceive of his entries as being numbers that are positive, negative, or zero. All numbers are positive, but some will be lacking and others will be appended in the final amount, and a zero still sits in a place where there is no number. If al-Samawʾal or anyone else took a formal view of the operations he describes, it has not come to light in our extant texts.

9. Operating on nothing in a passage of al-Hawārī

There is one last noteworthy passage to review, from al-Hawārī’s Essential commentary, a work that supplies numerical examples and clarifying remarks to Ibn al-Bannāʾ’s Condensed book. In the chapter on algebra al-Hawārī discusses the rules given by Ibn al-Bannāʾ for solving the six simplified equations of degree one and two. The fifth type of equation had been expressed as ‘some māls and a number equal some roots’ since the time of al-Khwārazmī (2009, 101.3). Rewritten in modern notation, this is the general equation $a{x}^2+c=bx$. Ibn al-Bannāʾ stated the rule for finding the thing for equations in which $a=1$:

You subtract the number from a square of half of the number of roots, and you take a root of the remainder. If you add it to the half, it gives a root of the greater māl, and if you subtract it, it gives a root of the smaller māl. (Ibn al-Bannāʾ 1969, 75.5; Abdeljaouad and Oaks 2021, 112)

Contorting the sequence of steps of the solution into a modern, static formula, this becomes $x={\displaystyle \frac{1}{2}b\pm \sqrt{{\left({\displaystyle \frac{1}{2}b}\right)}^2-c}}$. There are often two (positive) solutions to this equation type, which is why he calculates ‘a root of the greater māl’ and ‘a root of the smaller māl’. Then, Ibn al-Bannāʾ observes that ‘whenever a square of the half is equal to the number, then the half is the root, and the māl is the number’. In modern terms, whenever ${\left({\displaystyle \frac{1}{2}b}\right)}^2=c$, then $x={\displaystyle \frac{1}{2}b}$ and $x^2=c$. Al-Hawārī illustrates this case with the example we write as $x^2+9=6x$, and then takes the unusual step of ‘continu[ing] the solution’ by performing the operations according to the general rule:

For example, suppose someone said, ‘A māl and nine equal six things’. We square half of the things, giving nine, and this is equal to the number. So the number is the māl, and the half is the root. And if we continue the solution, we subtract the number from the square, leaving nothing. We take its root, giving nothing. We add nothing to the half, or we subtract it from it, leaving the half. It is the root, and its square is the number. So know it. (Abdeljaouad and Oaks 2021, 113)

Here al-Hawārī explicitly operates on ‘nothing’ in a context unrelated to calculation with Indian numerals, and without mentioning zero. Incidentally, the same calculations on nothing for the solution to the same equation are also found in the brief chapter on algebra in the Toledo Regule, a twelfth-century Latin translation from a different Arabic text (Burnett et al. 2007, 197). These calculations, together with some of the explanations of the operations on ‘nothing’ in Indian calculation quoted above, show that Arabic authors could conceive of ‘nothing’ as a kind of departed amount with which one can calculate. But it is still nothing, that is, it is not anything at all, and thus it is not a number of any species of unit.

10. Synthesis

We are fortunate that so many medieval Arabic arithmetic books are extant and that the authors took the trouble to explain what the zero is. Their remarks are all the better understood because we are able to relate them with what various authors have to say about the nature of practical Arabic numbers. If all we had were dust-board calculations without any explanatory text, it would be impossible for us to understand what the zero meant to the medieval authors. Similarly, it is because of what al-Samawʾal and other algebraists write about monomials and polynomials that we know that they did not work with negative numbers.

Numbers in practical Arabic arithmetic consist of a quantity–species pair, like ten dirhams, twenty-four starlings, $2{\displaystyle \frac{10}{19}}$ hours, $29{\displaystyle \frac{2}{3}}$ inches, or three fourths of a unit.⁷⁹ A number is a collection of counted objects or of something measured as seen from the perspective of ‘quantity’. Fifteen dirhams is composed of dirhams, four and a half mithqals of grain is composed of grain, etc. Addition, subtraction, and multiplication take the physical meanings of gathering together, taking away, and duplicating, respectively, even in the case of intelligible units. To add nothing to fifteen dirhams is simply not augmenting it with anything, subtracting nothing from it means not taking anything away, and multiplying it by zero or zero by it can be seen as taking none of the fifteen dirhams or as duplicating nothing fifteen times. Nothing is not an amount of any species, so it was not considered to be a number. It was natural, then, that most authors would not perform operations with zero, and for those who did, they could easily make sense of adding, subtracting, or multiplying nothing. The authors who explain the meaning of zero across the span of the Islamicate world, both geographically and temporally, are unanimous in regarding it as a sign for an empty place, and this view is consistent with the ways they perform and explain their operations. The ‘nothing’ that the zero signifies does not become something because of these manipulations.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Notes

1 In this article both Muslim and Christian dates are given in most instances.

2 Talkhīṣ aʿmāl al-ḥisāb (#696 [M1]), published with a French translation in (Ibn al-Bannāʾ 1969). The entire text is included in the commentary by al-Hawārī, which is published with an English translation in (Abdeljaouad and Oaks 2021). ‘#696 [M1]’ means book [M1] by author #696 in (Rosenfeld and İhsanoğlu 2003). Similarly for subsequent references of this form.

3 Kitāb fī uṣūl ḥisāb al-hindī (#308 [M1]), published with an English translation in (Kūshyār ibn Labbān 1965).

4 The introductions to (Abdeljaouad and Oaks 2021) and (al-Uqlīdisī 1978) give overviews of Arabic arithmetic.

5 Kitāb fīmā yaḥtāju ilayhi al-kuttāb wa l-ʿummāl wa ghayruhum min ʿilm al-ḥisāb (#256 [M2]), published in (Saidan 1971).

6 al-Kitāb fī l-ḥisāb al-Hindī (#41 [M1]). The redaction of the Latin translation with a German translation is published in (al-Khwārazmī 1997). An English translation of roughly the first half is published in (Crossley and Henry 1990).

7 al-Fuṣūl fī l-ḥisāb al-Hindī (#232 [M1]), published in (al-Uqlīdisī 1984). An English translation is published in (al-Uqlīdisī 1978).

8 (Berkey 1992; Chamberlain 1994).

9 (Ibn Sīnā 2005, 18), Marmura’s translation.

10 For the first three authors, these are the books already mentioned above. The other two are (al-Samawʾal MS A) and (al-Kāshī 1969; al-Kāshī 2019).

11 (al-Nīsābūrī MS, 7.1; al-Ḥaṣṣār MS, fol. 3v.4). It is only after describing the nine numerals that the Latin text of al-Khwārazmī gives what amounts to a paragraph to explaining that one is the origin of number and that a number is ‘a collection of ones’. The fact that this paragraph ends with ‘But now let us return to the book’ indicates that it was added later by an editor (Crossley and Henry 1990, 110–111).

12 Asās al-qawāʿid fī uṣūl al-fawāʾid (#674 [M2]), published in (al-Fārisī 1994).

13 Maqālāt fī l-ḥisāb (#696 [M2]), published in (Ibn al-Bannāʾ 1984).

14 Rafʿ al-ḥijāb ʿan wujūh aʿmāl al-ḥisāb (#696 [M8]), published in (Ibn al-Bannāʾ 1994).

15 (Ibn al-Bannāʾ 1994, 207; Aballagh 1988, 142). Compare with (Ibn Sīnā 2005, 91).

16 Kitāb al-tafhīm li-awāʾil ṣināʿat al-tanjīm (#348 [A2]), published with an English translation in (al-Bīrūnī 1934).

17 (al-Bīrūnī 1934, 24), modified from Wright’s translation.

18 Iḥṣāʾ al-ʿulūm, published with a French translation in (al-Fārābī 2015). In this section he considers practical numbers that come from counting. In the next section he distinguishes between practical and theoretical geometry, and there he addresses non-integral measure.

19 (al-Fārābī 2015, 127.5). A dinar was a denomination of gold coin. He then goes on to discuss theoretical numbers, which coincide with the intelligible numbers of the Greek texts.

20 This use of the word ‘species’ is not the same as the species (kinds) of number in Greek number theory, which begin with the even and the odd. Three horses and five horses are the same species by our meaning because they are both horses, while they are of the same species according to Nicomachus because they are both odd.

21 al-Maʿunah fī ʿilm al-ḥisāb al-hawāʿī (#783 [M1]), published in (Ibn al-Hāʾim 1988).

22 (Ibn al-Hāʾim 1988, 91.1). He gives essentially the same explanation in (Ibn al-Hāʾim 1999, 107).

23 The phrase can also be translated ‘divide ten dirhams [equally] among five men’.

24 An irdabb (pl. arādib) is a dry measure equivalent to a little over 5 bushels.

25 (Ibn Ghāzī 1983, 102; Sibṭ al-Māridīnī 2004, 109). Ibn Ghāzī’s book was completed in 890/1483. He quotes Ibn al-Bannāʾ in his definitions.

26 For a more complete discussion of plus/minus vs. and/less, see (Oaks 2009; Abdeljaouad and Oaks 2021, 214ff).

27 See (Oaks and Alkhateeb 2007; Oaks 2009, 2010, 2017) for studies of the nature of Arabic algebraic expressions.

28 al-Fakhrī fī ṣināʿat al-jabr wa l-muqābala (#309 [M2]), in manuscript (al-Karajī MS) and published in (Saidan 1986).

29 While it is true that we can also view our $12x$ as being twelve copies of the $x$, this premodern way does not make sense for terms that are just a little more intricate, like $\sqrt{5}x$, $\pi r^2$, or 3xy. The aggregations interpretation of polynomials is presented in (Oaks 2009, 2010, 2017; Abdeljaouad and Oaks 2021, 214–219).

30 Kitāb fī l-jabr wa l-muqābala (#124 [M1]), published with a French translation in (Abū Kāmil 2012).

31 Here the word māl takes its usual meaning as ‘money’, and is not the name of the second power in algebra.

32 (Abū Kāmil 2012, 427.12). If we convert this to a modern algebra problem, it asks for $a$ and $b$ such that $a+b=10$ and ${\displaystyle \frac{a}{b}+{\displaystyle \frac{b}{a}=\sqrt{5}}}$. The enunciation and first solution are translated in (Oaks 2017, 145–146).

33 Talqīḥ al-afkār fī l-ʿilm bi-rushūm al-ghubār (#521 [M3]), published in (Zemouli 1993).

34 (Zemouli 1993, 209.18). Converting this arithmetic problem into an algebra problem, it asks for x such that ${\displaystyle \frac{1}{3}x+{\displaystyle \frac{1}{4}x+2=2x}}$. The problem is worked out twice, the first time by single false position and the second time by algebra.

35 Murshidat al-ṭālib ilā asnā al-maṭālib fī ʿilm al-ḥisāb (#783 [M5]), published in (Ibn al-Hāʾim 1999).

36 That is, a third and a fourth of the sum, not of the original quantity.

37 The common denominator of ‘a third and a fourth’ is 12. This is repeated, so presuming a value of 144 will result in a whole number after passing it through the operations in the enunciation, disregarding the operations on the added dirham. The terms ‘numerator’ and ‘denominator’ are used because these operations result in ${\displaystyle \frac{95}{144}}$ of the unknown.

38 The third and a fourth are removed from the first dirham, then the remainder is subtracted from ‘the subtracted dirham’, making the new remainder a third and a fourth of a dirham.

39 To ‘denominate’ (from sammā) 84 ‘from’ (min) 95 means to make the name, or species, of the 84 ‘95ths’. This forms the fraction 84/95. In Arabic arithmetic one ‘divides’ (from qasama) a greater number by a smaller number, but one ‘denominates’, or ‘relates’ (from nasaba), a smaller number from a greater number.

40 These books are: #124 Abū Kāmil [M1], #179 Liber augmenti et dimintionis (a Latin translation of an Arabic book) [M1], #256 Abū l-Wafāʾ [M2], #267 ʿAlī al-Sulamī [M1], #309 al-Karajī [M2], [M3], #310 Ibn al-Samḥ [M1], #521 Ibn al-Yāsamīn [M3], #587 Ibn Badr [M1], #657 Ibn al-Khawwām [M2] (for his [M1], see al-Fārisī), #674 al-Fārisī [M2], #696 Ibn al-Bannāʾ [M6], #780 Ibn al-Qunfūdh [M1], #783 Ibn al-Hāʾim [M1], [M5], #1045 al-Qabāqibī [M1], #873 Sibṭ al-Māridīnī [M7], #924 Zakarīyā al-Anṣārī [M2], #997 al-Ghazzī [M1], #1058 al-ʿĀmilī [M1], #1066 Nūr al-Dīn al-Anṣārī [M2]. If an author repeats a problem in two different books, I only count it once.

41 Kitāb al-uṣūl wa l-muqaddimāt fī l-jabr wa l-muqābala (#696 [M6]), published in (Saidan 1986). The other three are in the books of Ibn Badr, al-Fārisī, and Ibn al-Qunfūdh.

42 This ‘restore and confront’, conjugated from al-jabr wa l-muqābala, means to simplify the equation by restoration and/or confrontation (Oaks and Alkhateeb 2007, §4.1).

43 Ḥaṭṭ al-niqāb ʿan wujūh aʿmāl al-ḥisāb (#780 [M1]), in manuscript (Ibn al-Qunfūdh, MS).

44 For an overview of this algebraic notation, see (Oaks 2012).

45 The 35 books are: #41 al-Khwārazmī [M1], #218 al-Nīsābūrī [M1], #232 al-Uqlīdisī [M1], #308 Kūshyār ibn Labbān [M1], #320 al-Baghdādī [M1], #411 al-Ṣardafī [M1], #487 al-Samawʾal [M4], #521 Ibn al-Yāsamīn [M3], #532 al-Ḥaṣṣār [M1], #566 Ibn Munʿim [M1], #606 Naṣīr al-Dīn al-Ṭūsī [M17], #682 al-Abharī [M1], #696 Ibn al-Bannāʾ [M1], [M2], #747 al-Hawārī [M1], al-Mawāḥidī (#M176 in (Lamrabet 2014)), #780 Ibn al-Qunfūdh [M1], #783 Ibn al-Hāʾim [M5], [M7], #802 al-Kāshī [M1], #815 Ibn al-Majdī [M3], #865 al-Qalaṣādī [M3], [M7], #980 Raḍī al-Dīn ibn al-Ḥanbalī [M3], #997 al-Ghazzī [M1], #1004 Taqī al-Dīn [M2], #1006 Yaḥyā al-Ruʿaynī [M1], #1026 al-Sakhāwī [M1], #1045 al-Qabāqibī [M1], #1058 al-ʿĀmilī [M1], #1066 Nūr al-Dīn al-Anṣārī [M2], #1186 Jawād ibn Saʿd ibn Jawād al-Kāẓimī [M1], #1355 Ḥusayn al-Maḥallī [M2], the guide by the lexicographer al-Khwārazmī (1895), and the anonymous Paris, BnF arabe 4441, copied in 1572.

46 Bulūgh al-ṭullāb fī ḥaqāʾiq ʿilm al-ḥisāb (#218 [M1]), in manuscript (al-Nīsābūrī MS).

47 (al-Nīsābūrī MS, 20; Ibn al-Qunfūdh MS, 12).

48 (Crossley and Henry 1990, 111), adjusted slightly from their translation.

49 (al-Uqlīdisī 1978, 42), adjusted slightly from Saidan’s translation.

50 Kitāb al-bayān wa l-tadhkār fī ṣanʿat ʿamal al-ghubār (#532 [M1]), in manuscript (al-Ḥaṣṣār MS).

51 Jāmiʿ al-ḥisāb bi l-takht wa l-turāb (#606 [M17]), published in (Saidan 1967).

52 Miftāḥ al-ḥisāb (#802 [M1]), published in al-Kāshī 1969; (al-Kāshī 2019), the latter covering the first, arithmetical part together with an English translation.

53 (al-Kāshī 1969, 46.16; 2019, 34.15). Our references to (al-Kāshī 2019) are for the page and line number of the Arabic.

54 Fatḥ al-wahhāb ʿalā nuzhat al-ḥussāb (#1066 [M2]), in manuscript (al-Anṣārī MS).

55 This is an oral instruction not to misspell ṣifr (‘zero’) as sifr (‘book of scripture’).

56 Ibn al-Bannāʾ’s [M1], Ibn al-Hāʾim’s [M5], and al-Qalaṣādī’s [M7] do not explain the meaning of zero, but their books [M2], [M7], and [M3] respectively do. Ḥusayn al-Maḥallī’s [M2] is a commentary on al-Sakhāwī’s [M1], and Jawād ibn Saʿd ibn Jawād al-Kāẓimī’s [M1] is a commentary on al-ʿĀmilī’s [M1]. Al-Kāẓimī was a student of al-ʿĀmilī.

57 al-Lubāb fī sharḥ Talkhīṣ aʿmāl al-ḥisāb (#747 [M1]), published with an English translation in (Abdeljaouad and Oaks 2021).

58 al-Takmila fī l-ḥisāb (#320 [M1]), published in (al-Baghdādī 1985).

59 (al-Uqlīdisī 1978, 46), Saidan’s translation.

60 Kitāb al-tabṣira fī ʿilm al-ḥisāb (#487 [M4]), in manuscript (al-Samawʾal MS A).

61 (Zemouli n.d., 11.5). Note that it is only the quantity, and not the quantity-species, of the multiplier that is applied. As some authors note, this definition only makes sense for whole numbers. Finger-reckoners had their own definition of multiplication based in proportion that is valid for fractional numbers. The Euclidean definition suffices for operating on Indian numerals because the nine possible entries are all whole numbers.

62 Mukhtaṣar al-hindī fī ʿilm al-ḥisāb (#411 [M1]), in manuscript (al-Ṣardafī MS).

63 (al-Uqlīdisī 1978, 190), Saidan’s translation.

64 (Crossley and Henry 1990, 116), their translation.

65 Fiqh al-ḥisāb (#556 [M1]), published in (Ibn Munʿim 2005).

66 (al-Kāshī 1969, 48.9; 2019, 38.15), Aydin’s and Hammoudi’s translation.

67 (Saidan 1967, 254). The ‘02’ is mistakenly shown as ‘03’ in the text. The word burj designates 1/12 of the circle, or 30 degrees, and takes the meaning of ‘sign’ of the zodiac. It is not a problem that the minuend is smaller than the subtrahend in this example. He adds 12 signs to the minuend and then performs the subtraction.

68 (al-Bīrūnī 1934, 42), Wright’s translation.

69 (al-Uqlīdisī 1978, 87, 88), adjusted from Saidan’s translations. For the second quotation, the figure again shows a pair of zeros.

70 (al-Kāshī 1969, 104.6; 2019, 178.18), Aydin’s and Hammoudi’s translation.

71 Translation by Toomer, adjusted slightly (Ptolemy 1898, 500.20; 1998, 295). One 0 is to be placed in the first line of the table and the other in the last line.

72 I thank Jan Hogendijk for pointing out this passage to me, and the translation is his.

73 al-Badīʿ fī l-ḥisāb (#309 [M3]), published with a French summary in (al-Karajī 1964).

74 al-Bāhir fī ʿilm al-ḥisāb (#487 [M1]), in manuscript (al-Samawʾal MS B) and published with a French translation in (Rashed 2021).

75 (al-Samawʾal MS B, fol. 28r; Rashed 2021, 59). We reproduce this table and the next based on MS Aya Sofia 2718, the only manuscript which shows the tables. We do not know why zeros are shown for only some empty places in the manuscript.

76 (al-Samawʾal MS B, fol. 29r; Rashed 2021, 61).

77 Sufficient introduction on calculation by algebra and what one can learn from its examples (al-Muqaddima al-kāfiyya fī ḥisāb al-jabr wa l-muqābala wa mā yuʿrafu bihi qiyāsuhū min al-amthila) (#267 [M1]), in manuscript (ʿAlī al-Sulamī).

78 (Ibn al-Bannāʾ 1994, 246.15; Abdeljaouad and Oaks 2021, 52). In our translation in the latter reference we wrote ‘deleted’ for ‘lacking’. Either translation fits the meaning.

79 Al-Hawārī writes of ‘twenty-four starlings’ (Abdeljaouad and Oaks 2021, 110), al-Karajī of ‘two hours and ten parts of nineteen parts of an hour’ (Saidan 1986, 185.16), and Abū l-Wafāʾ of ‘twenty-nine inches and two thirds of an inch’ (Saidan 1971, 205.11). ‘Ten dirhams’ and ‘three fourths of a unit’ are common.