Item Response Theory and Confirmatory Factor Analysis: Complementary Approaches for Scale Development

ABSTRACT

Purpose

This article demonstrates the advantages of using both confirmatory factor analysis (CFA) and item response theory (IRT) in the development and evaluation of social work scales with dichotomous or polytomous items. Social work researchers have commonly employed CFA and internal consistency reliability tests to validate scales for use in research- and evidence-based practice; IRT has been underused. We report findings from CFA and IRT analyses of a short social isolation scale for elementary school students to demonstrate that scale development and validation can benefit from complementary use of the two methods. Results provided evidence that scores from the scale are statistically sound, and each method contributed valuable information.

Method

Data collected from 626 third- through fifth-grade students using the social isolation scale from the Elementary School Success Profile (ESSP) were examined with both CFA and IRT.

Results

Complementary CFA and IRT results provide detailed information about item and scale performance of the social isolation scale.

Discussion

Evidence-based practice requires scales with known properties; knowledge of those properties is more complete when researchers use both CFA and IRT.

Conclusion

Using IRT modeling in combination with CFA can help social work researchers ensure the quality of scales they recommend to practitioners and researchers.

KEYWORDS:

• Confirmatory factor analysis
• item response theory
• scale development
• measurement
• psychometrics

Quality measures are a fundamental requirement of both social work practice and research. We take a broad argument-based perspective on measurement validity (Messick, 1988), which suggests that validity refers to the use of scores for drawing conclusions from research and making decisions in practice. In the current Standards for Psychological and Educational Testing (American Educational Research Association et al., 2014), validity refers to the “degree to which evidence and theory support the interpretations of test scores for proposed uses of tests. Validity is, therefore, the most fundamental consideration in developing tests and evaluating tests” (p. 11). The Standards also make clear that statements about validity should refer to interpretations for specific intended uses (p. 11). The intended use of measures in social work practice generally is to support decision-making that focuses on, for example, decisions about who will receive services and resources or which programs are effective. The importance of these and other practice and policy decisions requires the use of rigorously tested measures (Bowen, 2008a).

The purpose of this paper is to describe how item response theory (IRT) modeling can be used in conjunction with confirmatory factor analysis (CFA) to fully evaluate the quality of scales with dichotomous and polytomous (ordinal) items. CFA and IRT are sophisticated methods for examining scale quality. Each contributes unique information about item and scale quality that builds the argument for the validity of scale scores and their use in research and practice. CFA is more commonly used by social work researchers where its contributions to understanding scale quality are recognized (Bowen & Guo, 2012). IRT is less common in social work research measurement studies despite its substantial use in other disciplines (Unick & Stone, 2010). For example, IRT methods are cornerstones for scale development in educational testing (Baker & Kim, 2017), in the development of patient reported outcome measurement in healthcare (Stover et al., 2019), in personality research (Balsis et al., 2017), in adolescent development (Toland, 2014), in clinical assessment (Thomas, 2011), and in the study of change in human development research (Edwards & Wirth, 2009).

Brief background on CFA

CFA is commonly used in social work research to investigate and establish the psychometric qualities of scores from sets of items assessing common constructs. CFA is a latent variable modeling technique that assumes scores on sets of related questionnaire items reflect a common complex, unobservable phenomenon (construct). Researchers using CFA often begin with exploratory factor analysis (EFA) to obtain preliminary information about the factor structure of a set of items, that is, the number of factors and the pattern of relationships among items and factors. They then use CFA to test those models and potential competing factor structures with theoretical or empirical support. More factor and error structures can be tested in CFA than in EFA, and more sophisticated tests of model quality can be conducted. Researchers conducting CFAs can choose among estimation options based on the measurement level and distributional characteristics of observed variables – an important feature given that the majority of scales used in social work research and practice have items with dichotomous or ordinal response options that do not meet normality assumptions. Table 1 lists the types of information that can be obtained with CFA. We will refer to the table throughout the applied CFA example below.

Table 1. What can be learned about measures using CFA for ordinal level data

Model level analysis

1. Assessment of fit of the factor model based on an overall comparison of the analysis matrix to a new matrix implied by the model

2. Assessment of model fit based on a matrix of residuals – differences in values of corresponding elements of the analysis matrix and implied matrix.

Item level analysis

3. Estimate of the relationship between each indicator and the latent factor it measures in unstandardized and standardized metrics (factor loadings)

5. Estimates of cut points (thresholds) on the underlying theoretical normal distribution of the social isolation construct corresponding to the choice of different response options

6. Estimate of the amount of variance of each indicator that is explained and unexplained by an underlying factor

7. Estimates of relationships among error terms of observed indicators

8. Assessment of whether there are significant differences in parameter estimates across items, groups, time, or data collection methods

Scale level analysis

9. Confirmation of factor structure, including the number of factors, pattern of item loadings, and correlations among factors

10. Comparison of quality of competing alternative factor structures, such as second-order and bifactor structures

11. Estimates of the variance and mean of each factor in the model and weighted factor scores for individuals

12. Assessment of whether there are differences in means and variances of factors across subgroups of respondents

Brief background on IRT

Although IRT is referred to as modern measurement theory, its concepts and methodology have evolved steadily since the early 1900s (Baker & Kim, 2017). IRT was developed, in large part, as a response to limitations of classical test theory in educational test development. It is a set of model-based latent variable techniques designed to examine the process by which individuals respond to items in a measurement instrument (Chalmers, 2012; Edwards, 2009). Because the language of IRT might be new to some readers, what follows is a description of essential IRT concepts. See Nugent (2017) for a more detailed, accessible introduction to IRT for social work researchers.

IRT is a statistical process that links assessment, survey, or test item responses to a latent trait. An assumption is made that each respondent has a position on the latent trait (such as social isolation) that influences the probability he or she will select a particular item response category (such as “No, never”). For our analysis, the scale representing social isolation was expressed as theta (θ), which was in a standard score form with a mean of 0 and a standard deviation of 1. As illustrated below, θ is a key component in IRT model development and testing.

A product of the item-θ linking process is a set of model parameters that characterize the mathematical relationship between each item and θ. In general, the item–θ relationship is described by a slope parameter (also referred to as a discrimination or a-parameter) and one or more location parameters (also referred to as a difficulty or b-parameter). The slope parameter is interpreted as an item’s ability to discriminate between different levels on the θ scale. It is also interpreted as measure of the strength of the relationship between an item and the latent trait.

As the name implies, a location parameter serves to provide the location of an item on the θ scale. It is interpreted as the point on θ where a respondent has a 0.5 probability of endorsing a particular response category. The number of location parameters for an item varies by the number of response categories. For a dichotomous item, there is only one location parameter which is interpreted as the trait level necessary for an individual to have a 0.5 probability of endorsing one of the categories (e.g., answering “true” to a true/false question). For polytomous questions (three or more response categories), there are multiple location parameters; specifically, there are m-1 location parameters, where m refers to the number of response categories. For example, for a five-point Likert response scale, there will be four location parameters, each of which is interpreted as the trait level necessary to have a 0.5 probability of endorsing at or above a response category.

Typically, item parameters are estimated using a full information marginal maximum likelihood fitting function. For our analysis, we fit a graded response model (GRM) which is the recommended model for ordered polytomous response data (Paek & Cole, 2020). Once the parameters are estimated, a variety of indexes are available to assess model fit. If the model adequately fits the data, it is possible to compute various IRT components that provide insights into the item and scale attributes that form the basis for a comprehensive evaluation. These attributes include item and scale information, conditional standard errors, conditional reliability, model-based person scores in both the θ metric and transformed estimated true scores, differential item functioning, and differential scale functioning.

Table 2 presents a list of the types of information that can be obtained with IRT. The table also mirrors the process used to conduct an IRT analysis of a set of items and will be referred to in the IRT example below.

Table 2. What can be learned about measures using IRT for ordinal level data

Model level analysis

1. Assessment of model fit using indexes developed specifically for ordinal response IRT models

Item level analysis

2. Assessment of item fit

3. Estimates of IRT item slope parameters (a-parameters) and location (b-parameters) using marginal maximum likelihood methods

4. Assessment of item category response coverage: distribution of category response functions over θ

5. Assessment of item information: distribution of item information over θ

6. Assessment of differential item functioning across subgroups of respondent

Scale level analysis

7. Assessment of scale information, conditional standard errors, and conditional reliability

8. Estimates of person parameters (θ estimates, factor scores); assessment of score estimate precision using conditional standard errors

9. Estimates of expected true scores in original item metrics from model-based θ estimates

10. Assessment of differential scale functioning across subgroups of respondents

Method

Sample and data collection

Data used in the study were collected from 1,172 third- through fifth-grade students in 13 schools in four districts in a southeastern state during the 2008–2009 school year. Children completed the ESSP on computers at their schools. Schools in each district were taking part in school team efforts to use ESSP data in decision-making about prevention strategies to best support student success. Projects were funded with state, federal, and foundation funding. More information on the data collection and sample is available elsewhere (Bowen, 2011). Human subjects and data use procedures were approved by institutional review boards through the Behavioral Sciences IRB at the University of North Carolina and The Ohio State University IRB.

Combining data from multiple ESSP projects provided a large and diverse sample that was useful for the current study. Parent-report demographic data were available for 655 of the cases. These cases were retained for the analysis. Of the 655, 29 cases (4.4%) were missing data between one and five of the social isolation variables. To ensure that the samples were the same for the CFA and IRT analyses, we deleted the 29 cases, leaving 626 child cases for the analyses. Cross-tab/chi-square tests indicated that cases with and without complete data on the social isolation variables did not differ by race/ethnicity (Pearson χ² p = .499); participation in the free and reduced lunch program (Pearson χ² p = .564) or gender (Pearson χ² p = .051).

Girls constituted 53% of the sample (n = 332). The largest racial/ethnic group was White (45.4%, n = 284); followed by African Americans (37.4%, n = 284). Seven percent (7.3%, n = 46) was Hispanic/Latino. About 5% (5.1%, n = 32) were multiracial; the remainder of the sample (4%, n = 25) comprised small percentages of students who were Asian, Native American, Alaska Native, or Other race. Race/ethnicity data were missing for five students.

Measure

The Social Isolation Scale on the ESSP for Children, which has been called the “adjustment” scale in the past, has five items:

1. Do you ever wish you could run away from home?

2. Do you ever feel nobody cares about you?

3. Do you ever feel like you don’t know what to do?

4. Do you ever feel all alone?

5. Do you ever feel no one listens to you?

Response options for the items are 1 (No, never), 2 (Yes, sometimes), and 3 (Yes, often). Rigorous scale development steps were taken to promote the validity and reliability of all scales on the ESSP for Children (Bowen, 2008b, 2011; Bowen et al., 2004).

Item response frequencies are shown in Table 3. A relatively small percentage of students (6% to 15%) chose the response “Yes, often” for any of the five variables. There was more variability among the “No, never” and “Yes, sometimes” options. For example, most students (69.2%) choose “No, never” in response to the item about running away. Only about one-quarter of the students (26.4%) chose that response for the item about not knowing what to do. The fact that only about one-half or fewer of the students chose “No, never” for four of the five indicators, means most students experienced different aspects of a sense of isolation at least sometimes. We computed two reliability coefficients for the scale – coefficient alpha = .72 and omega = .75. Using a recommended threshold of ≥ .70, both coefficients indicated that the scale had adequate internal consistent reliability, especially for scales using collected data from children from ages 7 to 10.

Table 3. Item response frequencies

Item	No, Never	Yes, Sometimes	Yes, Often
1. Do you ever wish you could run away from home?	433	156	37
	69.2%	24.9%	5.9%
2. Do you ever feel nobody cares about you?	330	229	67
	52.7%	36.6%	10.7%
3. Do you ever feel like you don’t know what to do?	165	373	88
	26.4%	59.6%	14.1%
4. Do you ever feel all alone?	278	253	95
	44.4%	40.4%	15.2%
5. Do you ever feel no one listens to you?	314	246	66
	50.2%	39.3%	10.5%

Results

CFA analysis of the social isolation scale

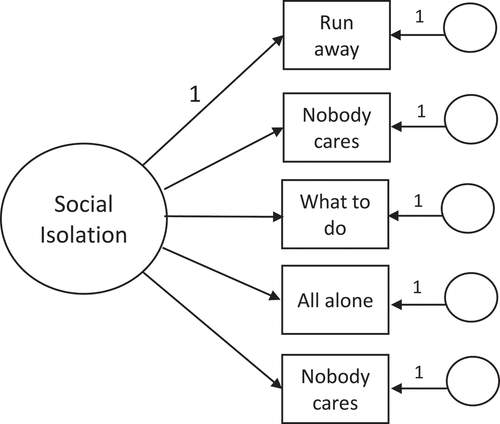
Recommended methods for analyzing ordinal data (Bollen, 1989; Flora & Curran, 2004; Jöreskog et al., 2016) were used in Mplus, version 7.31 (Muthén & Muthén, 2015) for the CFA of the social isolation variables. The variables were specified as categorical (which in Mplus includes ordinal), and a mean and variance-adjusted weighted least-squares estimator (WLSMV) was requested. With these specifications, the analysis matrix consisted of polychoric correlations between all pairs of analysis variables. The joint distribution of cases in a two-by-two cross-tabulation table of each pair of variables is used to generate the polychoric correlations (Bollen, 1989). Through the polychoric correlations, observed scores on indicators are linked to a theoretical underlying normal distribution of levels of the latent construct. Because a summary matrix is analyzed instead of the full raw data matrix, the approach is called a limited information approach. Polychoric correlations among the five indicator variables ranged from .39 to .60. Based on previous empirical work with the scale, we specified a one-factor, first-order factor model in which all five items directly measured the isolation construct (Figure 1).

Figure 1. First-order factor model of the ESSP Social Isolation Scale

CFA results

Model level analysis

Researchers using CFA typically examine fit statistics (see Table 1, #1) before proceeding to interpret parameter estimates because a model with inadequate fit should not be retained. The null hypothesis in a CFA analysis is that the matrix implied or reproduced by the data and specified model is statistically the same as the input or analysis matrix. Overall model fit refers, therefore, to how well the specified model can reproduce the original polychoric correlation analysis matrix. Researchers hope to accept the null hypothesis that the two matrices are statistically the same. An adjusted χ^{2 –} the Satorra-Bentler χ² (Satorra & Bentler, 1994) – is used with the WLSMV estimator to evaluate overall fit of a model. A nonsignificant χ² is desired but is often not obtained due to large sample sizes even when all other fit indicators are adequate. The χ²(df) for the social isolation factor model was 12.19(5), which was statistically significant at the p = .03 level. We used additional common measures of fit with recommended cutoffs (West et al., 2012). The root-mean-square error of approximation (RMSEA) point estimate was .05 with a 90% confidence interval of .01 to .08. Although the point estimate was good, the upper confidence interval of the RMSEA exceeded the recommended maximum of .06. At .99 and .98, respectively, the Comparative Fit index (CFI), Tucker–Lewis Index (TLI) values were well above the recommended .95 minimum. The Weighted Root Mean Square Residual (WRMR) was .43, well below the recommended maximum of .90.

Correlation residuals, which provide information about specific locations of fit or misfit (see Table 1, #2), ranged from −.004 to .04, well below the pre-specified .10 maximum cutoff (Kline, 2016). Unfortunately, it is not uncommon to obtain fit indices that lead to inconsistent conclusions about fit. Although the model χ² was significant, and the upper CI of the RMSEA exceeded our pre-specified cutoff, the low residuals suggested that all input correlations were adequately reproduced. Given the low residuals and desirable CFI, TLI, and WRMR values, we can argue that the factor model has adequate fit and will do so for this demonstration.

Item level analysis

Table 4 presents the unstandardized and standardized factor loadings of the five items on the social isolation latent variable and their standard errors (refer Table 1, #3). Confidence intervals (95%) are also presented for the unstandardized loadings and indicate the precision of the estimates. All loadings were statistically significant. Results support the conclusion that the social isolation scale is unidimensional. Standardized loadings ranged from .60 to .78, indicating the magnitude of the relationships of items to the factor was adequate (although there are no strict cutoffs for acceptable loadings). Loadings provide useful information to researchers; they indicate how much scores on an item change with a one-unit change in the latent factor. Items with higher loadings are more sensitive to changes in levels of the latent construct the items measure and play a larger role in defining the construct than items will lower loadings.

Table 4. CFA parameter estimates

Item	^Factor loadings (SE)	95% CIs	^^Factor loadings (S)	Item R^2	Thresholds
1. Do you ever wish you could run away from home?	1.00 (0.00)	–	0.65	0.42	.50 1.56
2. Do you ever feel nobody cares about you?	1.20 (.100)	[1.007, 1.400]	0.78	0.61	.07 1.24
3. Do you ever feel like you don’t know what to do?	0.92 (.094)	[0.735, 1.104]	0.60	0.36	−.63 1.08
4. Do you ever feel all alone?	1.11 (.080)	[0.958,1.270]	0.73	0.53	−.14 1.03
5. Do you ever feel no one listens to you?	1.18 (.101)	[0.982,1.378]	0.77	0.59	.00 1.25

^ = unstandardized; ^^ = standardized. SE = standard error. CI = confidence interval.

All loadings were statistically significant at the p < .001 level.

The last column in Table 4 presents the two thresholds for each item that divide its hypothetical underlying normal distribution into the “No, never,” “Yes sometimes,” and “Yes, often” response categories. Thresholds define the range of levels of the underlying social isolation phenomenon associated with each response option (see Table 1, #4). More specifically, a threshold indicates the level of social isolation at which respondents have a 50% chance of transitioning from one response choice on an item (e.g., “No, never”) to a higher one (e.g., “Yes, sometimes” or “Yes, often”).

It is apparent in Table 4 that threshold values differ across items. The differences signify that different responses correspond to different levels of social isolation across the items. The normal distribution has a mean of 0 and a standard deviation of 1; technically the distribution extends from minus to plus infinity, but graphs usually plot scores between −3 and +3. The table indicates that a score of 1 (“No, never”) for item 3 corresponds to all levels of social isolation between −3.0 and −.63 (below the mean of social isolation). In contrast, a score of 1 on item 1 corresponds to social isolation values from −3.0 to .5 (above the mean of social isolation).

Related to factor loadings are the item R²s, also called squared multiple correlations or SMCs (Table 1, #5). R²s are the squared standardized loadings of items; they indicate the percentage of variance of each item that is explained by the social isolation factor. The higher the percentage of variance of an item that is explained by the factor, the better the item is at measuring the factor. The values presented in Table 4 range from .36 to .61. There is no strict cutoff for acceptable R²s, but over .50 is desirable and higher is better. The percentage of unexplained variance (error, unique, or residual variance) is the complement of the R², that is, explained and unexplained variance of an item add up to 100% of its observed variance.

A desirable feature of CFA is that it can identify and accommodate correlations among error terms of items (Table 1, #6), that is, correlations between the unexplained variance of pairs of indicators. A correlation among error terms for two items indicates that one or more unmeasured influences predict some of the variance in both that is not associated with the factor. Failing to specify the correlated error reduces model fit. Correlated errors are not desirable but are acceptable if they can be justified theoretically. The low residuals and acceptable fit statistics obtained in the CFA of social isolation without correlated errors suggest there were no significant correlations among error terms.

For this demonstration of CFA, we did not conduct invariance testing (see Table 1, #7), which is testing for significant differences in factor structure, loadings, and thresholds, most often across sample subgroups defined by demographic characteristics. Such tests give in-depth understanding of how items may have different relationships to the latent variable across groups. Significant differences may indicate that scale scores have different meanings across groups. Invariance tests can also be used to determine if a scale performs comparably at two different time points; an important scale feature for measuring change across time.

Scale level analysis

First-order models are the simplest and most common type of factor structure. Due to the simplicity of the Social Isolation scale and previous research, we specified a first-order model (Table 1, #8). This factor structure was supported by the analysis, so we did not specify alternative models (Table 1, #9). Numerous alternative factor structures can be tested when there are many items, multiple hypothesized factors, and more complex relationships between scale items and latent factors. One example is a second-order model, in which one or more higher order factors are measured by first-order factors, which in turn are measured by observed items (as in a first-order model). Another example is bifactor models, in which observed items measure both a general factor and one or more specific factors. Factors representing the effects of different data sources and collection methods (e.g., self-report and observation) on item scores can also be added to factor models. The flexibility of CFA to accommodate such a variety of potential factor structures is a unique and significant advantage of the approach.

Our CFA output also indicated that the social isolation latent variable had a statistically significant variance of .42 (p < .0001, Table 1, #10), meaning it captured differences in social isolation across individuals. By default, the mean was centered at 0 in the Mplus analysis. Although in SEM models, testing theory analyses typically use latent factor scores, weighted observed factor scores can be saved and used in analyses. For this demonstration, we did not conduct a multiple-group analysis to determine if there were significant differences in means and variances across groups (Table 1, #11). Such information is often of substantive interest to researchers.

IRT analysis of the ESSP social isolation scale

We conducted IRT analyses using the R statistical computing environment (R Development Core Team, 2019) and the packages ltm: An R Package for Latent Variable Modeling for Item Response Theory Analyses (Rizopoulos, 2006) and mirt: A Multidimensional Item Response Theory Package for the R Environment (Chalmers, 2012). As noted, we fit and assess a graded response model using a recommended full-information marginal maximum likelihood fitting function with an expectation-maximization algorithm (Paek & Cole, 2020).

IRT results

Model level analysis

We examined various indexes to assess model adequacy (Table 2, #1). For overall model fit, we used an index, C_2, which is specifically designed to assess the fit of item response models for ordinal data (Cai & Monroe, 2014). In addition, we used the standardized root-mean-square residual (SRMSR) to assess adequacy of model fit based on suggestions made by Maydeu-Olivares and Joe (2014). Note that although the model fit indexes discussed here are conceptually similar to those presented for the CFA analysis reported above, the C₂-RMSEA and standardized root-mean-square residual (SRMSR) were developed specifically for assessing ordinal IRT models (Cai & Monroe, 2014). The obtained C₂-RMSEA = .03 (95% CI [.00, .06]) and SRMSR = .03 indicated adequate model fit using the recommended cutoffs of $\le$.06 for the C₂-RMSEA and its upper confidence interval and ≤ .05 for the SRMSR (Maydeu-Olivares & Joe, 2014).

A second step in assessing the fit of a graded response model is to examine how well each item fits the data (see Table 2, #2). For this analysis, we used an item fit index, the generalized S-χ², recommended for graded response models (DeMars, 2010; Reise, 2015). The generalized S-χ² tests the difference between observed responses to an item and model-based responses. A well-fitting item will have a nonsignificant generalized S-χ² p-value with a small

RMSEA value. Results from this analysis are shown in Table 5. Based on the RMSEA values, each item fit the data well. Item 3, Item 4, and Item 5 were the best-fitting items with nonsignificant p-values and small RMSEA values. Item 1 and Item 2 had significant p-values but had acceptable RMSEA values. Although the point estimates were acceptable for these items, the upper confidence interval of the RMSEA exceeded the recommended maximum of .06. That notwithstanding, our conclusion for this demonstration was that each item demonstrated adequate fit.

Table 5. Item generalized S-χ² and RMSEA indexes

Item	S-χ^2 (df)	p	RMSEA	95% CI
1. Do you ever wish you could run away from home?	30.77(10)	.00	.06	[.03, .08]
2. Do you ever feel nobody cares about you?	16.35(8)	.04	.04	[.00, .07]
3. Do you ever feel like you don’t know what to do?	11.12(9)	.27	.02	[.00, .05]
4. Do you ever feel all alone?	11.94(9)	.22	.02	[.00, .05]
5. Do you ever feel no one listens to you?	6.97(8)	.54	.00	[.00, .05]

As noted above, two types of item parameters are estimated in a graded response model: a slope parameter and a set of location parameters (see Table 2, #3). The estimated parameters for the model and their standard errors are shown in Table 6. The values of the slope parameters (a) ranged from 1.39 (Item 3) to 2.52 (Item 5). Baker and Kim (2017) define cutoffs that can be used to assess slope parameter magnitudes in terms of their ability to differentiate levels of the trait. Their cutoff labels are as follows: 0 = No ability; .01 to .04 = Very low; .35 to .64 = Low; .65 to 1.34 = Moderate; 1.35 to 1.69 = High; >1.70 = Very high. Based on these rules-of-thumb, we considered our slope estimates to be high (Items 1 and 3), and very high (Items 2, 4, and 5) in their ability to differentiate respondents with different levels of θ.

Table 6. Item graded response model parameter estimates

Item	a (se)	b1 (se)	b2 (se)
1. Do you ever wish you could run away from home?	1.59 (.18)	.78 (.09)	2.29 (.21)
2. Do you ever feel nobody cares about you?	2.42 (.24)	.12 (.06)	1.57 (.12)
3. Do you ever feel like you don’t know what to do?	1.39 (.14)	−1.00 (.11)	1.71 (.15)
4. Do you ever feel all alone?	1.93 (.19)	−.17 (.07)	1.38 (.11)
5. Do you ever feel no one listens to you?	2.52 (.24)	.03 (.06)	1.57 (.11)

Estimates of location parameters (b₁, b₂) also are listed for each item in Table 6. Location parameters for Item 1 can be interpreted as follows: b₁ = .78 represents the point on θ where a respondent has a .5 probability of endorsing the “Yes, sometimes” or the “Yes, often” categories; the b₂ = 2.29 parameter represents the point on θ where a respondent has a .5 probability of responding to the “Yes, often” category. Location parameters provide insights into how levels of the latent trait – social isolation – influence responses. For example. it takes a fairly high level of social isolation to have a higher probability of responding “Yes, sometimes” and “Yes, often” to the Item 1 compared to Item 2 as indicated by the lower b₁ = .12 and b₂ = 1.57 values for that item. Other items can be similarly interpreted.

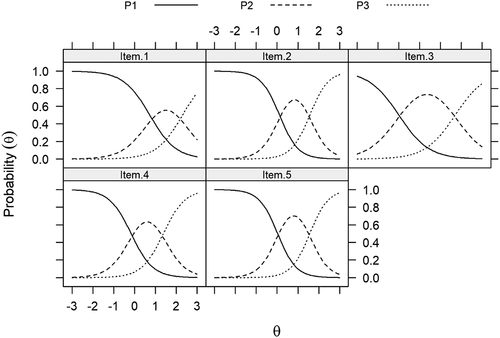
IRT results often are displayed in graphs that are helpful for visually inspecting and interpreting item and scale characteristics and functioning. For example, detail about item responses is displayed in category response curves (CRCs), which show the probabilities of responding to specific response categories for any given value of θ (see Table 2, #4). CRCs for our items are presented in Figure 2. Each curve reflects the probability of endorsing a response category ranging from P1 (“No, never”) to P3 (“Yes, often”). These curves have a functional relationship with θ; as θ increases, the probability of choosing a response category increases and then decreases when responses transition to the next higher category. The CRCs shown in Figure 2 indicated that, except for Item 3, it took fairly high levels of θ for a respondent to endorse a 2 or 3 on the response scale (e.g., the peaks of the curves for score 2 are shifted further to the right than for item 3). This is especially evident for Item 1 where category 2 or category 3 endorsements substantively started at θ levels ≥0. In addition, the impact of slope parameters was evident in each CRC. For example, the curves for Item 3 (slope = 1.39) were relatively flat – or more spread out horizontally – compared to the steeper curves for Item 5 (slope = 2.52).

Figure 2. Category response curves for 3 response options (Ps) per item

P1 = probability of responding 1 (No, never); P2 = probability of responding 2 (Yes, sometimes); P3 = probability of responding 3 (Yes, always)

Item and scale information

Overview

The primary purpose for using a scale is to estimate a score that represents where a respondent is located on the continuum of the measured construct. For example, if conventional scoring is used for our scale, a student’s summed score will fall somewhere between 5 and 15 with a higher score corresponding to a higher level of social isolation. That same student also will have an IRT model-based estimated θ score. This score will be expressed in the θ metric and will usually fall somewhere in the −3 < θ < +3 range. Higher scores on this scale correspond to higher trait levels of θ (higher levels of social isolation).

When we make estimates of respondents’ θ scores we are interested in the precision of those estimates. Precision here refers to the assumption that statistical estimates are not exact, that is, they are approximate representations of population values. Therefore, it is important to assess how close an estimate is to a population value by using measures of precision such as standard errors and confidence intervals. IRT models can provide substantive detail about the precision of θ score estimates. Two related components used in the score estimation process that provide insights into estimate precision are information and conditional standard errors (Table 2, #5). Information is a statistical concept that refers to the ability of an item and a scale (composite of items) to accurately estimate scores on θ (Baker & Kim, 2017). Information is computed at both the item level and at the scale level, with higher levels of information leading to more accurate score estimates. Item level information clarifies how well each item contributes to score estimation precision. Scale information (sometimes referred to as test information) is the total of the information values of items used to form the scale (Baker & Kim, 2017). A key characteristic of item and scale information is that both types are conditional on θ; conditional referring to the fact that each θ value has a linked item and a scaled information value.

Item information

In polytomous models, the amount of information an item contributes depends on its slope parameter – the larger the parameter, the more information the item provides. Further, the farther apart the location parameters (b₁, b₂), the more information the item provides (see Table 2, #5). Typically, an optimally informative polytomous item will have a large location and broad category coverage (as indicated by location parameters) over θ (DeMars, 2010; Reise, 2015)

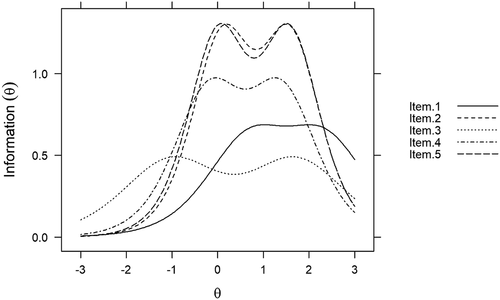
Information functions are best illustrated by the item information curves (IICs) for each item as displayed in Figure 3. These curves show that item information is not a static quantity, rather, it is conditional on levels of θ. Item 3 provides the greatest coverage over θ (given the spread of b₁ and b₂) but is the least informative item. Items 2 and 5 are the most informative items as illustrated by the noticeably higher curves for the two items in Figure 3. Except for Item 3, items tended to provide the most information between 0 ≤ θ ≤ + 2 range. The “wavy” form of the curves reflects the fact that item information is a composite of category information, that is, each category has an information function which is then combined to form the item information function.

Figure 3. Item information curves

Information (θ) = conditional scale information function for each item. Information values are not bounded by a value of 1, they can be >1 at points along θ.

Scale information

One particularly helpful IRT capacity is that information for individual items can be summed to form a scale information function (SIF, Table 2, #7). A scale information function is a summary of how well items, overall, provide statistical information about the latent trait. Further, scale information values can be used to compute conditional standard errors which indicate how precisely scores can be estimated across different values of θ. The relationship between scale information and conditional standard errors is illustrated in Figure 4. The solid Information (θ) line represents the scale information function. The overall scale provided the most information in the range 0 ≤ θ ≤ +2 (52.2% of the total scale information fell in this range). The dotted Standard Error (θ) line provides a visual reference about how estimate precision varies across θ with smaller values corresponding to better estimate precision. Because conditional standard errors mirror the SIF, estimated score precision was best in the 0 ≤ θ ≤ +2 range.

Figure 4. Scale information curve and conditional standard error curve

Information (θ) = conditional-scale information function (solid line); Standard Error (θ) = conditional scale standard errors (dotted line). The curves are mathematical functions of each other where Standard Error (θ) = 1 – √ Information (θ). Higher information along the θ scale gives rise to lower standard errors resulting in more precise θ estimates.

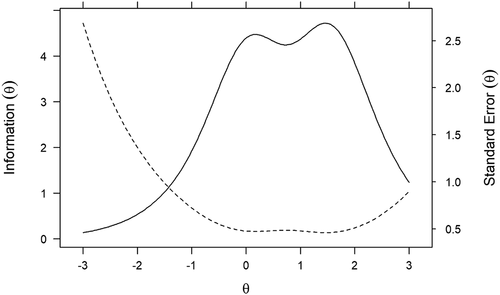
Scale reliability

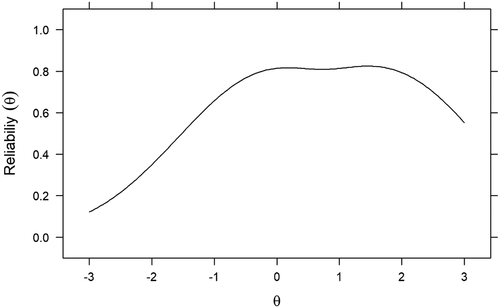
As noted above scale information and conditional standard errors are closely related. A scale or test that has high total information is more precise in its ability to estimate respondent scores on the latent trait than is a scale with limited total information as indicated by smaller standard errors. A third key concept related to information and conditional standard error is conditional reliability. Conditional reliability means that a scale may be more (or less) reliable at points along θ (see Table 2, #6). This approach to reliability stands in contrast to classical test theory reliability where one measure of reliability – coefficient alpha, for example, – is computed and interpreted under the assumption it covers the entire scale score range. Reliability in IRT takes a different view by assuming that test reliability is more dynamic that the ability to reliably estimate scores may potentially vary across the latent trait scores.

The conditional reliability curve is shown in Figure 5. Because conditional reliability mirrors the SIF and conditional standard errors, estimated score reliability was best in the 0 ≤ θ ≤ +2 range. Further, it is possible to compute a summary reliability coefficient in IRT. One such measure is called marginal reliability, which is useful for models with a single latent trait. The marginal reliability for our model was .75 which is similar in value to both the coefficient alpha = .72 and omega = .75 reported above.

Figure 5. Conditional reliability

Reliability (θ) = conditional-scale reliability function. Higher values along the θ scale indicate more reliable score estimates. Information, conditional standard errors, and conditional reliability are mathematically related.

Score estimation and the scale characteristic curve

As a next step, we used model parameters to generate estimates of student θ scores (see Table 2, #8) [See Figure 6 where estimated scores are used to compute expected true scores]. These scores are referred to as person parameters in IRT (they are called factor scores in CFA). We used a latent trait scoring procedure called expected a posteriori (EAP) estimation to generate the scores. Keep in mind the estimates are in the θ (standard normal) metric, so they are z-like scores. Further, as noted above, estimated precision varies across θ as indicated by conditional standard errors shown in Figure 4. The average for estimated θs was .00, the standard deviation was .86, and the range of scores was −1.31 to 2.37. Edwards (2009) suggested that IRT model-based scores have favorable properties that improve on a summed score approach. First, model-based scores reflect the impacts of parameter estimates obtained from the IRT model used. As a result, because they are weighted by item parameters, θ score estimates often show more variability than summed scores.

Figure 6. Scale characteristic curve linking estimated θ scores and expected true scores

Scale characteristic curves map model-based estimated θ scores to expected true scores. For example, an estimated θ score of 0 would translate into an expected true score of 8; an estimated θ score of 1 would translate into an expected true score of 10. As noted, these θ transformation scores provide model-based estimated true scores that are in the original scale score metric.

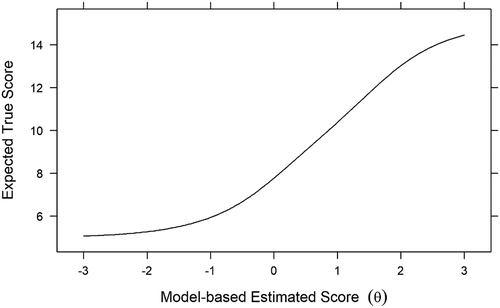
The second favorable property of IRT model-based scores is that because they are given in a standard normal metric, we can use our knowledge of the standard normal distribution to make score comparisons across individuals. For example, someone with a θ score of 1.0 is one standard deviation above average and we can expect that 84% of the sample to have lower scores and 16% to have higher scores (Edwards, 2009, p. 519). Other comparisons of interest based on standard normal characteristics are possible.

Once model-based θ score estimates are computed, it often is of interest to transform those estimates into the original scale metric (Table 2, #9). A scale characteristic function provides a means of transforming estimated θ scores to expected true scores in the original scale metric. This transformation back into the original scale metric provides a more familiar frame of reference for interpreting scores (Baker & Kim, 2017, p. 59). In this study, expected true scores refer to scores on the isolation scale metric (5 to 15) that are expected as a function of estimated student θ scores.

Scale characteristic functions can be graphically displayed in a scale characteristic curve (SCC). The SCC for our model is shown in Figure 6. It has a straightforward use; it illustrates that for any given estimated θ score we can easily find a corresponding expected true score in the summed scale score metric. For example, an estimated θ score of 0 would translate into an expected true score of 8; an estimated θ score of +1 would translate into an expected true score of 10. These true score transformations often are of interest in practical situations where scale users are not familiar with θ scores. Also, true score estimates can be used in other important statistical analyses and are often improvements over traditional summed scores.

Discussion

Information we gained about the ESSP Social Isolation scale from the CFA and IRT analyses is integrated in Table 7. The table illustrates the detailed information about a scale that can be obtained using a combination of CFA and IRT. Some information from the two approaches overlapped, providing triangulated evidence of item quality. Other information was unique to each method.

Table 7. Integrated performance information about the social isolation scale based on CFA and IRT results

CFA	IRT
Model level analysis	Model Level Analysis
1. The Social Isolation scale had overall good fit according to multiple indices.	The graded response model for the scale had good fit according to multiple indices.
2. The scale had good fit across all elements of the analysis matrix based on the residual matrix.
Item level analysis	Item level analysis
	3. Individual items had good fit based on S-χ^2 p-values and S-χ^2-RMSEA values.
4. Unstandardized factor loadings indicated that scores on items were responsive to 1-unit changes in the social isolation construct; item scores changed between .92 and 1.20 units on a 3-point scale.	4. Slope parameters indicated items were able to differentiate at high and very high levels among students with different levels of social isolation. Location parameters indicated that all items except item 3 measured higher levels of social isolation (θ) better than lower levels
5. According to item thresholds, only two of the five items (3 & 4) captured below-average levels of social isolation (between −3.0 and 0). For the three other items, latent social isolation values from −3.0 to 0 or above 0 were all captured in the first response option.	5. Response category probabilities tended to concentrate in higher levels of θ; this pattern suggested that it took higher levels of social isolation to endorse the “Yes, sometimes” or the “Yes, often” response categories
6. Because the social isolation construct explained less than 50% of the variance of items 1 and 3, they were not strong measures of the construct and contributed less to its definition.	7. All items contributed substantive information to the precision and reliability with which scores across values of social isolation could be estimated.
8. No correlations among item error terms (unexplained variances) were indicated, which is desirable.
9. We did not conduct invariance tests in this study.	9. We did not test for DIF in this study.
Scale level analysis
10. Results indicated the Social Isolation scale is unidimensional. Because the 5 social isolation items loaded on one factor, no alternative factor structures were tested.	11. High scale information values, low conditional standard errors, and high conditional reliability indicated that the scale operated best over the 0 ≤ θ ≤ +2 range of the social isolation scale (θ)
12. The social isolation factor had a statistically significant variance of .46 on a Z score scale, which means the factor captured meaningful differences in scores. The mean, standard deviation, and range of the factor scores were .015, .55, and −.791 to 1.5, respectively.	12. According to expected a posteriori (EAP) estimation of student θ scores (person parameters), the average estimated θ score was .00, the standard deviation was .86, and the range of scores was −1.31 to 2.37.
	13. We transformed estimated θ scores into model-based expected true scores so they could be understood in terms of the items’ observed metric. The average estimated true score was 8.68, the standard deviation was 3.27, and the range of scores was 5 to 15.
14. We did not conduct multiple group comparisons of the mean or variance of social isolation factor scores for this study.	14. We did not test for DTF for this study.

The Social Isolation scale had good overall fit according to both CFA and IRT analyses (see Table 7, #1). The CFA approach provided additional information about local fit based on how well the model reproduced the analysis correlation matrix (Table 7, #2). In our example, information from the residual matrix was consistent with overall fit indices. However, when standardized individual residuals are large (e.g., > .10), they can help researchers improve factors models. The IRT model also indicated that individual items had good fit (Table 7, #3), according to S-χ²-RMSEA values. Findings from both the CFA and IRT analyses also suggested that the five social isolation items adequately differentiated among levels of the latent construct or θ (see Table 7, #4). In the IRT framework, there are quantitative guidelines for interpreting the magnitude of the relationship between an item and the construct. In our example, items performed at high levels on this metric.

CFA thresholds and IRT response category probabilities (see Table 7, #5) provided additional information about item quality, some of which suggested the scale could be improved. The first CFA threshold for three items was at or above 0 on the −3 to +3 latent continuum of social isolation scores (items 1, 2, and 5). Those items, therefore, did not distinguish among various below-average levels of social isolation. IRT is especially well suited to identify and describe how items capture information across the full range of a latent construct and how well the scale operates across levels of the latent trait. Specifically, category response curves convey detailed information about how well items capture information across levels of θ and where there are gaps in coverage. Conversely, the conditional look at scale performance can help a researcher assess where the scale operates best – is most informative, provides the most precise score estimates, and is most reliable. For example, the IRT analysis of the ESSP scale indicated that the items tended to be most statistically informative in the upper range of the construct (in 0 ≤ θ ≤ +2 range). Together the CFA and IRT findings suggest that the Social Isolation scale could be improved by either modifying one or more existing items to make them more sensitive to gradations of lower levels of social isolation, or preferably, by adding one or more items that tap into lower levels of the construct.

CFA results provide another measure of the quality of individual items: the percentage of observed variance of the items that is explained by the latent social isolation construct (see Table 7, #6). Items with high amounts of explained variance are stronger measures of the latent construct and are more desirable indicators. Similarly, IRT item analysis indicated that each item provided statistical information which contributed to score estimation precision (see Table 7, #7). There was variability in item-level information with Item 5 (“Do you ever feel no one listens to you?” being the most informative and Item 3 (“Do you ever feel like you don’t know what to do?” In combination with other CFA and IRT findings, this information can inform item modifications or deletions.

CFA results can indicate when the error terms (representing variance unexplained by the factor) of two items are correlated (see Table 7, #8). As described above in the summary of CFA, correlated errors are not desirable in measurement models, but they do provide useful information about problematic relationships among items. In the latent variable framework, existing correlations can be modeled, rather than ignored in the measurement component of general structural equation models. Alternatively, researchers may choose to modify or delete at least one of the problematic items to avoid correlated errors. Although we did not conduct tests to determine if parameters of the social isolation operated differently across groups, such tests can be conducted with CFA and IRT (see Table 7, #9).

Although the quality of IRT results can suggest a scale has a unidimensional factor structure, the possibility of alternative factor structures can be tested in CFA (Table 7, #10). In the case of the Social Isolation scale, past studies and the current factor analysis results clearly supported a one-factor solution. Further, our IRT analysis found that each item substantively contributed to scale information, conditional standard errors, and conditional reliability, all of which indicated the scale operated with most precision in the 0 ≤ θ ≤ +2 range (see Table 7, #11).

In both CFA and IRT, standardized scale scores based on the analysis can be saved, summarized, and used in future analyses as observed composite scores (see Table 7, #12). CFA results also provide a latent variable mean and variance. It is important to confirm that a latent variable has a statistically significant variance; if it does not, its scores do not capture differences among individuals, and it is not a useful variable. IRT also has a mechanism for converting estimated θ scores into the metric of the original indicators, facilitating evaluation of individual and aggregate scale scores (Table 7, #13).

Both CFA and IRT can be used to identify if the parameters or scores on a latent construct differ across groups (see Table 7, #14). Loadings and slopes, thresholds and location parameters can be evaluated at both the item and scale levels (through measurement invariance and multiple group analysis in CFA, differential item, and test analysis in IRT). We did not conduct tests of group differences for the current study.

Finally, Wirth and Edwards (2007) discussed the situations where a researcher might choose either an IRT method or a CFA method in assessing a set of items. They note that IRT methods are helpful if the interest is in examining individual item characteristics or in estimating scores for respondents. As the name implies, item response theory focuses on items; it provides a broad range of statistical and visual analytic tools that allows a researcher to focus on item-specific relationships with the latent trait. If the goal of the ESSP scale is to provide an assessment of the full range of the social isolation construct, implications of the IRT analysis would be that items measuring lower levels of social isolation should be identified and tested.

On the other hand, Wirth and Edwards (2007) suggest that CFA would be the method of choice if research questions focus on the structural make-up of a scale (e.g., number of factors, cross-loadings of items, correlated errors, higher order factors). CFA results indicate whether a set of items can appropriately be used collectively to measure a construct, either for research or in practice. (Scale items supported in a factor analysis are often subsequently subjected to an internal consistency reliability test to further support their collective use.) We should note, however, that examination of item thresholds obtained in the CFA analysis also provided insights into the range of the social isolation construct captured with items and corroborated the findings from the IRT analysis. IRT analyses, however, examine many more aspects of item performance.

We contend it is ideal to employ both methods to obtain the most comprehensive and informative picture of scale and item quality. Whether or not findings of the two approaches indicate the need for item or scale revisions, they ultimately contribute to a robust argument for the validity of the use of scale scores in social work practice or research.

Conclusion

Used in combination, findings from CFA and IRT can help build the validity argument for the use of scales in research and practice. Our example examined 14 aspects of scale quality, including evidence about model fit, the adequacy of internal structure, and the reliability and precision of scale and item scores (American Educational Research Association et al., 2014). Two potential outcomes of the evaluation of a scale with both approaches are (a) demonstration of scale adequacy and (b) identification of specific ways in which the scale can be improved. Although it would be ideal to “pass” all 14 tests, as with all statistical analyses, researchers must use their judgment about the combination of findings and their implications for the validity argument for a scale. In addition, scale constructs and items must be informed by theory, not only statistical features.

The CFA and IRT analyses of the Social Isolation Scale identified many strengths of the scale, but also several limitations that could guide efforts to improve the scale. Results of the two approaches supported the conclusion of unidimensionality and adequate overall model fit. Both CFA factor loadings and IRT slope parameters indicated items were responsive to differences in levels of the latent construct or θ. However, findings from the two methods also converged around the conclusion that scale failed to measure lower levels of social isolation. Both the CFA thresholds and the IRT location parameters highlighted the fact that below-average levels of social isolation were not distinguished well with the five items, suggesting construct underrepresentation (American Educational Research Association et al., 2014, p. 12). These convergent findings indicate the need to refine the scale; adding items that better capture lower levels of isolation would improve the validity of its scores.

CFA and IRT also contribute unique information about the quality and performance of scales. CFA, for example, can identify error structures that include systematic and random sources of error. No correlated errors were indicated in the CFA results for the Social Isolation Scale. Correlated errors are acceptable but not desirable. They can be modeled in research analyses, however, in practice, when item scores are summed or averaged, correlated errors are ignored. In the development of scales to be used primarily in practice, researchers may need to consider deleting or revising at least one of the problem items.

Unlike in CFA results, IRT provides extensive item-level detail that can inform scale revisions. The traditional assessment of the reliability and precision of score estimates is based on an internal consistency reliability coefficient (e.g., coefficient alpha, omega) and a standard error of measurement coefficient based on a classical test theory model. These coefficients assume that scale reliability and estimated precision using standard error of measurement confidence intervals are the same for all scores (DeMars, 2010). In contrast, in IRT models the scale information function, conditional standard error function, and conditional reliability make it possible to identify where along θ scores are optimal. For example, we determined that the isolation scale operated with most precision and highest reliability in the 0 ≤ θ ≤ +2 range. This is not to say the scores outside this range are not useful, but that scale users should be aware that low scores (θ ≤ 0) and higher scores (θ ≥ +2) may not be estimated with the same precision.

Our internal structure, reliability, and precision results underscore the relationship between reliability and the validity argument. By adding items designed to measure lower levels of social isolation, we improve both construct representation (validity) and extend scale information, conditional standard errors, and conditional reliability across a broader range of θ. Note that this is not same as the common practice of adding items to a scale to increase internal consistency reliability (per the Spearman-Brown prophecy formula), rather, it is a focused, intentional effort to add items targeted to measure a level of θ.

Despite their many valuable features, there are barriers to the use of CFA and IRT in social work research. Specialized software is required for advanced CFA modeling that takes into account common characteristics of social work data, such as ordinal variables, non-normal distributions, weights, missing values, and clustering of cases. Both SEM and IRT software can be expensive; however, the open-source R statistical computing environment and a wide array of specialized R packages can be used for both types of analyses. Separate from the software cost is the issue of statistical training to properly conduct and interpret CFA and IRT analyses. As more free resources are developed by social workers and for social workers (for example, see https://rpubs.com/JBean), the training barrier can be reduced.

Two additional important issues were beyond the scope of this article but should be the focus of future studies: (a) an examination about how the Social Isolation Scale works in assessing change, and (b) an examination of item and scale invariance or differential functioning across time and groups. Both CFA and IRT can be used for this extended look at the scale. In a recent article, Nugent, (2017) stressed the need to examine differential item functioning and differential test function in the context of IRT. He discussed the implications of ignoring item and test differential functioning the most egregious of which is that a relationship between measures may be more a function of measurement nonequivalence than of substantive differences if differential functioning is present (Nugent, 2017, p. 306). There is a large set of factors and characteristics that potentially could drive differences in how students perceive social isolation: gender, race, socioeconomic status, and neighborhood are just a few examples. Ignoring differential functioning or measurement invariance across populations, for example, based on race, can lead to erroneous and potentially harmful comparisons about the attitudes, behaviors, and well-being of different groups.

As with all studies, our conclusions must be tempered by a few cautions and limitations. First, the study used a purposive sample of students. In addition, students whose parents failed to provide data were excluded due to the absence of demographic information. Although the article was designed to illustrate to complementary nature of CFA and IRT, these sample limitations reduce the generalizability of our findings. This limitation is less relevant to the IRT analysis. A particular strength of IRT is that parameter estimates are not completely sample dependent (Reise, 2015), that is, the estimated item parameters (slopes and thresholds) theoretically will be the same (or nearly the same) in different populations (DeMars, 2010). These limitations notwithstanding, we think our comprehensive analysis of the Social Isolation Scale adds substantively to the validity of its use in schools.

Replication

For readers interested in replicating the IRT analysis presented in this article, data and R files can be downloaded from: https://github.com/JerryBean46/Isolation-Markdown. Follow the directions listed in the README.md document. If you require assistance, contact the first author.