Preferential orientation of diamond formation on TaC: Diamond(111)//TaC(111)

Abstract

Experimental results showed that for the diamond film prepared by hot filament chemical vapor deposition (HFCVD) using Ta filament, TaC existed between diamond and the silicon substrate, and diamond grew directly on TaC, while the inherent mechanism was not clear. Here, a special coherent interface Diamond(111)//TaC(111) is observed using high resolution transmission electron microscopy, and then we explore the effects of the TaC with different lattice planes on the diamond formation by first-principle calculations. The results show that C tends to adsorb on the TaC(111) C-terminated surface. The strong covalent bond between C from diamond and Ta from TaC is formed in the Diamond(111)//TaC(111) interface, while only C–C covalent bonds are formed at the Graphite(002)/TaC(111). This makes diamond thermodynamically more stable than graphite on the TaC surfaces. Our investigations provide critical information to understand the complex diamond formation mechanism, especially with the presence of TaC.

Keywords:

• Diamond film
• HFCVD
• TaC
• Diamond(111)/TaC(111) interface
• Graphite(002)/TaC(111) interface

1. Introduction

Hot filament chemical vapor deposition (HFCVD) is a widely used method for the preparation of diamond film at low-pressure, since it has the advantage of a fast growth rate and large deposition area [1–4]. Eversole et al. successfully deposited diamonds at low pressure using the CVD method, and then Matsumoto et al. had been able to increase the growth rate of diamond by using hot metal filaments [5]. The growth of diamond by HFCVD is influenced by many factors because of the complexity of the experimental condition. Song et al. [6] found that when methane was used as the carbon source for diamond deposition, excessively high concentrations of methane increased the non-diamond phase, which reduced the growth rate of diamond. Yue et al. [7] indicated that the temperature of the filament affected the reaction at its surface and thus governed the diamond film deposition.

Non-diamond phases are produced and affect the formation of diamond during the complex HFCVD deposition process. Various carbon allotropes, such as i-carbon [8] and n-diamond [9], provided new perspectives on the growth mechanism of nanodiamond vapor phase synthesis and HFCVD diamond. Park et al. [10] observed that i-carbon and n-diamond were formed during the initial stages of diamond growth. Zhu et al. [11] found that i-carbon occurred as a phase transition intermediate during the transformation of graphite to diamond at ordinary pressure. Furthermore, due to the use of hot metal filaments, the metal carbides phase inevitably be formed, which affects the nucleation and growth of diamond. Zhang et al. [12] found that the WC interlayer acted as a diffusion barrier for carbon, thus significantly enhancing the nucleation properties of diamond. Aoki et al. [13] reported that the WC transition layer provided nucleation sites for diamond growth, and the diamond(111) surface grew epitaxially on the WC(001) surface.

In addition to tungsten (W), tantalum (Ta) wire served as another prevalent metal filament [7,11,14,15]. Various methods involved the incorporation of Ta into diamond films during deposition. The introduction of monodisperse Ta atoms effectively reduced the potential barrier necessary for the phase transition, facilitating the ordinary-pressure transformation of graphite into diamond [15]. Moreover, the formation of tantalum carbide (TaC) was an inevitable outcome during the growth of diamond films in HFCVD systems utilizing Ta filaments [14,16,17]. TaC was assumed as a crucial role in the nucleation of diamond. Soto et al. [18] undertook the preparation of TaC through HFPVD, transitioning from PVD to CVD. This strategic shift enabled the successful growth of diamond on in-situ deposited TaC. Interestingly, a composite of TaC and diamond powders exhibited a greater promotion of CVD diamond nucleation compared to using pure diamond powders [19]. Nevertheless, the precise mechanism underlying diamond formation on TaC remains unclear.

In this work, we used Ta wire as the metal filament to grow nanodiamond film on the single-crystal silicon substrate in the HFCVD system. TaC was found to exist between silicon and diamond, and the diamond was grown directly on TaC, satisfying a special interface relationship: Diamond(111)//TaC(111). And then we investigated the structural stability and bonding properties of the interface by first-principles calculation. The results show that diamond is more stable than graphite on the TaC surface. Our results provide critical information to understand the complex diamond film formation, especially with the presence of TaC.

2. Experimental and calculation methods

2.1 Experimental method

2.1.1 Pretreatment of substrate

The nanodiamond films were deposited using the HFCVD method with single-crystal silicon, orienting along [100] axis, as the substrate (size of 10 × 10 mm²). Before deposition, the nanodiamond powder was mixed with deionized water in a ratio of 1:100 and sonicated in an ultrasonic machine for 5 min to obtain the abrasive solution. The silicon wafer was placed on a polishing cloth and polished with an abrasive solution for 30 min and sonicated in the abrasive solution for 30 min, then rinsed with deionized water and sonicated in an acetone solution for 5 min.

2.1.2 Preparation of nanodiamond films

Ta wires were used as the hot filaments and carbonized before the deposition of the nanodiamond films. (filament number = 6, diameter = 0.8 mm). The 8 pre-treated samples were placed 7 mm below the Ta filaments. During the diamond deposition, acetone as a carbon source, H₂ gas was bubbling through acetone (∼80 sccm, maintained at 0°C), and extra amount of H₂ gas (∼200 sccm) was introduced into the reaction chamber. The pressure of the chamber was maintained at 1 kPa. The growth power was set as 4400 W and the deposition time was 1 h. The temperatures of the Ta filament and the substrate were about 2200°C and 650°C, respectively.

2.2 Calculation method

In this work, the Vienna Ab initio Simulation Package (VASP) software package based on density functional theory (DFT) was adopted for all calculations [20]. The Perdew–Burke–Emzerh (PBE) functional under the generalized gradient approximation (GGA) was used to describe the exchange-correlation energy [21] and projector augmented wave potential (PAW) [22] was used to deal with the interaction between ion and valence electrons. The Brillouin region was sampled by k-point grid of Monkhorst-pack method [23]. In the calculations, the cut-off energy for bulk TaC and diamond was all set at 500 eV. The k-point sampling grids for bulk TaC and diamond were all set to 8 × 8 × 8, while that for the surfaces and interfaces were set to 7 × 7 × 1. The SCF convergence tolerance of the total energy was 10⁻⁶eV/atom, and the maximum force was 0.001 eVÅ⁻¹.

3. Result and discussion

3.1 Interfacial selectivity of diamond growth on TaC

We prepared diamond films in HFCVD system using Ta filaments. There is an obvious peak of 1332 cm⁻¹ in the Raman spectrum (see Figure 1(a)), corresponding to diamond. SEM (see Figure 1(b)) also shows the typical morphology of nanodiamond films. To investigate the growth of diamond on the Si substrate, the sample was cut in cross-section using the focused ion beam (FIB) method and then characterized for the microstructure of the interface region between the diamond and Si substrate As shown in Figure 1(c), there is a transition region between the diamond and Si substrate with the thickness of about 10 nm. The elemental distribution shows that the region is rich in Ta and C elements. O atoms are uniformly dispersed in this interface region and the amount of O atoms is very little compared to other elemental atoms (see Figure S1). Further, the transition layer was characterized at a higher magnification, and the composition of the transition layer was studied in region 1 near the diamond and region 2 near the Si substrate, and the regions were subjected to Fourier transform (FT). The FT of region 1 (Figure 1 d-1 and FT-d1) shows the presence of two pairs of bright diffraction point, corresponding to diamond (111) plane with a crystalline spacing of 0.206 nm and the TaC(111) plane with a crystalline spacing of 0.264 nm. The lattice stripes are marked in red and yellow respectively in region 1, which are parallel to each other. In region 2, in addition to diamond (111) and TaC(111), there is a diffraction point corresponding to the Si(311) with a crystalline spacing of 0.131 nm (see Figure 1 d-2 and FT-d2). The results show that during the growth of diamond on Si substrate, TaC forms on the Si surface firstly, and then diamond grows directly on the surface of TaC, forming a coherent interface and a special orientation relationship: Diamond(111)//TaC(111).

Figure 1. (a) Raman spectrum and (b) FESEM image of the as-deposited nanocrystalline diamond film; (c) low-magnification TEM image of the interface region; (I) the HAADF image; (II)-(IV) EDX mapping information of Si, Ta, and C, respectively. (d) High-magnification TEM image of the interface region, corresponding enlarged images and FT images of regions 1 and 2 in (b).

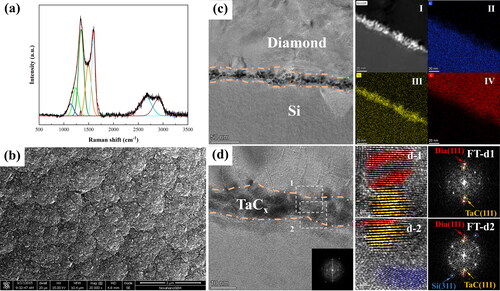
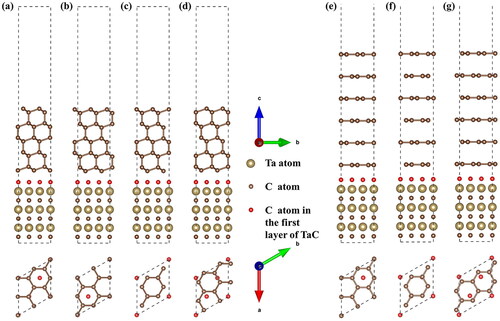
Figure 2. Side view and top view of the four different Diamond111)/TaC (111) interface models: (a) Dia-Model I, (b) Dia-Model II, (c) Dia-Model III, (d) Dia-Model IV, and the three different graphite (002)/TaC (111) interface models: (e) Gra-Model Ⅴ, (f) Gra-Model Ⅵ, (g) Gra-Model Ⅶ.

In Soto’s work [18], TaC substrate provided excellent nucleation sites for diamond. Significantly, the XRD of the substrate showed a distinct peak corresponding to TaC(111). Li and coworkers [16] clarified that TaC was formed during the deposition of the BDD films, and XRD profile of the diamond films deposited on the TaC exhibited the diffraction peaks characteristic of the Diamond(111) facet. The co-existence of two strong peaks, TaC(111) and Diamond(111), was observed by Mahtab [17] in the XRD patterns of diamond films grown using Ta filaments. These are consistent with our conclusions. The special orientation growth relationship between TaC and diamond provides a clearer understanding of the complex formation process of diamond films deposited in HFCVD systems.

3.2 First-principles calculations of Diamond/TaC interfacial properties

To understand the formation mechanism of the interfacial structure, we studied the adsorption energy, structural stability and bonding properties of the interface by performing first-principles calculations.

3.2.1 Adsorption energy of C atom on the TaC surfaces

In order to clarify on which TaC surface C atom is more likely to adsorb during the deposition process, we calculated the adsorption energy of the C atom on three common TaC surfaces: TaC(111), TaC(110), and TaC(100). The convergence of these surfaces was carefully tested to determine the number of atomic layers required for the surface model to deliver accurate results with reasonable computation cost. It is noted that there are two types of termination for the TaC(111) surface: C-terminated and Ta-terminated. When the number of atomic layers (n) is odd, the plate model is symmetric, which can eliminate the dipole effect [24]. So, the model with an odd atomic layer is applied in the following calculation. To determine the appropriate number of atomic layers, the change percentage (${\Delta }_{\mathit{\text{ij}}}$) in the interlayer is calculated according to Equation (1)(1) $${\Delta }_{\mathit{\text{ij}}}=\frac{d_{\mathit{\text{ij}}}-d_{\mathit{\text{ij}}}^0}{d_{\mathit{\text{ij}}}^0}\times 100\mathrm{\%}$$(1) as below: (1) $${\Delta }_{\mathit{\text{ij}}}=\frac{d_{\mathit{\text{ij}}}-d_{\mathit{\text{ij}}}^0}{d_{\mathit{\text{ij}}}^0}\times 100\mathrm{\%}$$(1) where $d_{\mathit{\text{ij}}}^0$ represents the spacing between i and j layers in the unrelaxed crystal, $d_{\mathit{\text{ij}}}$ represents the spacing between i and j layers in the crystal after relaxation. The calculation results are shown in Table S1. Note that the increase of atomic layers, Δ₁₂ and Δ₂₃, reach converge gradually as the slab interiors exhibit bulk-like properties. The change in $d_{\mathit{\text{ij}}}$ of the first four layers of atoms is small when the number of atomic layers is increased to 7.

TaC(110) and TaC(100) are non-polar surfaces and surface energy equation is defined as Equation (2)(2) $$E_{\mathit{\text{surf}}}=\frac{{E_{\mathit{\text{Slab}}}^{\mathit{\text{surf}}}}_{\mathrm{ }}-\left(\frac{N_{\mathit{\text{slab}}}}{N_{\mathit{\text{bulk}}}}\right)E_{\mathrm{\text{bulk}}}}{2A}$$(2) : (2) $$E_{\mathit{\text{surf}}}=\frac{{E_{\mathit{\text{Slab}}}^{\mathit{\text{surf}}}}_{\mathrm{ }}-\left(\frac{N_{\mathit{\text{slab}}}}{N_{\mathit{\text{bulk}}}}\right)E_{\mathrm{\text{bulk}}}}{2A}$$(2) where $E_{\mathit{\text{surf}}}$ is the surface energy of the TaC(110) or TaC(100), $E_{\mathit{\text{Slab}}}^{\mathit{\text{surf}}}$ is the total energy of the relaxed TaC(110) or TaC(100) surface model, $N_{\mathit{\text{slab}}}$ is the number of atoms of the TaC(110) or TaC(100) model, $N_{\mathit{\text{bulk}}}$ is the number of atoms of the bulk TaC cell, $E_{\mathit{\text{bulk}}}$ is the energy of the bulk TaC;, and $A$ signifies the TaC(110) or TaC(100) surface area.

As shown in Figure S2, 6-layer TaC(110) and TaC(100) surface are convergent and used to calculate in this work. The results of adsorption energy are listed in Table 1. It is observed that the adsorption energy of the TaC(111) C-terminated surface is the smallest. So C atoms are more easily adsorbed on the TaC(111) C-terminated surface, which is consistent with our TEM results. Therefore, the 7-layer TaC(111) C-terminated surface is selected for the study of the interface.

Table 1. Adsorption energy of C atom on TaC surfaces.

Plane of TaC	Termination	Site	Eads/eV
(111)	C-ter	FCC	−1.533
		HCP	−1.601
		Bridge	−2.385
	Ta-ter	HCP	0.242
		FCC	−0.262
(110)		Top_C	−0.012
		Bridge_C	−0.333
		Top_Ta	0.929
		Bridge_Ta	1.795
(100)		Top_C	1.803
		Top_Ta	5.031
		Bridge	1.452

3.2.2 Model construction and optimization

Based on our theoretical calculations and TEM results, we constructed the Diamond(111)/TaC(111) interface model. Considering that graphite is a competing phase for diamond during the deposition process [25,26], we constructed the Graphite(002)/TaC(111) interface model to compare the interfacial properties. The surface energy of diamond (111) with different atomic layers is shown in Table S2, which reveals that 10-layer Diamond(111) surface model is similar to the bulk structure, which is consistent with the calculations of Yue et al. [27]. According to the calculation results of the above convergence test, the model of Diamond/TaC interface was built with a superlattice geometry, in which a 10-layer Diamond(111) slab and a 7-layer TaC(111) slab are combined with the orientation relationship: Diamond[1 $\overline{1}$ 0]ǁTaC[2 $\overline{1}\mathrm{ }\overline{1}$] and Diamond(111)//TaC(111). Based on the Bramfitt lattice mismatch theory [28] that the lattice mismatch between two surfaces should be less than 6%, the lattice mismatches of Diamond(111)/TaC(111) are both about 4.42%, suggesting the formation of a coherent interface. Moreover, 6-layer graphite (002) slab and 7-layer TaC (111) slab are used to build the interface models, the lattice mismatches are about 5.4%. A 15 Å vacuum layer was added along the c direction in the model to avoid the interaction between the top and bottom layers.

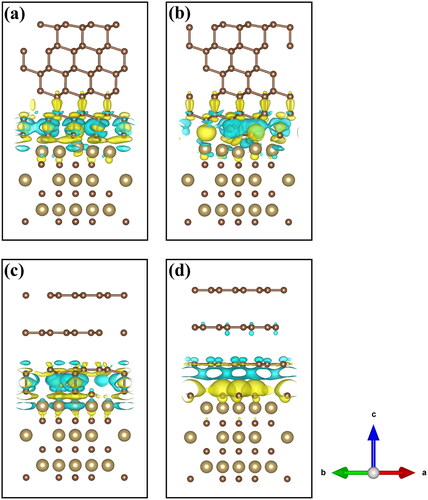
There are four Diamond(111)/TaC(111) interface models and three Graphite (002)/TaC(111) interface models constructed, as shown in Figure 2. The Dia-Model I, II, III, IV represent C atom in the first layer of TaC is located above the first layer of diamond, above the carbon atoms of the second diamond layer, above the carbon atom of diamond in the third layer, and between the two nearest carbon atoms in the first layer of the diamond, respectively. The Gra-Model Ⅴ, Ⅵ, and Ⅶ represents the C atom is located above the first layer of the graphite carbon atom, above the carbon atoms of the second graphite layer, and between the two nearest carbon atoms in the first layer of the graphite, respectively.

To construct the stable interfacial structure, we calculated the ideal adhesion work (W_ad), which is defined as the reversible work required to separate the interface into two free surfaces. The greater the value of adhesion work, the more stable the interface structure. The W_ad of these interfaces was calculated using a two-step approach. Firstly, according to the Universal Binding Energy Method (UBER) [29], the total energy of the unrelaxed interface with different interface distances was calculated and the relationship between W_ad and the different interface distances is shown in Figure 3. The highest point of the curve corresponds to the maximum W_ad and its optimal interface distance is listed in the “Unrelaxed (UBER)” column of Table 2. Secondly, the interfaces with the above optimal interface distance are fully relaxed and their W_ad are listed in the “Fully relaxed” column of Table 2. The W_ad is calculated by the following formula [30]: (3) $$W_{\mathit{\text{ad}}}=\frac{E_A+E_B-E_{\mathrm{A}/\mathrm{B}}}{A}$$(3) where $E_A$ and $E_B$ represents the total energy of diamond or graphite and TaC surface after fully relaxation, respectively, $E_{\mathrm{A}/\mathrm{B}}$ denotes the total energy of the diamond or graphite/TaC interface, and $A$ represents the interface area. Generally, when the adhesion work is larger, the bonding strength of the interface should be stronger and more stable.

Figure 3. Universal binding energy relation curves of four Diamond(111)/TaC (111) interfaces and three graphite (002)/TaC (111) interfaces.

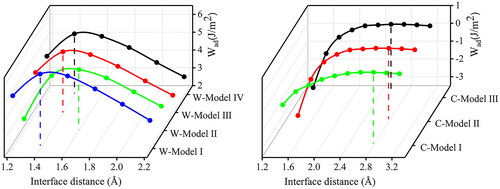
Table 2. Interface distance (d₀), adhesion work (W_ad) calculated using the two different methods (UBER and fully relaxation).

Models	Unrelaxed (UBER)		Fully relaxed
	d0 (Å)	Wad (J/m^2)	d0 (Å)	Wad (J/m^2)
Dia-Model I	1.470	4.688	1.479	5.659
Dia-Model II	1.479	4.689	1.436	6.186
Dia-Model III	1.579	4.697	1.435	6.187
Dia-Model IV	1.383	5.357	1.461	5.660
Gra-Model Ⅴ	2.625	0.618	1.607	0.964
Gra-Model Ⅵ	2.809	0.618	1.607	0.965
Gra-Model Ⅶ	2.818	0.610	2.935	0.547

Among the four models for Diamond/TaC interface, Dia-Model I and Dia-Model IV, Dia-Model II and Dia-Model III have similar W_ad, respectively. To explain the changes in W_ad, we examined these atomic structures after relaxation (see Figure S3) and it was found that Dia-Model I and Dia-Model IV, Dia-Model II and Dia-Model III are similar, respectively, which is consistent with the result of the W_ad. Among the three models of Graphite/TaC interface, Gra-Model Ⅴ and Gra-Model Ⅵ have similar W_ad, and it is worth noting that the interface distance has been reduced significantly after the relaxation. In Figure S3, it is observed that a fraction of the C atoms in the first graphite layer in Gra-Model Ⅴ after relaxation have moved downwards to form elongated sigma bonds with the C atoms on the TaC surface, with the bond length of 1.61 Å. Gra-Model Ⅶ has the largest interface distance and the smallest value of W_ad. The C atoms do not move and form bond with atoms in the TaC since the interface only relies on van der Waals force interactions and Coulomb forces paly an insignificant role. Moreover, W_ad of Diamond/TaC interface (6.186 J/m²) is about 6.4 times greater than that of Graphite/TaC interface (0.965 J/m²), which indicates that Diamond/TaC interface is more stable.

3.2.3 Bonding properties of interface

The bonding characteristic between atoms at the interface determines the interface bonding strength. In this work, the charge density difference of four fully relaxed interfaces is calculated. The formula for calculating the charge density difference is as follows: (4) $$\Delta \rho ={\rho }_{\mathrm{A}/\mathrm{B}\mathrm{ }}-{\rho }_{\mathrm{A}}-{\rho }_{\mathrm{B}}$$(4) where $\Delta \rho$ is the charge density difference, ${\rho }_{\mathrm{A}/\mathrm{B}\mathrm{ }}$, ${\rho }_{\mathrm{A}}$, and ${\rho }_{\mathrm{B}}$ are the charge density distribution of diamond or graphite/TaC interface, diamond or graphite interface and TaC interface, respectively.

The calculated charge density difference of the diamond or graphite/TaC interfaces is shown in Figure 4, in which blue cyan and yellow regions represent electron depletion and aggregation, respectively. As shown in Figure 4(a,b), not only there is an obvious charge accumulation between the first layer of C atoms on the top surface of TaC and C atoms on the under surface of diamond, but also there is an obvious charge accumulation between the second layer of Ta atoms on the upper surface of TaC and the C atoms on the under surface of diamond, implying that the C–C covalent bond and C–Ta polar covalent bond are formed. In comparison, there is no charge accumulation between the Ta atoms and C atom of graphite, only the formation of covalent bonds between the carbon atoms. As shown in Figure 4(d), the electrons do not overlap between the interfaces and no bonding is formed. This is consistent with the results of the adhesion work.

Figure 4. Charge density differences for fully relaxed Diamond(111)/Tac(111) and Graphite(002)/Tac(111) interfaces, (a) Relaxed-Dia-Model I; (b) Relaxed-Dia-Model II; (c) Relaxed-Gra-Model Ⅴ; (d) Relaxed-Gra-Model Ⅶ.

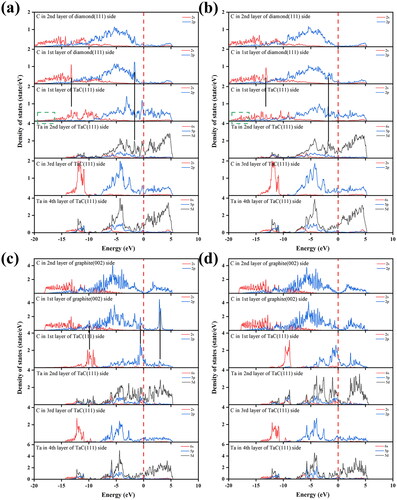
To further understand the bonding information of the diamond or graphite/TaC interfaces, we calculated the partial density of states (PDOS) at the interface, as shown in Figure 5. It is observed from Figure 5 (a) that the C-2s orbital of diamond forms a clear overlapping peak at –13.2 eV with the C-2s orbital of TaC, while the C-2p orbital of diamond forms a clear overlapping peak at –1.7 eV with the Ta-5d orbital of TaC. These overlapping peaks indicate that C–C and C–Ta covalent bonds are formed between diamond surface and TaC surface. Similarly, we also observe the presence of these two overlapping peaks in the PDOS of the Relaxed-Dia-Model II interface. Moreover, in the energy region around –17.2 eV, the first layer C atoms of TaC at the Relaxed-Dia-Model II interface form overlapping peaks with the first layer C atoms of diamond, which is not present at the Relaxed-Dia-Model I interface. This indicates that the covalent bonds formed at the Relaxed-Dia-Model II interface are stronger, resulting in a greater work of adhesion, which is consistent with the results of the adhesion work. C-Ta strong covalent bond makes Diamond/TaC interface bonding more stable. As can be observed in Figure 5c, there are two overlapping peaks at 2.9 and –9.9 eV, contributed by the 2p orbitals of the C atoms in graphite with the 2p orbitals of the C atoms in TaC and the 2s, 2p orbitals of the C atoms in graphite with the 2s orbitals of the C atoms in TaC, respectively. This indicates that C–C covalent bond is formed between the two layers of carbon atoms. Also, there are no overlapping peaks between the two layers of carbon atoms at the Relaxed-Gra-Model Ⅶ interface in Figure 5d, which indicates that the interface interacts with each other only by van der Waals forces.

Figure 5. Partial density of states (PDOS) for fully relaxed Diamond(111)/Tac(111) and Graphite(002)/Tac(111) interfaces, (a) Relaxed-Dia-Model I; (b) Relaxed-Dia- Model II; (c) Relaxed-Gra-Model Ⅴ; (d) Relaxed-Gra-Model Ⅶ.

4. Conclusion

We deposited nanodiamond films on the silicon substrate using Ta filament by HFCVD. TEM results revealed that TaC transition layer was found to be formed between diamond and substrate, and TaC formed a coherent interface with a special phase relationship: Diamond(111)//TaC(111). First-principles calculated adsorption energy of C atom on the TaC surfaces. The result indicates that C atoms are more likely to adsorb on the TaC (111) C-terminated surface. The structural stability and bonding properties of Diamond/TaC and Graphite/TaC interfaces were further calculated. Diamond(111)/TaC(111) interfacial adhesion work (6.186 J/m²) was much greater than the Graphite(002)/TaC(111) interfacial adhesion work (0.965 J/m²), which indicates that diamond is more stable than graphite on the TaC surface. The results of differential charge and electron density of states show that not only C–C covalent bond but also C–Ta covalent bond are formed, making the Diamond(111)/TaC(111) interface more stable, while only C–C covalent bonds are formed at the Graphite(002)/TaC(111). Our investigations provide critical information to understand the complex diamond formation mechanism, especially with the presence of TaC.

Authors’ contributions

Shaohua Lu: investigation, data curation, writing—original draft, visualization. Xiongtao Zhang: investigation, data curation, writing the original draft. Yuhao Zheng: investigation, data curation. Meiyan Jiang: formal analysis. Chengke Chen: formal analysis. Xiaojun Hu: funding acquisition, conceptualization, supervision, writing—review & editing.

Disclosure statement

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Funding

This work was supported by Key Project of National Natural Science Foundation of China (Grant No. U1809210) and National Natural Science Foundation of China (Grant Nos. 52102052, 11504325, 52002351, 50972129 and 50602039); International Science and Technology Cooperation Program of China (2014DFR51160); Natural Science Foundation of Zhejiang Province (LQ15A040004, LY18E020013 and LGC21E020001); and Key Research and Development Program of Zhe Jiang Province (2018C04021).