Some mathematical properties of Odd Kappa-G family

ABSTRACT

We present in this paper further mathematical properties of the Odd Kappa-G family of distributions. These structural properties of this family hold for any baseline model including characterizations results based on two truncated moments and hazard and reversed hazard functions. In addition, $k$th lower record values and extreme values of this Odd Kappa-G family are introduced. Lastly, the bivariate probability distributions of the Odd Kapp-G (BFGMOKG) family based on FGM copula are obtained.

KEYWORDS:

• Kappa distribution
• characterizations
• truncated moments
• hazard function
• record values
• extreme values
• FGM copula

View correction statement:

Correction

1. Introduction

In recent decades, many classical distributions have been widely employed for data modeling in a variety of fields such as demographics, economics, finance, insurance, biological research, medicine, engineering, environment and actuarial sciences. However, because of their lack of flexibility, various methods for generating new distributions from these old ones have piqued the interest of theoretical and applied statisticians in recent years

Albert & Olkin (1997) suggested an innovative method for adding a new parameter to an existing distribution in order to create a more flexible new family of distributions. Eugene et al. (2002) proposed a new class of distributions based on the beta distribution. M.C. Jones (2009) and Gauss & de Castro (2011) extended the beta-generated technique with the Kumaraswamy distribution as a generator instead of beta distribution.

Other known generators, just to mention a few, include gamma-G type 1 by Zografos & Balakrishnan (2009), gamma-G type 2 by Miroslav & Balakrishnan (2012), gamma-G type 3 by Torabi & Montazeri Hedesh (2012), McDonald-G (Mc-G) by Alexander et al. (2012), Weibull-G by Bourguignon et al. (2014), Transformed-Transformer (T-X) by Alzaatreh et al. (2013), exponentiated (T-X) by Alzaghal et al. (2013), T-X $\{$ Y $\}$ -quantile based approach by Aljarrah et al. (2014), T-R $\{$ Y $\}$ by Alzaatreh et al. (2014). alpha power transformation introduced by Mahdavi & Kundu (2017). Furthermore, Al-Shomrani et al. (2016) established the Topp–Leone family of distributions by employing the Topp–Leone distribution. Moreover, Al-Shomrani (2018) introduced new generalized statistical probability distributions based on extensions of beta and hypergeometric distributions. For other revisions of other generators, see M. C. Jones (2015), Famoye et al. (2013), Lee et al. (2013), Tahir & Nadarajah (2015) and Muhammad & Gauss (2016).

The Kappa distribution, an attractive asymmetric distribution, was introduced by Paul (1973) and Paul & Earl (1973). This distribution has recently received increased attention in hydro-logical research for the use in the evaluation of precipitation, stream-flow and wind speed data. The three-parameter Kappa cumulative distribution function (cdf; (Paul & Earl, 1973)) is

(1.1) $R\left(t\right)=\frac{{\left(\frac{t}{b}\right)}^{\lambda }}{{\left[a+{\left(\frac{t}{b}\right)}^{a\lambda }\right]}^{\left(\frac{1}{a}\right)}}\mathrm{f}\mathrm{o}\mathrm{r}t,a,b\mathrm{a}\mathrm{n}\mathrm{d}\lambda >0,$(1.1)

where $a$ and $\lambda$ are shape parameters and $b$ is a scale parameter. The probability density function (pdf) is

(1.2) $r\left(t\right)=\frac{a\lambda }{b}{\left(\frac{t}{b}\right)}^{\lambda -1}{\left[a+{\left(\frac{t}{b}\right)}^{a\lambda }\right]}^{-\left(\frac{a+1}{a}\right)}\mathrm{f}\mathrm{o}\mathrm{r}t,a,b\mathrm{a}\mathrm{n}\mathrm{d}\lambda >0.$(1.2)

Note that if $\lambda =b=1$, the three-parameter Kappa distribution reduces to one-parameter Kappa distribution. Also, if $\lambda =1$, the three-parameter Kappa distribution reduces to two-parameter Kappa distribution.

The Kappa distribution was extended in certain ways. Hussain (2015) suggested three expanded versions of the Kappa distribution: Kumaraswamy generalized Kappa (KGK), McDonald generalized Kappa (McGK) and Exponentiated generalized Kappa (EGK). The author examined the different statistical characteristics of those new extended forms, used different approaches to assess their unknown parameters and applied these models to real-world datasets. Javed et al. (2019) proposed the Marshall-Olkin Kappa (MOK) distribution while Nawaz et al. (2020), derived from Hussain (2015), offered the Kumaraswamy generalized Kappa (KGK) distribution.

As an extension of Kappa distribution with its cdf and pdf is shown, respectively, in Equation (1.1)(1.1) $R\left(t\right)=\frac{{\left(\frac{t}{b}\right)}^{\lambda }}{{\left[a+{\left(\frac{t}{b}\right)}^{a\lambda }\right]}^{\left(\frac{1}{a}\right)}}\mathrm{f}\mathrm{o}\mathrm{r}t,a,b\mathrm{a}\mathrm{n}\mathrm{d}\lambda >0,$(1.1) and (1.2(1.2) $r\left(t\right)=\frac{a\lambda }{b}{\left(\frac{t}{b}\right)}^{\lambda -1}{\left[a+{\left(\frac{t}{b}\right)}^{a\lambda }\right]}^{-\left(\frac{a+1}{a}\right)}\mathrm{f}\mathrm{o}\mathrm{r}t,a,b\mathrm{a}\mathrm{n}\mathrm{d}\lambda >0.$(1.2) ), Al-Shomrani & Al-Arfaj (2021) presented a new flexible family of distributions called the Odd Kappa-G family whose cdf is defined as

(1.3) $F\left(x;\alpha ,\beta ,\theta ,\vartheta \right)={\left[\frac{{\left(\frac{G(x;\vartheta )}{\beta \left[1-G(x;\vartheta )\right]}\right)}^{\alpha \theta }}{\alpha +{\left(\frac{G(x;\vartheta )}{\beta \left[1-G(x;\vartheta )\right]}\right)}^{\alpha \theta }}\right]}^{\left(\frac{1}{\alpha }\right)},x\in R.$(1.3)

The pdf of the Odd Kappa-G family of distributions can be expressed as follows:

$f\left(x;\alpha ,\beta ,\theta ,\vartheta \right)=\frac{\alpha \theta }{\beta }\left(\frac{g\left(x;\vartheta \right)}{{\left[1-G\left(x;\vartheta \right)\right]}^2}\right){\left(\frac{G\left(x;\vartheta \right)}{\beta \left[1-G\left(x;\vartheta \right)\right]}\right)}^{\theta -1}\times$

(1.4) ${\left[\alpha +{\left(\frac{G(x;\vartheta )}{\beta \left[1-G(x;\vartheta )\right]}\right)}^{\alpha \theta }\right]}^{-\left(\frac{\alpha +1}{\alpha }\right)}.$(1.4)

where $f\left(x;\alpha ,\beta ,\theta ,\vartheta \right)=\frac{d}{dx}F\left(x;\alpha ,\beta ,\theta ,\vartheta \right)$ and $g\left(x;\vartheta \right)=\frac{d}{dx}G\left(x;\vartheta \right)$ . $G\left(x;\vartheta \right)$ and $g\left(x;\vartheta \right)$ are, respectively, the cdf and pdf of the baseline distribution with parameter(s) $\vartheta$. Moreover, the survival or reliability function (sf) of the Odd Kappa-G family of distributions is defined as the following:

(1.5) $S\left(x;\alpha ,\beta ,\theta ,\vartheta \right)=1-{\left[\frac{{\left(\frac{G(x;\vartheta )}{\beta \left[1-G(x;\vartheta )\right]}\right)}^{\alpha \theta }}{\alpha +{\left(\frac{G(x;\vartheta )}{\beta \left[1-G(x;\vartheta )\right]}\right)}^{\alpha \theta }}\right]}^{\left(\frac{1}{\alpha }\right)},$(1.5)

Let $F\left(x\right)=F\left(x;\alpha ,\beta ,\theta ,\vartheta \right)$, $f\left(x\right)=f\left(x;\alpha ,\beta ,\theta ,\vartheta \right)$, $G\left(x\right)=G\left(x;\vartheta \right)$ and $g\left(x\right)=g\left(x;\vartheta \right)$. These shortcuts will be used throughout the paper when there is no confusion involved. Equation (1.4)(1.4) ${\left[\alpha +{\left(\frac{G(x;\vartheta )}{\beta \left[1-G(x;\vartheta )\right]}\right)}^{\alpha \theta }\right]}^{-\left(\frac{\alpha +1}{\alpha }\right)}.$(1.4) is most tractable when the cdf $G\left(x\right)$ and the pdf $g\left(x\right)$ have simple analytic expressions

Al-Shomrani & Al-Arfaj (2021) provided a comprehensive study of the mathematical properties of this new family; for instance, linear expansions for its cdf and pdf and explicit expressions for quantile function, the ordinary and incomplete moments, moment generating function, order statistics, Bonferroni and Lorenz curves, mean residual life, mean waiting time, mean deviations, entropy and other mathematical properties are derived. In this paper, further mathematical properties of this family such as characterization results of the Odd Kappa-G family based on two truncated moments and hazard and reversed hazard functions will be discussed. In addition, $k$th lower record values and extreme values of this Odd Kappa-G family are introduced. Lastly, the bivariate probability distributions of the Odd Kapp-G (BFGMOKG) family based on FGM copula are obtained. These topics will be introduced and studied thoroughly in this paper.

The rest of the paper is organized as follows. In Section 2, we introduce some characterization results of the Odd Kappa-G family including characterizations based on two truncated moments, hazard and reversed hazard functions. We discuss the $k$th lower record values of the Odd Kappa-G family in Section 3. In Section 4, extreme values for this family are presented. The bivariate cdf, pdf and sf of the Odd Kappa-G family based on FGM copula are obtained in Section 5. Finally, we give some concluding remarks in Section 6.

2. Characterizations results

2.1. Characterizations based on two truncated moments

In this section, we give characterizations of the Odd Kappa-G family of distributions in terms of a simple connection between two truncated moments. The characterization findings reported here will make use of intriguing theorem from Glänzel (1987) stated below. Because of the nature of the Odd Kappa-G family of distributions, we feel that our characterizations of Odd Kappa-G distribution may be the only ones conceivable. In this regard, we would like to highlight the work of Glänzel (1987, 1990), Glänzel & Hamedani (2001) and Hamedani (2010).

Theorem 2.1 (Glänzel, 1987). Suppose $\left(\mathrm{\Omega },\mathcal{A},\mathrm{P}\right)$ be a given probability space and let $X:\mathrm{\Omega }\to \mathrm{\Xi }$ be a continuous random variable with distribution function $F$, where $\mathrm{\Xi }=\left[a,b\right]$ for some $a<b$; $a=-\mathrm{\infty }$ and $b=+\mathrm{\infty }$ are not excluded. Let ${\xi }_1$ and ${\xi }_2$ be two real functions defined on $\mathrm{\Xi }$ such that $E\left[{\xi }_1\left(X\right)|X\ge x\right]=E\left[{\xi }_2\left(X\right)|X\ge x\right]$ $\delta \left(x\right),x\in \mathrm{\Xi }$, is defined with some real function $\delta$. Assume that ${\xi }_1,{\xi }_2\in C^1\left(\mathrm{\Xi }\right),\delta \in C^2\left(\mathrm{\Xi }\right)andF$ is twice continuously differentiable and strictly monotone function on the set $\mathrm{\Xi }$. Finally, assume that the equation $\delta {\xi }_2={\xi }_1$ has no real solution in the interior of $\mathrm{\Xi }$. Then, $F$ is uniquely determined by the functions ${\xi }_1,{\xi }_{2}and\delta$, particularly

$F\left(x\right)={\int }_a^{x}C\left|\frac{{\delta }^{\prime }\left(t\right)}{\delta \left(t\right){\xi }_2\left(t\right)-{\xi }_1\left(t\right)}\right|e^{-s\left(t\right)}dt,$

where the function $s$ is a solution of the differential equation $s^{\prime }=\frac{{\delta }^{\prime }{\xi }_2}{\delta {\xi }_2-{\xi }_1}$ and $C$ is a constant, chosen to make ${\int }_{\mathrm{\Xi }}dF=1$.

Remark 1. In the aforementioned Theorem 2.1, we could take ${\xi }_2\left(X\right)=1$ which reduces the condition to $E\left[{\xi }_1\left(X\right)|X\ge x\right]=\delta \left(x\right)$ but in terms of application, adding this function provides a lot more flexibility.

Proposition 1. Suppose $X:\mathrm{\Omega }\to \mathbb{R}$ be a continuous random variable and let

${\xi }_2\left(x\right)={\left(\beta \left[1-G\left(x\right)\right]\right)}^{\left(1+\theta \right)}{\left[\alpha +{\left(\frac{G\left(x\right)}{\beta \left[1-G\left(x\right)\right]}\right)}^{\alpha \theta }\right]}^{\left(\frac{\alpha +1}{\alpha }\right)}$

and ${\xi }_1\left(x\right)={\xi }_2\left(x\right)G\left(x\right)$ for $x\in \mathbb{R}$. The pdf of $X$ is (1.4) if and only if the function $\delta$ defined in Theorem 2.1 has the form

(2.1) $\delta \left(x\right)=\left(\frac{\theta }{\left(\theta +1\right)}\right)\frac{\left(1-{\left(G\left(x\right)\right)}^{\left(\theta +1\right)}\right)}{\left(1-{\left(G\left(x\right)\right)}^{\theta }\right)},x\in \mathbb{R}.$(2.1)

Proof. Using the same proof techniques used in Proposition 6 on page 83 in the work by Merovci et al. (2016), let $X$ has pdf (1.4); then, for $x\in \mathbb{R}$,

$\left[1-F_X\left(x\right)\right]E\left\{{\xi }_2\left(X\right)|X\ge x\right\}=\alpha \beta \left(1-{\left(G\left(x\right)\right)}^{\theta }\right),$

and

$\left[1-F_X\left(x\right)\right]E\left\{{\xi }_1\left(X\right)|X\ge x\right\}=\frac{\alpha \theta \beta \left(1-{\left(G\left(x\right)\right)}^{\left(\theta +1\right)}\right)}{\left(\theta +1\right)},$

and lastly,

$\begin{array}{rl}& \delta \left(x\right){\xi }_2\left(x\right)-{\xi }_1\left(x\right)=\frac{{\xi }_2\left(x\right)}{\left(\theta +1\right)\left(1-{\left(G\left(x\right)\right)}^{\theta }\right)}\\ & \left\{\theta -G\left(x\right)\left(\theta +\left(1-{\left(G\left(x\right)\right)}^{\theta }\right)\right)\right\}>0.\end{array}$

Conversely, if $\delta \left(x\right)$ is stated as in Equation (2.1(2.1) $\delta \left(x\right)=\left(\frac{\theta }{\left(\theta +1\right)}\right)\frac{\left(1-{\left(G\left(x\right)\right)}^{\left(\theta +1\right)}\right)}{\left(1-{\left(G\left(x\right)\right)}^{\theta }\right)},x\in \mathbb{R}.$(2.1) ), then

$s^{\prime }\left(x\right)=\frac{{\delta }^{\prime }\left(x\right){\xi }_2\left(x\right)}{\delta \left(x\right){\xi }_2\left(x\right)-{\xi }_1\left(x\right)}=\frac{\theta g\left(x\right){\left(G\left(x\right)\right)}^{\left(\theta -1\right)}}{\left(1-{\left(G\left(x\right)\right)}^{\theta }\right)},x\in \mathbb{R},$

from which we have

$s\left(x\right)=-log\left(1-{\left(G\left(x\right)\right)}^{\theta }\right),x\in \mathbb{R}.$

Hence, in light of Theorem 2.1, $X$ has pdf (1.4).

Corollary 2.2. Suppose $X:\mathrm{\Omega }\to \mathbb{R}$ be a continuous random variable and let ${\xi }_1\left(x\right)$ be as in Proposition 1. The pdf of $X$ is (1.4) if and only if there exist functions ${\xi }_2\left(x\right)$ and $\delta \left(x\right)$ defined in Theorem 2.1 satisfying the differential equation

$\frac{{\delta }^{\prime }\left(x\right){\xi }_2\left(x\right)}{\delta \left(x\right){\xi }_2\left(x\right)-{\xi }_1\left(x\right)}=\frac{\theta g\left(x\right){\left(G\left(x\right)\right)}^{\left(\theta -1\right)}}{\left(1-{\left(G\left(x\right)\right)}^{\theta }\right)},x\in \mathbb{R}.$

Remark 2. (1) The general solution of this differential equation in Corollary 2.2 is

$\delta \left(x\right)={\left(1-{\left(G\left(x\right)\right)}^{\theta }\right)}^{-1}\left\{-\int \theta g\left(t\right){\left(G\left(t\right)\right)}^{\left(\theta -1\right)}\frac{{\xi }_1\left(t\right)}{{\xi }_2\left(t\right)}dt+D\right\},$

where $D$ is a constant. One set of appropriate functions $\left({\xi }_1,{\xi }_2,\delta \right)$ that fulfill the aforementioned differential equation is given in Proposition 1 with $D=0$.

(2) It should be observed, however, that there are triplets $\left({\xi }_1,{\xi }_2,\delta \right)$ that meet the criteria of Theorem 2.1.

2.2. Characterizations based on hazard function

Definition 2.3. Assume that $F\left(x\right)$ be an absolutely continuous distribution with the associated pdf $f\left(x\right)$. The hazard function indicated by $h\left(x\right)$ and corresponding to $F\left(x\right)$ is defined by

$h\left(x\right)=\frac{f\left(x\right)}{1-F\left(x\right)}forx\in supportofF.$

The hazard function ($h\left(x\right)$) of a twice differentiable distribution function ($F\left(x\right)$) is known to satisfy the first-order differential equation

(2.2) $\frac{f^{\prime }\left(x\right)}{f\left(x\right)}=\frac{h^{\prime }\left(x\right)}{h\left(x\right)}-h\left(x\right)$(2.2)

The Proposition 2 that follows offers a non-trivial characterization of the Odd Kappa-G distribution, which does not have the trivial form given in Equation (2.2).

Proposition 2. Assume $X:\mathrm{\Omega }\to \mathbb{R}$ be a continuous random variable. For $\alpha =1$, the pdf of $X$ is (1.4) if and only if its hazard function $h\left(x\right)$ satisfies the differential equation

$h^{\prime }\left(x\right)-\frac{g^{\prime }\left(x\right)}{g\left(x\right)}h\left(x\right)=\theta {\left(g\left(x\right)\right)}^2{\left(\frac{G\left(x\right)}{\beta \left[1-G\left(x\right)\right]}\right)}^{\theta }\times$

(2.3) $\left\{\frac{\theta +\left(2G\left(x\right)-1\right)\left[1+{\left(\frac{G\left(x\right)}{\beta \left[1-G\left(x\right)\right]}\right)}^{\theta }\right]}{{\left(G\left(x\right)\left[1-G\left(x\right)\right]\right)}^2{\left[1+{\left(\frac{G\left(x\right)}{\beta \left[1-G\left(x\right)\right]}\right)}^{\theta }\right]}^2}\right\}$(2.3)

Proof. Suppose $X$ has pdf (1.4), then the above differential equation (2.3(2.3) $\left\{\frac{\theta +\left(2G\left(x\right)-1\right)\left[1+{\left(\frac{G\left(x\right)}{\beta \left[1-G\left(x\right)\right]}\right)}^{\theta }\right]}{{\left(G\left(x\right)\left[1-G\left(x\right)\right]\right)}^2{\left[1+{\left(\frac{G\left(x\right)}{\beta \left[1-G\left(x\right)\right]}\right)}^{\theta }\right]}^2}\right\}$(2.3) ) clearly holds. Conversely, if the differential equation (2.3(2.3) $\left\{\frac{\theta +\left(2G\left(x\right)-1\right)\left[1+{\left(\frac{G\left(x\right)}{\beta \left[1-G\left(x\right)\right]}\right)}^{\theta }\right]}{{\left(G\left(x\right)\left[1-G\left(x\right)\right]\right)}^2{\left[1+{\left(\frac{G\left(x\right)}{\beta \left[1-G\left(x\right)\right]}\right)}^{\theta }\right]}^2}\right\}$(2.3) ) holds, then

$\frac{d}{dx}\left[{\left(g\left(x\right)\right)}^{-1}h\left(x\right)\right]=\left(\frac{\theta }{\beta }\right)\frac{d}{dx}[\left(\frac{1}{{\left[1-G\left(x\right)\right]}^2}\right){\left(\frac{G\left(x\right)}{\beta \left[1-G\left(x\right)\right]}\right)}^{\theta -1}$

$\left.{\left[1+{\left(\frac{G(x)}{\beta \left[1-G(x)\right]}\right)}^{\theta }\right]}^{-1}\right],$

or

$\begin{array}{rl}& h\left(x\right)=\frac{\theta }{\beta }\left(\frac{g\left(x\right)}{{\left[1-G\left(x\right)\right]}^2}\right){\left(\frac{G\left(x\right)}{\beta \left[1-G\left(x\right)\right]}\right)}^{\theta -1}\\ & {\left[1+{\left(\frac{G(x)}{\beta \left[1-G(x)\right]}\right)}^{\theta }\right]}^{-1},\end{array}$

which is the hazard function of the Odd Kappa-G distribution for $\alpha =1$.

2.3. Characterizations based on the reversed hazard function

Definition 2.4. Assume that $F\left(x\right)$ be an absolutely continuous distribution with the associated pdf $f\left(x\right)$. The reversed hazard function indicated by $r\left(x\right)$ and corresponding to $F\left(x\right)$ is defined by

$r\left(x\right)=\frac{f\left(x\right)}{F\left(x\right)}forx\in supportofF.$

The reversed hazard function ($r\left(x\right)$) of a twice differentiable distribution function ($F\left(x\right)$) is known to satisfy the first-order differential equation

(2.4) $\frac{f^{\prime }\left(x\right)}{f\left(x\right)}=\frac{r^{\prime }\left(x\right)}{r\left(x\right)}+r\left(x\right)$(2.4)

The following Proposition 3 provides a non-trivial characterization of the Odd Kappa-G distribution, which does not have the simple form provided in Equation (2.4).

Proposition 3. Let $X:\mathrm{\Omega }\to \mathbb{R}$ be a continuous random variable. For $\alpha =1$, the pdf of $X$ is (1.4) if and only if its reversed hazard function $r\left(x\right)$ satisfies the differential equation

(2.5) $\begin{array}{rl}& r^{\prime }\left(x\right)-\frac{g^{\prime }\left(x\right)}{g\left(x\right)}r\left(x\right)=\theta {\left(g\left(x\right)\right)}^2\\ & \times \left\{\frac{\left(2G\left(x\right)-1\right)\left[1+{\left(\frac{G\left(x\right)}{\beta \left[1-G\left(x\right)\right]}\right)}^{\theta }\right]-\theta {\left(\frac{G\left(x\right)}{\beta \left[1-G\left(x\right)\right]}\right)}^{\theta }}{{\left(G\left(x\right)\left[1-G\left(x\right)\right]\right)}^2{\left[1+{\left(\frac{G\left(x\right)}{\beta \left[1-G\left(x\right)\right]}\right)}^{\theta }\right]}^2}\right\}\end{array}$(2.5)

Proof. let $X$ has pdf (1.4), then the above differential equation (2.5(2.5) $\begin{array}{rl}& r^{\prime }\left(x\right)-\frac{g^{\prime }\left(x\right)}{g\left(x\right)}r\left(x\right)=\theta {\left(g\left(x\right)\right)}^2\\ & \times \left\{\frac{\left(2G\left(x\right)-1\right)\left[1+{\left(\frac{G\left(x\right)}{\beta \left[1-G\left(x\right)\right]}\right)}^{\theta }\right]-\theta {\left(\frac{G\left(x\right)}{\beta \left[1-G\left(x\right)\right]}\right)}^{\theta }}{{\left(G\left(x\right)\left[1-G\left(x\right)\right]\right)}^2{\left[1+{\left(\frac{G\left(x\right)}{\beta \left[1-G\left(x\right)\right]}\right)}^{\theta }\right]}^2}\right\}\end{array}$(2.5) ) clearly holds. Conversely, if the differential equation (2.5(2.5) $\begin{array}{rl}& r^{\prime }\left(x\right)-\frac{g^{\prime }\left(x\right)}{g\left(x\right)}r\left(x\right)=\theta {\left(g\left(x\right)\right)}^2\\ & \times \left\{\frac{\left(2G\left(x\right)-1\right)\left[1+{\left(\frac{G\left(x\right)}{\beta \left[1-G\left(x\right)\right]}\right)}^{\theta }\right]-\theta {\left(\frac{G\left(x\right)}{\beta \left[1-G\left(x\right)\right]}\right)}^{\theta }}{{\left(G\left(x\right)\left[1-G\left(x\right)\right]\right)}^2{\left[1+{\left(\frac{G\left(x\right)}{\beta \left[1-G\left(x\right)\right]}\right)}^{\theta }\right]}^2}\right\}\end{array}$(2.5) ) holds, then

$\frac{d}{dx}\left[{\left(g\left(x\right)\right)}^{-1}r\left(x\right)\right]=\theta \frac{d}{dx}[\left(\frac{1}{G\left(x\right)\left[1-G\left(x\right)\right]}\right){\left[1+{\left(\frac{G(x)}{\beta \left[1-G(x)\right]}\right)}^{\theta }\right]}^{-1},$

or

$r\left(x\right)=\theta \left(\frac{g\left(x\right)}{G\left(x\right)\left[1-G\left(x\right)\right]}\right){\left[1+{\left(\frac{G(x)}{\beta \left[1-G(x)\right]}\right)}^{\theta }\right]}^{-1},$

which is the reversed hazard function of the Odd Kappa-G distribution for $\alpha =1$.

3. $k$th Lower record values

Chandler (1952) developed the notion of record values as a model for dependence structure of successive extremes in a sequence of randomly independently and identically generated variables. This indicates that the distribution of system component life-lengths may shift once each component fails. Many real-world applications requiring data relating to economics, sports, weather and life testing problems use record values. Therefore, the statistical analysis of record values has now been extended in many ways. Dziubdziela & Kopociński (1976) proposed the limiting distribution of $k$th upper record values by observing successive $k$ largest values in a sequence, where $k$ is a positive integer. Many researchers have thought about characterizing distributions using conditional expectation of record values (Al-Shomrani, 2016a; Al-Shomrani & Shawky, 2016; M. Franco & Ruiz, 1996; Hamid Khan et al., 2010; López Bláquez & Luis Moreno Rebollo, 1997; Manuel Franco & Jose, 1997; H. N. Nagaraja, 1988a and Al-Shomrani, 2016b). Further information on the theory of records and their characterizations and distributional properties can be found in, for example, Ahsanullah (1995, 2004), Barry et al. (1998), Deheuvels (1984), H.N. Nagaraja (1988b; Nevzorov (2001) and references therein.

Let $X_r^{\left(k\right)}$ denote the $k$th lower record value. The pdf $f_{X_r^{\left(k\right)}}\left(x\right)$ of the $k$th lower record value, for $k=1,\dots ,r$, from independently and identically distributed (iid) random variables $X_1,\dots ,X_r$ from the Odd Kappa-G distribution is given by (Ahsanullah, 2004; Barry et al., 1998)

$f_{X_r^{\left(k\right)}}\left(x\right)=\frac{k^r}{\mathrm{\Gamma }\left(r\right)}{\left(-log\left[F\left(x\right)\right]\right)}^{r-1}{\left(F\left(x\right)\right)}^{k-1}f\left(x\right)forr\ge 1$

By expanding the logarithm function in power series, we obtain

$\begin{array}{rl}{f}_{X_r^{\left(k\right)}}\left(x\right)=& \frac{k^r}{\mathrm{\Gamma }\left(r\right)}{\left(\sum _{i=1}^{\mathrm{\infty }}{\left(-1\right)}^i\frac{{\left[F\left(x\right)-1\right]}^i}{i}\right)}^{r-1}\\ & {\left(F\left(x\right)\right)}^{k-1}f\left(x\right)\end{array}$

See equation (1.512) on page 53 in the work by Solomonovich Gradshteyn & Moiseevich Ryzhik (2007).

By using the binomial expansion, we have

$\begin{array}{rl}{f}_{X_r^{\left(k\right)}}\left(x\right)=& \frac{k^r}{\mathrm{\Gamma }\left(r\right)}{\left(\sum _{i=1}^{\mathrm{\infty }}\sum _{j=0}^i\frac{{\left(-1\right)}^j}{i}\left(\begin{array}{c}i\\ j\end{array}\right){\left[F\left(x\right)\right]}^j\right)}^{r-1}\\ & {\left(F\left(x\right)\right)}^{k-1}f\left(x\right)\end{array}$

See equation (1.111) on page 25 in the work by Solomonovich Gradshteyn & Moiseevich Ryzhik (2007). This is the same as

$\begin{array}{rl}{f}_{X_r^{\left(k\right)}}\left(x\right)=& \frac{k^r}{\mathrm{\Gamma }\left(r\right)}{\left(\sum _{i=1}^{\mathrm{\infty }}\sum _{j=0}^{\mathrm{\infty }}\frac{{\left(-1\right)}^j}{i}\left(\begin{array}{c}i\\ j\end{array}\right){\left[F\left(x\right)\right]}^j\right)}^{r-1}\\ & {\left(F\left(x\right)\right)}^{k-1}f\left(x\right),\end{array}$

since $\left(\begin{array}{c}i\\ j\end{array}\right)=0ifj>i$. Therefore,

$\begin{array}{rl}{f}_{X_r^{\left(k\right)}}\left(x\right)=& \frac{k^r}{\mathrm{\Gamma }\left(r\right)}{\left(\sum _{j=0}^{\mathrm{\infty }}\sum _{i=1}^{\mathrm{\infty }}\frac{{\left(-1\right)}^j}{i}\left(\begin{array}{c}i\\ j\end{array}\right){\left[F\left(x\right)\right]}^j\right)}^{r-1}\\ & {\left(F\left(x\right)\right)}^{k-1}f\left(x\right).\end{array}$

From which we have

$f_{X_r^{\left(k\right)}}\left(x\right)=\frac{k^r}{\mathrm{\Gamma }\left(r\right)}{\left(\sum _{j=0}^{\mathrm{\infty }}{a}_j{\left[F\left(x\right)\right]}^j\right)}^{r-1}{\left(F\left(x\right)\right)}^{k-1}f\left(x\right),$

where $a_j={\sum }_{i=1}^{\mathrm{\infty }}\frac{{\left(-1\right)}^j}{i}\left(\begin{array}{c}i\\ j\end{array}\right)$. Then,

$f_{X_r^{\left(k\right)}}\left(x\right)=\frac{k^r}{\mathrm{\Gamma }\left(r\right)}\left(\sum _{j=0}^{\mathrm{\infty }}{b}_j{\left[F\left(x\right)\right]}^j\right){\left(F\left(x\right)\right)}^{k-1}f\left(x\right),$

where

$b_0={\left(a_0\right)}^{r-1}andforj\ge 1,b_j=\frac{1}{\left(j{a}_0\right)}\sum _{k=1}^j\left[kr-j\right]a_k{b}_{j-k},$

See equation (0.314) on page 17 in the work by Solomonovich Gradshteyn & Moiseevich Ryzhik (2007). Therefore,

(3.1) $f_{X_r^{\left(k\right)}}\left(x\right)=\frac{k^r}{\mathrm{\Gamma }\left(r\right)}\sum _{j=0}^{\mathrm{\infty }}{b}_j{\left[F\left(x\right)\right]}^{j+k-1}f\left(x\right).$(3.1)

From Proposition 5.1 in the work by Al-Shomrani & Al-Arfaj (2021), we have

(3.2) $F\left(x\right)=\sum _{p=0}^{\mathrm{\infty }}{w}_p{\left[G\left(x\right)\right]}^p,$(3.2)

and

(3.3) $f\left(x\right)=\sum _{p=0}^{\mathrm{\infty }}p{w}_{p}g\left(x\right){\left[G\left(x\right)\right]}^{p-1},$(3.3)

Substituting (3.2) and (3.3) into (3.1), we obtain

$\begin{array}{rl}& f_{X_r^{\left(k\right)}}\left(x\right)=\frac{k^r}{\mathrm{\Gamma }\left(r\right)}\sum _{j=0}^{\mathrm{\infty }}{b}_j{\left[\sum _{p=0}^{\mathrm{\infty }}{w}_p{\left[G\left(x\right)\right]}^p\right]}^{j+k-1}\\ & \left(\sum _{q=0}^{\mathrm{\infty }}q{w}_{q}g\left(x\right){\left[G\left(x\right)\right]}^{q-1}\right).\end{array}$

From which we have

(3.4) $\begin{array}{rl}& f_{X_r^{\left(k\right)}}\left(x\right)=\frac{k^r}{\mathrm{\Gamma }\left(r\right)}\sum _{j=0}^{\mathrm{\infty }}{b}_j\left(\sum _{p=0}^{\mathrm{\infty }}{c}_p{\left[G\left(x\right)\right]}^p\right)\\ & \left(\sum _{q=0}^{\mathrm{\infty }}q{w}_{q}g\left(x\right){\left[G\left(x\right)\right]}^{q-1}\right).\end{array}$(3.4)

where

$c_0={\left(w_0\right)}^{\left(j+k\right)-1}andforp\ge 1,c_p=\frac{1}{\left(p{w}_0\right)}\sum _{m=1}^p\left[m\left(j+k\right)-p\right]w_m{c}_{p-m},$

See equation (0.314) on page 17 in the work by Solomonovich Gradshteyn & Moiseevich Ryzhik (2007). Then, from Equation (3.4)(3.4) $\begin{array}{rl}& f_{X_r^{\left(k\right)}}\left(x\right)=\frac{k^r}{\mathrm{\Gamma }\left(r\right)}\sum _{j=0}^{\mathrm{\infty }}{b}_j\left(\sum _{p=0}^{\mathrm{\infty }}{c}_p{\left[G\left(x\right)\right]}^p\right)\\ & \left(\sum _{q=0}^{\mathrm{\infty }}q{w}_{q}g\left(x\right){\left[G\left(x\right)\right]}^{q-1}\right).\end{array}$(3.4) , we have

(3.5) $f_{X_r^{\left(k\right)}}\left(x\right)=\sum _{j,p,q=0}^{\mathrm{\infty }}{\phi }_{j,p,q}{h}_{p+q}\left(x\right),$(3.5)

where

${\phi }_{j,p,q}=\frac{k^r}{\mathrm{\Gamma }\left(r\right)}\frac{q{b}_j{c}_p{w}_q}{\left(p+q\right)}and{h}_{p+q}\left(x\right)=\left(p+q\right)g\left(x\right){\left[G\left(x\right)\right]}^{p+q-1}$

Equation (3.5)(3.5) $f_{X_r^{\left(k\right)}}\left(x\right)=\sum _{j,p,q=0}^{\mathrm{\infty }}{\phi }_{j,p,q}{h}_{p+q}\left(x\right),$(3.5) is the main result of this section. This shows that the pdf of the Odd Kappa-G $k$th lower record values is a triple linear combination of Exp-G densities. Some properties of the exp-G distributions are discussed by Gupta et al. (1998), Nadarajah & Kotz (2006) and Al-Hussaini & Ahsanullah (2015) among others.

4. Extreme values

Let $X_1,\dots ,X_n$ be a random sample from the pdf of the Odd Kappa-G distribution as in Equation (1.4)(1.4) ${\left[\alpha +{\left(\frac{G(x;\vartheta )}{\beta \left[1-G(x;\vartheta )\right]}\right)}^{\alpha \theta }\right]}^{-\left(\frac{\alpha +1}{\alpha }\right)}.$(1.4) and $\bar{X}=\left(X_1+\dots +X_n\right)/n$ denote the sample mean; then, the distribution of $\sqrt{n}\left(\bar{X}-E\left(X\right)\right)/\sqrt{Var\left(X\right)}$ approaches the standard normal distribution as $n\to \mathrm{\infty }$ by the usual central limit theorem under suitable conditions. In some cases, it is of interest to consider the asymptotic distributions of the extremes of order statistics $M_n=\mathrm{m}\mathrm{a}\mathrm{x}\left(X_1,\dots ,X_n\right)$ and $m_n=\mathrm{m}\mathrm{i}\mathrm{n}\left(X_1,\dots ,X_n\right)$. For further information in this topic, see, for instance, Coles (2001), Galambos (1987), Haan & Ferreira (2006), Kotz & Nadarajah (2000), Sidney (1987) and Arnold et al. (2008).

First, suppose that $G$ belongs to the maximal domain of attraction of the Gumbel extreme value distribution (see, Leadbetter et al., 2012). Let $\omega \left(G\right)=\mathrm{s}\mathrm{u}\mathrm{p}\left\{x|G\left(x\right)<1\right\}\le \mathrm{\infty }$ be the upper (right) end point of the cdf $G$. Then, there must exist a strictly positive function, say $\rho \left(t\right)>0$, such that

$\underset{t\uparrow \omega \left(G\right)}{lim}\frac{1-G\left(t+x\rho \left(t\right)\right)}{1-G\left(t\right)}=\mathrm{e}\mathrm{x}\mathrm{p}\left(-x\right)$

for every $x\in \mathbb{R}$. Let $\omega \left(F\right)=\mathrm{s}\mathrm{u}\mathrm{p}\left\{x|F\left(x\right)<1\right\}\le \mathrm{\infty }$ be the upper (right) end point of the cdf $F$. But, using L’Hopital’s rule and assuming $\omega \left(F\right)=\omega \left(G\right)$, we have

$\underset{t\uparrow \omega \left(F\right)}{lim}\frac{1-F\left(t+x\rho \left(t\right)\right)}{1-F\left(t\right)}=\underset{t\uparrow \omega \left(F\right)}{lim}\frac{\left[1+x{\rho }^{\prime }\left(t\right)\right]f\left(t+x\rho \left(t\right)\right)}{f\left(t\right)}$

$=\underset{t\uparrow \omega \left(G\right)}{lim}\frac{\left[1+x{\rho }^{\prime }\left(t\right)\right]g\left(t+x\rho \left(t\right)\right)}{g\left(t\right)}{\left[\frac{1-G\left(t+x\rho \left(t\right)\right)}{1-G\left(t\right)}\right]}^{-2}\times$

${\left(\frac{G\left(t+x\rho \left(t\right)\right)}{G\left(t\right)}\right)}^{\theta -1}{\left(\frac{1-G\left(t+x\rho \left(t\right)\right)}{1-G\left(t\right)}\right)}^{1-\theta }\times$

${\left[\frac{\alpha {\left(\beta \left[1-G(t+x\rho \left(t\right))\right]\right)}^{\alpha \theta }+{\left(G(t+x\rho \left(t\right))\right)}^{\alpha \theta }}{\alpha {\left(\beta \left[1-G(t)\right]\right)}^{\alpha \theta }+{\left(G(t)\right)}^{\alpha \theta }}\right]}^{-\left(\frac{\alpha +1}{\alpha }\right)}\times$

${\left[\frac{1-G(t+x\rho \left(t\right))}{1-G(t)}\right]}^{\left(\theta \left(\alpha +1\right)\right)}$

$=\mathrm{e}\mathrm{x}\mathrm{p}(-\alpha \theta x)$

for every $x\in \mathbb{R}$. Hence, it follows that $F$ also belongs to the maximal domain of attraction of the Gumbel extreme value distribution with

$\underset{n\to \mathrm{\infty }}{lim}\mathrm{P}\mathrm{r}\left(\left(M_n-a_n\right)/b_n\le x\right)=\mathrm{e}\mathrm{x}\mathrm{p}\left(-\mathrm{e}\mathrm{x}\mathrm{p}(-\alpha \theta x)\right),-\mathrm{\infty }<x<\mathrm{\infty }$

for some appropriate choices of the norming constants $a_n$ and $b_n>0$, where $a_n$ represents a shift in location and $b_n$ represents a change in scale. For instance, it follows from Corollary 1.6.3 in the work by Leadbetter et al. (2012) that the normalizing constants are $a_n=F^{-1}\left(1-1/n\right)$ and $b_n=\rho \left(a_n\right)>0$.

Second, assume that $G$ belongs to the maximal domain of attraction of the Fréchet extreme value distribution (see, Leadbetter et al., 2012). Then, $\omega \left(G\right)=\mathrm{\infty }$ and there must exist a $\tau >0$ such that

$\underset{t\to \mathrm{\infty }}{lim}\frac{1-G\left(tx\right)}{1-G\left(t\right)}=x^{-\tau }$

for every $x>0$. Therefore, $\omega \left(F\right)=\omega \left(G\right)=\mathrm{\infty }$ and by using L’Hopital’s rule, we note that

$\underset{t\to \mathrm{\infty }}{lim}\frac{1-F\left(tx\right)}{1-F\left(t\right)}=\underset{t\to \mathrm{\infty }}{lim}\frac{xf\left(tx\right)}{f\left(t\right)}=\underset{t\to \mathrm{\infty }}{lim}\frac{xg\left(tx\right)}{g\left(t\right)}{\left[\frac{1-G\left(tx\right)}{1-G\left(t\right)}\right]}^{-2}\times$

${\left(\frac{G\left(tx\right)}{G\left(t\right)}\right)}^{\theta -1}{\left(\frac{1-G\left(tx\right)}{1-G\left(t\right)}\right)}^{1-\theta }\times$

${\left[\frac{\alpha {\left(\beta \left[1-G(tx)\right]\right)}^{\alpha \theta }+{\left(G(tx)\right)}^{\alpha \theta }}{\alpha {\left(\beta \left[1-G(t)\right]\right)}^{\alpha \theta }+{\left(G(t)\right)}^{\alpha \theta }}\right]}^{-\left(\frac{\alpha +1}{\alpha }\right)}{\left[\frac{1-G(tx)}{1-G(t)}\right]}^{\left(\theta \left(\alpha +1\right)\right)}\times$

$=x^{-\alpha \theta \tau }$

for every $x>0$. So, it follows that $F$ also belongs to the maximal domain of attraction of the Fréchet extreme value distribution with

$\underset{n\to \mathrm{\infty }}{lim}\mathrm{P}\mathrm{r}\left(\left(M_n-a_n\right)/b_n\le x\right)=\mathrm{e}\mathrm{x}\mathrm{p}\left(-x^{-\alpha \theta \tau }\right),x>0$

for some appropriate choices of the norming constants $a_n$ and $b_n>0$. For example, it follows from Corollary 1.6.3 in the work by Leadbetter et al. (2012) that the normalizing constants are $a_n=0$ and that $b_n>0$ satisfies $1-F\left(b_n\right)\sim 1/n$.

Third, Let $G$ belong to the maximal domain of attraction of the Weibull extreme value distribution (see, Leadbetter et al., 2012). Then, $\omega \left(G\right)<\mathrm{\infty }$ and there must exist a $\varphi >0$ such that

$\underset{t\to 0}{lim}\frac{1-G\left(\omega \left(G\right)-tx\right)}{1-G\left(\omega \left(G\right)-t\right)}=x^{\varphi }$

for every $x<0$. Then, since $\omega \left(F\right)=\omega \left(G\right)<\mathrm{\infty }$ and by using L’Hopital’s rule, we have

$\underset{t\to 0}{lim}\frac{1-F\left(\omega \left(F\right)-tx\right)}{1-F\left(\omega \left(F\right)-t\right)}$

$=\underset{t\to 0}{lim}\frac{xf\left(\omega \left(F\right)-tx\right)}{f\left(\omega \left(F\right)-t\right)}$

$=\underset{t\to 0}{lim}\frac{xg\left(\omega \left(G\right)-tx\right)}{g\left(\omega \left(G\right)-t\right)}{\left[\frac{1-G\left(\omega \left(G\right)-tx\right)}{1-G\left(\omega \left(G\right)-t\right)}\right]}^{-2}\times$

${\left(\frac{G\left(\omega \left(G\right)-tx\right)}{G\left(\omega \left(G\right)-t\right)}\right)}^{\theta -1}{\left(\frac{1-G\left(\omega \left(G\right)-tx\right)}{1-G\left(\omega \left(G\right)-t\right)}\right)}^{1-\theta }\times$

${\left[\frac{\alpha {\left(\beta \left[1-G(\omega \left(G\right)-tx)\right]\right)}^{\alpha \theta }+{\left(G(\omega \left(G\right)-tx)\right)}^{\alpha \theta }}{\alpha {\left(\beta \left[1-G\left(\omega \left(G\right)-t\right)\right]\right)}^{\alpha \theta }+{\left(G\left(\omega \left(G\right)-t\right)\right)}^{\alpha \theta }}\right]}^{-\left(\frac{\alpha +1}{\alpha }\right)}\times$

${\left[\frac{1-G(\omega \left(G\right)-tx)}{1-G\left(\omega \left(G\right)-t\right)}\right]}^{\left(\theta \left(\alpha +1\right)\right)}=x^{\theta \varphi }$

for every $x<0$. Hence, it follows that $F$ also belongs to the maximal domain of attraction of the Weibull extreme value distribution with

$\underset{n\to \mathrm{\infty }}{lim}\mathrm{P}\mathrm{r}\left(\left(M_n-a_n\right)/b_n\le x\right)=\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\left(-x\right)}^{\theta \varphi }\right),x<0$

for some suitable choices of the norming constants $a_n$ and $b_n>0$. For instance, it follows from Corollary 1.6.3 in the work by Leadbetter et al. (2012) that the normalizing constants are $a_n=\omega \left(F\right)=F^{-1}(1)$ and $b_n=\omega \left(F\right)-F^{-1}\left(1-1/n\right)>0$.

Similar arguments can be obtained for minimal domains of attraction. That is, $F$ belongs to the same minimal domain of attraction as that of $G$. For instance, since the normal distribution belongs to the maximal/minimal domain of attraction of the Gumbel extreme value distribution, it follows that the Odd-Kappa normal distribution also belongs to the maximal/minimal domain of attraction of the Gumbel extreme value distribution.

5. FGM copula

Copulas were introduced by Roger (2006) as a function that combines multivariate distribution functions with uniform [0,1] margins. Sklar (1996) defined the cdf and pdf for two-dimensional copulas as follows: given two random variables X and Y with, respectively, distribution functions F(x) and F(y), the cdf and pdf for bivariate copulas were provided, respectively, as

(5.1) $F\left(x,y\right)=C\left(F\left(x;{\vartheta }_1\right),F\left(y;{\vartheta }_2\right)\right),$(5.1)

and

(5.2) $f\left(x,y\right)=f\left(x;{\vartheta }_1\right)f\left(y;{\vartheta }_2\right)c\left(F\left(x;{\vartheta }_1\right),F\left(y;{\vartheta }_2\right)\right),$(5.2)

where $\left(x,y\right)\in \left(-\mathrm{\infty },\mathrm{\infty }\right)\times \left(-\mathrm{\infty },\mathrm{\infty }\right)$ and ${\vartheta }_1$ is a parameter vector for the first variable $X$, and ${\vartheta }_2$ is a parameter vector for the second variable $Y$. Moreover, the sf for bivariate copulas was defined by Roger (2006) as

$S\left(x,y\right)=\hat{C}\left(\bar{F}\left(x\right),\bar{F}\left(y\right)\right)$

(5.3) $=\bar{F}\left(x;{\vartheta }_1\right)+\bar{F}\left(y;{\vartheta }_2\right)-1+C\left(1-\bar{F}\left(x;{\vartheta }_1\right),1-\bar{F}\left(y;{\vartheta }_2\right)\right).$(5.3)

From Sklar’s theorem and using Equation (5.1)(5.1) $F\left(x,y\right)=C\left(F\left(x;{\vartheta }_1\right),F\left(y;{\vartheta }_2\right)\right),$(5.1) -(5.3(5.3) $=\bar{F}\left(x;{\vartheta }_1\right)+\bar{F}\left(y;{\vartheta }_2\right)-1+C\left(1-\bar{F}\left(x;{\vartheta }_1\right),1-\bar{F}\left(y;{\vartheta }_2\right)\right).$(5.3) ) and Odd Kappa-G family Equation (1.3)(1.3) $F\left(x;\alpha ,\beta ,\theta ,\vartheta \right)={\left[\frac{{\left(\frac{G(x;\vartheta )}{\beta \left[1-G(x;\vartheta )\right]}\right)}^{\alpha \theta }}{\alpha +{\left(\frac{G(x;\vartheta )}{\beta \left[1-G(x;\vartheta )\right]}\right)}^{\alpha \theta }}\right]}^{\left(\frac{1}{\alpha }\right)},x\in R.$(1.3) -(1.5(1.5) $S\left(x;\alpha ,\beta ,\theta ,\vartheta \right)=1-{\left[\frac{{\left(\frac{G(x;\vartheta )}{\beta \left[1-G(x;\vartheta )\right]}\right)}^{\alpha \theta }}{\alpha +{\left(\frac{G(x;\vartheta )}{\beta \left[1-G(x;\vartheta )\right]}\right)}^{\alpha \theta }}\right]}^{\left(\frac{1}{\alpha }\right)},$(1.5) ), we get the joint cdf, pdf and sf of bivariate Odd Kappa-G family based on any copula function, respectively, as the following:

(5.4) $\begin{array}{rl}& F\left(x,y\right)=C\left({\left[\frac{{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}}{{\alpha }_1+{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}}\right]}^{\left(\frac{1}{{\alpha }_1}\right)},\right.\\ & \left.{\left[\frac{{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}{{\alpha }_2+{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}\right]}^{\left(\frac{1}{{\alpha }_2}\right)}\right),\end{array}$(5.4)

$f\left(x,y\right)=\left(\frac{{\alpha }_1{\theta }_{1}g\left(x;{\vartheta }_1\right)}{{\beta }_1{\left[1-G\left(x;{\vartheta }_1\right)\right]}^2}\right){\left(\frac{G\left(x;{\vartheta }_1\right)}{{\beta }_1\left[1-G\left(x;{\vartheta }_1\right)\right]}\right)}^{{\theta }_1-1}\times$

$\begin{array}{rl}& {\left[{\alpha }_1+{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}\right]}^{-\left(\frac{{\alpha }_1+1}{{\alpha }_1}\right)}\\ & \left(\frac{{\alpha }_2{\theta }_{2}g\left(y;{\vartheta }_2\right)}{{\beta }_2{\left[1-G\left(y;{\vartheta }_2\right)\right]}^2}\right)\times \end{array}$

${\left(\frac{G\left(y;{\vartheta }_2\right)}{{\beta }_2\left[1-G\left(y;{\vartheta }_2\right)\right]}\right)}^{{\theta }_2-1}{\left[{\alpha }_2+{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}\right]}^{-\left(\frac{{\alpha }_2+1}{{\alpha }_2}\right)}\times$

(5.5) $c\left({\left[\frac{{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}}{{\alpha }_1+{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}}\right]}^{\left(\frac{1}{{\alpha }_1}\right)},{\left[\frac{{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}{{\alpha }_2+{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}\right]}^{\left(\frac{1}{{\alpha }_2}\right)}\right),$(5.5)

and

$S\left(x,y\right)=1-{\left[\frac{{\left(\frac{G\left(x;{\vartheta }_1\right)}{{\beta }_1\left[1-G\left(x;{\vartheta }_1\right)\right]}\right)}^{{\alpha }_1{\theta }_1}}{{\alpha }_1+{\left(\frac{G\left(x;{\vartheta }_1\right)}{{\beta }_1\left[1-G\left(x;{\vartheta }_1\right)\right]}\right)}^{{\alpha }_1{\theta }_1}}\right]}^{\left(\frac{1}{{\alpha }_1}\right)}-{\left[\frac{{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}{{\alpha }_2+{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}\right]}^{\left(\frac{1}{{\alpha }_2}\right)}+$

(5.6) $C\left({\left[\frac{{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}}{{\alpha }_1+{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}}\right]}^{\left(\frac{1}{{\alpha }_1}\right)},{\left[\frac{{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}{{\alpha }_2+{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}\right]}^{\left(\frac{1}{{\alpha }_2}\right)}\right)$(5.6)

Many copulas, such as Farlie-Gumbel-Morgenstern (FGM), have been defined using Equation (5.1)(5.1) $F\left(x,y\right)=C\left(F\left(x;{\vartheta }_1\right),F\left(y;{\vartheta }_2\right)\right),$(5.1) -(5.3(5.3) $=\bar{F}\left(x;{\vartheta }_1\right)+\bar{F}\left(y;{\vartheta }_2\right)-1+C\left(1-\bar{F}\left(x;{\vartheta }_1\right),1-\bar{F}\left(y;{\vartheta }_2\right)\right).$(5.3) ). The FGM copula is one of the most well-known parametric families of copulas explored by Gumbel (1960), Morgenstern (1956) and Farlie (1960). In addition, it is considered to be the most effective in describing quantity dependence. Sriboonchitta & Kreinovich (2018), Almetwally (2019) and El-Sherpieny et al. (2021) discussed the FGM copula in order to introduce the bivariate Weibull distribution.

For the FGM copula, we know that its copula function and the associated copula density are, respectively

(5.7) $\begin{array}{rll}& C\left(F\left(x;{\vartheta }_1\right),F\left(y;{\vartheta }_2\right)\right)=F\left(x;{\vartheta }_1\right)F\left(y;{\vartheta }_2\right)& \\ & \left\{1+\rho \left[\left(1-F\left(x;{\vartheta }_1\right)\right)\left(1-F\left(y;{\vartheta }_2\right)\right)\right]\right\},\end{array}$(5.7)

and

(5.8) $c\left(F\left(x;{\vartheta }_1\right),F\left(y;{\vartheta }_2\right)\right)=1+\rho [\left(1-2F\left(x;{\vartheta }_1\right)\right)\left(1-2F\left(y;{\vartheta }_2\right)\right),$(5.8)

where $-1\le \rho \le 1$. Note that, if $\rho =0$, then $X$ and $Y$ are independent.

Using the FGM copula function given in Equation (5.7)(5.7) $\begin{array}{rll}& C\left(F\left(x;{\vartheta }_1\right),F\left(y;{\vartheta }_2\right)\right)=F\left(x;{\vartheta }_1\right)F\left(y;{\vartheta }_2\right)& \\ & \left\{1+\rho \left[\left(1-F\left(x;{\vartheta }_1\right)\right)\left(1-F\left(y;{\vartheta }_2\right)\right)\right]\right\},\end{array}$(5.7) and (5.8(5.8) $c\left(F\left(x;{\vartheta }_1\right),F\left(y;{\vartheta }_2\right)\right)=1+\rho [\left(1-2F\left(x;{\vartheta }_1\right)\right)\left(1-2F\left(y;{\vartheta }_2\right)\right),$(5.8) ) and the bivariate Odd Kapp-G family based on any copula function in Equation (5.4)(5.4) $\begin{array}{rl}& F\left(x,y\right)=C\left({\left[\frac{{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}}{{\alpha }_1+{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}}\right]}^{\left(\frac{1}{{\alpha }_1}\right)},\right.\\ & \left.{\left[\frac{{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}{{\alpha }_2+{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}\right]}^{\left(\frac{1}{{\alpha }_2}\right)}\right),\end{array}$(5.4) -(5.6(5.6) $C\left({\left[\frac{{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}}{{\alpha }_1+{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}}\right]}^{\left(\frac{1}{{\alpha }_1}\right)},{\left[\frac{{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}{{\alpha }_2+{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}\right]}^{\left(\frac{1}{{\alpha }_2}\right)}\right)$(5.6) ), we get the bivariate cdf, pdf and sf of the Odd Kapp-G (BFGMOKG) family based on FGM copula as follows:

$\begin{array}{rl}& F_{\mathrm{B}\mathrm{F}\mathrm{G}\mathrm{M}\mathrm{O}\mathrm{K}\mathrm{G}}\left(x,y\right)={\left[\frac{{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}}{{\alpha }_1+{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}}\right]}^{\left(\frac{1}{{\alpha }_1}\right)}\\ & {\left[\frac{{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}{{\alpha }_2+{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}\right]}^{\left(\frac{1}{{\alpha }_2}\right)}\times \end{array}$

$\left\{1+\rho \left\{\left(1-{\left[\frac{{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}}{{\alpha }_1+{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}}\right]}^{\left(\frac{1}{{\alpha }_1}\right)}\right)\right.\right.\times$

$\left.\left.\left(1-{\left[\frac{{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}{{\alpha }_2+{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}\right]}^{\left(\frac{1}{{\alpha }_2}\right)}\right)\right\}\right\},$

$f_{\mathrm{B}\mathrm{F}\mathrm{G}\mathrm{M}\mathrm{O}\mathrm{K}\mathrm{G}}\left(x,y\right)=\left(\frac{{\alpha }_1{\theta }_{1}g\left(x;{\vartheta }_1\right)}{{\beta }_1{\left[1-G\left(x;{\vartheta }_1\right)\right]}^2}\right){\left(\frac{G\left(x;{\vartheta }_1\right)}{{\beta }_1\left[1-G\left(x;{\vartheta }_1\right)\right]}\right)}^{{\theta }_1-1}$

${\left[{\alpha }_1+{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}\right]}^{-\left(\frac{{\alpha }_1+1}{{\alpha }_1}\right)}\left(\frac{{\alpha }_2{\theta }_{2}g\left(y;{\vartheta }_2\right)}{{\beta }_2{\left[1-G\left(y;{\vartheta }_2\right)\right]}^2}\right)\times$

${\left(\frac{G\left(y;{\vartheta }_2\right)}{{\beta }_2\left[1-G\left(y;{\vartheta }_2\right)\right]}\right)}^{{\theta }_2-1}{\left[{\alpha }_2+{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}\right]}^{-\left(\frac{{\alpha }_2+1}{{\alpha }_2}\right)}\times$

$\left\{1+\rho \left\{\left(1-2{\left[\frac{{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}}{{\alpha }_1+{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}}\right]}^{\left(\frac{1}{{\alpha }_1}\right)}\right)\right.\right.\times$

(24) $\left.\left.\left(1-2{\left[\frac{{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}{{\alpha }_2+{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}\right]}^{\left(\frac{1}{{\alpha }_2}\right)}\right)\right\}\right\},$(24)

and

$S_{\mathrm{B}\mathrm{F}\mathrm{G}\mathrm{M}\mathrm{O}\mathrm{K}\mathrm{G}}\left(x,y\right)=1-$

${\left[\frac{{\left(\frac{G\left(x;{\vartheta }_1\right)}{{\beta }_1\left[1-G\left(x;{\vartheta }_1\right)\right]}\right)}^{{\alpha }_1{\theta }_1}}{{\alpha }_1+{\left(\frac{G\left(x;{\vartheta }_1\right)}{{\beta }_1\left[1-G\left(x;{\vartheta }_1\right)\right]}\right)}^{{\alpha }_1{\theta }_1}}\right]}^{\left(\frac{1}{{\alpha }_1}\right)}-{\left[\frac{{\left(\frac{G\left(y;{\vartheta }_2\right)}{{\beta }_2\left[1-G\left(y;{\vartheta }_2\right)\right]}\right)}^{{\alpha }_2{\theta }_2}}{{\alpha }_2+{\left(\frac{G\left(y;{\vartheta }_2\right)}{{\beta }_2\left[1-G\left(y;{\vartheta }_2\right)\right]}\right)}^{{\alpha }_2{\theta }_2}}\right]}^{\left(\frac{1}{{\alpha }_2}\right)}+$

${\left[\frac{{\left(\frac{G\left(x;{\vartheta }_1\right)}{{\beta }_1\left[1-G\left(x;{\vartheta }_1\right)\right]}\right)}^{{\alpha }_1{\theta }_1}}{{\alpha }_1+{\left(\frac{G\left(x;{\vartheta }_1\right)}{{\beta }_1\left[1-G\left(x;{\vartheta }_1\right)\right]}\right)}^{{\alpha }_1{\theta }_1}}\right]}^{\left(\frac{1}{{\alpha }_1}\right)}{\left[\frac{{\left(\frac{G\left(y;{\vartheta }_2\right)}{{\beta }_2\left[1-G\left(y;{\vartheta }_2\right)\right]}\right)}^{{\alpha }_2{\theta }_2}}{{\alpha }_2+{\left(\frac{G\left(y;{\vartheta }_2\right)}{{\beta }_2\left[1-G\left(y;{\vartheta }_2\right)\right]}\right)}^{{\alpha }_2{\theta }_2}}\right]}^{\left(\frac{1}{{\alpha }_2}\right)}\times$

$\left\{1+\rho \left\{\left(1-{\left[\frac{{\left(\frac{G\left(x;{\vartheta }_1\right)}{{\beta }_1\left[1-G\left(x;{\vartheta }_1\right)\right]}\right)}^{{\alpha }_1{\theta }_1}}{{\alpha }_1+{\left(\frac{G\left(x;{\vartheta }_1\right)}{{\beta }_1\left[1-G\left(x;{\vartheta }_1\right)\right]}\right)}^{{\alpha }_1{\theta }_1}}\right]}^{\left(\frac{1}{{\alpha }_1}\right)}\right)\right.\right.\times$

$\left.\left.\left(1-{\left[\frac{{\left(\frac{G\left(y;{\vartheta }_2\right)}{{\beta }_2\left[1-G\left(y;{\vartheta }_2\right)\right]}\right)}^{{\alpha }_2{\theta }_2}}{{\alpha }_2+{\left(\frac{G\left(y;{\vartheta }_2\right)}{{\beta }_2\left[1-G\left(y;{\vartheta }_2\right)\right]}\right)}^{{\alpha }_2{\theta }_2}}\right]}^{\left(\frac{1}{{\alpha }_2}\right)}\right)\right\}\right\}.$

The bivariate pdf of the BFGMOKG family given in Equation (5.9) has Odd Kappa-G family marginals. The marginal density functions for X and Y, respectively, are

$f\left(x;{\alpha }_1,{\beta }_1,{\theta }_1,{\vartheta }_1\right)=\left(\frac{{\alpha }_1{\theta }_{1}g\left(x;{\vartheta }_1\right)}{{\beta }_1{\left[1-G\left(x;{\vartheta }_1\right)\right]}^2}\right){\left(\frac{G\left(x;{\vartheta }_1\right)}{{\beta }_1\left[1-G\left(x;{\vartheta }_1\right)\right]}\right)}^{{\theta }_1-1}$

${\left[{\alpha }_1+{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}\right]}^{-\left(\frac{{\alpha }_1+1}{{\alpha }_1}\right)}$

and

$f\left(y;{\alpha }_2,{\beta }_2,{\theta }_2,{\vartheta }_2\right)=\left(\frac{{\alpha }_2{\theta }_{2}g\left(y;{\vartheta }_2\right)}{{\beta }_2{\left[1-G\left(y;{\vartheta }_2\right)\right]}^2}\right){\left(\frac{G\left(y;{\vartheta }_2\right)}{{\beta }_2\left[1-G\left(y;{\vartheta }_2\right)\right]}\right)}^{{\theta }_2-1}$

${\left[{\alpha }_2+{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}\right]}^{-\left(\frac{{\alpha }_2+1}{{\alpha }_2}\right)}.$

The conditional cdf and pdf of X given Y, respectively, are

$F\left(x|y\right)={\left[\frac{{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}}{{\alpha }_1+{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}}\right]}^{\left(\frac{1}{{\alpha }_1}\right)}\times$

$\left\{1+\rho \left(1-{\left[\frac{{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}}{{\alpha }_1+{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}}\right]}^{\left(\frac{1}{{\alpha }_1}\right)}\right)\right.\times$

$\left.\left(1-2{\left[\frac{{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}{{\alpha }_2+{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}\right]}^{\left(\frac{1}{{\alpha }_2}\right)}\right)\right\}$

and

$f\left(x|y\right)=\left(\frac{{\alpha }_1{\theta }_{1}g\left(x;{\vartheta }_1\right)}{{\beta }_1{\left[1-G\left(x;{\vartheta }_1\right)\right]}^2}\right){\left(\frac{G\left(x;{\vartheta }_1\right)}{{\beta }_1\left[1-G\left(x;{\vartheta }_1\right)\right]}\right)}^{{\theta }_1-1}\times$

${\left[{\alpha }_1+{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}\right]}^{-\left(\frac{{\alpha }_1+1}{{\alpha }_1}\right)}\times$

$\left\{1+\rho \left\{\left(1-2{\left[\frac{{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}}{{\alpha }_1+{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}}\right]}^{\left(\frac{1}{{\alpha }_1}\right)}\right)\right.\right.\times$

$\left.\left.\left(1-2{\left[\frac{{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}{{\alpha }_2+{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}\right]}^{\left(\frac{1}{{\alpha }_2}\right)}\right)\right\}\right\}.$

Similarly, the conditional cdf and pdf of Y given X, respectively, are

$F\left(y|x\right)={\left[\frac{{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}{{\alpha }_2+{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}\right]}^{\left(\frac{1}{{\alpha }_2}\right)}\times$

$\left\{1+\rho \left(1-{\left[\frac{{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}{{\alpha }_2+{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}\right]}^{\left(\frac{1}{{\alpha }_2}\right)}\right)\right.\times$

$\left.\left(1-2{\left[\frac{{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}}{{\alpha }_1+{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}}\right]}^{\left(\frac{1}{{\alpha }_1}\right)}\right)\right\}$

and

$f\left(y|x\right)=\left(\frac{{\alpha }_2{\theta }_{2}g\left(y;{\vartheta }_2\right)}{{\beta }_2{\left[1-G\left(y;{\vartheta }_2\right)\right]}^2}\right){\left(\frac{G\left(y;{\vartheta }_2\right)}{{\beta }_2\left[1-G\left(y;{\vartheta }_2\right)\right]}\right)}^{{\theta }_2-1}\times$

${\left[{\alpha }_2+{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}\right]}^{-\left(\frac{{\alpha }_2+1}{{\alpha }_2}\right)}\times$

$\left\{1+\rho \left\{\left(1-2{\left[\frac{{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}}{{\alpha }_1+{\left(\frac{G(x;{\vartheta }_1)}{{\beta }_1\left[1-G(x;{\vartheta }_1)\right]}\right)}^{{\alpha }_1{\theta }_1}}\right]}^{\left(\frac{1}{{\alpha }_1}\right)}\right)\right.\right.\times$

$\left.\left.\left(1-2{\left[\frac{{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}{{\alpha }_2+{\left(\frac{G(y;{\vartheta }_2)}{{\beta }_2\left[1-G(y;{\vartheta }_2)\right]}\right)}^{{\alpha }_2{\theta }_2}}\right]}^{\left(\frac{1}{{\alpha }_2}\right)}\right)\right\}\right\}.$

Some measures of dependence were presented by Roger (2006). One of these is Kendall’s tau correlation ($\tau$), which is defined as the difference between the probabilities of concordance and discordance, given in terms of any copula function as

$\tau =4E\left(C\left(U,V\right)\right)-1=4{\int }_0^1{\int }_0^{1}C\left(u,v\right)c\left(u,v\right)dudv-1$

Using FGM copula function, Kendall’s tau correlation ($\tau$) is

$\tau =4{\int }_0^1{\int }_0^{1}C\left(u,v\right)\left[1+\rho \left(1-2u\right)\left(1-2v\right)\right]dudv-1=4\left\{\frac{9+2\rho }{36}\right\}-1=\frac{2\rho }{9}.$

The other one is the median regression curve of Y on X, which is a method for describing the dependence of one random variable on another, for any copula as follows:

$Pr\left(Y\le y|X=x\right)=F\left(y|x\right)=\frac{\mathrm{\partial }C\left(F\left(x\right),F\left(y\right)\right)}{\mathrm{\partial }F\left(x\right)}=\frac{1}{2}.$

By using FGM copula function, the median regression model of BFGMOKG family is as the following:

$\frac{1}{2}=Pr\left(Y\le y|X=x\right)={\left[\frac{{\left(\frac{G\left(y;{\vartheta }_2\right)}{{\beta }_2\left[1-G\left(y;{\vartheta }_2\right)\right]}\right)}^{{\alpha }_2{\theta }_2}}{{\alpha }_2+{\left(\frac{G\left(y;{\vartheta }_2\right)}{{\beta }_2\left[1-G\left(y;{\vartheta }_2\right)\right]}\right)}^{{\alpha }_2{\theta }_2}}\right]}^{\left(\frac{1}{{\alpha }_2}\right)}\times$

$\left\{1+\rho \left[\left(1-{\left[\frac{{\left(\frac{G\left(y;{\vartheta }_2\right)}{{\beta }_2\left[1-G\left(y;{\vartheta }_2\right)\right]}\right)}^{{\alpha }_2{\theta }_2}}{{\alpha }_2+{\left(\frac{G\left(y;{\vartheta }_2\right)}{{\beta }_2\left[1-G\left(y;{\vartheta }_2\right)\right]}\right)}^{{\alpha }_2{\theta }_2}}\right]}^{\left(\frac{1}{{\alpha }_2}\right)}\right)\right.\right.\times$

$\left.\left.\left(1-2{\left[\frac{{\left(\frac{G\left(x;{\vartheta }_1\right)}{{\beta }_1\left[1-G\left(x;{\vartheta }_1\right)\right]}\right)}^{{\alpha }_1{\theta }_1}}{{\alpha }_1+{\left(\frac{G\left(x;{\vartheta }_1\right)}{{\beta }_1\left[1-G\left(x;{\vartheta }_1\right)\right]}\right)}^{{\alpha }_1{\theta }_1}}\right]}^{\left(\frac{1}{{\alpha }_1}\right)}\right)\right]\right\}.$

Let $u=F\left(x\right)={\left[\frac{{\left(\frac{G\left(x;{\vartheta }_1\right)}{{\beta }_1\left[1-G\left(x;{\vartheta }_1\right)\right]}\right)}^{{\alpha }_1{\theta }_1}}{{\alpha }_1+{\left(\frac{G\left(x;{\vartheta }_1\right)}{{\beta }_1\left[1-G\left(x;{\vartheta }_1\right)\right]}\right)}^{{\alpha }_1{\theta }_1}}\right]}^{\left(\frac{1}{{\alpha }_1}\right)}$ and $v=F\left(y\right)={\left[\frac{{\left(\frac{G\left(y;{\vartheta }_2\right)}{{\beta }_2\left[1-G\left(y;{\vartheta }_2\right)\right]}\right)}^{{\alpha }_2{\theta }_2}}{{\alpha }_2+{\left(\frac{G\left(y;{\vartheta }_2\right)}{{\beta }_2\left[1-G\left(y;{\vartheta }_2\right)\right]}\right)}^{{\alpha }_2{\theta }_2}}\right]}^{\left(\frac{1}{{\alpha }_2}\right)}$. After simplifications, we have

$v=\frac{\sqrt{1+{\rho }^2-4u{\rho }^2+4{\rho }^2{u}^2}+2\rho u-\rho -1}{2\rho \left(2u-1\right)}$

Thus, the median regression curve of V on U is the line in ${\mathbf{I}}^2$ connecting the points $\left(1,\frac{\rho -1+\sqrt{1+{\rho }^2}}{2\rho }\right)$ and $\left(0,\frac{1+\rho -\sqrt{1+{\rho }^2}}{2\rho }\right)$. Furthermore, the median regression line is $v=\frac{2u-\sqrt{2-4u+4u^2}}{2\left(2u-1\right)}$ when $\rho =-1$, and $v=\frac{2\left(u-1\right)+\sqrt{2-4u+4u^2}}{2\left(2u-1\right)}$ when $\rho =1$. 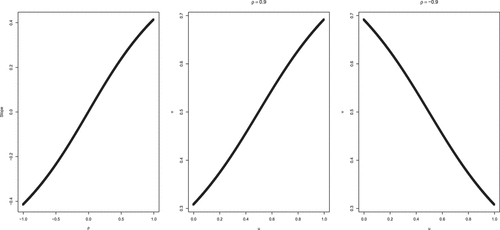Moreover, the slope of the median regression line is $\frac{-1+\sqrt{1+{\rho }^2}}{\rho }$. As an illustration, see Figure 1.

Figure 1. Plots of slope and regression curve of V on U of BFGMOKG family.

6. Concluding remarks

In this research paper, more mathematical properties of Odd Kappa-G family are introduced. We study some characterization results of the Odd Kappa-G family including characterizations based on two truncated moments, hazard and reversed hazard functions. We present the $k$th lower record values of the Odd Kappa-G family. Extreme values for this family are discussed. The bivariate cdf, pdf and sf of the Odd Kappa-G family based on FGM copula are obtained. Finally, we hope that this paper will encourage more researchers to study this attractive new family of distributions and inspire practitioners to apply it in their fields.

Data Availability

Data sharing not applicable to this article as no real data set was analyzed during the current study.

Acknowledgements

The author would like to thank the editor and anonymous referees for their insightful comments that helped to enhance the paper.

Disclosure statement

No potential conflict of interest was reported by the author.

Additional information

Funding

The author received no direct funding for this research.