Solving singularly perturbed delay differential equations via fitted mesh and exact difference method

ABSTRACT

In this paper, different numerical schemes are developed and investigated for solving singularly perturbed delay differential equations (DDEs). The solution of the considered equations exhibits a strong boundary layer when the perturbation parameter approaches zero. Standard numerical methods developed for solving regular problems fail to treat accurately the considered equations. We developed three numerical schemes for treating the considered equations. The first scheme (Scheme I) uses a non-standard mid-point upwind finite difference method on uniform mesh; the second scheme (Scheme II) uses a standard mid-point upwind finite difference method on Shiskin mesh and the third scheme (Scheme III) uses a non-standard mid-point upwind finite difference method on Shiskin mesh. The existence of a unique discrete solution is investigated using the discrete maximum principle. The stability and uniform convergence of the schemes are investigated and proved. Scheme III gives better accuracy and order of convergence than Scheme I. It has a boundary layer resolving behaviour which is the main drawback of Scheme II. Numerical examples are considered and treated to validate the theoretical finding of the schemes for different values of the perturbation parameter and delay parameter.

KEYWORDS:

• Mid-point upwind
• Shishkin mesh
• singularly perturbed
• uniformly convergent

1. Introduction

Differential equations are commonly used to model a process in which its evolution depends on the current state of the system. If the evolution depends on the current state and the history of the system, it is commonly modelled using a delay differential equation (DDEs). Most processes in bioscience, control theory, economics, and engineering are common examples of the DDEs model (Bellen & Zennaro, 2003). Some of the well-known applications areas are the mathematical modelling of epidemiology and population dynamics (Kuang, 1993; Salpeter & Salpeter, 1998), physiological kinetics (Baker et al., 1999), dynamics of diabetes (Makroglou et al., 2006), blood cell production (Mahaffy et al., 1999), classical electrodynamics (Lopez, 2020) and so on. Fractional-order differential equations, integral equations, and integro-differential equations can also be used for modelling different types of processes. The interested reader can refer (Bushnaq et al., 2022; Izadi et al., 2021; Shah et al., 2022; Sitthiwirattham et al., 2021; Usta et al., 2022) and the reference therein.

A singularly perturbed delay differential equation (SPDDE) is a differential equation in which its highest order derivative is multiplied by a small perturbation parameter and that involves at least one delay term. SPDDE appears in several research areas of applied mathematics (Kumar & Kadalbajoo, 2012), to list a few of them: in neuronal variability model in computational neuroscience and in control theory.

In general, when the perturbation parameter tends to zero, smoothness of the solution of singularly perturbed problems deteriorates and it forms a boundary layer (Miller et al., 2012). A boundary layer is a region on the solution domain, in which the solution shows a very rapid change. The commonly used classical numerical methods in FDM, FEM, and collocation method do not give accurate results for solving singularly perturbed problems and it leads to oscillations in the computed solution. While using the classical numerical methods to handle the oscillation, a large number of mesh points are required when $\epsilon$ is very small. It is not practical due to round-off error, limitation of computer memory, and computer processing ability (Roos et al., 2008).

There are two common strategies to develop numerical schemes which give an accurate computed solution. The first approach is the fitted mesh methods which consist of choosing a fine mesh in the boundary layer region and a coarse mesh on the outer layer region. The second approach is the fitted operator methods (the exponentially fitted method or the non-standard FDM) in which the mesh remains uniform and the difference schemes reflect the qualitative behaviour of the solution inside the layer region(s).

Several schemes have been developed using non-standard FDM on uniform mesh for solving singularly perturbed ODEs and PDEs. Interested readers can refer (Elsheikh et al., 2014; Kadalbajoo & Ramesh, 2007; Mickens, 2002; Patidar, 2008; Woldaregay & Duressa, 2021b) and the references therein. In review papers (Patidar, 2016, 2005), Patidar addresses on the use and recent developments of non-standard FDMs on uniform mesh. The non-standard FDMs are relatively superior to the equivalent fitted mesh methods in terms of accuracy and order of convergence (Kadalbajoo et al., 2006). But the non-standard FDMs on uniform mesh fail to have boundary layer resolving property (there is no sufficient number of mesh points in the boundary layer region). He and Wang in (He & Wang, 2018) developed a new class of non-standard FDM for a stationary singularly perturbed convection-diffusion equation using infinite Taylor’s series expansion. The authors conclude without proof that their scheme works on Shishkin mesh. The result in (He & Wang, 2018) motivates us for developing non-standard FDM on uniform mesh and for extending it on Shishkin mesh.

In this paper, we developed three numerical schemes: In Scheme I, we used the non-standard mid-point upwind finite difference method on a uniform mesh. Even if the scheme gives accurate results, it misses the boundary layer resolving property. In Scheme II, we used the standard mid-point upwind finite difference method on the Shiskin mesh. It gives moderately accurate and boundary layer resolving results since it uses layer-adapted mesh. In Scheme III, we used the non-standard mid-point upwind finite difference method on Shiskin mesh. Scheme III gives a more accurate and relatively higher order of convergence than the standard mid-point upwind FDM on Shishkin mesh. In Scheme III, half of the mesh points and the computed solutions are in the boundary layer region.

Notation: Throughout this paper, $N$ is denoted for the number of mesh intervals in the domain discretization; $C$ is denoted for the positive constant independent of the perturbation parameter $\epsilon$, and $N$. The norm $\parallel .\parallel$ represent the maximum norm $\parallel f\parallel =\text{break}max|f(t)|,t\in \mathrm{\Omega }$.

2. Continuous problem

We considered singularly perturbed DDE of the form:

(1) $\left\{\begin{array}{c}-\epsilon y{ }^{\mathrm{\prime }\mathrm{\prime }}(t)+a(t)y{ }^{\mathrm{\prime }}(t-\delta )+\alpha (t)y(t-\delta )+\beta (t)y(t)\\ =f(t),t\in \mathrm{\Omega }=(0,1),\\ y(t)=\varphi (t),t\in [-\delta ,0],y(1)=\varphi (1),\end{array}\right.$(1)

where $\epsilon ,0<\epsilon \ll 1$ is singular perturbation parameter and $\delta$ is delay parameter satisfying $\delta <\epsilon$. The functions $a(t),\alpha (t),\beta (t),f(t)$ and $\varphi (t)$ are assumed to be sufficiently smooth and bounded for guaranteeing the existence of unique continuous solution. The coefficient functions $\alpha (t),\beta (t)$ are assumed to satisfy

$\alpha (t)+\beta (t)\ge \zeta >0,t\in \mathrm{\Omega },$

for some constant $\zeta$.

In case $\delta =0$, the equation reduces to a singularly perturbed boundary value problem, in which for small $\epsilon$, it exhibits a boundary layer. The boundary layer is maintained for $\delta \ne 0$, but sufficiently small (Kumar & Kadalbajoo, 2012; Woldaregay & Duressa, 2021a).

2.1. Asymptotic approximation and bounds

If $\delta <\epsilon$, using Taylor’s series approximation for the terms with the shift is appropriate (Tian, 2002). Using Taylor series approximation, we approximate $y{ }^{\mathrm{\prime }}(t-\delta )$ and $y(t-\delta )$ as

(2) $\begin{array}{rl}& y{ }^{\mathrm{\prime }}(t-\delta )\approx y{ }^{\mathrm{\prime }}(t)-\delta y{ }^{\mathrm{\prime }\mathrm{\prime }}(t)+O({\delta }^2),\mathrm{a}\mathrm{n}\mathrm{d}\\ & y(t-\delta )\approx y(t)-\delta y{ }^{\mathrm{\prime }}(t)+\frac{{\delta }^2}{2}y{ }^{\mathrm{\prime }\mathrm{\prime }}(t)+O({\delta }^3).\end{array}$(2)

Using the approximation in (2) into (1) gives

(3) $\left\{\begin{array}{c}-c_{\epsilon }(t)y{ }^{\mathrm{\prime }\mathrm{\prime }}(t)+d(t)y{ }^{\mathrm{\prime }}(t)+b(t)y(t)=f(t),t\in \mathrm{\Omega },\\ y(0)=\varphi (0),y(1)=\varphi (1),\end{array}\right.$(3)

where $c_{\epsilon }(t)=\epsilon +\delta a(t)-\frac{{\delta }^2}{2}\alpha (t)$, $d(t)=a(t)-\delta \alpha (t)$ and $b(t)=\alpha (t)+\beta (t)$

For small values of $\delta$, (1) and (3) are asymptotically equivalent, since the difference between the two is $O({\delta }^2)$ (Kumar & Kadalbajoo, 2012). We assume $0<c_{\epsilon }(x)\le \epsilon +\delta a^{\ast }-\frac{{\delta }^2}{2}{\alpha }^{\ast }=c_{\epsilon }$, where $\alpha (x)\ge {\alpha }^{\ast }$ and $a(x)\ge a^{\ast }$. The problem in (1) exhibits a regular boundary layer and position of the layer depends on the conditions: For $d(t)<0$, left boundary layer exist and if $d(t)>0$, right boundary layer exist. In case $d(t)$ changes sign, interior layer will exist (Kadalbajoo & Ramesh, 2007). For the case $d(t)\ge d>0,$ implies occurrence of right boundary layer. The equation obtained by setting $c_{\epsilon }=0$ in (3) is called reduced problem and given as

(4) $\left\{\begin{array}{c}d(t){y{ }^{\mathrm{\prime }}}_0(t)+b(t)y_0(t)=f(t),t\in \mathrm{\Omega },\\ y_0(0)=\varphi (0),y_0(1)\ne \varphi (1).\end{array}\right.$(4)

For small values of $c_{\epsilon }$, the solution $y(t)$ of (3) is very close to the solution $y_0(t)$ of (4). Let $\varsigma$ be the differential operator denoted for $\xi z(t)=-c_{\epsilon }z{ }^{\mathrm{\prime }\mathrm{\prime }}(t)+d(t)z{ }^{\mathrm{\prime }}(t)+b(t)z(t)$.

Lemma 2.1. The maximum principle (Kadalbajoo et al., 2006). Let $z$ be any sufficiently smooth function defined on $\mathrm{\Omega }$ and which satisfies $z(0)\ge 0$ and $z(1)\ge 0$. Then, $\text{pound}z(t)\ge 0,t\in \mathrm{\Omega }$ implies that $z(t)\ge 0,\mathrm{\forall }t\in \bar{\mathrm{\Omega }}$.

Lemma 2.2. Stability estimate. The solution $y(t)$ of the continuous equation in (3) satisfies the bounded

(5) $|y(t)|\le {\zeta }^{-1}\parallel f\parallel +\parallel y{\parallel }_{\mathrm{\partial }\mathrm{\Omega }},$(5)

for $b(t)\ge \zeta$ and $\parallel y{\parallel }_{\mathrm{\partial }\mathrm{\Omega }}=max\{|\varphi (0)|,|\varphi (1)|\}$.

Proof. We define two barrier functions ${\vartheta }_{\pm }$ as ${\vartheta }_{\pm }(t)={\zeta }^{-1}\parallel f\parallel +\parallel y{\parallel }_{\mathrm{\partial }\mathrm{\Omega }}\pm y(t).$ On the boundaries, we obtain

${\vartheta }_{\pm }(0)={\zeta }^{-1}\parallel f\parallel +\parallel y{\parallel }_{\mathrm{\partial }\mathrm{\Omega }}\pm y(0)\ge 0,and{\vartheta }_{\pm }(1)={\zeta }^{-1}\parallel f\parallel +\parallel y{\parallel }_{\mathrm{\partial }\mathrm{\Omega }}\pm y(1)\ge 0.$

On the domain $\mathrm{\Omega }$, we have

$\begin{array}{rl}\text{pound}{\vartheta }_{\pm }(t)& =-c_{\epsilon }{\vartheta { }^{\mathrm{\prime }\mathrm{\prime }}}_{\pm }(t)+d(t){\vartheta { }^{\mathrm{\prime }}}_{\pm }(t)+b(t){\vartheta }_{\pm }(t)\\ \hspace{0.17em}& =-c_{\epsilon }(0\pm y{ }^{\mathrm{\prime }\mathrm{\prime }}(t))+d(t)(0\pm y{ }^{\mathrm{\prime }}(t))\\ & +b(t)({\zeta }^{-1}\parallel f\parallel +\parallel y{\parallel }_{\mathrm{\partial }\mathrm{\Omega }}\pm y(t))\\ \hspace{0.17em}& =b(t)({\zeta }^{-1}\parallel f\parallel +\parallel y{\parallel }_{\mathrm{\partial }\mathrm{\Omega }})\mp c_{\epsilon }y{ }^{\mathrm{\prime }\mathrm{\prime }}(t)\\ & \pm d(t)y{ }^{\mathrm{\prime }}(t)\pm b(t)y(t)\\ \hspace{0.17em}& =b(t)({\zeta }^{-1}\parallel f\parallel +\parallel y{\parallel }_{\mathrm{\partial }\mathrm{\Omega }})\pm f(t)\ge 0,\\ & \mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{e},b(t)\ge \zeta >0.\end{array}$

With the hypothesis of the maximum principle in Lemma 2.1, ${\vartheta }_{\pm }(t)\ge 0,t\in \bar{\mathrm{\Omega }},$ which implies the required bound.

2.2. Solution decomposition

For the proof of uniform convergence, the bounds on the derivatives of the solution are not sharp enough (Miller et al., 2012). So we need to derive stronger bounds. To achieve the required stronger bound, we decompose the solution $y(t)$ into regular component $v(t)$ and singular component $w(t)$ as

(6) $y(t)=v(t)+w(t),t\in \bar{\mathrm{\Omega }}.$(6)

The regular and the singular components are, respectively, solution to the non-homogeneous equation and to the homogeneous equation

(7) $\left\{\begin{array}{c}-c_{\epsilon }v{ }^{\mathrm{\prime }\mathrm{\prime }}(t)+d(t)v{ }^{\mathrm{\prime }}(t)+b(t)v(t)=f(t),t\in \mathrm{\Omega },\\ v(0)=y(0),v(1)\ne y(1),\end{array}\right.$(7)

and

(8) $\left\{\begin{array}{c}-c_{\epsilon }w{ }^{\mathrm{\prime }\mathrm{\prime }}(t)+d(t)w{ }^{\mathrm{\prime }}(t)+b(t)w(t)=0,t\in \mathrm{\Omega },\\ w(0)=0,w(1)=y(1)-v(1),\end{array}\right.$(8)

Lemma 2.3. The regular component solution $v(t)$ and its derivatives satisfy the bound

(9) $|v^{(k)}(t)|\le C,k=0,1,2,3,4,$(9)

the boundary layer component solution $w(t)$ and its derivatives satisfy the bound

(10) $|w^{(k)}(t)|\le C{c}_{\epsilon }^{-k}exp(\frac{-d(1-t)}{c_{\epsilon }}),k=0,1,2,3,4,$(10)

where $d$ is lower bound of $d(t)$.

Proof. See, in (Miller et al., 2012; Roos et al., 2008).

Lemma 2.4. Derivatives of the solution $y(t)$ of the equation (3)(3) $\left\{\begin{array}{c}-c_{\epsilon }(t)y{ }^{\mathrm{\prime }\mathrm{\prime }}(t)+d(t)y{ }^{\mathrm{\prime }}(t)+b(t)y(t)=f(t),t\in \mathrm{\Omega },\\ y(0)=\varphi (0),y(1)=\varphi (1),\end{array}\right.$(3) satisfy the bound

(11) $|y^{(k)}(t)|\le C(1+c_{\epsilon }^{-k}exp(\frac{-d(1-t)}{c_{\epsilon }})),k=0,1,2,3,4.$(11)

Proof. Interested reader can refer the proof in (Kellogg & Tsan, 1978; Miller et al., 2012; Roos et al., 2008).

3. Numerical schemes

In this section, first we discuss the exact finite difference and then discuss the three numerical schemes: (i) non-standard mid-point upwind FDM on uniform mesh, (ii) standard mid-point upwind FDM on Shishkin mesh, and (iii) the non-standard mid-point upwind FDM on Shishkin mesh. The non-standard FDM on Shishkin mesh is formulated using the concept of non-standard FDM together with the fitted mesh.

Exact Finite Difference

For the second-order singularly perturbed differential equation of the form in (3), in order to construct an exact finite difference, we follow the techniques in (Mickens, 2005). We consider the constant coefficient sub-equations of (3) as

(12) $-c_{\epsilon }y{ }^{\mathrm{\prime }\mathrm{\prime }}(t)+dy{ }^{\mathrm{\prime }}(t)+\zeta y(t)=0,$(12)

(13) $-c_{\epsilon }y{ }^{\mathrm{\prime }\mathrm{\prime }}(t)+dy{ }^{\mathrm{\prime }}(t)=0,$(13)

where $d(t)\ge d$ and $b(t)\ge \zeta$. Since (12) is a constant coefficient second-order differential equation, it has two independent solutions

(14) $y(t)=A_{1}exp({\lambda }_{1}t)+A_{2}exp({\lambda }_{2}t),$(14)

where ${\lambda }_{1,2}=\frac{-d\pm \sqrt{d^2+4c_{\epsilon }\zeta }}{-2c_{\epsilon }}.$

We introduce a uniform mesh with mesh length $\mathrm{\Delta }t$ such that {$t_i=t_0+i\mathrm{\Delta }t,i=1,2,\dots ,N,t_0=0,\text{break}{t}_N=1,\mathrm{\Delta }t=\frac{1}{N}\}$ where $N$ is the number of mesh intervals in the discretization. The target is to design a difference equation which has the same general solution as the differential equation in (13) at the mesh point $t_i$ given by

$Y_i=A_{1}exp({\lambda }_1{t}_i)+A_{2}exp({\lambda }_2{t}_i).$

Using the theory of difference equations for second-order linear difference equations and substituting the values of ${\lambda }_1$ and ${\lambda }_2$, we obtain:

(15) $exp(\frac{d\mathrm{\Delta }t}{2c_{\epsilon }})Y_{i-1}-2cosh(\frac{\mathrm{\Delta }t\sqrt{d^2+4c_{\epsilon }\zeta }}{2c_{\epsilon }})Y_i+exp(-\frac{d\mathrm{\Delta }t}{2c_{\epsilon }})Y_{i+1}=0$(15)

is an exact difference scheme for (12). For $c_{\epsilon }\to 0$, we use the approximation $\frac{\mathrm{\Delta }t\sqrt{d^2+4c_{\epsilon }\zeta }}{2c_{\epsilon }}\approx \frac{d\mathrm{\Delta }t}{2c_{\epsilon }}$ in (15). Hence, multiplying both sides by $exp(\frac{d\mathrm{\Delta }t}{2c_{\epsilon }})$, simplifying we obtain

(16) $-c_{\epsilon }\frac{Y_{i-1}-2Y_i+Y_{i+1}}{\frac{\mathrm{\Delta }t{c}_{\epsilon }}{d}(exp(\frac{d\mathrm{\Delta }t}{c_{\epsilon }})-1)}+d\frac{Y_i-Y_{i-1}}{\mathrm{\Delta }t}=0.$(16)

The denominator function for second derivative approximation is obtained as ${\gamma }^2=\frac{\mathrm{\Delta }t{c}_{\epsilon }}{d}(exp(\frac{d\mathrm{\Delta }t}{c_{\epsilon }})-1)$. Adopting it for the variable coefficient equations written as

(17) ${\gamma }_i^2=\frac{\mathrm{\Delta }t{c}_{\epsilon }}{d(t_i)}(exp(\frac{\mathrm{\Delta }td(t_i)}{c_{\epsilon }})-1).$(17)

3.1. Scheme I: Non-standard mid-point upwind scheme on uniform mesh

For $i=1,2,\dots ,N-1,$ using the denominator function ${\gamma }_i^2$ in (17), the non-standard mid-point upwind finite difference scheme given as

(18) $\begin{array}{l}{\{{\pounds }_1^{N}Y}_i=-c_{\epsilon }\frac{Y_{i+1}-2Y_i+Y_{i-1}}{{\gamma }_i^2}+d_{i-1/2}\frac{Y_i-Y_{i-1}}{\Delta t}+b_{i-1/2}\\ Y_i=f_{i-1/2},Y_0=\varphi (0),Y_N=\varphi (1),\end{array}$(18)

where $d_{i-1/2},b_{i-1/2}$ and $f_{i-1/2}$ are denoted for $\frac{1}{2}[d(t_i)+d(t_{i-1})]$, $\frac{1}{2}[b(t_i)+b(t_{i-1})]$ and $\frac{1}{2}[f(t_i)+f(t_{i-1})]$ respectively.

3.1.1. Uniform convergence of scheme I

In the following few lemmas, we show that the discrete scheme in (18) satisfies the discrete maximum principle, uniform stability estimate and uniform convergence.

Lemma 3.1. The operator defined by the discrete scheme in (18) satisfies a discrete maximum principle. i.e. Let $Y_i$ be any mesh function satisfying $Y_0\ge 0,Y_N\ge 0$. Then, ${\text{pound}}_1^N{Y}_i\ge 0,\mathrm{\forall }i=1,2,\dots ,N-1$ implies that $Y_i\ge 0,i=0,1,\dots ,N.$

Proof. Suppose there exist $k\in \{0,1,\dots ,N\}$ such that $Y_k=\underset{0\le i\le N}{min}{Y}_i$. Suppose that $Y_k<0$ which implies $k\ne 0,N$. Also we assume that $Y_{k+1}-Y_k>0$ and $Y_k-Y_{k-1}<0$. Now, using the assumptions made above, we obtain ${\xi }_1^N{Y}_k<0$ for $k=1,2,3,\dots ,N-1$. Thus, the supposition $Y_i<0$, for $i=0,1,\dots ,N$ is wrong. Hence, we obtain $Y_i\ge 0,\mathrm{\forall }i=0,1,\dots ,N$.

Using this discrete maximum principle, we now prove that the discrete scheme in (18) also satisfies the uniform stability result given in the following lemma.

Lemma 3.2. The solution $Y_i$ of the discrete scheme in (18) satisfies the following bound

$\left|Y_i\right|\le {\zeta }^{-1}\parallel {\xi }_1^N{Y}_i\parallel +\parallel Y{\parallel }_{\mathrm{\partial }\mathrm{\Omega }}.$

Proof. Let $D={\zeta }^{-1}\parallel {\xi }_1^N{Y}_i\parallel +\parallel Y{\parallel }_{\mathrm{\partial }\mathrm{\Omega }}$ and define the barrier function ${\vartheta }_i^{\pm }$ by ${\vartheta }_i^{\pm }=D\pm Y_i$. At the boundary points, we have

${\vartheta }_0^{\pm }=D\pm Y_0={\zeta }^{-1}\parallel {\xi }_1^N{Y}_i\parallel +\parallel Y{\parallel }_{\mathrm{\partial }\mathrm{\Omega }}\pm \varphi (0)\ge 0,$

${\vartheta }_N^{\pm }=D\pm Y_N={\zeta }^{-1}\parallel {\xi }_1^N{Y}_i\parallel +\parallel Y{\parallel }_{\mathrm{\partial }\mathrm{\Omega }}\pm \varphi (1)\ge 0.$

On the discretized domain $t_i,0<i<N$, we obtain

${\text{pound}}_1^N{\vartheta }_i^{\pm }=-c_{\epsilon }\left(\frac{D\pm Y_{i+1}-2(D\pm Y_i)+D\pm Y_{i-1}}{{\gamma }_i^2}\right)+d_{i-1/2}(\frac{D\pm Y_i-D\pm Y_{i-1}}{\mathrm{\Delta }t})$

$+b_{i-1/2}(D\pm Y_i)$

$=b_{i-1/2}D\pm {\xi }_1^N{Y}_i$

$=b_{i-1/2}({\zeta }^{-1}\parallel {\text{pound}}_1^N{Y}_i\parallel +\parallel Y{\parallel }_{\mathrm{\partial }\mathrm{\Omega }})\pm f_{i-1/2}\text{break}\ge 0,since{b}_{i-1/2}\ge \zeta .$

Using the discrete maximum principle in Lemma 3.1, we obtain ${\vartheta }_i^{\pm }\ge 0,i=0,1,\dots ,N.$ Hence, the required bound is obtained.

Next, we want to prove uniform convergence of the scheme in (18). Let us denote the forward and backward finite differences operators for the first derivative as

$D^{+}z(t_i)=\frac{z(t_{i+1})-z(t_i)}{\mathrm{\Delta }t},D^{-}z(t_i)=\frac{z(t_i)-z(t_{i-1})}{\mathrm{\Delta }t}$

respectively, and the second-order finite difference operator as

$D^{+}{D}^{-}z(t_i)=\frac{D^{+}z(t_i)-D^{-}z(t_i)}{\mathrm{\Delta }t}.$

Lemma 3.3. For uniform mesh discretization, we obtain the estimate

(19) $c_{\epsilon }\left|\frac{{(\mathrm{\Delta }t)}^2}{{\gamma }_i^2}-1\right|\le C\mathrm{\Delta }t.$(19)

Proof. Let us define $\rho =d_i\mathrm{\Delta }t/c_{\epsilon },\rho \in (0,\mathrm{\infty })$. Then, using the expression for ${\gamma }_i^2$, we obtain

$c_{\epsilon }\left|\frac{{(\mathrm{\Delta }t)}^2}{{\gamma }_i^2}-1\right|=d_i\mathrm{\Delta }t\left|\frac{1}{exp(\rho )-1}-\frac{1}{\rho }\right|=:d_i\mathrm{\Delta }tQ(\rho ),$

where $Q(\rho )=\frac{exp(\rho )-1-\rho }{\rho (exp(\rho )-1)}$. We obtain the bounds

$\underset{\rho \to 0}{lim}Q(\rho )=\frac{1}{2},\underset{\rho \to \mathrm{\infty }}{lim}Q(\rho )=0.$

Giving that

(20) $Q(\rho )\le C_2,\rho \in (0,\mathrm{\infty }).$(20)

Hence, the estimate $c_{\epsilon }\left|\frac{{(\mathrm{\Delta }t)}^2}{{\gamma }_i^2}-1\right|\le C\mathrm{\Delta }t$.

Theorem 3.4. The discrete solution $Y_i$ of (18) satisfies the truncation error bound

(21) $\left|{\text{pound}}_1^N(y(t_i)-Y_i)\right|\le C\mathrm{\Delta }t(1+\underset{i}{max}\frac{exp(-d(1-t_i)/c_{\epsilon })}{c_{\epsilon }^3}).$(21)

Proof. From the truncation error, we obtain

$\begin{array}{c}|{\text{pound}}_1^N(y(t_i)-Y_i)|\le \left|c_{\epsilon }\left(y{ }^{\mathrm{\prime }\mathrm{\prime }}(t_i)-{(\mathrm{\Delta }t)}^2\frac{D^{+}{D}^{-}y(t_i)}{{\gamma }_i^2}\right)\right|+|y{ }^{\mathrm{\prime }}(t_i)-D^{-}y(t_i)|\\ \hspace{0.17em}\le C{c}_{\epsilon }|y{ }^{\mathrm{\prime }\mathrm{\prime }}(t_i)-D^{+}{D}^{-}y(t_i)|\text{break}+C{c}_{\epsilon }\left|\left(\frac{{(\mathrm{\Delta }t)}^2}{{\gamma }_i^2}-1\right)D^{+}{D}^{-}y(t_i)|+C\mathrm{\Delta }t|y{ }^{\mathrm{\prime }\mathrm{\prime }}(t_i)\right|\\ \hspace{0.17em}\le C{c}_{\epsilon }{(\mathrm{\Delta }t)}^2|y^{(4)}(t_i)|+C\mathrm{\Delta }t|y{ }^{\mathrm{\prime }\mathrm{\prime }}(t_i)|.\end{array}$

Using the bound in Lemma 3.3, we obtain

(22) $\left|{\text{pound}}_1^N(y(t_i)-Y_i)\left|\le C{c}_{\epsilon }{(\mathrm{\Delta }t)}^2\right|y^{(4)}(t_i)\left|+C\mathrm{\Delta }t\right|y{ }^{\mathrm{\prime }\mathrm{\prime }}(t_i)\right|.$(22)

Using the boundedness of the derivatives of the solution in Lemma 2.4 into (22) gives the required bound

$\begin{array}{cc}|{\text{pound}}_1^N(y(t_i)-Y_i)|& \le C{c}_{\epsilon }{(\mathrm{\Delta }t)}^2\left|1+c_{\epsilon }^{-4}{e}^{\frac{-d(1-t_i)}{c_{\epsilon }}}\right|+C\mathrm{\Delta }t\left|1+c_{\epsilon }^{-2}{e}^{\frac{-d(1-t_i)}{c_{\epsilon }}}\right|\\ \hspace{0.17em}& \le C\mathrm{\Delta }t(1+\underset{i}{max}{c}_{\epsilon }^{-3}{e}^{\frac{-d(1-t_i)}{c_{\epsilon }}}),\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{e},c_{\epsilon }^{-3}\ge c_{\epsilon }^{-2}.\end{array}$

Lemma 3.5. For a fixed mesh and for $\epsilon \to 0,$ it holds

(23) $\underset{c_{\epsilon }\to 0}{lim}\underset{1\le j\le N-1}{max}{c}_{\epsilon }^{-m}{e}^{\frac{-d(1-t_j)}{c_{\epsilon }}}=0,m=1,2,3,\dots$(23)

where $t_j=j\mathrm{\Delta }t,\mathrm{\Delta }t=1/N$.

Proof. See, in (Woldaregay & Duressa, 2021a).

Theorem 3.6. The error for the discretization of the non-standard FDM on uniform mesh satisfies the bound

(24) $\underset{\epsilon }{max}\parallel y(t_i)-Y_i\parallel \le C\mathrm{\Delta }t.$(24)

Proof. Using Lemma 3.5, into Theorem 3.4 gives $\left|{\xi }_1^N(y(t_i)-Y_i)\right|\le C\mathrm{\Delta }t$. By the discrete maximum principle in Lemma 3.1, we obtain the bound $|y(t_i)-Y_i|\le C\mathrm{\Delta }t$.

3.2. Scheme II: Standard mid-point upwind scheme on Shishkin Mesh

Let $\{t_i{\}}_{i=0}^N$ be the discretized domain where $N$ is the number of grid points, and be an even positive integer. For each $i\ge 1$, we define $h_i=t_i-t_{i-1}$. Since the considered problem exhibits right boundary layer we set a mesh transition parameter $\tau$ which divides the domain $[0,1]$ in to outer layer region ${\mathrm{\Omega }}_1=[0,1-\tau ]$ and inner (boundary) layer region ${\mathrm{\Omega }}_2=[1-\tau ,1]$. The mesh transition parameter $\tau$ is defined as

(25) $\tau =min\{\frac{1}{2},\frac{\sigma c_{\epsilon }}{\zeta }lnN\},$(25)

where $N$ denotes the number of mesh points in discretization and $\sigma$ denotes a constant that represents the order of the scheme and $\zeta$ denotes the lower bound of $b(t)$. Now we set a uniform mesh $N/2$ in ${\mathrm{\Omega }}_1$ with mesh spacing $H=\frac{2(1-\tau )}{N}$ and similarly a uniform mesh $N/2$ is placed in ${\mathrm{\Omega }}_2$ with the mesh spacing $h=\frac{2\tau }{N}$. So that the mesh points $t_i$ are given as

(26) $t_i=\left\{\begin{array}{c}\frac{2(1-\tau )}{N}i,fori=0,1,2,\dots ,N/2,\\ 1-\tau +\frac{2\tau }{N}(i-N/2),fori=N/2+1,\dots ,N.\end{array}\right.$(26)

Similarly, one can generate a Shishkin mesh for the left boundary layer problem.

For the mesh function $y(t_i)$ at the grid points $t_i$, the first and second derivatives approximation is given as

$D^{-}y(t_i)=\frac{Y_i-Y_{i-1}}{h_i},D^{+}y(t_i)=\frac{Y_{i+1}-Y_i}{h_{i+1}},$

and

$D^{+}{D}^{-}y(t_i)=\frac{2}{h_i+h_{i+1}}\left(\frac{Y_{i+1}-Y_i}{h_{i+1}}-\frac{Y_i-Y_{i-1}}{h_i}\right).$

The mid-point upwind discrete scheme on the piecewise uniform Shishkin mesh is given as

(27) $\{{}_{Y_0=\varphi (0),Y_N=\varphi (1),}^{{\pounds }_2^N{Y}_i=-\frac{c_{\epsilon }}{h_i+h_{i+1}}\left(\frac{Y_{i+1}-Y_i}{h_{i+1}}-\frac{Y_i-Y_{i-1}}{h_i}\right)+d_{i-1/2}\frac{Y_i-Y_{i-1}}{h_i}+b_{i-1/2}{Y}_i=f_{i-1/2},}$(27)

for $i=1,2,\dots ,N-1$.

Theorem 3.7. The maximum absolute error for the discretization of the mid-point upwind FDM on Shishkin mesh satisfies the bound

(28) $\underset{i}{max}|y(t_i)-Y_i|\le C{N}^{-1}(c_{\epsilon }+N^{-4(1-i/N)})lnN.$(28)

Proof. See, in (Kadalbajoo & Ramesh, 2007).

3.3. Scheme III: Non-standard mid-point upwind scheme on Shishkin Mesh

Here, we introduce a hybrid method that is constructed using concepts from the non-standard FDM and fitted mesh method. We use the mesh transition parameter defined in (25) and the Shishkin mesh defined in (26). It is well documented that the non-standard FDM is superior in accuracy to that of fitted mesh FDM. The fitted mesh methods have a layer resolving behaviour ($N/2$ mesh points are computed in the boundary layer region) which is the drawback of Scheme I. Scheme III uses the denominator function constructed for Scheme I together with the fitted mesh technique. The non-standard FDM is traditionally applied on uniform meshes while using it on fitted mesh necessitates the following modifications

(29) ${\gamma }_i=\frac{c_{\epsilon }}{d_i}(exp(\frac{h_i{d}_i}{c_{\epsilon }})-1),and{\gamma }_{i+1}=\frac{c_{\epsilon }}{d_i}(exp(\frac{h_{i+1}{d}_i}{c_{\epsilon }})-1).$(29)

For the mesh function $y(t_i)$ at the grid points $t_i$, we have the approximation of the first and second derivatives as

$D^{-}y(t_i)=\frac{Y_i-Y_{i-1}}{h_i},and(D^{+}{D}^{-}{)}_{\gamma }y(t_i)=\frac{2}{h_i+h_{i+1}}\left(\frac{Y_{i+1}-Y_i}{{\gamma }_{i+1}}-\frac{Y_i-Y_{i-1}}{{\gamma }_i}\right).$

Non-standard mid-point upwind FDM on Shishkin mesh for $i=1,2,\dots ,N-1,$ is given as

(30) $\begin{array}{l}\{{}_{Y_0=\varphi (0),Y_N=\varphi (1).}^{{\pounds }_3^N{Y}_i=-\frac{2c_{\epsilon }}{h_i+h_{i+1}}\left(\frac{Y_{i+1}-Y_i}{{\gamma }_{i+1}}-\frac{Y_i-Y_{i-1}}{{\gamma }_i}\right)+d_{i-1/2}\frac{Y_i-Y_{i-1}}{h_i}+b_{i-1/2}{Y}_i=f_{i-1/2},}\\ \end{array}$(30)

3.3.1. Uniform convergence of scheme III

We assumed that $\tau =min\{\frac{1}{2},\frac{\sigma c_{\epsilon }}{\zeta }lnN\}$. Now, we assign each of the subintervals $[0,1-\tau ]$ and $[1-\tau ,1]$ with $N/2$ number of equidistant grid points. Let $H$ be the mesh width in the subinterval $[0,1-\tau ]$ and $h$ be the mesh width in $[1-\tau ,1]$. These mesh widths satisfy

(31) $N^{-1}\le H\le 2N^{-1},h\le N^{-1},and,h=\frac{\sigma c_{\epsilon }}{\zeta }{N}^{-1}lnN.$(31)

Lemma 3.8. The discrete maximum principle. The discrete scheme ${\xi }_3^N{Y}_i=f_{i-1/2},i=1,2,\dots ,N-1$ and for given $Y_0$ and $Y_N$ has a solution. If ${\xi }_3^N{Y}_i\le {\xi }_3^N{U}_i$ for $i=1,2,\dots ,N-1$, and if $Y_0\le U_0$ and $Y_N\le U_N$ then $Y_i\le U_i$, $\mathrm{\forall }i=0,1,2,\dots ,N.$

Proof. The matrix associated with operator ${\xi }_3^N{Y}_i$ is of size $(N+1)\times (N+1)$ and satisfies the property of $M$-matrix with the given condition in (31). See the detailed proof in (Kellogg & Tsan, 1978).

Lemma 3.9. The solution $Y_i$ of the discrete scheme in (30) satisfies the bound

$\left|Y_i\right|\le {\zeta }^{-1}\parallel {\xi }_3^N{Y}_i\parallel +\parallel Y{\parallel }_{\mathrm{\partial }\mathrm{\Omega }}.$

Proof. Let $D={\zeta }^{-1}\parallel {\xi }_3^N{Y}_i\parallel +\parallel Y{\parallel }_{\mathrm{\partial }\mathrm{\Omega }}$ and define the barrier function ${\vartheta }_i^{\pm }$ by ${\vartheta }_i^{\pm }=D\pm Y_i$. At the boundary points, we have

$\begin{array}{c}{\vartheta }_0^{\pm }=D\pm Y_0={\zeta }^{-1}\parallel {\zeta }_3^N{Y}_i\parallel +\parallel Y{\parallel }_{\mathrm{\partial }\mathrm{\Omega }}\pm \varphi (0)\ge 0,\\ {\vartheta }_N^{\pm }=D\pm Y_N={\zeta }^{-1}\parallel {\zeta }_3^N{Y}_i\parallel +\parallel Y{\parallel }_{\mathrm{\partial }\mathrm{\Omega }}\pm \varphi (1)\ge 0.\end{array}$

On the discretized spatial domain $t_i,0<i<N$, we obtain

$\begin{array}{rl}& {\text{pound}}_3^N{\vartheta }_i^{\pm }=-c_{\epsilon }\left(\frac{D\pm Y_{i+1}-(D\pm Y_i)}{{\gamma }_{i+1}}-\frac{(D\pm Y_i)-(D\pm Y_{i-1})}{{\gamma }_i}\right)\\ & +d_{i-1/2}\left(\frac{D\pm Y_i-D\pm Y_{i-1}}{h_i}\right)+b_{i-1/2}(D\pm Y_i)\\ & =b_{i-1/2}D\pm {\xi }_3^N{Y}_i\\ & =b_{i-1/2}({\zeta }^{-1}\parallel {\xi }_3^N{Y}_i\parallel +\parallel Y{\parallel }_{\mathrm{\partial }\mathrm{\Omega }})\pm f_{i-1/2}\\ & \ge 0,since{b}_{i-1/2}\ge \zeta .\end{array}$

Using the discrete maximum principle in Lemma 3.1, we obtain ${\vartheta }_i^{\pm }\ge 0,i=0,1,\dots ,N.$ Hence, the required bound is obtained.

Lemma 3.10. Let $t_i\in {\mathrm{\Omega }}^N$ for a given mesh ${\mathrm{\Omega }}^N=\{t_i{\}}_{i=0}^N$. Then, for any $z\in C^4(\bar{\mathrm{\Omega }})$

$|D^{-}z(t_i)-z{ }^{\mathrm{\prime }}(t_i)|\le C{h}_i|z{ }^{\mathrm{\prime }\mathrm{\prime }}(\xi )|,and|D^{+}{D}^{-}z(x_i)-z{ }^{\mathrm{\prime }\mathrm{\prime }}(x_i)|\le C{h}_i^2|z^{(4)}(\xi )|.$

Proof. See, in ((Miller et al., 2012), Lemma 4.1).

3.3.2. Decomposition of the Numerical Solution

We decompose the numerical solution $Y_i$ into regular and singular components in a similar way to the continuous case as,

(32) $Y_i=V_i+W_i,i=0,1,2,\dots ,N,$(32)

where the regular part satisfied the non-homogeneous equation

(33) $\{{}_{V(0)=v(0),V(1)=v(1),}^{{\pounds }_3^N{V}_i=-\frac{2c_{\epsilon }}{h_i+h_{i+1}}\left(\frac{V_{i+1}-V_i}{{\gamma }_{i+1}}-\frac{V_i-V_{i-1}}{{\gamma }_i}\right)+d_{i-1/2}\frac{V_i-V_{i-1}}{h_i}+b_{i-1/2}{V}_i=f_{i-1/2}}$(33)

and the singular component $W_i$ satisfies the homogeneous equation

(34) $\{{}_{W(0)=w(0),W(1)=w(1),}^{{\pounds }_3^N{W}_i=-\frac{2c_{\epsilon }}{h_i+h_{i+1}}\left(\frac{W_{i+1}-W_i}{{\gamma }_{i+1}}-\frac{W_i-W_{i-1}}{{\gamma }_i}\right)+d_{i-1/2}\frac{W_i-W_{i-1}}{h_i}+b_{i-1/2}{W}_i=0,}$(34)

Now the error in the numerical solution can also be decomposed as

(35) $Y_i-y(t_i)=V_i-v(t_i)+W_i-w(t_i).$(35)

We estimate the error in the regular and singular solutions separately. For the case $\tau =\frac{1}{2}$, the mesh becomes uniform on the entire domain. So, we have

$\begin{array}{rl}& (D^{+}{D}^{-}{)}_{\gamma }w(t_i)=\frac{2}{h_i+h_{i+1}}\left[\frac{W_{i+1}-W_i}{{\gamma }_{i+1}}-\frac{W_i-W_{i-1}}{{\gamma }_i}\right]\\ & =\frac{W_{i+1}-W_i}{\frac{h{c}_{\epsilon }}{d_i}(exp(\frac{h{d}_i}{c_{\epsilon }})-1)}-\frac{W_i-W_{i-1}}{\frac{h{c}_{\epsilon }}{d_i}(exp(\frac{h{d}_i}{c_{\epsilon }})-1)}\\ & =\frac{W_{i+1}-2W_i+W_{i-1}}{\frac{h{c}_{\epsilon }}{d_i}(exp(\frac{h{d}_i}{c_{\epsilon }})-1)},\end{array}$

So, the scheme becomes non-standard FDM on uniform mesh in (18). Here, we prove the uniform convergence for the case $\tau =\frac{\sigma c_{\epsilon }}{\zeta }lnN$ only.

For the case $\tau =\frac{\sigma c_{\epsilon }}{\zeta }lnN$, we estimate the error in the regular and singular solution separately. In this case $\frac{\sigma c_{\epsilon }}{\zeta }lnN\le 0.5$, which implies that $\frac{1}{c_{\epsilon }}\le ClnN$.

Theorem 3.11. The error in the regular component satisfies the bound

(36) $|v(t_i)-V_i|\le C{N}^{-1}.$(36)

Proof. On outer layer region ${\mathrm{\Omega }}_1=[0,1-\tau ]$ it is clear that the mesh is uniform i.e. $h_i=h_{i+1}=H\le 2N^{-1},i=1,2,\dots ,N/2$. Using the bound in Lemma 2.3, the truncation error in the regular component is given as

$\begin{array}{l}|{\pounds }_3^N(v(t_i)-V_i)|=|c_{\epsilon }\left(\frac{d^2}{d{t}^2}-{(D^{+}{D}^{-})}_{\gamma }\right)v(t_i)+d_{i-1/2}(\frac{d}{dt}-D^{-})v(t_i)|\\ \le C{c}_{\epsilon }{N}^{-2}|v^{(4)}(x_i)|+C{N}^{-1}|v(t_i)|,since,H\le 2N^{-1}\\ \le C\epsilon N^{-2}+C{N}^{-1},since|v^i(t_i)|\le C,i=0,1,2,3,4\\ \le C{N}^{-1}.\end{array}$

In the layer region ${\mathrm{\Omega }}_2=[1-\tau ,1]$, the mesh is fine but still uniform i.e. $h_i=h_{i+1}=h\le N^{-1},\text{break}i=N/2+1,\dots ,N-1$. Using the bound in Lemma 2.3, the truncation error is given as

$\begin{array}{rl}& |{\text{pound}}_3^N(v(t_i)-V_i)|=\hspace{0.17em}|c_{\epsilon }\left(\frac{d^2}{d{t}^2}-(D^{+}{D}^{-}{)}_{\gamma }\right)v(t_i)+d_{i-1/2}(\frac{d}{dt}-D^{-})v(t_i)|\\ & \le C{c}_{\epsilon }{N}^{-2}|v^{(4)}(x_i)|+C{N}^{-1}|v^{\mathrm{\prime }\mathrm{\prime }}(t_i)|,since,h\le N^{-1}\\ & \le C\epsilon N^{-2}+C{N}^{-1},since|v^i(t_i)\\ & |\le C,i=0,1,2,3,4\\ & \le C{N}^{-1}.\end{array}$

Using the discrete maximum principle, we obtain $|v(t_i)-V_i|\le C{N}^{-1}.$

Theorem 3.12. Error in the singular component satisfies the bound

(37) $|w(t_i)-W_i|\le C{N}^{-1}(lnN{)}^2.$(37)

Proof. On outer layer region ${\mathrm{\Omega }}_1=[0,1-\tau ]$, we have $h_i=h_{i+1}=H\le 2N^{-1},i=1,2,\dots ,N/2$. Using the bound in Lemma 2.3, the truncation error becomes

$\begin{array}{rl}& |{\text{pound}}_3^N(w(t_i)-W_i)|=|c_{\epsilon }\left(\frac{d^2}{d{t}^2}-(D^{+}{D}^{-}{)}_{\gamma }\right)w(t_i)\\ & +d_{i-1/2}(\frac{d}{dt}-D^{-})w(t_i)|\\ & \le C{c}_{\epsilon }{N}^{-2}|w^{(4)}(t_i)|+C{N}^{-1}|w^{\mathrm{\prime }\mathrm{\prime }}(t_i)|,\\ & \mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{e}H\le 2N^{-1}\\ & \le C{c}_{\epsilon }{N}^{-2}\left(c_{\epsilon }^{-4}exp\left(\frac{-d(1-t_i)}{c_{\epsilon }}\right)\right)\\ & +C{N}^{-1}\left(c_{\epsilon }^{-2}exp\left(\frac{-d(1-t_i)}{c_{\epsilon }}\right)\right)\\ & since|w^{(i)}(t_i)|\le c_{\epsilon }^{-i}exp\left(\frac{-d(1-t_i)}{c_{\epsilon }}\right),\\ & i=0,1,2,3,4\\ & \le C\left(N^{-2}{c}_{\epsilon }^{-3}+N^{-1}{c}_{\epsilon }^{-2})exp\left(\frac{-d(1-t_i)}{c_{\epsilon }}\right)\right)\\ & \le C(N^{-2}{c}_{\epsilon }^{-3}+N^{-1}{c}_{\epsilon }^{-2})N^{-1},\\ & sinceexp\left(\frac{-d(1-\{t_i=0\})}{c_{\epsilon }}\right)\\ & \le C{N}^{-1},\le C{N}^{-2}(lnN{)}^2,since\frac{1}{c_{\epsilon }}\le ClnN.\end{array}$

In the boundary layer region ${\mathrm{\Omega }}_2=[1-\tau ,1]$, the mesh is also uniform i.e. $h_i=h_{i+1}=h,i=N/2+1,\dots ,N-1$. Hence, we have

$\begin{array}{rl}& |{\text{pound}}_3^N(w(t_i)-W_i)|=|c_{\epsilon }(\frac{d^2}{d{t}^2}-(D^{+}{D}^{-}{)}_{\gamma })w(t_i)\\ & +d_{i-1/2}(\frac{d}{dt}-D^{-})w(t_i)|\\ & \le C{c}_{\epsilon }{N}^{-2}|w^{(4)}(t_i)|\\ & +C{N}^{-1}|w^{\mathrm{\prime }\mathrm{\prime }}(t_i)|,sinceh\le N^{-1}\\ & \le C{c}_{\epsilon }{N}^{-2}(c_{\epsilon }^{-4}exp(\frac{-d(1-t_i)}{\epsilon }))\\ & +C{N}^{-1}(c_{\epsilon }^{-2}exp(\frac{-d(1-t_i)}{c_{\epsilon }}))\\ & since|w^{(i)}(t_i)|\le c_{\epsilon }^{-i}exp(\frac{-d(1-t_i)}{c_{\epsilon }}),\\ & i=0,1,2,3,4\\ & \le C(N^{-2}{c}_{\epsilon }^{-3}+N^{-1}{c}_{\epsilon }^{-2})exp(\frac{-d(1-t_i)}{c_{\epsilon }}),\\ & \le C{N}^{-1}{c}_{\epsilon }^{-2},since\underset{i}{max}exp(\frac{-d(1-t_i)}{c_{\epsilon }})\le 1,\\ & \le C{N}^{-1}(lnN{)}^2,since\frac{1}{c_{\epsilon }}\le ClnN.\end{array}$

Hence, from the outer layer and boundary layer region, we obtain the bound

$\begin{array}{ccc}\left|{\text{pound}}_3^N(w(t_i)-W_i)\right|& \le & max\left\{C{N}^{-2}{(lnN)}^2,\text{break}C{N}^{-1}{(lnN)}^2\right\}=C{N}^{-1}{(lnN)}^2.\end{array}$

Using the discrete maximum principle, we obtain $|w(t_i)-W_i|\le C{N}^{-1}(lnN{)}^2.$

Theorem 3.13. The error of the computed solution due to the hybrid scheme satisfies the bound

(38) $\underset{\epsilon }{max}\parallel y(t_i)-Y_i\parallel \le C{N}^{-1}(lnN{)}^2.$(38)

Proof. Combining the error estimate in the regular and singular components in Theorem 3.11 and 3.12 gives the result.

4. Numerical results and discussion

We consider numerical examples to illustrate the theoretical findings of the developed schemes.

Example 4.1. We consider the problem

$-\epsilon y{ }^{\mathrm{\prime }\mathrm{\prime }}(t)+(1+t)y{ }^{\mathrm{\prime }}(t-\delta )-exp(-2t)y(t-\delta )+exp(-t)y(t)=-exp(t-1)$

with interval-boundary conditions $y(t)=1,-\delta \le \text{break}t\le 0,y(1)=-1.$

Example 4.2. We consider the problem

$-\epsilon y{ }^{\mathrm{\prime }\mathrm{\prime }}(t)+(1+t)y{ }^{\mathrm{\prime }}(t-\delta )+sin(2t)y(t-\delta )-exp(-t)y(t)=sin(2t)+3exp(-t)$

with interval-boundary conditions $y(t)=-1,-\delta \le \text{break}t\le 0,y(1)=1.$

The exact solution to the considered examples is not known. So, using the procedure of double mesh techniques, we calculate the maximum absolute error. Let $Y_i^N$ be denoted for the computed solution of the problem for $N$ number of mesh points and $Y_i^{2N}$ be denoted for the computed solution on double number of mesh points $2N$ by including the mid-points $t_{i+1/2}=\frac{t_{i+1}+t_i}{2}$ into the mesh points.

The maximum point-wise absolute error is given by $E_{\epsilon ,\delta }^N=\underset{i}{max}|Y_i^N-Y_i^{2N}|,$ and the $\epsilon$-uniform error is calculated using $E^N=\underset{\epsilon ,\delta }{max}|E_{\epsilon ,\delta }^N|.$

The rate of convergence of the scheme is calculated using $r_{\epsilon ,\delta }^N={log}_2(E_{\epsilon ,\delta }^N/E_{\epsilon ,\delta }^{2N}).$ and the $\epsilon$- uniform rate of convergence is calculated using $r^N={log}_2(E^N/E^{2N}).$

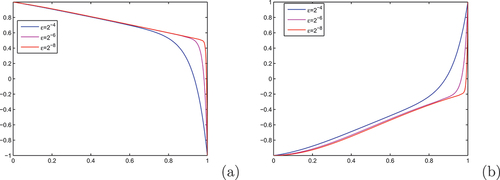
Solution of the considered problems in Example 4.1 and 4.2 exhibits a right boundary layer. As one observe in Figure 2$(a)$ and 2 $(b)$, as the perturbation parameter $\epsilon$ goes small the boundary layer formation becomes more visible. In Figure 3$(a)$ and Figure 4 $(a)$, the computed solution of Example 4.1 and 4.2 are depicted using Scheme I for $\epsilon =2^{-10}$. In these figures, we observe that there is no computed solution in the boundary layer region, which is the main drawback of the non-standard finite difference method and exponentially fitted operator methods. In Figure 3$(b)$ and Figure 4 $(b)$, the computed solution of Example 4.1 and 4.2 are depicted using Scheme III for $\epsilon =2^{-10}$. In these figures, one can observe that a sufficient amount of mesh points and computed solutions are in the boundary layer region. we call that, the boundary layer resolving property of the scheme. In Figure 5 and Figure 6, the absolute error of the three schemes are depicted for different mesh numbers $N=2^5,2^6$ and $2^7$. As the mesh numbers increases, the accuracy of the schemes increases. 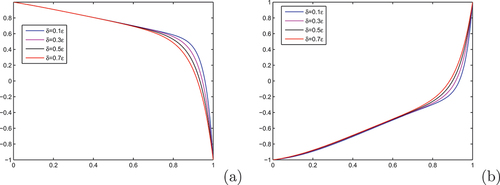In Figure 1, the effect of the delay parameter $(\delta )$ on the solution and the influence of $\delta$ on the thickness of the boundary layer are shown. As the magnitude of the delay parameter increase, the thickness of the boundary layer increases.

Figure 1. Effect of the delay parameter $(\delta )$ on solution: (a) Example 4.1 and (b) Example 4.2 for $\epsilon =2^{-4}$.

Figure 2. Formation of the boundary layer as $\epsilon$ goes small in (a) Example 4.1 in (b) Example 4.2.

Figure 3. Example 4.1, Layer resolving property of the schemes for $\epsilon =2^{-10}$: on (a) Scheme I, on (b) Scheme III for $N=2^6$

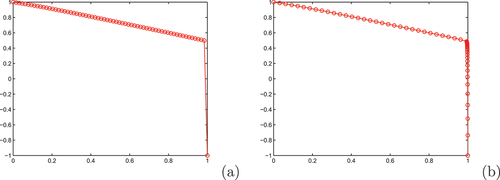
Figure 4. Layer resolving property of the schemes for $\epsilon =2^{-10}$ Example 4.2: in (a) Scheme I, in (b) Scheme III for $N=2^6$

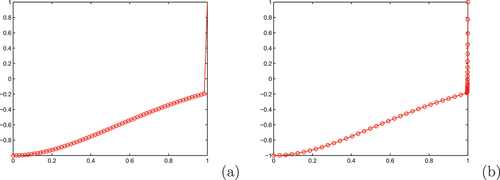
Figure 5. Example 4.1, absolute error of the schemes for different mesh numbers on (a) Scheme I, on (b) Scheme II and on (c) Scheme III for $\epsilon =2^{-20}$

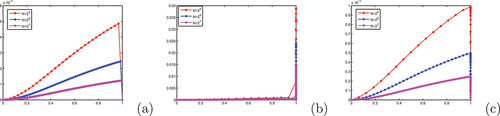
Figure 6. Example 4.2, absolute error of the schemes for different mesh numbers on (a) Scheme I, on (b) Scheme II and on (c) Scheme III for $\epsilon =2^{-20}$

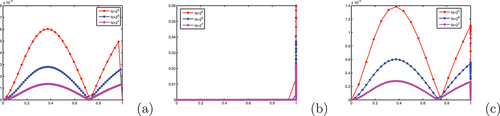
In Tables 1 and 5, the maximum absolute error, $\epsilon$-uniform error and $\epsilon$-uniform rate of convergence of Example 4.1 and 4.2 are given for the Scheme II. Similarly, in Tables, 2 and 6, the maximum absolute error, $\epsilon$-uniform error, and the $\epsilon$-uniform rate of convergence of Scheme III are given. As one can see from the results in these tables, Scheme II has inferior accuracy and rate of convergence to Scheme III. The results in Tables 2-6, show that the schemes are uniformly convergent(converges independent of the perturbation parameter as the perturbation parameter goes small) with an order of convergence one. In Tables 3 and 7, the maximum absolute error of Scheme III for different values of the delay parameter is given. As is seen in these tables, the scheme converges independently of the delay parameter. In Table 4, one can see the comparison of Scheme III with the results in (Kadalbajoo & Ramesh, 2007; Kumar & Kadalbajoo, 2012), and (Woldaregay & Duressa, 2021a). We confirm that the proposed Scheme III is more accurate than the results in (Kadalbajoo & Ramesh, 2007; Kumar & Kadalbajoo, 2012), and (Woldaregay & Duressa, 2021a).

Table 1. Example 4.1, maximum absolute error of Scheme II in (27) for $\delta =0.5\epsilon$

$\epsilon \downarrow$	N $\to$ $2^5$	$2^6$	$2^7$	$2^8$	$2^9$	$2^{10}$
$2^{-1}$	4.4251e-03	2.2784e-03	1.1565e-03	5.8257e-04	2.9238e-04	1.4646e-04
$2^{-4}$	3.2208e-02	2.0620e-02	1.2640e-02	7.1665e-03	3.6525e-03	1.8441e-03
$2^{-8}$	3.1420e-02	1.9795e-02	1.2021e-02	7.0567e-03	4.0454e-03	2.2756e-03
$2^{-12}$	3.8756e-02	2.4129e-02	1.4568e-02	8.5257e-03	4.8728e-03	2.7339e-03
$2^{-16}$	3.8722e-02	2.4105e-02	1.4552e-02	8.5148e-03	4.8664e-03	2.7306e-03
$2^{-20}$	3.8720e-02	2.4103e-02	1.4551e-02	8.5140e-03	4.8658e-03	2.7302e-03
$2^{-24}$	3.8720e-02	2.4103e-02	1.4551e-02	8.5139e-03	4.8657e-03	2.7302e-03
$2^{-30}$	3.8720e-02	2.4103e-02	1.4551e-02	8.5139e-03	4.8657e-03	2.7302e-03
$E^N$	3.8756e-02	2.4129e-02	1.4568e-02	8.5257e-03	4.8728e-03	2.7339e-03
$r^N$	0.6837	0.7279	0.7729	0.8071	0.8338	-

Table 2. Example 4.1, maximum absolute error of Scheme III in (30) for $\delta =0.5\epsilon$

$\epsilon \downarrow$	N $\to$ $2^5$	$2^6$	$2^7$	$2^8$	$2^9$	$2^{10}$
$2^{-1}$	5.4777e-04	2.8329e-04	1.4398e-04	7.2573e-05	3.6432e-05	1.8252e-05
$2^{-4}$	5.4013e-04	3.0846e-04	1.1991e-04	8.7367e-05	4.3864e-05	1.9777e-05
$2^{-8}$	6.5860e-04	1.7524e-04	1.8706e-04	5.4203e-05	5.3422e-05	2.1310e-05
$2^{-12}$	9.9983e-04	5.0405e-04	2.5259e-04	1.2650e-04	6.3418e-05	3.2934e-05
$2^{-16}$	9.8946e-04	4.9744e-04	2.4859e-04	1.2417e-04	6.2046e-05	3.1014e-05
$2^{-20}$	9.8881e-04	4.9702e-04	2.4834e-04	1.2402e-04	6.1963e-05	3.0968e-05
$2^{-24}$	9.8877e-04	4.9700e-04	2.4832e-04	1.2402e-04	6.1958e-05	3.0965e-05
$2^{-30}$	9.8876e-04	4.9700e-04	2.4832e-04	1.2401e-04	6.1958e-05	3.0965e-05
$E^N$	9.9983e-04	5.0405e-04	2.5259e-04	1.2650e-04	6.3418e-05	3.2934e-05
$r^N$	0.9881	0.9968	0.9977	0.9962	0.9453	-

Table 3. Example 4.1, maximum absolute error of Scheme III in (30) for different values of $\delta$ with $\epsilon =2^{-20}$

$\delta \downarrow ,$	$N\to 2^5$	$2^6$	$2^7$	$2^8$	$2^9$	$2^{10}$
$0$	9.8881e-04	4.9702e-04	2.4834e-04	1.2402e-04	6.1963e-05	3.0968e-05
$0.1\epsilon$	9.8468e-04	4.9622e-04	2.4820e-04	1.2400e-04	6.1960e-05	3.0968e-05
$0.3\epsilon$	9.8305e-04	4.9553e-04	2.4803e-04	1.2397e-04	6.1954e-05	3.0967e-05
$0.5\epsilon$	9.8848e-04	4.9616e-04	2.4809e-04	1.2397e-04	6.1954e-05	3.0967e-05
$0.7\epsilon$	9.9791e-04	4.9776e-04	2.4836e-04	1.2402e-04	6.1963e-05	3.0969e-05

Table 4. Example 4.1, comparison of maximum absolute error of Scheme III in (30) with results in (Kadalbajoo & Ramesh, 2007; Kumar & Kadalbajoo, 2012) and (Woldaregay & Duressa, 2021a)

$\epsilon \downarrow$	N $\to$ $2^5$	$2^6$	$2^7$	$2^8$	$2^9$	$2^{10}$
	Scheme III in (30)
$2^{-16}$	9.8946e-04	4.9744e-04	2.4859e-04	1.2417e-04	6.2046e-05	3.1014e-05
$2^{-20}$	9.8881e-04	4.9702e-04	2.4834e-04	1.2402e-04	6.1963e-05	3.0968e-05
$2^{-24}$	9.8877e-04	4.9700e-04	2.4832e-04	1.2402e-04	6.1958e-05	3.0965e-05
	Result in (Kumar & Kadalbajoo, 2012)
$2^{-16}$	3.6701e-02	1.2463e-02	4.1666e-03	1.4086e-03	4.7513e-04	1.5946e-04
$2^{-20}$	3.6709e-02	1.2478e-02	4.1763e-03	1.3898e-03	4.5369e-04	1.5379e-04
$2^{-24}$	3.6710e-02	1.2479e-02	4.1785e-03	1.3936e-03	4.5637e-04	1.4895e-04
	Method 1 in (Kadalbajoo & Ramesh, 2007)
$2^{-16}$	3.19e-2	1.90e-2	1.10e-2	6.21e-3	3.47Ee-3	1.93e-3
$2^{-20}$	3.19e-2	1.90e-2	1.09e-2	6.19e-3	3.46e-3	1.91e-3
$2^{-24}$	3.19e-2	1.90e-2	1.09e-2	6.19e-3	3.46e-3	1.91e-3
	Method 2 in (Kadalbajoo & Ramesh, 2007)
$2^{-16}$	3.39e-2	1.99e-2	1.14e-2	6.41e-3	3.57e-3	1.97e-3
$2^{-20}$	3.39e-2	1.99e-2	1.14e-2	6.39e-3	3.56e-3	1.96e-3
$2^{-24}$	3.39e-2	1.99e-2	1.14e-2	6.39e-3	3.56e-3	1.96e-3
	Method 3 in (Kadalbajoo & Ramesh, 2007)
$2^{-16}$	9.11e-3	3.84e-3	1.68e-3	7.71e-4	3.72e-4	1.89e-4
$2^{-20}$	9.09e-3	3.82e-3	1.66e-3	7.51e-4	3.52e-4	1.69e-4
$2^{-24}$	9.08e-3	3.82e-3	1.66e-3	7.50e-4	3.50e-4	1.68e-4
	Result in (Woldaregay & Duressa, 2021a)
$2^{-16}$	1.0745e-03	5.5307e-04	2.8038e-04	1.4117e-04	7.0825e-05	3.5473e-05
$2^{-20}$	1.0745e-03	5.5307e-04	2.8039e-04	1.4117e-04	7.0826e-05	3.5473e-05
$2^{-24}$	1.0745e-03	5.5307e-04	2.8039e-04	1.4117e-04	7.0826e-05	3.5473e-05

Table 5. Example 4.2, maximum absolute error of Scheme II in (27) for $\delta =0.5\epsilon ,$ for $\sigma =1$

$\epsilon \downarrow$	N $\to 2^5$	$2^6$	$2^7$	$2^8$	$2^9$	$2^{10}$
$2^{-1}$	4.9803e-03	2.5564e-03	1.2951e-03	6.5187e-04	3.2703e-04	1.6379e-04
$2^{-4}$	2.7963e-02	1.8022e-02	1.1082e-02	6.2982e-03	3.2111e-03	1.6215e-03
$2^{-8}$	3.0497e-02	1.9057e-02	1.1510e-02	6.7282e-03	3.8424e-03	2.1557e-03
$2^{-12}$	3.0453e-02	1.9034e-02	1.1513e-02	6.7419e-03	3.8552e-03	2.1638e-03
$2^{-16}$	3.0438e-02	1.9021e-02	1.1502e-02	6.7348e-03	3.8509e-03	2.1616e-03
$2^{-20}$	3.0437e-02	1.9020e-02	1.1502e-02	6.7342e-03	3.8504e-03	2.1613e-03
$2^{-24}$	3.0437e-02	1.9020e-02	1.1502e-02	6.7342e-03	3.8504e-03	2.1612e-03
$2^{-30}$	3.0437e-02	1.9020e-02	1.1502e-02	6.7342e-03	3.8504e-03	2.1612e-03
$E^N$	3.0453e-02	1.9034e-02	1.1513e-02	6.7419e-03	3.8552e-03	2.1638e-03
$r^N$	0.6780	0.7253	0.7720	0.8064	0.8333	-

Table 6. Example 4.2, maximum absolute error of Scheme III in (30) for $\delta =0.5\epsilon$

$\epsilon \downarrow$	N $\to 2^5$	$2^6$	$2^7$	$2^8$	$2^9$	$2^{10}$
$2^{-1}$	7.5977e-04	3.7960e-04	1.8981e-04	9.4937e-05	4.7478e-05	2.3742e-05
$2^{-4}$	1.3153e-03	4.9853e-04	1.9598e-04	1.0356e-04	5.3303e-05	2.6682e-05
$2^{-8}$	1.1163e-03	5.1315e-04	1.4435e-04	1.2709e-04	5.0211e-05	2.4331e-05
$2^{-12}$	1.3840e-03	6.0117e-04	2.7968e-04	1.3440e-04	6.3466e-05	2.4170e-05
$2^{-16}$	1.3861e-03	6.0216e-04	2.8020e-04	1.3511e-04	6.6747e-05	3.3305e-05
$2^{-20}$	1.3862e-03	6.0223e-04	2.8023e-04	1.3513e-04	6.6596e-05	3.3220e-05
$2^{-24}$	1.3862e-03	6.0223e-04	2.8023e-04	1.3513e-04	6.6586e-05	3.3215e-05
$2^{-30}$	1.3862e-03	6.0223e-04	2.8023e-04	1.3513e-04	6.6586e-05	3.3215e-05
$E^N$	1.3862e-03	6.0223e-04	2.8023e-04	1.3513e-04	6.6586e-05	3.3215e-05
$r^N$	1.2027	1.1037	1.0523	1.0211	1.0034	-

Table 7. Example 4.2, maximum absolute error of Scheme III in (30) for different values of $\delta$ with $\epsilon =2^{-20}$

$\delta \downarrow ,$	$N=2^5$	$2^6$	$2^7$	$2^8$	$2^9$	$2^{10}$
$0$	1.3862e-03	6.0223e-04	2.8023e-04	1.3513e-04	6.6545e-05	3.3210e-05
$0.1\epsilon$	1.3862e-03	6.0223e-04	2.8023e-04	1.3513e-04	6.6545e-05	3.3210e-05
$0.3\epsilon$	1.3862e-03	6.0223e-04	2.8023e-04	1.3513e-04	6.6545e-05	3.3210e-05
$0.5\epsilon$	1.3862e-03	6.0223e-04	2.8023e-04	1.3513e-04	6.6545e-05	3.3210e-05
$0.7\epsilon$	1.3862e-03	6.0223e-04	2.8023e-04	1.3513e-04	6.6545e-05	3.3210e-05

5. Conclusion

In this paper, three numerical schemes are developed and investigated for solving singularly perturbed DDEs. Solution of the considered equation exhibits boundary layer. The developed numerical schemes: Scheme I (non-standard mid-point upwind FDM on uniform mesh), Scheme II (standard mid-point upwind FDM on Shishkin mesh), and Scheme III (non-standard mid-point upwind FDM on Shishkin mesh). The stability of the schemes is investigated using the construction of a barrier function for the solution bound. Uniform convergence of the schemes is stated and proved. The applicability of the schemes is investigated by considering two test examples for different mesh sizes and parameter values. The effect of the perturbation parameter and the delay parameter on the solution is shown using figures and tables. The proposed Scheme III is layer resolving and uniformly convergent with an order of convergence one. It gives more accurate numerical results than Scheme II. Scheme III can be extendible for solving higher dimensional singularly perturbed problems. In future works, we extend Scheme III for semi-linear and higher dimensional singularly perturbed problems.

Acknowledgements

I would like to thank the editor and anonymous referees for careful reading and giving fruitful comments for improving the quality and content of the manuscript.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

The author(s) reported there is no funding associated with the work featured in this article.

Notes on contributors

Mesfin Mekuria Woldaregay

Mesfin Mekuria Woldaregay received his Ph.D. in Mathematics from Jimma University in 2021. Currently, he is working at Adama Science and Technology University, Department of Applied Mathematics as a researcher and lecturer. His research interests span the areas of numerical solution of differential equations, focusing on singularly perturbed problems. He has published more than 25 research articles in reputable journals. He also made numerous contributions in serving as a reviewer, and he is currently serving as an associate editor for the Ethiopian journal of sciences and sustainable development. So far, he has supervised four MSc students to completion and currently supervising four MSc students.