On allowable properties and spectrally arbitrary sign pattern matrices

ABSTRACT

In this paper, we give a geometric construction for different allowable properties for sign pattern matrices. In Section 2, we give a construction for detecting a sign pattern matrix to be potentially nilpotent and also compute the nilpotent matrix realization for a given sign pattern matrix if it exists. In Section 3, we develop a geometric construction for potential stability. In Section 4, we establish a necessary and sufficient condition for a sign pattern matrix $S$ to be spectrally arbitrary. For a given sign pattern matrix of order $n$, we prove that there exists a surface of dimension at most $m$ for $m\le n$ such that for every vector $\left(a_1,a_2,\cdots ,a_n\right)$ on the same surface, there exists a matrix $A\in Q(S)$, a qualitative class of $S$ whose characteristic polynomial is $x^n-a_1{x}^{n-1}+\cdots +(-1{)}^n{a}_n$.

KEYWORDS:

• Potentially nilpotent
• potentially stable
• spectrally arbitrary sign patterns

1. Introduction

A sign pattern matrix of order $n$ is an $n\times n$ matrix whose entries belong to the sign set $\{+,-,0\}$. A qualitative class of a sign pattern matrix $S$ is denoted by $Q(S)$ and is defined as

$Q(S):=\{A=(a_{ij})\in M_n(\mathbb{R}):\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}{a}_{ij}=s_{ij}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}i,j\},$

where $s_{ij}$ is the $i{j}^{th}$ entry of a sign pattern matrix $S$. A property $P$ of an $n\times n$ matrix is said to be an allowable property for a given sign pattern matrix $S$ if there exists an $n\times n$ matrix $A\in Q(S)$ such that $A$ satisfies property $P$. A sign pattern matrix $S$ requires a property $P$ if every matrix in $Q(S)$ satisfies property $P$.

A permutation pattern is a square sign pattern matrix with entries $0$ and $+$, where the entry $+$ occurs precisely once in each row and in each column. A signature sign pattern is a square sign pattern $S$ having diagonal entries either $+$ or $-$ and off-diagonal entries $0$. Sign patterns $S_1$ and $S_2$ are said to be permutationally similar if there exists a permutation pattern matrix $P$ such that $S_1=P^T{S}_{2}P$. Sign patterns $S_1$ and $S_2$ are said to be signature similar if there exists a signature sign pattern matrix $S$ such that $S_1=S{S}_{2}S$. Two sign patterns are said to be equivalent if one of them can be obtained from other by using any combination of transpositions, permutation similarity and signature similarity. In 1947, an economist P. A. Samuelson considered special matrices while studying mathematical modeling of problems from economics. Entries of these matrices were signs instead of real numbers. Such matrices also arise in population biology, chemistry, sociology and many other situations. A study of these matrices falls under the branch of combinatorial matrix theory. In this paper, we have studied some of these qualitative matrix problems.

In Section 2, we have discussed about potentially nilpotent sign pattern matrices, computed nilpotent realization for a given sign pattern matrix if it exists, and also discussed about an index of nilpotency for computed nilpotent realizations. In Section 3, we have introduced the concept of arbitrary potentially stable sign pattern matrices, a method for detecting arbitrary potential stability of a sign pattern matrix. In the same section, we have characterized order 2 arbitrary potentially stable sign pattern matrices. In Section 4, spectrally arbitrary sign pattern matrices have been investigated. This section also generalizes some results from Section 2.

2. Potentially nilpotent sign pattern matrices

A non-zero matrix $A$ of order $n$ is said to be nilpotent if there exists a positive integer $k$ with $A^k=0$. The smallest positive integer $k$ is called as an index of nilpotency for the matrix $A$.

Definition 2.1 (Hogben et al., 2018). A sign pattern matrix $S$ of order $n$ is said to be potentially nilpotent if $S$ allows a nilpotent matrix, i.e., there exists a nilpotent matrix in the qualitative class of $S$.

We will assign a one-to-one correspondence between vectors in ${\mathbb{R}}^n$ and coefficients of a characteristic polynomial for a matrix in $M_n(\mathbb{R})$. For a vector $v=(a_1,a_2,\dots ,a_{n-1},a_n)$, there is a characteristic polynomial $x^n-a_1{x}^{n-1}+a_2{x}^{n-2}-\dots +(-1{)}^{n-1}{a}_{n-1}x+(-1{)}^n{a}_n$ for some square matrix $A$ of order $n$.

Definition 2.2 (Jadhav & Deore, 2022). Let $S$ be a given sign pattern matrix of order $n$. A matrix $A\in Q(S)$ is said to be a realization for a given vector $v=(a_1,a_2,\dots ,a_{n-1},a_n)$ in ${\mathbb{R}}^n$ if the characteristic polynomial of $A$ is $x^n-a_1{x}^{n-1}+a_2{x}^{n-2}-\dots +(-1{)}^{n-1}{a}_{n-1}x+(-1{)}^n{a}_n.$

Here, we discuss about two open questions, the first question has been listed in Catral et al. (2009) and Eschenbach and Johnson (1988) and the second question which has not been directly appeared in the literature. Bergsma et al., 2012; Luo et al., (2015) have discussed about potentially nilpotent sign pattern matrices. However, in Catral et al. (2009), we observe that the nilpotent-Jacobian method for proving spectral arbitrariness of a given sign pattern matrix requires the explicit computation of the nilpotent matrix from the qualitative class of a given sign pattern matrix.

Question 1. Is a sign pattern matrix $S$ potentially nilpotent?

If we want to check whether a given sign pattern matrix $S$ is potentially nilpotent, it is sufficient to find a matrix realization for the vector $(0,0,\cdots ,0)$.

Question 2. If a sign pattern $S$ is potentially nilpotent, then how do we find a nilpotent matrix in the qualitative class of $S$?

In Theorem 2.4, we prove the sufficient condition for sign pattern matrices to be potentially nilpotent. Throughout this article, the characteristic polynomial of a square matrix $A$ will be denoted by $ch(A)$.

Lemma 2.3 (Jadhav & Deore, 2022). Let $A$ and $B$ be two $n\times n$ matrices over the field of real numbers such that they vary either in a fixed row or in a fixed column. Then

$ch((1-s)A+sB)=(1-s)ch(A)+sch(B),\mathrm{\forall }0\le s\le 1.$

Above lemma is easy to prove and can be extended to the convex linear combination of $n$ matrices.

Theorem 2.4. Let $S$ be a sign pattern matrix of order $n$. Suppose $A$ and $B$ are two matrices in $Q(S)$ such that $A$ and $B$ vary exactly either in one row or in one column. If the vectors correspond to $A$ and $B$ are with same magnitude and in opposite direction of each other, then a sign pattern $S$ is potentially nilpotent.

Proof. Suppose that matrix realizations $A$ and $B$ vary exactly either in a row or a column. Let $p_1(x)=x^n-a_1{x}^{n-1}+\cdots +(-1{)}^{n-1}{a}_{n-1}x+(-1{)}^n{a}_n$ and $p_2(x)=x^n-b_1{x}^{n-1}+\cdots +(-1{)}^{n-1}{b}_{n-1}x+(-1{)}^n{b}_n$ be the characteristic polynomials of $A$ and $B$, respectively, so that the vector $v_1=(a_1,a_2,\cdots ,a_n)$ corresponds to matrix $A$ and the vector $v_2=(b_1,b_2,\cdots ,b_n)$ corresponds to matrix $B$. Now, by hypothesis, we have $v_1=-v_2$, i.e., $(a_1,a_2,\cdots ,a_n)=-(b_1,b_2,\cdots ,b_n)$. From Lemma 2.3, the characteristic polynomial of the matrix $N_p=\frac{1}{2}(A+B)$ is given by $p(x)=\frac{1}{2}(p_1(x)+p_2(x))$. Since $v_1=-v_2$, we have $p(x)=x^n$. This shows that $N_p$ is nilpotent and $N_p\in Q(S)$. Thus, $N_p$ gives a required nilpotent matrix realization for a sign pattern $S$. Hence, $S$ is potentially nilpotent.

A generalization of Theorem 2.4 is the following.

Theorem 2.5. Let $S$ be a sign pattern matrix of order $n$. Suppose $A$ and $B$ are matrices in $Q(S)$ such that $A$, $B$ vary exactly either in one row or in one column. If $u$ and $v$ are the vectors corresponding to $A$ and $B$, respectively, and satisfy $(1-s_0)u+s_{0}v=0$ for some $s_0\in [0,1]$, then $S$ is a potentially nilpotent sign pattern matrix.

Proof. In view of Lemma 2.3, the characteristic polynomial of $(1-s_0)A+s_{0}B$ is $(1-s_0)ch(A)+s_{0}ch(B)$. As $A$ and $B$ are realizations of vectors $u$ and $v$ such that they vary exactly in a row or a column, the matrix $(1-s_0)A+s_{0}B$ is a realization for the vector $(1-s_0)u+s_{0}v=0$. Also, $(1-s_0)A+s_{0}B\in Q(S)$. Thus, $(1-s_0)A+s_{0}B$ is the required nilpotent matrix. Hence, the result.

Remark 1. Considering an appropriate convex linear combination, Theorem 2.5 holds for any number of matrices.

Example 2.1. Consider an example of a sign pattern matrix of order 5 as given below

$S=\left[\begin{array}{ccccc}+& 0& 0& 0& -\\ +& 0& 0& 0& -\\ 0& +& 0& 0& -\\ 0& 0& +& 0& -\\ 0& 0& 0& +& -\end{array}\right]$

Consider a matrix $A=\left[\begin{array}{ccccc}2& 0& 0& 0& -16\\ 1& 0& 0& 0& -8\\ 0& 1& 0& 0& -4\\ 0& 0& 1& 0& -2\\ 0& 0& 0& 1& -1\end{array}\right]$ $\in Q(S)$, its characteristic polynomial is $x^5-x^4$ which corresponds to the vector $(1,0,0,0,0)$. Also, consider the matrix $B=\left[\begin{array}{ccccc}2& 0& 0& 0& -48\\ 1& 0& 0& 0& -24\\ 0& 1& 0& 0& -12\\ 0& 0& 1& 0& -6\\ 0& 0& 0& 1& -3\end{array}\right]\in Q(S)$, its characteristic polynomial is $x^5+x^4$ which corresponds to the vector $(-1,0,0,0,0)$. If we take a matrix $N_p=\frac{1}{2}(A+B)=\left[\begin{array}{ccccc}2& 0& 0& 0& -32\\ 1& 0& 0& 0& -16\\ 0& 1& 0& 0& -8\\ 0& 0& 1& 0& -4\\ 0& 0& 0& 1& -2\end{array}\right]$, which is also in $Q(S)$, a qualitative class of $S$ and its characteristic polynomial is $x^5$. So the matrix $N_p$ gives the required nilpotent matrix realization in the qualitative class of $S$.

Lemma 2.6. If nilpotent matrices $A$ and $B$ of order $n$ vary only in a row or in a column, then $(1-s)A+sB$ is nilpotent for all $0\le s\le 1$.

Proof. As $A$ and $B$ are nilpotent matrices of order $n$, the characteristic polynomial of $A$ and $B$ is $x^n$. Thus, Lemma 2.3 says that the characteristic polynomial of $(1-s)A+sB$ is $x^n$ for all $0\le s\le 1$. Hence, the matrix $(1-s)A+sB$ is nilpotent for every $0\le s\le 1$.

Lemma 2.7. Let $A$ and $B$ be square matrices that vary exactly either in a row or in a column and $detA>0,detB>0(ordetA<0,detB<0)$. Then, $det((1-s)A+sB)>0(ordet((1-s)A+sB)<0)$ for all $0\le s\le 1$.

Proof. If $A$ and $B$ vary exactly in the $i^{th}$ column, then by splitting determinant of $(1-s)A+sB$ along the $i^{th}$ column, we get $det((1-s)A+sB)=(1-s)detA+sdetB$ for all $0\le s\le 1$, hence the result.

Remark 2. For square matrices $A$ and $B$, the determinant of $(1-s)A+sB$ is zero for all $0\le s\le 1$ if determinant of $A$ and $B$ is zero with $A$ and $B$ varying exactly either in a row or in a column.

We denote the $i^{th}$ column of a matrix $A$ by $A^{(i)}$ for all values of $i$ in the proof of the following Lemma. Now, we analyze an index of nilpotent matrices obtained from the construction as given in Theorems 2.4 and 2.5.

Lemma 2.8. Let $A$ and $B$ be square matrices of order $n$ with rank $k$ such that they vary exactly in a row or in a column. Then, rank of $(1-s)A+sB$ is either $k$ for all $0\le s\le 1$ or $k-1$ for some $s\in (0,1)$.

Proof. The rank of a matrix is preserved under permutation similarity. Without loss of generality, assume that matrices $A$ and $B$ vary in the last column. Let $A^{(1)},A^{(2)},\dots ,A^{(n)}$ be the columns of $A$ and let $A^{(1)},A^{(2)},\cdots ,A^{(n-1)},B^{(n)}$ be the columns of $B$. As $1\le k\le n$, we have the following two cases:

Case 1. Column $A^{(n)}$ does not belong to a set of linearly independent columns of $A$. By rearranging the columns (if necessary), assume that the first $k$ columns of $A$ are linearly independent. Thus, remaining $n-k$ columns are linearly dependent on first $k$ columns. Hence, we have $A^{(n)}={\alpha }_1{A}^{(1)}+\cdots +{\alpha }_k{A}^{(k)}$ and $B^{(n)}={\beta }_1{A}^{(1)}+\cdots +{\beta }_k{A}^{(k)}$. Therefore, the $n^{th}$ column of $(1-s)A+sB$, i.e., $((1-s)A+sB{)}^{(n)}=(1-s)A^{(n)}+s{B}^{(n)}=(1-s)\left({\alpha }_1{A}^{(1)}+\cdots +{\alpha }_k{A}^{(k)}\right)\text{break}+s\left({\beta }_1{A}^{(1)}+\cdots +{\beta }_k{A}^{(k)}\right)=((1-s){\alpha }_1+s{\beta }_1)A^{(1)}\text{break}+\cdots +((1-s){\alpha }_k+s{\beta }_k)A^{(k)}={\gamma }_1{A}^{(1)}+\cdots +{\gamma }_k{A}^{(k)}$ where ${\gamma }_i=(1-s){\alpha }_i+s{\beta }_i$ for all $1\le i\le k$. Thus, in a matrix $(1-s)A+sB$, the $n^{th}$ column is linearly dependent on its first $k$ columns, and the remaining columns are already linearly dependent on first $k$ columns, as they are the same as in matrices $A$ and $B$. It follows that the rank of $(1-s)A+sB$ is $k$.

Case 2. Column $A^{(n)}$ belongs to the set of linearly independent $k$ columns. In this case for all $s\in [0,1]$, if the column $((1-s)A+sB{)}^{(n)}$ is linearly independent to remaining $k-1$ linearly independent columns, then rank of $(1-s)A+sB$ still remains as $k$. Otherwise, for some $s\in (0,1)$, the column $((1-s)A+sB{)}^{(n)}$ is linearly dependent on remaining $k-1$ linearly independent columns, and then the rank of $(1-s)A+sB$ is $k-1$ for these values of $s$.

By the rank-nullity theorem, for a nilpotent matrix of rank $k$, the dimension of its kernel space is $n-k$; it means that the dimension of the eigenspace corresponding to an eigenvalue $0$ is $n-k$. Hence, the number of Jordan blocks corresponding to an eigenvalue $0$, which is equal to the geometric multiplicity of an eigenvalue $0$, has to be $n-k$. Therefore, the largest possible size of a Jordan block is $k+1$, and when we distribute $n$ over $n-k$ blocks almost equally, the minimal possible size of a larger Jordan block amongst them is $⌈n/(n-k)⌉$ (where $⌈x⌉$ denotes the smallest integer but not smaller than $x$). Now for any nilpotent matrix, its index is nothing but the size of a larger Jordan block in its Jordan canonical form. Hence, the index of nilpotency for a rank $k$ nilpotent matrix is at most $k+1$ and at least $⌈n/(n-k)⌉$.

Theorem 2.9. Let $S$ be a sign pattern matrix of order $n$. The nilpotent realization $N_p$ of $S$ obtained by Theorems 2.4 and 2.5 has index of nilpotency at most $k$ or $k+1$ and at least $⌈n/(n-k+1)⌉$ or $⌈n/(n-k)⌉$ for matrices $A$ and $B$ of rank $k$.

Proof. Given that $N_p$ is a nilpotent matrix realization of a sign pattern matrix $S$, computed by Theorem 2.4 or 2.5. Moreover, $A$ and $B$ are matrices of rank $k$. By using Lemma 2.8, the nilpotent matrix $N_p$ has rank $k-1$ or $k$. Therefore, as discussed in the above paragraph before Theorem 2.9, we conclude that the index of nilpotency for a matrix $N_p$ is at most $k$ or $k+1$ and at least $⌈n/(n-k+1)⌉$ or $⌈n/(n-k)⌉$.

In example 2.1, we observe that the index of nilpotency for the matrix $N_p$ is $5=k+1$.

3. Potentially stable sign pattern

An $n\times n$ matrix $A$ is said to be a stable matrix if all of its eigenvalues have negative real parts. A sign pattern $S$ is said to be potentially stable if it allows stability, i.e., there exists a stable matrix in its qualitative class. Grundy et al. (2012) discussed about constructions of potentially stable sign pattern matrices. Cavers (2021) used polynomial stability to show that certain sign patterns are not potentially stable. In this section, we are introducing arbitrary potential stability of sign pattern matrices.

Let $A$ be an $n\times n$ matrix with real entries. If all eigenvalues of $A$ have negative real parts, then all the coefficients of its characteristic polynomial are positive. Let $A$ and $B$ be stable matrices of order $n$. Is $sA+(1-s)B$ a stable matrix?

Example 3.1. Let $A=\left[\begin{array}{ccc}-2& -8& 0\\ 1& 0& -4\\ -5& 4& -5\end{array}\right]$ and$B=\left[\begin{array}{ccc}-4& -16& 0\\ 1& 0& -4\\ -5& 4& -5\end{array}\right]$. Then $A$ and $B$ are stable matrices, and they differ only in the first row, but $0.5(A+B)$ is not stable.

But nevertheless, we have the following result true.

Theorem 3.1. Let $S$ be a sign pattern matrix. Suppose $A$ and $B$ are two stable matrices in the qualitative class $Q(S)$ such that they vary either in a row (or a column). Then, real eigenvalues of $sA+(1-s)B$ for $0\le s\le 1$ are negative.

Proof. Without loss of generality, assume that matrices $A$ and $B$ vary in the $i^{th}$ row. Since $A$ and $B$ are stable matrices, all eigenvalues of $A$ and $B$ have negative real parts. Hence, all the coefficients of the characteristic polynomial of $A$ as well as the coefficients of the characteristic polynomial of $B$ are positive. Let $x^n+a_1{x}^{n-1}+\cdots +a_{n-1}x+a_n$ and $x^n+b_1{x}^{n-1}+\cdots +b_{n-1}x+b_n$ be characteristic polynomials of $A$ and $B$, respectively, where all $a_i$s and $b_i$s are positive. Let $s\in [0,1]$. By Lemma 2.3, the characteristic polynomial

(1) $\begin{array}{cc}ch(sA+(1-s)B)& \hspace{0.17em}\\ =x^n+(s{a}_1+(1-s)b_1)x^{n-1}+\cdots +(s{a}_n+(1-s)b_n).& \hspace{0.17em}\end{array}$(1)

As all $a_i$s and $b_i$s are positive, we have $s{a}_i+(1-s)b_i$ is positive for all $1\le i\le n$. If a real number $\lambda \ge 0$ is an eigenvalue of $sA+(1-s)B$, then from Equation 1(1) $\begin{array}{cc}ch(sA+(1-s)B)& \hspace{0.17em}\\ =x^n+(s{a}_1+(1-s)b_1)x^{n-1}+\cdots +(s{a}_n+(1-s)b_n).& \hspace{0.17em}\end{array}$(1) , we have

${\lambda }^n+(s{a}_1+(1-s)b_1){\lambda }^{n-1}+\cdots +(s{a}_{n-1}+(1-s)b_{n-1})\lambda =-(s{a}_n+(1-s)b_n),$

which is not possible as the left hand side of the above equation is non-negative, but the right hand side is strictly negative. Hence, every real eigenvalue of $sA+(1-s)B$ has to be negative.

Remark 3. Theorem 3.1 can also be extended to $n$ matrices corresponding to $n$ unit vectors surrounding a hyperoctant in ${\mathbb{R}}^n$.

We give here the sufficient condition for potential stability of a sign pattern matrix of order $n$. Note that the proof of the following theorem is essentially as similar to the proof of Theorem 2.7 given in Jadhav and Deore (2022). For the sake of completeness, we have incorporated the same.

Theorem 3.2. Let $S$ be a sign pattern matrix of order $n$. Suppose there exist matrices $A_1,A_2,\cdots ,A_n$ in $Q(S)$, which are realizations of the vectors $-e_1,e_2,-e_3,\cdots ,(-1{)}^n{e}_n$ respectively. Further, assume that all these matrices $A_1,A_2,\cdots ,A_n$ vary exactly either in a row or in a column. Then the sign pattern $S$ is potentially stable.

Proof. We shall prove that every point lying in the hyperoctant surrounded by the vectors $-e_1,e_2,-e_3,\cdots ,(-1{)}^n{e}_n$ (denote it by $H$) is realized by a matrix in $Q(S)$. Let $p=(a_1,a_2,\cdots ,a_n)$ be any point lying in the hyperoctant $H$. Consider the curve $(t{a}_1,t^2{a}_2,\cdots ,t^n{a}_n)$ for all $t\ge 0$ and part of the plane $-x_1+x_2-x_3+\cdots +(-1{)}^n{x}_n=1$ lying in the hyperoctant $H$. Note that the plane and the curve intersect exactly at one point say $q$. Assume that the point $q$ corresponds to $t=t_0$ on the curve. Also, note that $t_0>0$. As $A_1,A_2,\cdots ,A_n$ are realizations for the vectors $-e_1,e_2,-e_3,\cdots ,(-1{)}^n{e}_n$, in $Q(S)$, by Lemma 2.3, every point on the convex linear combination of $-e_1,e_2,-e_3,\cdots ,(-1{)}^n{e}_n$ has a matrix realization lying in $Q(S)$. Thus, $q$ has a matrix realization say $A$ in $Q(S)$. But then $(1/t_0)A$ lying in $Q(S)$, provides a matrix realization for the point $p$. So every point in the hyperoctant $H$ has a matrix realization in $Q(S)$.

In particular, the point $(-\left(\begin{array}{c}n\\ 1\end{array}\right),\left(\begin{array}{c}n\\ 2\end{array}\right),\cdots ,(-1{)}^n\left(\begin{array}{c}n\\ n\end{array}\right))$ lies in the hyperoctant $H$; hence, it has a matrix realization in $Q(S)$. Also, polynomial corresponding to this point is $(x+1{)}^n$; this proves $S$ is potentially stable sign pattern.

Let us illustrate the above theorem with the help of an example.

Example 3.2. Consider a sign pattern matrix of order $5$ as given below:

$S=\left[\begin{array}{ccccc}-& +& -& +& -\\ +& +& 0& 0& 0\\ +& 0& +& 0& 0\\ +& 0& 0& +& 0\\ +& 0& 0& 0& +\end{array}\right]$

Consider a realization $A=\left[\begin{array}{ccccc}-a& b& -c& d& -e\\ 1& 1& 0& 0& 0\\ 1& 0& 2& 0& 0\\ 1& 0& 0& 3& 0\\ 1& 0& 0& 0& 4\end{array}\right]$ in a qualitative class of $S$ where $a,b,c,d,e$ are positive real numbers. Its characteristic polynomial is given as follows

$p(x)=x^5-(-a+10)x^4+(-10a-b+c-d+e+35)x^3$

$-(-35a-9b+8c-7d+6e+50)x^2$

$+(-50a-26b+19c-14d+11e+24)x$

(2) $-(-24a-24b+12c-8d+6e).$(2)

Now to find the values of $a,b,c,d$ and $e$ so that the polynomial $p(x)$ in 2 corresponds to a vector $-e_1$, i.e, it becomes $x^5+x^4$. Equating $p(x)$ with $x^5+x^4$, we get a system of linear equations in variables $a,b,c,d$ and $e$. Solving this system of equations, we get $a=11,b=1/3,c=24,d=162,e=640/3$. Therefore, we get a matrix $A_1=\left[\begin{array}{ccccc}-11& \frac{1}{3}& -24& 162& \frac{-640}{3}\\ 1& 1& 0& 0& 0\\ 1& 0& 2& 0& 0\\ 1& 0& 0& 3& 0\\ 1& 0& 0& 0& 4\end{array}\right]$ in the qualitative class of $S$ whose characteristic polynomial is $x^5+x^4$. Similarly, we obtained the matrices

$A_2=\left[\begin{array}{ccccc}-10& 1/3& -20& 135& \frac{-544}{3}\\ 1& 1& 0& 0& 0\\ 1& 0& 2& 0& 0\\ 1& 0& 0& 3& 0\\ 1& 0& 0& 0& 4\end{array}\right]$, $A_3=\left[\begin{array}{ccccc}-10& \frac{1}{3}& -18& 126& \frac{-520}{3}\\ 1& 1& 0& 0& 0\\ 1& 0& 2& 0& 0\\ 1& 0& 0& 3& 0\\ 1& 0& 0& 0& 4\end{array}\right]$, $A_4=\left[\begin{array}{ccccc}-10& \frac{1}{3}& -17& 123& \frac{-514}{3}\\ 1& 1& 0& 0& 0\\ 1& 0& 2& 0& 0\\ 1& 0& 0& 3& 0\\ 1& 0& 0& 0& 4\end{array}\right]$ and $A_5=\left[\begin{array}{ccccc}-10& \frac{1}{3}& \frac{-33}{2}& 122& \frac{-1025}{6}\\ 1& 1& 0& 0& 0\\ 1& 0& 2& 0& 0\\ 1& 0& 0& 3& 0\\ 1& 0& 0& 0& 4\end{array}\right]$ having the characteristic polynomials $x^5+x^3,x^5+x^2,x^5+x$ and $x^5+1$, respectively. Observe that all the matrices $A_1,A_2,A_3,A_4,A_5$ have the same sign pattern and they vary only in the first row. Also they are realizations of vectors $-e_1,e_2,-e_3,e_4,-e_5$, respectively. Hence, by Theorem 3.2, a sign pattern matrix given by $\left[\begin{array}{ccccc}-& +& -& +& -\\ +& +& 0& 0& 0\\ +& 0& +& 0& 0\\ +& 0& 0& +& 0\\ +& 0& 0& 0& +\end{array}\right]$ is potentially stable.

Remark 4. Theorem 3.2 says something extra rather than only saying potential stability of a sign pattern matrix $S$. Potential stability means that a sign pattern allows a stable matrix. But for sign pattern matrices whose potential stability is proved by Theorem 3.2, we have for any size $n$ multiset of complex numbers with real parts negative and closed under complex conjugation, there exists a matrix in $Q(S)$ whose set of eigenvalues is the given multiset. Therefore, a sign pattern $S$ allows all possible stable matrices which have the sign pattern as that of $S$.

Definition 3.3. A square sign pattern matrix $S$ is said to be an arbitrary potentially stable sign pattern if for every multiset of $n$ complex numbers with real parts negative and closed under complex conjugation, there exists a matrix in $Q(S)$ whose set of eigenvalues is the given multiset.

A sign pattern given in Example 3.2 is arbitrary potentially stable. A potentially stable sign pattern matrix is not need to be arbitrary potentially stable, and we can see the same in the following example.

Example 3.3. Consider a sign pattern given by $S=\left[\begin{array}{cccc}0& +& 0& +\\ 0& 0& +& 0\\ -& 0& 0& 0\\ -& 0& 0& -\end{array}\right]$. From Catral et al. (2009), we note that $S$ allows a stable matrix specifically $A=\left[\begin{array}{cccc}0& 1& 0& 1\\ 0& 0& 1& 0\\ -1& 0& 0& 0\\ -3& 0& 0& -1\end{array}\right]$, so it is potentially stable. Consider a realization of $S$ obtained by replacing all non-zero entries by variables say $B=\left[\begin{array}{cccc}0& a& 0& b\\ 0& 0& c& 0\\ -d& 0& 0& 0\\ -e& 0& 0& -f\end{array}\right]$ where $a,b,c,d,e,f$ are all positive real numbers. The matrix $B$ corresponds to a vector $u=(-f,be,-acd,acdf)$. By equating vector $u$ with $(-4,6,-4,1)$, we get $f=4,be=6,acd=4$ and $acdf=1$. Substituting back the value of $f=4$, we observe that $acd=4$ and $acd=1/4$, which is not possible. Thus, a vector $u$ can never be equal to $(-4,6,-4,1)$. It means a vector $(-4,6,-4,1)$ can never be realized by a matrix in the qualitative class of sign pattern $S$. Thus, a polynomial $(x+1{)}^4$ can never be a characteristic polynomial of any matrix in the qualitative class of $S$. Thus, $S$ is not arbitrary potentially stable.

However, Theorem 3.2 gives only a sufficient condition for an arbitrary potentially stable sign pattern. It is not a necessary condition, observed from the following example of order $2$ sign pattern matrix.

Example 3.4. Consider a sign pattern matrix $S=\left[\begin{array}{cc}-& -\\ +& -\end{array}\right]$.Let $A=\left[\begin{array}{cc}-a& -b\\ c& -d\end{array}\right]$ be a matrix realization of sign pattern $S$, where $a,b,c,d$ are all positive real numbers. This matrix $A$ corresponds to a vector $(-a-d,ad+bc)$. It can be observed that for any vector lying in the second quadrant $(-p,q)$, there exist values of $a,b,c,d$ with $-a-d=-p$ and $ad+bc=q$. It means that a sign pattern $S$ is an arbitrary potentially stable sign pattern matrix. If we equate vector $(-a-d,ad+bc)$ with $(-1,0)$, we get $a+d=1$ and $ad+bc=0$. As being all $a,b,c,d$ are positive real numbers, we cannot have a solution to $ad+bc=0$. Similarly, vector $(-a-d,ad+bc)$ cannot be equal to $(0,1)$, so that Theorem 3.2 is not applicable but still sign pattern $S$ is arbitrary potentially stable.

Now, we will give the characterizations of $2\times 2$ arbitrary potentially stable sign pattern matrices. It should be noted that every spectrally arbitrary sign patterns (Definition 4.1) are always arbitrary potential stable.

Theorem 3.1. A $2\times 2$ sign pattern matrix is arbitrary potentially stable if it is a transposition or a permutation similarity equivalent to any of the following sign patterns

$\left[\begin{array}{cc}-& +\\ -& +\end{array}\right],\left[\begin{array}{cc}-& -\\ +& -\end{array}\right],\left[\begin{array}{cc}-& +\\ -& 0\end{array}\right]$

Proof. A sign pattern matrix $\left[\begin{array}{cc}-& +\\ -& +\end{array}\right]$ is arbitrary potentially stable as being spectrally arbitrary. Working out as in Example 3.4, we get sign pattern matrices $\left[\begin{array}{cc}-& -\\ +& -\end{array}\right],\left[\begin{array}{cc}-& +\\ -& 0\end{array}\right]$ are arbitrary potentially stable. Now, sign pattern matrices containing either four zero or three zero entries cannot be potentially stable as being every matrix in their qualitative class has zero determinant. Similarly, sign pattern matrices having two zero entries in the same row or in the same column cannot be potentially stable as being zero determinant. Sign pattern matrices having two zero entries on the diagonal cannot be potentially stable as being every matrix in their qualitative class has trace zero. Similarly, sign pattern matrices $\left[\begin{array}{cc}+& 0\\ 0& \ast \end{array}\right]$ and $\left[\begin{array}{cc}\ast & 0\\ 0& +\end{array}\right]$, where $\ast$ denotes either $+$ or $-$, cannot be potentially stable, as matrices in their qualitative class have either positive trace or negative determinant. Let $[\begin{array}{cc}-a& 0\\ 0& -b\end{array}]$ be any matrix in the qualitative class of a sign pattern matrix $\left[\begin{array}{cc}-& 0\\ 0& -\end{array}\right]$, where $A,B$ are positive real numbers. It has a corresponding vector $(-a-b,ab)$ in ${\mathbb{R}}^2$. If we equate $(-a-b,ab)=(-0.5,5)$, then there is no solution with $a$ and $b$ in positive real numbers. However, the roots of the polynomial $x^2+0.5x+5=0$ have negative real parts. Thus, a sign pattern matrix $\left[\begin{array}{cc}-& 0\\ 0& -\end{array}\right]$ is not arbitrary potentially stable. Similarly, it can be proved that the remaining order $2$ sign pattern matrices cannot be arbitrary potentially stable.

It should be noted that an arbitrary potential stability is not preserved under signature similarity, as explained in the following example.

Example 3.2. Consider an arbitrary potentially stable sign pattern matrix $S_1=\left[\begin{array}{cc}-& -\\ +& -\end{array}\right]$ and a signature matrix $S=\left[\begin{array}{cc}-& 0\\ 0& +\end{array}\right]$. Then, $S{S}_{1}S=\left[\begin{array}{cc}+& -\\ +& +\end{array}\right]$, which is not arbitrary potentially stable because every matrix in the qualitative class of $S{S}_{1}S$ has positive trace.

4. Spectrally arbitrary sign pattern matrices

Definition 4.1 (Catral et al., 2009). A sign pattern matrix $S$ of order $n\times n$ is said to be spectrally arbitrary if every monic polynomial of degree n is the characteristic polynomial of some matrix $A$ in the qualitative class of $S$.

Henceforth, we will denote the columns of a square matrix $A$ by $A^{(1)},A^{(2)},\cdots ,A^{(n)}$.

Let $A_1$ and $A_2$ be any two square matrices of order$2$. We denote $B[1,1]=\left(A_1^{(1)}{A}_1^{(2)}\right)=A_1,B[1,2]=\left(A_1^{(1)}{A}_2^{(2)}\right),B[2,1]=\left(A_2^{(1)}{A}_1^{(2)}\right)$ and $B[2,2]=\text{break}\left(A_2^{(1)}{A}_2^{(2)}\right)=A_2$, the matrices formed by using the columns of $A_1,A_2$.

Lemma 4.2. For any two square matrices $A_1$ and $A_2$ of order $2$,

$ch(s{A}_1+(1-s)A_2)$

(3) $=s^{2}ch(B[1,1])+s(1-s)ch(B[1,2])+s(1-s)ch(B[2,1])+(1-s{)}^{2}ch(B[2,2]).$(3)

Proof. With the above notations, the matrix $s{A}_1\text{break}+(1-s)A_2=\left(s{A}_1^{(1)}+(1-s)A_2^{(1)}s{A}_1^{(2)}+(1-s)A_2^{(2)}\right).$ Therefore, the characteristic polynomial of $s{A}_1+(1-s)A_2$ is

$det(xI-(s{A}_1+(1-s)A_2))$

$=det((x{I}^{(1)}x{I}^{(2)})-(s{A}_1^{(1)}+(1-s)A_2^{(1)}s{A}_1^{(2)}+(1-s)A_2^{(2)}))$

$=det(x{I}^{(1)}-s{A}_1^{(1)}-(1-s)A_2^{(1)}x{I}^{(2)}-s{A}_1^{(2)}-(1-s)A_2^{(2)})$

$=det(s(x{I}^{(1)}-A_1^{(1)})+(1-s)(x{I}^{(1)}-A_2^{(1)})s(x{I}^{(2)}-A_1^{(2)})+(1-s)(x{I}^{(2)}-A_2^{(2)}))$

$=sdet(x{I}^{(1)}-A_1^{(1)}s(x{I}^{(2)}-A_1^{(2)})+(1-s)(x{I}^{(2)}-A_2^{(2)}))$

$+(1-s)det(x{I}^{(1)}-A_2^{(1)}s(x{I}^{(2)}-A_1^{(2)})+(1-s)(x{I}^{(2)}-A_2^{(2)}))$

$=s^{2}det(x{I}^{(1)}-A_1^{(1)}x{I}^{(2)}-A_1^{(2)})+s(1-s)det(x{I}^{(1)}-A_1^{(1)}x{I}^{(2)}-A_2^{(2)})$

$+(1-s)sdet(x{I}^{(1)}-A_2^{(1)}x{I}^{(2)}-A_1^{(2)})+(1-s{)}^{2}det(x{I}^{(1)}-A_2^{(1)}x{I}^{(2)}-A_2^{(2)})$

$=s^{2}det((x{I}^{(1)}x{I}^{(2)})-(A_1^{(1)}{A}_1^{(2)}))+s(1-s)det((x{I}^{(1)}x{I}^{(2)})-(A_1^{(1)}{A}_2^{(2)}))$

$+(1-s)sdet((x{I}^{(1)}x{I}^{(2)})-(A_2^{(1)}{A}_1^{(2)}))+(1-s{)}^{2}det((x{I}^{(1)}x{I}^{(2)})-(A_2^{(1)}{A}_2^{(2)}))$

$=s^{2}det(xI-B[1,1])+s(1-s)det(xI-B[1,2])$

$+(1-s)sdet(xI-B[2,1])+(1-s{)}^{2}det(xI-B[2,2]).$

Hence the result.

In the above lemma, the sum of the coefficients of the terms on the right hand side of an expression in Equation 3(3) $=s^{2}ch(B[1,1])+s(1-s)ch(B[1,2])+s(1-s)ch(B[2,1])+(1-s{)}^{2}ch(B[2,2]).$(3) is 1.

Example 4.3. Let $S=\left[\begin{array}{cc}+& -\\ +& -\end{array}\right]$ be a sign pattern matrix of order 2. Then, $S$ is spectrally arbitrary by Catral et al. (2009). Let $A_1=\left[\begin{array}{cc}1& -2\\ 1& -3\end{array}\right]$, $A_2=\left[\begin{array}{cc}3& -2\\ 4& -2\end{array}\right]$ be square matrices of order $2$ in the qualitative class of $S$. Then, we can observe that $B[2,1]=\left[\begin{array}{cc}3& -2\\ 4& -3\end{array}\right]$, $B[1,2]=\left[\begin{array}{cc}1& -2\\ 1& -2\end{array}\right]$. Also, $B[1,1]=A_1,B[2,2]=A_2$. Note that matrices $B[1,1],B[2,2],B[1,2],B[2,1]$ are in $Q(S)$, a qualitative class of $S$. The matrices $A_1$, $A_2,B[2,1]$ and $B[1,2]$ correspond to the vectors $u_{11}=(-2,-1)$, $u_{22}=(1,2),u_{21}=(0,-1)$ and $u_{12}=(-1,0)$, respectively.

Theorem 4.4 (Jadhav & Deore, 2022). Let $S$ be a potentially nilpotent sign pattern matrix of order $n$ and let $\pm e_1,\pm e_2,\dots ,\pm e_n$ be the unit vectors along the axes. Suppose there exist at least $2n$ matrices which are realization of these $2n$ vectors corresponding to a sign pattern $S$. If $n$ matrices corresponding to $n$ vectors surrounding each hyperoctant differ only in one fixed row (or column), then the sign pattern $S$ is spectrally arbitrary. Moreover, any particular non-nilpotent matrix realization can be constructed as an affine combination of matrices corresponding to a hyperoctant (i.e., the unit vectors).

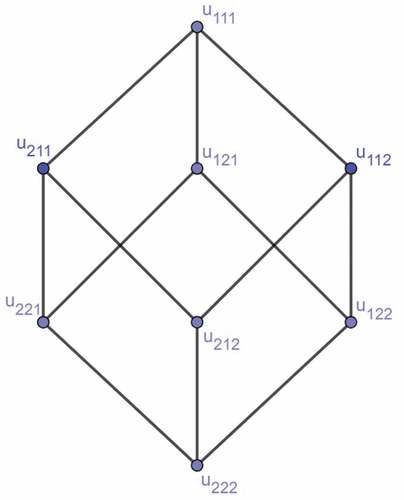
We can visualize all these four vectors in the above figure, wherein the region bounded by the quadrilateral contains the origin in its interior. Moreover, any two matrices corresponding to the adjacent vertices in Figure 4.3 vary only in a column. Thus, by Theorem 4.4, a sign pattern $S$ is spectrally arbitrary.

Theorem 4.5. Let $S$ be a sign pattern matrix of order $2$. Let $A_1,A_2\in Q(S)$ such that the vectors corresponding to $A_1,A_2$ are $u_{11},u_{22}$. Then, there exists a curve in ${\mathbb{R}}^2$ joining the points $u_{11}$ and $u_{22}$, such that every point on this curve is realizable by a sign pattern matrix $S$.

Proof. Let $B[2,1]=(A_2^{(1)}{A}_1^{(2)})$ and $B[1,2]=(A_1^{(1)}{A}_2^{(2)})$ be the matrices correspond to the vectors $u_{21},u_{12}$ in ${\mathbb{R}}^2$. Then from Lemma 4.2, $s^{2}ch(A_1)+s(1-s)ch(B[2,1])+s(1-s)ch(B[1,2])+(1-s{)}^{2}ch(A_2)=ch(s{A}_1+(1-s)A_2)$ for $0\le s\le 1$. If we consider the same affine combination of the corresponding vectors, then we get a vector $s^2{u}_{11}+s(1-s)u_{21}+s(1-s)u_{12}+(1-s{)}^2{u}_{22}$, which has a matrix realization $s{A}_1+(1-s)A_2$ in $Q(S)$ for each $0\le s\le 1$. Hence, $s^2{u}_{11}+s(1-s)u_{21}+s(1-s)u_{12}+(1-s{)}^2{u}_{22}$ for $0\le s\le 1$ establishes the required realizable curve in $Q(S)$ joining the points $u_{11}$ and $u_{22}$.

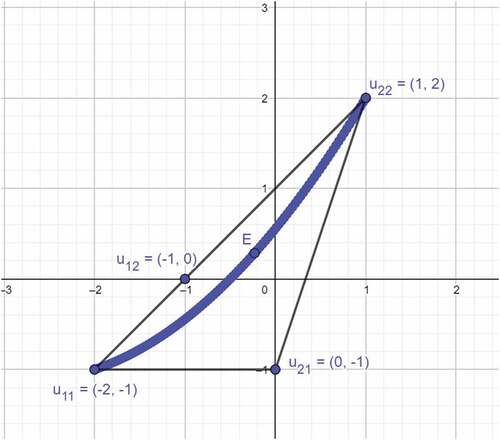
In Figure 1, the curve traced by $E$ lies in the affine combination of the vectors $u_{11},u_{12},u_{21},u_{22}$.

Figure 1. Quadrilateral formed by vertices $u_{11},u_{12},u_{22},u_{21}$ The image is plotted by using open source software “GeoGebra”

Let $A$ and $B$ be any two square matrices of order $3$. We denote $C[1,1,1]=A,C[2,1,1]=(B^{(1)}{A}^{(2)}{A}^{(3)}),C[1,2,1]=(A^{(1)}{B}^{(2)}{A}^{(3)}),C[1,1,2]\text{break}=(A^{(1)}{A}^{(2)}{B}^{(3)}),C[2,2,1]=(B^{(1)}{B}^{(2)}{A}^{(3)}),\text{break}C[2,1,2]=(B^{(1)}{A}^{(2)}{B}^{(3)}),C[1,2,2]=(A^{(1)}{B}^{(2)}{B}^{(3)})$ and $C[2,2,2]=(B^{(1)}{B}^{(2)}{B}^{(3)})=B$, the matrices formed by using columns of matrices $A$ and $B$. Then, we have the following.

Lemma 4.6. Let $A$ and $B$ be any two square matrices of order $3$. Then

$ch(sA+(1-s)B)$

(4) $=s^{3}ch(A)+s^2(1-s)(ch(C[2,1,1])+ch(C[1,2,1])+ch(C[1,1,2]))+s(1-s{)}^2(ch(C[2,2,1])+ch(C[2,1,2])+ch(C[1,2,2]))+(1-s{)}^{3}ch(B).$(4)

Proof. Proof follows by the multilinearity property of the determinant function, similar to proof of Lemma 4.2.

We observe that the sum of the coefficients of the terms from right hand side of Equation 4(4) $=s^{3}ch(A)+s^2(1-s)(ch(C[2,1,1])+ch(C[1,2,1])+ch(C[1,1,2]))+s(1-s{)}^2(ch(C[2,2,1])+ch(C[2,1,2])+ch(C[1,2,2]))+(1-s{)}^{3}ch(B).$(4) is

$s^3+3s^2(1-s)+3s(1-s{)}^2+(1-s{)}^3=1.$

Let $S$ be any square sign pattern matrix of order $3$ and $A,B\in Q(S)$. Then, the matrices constructed from $A$ and $B$ as above are also in $Q(S)$. As per the correspondence, suppose these eight matrices $C[1,1,1]=A,C[2,1,1],C[1,2,1],C[1,1,2],C[2,2,1],C[2,1,2],\text{break}C[1,2,2]$ and $C[2,2,2]=B$ correspond to vectors $u_{111},u_{211},u_{121},u_{112},u_{221},u_{212},u_{122}$ and $u_{222}$ in ${\mathbb{R}}^3$, respectively. If we plot all these eight vectors as vertices, and two vertices are adjacent if and only if the corresponding matrices vary only in one column, then we get a graph isomorphic to the following graph in ${\mathbb{R}}^3$ as shown in Figure 2.

Figure 2. Graph formed by vertices $u_{111},u_{112},u_{121},u_{211},u_{122},u_{212},u_{221},u_{222}$The image is plotted by using open-source software “GeoGebra”.

From Lemma 2.3, as the matrices corresponding to the adjacent vertices vary only in a column, all the vectors lying on edges of the above graph are realizable by a sign pattern matrix $S$. In view of Lemma 4.6, a vector inside the convex linear combination of vectors $u_{111},\dots ,u_{222}$ of the type $s^3{u}_{111}+s^2(1-s)(u_{211}+u_{121}+u_{112})+s(1-s{)}^2(u_{221}\text{break}+u_{212}+u_{122})+(1-s{)}^3{u}_{222}$, for some $0\le s\le 1$ is realizable by a sign pattern matrix $S$. Therefore, there exists a curve joining the points $u_{111}$ and $u_{222}$ such that every point on the curve is realizable by a sign pattern matrix $S$.

Example 4.7. Consider $S=\left[\begin{array}{ccc}-& +& 0\\ -& 0& +\\ 0& -& +\end{array}\right]$, a square sign pattern matrix of order $3$. Let $A=\left[\begin{array}{ccc}-1& 1& 0\\ -2& 0& 1\\ 0& -3& 4\end{array}\right]$ and $B=\left[\begin{array}{ccc}-2& 1& 0\\ -1& 0& 2\\ 0& -2& 1\end{array}\right]$ be two matrices in $Q(S)$. Then, $u_{111}=(3,1,5),u_{211}=(2,-4,-2),u_{121}=(3,0,6),u_{112}\text{break}=(0,7,-4),u_{221}=(2,-5,0),u_{212}=(-1,5,-11),u_{122}\text{break}=(0,5,-2),u_{222}=(-1,3,-7).$ If we choose $s=1/4$, then a vector $s^3{u}_{111}+s^2(1-s)(u_{211}+u_{121}+u_{112})+s(1-s{)}^2(u_{221}+u_{212}+u_{122})+(1-s{)}^3{u}_{222}$ becomes $\frac{1}{64}(0,136,-301)$ which has a matrix realization as $\frac{1}{4}A+\frac{3}{4}B=\frac{1}{4}\left[\begin{array}{ccc}-7& 4& 0\\ -5& 0& 7\\ 0& -9& 7\end{array}\right]\in Q(S)$.

Let $A_1$ and $A_2$ be square matrices of order $n$, say $A_1=\left[\begin{array}{cccc}{A}_1^{(1)}& A_1^{(2)}& \cdots & A_1^{(n)}\end{array}\right]$ and $A_2=\left[\begin{array}{cccc}{A}_2^{(1)}& A_2^{(2)}& \cdots & A_2^{(n)}\end{array}\right]$. Construct an another matrix $B$ by using columns of $A_1$ and $A_2$. More specifically, the $k^{th}$ column of the matrix $B$ is either $A_1^{(k)}$ or $A_2^{(k)}$ for $1\le k\le n$, then there are $2^n$ such possible matrices. For $1\le i_1,i_2,\cdots ,i_n\le 2$, let us denote $B[i_1,i_2,\cdots ,i_n]$ be the matrix, whose $k^{th}$ column is the $k^{th}$ column of the matrix $A_{i_k}$, for $1\le k\le n$.

Theorem 4.8. Let $A_1$ and $A_2$ be two square matrices of order $n$. Then

$ch(s_1{A}_1+s_2{A}_2)=\sum _{1\le i_1,i_2,\cdots ,i_n\le 2}{s}_{i_1}{s}_{i_2}\cdots s_{i_n}ch(B[i_1,i_2,\cdots ,i_n]),$

where $0\le s_1,s_2\le 1$ and $s_1+s_2=1$.

Proof. Proof follows by multilinearity property of the determinant function.

We would like to mention that Lemma 2.3 is a special case of Theorem 4.8. If $S$ is a square sign pattern matrix of order $n$ and the matrices $A_1,A_2\in Q(S)$, then the number of matrices obtained from $A_1$ and $A_2$ as above is $2^n$. All these matrices are the members of $Q(S)$. Moreover, these $2^n$ matrices correspond to $2^n$ vectors in ${\mathbb{R}}^n$. Two of these vectors can be joined by an edge if the corresponding matrices vary only in a column so that we get a graph on $2^n$ vertices in which degree of each vertex is at least $n$. We can observe that a point on every edge is realizable by a sign pattern matrix $S$, and also a vector which can be expressed as an affine combination of the type as in Theorem 4.8 for some $0\le s\le 1$ is also realizable.

Theorem 4.9. Let $S$ be a sign pattern matrix of order $n$. Let $A_1,A_2\in Q(S)$ and let $u_{11\cdots 1}$ and $u_{22\cdots 2}$ be vectors in ${\mathbb{R}}^n$ corresponding to matrices $A_1$ and $A_2$, respectively. Then, there exists a curve with every point on that curve is realizable by a sign pattern matrix $S$.

Let $A_1,A_2$ and $A_3$ be any three square matrices of order $3$ over the set of real numbers. Forming a matrix $B$ by using $A_1,A_2$ and $A_3$, where the first column of $B$ is the first column of $A_1$ or $A_2$ or $A_3$. Similarly, the second and third columns of $B$ is the second and third respective columns of $A_1$ or $A_2$ or $A_3$. Then, there are $27$ such possibilities for matrix $B$. Let us denote $B[i_1,i_2,i_3]$ be the matrix whose first column is the first column of $A_{i_1}$, second column is the second column of $A_{i_2}$ and the third column is the third column of matrix $A_{i_3}$ where $1\le i_1,i_2,i_3\le 3$, e.g., the matrix $B[1,1,1]=A_1,B[1,1,2]=\left(A_1^{(1)}{A}_1^{(2)}{A}_2^{(3)}\right)$, etc.

Theorem 4.10. Let $A_1,A_2$ and $A_3$ be any three matrices of order $3$. Then

(5) $ch(x_1{A}_1+x_2{A}_2+x_3{A}_3)=\sum _{1\le i_1,i_2,i_3\le 3}{x}_{i_1}{x}_{i_2}{x}_{i_3}ch(B[i_1,i_2,i_3]),$(5)

With $0\le x_1,x_2,x_3\le 1$ and$x_1+x_2+x_3=1$

Proof. Proof follows by multilinearity property of the determinant function.

Let $S$ be a sign pattern matrix of order 3 and let $A_1,A_2$ and $A_3$ be any three matrices lying in $Q(S)$. Let $B[i_1,i_2,i_3]$ be matrices as defined above. Note that $B[i_1,i_2,i_3]\in Q(S)$. Assume that for each $1\le i_1,i_2,i_3\le 3$, the matrix $B[i_1,i_2,i_3]$ corresponds to the vector $u_{i_1{i}_2{i}_3}$ in ${\mathbb{R}}^3$. Consider a graph in ${\mathbb{R}}^3$ with vertices $u_{i_1{i}_2{i}_3}$ and two of the vertices are joined by an edge if and only if the corresponding matrices differ only in one column. Then, we get a graph isomorphic to a graph on $27$ vertices with a degree of each vertex is at least $6$. Every point on this edge is realizable by a matrix in $Q(S)$. Also, a vector which can be expressed as an affine combination of the type as in Equation 5(5) $ch(x_1{A}_1+x_2{A}_2+x_3{A}_3)=\sum _{1\le i_1,i_2,i_3\le 3}{x}_{i_1}{x}_{i_2}{x}_{i_3}ch(B[i_1,i_2,i_3]),$(5) of Theorem 4.10 for some $0\le x_1,x_2,x_3\le 1$ and $x_1+x_2+x_3=1$ is realizable. In this case, we may get a degree of freedom at most $2$. Thus, we have the following statement true.

Theorem 4.11. Let $S$ be a sign pattern of order $3$. Let $A_1,A_2$ and $A_3$ be any three matrices in $Q(S)$. Assume that matrices $A_1,A_2$ and $A_3$ correspond to vectors $u_{111},u_{222}$ and $u_{333}$, respectively. Then there exists a curve or a surface in ${\mathbb{R}}^3$ such that every point on that curve or surface is realizable by a sign pattern $S$.

In general, if we have three matrices of order $n$, then we have the following result.

Theorem 4.12. Let $A_1,A_2$ and $A_3$ be any three matrices of order $n$. Then

(6) $ch(x_1{A}_1+x_2{A}_2+x_3{A}_3)=\sum _{1\le i_1,i_2,\cdots ,i_n\le 3}{x}_{i_1}{x}_{i_2}\cdots x_{i_n}ch(B[i_1,i_2,\cdots ,i_n]),$(6)

With $0\le x_1,x_2,x_3\le 1$ and $x_1+x_2+x_3=1$

Let $S$ be a sign pattern matrix of order $n$, let $A_1,A_2$ and $A_3$ be any three matrices in $Q(S)$ and let matrices $B[i_1,i_2,\cdots ,i_n]$ be constructed as above. Note that all these matrices $B[i_1,i_2,\cdots ,i_n]$ are in $Q(S)$. Assume that the matrix $B[i_1,i_2,\cdots ,i_n]$ corresponds to a vector $u_{i_1{i}_2\cdots i_n}$ in ${\mathbb{R}}^n$ for each $1\le i_1,i_2,\cdots ,i_n\le 3$. If we consider a graph with vertices as these $3^n$ points $u_{i_1{i}_2\cdots i_n}$ and connect two of these vertices by an edge if and only if the corresponding matrices vary only in a column. Then, the graph will have at least $2n$ edges. Note that every point on this edge is realizable by a sign pattern $S$. Also, a vector which can be expressed as an affine combination of the type as in Equation 6(6) $ch(x_1{A}_1+x_2{A}_2+x_3{A}_3)=\sum _{1\le i_1,i_2,\cdots ,i_n\le 3}{x}_{i_1}{x}_{i_2}\cdots x_{i_n}ch(B[i_1,i_2,\cdots ,i_n]),$(6) of Theorem 4.12, for some $0\le x_1,x_2,x_3\le 1$ and $x_1+x_2+x_3=1$, is realizable. Observe that degree of freedom is at most $2$.

Theorem 4.13. Let $S$ be a sign pattern matrix of order $n$. Let $A_1,A_2$ and $A_3$ be any three matrices in $Q(S)$. Assume that matrices $A_1,A_2$ and $A_3$ correspond to the vectors $u_{11\cdots 1},u_{22\cdots 2}$ and $u_{33\cdots 3}$ respectively. Then, there exists a surface of dimension at most $2$ in ${\mathbb{R}}^n$ such that every point on that surface is realizable by a sign pattern $S$.

In general, we can consider $m$ matrices say $A_1,A_2,\cdots ,A_m$ of order $n$, where $m\le n+1$. For each $1\le i_1,i_2,\cdots ,i_n\le m$, a matrix $B[i_1,i_2,\cdots ,i_n]$ is constructed by using $A_1,A_2,\cdots ,A_m$, i.e., the $k^{th}$ column of $B[i_1,i_2,\cdots ,i_n]$ is the $k^{th}$ column of $A_{i_k}$ for $1\le k\le n$. So we get $m^n$ such possible matrices.

Theorem 4.14. With the above notations, we have

(7) $ch(x_1{A}_1+x_2{A}_2+\cdots +x_m{A}_m)=\sum _{1\le i_1,i_2,\cdots ,i_n\le m}{x}_{i_1}{x}_{i_2}\cdots x_{i_m}ch(B[i_1,i_2,\cdots ,i_n]),$(7)

With $0\le x_1,x_2,\cdots x_m\le 1$ and $x_1+x_2+\cdots +x_m=1$

Let $S$ be any sign pattern matrix of order $n$ and $A_1,A_2,\cdots ,A_m$ be any $m$ matrices in $Q(S)$. Then, we get at most $(m-1)-$ dimensional surface in ${\mathbb{R}}^n$ with every point on that surface is realizable by a sign pattern matrix $S$.

Theorem 4.15. Let $S$ be a sign pattern matrix of order $n$. Let $A_1,A_2,\cdots ,A_m$ be any $m$ matrices in $Q(S)$ where $m\le n+1$. Then,there exists a surface of dimension at most $(m-1)$ in ${\mathbb{R}}^n$ such that every point on that surface is realizable by a sign pattern $S$.

It should be noted that if $S$ is a sign pattern matrix of order $n$ and $A_1,A_2,\cdots ,A_m$ are any $m$ matrices lying in $Q(S)$ where $m>n+1$, then there exists at most $n$-dimensional surface in ${\mathbb{R}}^n$ such that every point in that surface is realizable by a sign pattern $S$.

Let $S$ be a sign pattern matrix of order $n$. Let $A$ and $B$ be any two matrices in $Q(S)$. Let $C[i_1,i_2,\cdots ,i_n]$ be the matrix whose $k^{th}$ column is the $k^{th}$ column of the matrix $A$ if $i_k=1$ otherwise is the $k^{th}$ column of the matrix $B$, for all $1\le i_1,i_2,\cdots ,i_n\le 2$.

Theorem 4.16. With the above notations, we have

$det\left(\sum _{1\le i_1,i_2,\cdots ,i_n\le 2}{x}_{i_1{i}_2\cdots i_n}C[i_1,i_2,\cdots ,i_n]\right)=$

(8) $\sum _{1\le i_1,i_2,\cdots ,i_n\le 2}\left(\left[\prod _{1\le k\le n}\left(\sum _{1\le i_1,i_2,\cdots ,{\hat{i}}_k,\cdots ,i_n\le 2}{x}_{i_1{i}_2\cdots i_n}\right)\right]\text{break}detC[i_1,i_2,\cdots ,i_n]\right),$(8)

where the hat notation denotes the deletion of that entry from the sequence.

Proof. The proof follows by multilinearity property of the determinant function.

Theorem 4.17. Let $S$ be a sign pattern matrix of order $n$, $A$ and $B$ be any two matrices in $Q(S)$ and $C[i_1,i_2,\cdots ,i_n]$ be matrices as defined above for $1\le i_1,i_2,\cdots ,i_n\le 2$. Then

$ch\left(\sum _{1\le i_1,i_2,\cdots ,i_n\le 2}{x}_{i_1{i}_2\cdots i_n}C[i_1,i_2,\cdots ,i_n]\right)=$

(9) $\sum _{1\le i_1,i_2,\cdots ,i_n\le 2}\left(\left[\prod _{1\le k\le n}\left(\sum _{1\le i_1,i_2,\cdots ,{\hat{i}}_k,\cdots ,i_n\le 2}{x}_{i_1{i}_2\cdots i_n}\right)\right]\text{break}ch\left(C[i_1,i_2,\cdots ,i_n]\right)\right),$(9)

where the hat notation denotes the deletion of that entry from the sequence and each $x_{i_1{i}_2\cdots i_n}$ satisfies $0\le x_{i_1{i}_2\cdots i_n}\le 1$ and $\sum _{1\le i_1,i_2,\cdots ,i_n\le 2}{x}_{i_1{i}_2\cdots i_n}=1$.

Suppose the matrix $C[i_1,i_2,\cdots ,i_n]$ has the corresponding vector $u_{i_1{i}_2\cdots i_n}$ for each $1\le i_1,i_2,\cdots ,i_n\le 2$, then every vector in ${\mathbb{R}}^n$ which satisfies an affine linear combination as given in Equation 9(9) $\sum _{1\le i_1,i_2,\cdots ,i_n\le 2}\left(\left[\prod _{1\le k\le n}\left(\sum _{1\le i_1,i_2,\cdots ,{\hat{i}}_k,\cdots ,i_n\le 2}{x}_{i_1{i}_2\cdots i_n}\right)\right]\text{break}ch\left(C[i_1,i_2,\cdots ,i_n]\right)\right),$(9) of Theorem 4.17 will also belong to $Q(S)$. This implies that there exists at most $n-$ dimensional surface in a convex linear combination of these vectors $u_{i_1{i}_2\cdots i_n}$ such that every point on that surface is realizable by the matrix in $Q(S)$.

Definition 4.18. If the surface generated by the vectors $u_{i_1{i}_2\cdots i_n}$ by using the affine linear combination as given in Equation 9(9) $\sum _{1\le i_1,i_2,\cdots ,i_n\le 2}\left(\left[\prod _{1\le k\le n}\left(\sum _{1\le i_1,i_2,\cdots ,{\hat{i}}_k,\cdots ,i_n\le 2}{x}_{i_1{i}_2\cdots i_n}\right)\right]\text{break}ch\left(C[i_1,i_2,\cdots ,i_n]\right)\right),$(9) of Theorem 4.17 has dimension $n$, then it is called a solid, we denote this solid by $\mathrm{\Gamma }$.

If we plot a graph in ${\mathbb{R}}^n$ with vertices $u_{i_1{i}_2\cdots i_n}$ for $1\le i_1,i_2,\cdots ,i_n\le 2$, and two of the vertices are connected by an edge if and only if the corresponding matrices differ only in one column, then we get a graph on $2^n$ vertices with degree of each vertex is at least $n$. For a fixed value of $i_k$ either $1$ or $2$, the vertices $u_{i_1{i}_2\cdots i_n}$ for all $1\le i_1,\cdots ,i_{k-1},i_{k+1},\cdots ,i_n\le 2$ form the vertices of one of the faces. Theorem 4.17 is valid for corresponding to these $2^{n-1}$ matrices as well.

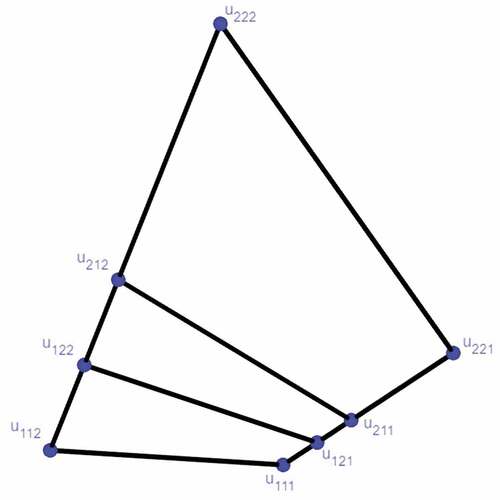
Example 4.19. Consider a sign pattern matrix $S=\left[\begin{array}{ccc}-& +& 0\\ -& 0& +\\ 0& -& +\end{array}\right]$. Let $A=\left[\begin{array}{ccc}-2& 1& 0\\ -1& 0& 2\\ 0& -1& 1\end{array}\right]$ and $B=\left[\begin{array}{ccc}-2& 2& 0\\ -3& 0& 1\\ 0& -1& 4\end{array}\right]$ be two matrices from $Q(S)$. Then, we get the set of eight vectors $u_{111}=(-1,1,-3),u_{211}=(-1,3,-1),u_{121}=(-1,2,-2),\text{break}{u}_{112}=(2,-6,2),u_{221}=(-1,6,2),u_{212}=(2,-4,10),\text{break}{u}_{122}=(2,-5,6),u_{222}=(2,-1,22)$. It is easy to verify that vectors $u_{222},u_{212},u_{122},u_{112}$ are co-linear and vectors $u_{221},u_{211},u_{121},u_{111}$ are also co-linear as shown in the following Figure 3. Hence, these sets of eight vectors span the two-dimensional surface in ${\mathbb{R}}^3$.

Figure 3. The image is plotted by using open-source software “GeoGebra”.

The above example shows that these $2^n$ vectors in ${\mathbb{R}}^n$ may span lesser than $n-$ dimensional surface.

Definition 4.20. Let $S$ be a sign pattern matrix of order $n$. We shall denote the set of all realized vectors of a sign pattern $S$ by $RV(S)$ and is defined as

$RV(S)=\left\{u\in {\mathbb{R}}^n:\mathrm{\exists }\mathrm{a}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{x}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{z}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\text{break}\mathrm{A}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{r}u\right\}.$

Lemma 4.21. Let $S$ be a sign pattern matrix of order $n$. If $u=(a_1,a_2,\cdots ,a_n)\in RV(S)$, then $(t{a}_1,t^2{a}_2,\cdots ,t^n{a}_n)$ also lies in $RV(S)$, for all $t>0$.

Proof. As $u=(a_1,a_2,\cdots ,a_n)\in RV(S)$, so there exists a matrix realization say $A$ for the vector $u$ in $Q(S)$. Therefore, the characteristic polynomial of a matrix $A$ is $x^n-a_1{x}^{n-1}+\cdots +(-1{)}^n{a}_n$. But then the characteristic polynomial of $tA$ would be $x^n-t{a}_1{x}^{n-1}+\cdots +(-1{)}^n{t}^n{a}_n$ for all $t>0$. Thus, the vector $(t{a}_1,t^2{a}_2,\cdots ,t^n{a}_n)$ has a matrix realization $tA$ for all $t>0$ in $Q(S)$. Hence, $(t{a}_1,t^2{a}_2,\cdots ,t^n{a}_n)\in RV(S)$ for all $t>0$.

Using Lemma 4.21, we can give a sufficient condition for a sign pattern matrix to be spectrally arbitrary.

Theorem 4.22. Let $S$ be a potentially nilpotent sign pattern matrix of order $n$. If every point $u$ on the unit sphere $S^{n-1}$ lies in $RV(S)$, then $S$ is spectrally arbitrary.

Proof. It is enough to prove that every non-zero point in ${\mathbb{R}}^n$ lies in $RV(S)$. For that, let $v=(a_1,a_2,\cdots ,a_n)$ be any non-zero point in ${\mathbb{R}}^n$. Consider the curve $\gamma (t)=(t{a}_1,t^2{a}_2,\cdots ,t^n{a}_n)$ for $t\ge 0$. This curve will intersect the unit sphere say at $u\in S^{n-1}$. Therefore, by the hypothesis $u\in RV(S)$. Thus by Lemma 4.21, $v\in RV(S)$.

It should be noted that if $S$ is a spectrally arbitrary sign pattern matrix, then obviously $S^{n-1}\subset RV(S)$. Thus, the above theorem establishes a necessary and sufficient condition for a potentially nilpotent sign pattern matrix to be spectrally arbitrary. We have used the unit sphere $S^{n-1}$ in the above theorem. However, any $n-1$-dimensional closed surface which encloses the origin in its interior would also work. If any such a closed surface lies in $RV(S)$, then the unit sphere $S^{n-1}$ would also belong to $RV(S)$.

Theorem 4.23. Let $S$ be a nilpotent sign pattern matrix of order $n$, and let $A$ and $B$ be any two matrices such that they generate a solid $\mathrm{\Gamma }$ lying in $Q(S)$. If $\mathrm{\Gamma }$ contains the origin in its interior, then a sign pattern $S$ is spectrally arbitrary.

Proof. Such a $n-$ dimensional solid lying in the qualitative class of $S$ has its closed boundary surface of dimension $n-1$ with the origin $0$ lying in its interior. Then, $S^{n-1}$ belongs to the qualitative class of $S$, and thus by Theorem 4.22, a sign pattern $S$ is spectrally arbitrary.

Finally, we discuss a very general case. Let $S$ be a sign pattern matrix of order $n$. Let $A_1,A_2,\cdots ,A_m$ be any $m$ matrices belonging to the qualitative class of $S$. Let $C[i_1,i_2,\cdots ,i_n]$ be the matrix whose $k^{th}$ column is the $k^{th}$ column of matrix $A_{i_k}$ for $1\le i_1,i_2,\cdots ,i_n\text{lem}$ and $1\le k\le n$. Then, there are $m^n$ such possible matrices. Similar to Theorem 4.17.

Theorem 4.24. With the above notations, we have

$ch\left(\sum _{1\le i_1,i_2,\cdots ,i_n\text{lem}}{x}_{i_1{i}_2\cdots i_n}C[i_1,i_2,\cdots ,i_n]\right)=$

$\sum _{1\le i_1,i_2,\cdots ,i_n\text{lem}}\left(\left[\prod _{1\le k\le n}\left(\sum _{1\le i_1,i_2,\cdots ,{\hat{i}}_k,\cdots ,i_n\text{lem}}{x}_{i_1{i}_2\cdots i_n}\right)\right]\text{break}ch\left(C[i_1,i_2,\cdots ,i_n]\right)\right),$

Where the hat notation denotes the deletion of that entry from the sequence and each $x_{i_1{i}_2\cdots i_n}$ satisfies $0\le x_{i_1{i}_2\cdots i_n}\le 1$ with $\sum _{1\le i_1,i_2,\cdots ,i_n\text{lem}}{x}_{i_1{i}_2\cdots i_n}=1$

Proof. Proof basically uses the multi-linearity property of the determinant function.

Assume that the matrix $C[i_1,i_2,\cdots ,i_n]$ corresponds to the vector $u_{i_1{i}_2\cdots i_n}$ in ${\mathbb{R}}^n$. We can consider a graph with these $m^n$ vectors as points in ${\mathbb{R}}^n$, and two of these points are joined if and only if matrices corresponding to them vary only in one column. So we get a graph containing a sub-graph isomorphic to the graph having $m^n$ vertices and degree of each vertex is at least $n(m-1)$. Theorem 4.24 says that every point which satisfies the affine combination as given above will also belong to the qualitative class of $S$. Thus, we get at most $m^n-1$ dimensional surface in ${\mathbb{R}}^n$ lying in the qualitative class of $S$ for $m^n-1\le n$. If $m^n-1>n$, then dimension of an affine surface generated by considering an affine combination given in Theorem 4.24 is at most $n$. If it has dimension exactly $n$, then it is a solid, and we denote this solid by $\mathrm{\Gamma }$.

Theorem 4.25. Let $S$ be a nilpotent sign pattern matrix of order $n$. Let $A_1,A_2,\cdots ,A_m$ be any $m$ matrices such that they generate a solid $\mathrm{\Gamma }$ lying in the qualitative class of $S$. If $\mathrm{\Gamma }$ contains the origin in its interior, then the sign pattern $S$ is spectrally arbitrary.

Proof. The proof is similar to the proof of Theorem 4.23.

5. Open question

In Section 4, we may raise an open question “If the set of vectors $u_{i_1{i}_2\cdots i_n}$ for $1\le i_1,i_2,\cdots ,i_n\le 2$ spans ${\mathbb{R}}^n$, then the surface $\mathrm{\Gamma }$ is a solid of dimension $n$”.

Acknowledgment

The authors would like to express their sincere gratitude to the learned referees for their valuable comments and suggestions.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

The authors received no direct funding for this research.