Fuzzy congruence relation on fuzzy lattice

ABSTRACT

Numerous scholars have studied fuzzy congruence relations in various algebraic structures. In this paper, we introduce a new kind of fuzzy congruence relations on a fuzzy algebraic structure (i.e. fuzzy lattice). Additionally, we provide a characterization of fuzzy congruence relations using its level sets and support. We also make a theoretical study of their basic properties analogous to those of ordinary congruence relations. Furthermore, we study the lattice of fuzzy congruence relations and also, we show that the lattice of all fuzzy congruence relations is complete, distributive and a special class of this lattice forms a modular lattice under certain conditions.

KEYWORDS:

• fuzzy Lattices
• fuzzy congruence relation
• permutable fuzzy congruences
• distributive lattice
• modular lattice

1. Introduction

The concept of a fuzzy set and fuzzy relation was first introduced by Zadeh in his pioneering paper (Zadeh, 1971). Since then many fuzzy algebraic structures have been developed by utilizing the concept of fuzzy relation in many directions. Starting from the earlier periods, several researchers have extensively studied fuzzy congruence relations on various crisp algebraic structures. A fuzzy congruence relation is a fuzzy equivalence relations which is fuzzy compatible with all basic operations of the algebras.

In (Murali, 1989, 1991), Murali studied fuzzy equivalence and congruence relations in universal algebra, developed some properties, and proved various results related to these relations. Furthermore, he developed certain lattice theoretic properties of fuzzy equivalence and congruence relations. Samhan (1993) discussed the fuzzy congruence generated by a fuzzy relation and studied on the lattice of fuzzy congruence relations on a semigroup. Kondo (2004) studied the notion of fuzzy congruence relation on a group, derived some of their fundamental properties. Also, he proved that there is an isomorphism between the set of fuzzy normal subgroups of a group and the set of fuzzy congruences on the group. More recently, Ullah in 2021 (Ullah et al., 2021), established the idea of fuzzy congruences on Abel-Grassmann’s group (AG-group) and studied different outcomes of fuzzy congruences on AG-groups. Similarly, numerous researchers have also examined the concept of fuzzy congruence relation with respect to different areas of algebra, including semi-group, group, ring, etc. (see Das, 1997; Debnath, 2022; Kim & Bae, 1997; Konwar & Debnath, 2018a, 2018b; Kuroki, 1992, 1997; Samhan, 1995; Tan, 2001), and more specifically, on different types of lattices (see Addis, 2022; Alaba & Mulat Addis, 2017; Alemayehu & Ayenew Ageze, 2022; Alemayehu et al., 2021, 2022; Rasuli, 2021).

On the other hand, the concept of fuzzy lattice was presented by (Chon, 2009) in 2009 as an extension of fuzzy partial order relation which is defined by (Zadeh, 1965). Developed some basic properties, characterized a fuzzy lattice using its level set, presented the ideas of distributive and modular fuzzy lattices, and measured several undeveloped properties of fuzzy lattices. Despite the fact that there are numerous papers about fuzzy congruence relations on algebraic structures, we were unable to find papers about fuzzy congruence’s defined on fuzzy algebraic structures. We are thus motivated to research on fuzzy congruence relation which are defined based on a fuzzy lattice.

Thus, in this work, using (Chon, 2009) definition of fuzzy lattices, we introduce the concept of fuzzy congruence relation, characterize its properties using its level sets and support, and finally, we prove that the lattice of all fuzzy congruence relations is a distributive lattice and special class of this lattice forms a modular lattice. We organized the remaining part of this paper as follows. In Section 2, some concepts, terminologies, notations, and important results on fuzzy relation, fuzzy posets, and fuzzy lattices are recalled. In Section 3, by the use of Chons’s definition of fuzzy lattice, a new kind of fuzzy algebraic structure, i.e. fuzzy congruence relation is introduced. Basic, fundamental properties of fuzzy congruence relation are presented. Finally, in Section 4, we investigate the lattice structure of fuzzy congruence relations on a fuzzy lattice.

2. Preliminaries

In this section, we summarize well-known definitions, and results that are required later in coming section of this paper. For contents of this section, we refer (Chon, 2009; Murali, 1989, 1991).

2.1. Fuzzy equivalence relation on a set

Definition 2.1.

(Zadeh, 1971) Let X be anon empty set. Then, any mapping $\mu :X\times X⟶[0,1]$ is called fuzzy relation on X (or a binary fuzzy relation on X).

Definition 2.2.

(Zadeh, 1971) Let µ be a fuzzy relation in on X. For $\alpha \in [0,1]$, the set (a crisp set)

(1) ${\mu }_{\alpha }=\{(x,y)\in X\times X:\mu (x,y)\ge \alpha \}$(1)

is called $\alpha -level$ (or $\alpha -cut$) subset of the fuzzy relation µ

Thus, the set µ_α form a nested sequence of crisp relations, with

(2) ${\alpha }_1\ge {\alpha }_2⟹{\mu }_{{\alpha }_1}\subseteq {\mu }_{{\alpha }_2}$(2)

Definition 2.3.

(Zadeh, 1971) Let X be a non empty set and let $\mu :X\times X⟶[0,1]$ be a fuzzy relation on X. Then the support of a fuzzy relation µ is denoted by $S(\mu )$ is defined to be the crisp relation on X over which $\mu (x,y)>0$ for every $x,y\in X$That is,

(3) $S(\mu )=\{(x,y)\in X\times X:\mu (x,y)>0\}$(3)

Definition 2.4.

Let X be a non-empty set and let µ₁ and µ₂ be fuzzy relations on X. Then

(1)	µ1 is said to be contained in fuzzy relation µ2 and is denoted by ${\mu }_1\subseteq {\mu }_2$ if and only if ${\mu }_1\le {\mu }_2$ which means, more explicitly, ${\mu }_1(x,y)\le {\mu }_2(x,y)$ for all (x, y) in X × X
(2)	µ1 and µ2 and are said to be equal denoted by µ1 = µ2 if and only if ${\mu }_1(x,y)={\mu }_2(x,y)$ for all (x, y) in X × X

Definition 2.5.

(Zadeh, 1971) Let X be a non-empty set and let µ₁ and µ₂ be fuzzy relations on X. Then

(1)	The union of fuzzy relations µ1 and µ2 is denoted by ${\mu }_1\cup {\mu }_2$ and is defined by (4) $({\mu }_1\cup {\mu }_2)(x,y)=max({\mu }_1(x,y),{\mu }_2(x,y))$(4) for all (x, y) in X × Y
(2)	The intersection of fuzzy relations µ1 and µ2 is denoted by ${\mu }_1\cap {\mu }_2$ and is defined by (5) $({\mu }_1\cap {\mu }_2)(x,y)=min({\mu }_1(x,y),{\mu }_2(x,y))$(5) for all (x, y) in X × X

Remark.

If $\{{\mu }_{\alpha }{\}}_{\alpha \in I}$ is a family of fuzzy relations, we shall write

(6) ${\displaystyle \bigcup _{\alpha }{\mu }_{\alpha }=sup\{{\mu }_{\alpha }{\}}_{\alpha \in I}}$(6)

(7) ${\displaystyle \bigcap _{\alpha }{\mu }_{\alpha }=inf\{{\mu }_{\alpha }{\}}_{\alpha \in I}}$(7)

Definition 2.6.

(Zadeh, 1965) Let X be a non empty set and let π₁ and π₂ be fuzzy relations on X, then the composition or, more specifically, the max-min composition of π₁ and π₂ is a fuzzy relation on X denoted by ${\pi }_1\circ {\pi }_2$ and is defined by

(8) $({\pi }_1\circ {\pi }_2)(x,z)=\underset{y\in X}{max}[min({\pi }_1(x,y),{\pi }_2(y,z))]$(8)

for every $x,z\in X$ and the sup is taken for every $y\in X$

Remark.

The composition of fuzzy relation is associative. That is, for any fuzzy relations ${\pi }_1,{\pi }_2,{\pi }_3$ on X we have,

${\pi }_1\circ ({\pi }_2\circ {\pi }_3)=({\pi }_1\circ {\pi }_2)\circ {\pi }_3$

Definition 2.7.

(Zadeh, 1971) Let X be a non empty set. A fuzzy relation π on X is said to be,

(a)	Reflexive:- If and only if $\pi (x,x)=1$, for every $x\in X$
(b)	Symmetric:- If and only if $\pi (x,y)=\pi (y,x)$, for every $x,y\in X$
(c)	Anti-symmetric:- If and only if $\mu (x,y)>0$ and $\mu (y,x)>0$ implies x = y, for every $x,y\in X$
(d)	Transitive:- If and only if ${\displaystyle \pi (x,z)\ge \underset{y\in X}{sup}min(\pi (x,y),\pi (y,z))}$, for every $x,z\in X$

Definition 2.8.

(Murali, 1989) Let X be a non empty set and π be a fuzzy relation on X. Then, π is said to be fuzzy equivalence relation on X if and only if π is Reflexive, Symmetric and Transitive fuzzy relation on set X.

Proposition 2.1.

If π₁ and π₂ are fuzzy relations on set X, then ${\pi }_1,{\pi }_2\subseteq {\pi }_1\circ {\pi }_2$

Proof. The proof is clear.

Proposition 2.2.

Let X be a non-empty set and π be a fuzzy relation on X. Then, π is transitive fuzzy relation on X if and only if $\pi \circ \pi \subseteq \pi$

Proof. See in (Murali, 1989) Proposition 3.1.

Notation.

Let X be a non-empty set then, the family of all fuzzy equivalence relations on set X is denoted by FEq(X)

Definition 2.9.

Let X be a crisp set . Define the fuzzy equivalence relations Δ and $\mathrm{\nabla }$ on set X by

(a)	$\mathrm{\Delta }(x,y)=\{\begin{array}{ll}{\displaystyle 1}& \text{if}x=y\\ 0& \text{if}x\ne y\end{array}$ for all $x,y\in X$
(b)	$\mathrm{\nabla }(x,y)=1$ for all $x,y\in X$

Remark.

It is clear that Δ and $\mathrm{\nabla }$ are fuzzy equivalence relations and are called the diagonal and total fuzzy relations on X, respectively.

Proposition 2.3.

(Murali, 1991)

Let $\{{\pi }_i{\}}_{i\in I}$ be a non-empty family of fuzzy equivalence relations on a set X. Then, $\underset{i\in I}{\bigwedge }{\pi }_i$ is a fuzzy equivalence relation on set X.

2.2. Fuzzy lattice

Definition 2.10.

(Zadeh, 1971) Let X be a non empty set and µ be a fuzzy relation on X, then µ is said to be fuzzy partial ordered relation on X if and only if µ is reflexive, anti-symmetric and transitive.

Definition 2.11.

(Chon, 2009) If µ is fuzzy partial ordered relation in X, then the ordered pair $(X,\mu )$ is called a fuzzy partially ordered set or a fuzzy poset.

Definition 2.12.

(Chon, 2009) If µ is fuzzy total order relation on X, then the ordered pair $(X,\mu )$ is called a fuzzy total ordered set or a fuzzy chain.

Remark.

(Mezzomo et al., 2015) Let $(X,\mu )$ is fuzzy poset and $x,y,z\in X$. If $\mu (x,y)>0$ and $\mu (y,z)>0$, then $\mu (x,z)>0$.

Theorem 2.4.

(Chon, 2009) Let $\{{\mu }_i:i\in I\}$ be a collection of fuzzy partial order relations in a set X, then $(X,\bigcap _{i\in I}{\mu }_i)$ is a fuzzy poset.

Remark.

It is easy to see that for fuzzy partial order relations µ₁ and µ₂ on a set X, $(X,{\mu }_1\cup {\mu }_2)$ and $(X,{\mu }_1\circ {\mu }_2)$ are not necessarily a fuzzy poset.

Example 2.13.

Let $X=\{x,y,z,\}$ and define the fuzzy relations µ₁ and µ₂ on X by the fuzzy relational matrices given in Table 1 and Table 2 respectively.

Then it is easily checked that, $(X,{\mu }_1)$ and $(X,{\mu }_2)$ are fuzzy posets. And also, as given in the table (Table 3) since, $({\mu }_1\cup {\mu }_2)(x,y)=0.1>0$ and $({\mu }_1\cup {\mu }_2)(y,x)=0.4>0$. Then, ${\mu }_1\cup {\mu }_2$ is not antisymmetric. Hence, ${\mu }_1\cup {\mu }_2$ is not fuzzy partial ordering relation. Therefore, $(X,{\mu }_1\cup {\mu }_2)$ is not a fuzzy poset.

Similarly, as given in the table 4, since, $({\mu }_1\circ {\mu }_2)(x,y)=0.4>0$ and $({\mu }_1\circ {\mu }_2)(y,x)=0.4>0$. Then, ${\mu }_1\circ {\mu }_2$ is not antisymmetric. Hence, ${\mu }_1\circ {\mu }_2$ is not fuzzy partial ordering relation. Therefore, $(X,{\mu }_1\circ {\mu }_2)$ is not a fuzzy poset.

Table 1. Relational matrix of the fuzzy relation µ₁ on X

µ1	x	y	z
x	1.0	0.1	0.4
y	0.0	1.0	0.2
z	0.0	0.0	1.0

Table 2. Relational matrix of the fuzzy relational µ₂ on X

µ2	x	y	z
x	1.0	0.0	0.0
y	0.4	1.0	0.0
z	0.8	0.4	1.0

Table 3. Relational matrix of the fuzzy relation ${\mu }_1\cup {\mu }_2$ on X

${\mu }_1\cup {\mu }_2$	x	y	z
x	1.0	0.1	0.4
y	0.4	1.0	0.2
z	0.8	0.0	1.0

Table 4. Relational matrix of the fuzzy relation ${\mu }_1\circ {\mu }_2$ on X

${\mu }_1\circ {\mu }_2$	x	y	z
x	1.0	0.4	0.4
y	0.4	1.0	0.2
z	0.8	0.4	1.0

The following Theorems show the characterization of fuzzy relations in terms of their level subsets.

Theorem 2.5.

(Mezzomo et al., 2015) Let µ be a fuzzy relation in X. Then µ is a fuzzy partial order relation if and only if every α-cut, µ_α is a partial order relation in X for all α such that $0<\alpha \le 1$.

Theorem 2.6.

(Mezzomo et al., 2015) Let µ be a fuzzy relation in X and let $S(\mu )=\{(x,y)\in X\times X:\mu (x,y)>0\}$ be a support of the fuzzy relation µ defined on X. If µ is a fuzzy partial order relation on X. Then, $S(\mu )$ is a partial order relation on X.

Definition 2.14.

(Chon, 2009) Let $(X,\mu )$ be a fuzzy poset and let $B\subseteq X$.

(1)	An element $u\in X$ is said to be an upper bound for a subset B if and only if $\mu (b,u)>0$ for all $b\in B$.
(2)	An upper bound u0 for B is said to be the least upper bound (lub) of B if and only if $\mu (u_0,u)>0$ for every upper bound u for B.
(3)	An element $v\in X$ is said to be a lower bound for a subset B if and only if $\mu (v,b)>0$ for all $b\in B$.
(4)	A lower bound v0 for B is said to be the greatest lower bound (glb) of B if and only if $\mu (v,v_0)>0$ for every lower bound v for B.

Notation.

We denote the least upper bound of the set $\{x,y\}$ if it exists by $x{\vee }_{F}y$ and denote the greatest lower bound of the set $\{x,y\}$ if it exists by $x{\wedge }_{F}y$.

Definition 2.15.

(Chon, 2009) Let $(X,\mu )$ be a fuzzy poset. Then, $(X,\mu )$ is said to be a fuzzy lattice if and only if $x{\vee }_{F}y$ and $x{\wedge }_{F}y$ exist for all $x,y\in X$.

Remark.

Let $(X,\mu )$ be a fuzzy poset and let $Y\subseteq X$. Then, the least upper bound and greatest lower bound of Y if it exists is unique.

Theorem 2.7.

(Chon, 2009) (Properties of Fuzzy Lattice)

Let $(X,\mu )$ be a fuzzy lattice and let $x,y,z\in X$. Then,

(i)	$\mu (x,x{\vee }_{F}y)>0$ and $\mu (y,x{\vee }_{F}y)>0$.
(ii)	$\mu (x{\wedge }_{F}y,x)>0$, and $\mu (x{\wedge }_{F}y,y)>0$.
(iii)	If $\mu (x,z)>0$ and $\mu (y,z)>0$ then $\mu (x{\vee }_{F}y,z)>0$.
(iv)	If $\mu (z,x)>0$ and $\mu (z,y)>0$, then $\mu (z,x{\wedge }_{F}y)>0$.
(v)	$\mu (y,z)>0$ then, $\mu (x{\wedge }_{F}y,x{\wedge }_{F}z)>0$ and $\mu (x{\vee }_{F}y,x{\vee }_{F}z)>0$.

Theorem 2.8.

(Chon, 2009) Let $\mu :X\times X⟶[0,1]$ be a fuzzy relation in X and let ${\mu }_{\alpha }=\{(x,y)\in X\times X:\mu (x,y)\text{break}\ge \alpha \}$ be $\alpha -level$ sub set of the fuzzy relation µ defined on X. If $(X,{\mu }_{\alpha })$ is a lattice for all $\alpha \in (0,1]$, then $(X,\mu )$ is a fuzzy lattice.

Remark.

The converse of the above Theorem is not necessarily true.

But we can find a lattice from a fuzzy lattice by specifying the α-cut as follow

Theorem 2.9.

(Chon, 2009) Let $\mu :X\times X⟶[0,1]$ be a fuzzy relation on X and let ${\mu }_{\alpha }=\{(x,y)\in X\times X:\mu (x,y)\text{break}\ge \alpha \}$ be $\alpha -level$ sub set of the fuzzy relation µ defined on X. If $(X,\mu )$ is a fuzzy lattice, then $(X,{\mu }_{\alpha })$ is a lattice for some $\alpha \in (0,1]$.

Proposition 2.10.

(Mezzomo et al., 2015) Let $(X,\mu )$ be a fuzzy lattice and let $x,y\in X$, then $x{\vee }_{F}y$ and $x{\wedge }_{F}y$ coincides with $x\vee y$ and $x\wedge y$ respectively in $(X,S(\mu ))$.

Theorem 2.11.

(Chon, 2009) Let µ be a fuzzy relation in X and let $S(\mu )$ be a support of the fuzzy relation µ defined on X. If $(X,\mu )$ is a fuzzy lattice, then $(X,S(\mu ))$ is a lattice on X.

3. Fuzzy congruence relation on fuzzy lattice

In this section, we introduce the notion of fuzzy congruence relations on a fuzzy lattice and discuss basic properties related to its level sets.

Remark.

Throughout the rest of this paper $(L,\mu )$ stands for a fuzzy lattice $(L,{\vee }_F,{\wedge }_F)$.

Definition 3.1.

Let $(L,\mu )$ be a fuzzy lattice as defined by (Chon, 2009) and let π be a fuzzy relation on L. Then, π is said to be

(i)	Fuzzy join compatible if $\pi (x,y)\le \pi (x{\vee }_{F}z,y{\vee }_{F}z)$ for all $x,y,z\in L$.
(ii)	Fuzzy meet compatible if $\pi (x,y)\le \pi (x{\wedge }_{F}z,y{\wedge }_{F}z)$ for all $x,y,z\in L$
(iii)	Fuzzy compatible if it is both fuzzy join and fuzzy meet compatible.

Definition 3.2.

Let $\pi \in FEq(L)$. Then, π is called fuzzy join congruence (fuzzy meet congruence, fuzzy congruence) relation on fuzzy lattice L if it is fuzzy join compatible (meet compatible, compatible) on fuzzy lattice L.

Notation.

Let $(L,\mu )$ be a fuzzy lattice then, the family of all fuzzy congruence relation on fuzzy lattice L is denoted by FCon(L).

Theorem 3.1

Let $(L,\mu )$ be a fuzzy lattice and $\pi \in FEq(L)$. Then, π is fuzzy compatible if and only if $min(\pi (x,y),\pi (z,t))\le \pi (x{\vee }_{F}z,y{\vee }_{F}t)$ and $min(\pi (x,y),\pi (z,t))\le \pi (x{\wedge }_{F}z,y{\wedge }_{F}t)$ for all $x,y,z,t\in L$.

Proof. Suppose π is fuzzy compatible. Let $x,y,z,t\in L$, then

$\begin{array}{ll}min(\pi (x,y),\pi (z,t))& \le min(\pi (x{\vee }_{F}z,y{\vee }_{F}z),\\ & \pi (y{\vee }_{F}z,y{\vee }_{F}t))\\ & \le \pi (x{\vee }_{F}z,y{\vee }_{F}t)\end{array}$

Similarly,

$min(\pi (x,y),\pi (z,t))\le \pi (x{\wedge }_{F}z,y{\wedge }_{F}t)$

Conversely, suppose the condition and to show π is fuzzy compatible. Let $x,y,z\in L$, then

$\begin{array}{ll}\pi (x,y)& =min(\pi (x,y),\pi (z,z))\\ & \le \pi (x{\vee }_{F}z,y{\vee }_{F}z)\end{array}$

Similarly, $\pi (x,y)\le \pi (x{\wedge }_{F}z,y{\wedge }_{F}z)$. Therefore, π is fuzzy compatible.

Based on the definition of fuzzy congruence relation and Theorem (2.11) we have the following result,

Theorem 3.2

Let $(L,\mu )$ be a fuzzy lattice and π be a fuzzy relation on L. Then $\pi \in FCon(L,\mu )$ if and only if ${\pi }_{\alpha }\in Con(L,S(\mu ))$ for all $\alpha \in (0,1]$ whenever ${\pi }_{\alpha }\ne \mathrm{\varnothing }$.

Proof. $(⟹)$ Suppose $\pi \in FCon(L,\mu )$ and let $\alpha \in (0,1]$ and assume ${\pi }_{\alpha }\ne \mathrm{\varnothing }$

(i)	Let $x\in L$. Since, $\pi (x,x)=1\ge \alpha$. Then, $(x,x)\in {\pi }_{\alpha }$. Thus, πα is reflexive.
(ii)	Let $x,y\in L$ such that $(x,y)\in {\pi }_{\alpha }$. Then, $\pi (x,y)\ge \alpha$. By symmetric of π, we have $\pi (y,x)\ge \alpha$. Thus,$(y,x)\in {\pi }_{\alpha }$ Therefore, πα is symmetric.
(iii)	Let $x,y,z\in L$ such that $(x,y)\in {\pi }_{\alpha }$ and $(y,z)\in {\pi }_{\alpha }$. Then, $\pi (x,y)\ge \alpha$ and $\pi (y,z)\ge \alpha$. Then, $\begin{array}{ll}\pi (x,z)& \ge \underset{s\in L}{sup}min(\pi (x,s),\pi (s,z))\\ & \ge min(\pi (x,y),\pi (y,z))\\ & \ge min(\alpha ,\alpha )\\ \pi (x,z)& \ge \alpha \end{array}$ Therefore, $(x,z)\in {\pi }_{\alpha }$ and hence πα is transitive.
(iv)	Let $x,y,z\in L$ such that $(x,y)\in {\pi }_{\alpha }$. Then, $\pi (x,y)\ge \alpha$. Since π is fuzzy compatible we have $\pi (x{\wedge }_{F}z,y{\wedge }_{F}z)\ge \pi (x,y)$ and $\pi (x{\vee }_{F}z,y{\vee }_{F}z)\ge \pi (x,y)$. Therefore, $(x{\wedge }_{F}z,y{\wedge }_{F}z)\in {\pi }_{\alpha }$ and $(x{\vee }_{F}z,y{\vee }_{F}z)\in {\pi }_{\alpha }$. Thus, πα is congruence relation on $(L,S(\mu ))$.

$(⟸)$ Conversely, suppose ${\pi }_{\alpha }\in Con(L,S(\mu ))$ for all $\alpha \in (0,1]$.

(i)	Let $x\in L$. Since $(x,x)\in {\pi }_1$ then $\pi (x,x)\ge 1$ and hence $\pi (x,x)=1$. Therefore, π is reflexive.
(ii)	Let $x,y\in L$ and suppose $\pi (x,y)=\alpha$. Then $\pi (x,y)\ge \alpha$ and hence $(x,y)\in {\pi }_{\alpha }$. Then by symmetric of πα we have $(y,x)\in {\pi }_{\alpha }$ and then $\pi (y,x)\ge \alpha$. Hence, $\pi (y,x)\ge \pi (x,y)$. Similarly, $\pi (x,y)\ge \pi (y,x)$. Therefore, $\pi (y,x)=\pi (x,y)$ which implies that π is symmetric.
(iii)	Let $x,y,z\in L$ and suppose $\pi (x,z)=\alpha$ and $\pi (z,y)=\beta$. Then, $(x,z)\in {\pi }_{\alpha }$ and $(z,y)\in {\pi }_{\beta }$. Now let $\gamma =min\{\alpha ,\beta \}$. Then, $\pi (x,z)\ge \gamma$ and $\pi (z,y)\ge \gamma$ and hence $(x,z)\in {\pi }_{\gamma }$ and $(z,y)\in {\pi }_{\gamma }$ and by transitivity of πγ we have $(x,y)\in {\pi }_{\gamma }$. Thus, $\begin{array}{ll}\pi (x,y)& \ge \gamma \\ & =min\{\alpha ,\beta \}\\ & =min(\pi (x,z),\pi (z,y))\end{array}$ Since $z\in L$ is arbitrary we have, $\pi (x,y)\ge \text{break}\underset{z\in L}{sup}[min(\pi (x,z),\pi (z,y))]$. Therefore, π is transitive.
(iv)	Let $x,y,t\in L$ and suppose $\pi (x,y)=\alpha$. Then, $(x,y)\in {\pi }_{\alpha }$ and hence $(x{\wedge }_{F}t,y{\wedge }_{F}t)\in {\pi }_{\alpha }$. Then, $\pi (x{\wedge }_{F}t,y{\wedge }_{F}t)\ge \alpha$. Hence, $\pi (x{\wedge }_{F}t,y{\wedge }_{F}t)\ge \pi (x,y)$. Similarly, $\pi (x{\vee }_{F}t,y{\vee }_{F}t)\ge \pi (x,y)$.

Hence, π is compatible and therefore, $\pi \in FCon(L,\mu )$.

Definition 3.3.

Let $(L,\mu )$ be a fuzzy lattice and a and b be pair of elements of L such that $\mu (a,b)>0$. We define the interval $[a,b]$ on L by

(9) $[a,b]=\{x\in L:\mu (a,x)>0\text{and}\mu (x,b)>0\}$(9)

Proposition 3.3.

Let $(L,\mu )$ be a fuzzy lattice and $\pi \in FCon(L)$. Then, the following are equivalent for all $a,b\in L$

(i)	$\pi (a,b)>0$
(ii)	$\pi (a{\wedge }_{F}b,a{\vee }_{F}b)>0$
(iii)	If $x,y\in L$ such that $x,y\in [a{\wedge }_{F}b,a{\vee }_{F}b]$, then $\pi (x,y)>0$

Proof. (i $⟹$ ii): Suppose $\pi (a,b)>0$. Since $\pi (b,b)=1>0$, then $\pi (a{\wedge }_{F}b,b)>0$. Similarly, $\pi (b,a{\vee }_{F}b)>0$. Thus by transitivity on π we have $\pi (a{\wedge }_{F}b,a{\vee }_{F}b)>0$.

(ii $⟹$ iii): Suppose $\pi (a{\wedge }_{F}b,a{\vee }_{F}b)>0$. Let $x,y\in L$ such that $x,y\in [a{\wedge }_{F}b,a{\vee }_{F}b]$. Then, $\pi ((a{\wedge }_{F}b){\vee }_{F}x,(a{\vee }_{F}b){\vee }_{F}x)>0$ and $\pi ((a{\wedge }_{F}b){\vee }_{F}y,(a{\vee }_{F}b){\vee }_{F}y)>0$. Hence, $\pi (x,a{\vee }_{F}b)>0$ and $\pi (y,a{\vee }_{F}b)>0$ and hence $\pi (x,a{\vee }_{F}b)>0$ and $\pi (a{\vee }_{F}b,y)>0$. Then, by transitivity of π we have $\pi (x,y)>0$.

(iii $⟹$ i): Suppose, if $x,y\in L$ such that $x,y\in [a{\wedge }_{F}b,a{\vee }_{F}b]$, then $\pi (x,y)>0$. Since $a,b\in [a{\wedge }_{F}b,a{\vee }_{F}b]$, then $\pi (a,b)>0$.

Definition 3.4.

Let $(L,\mu )$ be a fuzzy lattice and let ${\pi }_1,{\pi }_2\in FCon(L)$. Then, π₁ and π₂ are said to be permutable fuzzy congruences if ${\pi }_1\circ {\pi }_2={\pi }_2\circ {\pi }_1$.

Definition 3.5.

If every pair of elements of FCon(L) are permutable then the fuzzy lattice L is called fuzzy congruence permutable.

Lemma 3.4.

If π₁ and π₂ are compatible fuzzy congruences on $(L,\mu )$. Then, ${\pi }_1\circ {\pi }_2$ is also fuzzy compatible.

Proof. Let $x,y,a,b\in L$. Then,

$\begin{array}{ll}({\pi }_1\circ {\pi }_2)(x{\wedge }_{F}a,y{\wedge }_{F}b)& =\underset{z\in L}{sup}min({\pi }_1(x{\wedge }_{F}a,z),\\ & {\pi }_2(z,y{\wedge }_{F}b))\\ & \ge \underset{c,d\in L}{sup}min({\pi }_1(x{\wedge }_{F}a,\\ & c{\wedge }_{F}d),{\pi }_2(c{\wedge }_{F}d,y{\wedge }_{F}b))\\ & \ge \underset{c,d\in L}{sup}min[min({\pi }_1(x,c),\\ & {\pi }_1(a,d)),min({\pi }_2(c,y),\\ & {\pi }_2(d,b)])\\ & \ge min[\underset{c\in L}{sup}min({\pi }_1(x,c),\\ & {\pi }_2(c,y)),\underset{d\in L}{sup}(min({\pi }_1(a,d),\\ & {\pi }_2(d,b))]\\ & =min(({\pi }_1\circ {\pi }_2)(x,y),\\ & ({\pi }_1\circ {\pi }_2)(a,b))\end{array}$

Similarly, $({\pi }_1\circ {\pi }_2)(x{\vee }_{F}a,y{\vee }_{F}b)\ge min(({\pi }_1\circ {\pi }_2)(x,y),({\pi }_1\circ {\pi }_2)(a,b))$. Therefore, ${\pi }_1\circ {\pi }_2$ is fuzzy compatible.

Proposition 3.5.

Let ${\pi }_1,{\pi }_2\in FCon(L)$. Then, π₁ and π₂ are permutable fuzzy congruences if and only if ${\pi }_1\circ {\pi }_2\in FCon(L)$.

Proof. Suppose π₁ and π₂ are permutable fuzzy congruences.

(i)	Let $x\in L$. Then, $\begin{array}{ll}({\pi }_1\circ {\pi }_2)(x,x)& =\underset{z\in L}{sup}min({\pi }_1(x,z),{\pi }_2(z,x))\\ & \ge min({\pi }_1(x,x),{\pi }_2(x,x))\\ & =min(1,1)\\ & =1\end{array}$ Thus, $({\pi }_1\circ {\pi }_2)(x,x)=1$ and therefore ${\pi }_1\circ {\pi }_2$ reflexive.
(ii)	Let $x,y\in L$ $\begin{array}{ll}({\pi }_1\circ {\pi }_2)(x,y)& =\underset{z\in L}{sup}min({\pi }_1(x,z),{\pi }_2(z,y))\\ & =\underset{z\in L}{sup}min({\pi }_2(y,z),{\pi }_1(z,x))\\ & =({\pi }_2\circ {\pi }_1)(y,x)\\ & =({\pi }_1\circ {\pi }_2)(y,x)\text{(}\because {\pi }_1\text{and}{\pi }_2\\ & \text{are fuzzy permutable)}\end{array}$ Therefore, $({\pi }_1\circ {\pi }_2)(x,y)=({\pi }_1\circ {\pi }_2)(y,x)$ and hence ${\pi }_1\circ {\pi }_2$ symmetric.
(iii)	Since ${\pi }_1,{\pi }_2$ are permutable fuzzy congruences then apply associativity property we have, $\begin{array}{ll}({\pi }_1\circ {\pi }_2)\circ ({\pi }_1\circ {\pi }_2)& =({\pi }_1\circ {\pi }_1)\circ ({\pi }_2\circ {\pi }_2)\\ & \subseteq {\pi }_1\circ {\pi }_2\end{array}$ Thus, $({\pi }_1\circ {\pi }_2)\circ ({\pi }_1\circ {\pi }_2)\subseteq {\pi }_1\circ {\pi }_2$ and hence ${\pi }_1\circ {\pi }_2$ transitive.
(iv)	Fuzzy compatibility is clear by Lemma (3.4)

Therefore, ${\pi }_1\circ {\pi }_2\in FCon(L)$.

Conversely, suppose ${\pi }_1\circ {\pi }_2\in FCon(L)$ and let $x,y\in L$, then

$\begin{array}{ll}({\pi }_1\circ {\pi }_2)(x,y)& =({\pi }_1\circ {\pi }_2)(y,x)\\ & =\underset{z\in L}{sup}min({\pi }_1(y,z),{\pi }_2(z,x))\\ & =\underset{z\in L}{sup}min({\pi }_2(x,z),{\pi }_1(z,y))\\ & =({\pi }_2\circ {\pi }_1)(x,y)\end{array}$

Therefore, π₁ and π₂ permutable fuzzy congruences.

Lemma 3.6.

Let $(L,\mu )$ be fuzzy lattice and let ${\pi }_1,{\pi }_2\in Fcon(L)$. Then, ${\pi }_1\cap {\pi }_2\in Fcon(L)$

Proof. Suppose ${\pi }_1,{\pi }_2\in Fcon(L)$

(i)	Since ${\pi }_1(x,x)=1={\pi }_2(x,x)$. Then $({\pi }_1\cap {\pi }_2)(x,x)=1$. Thus, ${\pi }_1\cap {\pi }_2$ is reflexive.
(ii)	Let $x,y\in L$. Since ${\pi }_1(x,y)={\pi }_1(y,x)$ and ${\pi }_2(x,y)={\pi }_2(y,x)$. Then $({\pi }_1\cap {\pi }_2)(x,y)=({\pi }_1\cap {\pi }_2)(y,x)$ this shows ${\pi }_1\cap {\pi }_2$ is symmetric.
(iii)	Let $x,z\in L$, then $\begin{array}{ll}({\pi }_1\cap {\pi }_2)(x,z)=& min({\pi }_1(x,z),{\pi }_2(x,z))\\ \ge & min(\underset{y\in L}{sup}[min({\pi }_1(x,y),{\pi }_1(y,z))],\\ & \underset{y\in L}{sup}[min({\pi }_2(x,y),{\pi }_2(y,z))])\\ =& \underset{y\in L}{sup}[min(min({\pi }_1(x,y),{\pi }_2(x,y)),\\ & min({\pi }_1(y,z),{\pi }_2(y,z))])\\ =& \underset{y\in L}{sup}[min(({\pi }_1\cap {\pi }_2)(x,y),\\ & ({\pi }_1\cap {\pi }_2)(y,z))])\end{array}$ Hence, ${\pi }_1\cap {\pi }_2$ is transitive.
(iv)	Let $x,y,z\in L$. Then, $\begin{array}{ll}({\pi }_1\cap {\pi }_2)(x,y)& =min({\pi }_1(x,y),{\pi }_2(x,y))\\ & \le min({\pi }_1(x{\wedge }_{F}z,y{\wedge }_{F}z),\\ & {\pi }_2(x{\wedge }_{F}z,y{\wedge }_{F}z))\\ & =({\pi }_1\cap {\pi }_2)(x{\wedge }_{F}z,y{\wedge }_{F}z)\end{array}$ Similarly, $({\pi }_1\cap {\pi }_2)(x,y)\le ({\pi }_1\cap {\pi }_2)(x{\vee }_{F}z,y{\vee }_{F}z)$. Therefore, ${\pi }_1\cap {\pi }_2\in Fcon(L)$.

Remark.

However the union of two fuzzy congruence relations may not be a fuzzy congruence relation

Example 3.6.

Let $L_1=\{x,y,z,w\}$ and define a fuzzy relation µ₁ on X by the fuzzy relational matrix given in Figure 1

Figure 1. Representation of fuzzy lattice µ₁ on L₁ by relational matrix and Hasse diagram.

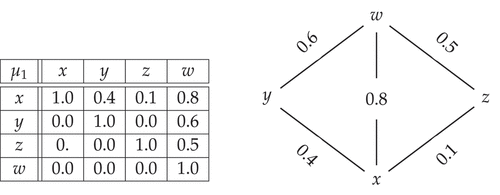
Thus, from figure 1 it is easy to verify that $(L_1,{\mu }_1)$ is fuzzy lattice.

Similarly consider the following fuzzy congruence relations π₁ and π₂ on L₁ whose represntations given in Table 5 and Table 6 respectively

Table 5. Representation of the fuzzy congruence relations π₁ and π₂ on fuzzy lattice L₁ by relational matrices

π1	x	y	z	w	π2	x	y	z	w
x	1.0	1.0	0.0	0.0	x	1.0	0.0	1.0	0.0
y	1.0	1.0	0.0	0.0	y	0.0	1.0	0.0	1.0
z	0.	0.0	1.0	1.0	z	1.0	0.0	1.0	0.0
w	0.0	0.0	1.0	1.0	w	0.0	1.0	0.0	1.0

Then, the relational matrix corresponds to the fuzzy relation ${\pi }_1\cup {\pi }_2$ is given in Table 6,

Table 6. Representation of fuzzy congruence relations ${\pi }_1\cup {\pi }_2$ on L₁ by relational matrix

${\pi }_1\cup {\pi }_2$	x	y	z	w
x	1.0	1.0	1.0	0.0
y	1.0	1.0	0.0	1.0
z	1.0	0.0	1.0	1.0
w	0.0	1.0	1.0	1.0

Now since, $({\pi }_1\cup {\pi }_2)(y,z)=0\ngeqq min(({\pi }_1\cup {\pi }_2)(y,w),({\pi }_1\cup {\pi }_2)(w,z))=1$. Then, ${\pi }_1\cup {\pi }_2$ is not a transitive and hence it is not a fuzzy congruence relation on L₁.

4. Lattice of fuzzy congruence relation

In this section, we discuss the lattice structure of the fuzzy congruence relations on the fuzzy lattice which is defined above.

Lemma 4.1.

Let $(L,\mu )$ be a fuzzy lattice. Then, $(FCon(L),\subseteq )$ is complete lattice where $\subseteq$ is a relation defined by ${\pi }_1\subseteq {\pi }_2$ if and only if ${\pi }_1(x,y)\subseteq {\pi }_2(x,y)$ for all $x,y\in L$ and ${\pi }_1,{\pi }_2\in FCon(L)$.

Proof. It is clear that $(FCon(L),\subseteq )$ is a poset with Δ and $\mathrm{\nabla }$ are the least and greatest elements of $(FCon(L),\subseteq )$. Now let $\{{\pi }_i{\}}_{i\in I}$ be any collection of fuzzy congruences on fuzzy lattice L and suppose $\pi (x,y)=\underset{i\in I}{inf}{\pi }_i(x,y)$ for $x,y\in L$. Then,

(i)	Since ${\pi }_i(x,x)=1$ for all $i\in I$, then $\underset{i\in I}{inf}{\pi }_i(x,x)=1$. Thus, $\pi (x,x)=1$ and hence π is reflexive.
(ii)	Let $x,y\in L$, since ${\pi }_i(x,y)={\pi }_i(y,x)$ for all $i\in I$ then $\pi (x,y)=\pi (y,x)$ and hence π is symmetric.
(iii)	Let $x,z\in L$, then $\begin{array}{ll}\pi (x,z)=& \underset{i\in I}{inf}{\pi }_i(x,z)\\ \ge & \underset{i\in I}{inf}(\underset{y\in X}{sup}[min({\pi }_i(x,y),{\pi }_i(y,z))])\\ =& \underset{y\in X}{sup}[min(\underset{i\in I}{inf}{\pi }_i(x,y),\underset{i\in I}{inf}{\pi }_i(y,z))]\\ =& \underset{y\in X}{sup}[min(\pi (x,y),\pi (y,z))]\end{array}$ Hence, π is transitive.
(iv)	Let $x,y,z\in L$. Then, $\begin{array}{ll}\pi (x,y)& =\underset{i\in I}{inf}{\pi }_i(x,y)\\ & \le \underset{i\in I}{inf}{\pi }_i(x{\wedge }_{F}z,y{\wedge }_{F}z)\\ & =\pi (x{\wedge }_{F}z,y{\wedge }_{F}z)\end{array}$ Similarly, $\pi (x,y)\le \pi (x{\vee }_{F}z,y{\vee }_{F}z)$. Then, $\pi =\underset{i\in I}{inf}{\pi }_i\in Fcon(L)$. Therefore, $(FCon(L),\subseteq )$ is complete lattice.

Theorem 4.2

Let $(L,\mu )$ be a fuzzy lattice and let ${\pi }_1,{\pi }_2\in Fcon(L)$. Then,

(a)

${\pi }_1\wedge {\pi }_2={\pi }_1\cap {\pi }_2$

(b)

${\pi }_1\vee {\pi }_2={\pi }_1\cup ({\pi }_1\circ {\pi }_2\circ {\pi }_1)\cup ({\pi }_1\circ {\pi }_2\circ {\pi }_1\circ {\pi }_2\circ {\pi }_1)\cup \cdots$ That is, for every $x,y\in L$ there exists $x=c_0,c_1,c_2,\cdots c_n=y\in L$ such that $\begin{array}{ll}({\pi }_1\vee {\pi }_2)(x,y)=& \underset{x=c_0,c_1,c_2,\cdots c_n=y\in L}{sup}[min({\pi }_1(x,c_1),\\ & {\pi }_2(c_1,c_2),\cdots ,{\pi }_1(c_{n-1},y)]\end{array}$

Proof. Let ${\pi }_1,{\pi }_2\in Fcon(L)$

(a)

Clearly ${\pi }_1\cap {\pi }_2\in Fcon(L)$ and ${\pi }_1\cap {\pi }_2\subseteq {\pi }_1,{\pi }_2$ (i.e ${\pi }_1\cap {\pi }_2$ is lower bound of $\{{\pi }_1,{\pi }_2\}$). Let $\theta \in Fcon(L)$ be lower bound of $\{{\pi }_1,{\pi }_2\}$. Then for any $x,y\in L$ we have $\theta (x,y)\le {\pi }_1(x,y)$ and $\theta (x,y)\le {\pi }_2(x,y)$. Then, $\theta (x,y)\le min({\pi }_1(x,y),{\pi }_2(x,y))$ and hence $\theta (x,y)\le ({\pi }_1\cap {\pi }_2)(x,y))$. Thus, $\theta \subseteq {\pi }_1\cap {\pi }_2$ and this shows ${\pi }_1\cap {\pi }_2$ is greatest lower bound of ${\pi }_1,{\pi }_2$. Therefore, ${\pi }_1\wedge {\pi }_2={\pi }_1\cap {\pi }_2$.

(b)

Let $\theta =\underset{x=c_0,c_1,c_2,\cdots c_n=y\in L}{sup}[min({\pi }_1(a,c_1),{\pi }_2(c_1,c_2),\text{break}\cdots ,{\pi }_1(c_{n-1},y)]$

(i)	Let $x\in L$. Since $1={\pi }_1(x,x)\le \theta (x,x)$. Then, $\theta (x,x)=1$. Therefore, θ is reflexive.
(ii)	Let $x,y\in L$. Then, $\begin{array}{ll}\theta (x,y)& =\underset{x=c_0,c_1,c_2,\cdots c_n=y\in L}{sup}[min({\pi }_1(x,c_1),{\pi }_2(c_1,c_2),\\ & \cdots ,{\pi }_1(c_{n-1},y)]\\ & =\underset{y=c_n,c_{n-1},\cdots c_0=x\in L}{sup}[min({\pi }_1(c_{n-1},y),\cdots ,\\ & {\pi }_1(c_1,c_2),{\pi }_2(x,c_1)]\\ & =\underset{y=c_n,c_{n-1},\cdots c_0=x\in L}{sup}[min({\pi }_1(y,c_{n-1}),\\ & {\pi }_2(c_{n-1},c_{n-2})\cdots ,,{\pi }_1(c_1,x)]\\ & =\theta (y,x)\end{array}$ which shows θ is symmetric.
(iii)	To show θ is transitive it is sufficient to show that $\theta \circ \theta \subseteq \theta$. Now, let $x,y\in L$. Then, $\begin{array}{ll}& \theta \circ \theta (x,y)\\ & =\underset{z\in L}{sup}[min(\theta (x,z),\theta (z,y))]\\ & =\underset{z\in L}{sup}[min[\underset{x=c_0,c_1,c_2,\cdots c_n=z\in L}{sup}[min({\pi }_1(x,c_1),\\ & {\pi }_2(c_1,c_2),\cdots ,{\pi }_1(c_{n-1},z)],\\ & \underset{z=d_0,d_1,d_2,\cdots d_m=y\in L}{sup}[min({\pi }_1(z,d_1),{\pi }_2(d_1,d_2),\\ & \cdots ,{\pi }_1(d_{m-1},y)]]]\\ & =\underset{z\in L}{sup}[\underset{x=c_0,c_1,c_2,\cdots c_n=z,d_1,d_2,\cdots d_m\in L}{sup}[min({\pi }_1(x,c_1),\\ & {\pi }_2(c_1,c_2),\cdots ,{\pi }_1(c_{n-1},z),{\pi }_1(z,d_1),\\ & {\pi }_2(d_1,d_2),\cdots ,{\pi }_1(d_{m-1},y)]]\\ & \le \underset{x=c_0,c_1,c_2,\cdots c_{n-1},d_1,d_2,\cdots d_m\in L}{sup}[min({\pi }_1(x,c_1),\\ & {\pi }_2(c_1,c_2),\cdots ,{\pi }_1(c_{n-1},d_1),{\pi }_2(d_1{d}_2),\\ & \cdots ,{\pi }_1(d_{m-1},y)](\because min({\pi }_1(c_{n-1},z),\\ & {\pi }_1(z,d_1))\le {\pi }_1(c_{n-1},d_1))\\ & =\theta (x,y)\end{array}$ Thus, $\theta \circ \theta \subseteq \theta$ and hence θ is transitive.
(iv)	Let $x,y,z\in L$. Then, $\begin{array}{ll}\theta (x,y)& =\underset{c_0,c_1,c_2,\cdots c_n}{sup}[min({\pi }_1(x,c_1),{\pi }_2(c_1,c_2),\cdots ,\\ & {\pi }_1(c_{n-1},y)]\\ & \le \underset{c_0{\wedge }_{F}z,c_1{\wedge }_{F}z,\cdots ,c_n{\wedge }_{F}z}{sup}[min({\pi }_1(x{\wedge }_{F}z,c_1{\wedge }_{F}z),\\ & {\pi }_2(c_1{\wedge }_{F}z,c_2{\wedge }_{F}z),\cdots ,\\ & {\pi }_1(c_{n-1}{\wedge }_{F}z,y{\wedge }_{F}z)]\\ & =\theta (x{\wedge }_{F}z,y{\wedge }_{F}z)\end{array}$ Similarly, $\theta (x,y)\le \theta (x{\vee }_{F}z,y{\vee }_{F}z)$. Hence, θ is fuzzy compatible and therefore $\theta \in Fcon(L)$
(v)	Finally to show that θ is least upper bound of $\{{\pi }_1,{\pi }_2\}$. Clearly ${\pi }_1,{\pi }_2\subseteq \theta$. Suppose $\alpha \in Fcon(L)$ be an upper bound of $\{{\pi }_1,{\pi }_2\}$ and let $x,y\in L$ then, $\begin{array}{ll}\theta (x,y)& =\underset{c_0,c_1,c_2,\cdots c_n}{sup}[min({\pi }_1(x,c_1),{\pi }_2(c_1,c_2),\cdots ,\\ & {\pi }_1(c_{n-1},y)]\\ & \le \underset{c_0,c_1,c_2,\cdots c_n}{sup}[min(\alpha (x,c_1),\alpha (c_1,c_2),\cdots ,\\ & \alpha (c_{n-1},y)]\\ & \le \alpha (x,y)\end{array}$ This shows θ is the least upper bound of $\{{\pi }_1,{\pi }_1\}$. Hence, $\begin{array}{ll}({\pi }_1\vee {\pi }_2)(x,y)=& \underset{c_0,c_1,c_2,\cdots c_n}{sup}[min({\pi }_1(x,c_1),{\pi }_2(c_1,c_2),\\ & \cdots ,{\pi }_1(c_{n-1},y)]\end{array}$ Therefore, ${\pi }_1\vee {\pi }_2={\pi }_1\cup ({\pi }_1\circ {\pi }_2\circ {\pi }_1)\cup ({\pi }_1\circ {\pi }_2\circ {\pi }_1\circ {\pi }_2\circ {\pi }_1)\cup \cdots$

Proposition 4.3.

Let ${\pi }_1,{\pi }_2\in FCon(L)$ such that ${\pi }_1\circ {\pi }_2\in FCon(L)$. Then ${\pi }_1\circ {\pi }_2={\pi }_1\vee {\pi }_2$

Proof. Let ${\pi }_1,{\pi }_2\in FCon(L)$ such that ${\pi }_1\circ {\pi }_2\in FCon(L)$. Then, for $x,y\in L$

$\begin{array}{ll}({\pi }_1\circ {\pi }_2)(x,y)& =\underset{z\in L}{sup}min({\pi }_1(x,z),{\pi }_2(z,y))\\ & \ge min({\pi }_1(x,y),{\pi }_2(y,y))\\ & \ge min({\pi }_1(x,y),1)\\ & ={\pi }_1(x,y)\\ ({\pi }_1\circ {\pi }_2)(x,y)& \ge {\pi }_1(x,y)\end{array}$

Therefore, ${\pi }_1\circ {\pi }_2\supseteq {\pi }_1$ and similarly ${\pi }_1\circ {\pi }_2\supseteq {\pi }_2$. Thus, ${\pi }_1\circ {\pi }_2$ is upper bound of $\{{\pi }_1,{\pi }_2\}$. Now let, $\theta \in FCon(L)$ be upper bound of $\{{\pi }_1,{\pi }_2\}$. Then for $x,y\in L$

$\begin{array}{ll}({\pi }_1\circ {\pi }_2)(x,y)& =\underset{z\in L}{sup}min({\pi }_1(x,z),{\pi }_2(z,y))\\ & \le \underset{z\in L}{sup}min(\theta (x,z),\theta (z,y))\\ & \le \theta (x,y)\\ ({\pi }_1\circ {\pi }_2)(x,y)& \le \theta (x,y)\end{array}$

Then, ${\pi }_1\circ {\pi }_2\subseteq \theta$. Which shows ${\pi }_1\circ {\pi }_2$ is least upper bound of $\{{\pi }_1,{\pi }_2\}$. Therefore, ${\pi }_1\circ {\pi }_2={\pi }_1\vee {\pi }_2$.

By combining Propositions (3.5) and (4.3) we have the following result:

Corollary 4.4.

Let ${\pi }_1,{\pi }_2\in FCon(L)$. If π₁ and π₂ are permutable fuzzy congruences, then ${\pi }_1\circ {\pi }_2={\pi }_1\vee {\pi }_2$

Theorem 4.5

Let $(L,\mu )$ be a fuzzy lattice and ${\pi }_1,{\pi }_2\in Fcon(L)$. Then, the following are equivalent.

(i)	${\pi }_1\circ {\pi }_2={\pi }_2\circ {\pi }_1$
(ii)	${\pi }_1\vee {\pi }_2={\pi }_1\circ {\pi }_2$
(iii)	${\pi }_2\circ {\pi }_1\subseteq {\pi }_1\circ {\pi }_2$

Proof. $(i)⟹(ii)$ : Suppose ${\pi }_1\circ {\pi }_2={\pi }_2\circ {\pi }_1$. Then ${\pi }_1\circ {\pi }_2\in Fcon(L)$ and also ,

$\begin{array}{l}\begin{array}{ll}{\pi }_1\vee {\pi }_2=& {\pi }_1\cup ({\pi }_1\circ {\pi }_2\circ {\pi }_1)\\ & \cup ({\pi }_1\circ {\pi }_2\circ {\pi }_1\circ {\pi }_2\circ {\pi }_1)\cup \cdots \\ =& {\pi }_1\cup ({\pi }_1\circ {\pi }_1\circ {\pi }_2)\\ & \cup ({\pi }_1\circ {\pi }_1\circ {\pi }_1\circ {\pi }_2\circ {\pi }_2)\cup \cdots \\ =& {\pi }_1\cup ({\pi }_1\circ {\pi }_2)\cup ({\pi }_1\circ {\pi }_1\circ {\pi }_2)\\ & \cup ({\pi }_1\circ {\pi }_1\circ {\pi }_2\circ {\pi }_2)\cup \cdots \\ =& {\pi }_1\cup ({\pi }_1\circ {\pi }_2)\cup ({\pi }_1\circ {\pi }_2)\\ & \cup ({\pi }_1\circ {\pi }_2)\cup \cdots \\ =& {\pi }_1\circ {\pi }_2\end{array}\end{array}$

$(ii)⟹(iii)$: Suppose ${\pi }_1\vee {\pi }_2={\pi }_1\circ {\pi }_2$. Now,

$\begin{array}{ll}{\pi }_2\circ {\pi }_1& \subseteq {\pi }_2\vee {\pi }_1\\ & ={\pi }_1\vee {\pi }_2\\ & ={\pi }_1\circ {\pi }_2\end{array}$

$(iii)⟹(i)$: Suppose ${\pi }_2\circ {\pi }_1\subseteq {\pi }_1\circ {\pi }_2$. Then,

$\begin{array}{ll}({\pi }_2\circ {\pi }_1{)}^{-1}& \subseteq ({\pi }_1\circ {\pi }_2{)}^{-1}\\ {\pi }_1^{-1}\circ {\pi }_2^{-1}& \subseteq {\pi }_2^{-1}\circ {\pi }_1^{-1}\\ {\pi }_1\circ {\pi }_2& \subseteq {\pi }_2\circ {\pi }_1\end{array}$

Therefore, ${\pi }_1\circ {\pi }_2={\pi }_2\circ {\pi }_1$

Definition 4.1.

A fuzzy lattice $(L,\mu )$ is said to be fuzzy congruence modular if Fcon(L) is modular lattice. That is, if ${\pi }_1,{\pi }_2,{\pi }_3\in Fcon(L)$ such that ${\pi }_1\subseteq {\pi }_3$, then ${\pi }_1\vee ({\pi }_2\wedge {\pi }_3)=({\pi }_1\vee {\pi }_2)\wedge {\pi }_3$

Similarly,

Definition 4.2.

A fuzzy lattice $(L,\mu )$ is said to be fuzzy congruence distributive if Fcon(L) is distributive lattice. That is, if ${\pi }_1,{\pi }_2,{\pi }_3\in Fcon(L)$ then, ${\pi }_1\wedge ({\pi }_2\vee {\pi }_3)=({\pi }_1\wedge {\pi }_2)\vee ({\pi }_1\wedge {\pi }_3)$.

Theorem 4.6

If a fuzzy lattice $(L,\mu )$ is fuzzy congruence permutable then $(Fcon(L),\subseteq )$ is modular lattice

Proof. Let ${\pi }_1,{\pi }_2,{\pi }_3\in Fcon(L)$ and suppose ${\pi }_1\subseteq {\pi }_3$. It is clear that ${\pi }_1\vee ({\pi }_2\wedge {\pi }_3)\subseteq ({\pi }_1\vee {\pi }_2)\wedge {\pi }_3$. To show ${\pi }_1\vee ({\pi }_2\wedge {\pi }_3)=({\pi }_1\vee {\pi }_2)\wedge {\pi }_3$ it is enough to show $({\pi }_1\vee {\pi }_2)\wedge {\pi }_3\subseteq {\pi }_1\vee ({\pi }_2\wedge {\pi }_3)$. Again, since Fcon(L) is fuzzy permutable we need to show $({\pi }_1\circ {\pi }_2)\cap {\pi }_3\subseteq {\pi }_1\circ ({\pi }_2\cap {\pi }_3)$. Now, let $x,y\in L$, then

$\begin{array}{ll}({\pi }_1\circ {\pi }_2)\cap {\pi }_3(x,y)& =min[({\pi }_1\circ {\pi }_2)(x,y),{\pi }_3(x,y)]\\ & =min[\underset{z\in L}{sup}[min({\pi }_1(x,z),{\pi }_2(z,y))],\\ & {\pi }_3(x,y)]\\ & =\underset{z\in L}{sup}[min[min({\pi }_1(x,z),{\pi }_2(z,y)),\\ & {\pi }_3(x,z)],{\pi }_3(x,y)]\\ & =\underset{z\in L}{sup}[min[min({\pi }_1(x,z),{\pi }_2(z,y)),\\ & min({\pi }_3(z,x),{\pi }_3(x,y))]]\\ & \le \underset{z\in L}{sup}[min({\pi }_1(x,z),min[{\pi }_2(z,y),\\ & {\pi }_3(z,y)]]\\ & =\underset{z\in L}{sup}[min({\pi }_1(x,z),{\pi }_2\cap {\pi }_3(z,y)]]\\ & ={\pi }_1\circ ({\pi }_2\cap {\pi }_3)(x,y)\end{array}$

Thus, $({\pi }_1\circ {\pi }_2)\cap {\pi }_3\subseteq {\pi }_1\circ ({\pi }_2\cap {\pi }_3)$. Therefore, $(Fcon(L),\subseteq )$ is modular lattice.

Proposition 4.7.

If a fuzzy lattice $(L,\mu )$ is fuzzy congruence permutable then $(Fcon(L),\subseteq )$ is distributive lattice.

Proof. Let ${\pi }_1,{\pi }_2,{\pi }_3\in Fcon(L)$. To show that ${\pi }_1\wedge ({\pi }_2\vee {\pi }_3)=({\pi }_1\wedge {\pi }_2)\vee ({\pi }_1\wedge {\pi }_3)$. Since L is fuzzy congruence permutable then ${\pi }_i\circ {\pi }_j={\pi }_i\vee {\pi }_j$ for all $i,j$. Thus to show Fcon(L) is distributive it is enough to show that ${\pi }_1\cap ({\pi }_2\circ {\pi }_3)=({\pi }_1\cap {\pi }_2)\circ ({\pi }_1\cap {\pi }_3)$. Now let $x,y\in L$. Then,

$\begin{array}{ll}& ({\pi }_1\cap {\pi }_2)\circ ({\pi }_1\cap {\pi }_3)(x,y)\\ & =\underset{z\in L}{sup}[min(({\pi }_1\cap {\pi }_2)(x,z),\\ & ({\pi }_1\cap {\pi }_3)(z,y))]\\ & =\underset{z\in L}{sup}[min(min({\pi }_1(x,z),\\ & {\pi }_2(x,z)),min({\pi }_1(z,y),{\pi }_3(z,y))]\\ & =min[\underset{z\in L}{sup}[min({\pi }_1(x,z),\\ & {\pi }_1(z,y)),min({\pi }_2(x,z),{\pi }_3(z,y))]\\ & =min[\underset{z\in L}{sup}min({\pi }_1(x,z),\\ & {\pi }_1(z,y)),\underset{z\in L}{sup}min({\pi }_2(x,z),{\pi }_3(z,y)]\\ & =min[({\pi }_1\circ {\pi }_1)(x,y),\\ & ({\pi }_2\circ {\pi }_3)(x,y))]\\ & =min[({\pi }_1)(x,y),({\pi }_2\circ {\pi }_3)(x,y)]]\\ & ={\pi }_1\cap ({\pi }_2\circ {\pi }_3)(x,y)\end{array}$

Hence, $({\pi }_1\cap {\pi }_2)\circ ({\pi }_1\cap {\pi }_3)={\pi }_1\cap ({\pi }_2\circ {\pi }_3)$. Therefore, Fcon(L) is distributive.

In the next theorem, we will prove the above theorem without the condition $(L,\mu )$ is fuzzy congruence permutable.

Theorem 4.8

If L is fuzzy lattice. Then, Fcon(L) is distributive.

Proof. Let ${\pi }_1,{\pi }_2,{\pi }_3\in Fcon(L)$. To show that ${\pi }_1\wedge ({\pi }_2\vee {\pi }_3)=({\pi }_1\wedge {\pi }_2)\vee ({\pi }_1\wedge {\pi }_3)$. Since, it is clear that ${\pi }_1\wedge ({\pi }_2\vee {\pi }_3)\supseteq ({\pi }_1\wedge {\pi }_2)\vee ({\pi }_1\wedge {\pi }_3)$ then it is enough to show that ${\pi }_1\wedge ({\pi }_2\vee {\pi }_3)\subseteq ({\pi }_1\wedge {\pi }_2)\vee ({\pi }_1\wedge {\pi }_3)$.

Now let $x,y\in L$. Then,

$\begin{array}{ll}& {\pi }_1\wedge ({\pi }_2\vee {\pi }_3)(x,y)\\ & =min[{\pi }_1(x,y),({\pi }_2\vee {\pi }_3)(x,y)]\\ & =min[{\pi }_1(x,y),\underset{x=c_0,c_1,c_2,\cdots c_n=y\in L}{sup}[min({\pi }_2(x,c_1),{\pi }_3(c_1,c_2),\\ & \cdots ,{\pi }_2(c_{n-1},y)]\\ & =min[\underset{x=c_0,c_1,c_2,\cdots c_n=y\in L}{sup}[min({\pi }_1(x,c_1),{\pi }_1(c_1,c_2),\cdots ,\\ & {\pi }_1(c_{n-1},y),\\ & \underset{x=c_0,c_1,c_2,\cdots c_n=y\in L}{sup}[min({\pi }_2(x,c_1),{\pi }_3(c_1,c_2),\cdots ,{\pi }_2(c_{n-1},y)]\\ & \le \underset{x=c_0,c_1,c_2,\cdots c_n=y\in L}{sup}[min({\pi }_1\wedge {\pi }_2(x,c_1),{\pi }_1\wedge {\pi }_3(c_1,c_2),\\ & \cdots ,{\pi }_1\wedge {\pi }_2(c_{n-1},y)]\\ & =({\pi }_1\wedge {\pi }_2)\vee ({\pi }_1\wedge {\pi }_3)(x,y)\end{array}$

This shows ${\pi }_1\wedge ({\pi }_2\vee {\pi }_3)\subseteq ({\pi }_1\wedge {\pi }_2)\vee ({\pi }_1\wedge {\pi }_3)$. Therefore, Fcon(L) is distributive lattice.

5. Discussion

As explained earlier in the introduction, a lot of authors have attempted to study fuzzy congruence relation on different algebraic structures. So, it is a natural question to extend these concept to the case of fuzzy congruence relation on fuzzy algebraic structures. Hence, the current study presented a novel approach to define fuzzy congruence relation on fuzzy lattice. The earlier publications, on the other hand, focused solely on fuzzy congruence relation on crisp algebraic structures. Additionally, our study showed that there is connection between a fuzzy congruence relation on fuzzy lattice with the congruence relation on a level set. Also, as expected we were able to show that the fuzzy congruence relation we defined here preserve the main properties that the classical congruence relation holds. Furthermore, in this study, we studied the lattice theoretic structure of the fuzzy congruence relations on the fuzzy lattice. Because the concept distributive fuzzy lattice was not thoroughly studied in literature, we are unable to explore the relationship between fuzzy congruence relation and an ideal (or fuzzy ideal) of fuzzy lattice. Because of this, we plan to expand the theory of distributive fuzzy lattice in more depth soon and explore the connection between fuzzy ideals and fuzzy congruences on a distributive fuzzy lattice, just as we found in the classical lattice theory.

One of the algebraic structures that are most extensively used and applied in the fuzzy mathematical theory is certainly the fuzzy congruence structure. Fuzzy congruence theory has several applications that are quite similar to those of the classical congruence theory, including those in physics, business, computer science, coding theory, and other fields. More specifically, congruences and their classes on the ring of integers are important tools in the design of round-robin tournaments (Childs, 1995), fuzzy congruence relations and their classes are important structures in the study of knowledge representation systems (De Baets & Kerre, 1994), congruence arithmetic has many applications in the foundation of modern cryptography in public-key encryption, secret sharing, wireless authentication, and many other applications for data security (Debnath & Mohiuddine, 2021; Nair & Mordeson, 2001; Schroeder, 2008; Yan, 2002).

6. Conclusions

In this paper, we have introduced and studied a new kind of fuzzy congruence relation on a fuzzy lattice, gave an equivalent definition for a fuzzy congruence relation on fuzzy lattice, investigated some of their properties, and also characterized a fuzzy congruence relation using its level set. Moreover, we constructed a lattice of fuzzy congruence relations, and characterize the join and meet of fuzzy congruence relation in the lattice. Finally, we have shown that the lattice of fuzzy congruence relation is complete, distributive lattice and also under certain conditions the lattice becomes a modular lattice.

Acknowledgements

The authors express their gratitude to the anonymous reviewers for providing valuable feedback and suggestions that significantly enhanced the quality of the paper.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Notes on contributors

Sileshe Gone Korma

Sileshe Gone Korma is a PhD scholar at the Department of Mathematics, College of Natural Sciences, Arba Minch University, Ethiopia. His research interest includes fuzzy algebra.