?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.ABSTRACT
This paper deals with the numerical treatment of a singularly perturbed parabolic differential-difference equation with time delay. Taylor’s series expansion is employed to approximate the terms with shift arguments in both spatial and time directions. The resulting problem is discretized using the implicit Euler method and fitted exponential cubic spline methods for time and space variables, respectively. The stability and uniform convergence of the proposed scheme are investigated. The scheme is proved to be uniformly convergent with the order of convergence . A model test problem is considered to validate the applicability and efficiency of the scheme. It is observed that the proposed scheme provides more accurate results than methods available in the literature.
1. Introduction
In this study, we consider the following singularly perturbed parabolic differential-difference equation (SPPDDE) with time delay on the domain of the form:
where and
are the left and right sides of the rectangular domain D corresponding to z = 0 and z = 1, respectively.
.
is a singular perturbation parameter, η is positive shift (advance) parameter, δ and ξ are negative shift (delay) parameters in space and time direction, respectively, and
. The functions
and
on Γ are assumed to be sufficiently smooth, bounded and independent of ɛ.
The model problem (Equation1.1(1.1)
(1.1) ) is used to describe the time evolution trajectories of the membrane potential when ξ = 0 (Musila & Lánsk’y, Citation1991) and used to describe a furnace used to process metal sheets when
(Wang, Citation1963). The dual presence of singular perturbations and shift arguments in both space and time directions in EquationEq. (1.1)
(1.1)
(1.1) increases the difficulty of obtaining oscillation-free solutions by applying classical numerical methods. To solve such types of equations, one can look for non-classical numerical methods. The most common non-classical competitive computational schemes developed for EquationEq. (1.1)
(1.1)
(1.1) and related problems are based on the fitted operator and the fitted mesh approach. For the details of these techniques, one can refer (Doolan et al., Citation1980; Roos et al., Citation2008; Shishkin & Shishkina, Citation2008).
Most of the published works to date have concentrated on singularly perturbed parabolic differential equations with either space delay(s) or time delay, but not both. For instance, the authors in (Daba & Duressa, Citation2021, Citation2021a, Citation2021b, Citation2021c, Citation2022a, Citation2022b, Citation2022c; Kumar, Citation2018; Nageshwar Rao & Chakravarthy, Citation2019; Ramesh & Priyanga, Citation2019) have suggested different computational techniques for singularly perturbed differential equations with delay/and advance parameter(s). In the articles (Govindarao & Mohapatra, Citation2020; Govindarao et al., Citation2019, Citation2019; Gupta et al., Citation2019; Negero & Duressa, Citation2022; Sumit et al., Citation2020), the authors have presented several parameter numerical schemes for singularly perturbed parabolic differential problems with a time lag. Recently, the numerical treatment of coupled systems of multiple scales, a class of singularly perturbed one- and two-dimensional non-smooth data and non-linear problems have been investigated. For example, an a posteriori based convergence analysis for a nonlinear singularly perturbed system of delay differential equations can observe on an adaptive mesh at (Das, Citation2019). A parameter uniform numerical method is developed for a two-parameter singularly perturbed parabolic partial differential equation with discontinuous convection coefficient and source term in (Chandru et al., Citation2019). (Saini et al., Citation2023) have proposed computational cost reduction for a coupled system of multiple-scale reaction-diffusion problems, with mixed-type boundary conditions having boundary layers. (Shiromani et al., Citation2023) have suggested a higher-order hybrid-numerical approximation for a class of singularly perturbed two-dimensional convection-diffusion elliptic problems with non-smooth convection and source terms. In (Srivastava et al., Citation2023), Srivastava et al. have introduced a theoretical study of the fractional-order p-Laplacian nonlinear Hadamard type turbulent flow models having the Ulam-Hyers stability.
More recently (Sahu & Mohapatra, Citation2021), and (Reddy & Mohapatra, Citation2023) have developed an uniform numerical scheme for singularly perturbed differential equations having both mixed shifts in space and delays in time directions. However, as we have seen from the literature survey, very limited competitive numerical methods exist for solving EquationEq. (1.1)
(1.1)
(1.1) . To minimize the observed gap, in this article, a parameter uniformly convergent numerical scheme is proposed for EquationEq. (1.1)
(1.1)
(1.1) .
When , the use of Taylor’s series expansion for the terms containing shift arguments is valid (Tian, Citation2002). Thus, on applying Taylor’s series expansion on the terms with shifts of EquationEq. (1.1)
(1.1)
(1.1) , we have
Substituting EquationEq. (1.2)(1.2)
(1.2) into EquationEq. (1.1)
(1.1)
(1.1) , we obtain
where
The choice of smaller
and ξ EquationEqs. (1.1)
(1.1)
(1.1) and (Equation1.3
(1.3)
(1.3) ) are asymptotically equivalent, because the difference between the two equations is of order of
. Assume that
, for
. For
and
, the problem exhibits a layer near z = 1. For
and
, the problem exhibits a layer near z = 0. Now, we consider the maximum principle and stability of the solution u in (Equation1.3
(1.3)
(1.3) ), which is important for the proposed numerical analysis (Das, Citation2019, Das et al., Citation2019, Das et al., Citation2020, Das et al., Citation2022).
Lemma 1.1.
(Maximum principle) If ,
and
, then
.
Proof.
See (Reddy & Mohapatra, Citation2023).
An immediate consequence of Lemma 1.1 for the solution of problem (Equation1.3(1.3)
(1.3) ) gives the next Lemma 1.2.
Lemma 1.2.
(Continuous stability estimate) Let be the solution of the problem (Equation1.3
(1.3)
(1.3) ), then we have
where is the
norm given by
Proof.
Let be two barrier functions defined by
Then at the initial value
and at the two end points
When we consider the differential operator , on D we have
We have , since
. Using this inequality in the above inequality, we obtain
Hence by Lemma 1.1 we have, , which gives
the proof is complete.
Lemma 1.3.
The bound on the derivative of the solution of the problem in (Equation1.3
(1.3)
(1.3) ) with respect to z is given by
Proof.
See (Das, Citation2015, Citation2018; Das & Vigo-Aguiar, Citation2019; Shakti et al., Citation2022)
2. Formulation of the numerical scheme
2.1. Temporal semi-discretization
We define the uniform mesh for the domain Gt as:
and we approximated the temporal derivative term of (Equation1.3(1.3)
(1.3) ) by employing the implicit Euler method, which gives
Since, EquationEq. (2.1)
(2.1)
(2.1) exhibits boundary located at z = 1 and admits a unique solution.
Lemma 2.1.
(Local Error Estimate) In the solution of EquationEq. (2.1)(2.1)
(2.1) , the local truncation error (LTE) estimate is bounded by
where C is a positive constant independent of ɛ and .
Proof.
On applying Taylor’s series expansion on yields
This implies
Substituting EquationEq. (1.3)(1.3)
(1.3) into EquationEq. (2.2)
(2.2)
(2.2) we have
Subtracting EquationEq. (2.1)(2.1)
(2.1) from EquationEq. (2.3)
(2.3)
(2.3) , and the local truncation error
at
is the solution of a BVP
Hence, applying the maximum principle on the operator gives
Lemma 2.2.
(Global Error Estimate (GEE)) The GEE in the temporal direction of EquationEq. (2.1)(2.1)
(2.1) is given by
Proof.
Using Lemma 2.1, we obtain the following GEE at time step
where are positive constants independent of ɛ and
.
Lemma 2.3.
The solution of the EquationEq. (2.1)
(2.1)
(2.1) is bounded by
Proof.
See (Reddy & Mohapatra, Citation2023).
2.1.1. Spatial discretization
We define the uniform mesh for the space domain as:
EquationEquation (2.1)(2.1)
(2.1) can be rewritten as:
where and
.
For the spatial discretization of EquationEq. (2.5)(2.5)
(2.5) , we use an exponential cubic spline method. The approximation solution
of EquationEq. (2.5)
(2.5)
(2.5) obtained by the segment
passing through the points
and
. Each mixed spline segment
has the form (Das & Natesan, Citation2012, Citation2013; Das et al., Citation2020; Zahra & Ashraf, Citation2013):
where and Di are constants and
is a free parameter that will be used to enhance the accuracy of the method. To find the values of
and Di in EquationEq. (2.6)
(2.6)
(2.6) , let us denote:
Differentiating twice both sides of EquationEq. (2.6)(2.6)
(2.6) , we get
Using the relation in EquationEq. (2.7)(2.7)
(2.7) into (Equation2.8
(2.8)
(2.8) ) at
, we get
and it yields
where and
.
Again, substituting EquationEq. (2.7)(2.7)
(2.7) into (Equation2.8
(2.8)
(2.8) ) at
, we obtain
and it gives
From EquationEqs. (2.9)(2.9)
(2.9) and (Equation2.10
(2.10)
(2.10) ), we have
Taking EquationEq. (2.7)(2.7)
(2.7) into EquationEq. (2.6)
(2.6)
(2.6) at
and
, we obtain
and which implies
The first derivative continuity condition at , that is
gives
where
Now from EquationEq. (2.5)(2.5)
(2.5) , we have
where we approximate and
as
Substituting EquationEq. (2.15)(2.15)
(2.15) into (Equation2.14
(2.14)
(2.14) ), we have
Substituting EquationEq. (2.16)(2.16)
(2.16) into EquationEq. (2.13)
(2.13)
(2.13) and rearranging, we get
To grip the effect of the perturbation parameter ɛ, we multiply the perturbation parameter of Eq.(Equation2.17(2.17)
(2.17) ) by fitting factor
, we obtain
where .
Evaluating the limit of EquationEq. (2.18)(2.18)
(2.18) as
:
When the boundary layer is on the right side of the domain, from the theory of singular perturbation (O’Malley, Citation1974), the solution of EquationEq. (2.5)(2.5)
(2.5) is of the form:
where is the solution of the reduced problem:
Using Taylor’s series expansion for p(z) about the point z = 1 and restricting to their first terms, EquationEq. (2.20)(2.20)
(2.20) becomes
EquationEquation (2.21)(2.21)
(2.21) at
and as
becomes
Plugging the above equations into EquationEq. (2.19)(2.19)
(2.19) , we get
Finally, from EquationEqs. (2.18)(2.18)
(2.18) and (Equation2.23
(2.23)
(2.23) ), we get
where
For sufficiently small mesh sizes the above matrix is non-singular and
(i.e., the matrix is diagonally dominant). Hence, by (Nichols, Citation1989), the matrix ϑ is M-matrix and has an inverse. Therefore, the system of equations can be solved by matrix inverse with the given boundary conditions.
3. Convergence analysis
Lemma 3.1.
(Discrete Maximum Principle) If the discrete function satisfies
, on
. Then
on
implies that
at each point of
Lemma 3.2.
(Discrete Uniform Stability) The solution of the discrete problem (Equation2.24
(2.24)
(2.24) ) at
time level and
, where χ is some positive constant satisfies
Proof.
Let define barrier functions as
where .
On the boundary points, we obtain
Now, on the discretized spatial domain , we have
By Lemma 3.1, we obtain . Hence, the required bound is obtained.
Lemma 3.3.
The local truncation error in space semi-discretization of the discrete problem (Equation2.24(2.24)
(2.24) ) is given as
where C is a positive constant independent of ɛ and .
Proof.
From the truncation error of EquationEq. (2.15)(2.15)
(2.15) , we have
where .
Substituting
into EquationEq. (2.13)(2.13)
(2.13) , we get
Considering the corresponding exact solution to EquationEq. (3.2)(3.2)
(3.2) , we have
Subtracting EquationEq. (3.2)(3.2)
(3.2) from EquationEq. (3.3)
(3.3)
(3.3) and denoting
, for
we arrive at
Inserting EquationEq. (3.1)(3.1)
(3.1) in EquationEq. (3.4)
(3.4)
(3.4) , we obtain
Using the expressions and
in EquationEq. (3.5)
(3.5)
(3.5) , we have
where . Hence, for the choice of
, we obtain
.
The matrix representation of EquationEq. (3.6)(3.6)
(3.6) is
where ,
,
and
.
Following [3], it can be shown that
where C is a constant, independent of and ɛ.
Theorem 3.1.
Let and
be the solution of EquationEqs. (1.1)
(1.1)
(1.1) and (Equation2.24
(2.24)
(2.24) ) at each grid point
, respectively. Then, the following uniform error bound holds
Proof.
By combining the result of Lemmas 2.2 and 3.3 the required bound is obtained.
4. Numerical examples, results and discussion
Some test examples have been presented to illustrate the efficiency of the proposed method. The exact solutions for these problems are unknown for comparison. Therefore, we use the double mesh principle to estimate the error as given in (Gupta et al., Citation2019).
where is the numerical solution with (N, M) mesh points and
is the numerical solution at the finer mesh with
mesh points. The rate of convergence is calculated as
For each N and M, the parameter uniform maximum absolute error and uniform rate of convergence are computed using
Example 4.1.
Consider the following SPPDDE with time lag:
The computed ,
, and
of the considered example using the proposed scheme is depicted in Tables . From these tables, one can observe that the developed scheme converges independently of the perturbation parameter with the first order of convergence. Also, from these Tables, one can see the comparison of the scheme with the results in the articles (Sahu & Mohapatra, Citation2021). The comparison confirms that the scheme provides a more accurate result than some schemes (Sahu & Mohapatra, Citation2021). In Figure , the 3D view of the solution of Example 4.1 is given for visualizing the boundary layer when
,
and
. This figure shows that as
a strong boundary layer is created near z = 1. In Figure , the effect of ɛ and δ on the solution profiles is shown. As one observes, as
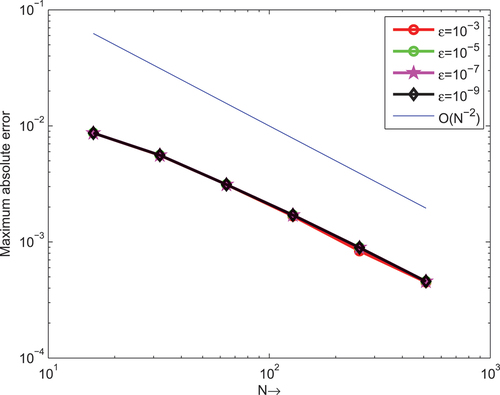
a strong boundary layer is created near z = 1 and the size of the boundary layer increases. Figure shows that as the values of δ increases the width of the boundary layer increases, whereas when the size of η increases, the thickness of the layer decreases (see, Figure ). Figure shows the uniform convergence of the proposed scheme in the Log–Log scale plot for Example 4.1. This figure reveals that the expected numerical order of convergence is correct in rehearsal
Figure 1. 3D view of numerical solution for example 4.1 with .
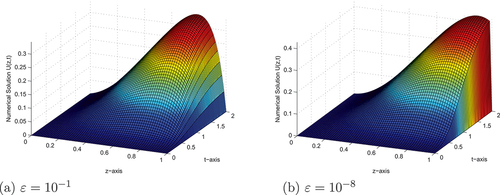
Figure 2. (a), (b) and (c) effect of the and η on the behaviour of the solution with layer formation when
, respectively.
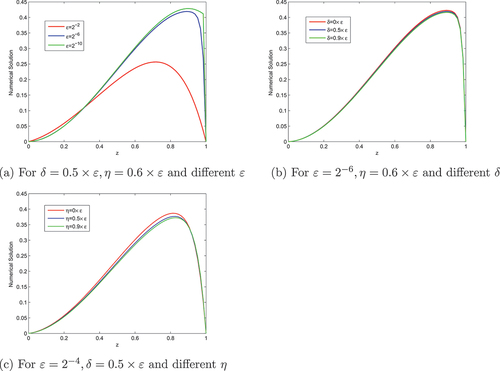
Table 1. and
for example 4.1 using the proposed method and results in (Sahu & Mohapatra, Citation2021) with
Table 2. and
for example 4.1 using the proposed method with
Figure . Example 4.1 Log–Log scale plot of the maximum absolute error for different values of ɛ.
5. Conclusion
A parameter uniform numerical scheme for singularly perturbed parabolic differential-difference equation with delay in time is presented. The developed scheme constitutes the implicit Euler in the time direction and the exponential cubic spline method in the space direction. The stability and parameter uniform convergence of the proposed scheme are investigated. The scheme is shown to be uniformly convergent with a linear order of convergence. A test example is presented to illustrate the efficiency of the proposed scheme. It is observed that the proposed computational technique gives more accurate numerical results than the method in (Sahu & Mohapatra, Citation2021).
Acknowledgements
The authors thankfully acknowledge the prolific comments from the anonymous referees.
Disclosure statement
No potential conflict of interest was reported by the author(s).
Funding
This research did not receive any funding.
Data availability statement
No data were used to support the study.
Additional information
Funding
Notes on contributors
Genanew Gofe Gonfa
Genanew Gofe Gonfa received his Ph.D. in Mathematics from Andhra University, India. He is presently working at Salale University as an associate professor of Mathematics and President, Salale University, Ethiopia. His research interests span on the areas of numerical solutions of differential equations, systems of equations, and singularly perturbed ordinary and partial differential equations. He published more than 13 research articles in national and international reputable journals. In addition, he made numerous contributions in serving as a reviewer, assistant editor, and editor for various national and international reputable journals. So far, he has supervised 40 M.Sc. graduates to completion and currently supervising 8 M.Sc. students.
Imiru Takele Daba
Imiru Takele Daba received his Ph.D. in Mathematics from Wollega University in 2021. His research interests span the areas of numerical solutions of partial differential equations, focusing on singularly perturbed problems. He has published more than 13 research articles in reputable journals. He also made numerous contributions while serving as a reviewer. So far, he has supervised 19 M.Sc. students to completion and currently supervising 8 M.Sc. students.
References
- Chandru, M., Prabha, T., Das, P., & Shanthi, V. (2019). A numerical method for solving boundary and interior layers dominated parabolic problems with discontinuous convection coefficient and source terms. Differential Equations and Dynamical Systems, 27, 91–112. https://doi.org/10.1007/s12591-017-0385-3
- Daba, I. T, & Duressa, G. F. (2021). A hybrid numerical scheme for singularly perturbed parabolic differential-difference equations arising in the modeling of neuronal variability. Computational and Mathematical Methods, 3(5), e1178. https://doi.org/10.1002/cmm4.1178
- Daba, I. T., & Duressa, G. F. (2021a). Extended cubic B-spline collocation method for singularly perturbed parabolic differential-difference equation arising in computational neuroscience. International Journal for Numerical Methods in Biomedical Engineering, 37(2). https://doi.org/10.1002/cnm.3418
- Daba, I. T., & Duressa, G. F. (2021b). Hybrid algorithm for singularly perturbed delay parabolic partial differential equations. Applications and Applied Mathematics: An International Journal (AAM), 16(1), 21.
- Daba, I. T., & Duressa, G. F. (2021c). Uniformly convergent numerical scheme for a singularly perturbed differential-difference equations arising in computational neuroscience. Journal of Applied Mathematics & Informatics, 39(5–6), 655–676.
- Daba, I. T., & Duressa, G. F. (2022a). Collocation method using artificial viscosity for time dependent singularly perturbed differential–difference equations. Mathematics and Computers in Simulation, 192, 201–220. https://doi.org/10.1016/j.matcom.2021.09.005
- Daba, I. T., & Duressa, G. F. (2022b). A novel algorithm for singularly perturbed parabolic differential-difference equations. Research in Mathematics, 9(1), 2133211. https://doi.org/10.1080/27684830.2022.2133211
- Daba, I. T., & Duressa, G. F. (2022c). A robust computational method for singularly perturbed delay parabolic convection-diffusion equations arising in the modeling of neuronal variability. Computational Methods for Differential Equations, 10(2), 475–488.
- Das, P., & Natesan, S. (2012). Higher-order parameter uniform convergent schemes for Robin type reaction-diffusion problems using adaptively generated grid. International Journal of Computational Methods, 9(4), 1250052. https://doi.org/10.1142/S0219876212500521
- Das, P., & Natesan, S. (2013). A uniformly convergent hybrid scheme for singularly perturbed system of reaction-diffusion Robin type boundary-value problems. Journal of Applied Mathematics and Computing, 41, 447–471. https://doi.org/10.1007/s12190-012-0611-7
- Das, P., Rana, S., & Ramos, H. (2019). Homotopy perturbation method for solving Caputo-type fractional-order Volterra-fredholm integro-differential equations. Computational and Mathematical Methods, 1(5), e1047. https://doi.org/10.1002/cmm4.1047
- Das, P., Rana, S., & Ramos, H. (2020). A perturbation-based approach for solving fractional-order Volterra-fredholm integro differential equations and its convergence analysis. International Journal of Computer Mathematics, 97(10), 1994–2014. https://doi.org/10.1080/00207160.2019.1673892
- Das, P., Rana, S., & Ramos, H. (2022). On the approximate solutions of a class of fractional order nonlinear Volterra integro-differential initial value problems and boundary value problems of first kind and their convergence analysis. Journal of Computational and Applied Mathematics, 404, 113116. https://doi.org/10.1016/j.cam.2020.113116
- Das, P., Rana, S., & Vigo-Aguiar, J. (2020). Higher order accurate approximations on equidistributed meshes for boundary layer originated mixed type reaction diffusion systems with multiple scale nature. Applied Numerical Mathematics, 148, 79–97. https://doi.org/10.1016/j.apnum.2019.08.028
- Das, P., & Vigo-Aguiar, J. (2019). Parameter uniform optimal order numerical approximation of a class of singularly perturbed system of reaction diffusion problems involving a small perturbation parameter. Journal of Computational and Applied Mathematics, 354, 533–544. https://doi.org/10.1016/j.cam.2017.11.026
- Das, P. (2015). Comparison of a priori and a posteriori meshes for singularly perturbed nonlinear parameterized problems. Journal of Computational and Applied Mathematics, 290, 16–25. https://doi.org/10.1016/j.cam.2015.04.034
- Das, P. (2018). A higher order difference method for singularly perturbed parabolic partial differential equations. Journal of Difference Equations and Applications, 24(3), 452–477. https://doi.org/10.1080/10236198.2017.1420792
- Das, P. (2019). An a posteriori based convergence analysis for a nonlinear singularly perturbed system of delay differential equations on an adaptive mesh. Numerical Algorithms, 81(2), 465–487. https://doi.org/10.1007/s11075-018-0557-4
- Doolan, E. P., Miller, J. J. H., & Schilders, W. H. A. (1980). Uniform numerical methods for problems with initial and boundary layers. Boole Press.
- Govindarao, L., & Mohapatra, J. (2020). Numerical analysis and simulation of delay parabolic partial differential equation involving a small parameter. Engineering Computations, 37(1), 289–312. https://doi.org/10.1108/EC-03-2019-0115
- Govindarao, L., Sahu, S. R., & Mohapatra, J. (2019). Uniformly convergent numerical method for singularly perturbed time delay parabolic problem with two small parameters. Iranian Journal of Science & Technology, Transactions A: Science, 43(5), 2373–2383. https://doi.org/10.1007/s40995-019-00697-2
- Govindarao, S. R., Mohapatra, J., & Sahu, L. (2019). Uniformly convergent numerical method for singularly perturbed two parameter time delay parabolic problem. International Journal of Applied and Computational Mathematics, 5(3), 1–9. https://doi.org/10.1007/s40819-019-0672-5
- Gupta, V., Kadalbajoo, M. K., & Dubey, R. K. (2019). A parameter-uniform higher order finite difference scheme for singularly perturbed time-dependent parabolic problem with two small parameters. International Journal of Computer Mathematics, 96(3), 474–499. https://doi.org/10.1080/00207160.2018.1432856
- Kumar, D. (2018). An implicit scheme for singularly perturbed parabolic problem with retarded terms arising in computational neuroscience. Numerical Methods for Partial Differential Equations, 34(6), 1933–1952. https://doi.org/10.1002/num.22269
- Musila, M., & Lánsk’y, P. (1991). Generalized stein’s model for anatomically complex neurons. BioSystems, 25(3), 179–191. https://doi.org/10.1016/0303-2647(91)90004-5
- Nageshwar Rao, R., & Chakravarthy, P. (2019). Fitted numerical methods for singularly perturbed one-dimensional parabolic partial differential equations with small shifts arising in the modelling of neuronal variability. Differential Equations and Dynamical Systems, 27(1–3), 1–18. https://doi.org/10.1007/s12591-017-0363-9
- Negero, N. T., & Duressa, G. F. (2022). An efficient numerical approach for singularly perturbed parabolic convection-diffusion problems with large time-lag. Journal of Mathematical Modeling, 10(2), 173–190.
- Nichols, N. (1989). On the numerical integration of a class of singular perturbation problems. Journal of Optimization Theory and Applications, 60(3), 2050034. https://doi.org/10.1007/BF00940347
- O’Malley, J. R. E. (1974). Introduction to singular perturbations. Technical report. New York Univ Ny Courant Inst of Mathematical Sciences. https://apps.dtic.mil/sti/citations/AD0787833.
- Ramesh, V. P., & Priyanga, B. (2019). Higher order uniformly convergent numerical algorithm for time-dependent singularly perturbed differential-difference equations. Differential Equations and Dynamical Systems, 29(1), 239–263. https://doi.org/10.1007/s12591-019-00452-4
- Reddy, N. R., & Mohapatra, J. (2023). A robust numerical scheme for singularly perturbed delay parabolic initial-boundary value problems involving mixed space shifts. Computational Methods for Differential Equations, 11(1), 42–51.
- Roos, H.-G., Martin, S., & Tobiska, L. (2008 24). Robust numerical methods for singularly perturbed differential equations: Convection-diffusion-reaction and flow problems. Springer Science & Business Media.
- Sahu, S. R., & Mohapatra, J. (2021). Numerical study of time delay singularly perturbed parabolic differential equations involving both small positive and negative space shift. Journal of Applied Analysis, 28(1), 121–134. https://doi.org/10.1515/jaa-2021-2064
- Saini, S., Das, P., & Kumar, S. (2023). Computational cost reduction for coupled system of multiple scale reaction diffusion problems with mixed type boundary conditions having boundary layers. Revista de la Real Academia de Ciencias Exactas Físicas y Naturales Serie A Matemáticas, 117(2), 66. https://doi.org/10.1007/s13398-023-01397-8
- Shakti, D., Mohapatra, J., Das, P., & Vigo-Aguiar, J. (2022). A moving mesh refinement based optimal accurate uniformly convergent computational method for a parabolic system of boundary layer originated reaction?diffusion problems with arbitrary small diffusion terms. Journal of Computational and Applied Mathematics, 404, 113167. https://doi.org/10.1016/j.cam.2020.113167
- Shiromani, R., Shanthi, V., & Das, P. (2023). A higher order hybrid-numerical approximation for a class of singularly perturbed two-dimensional convection-diffusion elliptic problem with non-smooth convection and source terms. Computers & Mathematics with Applications, 142, 9–30. https://doi.org/10.1016/j.camwa.2023.04.004
- Shishkin, G. I., & Shishkina, L. P. (2008). Difference methods for singular perturbation problems. CRC Press.
- Srivastava, H. M., Nain, A. K., Vats, R. K., & Das, P. (2023). A theoretical study of the fractional-order p-Laplacian nonlinear hadamard type turbulent flow models having the ulam-Hyers stability. Revista de la Real Academia de Ciencias Exactas Físicas y Naturales Serie A Matemáticas, 117(4), 160. https://doi.org/10.1007/s13398-023-01488-6
- Sumit, K., Kuldeep, S., Kumar, M., & Kumar, M. (2020). A robust numerical method for a two-parameter singularly perturbed time delay parabolic problem. Computational & Applied Mathematics, 39(3). https://doi.org/10.1007/s40314-020-01236-1
- Tian, H. (2002). The exponential asymptotic stability of singularly perturbed delay differential equations with a bounded lag. Journal of Mathematical Analysis and Applications, 270(1), 143–149. https://doi.org/10.1016/S0022-247X(02)00056-2
- Wang, P. K. C. (1963). Asymptotic stability of a time-delayed diffusion system. Journal of Applied Mechanics, 30(4), 500–504. https://doi.org/10.1115/1.3636609
- Zahra, W. K., & Ashraf, M. E. M. (2013). Numerical solution of two-parameter singularly perturbed boundary value problems via exponential spline. Journal of King Saud University-Science, 25(3), 201–208. https://doi.org/10.1016/j.jksus.2013.01.003