First irregularity Sombor index of trees with fixed maximum degree

ABSTRACT

The Sombor index as a new degree-based topological index was first put forward in 2021 by Gutman. Recently, Kulli introduced a variant of the Sombor index called first irregularity Sombor index. The first irregularity Sombor index of a graph G, denoted by $\mathit{IS}{O}_1(\mathit{G})$, is defined as the sum of weights $|d_G^2(\mathit{v})-d_G^2(\mathit{w})|$ of all edges vw of E(G), where $d_G(\mathit{v})$ denotes the degree of a node v in G. In this paper we show that for any tree T of order n with maximum degree Δ,

$\mathit{IS}{O}_1\left(\mathit{T}\right)\ge \{\begin{array}{l}(\mathrm{△}-1)\sqrt{{\mathrm{△}}^2-1}+\sqrt{{\mathrm{△}}^2-4}+\sqrt{3}\mathit{if}\mathrm{△}<\mathit{n}-1,\\ \mathrm{△}\sqrt{{\mathrm{△}}^2-1}\mathit{if}\mathrm{△}=\mathit{n}-1.\end{array}$

We also characterize the extremal trees.

KEYWORDS:

• First irregularity Sombor index
• lower bound
• trees

MATHEMATICS SUBJECT CLASSIFICATION:

• 05C07

1. Introduction

Let G be a simple graph of order n. The node and edge sets of G are shown by V(G) and E(G), respectively. For $\mathit{w}\in \mathit{V}(\mathit{G})$, the open neighborhood of w in G, $N_G(\mathit{w})$, is the set $N_G(\mathit{w})=\{\mathit{v}\in \mathit{V}(\mathit{G})\mid \mathit{wv}\in \mathit{E}(\mathit{G})\}$. The degree of a node $\mathit{w}\in \mathit{V}(\mathit{G})$ is $d_G(\mathit{w})=|N_G(\mathit{w})|$. We consider $\mathrm{\Delta }(\mathit{G})=\mathrm{\Delta }$ as the maximum degree of G. The distance between two nodes of G is the length of any shortest path in G connecting them.

In the last decade, some variants of topological indices introduced, such as multiplicative Zagreb indices (Gutman, 2011; Xu & Hua, 2012), irregularity (Ali et al., 2021; Azari et al., 2023; Ma et al., 2019; Yousaf et al., 2020; Zhou & Luo, 2008), Zagreb coindices (Ashrafi et al., 2010; Došlić, 2008; Gutman et al., 2015; Rasi et al., 2017), Lanzhou index (Dehgardi & Liu, 2021; Vukičević et al., 2018), eccentricity index (Akhter & Farooq, 2020; Farooq et al., 2022, 2023), etc. One of such variants is the Sombor index which was introduced by Gutman (Gutman, 2021) as:

$\mathit{SO}(\mathit{G})=\sum _{\mathit{vw}\in \mathit{E}(\mathit{G})}\sqrt{d_G^2(\mathit{v})+d_G^2(\mathit{w})}.$

Recently, some novel variants of Sombor index introduced, such as the reduced Sombor index, multiplicative Sombor index, KG-Sombor index, first irregularity Sombor index, etc. For more information about variants of the Sombor see (Cruz & Rada, 2021; Das & Shang, 2021; Das et al., 2021; Došlić et al., 2021; Gutman et al., 2022; Kosari et al., 2023; Kulli, 2021; Kulli & Gutman, 2021; Liu et al., 2021; Ramane et al., 2023; Shang, 2022) and the references therein.

In this paper we focus on first irregularity Sombor index. The first irregularity Sombor index defined as:

$\mathit{IS}{O}_1(\mathit{G})=\sum _{\mathit{vw}\in \mathit{E}(\mathit{G})}\sqrt{|d_G^2(\mathit{v})-d_G^2(\mathit{w})|}.$

We obtain a lower bound on the first irregularity Sombor index of trees with given their nodes number and maximum degree. Finally, we determine the extremal trees achieve this bound.

2. Trees with minimum first irregularity Sombor index

A tree is a connected acyclic graph. A node of degree one of a tree is called a leaf. A node adjacent to a leaf and a node adjacent to at least two leaves are called support node and strong support node respectively. A rooted tree is a tree with a special node chosen as the root of the tree.

A starlike is a tree with one node of degree at least three. The node with degree at least three in a starlike is called the center. The leg of a starlike is a path from the center node to a leaf. A star is a starlike with all legs of length one. Also the path is a starlike with one or two leg.

In this section, T denote a tree rooted at x such that $d_T(\mathit{x})=\mathrm{\Delta }$. Also, ${\mathcal{T}}_{\mathit{n},\mathrm{\Delta }}$, is the set of all trees with n nodes and maximum degree Δ.

Lemma 1.

If $\mathit{T}\in {\mathcal{T}}_{\mathit{n},\mathrm{\Delta }}$ contains a node of degree greater than two except x, then there is $T^{\ast }\in {\mathcal{T}}_{\mathit{n},\mathrm{\Delta }}$ such that $\mathit{IS}{O}_1(T^{\ast })<\mathit{IS}{O}_1(\mathit{T})$.

Proof.

Assume that y is a node with maximum distance from x such that $d_T(\mathit{y})=\mathit{\lambda }\ge 3$. Let $N_T(\mathit{y})=\{y_1,y_2,\dots ,y_{\mathit{\lambda }}\}$ such that y_λ lies on the path from y to x and $d_T(y_{\mathit{\lambda }})=\mathit{\ell }$. Consider the following cases.

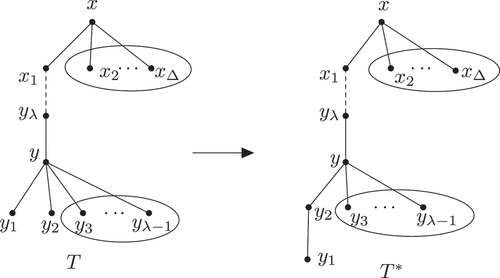
Case 1. y is a strong support node of T.

Let y₁ and y₂ be two leaves. Denote by $T^{\ast }$ the tree achieved by attaching the edge $y_1{y}_2$ to $\mathit{T}-\{\mathit{y}{y}_1\}$ (see Figure 1). Hence

$\begin{array}{ll}\mathit{IS}{O}_1(\mathit{T})-\mathit{IS}{O}_1(T^{\ast })& \mathit{ }=\sum _{\mathit{vw}\in \mathit{E}(\mathit{T})}\sqrt{|d_T^2(\mathit{v})-d_T^2(\mathit{w})|}-\sum _{vw\in E(T^{\ast })}\sqrt{|d_{T^{\ast }}^2(\mathit{v})-d_{T^{\ast }}^2(\mathit{w})|}\\ \mathit{ }=\sum _{\mathit{i}=3}^{\mathit{\lambda }-1}\sqrt{|d_T^2(\mathit{y})-d_T^2(y_i)|}+\sqrt{|d_T^2(\mathit{y})-d_T^2(y_{\mathit{\lambda }})|}\\ +\sqrt{|d_T^2(\mathit{y})-d_T^2(y_1)|}+\sqrt{|d_T^2(\mathit{y})-d_T^2(y_2)|}\\ -\sum _{\mathit{i}=3}^{\mathit{\lambda }-1}\sqrt{|d_{T^{\ast }}^2(\mathit{y})-d_{T^{\ast }}^2(y_i)|}-\sqrt{|d_{T^{\ast }}^2(\mathit{y})-d_{T^{\ast }}^2(y_{\mathit{\lambda }})|}\\ -\sqrt{|d_{T^{\ast }}^2(\mathit{y})-d_{T^{\ast }}^2(y_2)|}-\sqrt{|d_{T^{\ast }}^2(y_2)-d_{T^{\ast }}^2(y_1)|}\\ \mathit{ }=\sum _{\mathit{i}=3}^{\mathit{\lambda }-1}\sqrt{{\lambda }^2-d_T^2(y_i)}+\sqrt{|{\lambda }^2-{\ell }^2|}+\sqrt{{\lambda }^2-1}+\sqrt{{\lambda }^2-1}\\ -\sum _{\mathit{i}=3}^{\mathit{\lambda }-1}\sqrt{(\mathit{\lambda }-1{)}^2-d_{T^{\ast }}^2(y_i)}-\sqrt{|(\mathit{\lambda }-1{)}^2-{\ell }^2|}\\ -\sqrt{(\mathit{\lambda }-1{)}^2-4}-\sqrt{3}\\ \mathit{ }\ge 2\sqrt{{\lambda }^2-1}+\sqrt{|{\lambda }^2-{\ell }^2|}-\sqrt{|(\mathit{\lambda }-1{)}^2-{\ell }^2|}\\ -\sqrt{(\mathit{\lambda }-1{)}^2-4}-\sqrt{3}.\end{array}$

If $\mathit{\lambda }>\mathit{\ell }$, then

$\begin{array}{l}\mathit{IS}{O}_1(\mathit{T})-\mathit{IS}{O}_1(T^{\ast })\ge 2\sqrt{{\lambda }^2-1}+\sqrt{{\lambda }^2-{\ell }^2}\\ -\sqrt{(\mathit{\lambda }-1{)}^2-{\ell }^2}-\sqrt{(\mathit{\lambda }-1{)}^2-4}-\sqrt{3}>0.\end{array}$

Now let $\mathit{\lambda }\le \mathit{\ell }$. Then

$\begin{array}{ll}\sqrt{|{\lambda }^2-{\ell }^2|}& \mathit{ }-\sqrt{|(\mathit{\lambda }-1{)}^2-{\ell }^2|}=\sqrt{{\ell }^2-{\lambda }^2}\\ \mathit{ }-\sqrt{{\ell }^2-(\mathit{\lambda }-1{)}^2}\ge -\sqrt{2\mathit{\lambda }-1}.\end{array}$

Since $\mathit{\lambda }\ge 3$, then we have

$\begin{array}{ll}\mathit{IS}{O}_1(\mathit{T})& \mathit{ }-\mathit{IS}{O}_1(T^{\ast })\ge 2\sqrt{{\lambda }^2-1}+\sqrt{{\ell }^2-{\lambda }^2}\\ \mathit{ }-\sqrt{{\ell }^2-(\mathit{\lambda }-1{)}^2}-\sqrt{(\mathit{\lambda }-1{)}^2-4}-\sqrt{3}\\ \mathit{ }\ge 2\sqrt{{\lambda }^2-1}-\sqrt{2\mathit{\lambda }-1}-\sqrt{(\mathit{\lambda }-1{)}^2-4}\\ \mathit{ }-\sqrt{3}>0.\end{array}$

Figure 1. Case 1.

Case 2. y is a support node of T.

We can assume that, y₁ be a leaf and $\mathit{y}{z}_1{z}_2\dots z_k$ be a path in T such that $\mathit{k}\ge 2$ and $z_1=y_2$. Let $T^{\ast }$ be the tree derived from $\mathit{T}-\{\mathit{y}{y}_1\}$ by adding the path $z_k{y}_1$ (see Figure 2). then

$\begin{array}{ll}\mathit{IS}{O}_1(\mathit{T})-\mathit{IS}{O}_1(T^{\ast })=& \mathit{ }\sum _{\mathit{vw}\in \mathit{E}(\mathit{T})}\sqrt{|d_T^2(\mathit{v})-d_T^2(\mathit{w})|}-\sum _{vw\in E(T^{\ast })}\sqrt{|d_{T^{\ast }}^2(\mathit{v})-d_{T^{\ast }}^2(\mathit{w})|}\\ =& \mathit{ }\sum _{\mathit{i}=2}^{\mathit{\lambda }-1}\sqrt{|d_T^2(\mathit{y})-d_T^2(y_i)|}+\sqrt{|d_T^2(\mathit{y})-d_T^2(y_{\mathit{\lambda }})|}\\ \mathit{ }+\sqrt{|d_T^2(\mathit{y})-d_T^2(y_1)|}+\sqrt{|d_T^2(z_k)-d_T^2(z_{\mathit{k}-1})|}\\ \mathit{ }-\sum _{\mathit{i}=2}^{\mathit{\lambda }-1}\sqrt{|d_{T^{\ast }}^2(\mathit{y})-d_{T^{\ast }}^2(y_i)|}-\sqrt{|d_{T^{\ast }}^2(\mathit{y})-d_{T^{\ast }}^2(y_{\mathit{\lambda }})|}\\ \mathit{ }-\sqrt{|d_{T^{\ast }}^2(z_{\mathit{k}})-d_{T^{\ast }}^2(y_1)|}-\sqrt{|d_{T^{\ast }}^2(z_{\mathit{k}})-d_{T^{\ast }}^2(z_{\mathit{k}-1})|}\\ =& \mathit{ }\sum _{\mathit{i}=2}^{\mathit{\lambda }-1}\sqrt{{\lambda }^2-d_T^2(y_i)}+\sqrt{|{\lambda }^2-{\ell }^2|}+\sqrt{{\lambda }^2-1}+\sqrt{3}\\ \mathit{ }-\sum _{\mathit{i}=2}^{\mathit{\lambda }-1}\sqrt{(\mathit{\lambda }-1{)}^2-d_{T^{\ast }}^2(y_i)}-\sqrt{|(\mathit{\lambda }-1{)}^2-{\ell }^2|}-\sqrt{3}\\ \ge & \sqrt{{\lambda }^2-1}+\sqrt{|{\lambda }^2-{\ell }^2|}-\sqrt{|(\mathit{\lambda }-1{)}^2-{\ell }^2|}.\end{array}$

If $\mathit{\lambda }>\mathit{\ell }$, then

$\begin{array}{ll}\mathit{IS}{O}_1(\mathit{T})-\mathit{IS}{O}_1(T^{\ast })\ge & \sqrt{{\lambda }^2-1}+\sqrt{{\lambda }^2-{\ell }^2}\\ \mathit{ }-\sqrt{(\mathit{\lambda }-1{)}^2-{\ell }^2}>0.\end{array}$

Now let $\mathit{\lambda }\le \mathit{\ell }$. Then

$\begin{array}{ll}\mathit{IS}{O}_1(\mathit{T})-\mathit{IS}{O}_1(T^{\ast })\ge & \sqrt{{\lambda }^2-1}+\sqrt{{\ell }^2-{\lambda }^2}\\ \mathit{ }-\sqrt{{\ell }^2-(\mathit{\lambda }-1{)}^2}\\ \ge & \sqrt{{\lambda }^2-1}-\sqrt{2\mathit{\lambda }-1}>0.\end{array}$

Figure 2. Case 2.

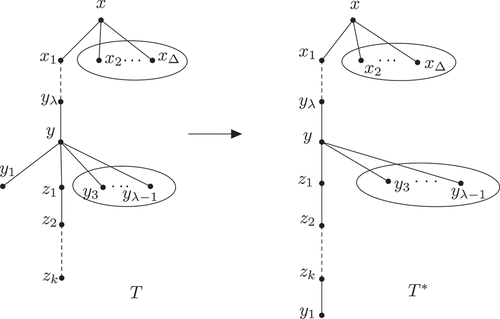
Case 3. All nodes adjacent to y are of degree at least two.

Let $\mathit{y}{v}_1{v}_2\dots v_{\mathit{t}}$ and $\mathit{y}{u}_1{u}_2\dots u_s$ be two paths in T such that $\mathit{t},\mathit{s}\ge 2$, $v_1=y_1$ and $u_1=y_2$. Assume $T^{\ast }$ be the tree derived from $\mathit{T}-\{\mathit{y}{y}_1\}$ by adding the path $u_s{v}_1\dots v_t$ (see Figure 3). Then

$\begin{array}{ll}\mathit{IS}{O}_1(\mathit{T})-\mathit{IS}{O}_1(T^{\ast })=& \mathit{ }\sum _{\mathit{vw}\in \mathit{E}(\mathit{T})}\sqrt{|d_T^2(\mathit{v})-d_T^2(\mathit{w})|}-\sum _{vw\in E(T^{\ast })}\sqrt{|d_{T^{\ast }}^2(\mathit{v})-d_{T^{\ast }}^2(\mathit{w})|}\\ =& \mathit{ }\sum _{\mathit{i}=2}^{\mathit{\lambda }-1}\sqrt{|d_T^2(\mathit{y})-d_T^2(y_i)|}+\sqrt{|d_T^2(\mathit{y})-d_T^2(y_{\mathit{\lambda }})|}\\ \mathit{ }+\sqrt{|d_T^2(\mathit{y})-d_T^2(y_1)|}+\sqrt{|d_T^2(u_{\mathit{s}})-d_T^2(u_{\mathit{s}-1})|}\\ \mathit{ }-\sum _{\mathit{i}=2}^{\mathit{\lambda }-1}\sqrt{|d_{T^{\ast }}^2(\mathit{y})-d_{T^{\ast }}^2(y_i)|}-\sqrt{|d_{T^{\ast }}^2(\mathit{y})-d_{T^{\ast }}^2(y_{\mathit{\lambda }})|}\\ \mathit{ }-\sqrt{|d_{T^{\ast }}^2(u_{\mathit{s}})-d_{T^{\ast }}^2(y_1)|}-\sqrt{|d_{T^{\ast }}^2(u_{\mathit{s}})-d_{T^{\ast }}^2(u_{\mathit{s}-1})|}\\ =& \mathit{ }\sum _{\mathit{i}=2}^{\mathit{\lambda }-1}\sqrt{{\lambda }^2-d_T^2(y_i)}+\sqrt{|{\lambda }^2-{\ell }^2|}+\sqrt{{\lambda }^2-4}+\sqrt{3}\\ \mathit{ }-\sum _{\mathit{i}=2}^{\mathit{\lambda }-1}\sqrt{(\mathit{\lambda }-1{)}^2-d_{T^{\ast }}^2(y_i)}-\sqrt{|(\mathit{\lambda }-1{)}^2-{\ell }^2|}\\ \ge & \sqrt{{\lambda }^2-4}+\sqrt{3}+\sqrt{|{\lambda }^2-{\ell }^2|}-\sqrt{|(\mathit{\lambda }-1{)}^2-{\ell }^2|}.\end{array}$

If $\mathit{\lambda }>\mathit{\ell }$, then

$\begin{array}{ll}\mathit{IS}{O}_1(\mathit{T})-\mathit{IS}{O}_1(T^{\ast })\ge & \sqrt{{\lambda }^2-4}+\sqrt{3}+\sqrt{{\lambda }^2-{\ell }^2}\\ \mathit{ }-\sqrt{(\mathit{\lambda }-1{)}^2-{\ell }^2}>0.\end{array}$

Now let $\mathit{\lambda }\le \mathit{\ell }$. Then

$\begin{array}{ll}\mathit{IS}{O}_1(\mathit{T})-\mathit{IS}{O}_1(T^{\ast })\ge & \sqrt{{\lambda }^2-4}+\sqrt{3}+\sqrt{{\ell }^2-{\lambda }^2}\\ \mathit{ }-\sqrt{{\ell }^2-(\mathit{\lambda }-1{)}^2}\\ \ge & \sqrt{{\lambda }^2-4}+\sqrt{3}-\sqrt{2\mathit{\lambda }-1}>0.\end{array}$

This completes the proof.

Figure 3. Case 3.

Lemma 2.

Let $\mathit{T}\in {\mathcal{T}}_{\mathit{n},\mathrm{\Delta }}$ be a starlike with $\mathrm{\Delta }\ge 3$. If T has at least two legs of length greater than one, then there exists a starlike $T^{\ast }\in {\mathcal{T}}_{\mathit{n},\mathrm{\Delta }}$ such that $\mathit{IS}{O}_1(T^{\ast })<\mathit{IS}{O}_1(\mathit{T})$.

Proof.

Let T be a starlike with center x and $N_T(\mathit{x})=\{x_1,x_2,\dots ,x_{\mathrm{\Delta }}\}$. Assume that $\mathit{x}{y}_1{y}_2\dots y_t$, $\mathit{x}{z}_1{z}_2\dots z_s$, $(\mathit{s},\mathit{t}\ge 2)$ be two legs of length greater than one in T such that $x_1=y_1$ and $x_2=z_1$. Suppose that $T^{\ast }$ be the tree derived from $\mathit{T}-\{y_1{y}_2\}$ by attaching the path $z_s{y}_2\dots y_t$. Hence

$\begin{array}{ll}\mathit{IS}{O}_1(\mathit{T})-\mathit{IS}{O}_1(T^{\ast })=& \mathit{ }\sum _{\mathit{vw}\in \mathit{E}(\mathit{T})}\sqrt{|d_T^2(\mathit{v})-d_T^2(\mathit{w})|}-\sum _{vw\in E(T^{\ast })}\sqrt{|d_{T^{\ast }}^2(\mathit{v})-d_{T^{\ast }}^2(\mathit{w})|}\\ =& \mathit{ }\sum _{\mathit{i}=2}^{\mathrm{\Delta }}\sqrt{|d_T^2(\mathit{x})-d_T^2(x_i)|}+\sqrt{|d_T^2(y_1)-d_T^2(y_2)|}\\ \mathit{ }+\sqrt{|d_T^2(\mathit{x})-d_T^2(x_1)|}+\sqrt{|d_T^2(z_{\mathit{s}})-d_T^2(z_{\mathit{s}-1})|}\\ \mathit{ }-\sum _{\mathit{i}=2}^{\mathrm{\Delta }}\sqrt{|d_{T^{\ast }}^2(\mathit{x})-d_{T^{\ast }}^2(x_i)|}-\sqrt{|d_{T^{\ast }}^2(\mathit{x})-d_{T^{\ast }}^2(x_1)|}\\ \mathit{ }-\sqrt{|d_{T^{\ast }}^2(z_{\mathit{s}})-d_{T^{\ast }}^2(y_2)|}-\sqrt{|d_{T^{\ast }}^2(z_{\mathit{s}})-d_{T^{\ast }}^2(z_{\mathit{s}-1})|}\\ =& \mathit{ }\sum _{\mathit{i}=2}^{\mathrm{\Delta }}\sqrt{{\mathrm{\Delta }}^2-d_T^2(x_i)}+\sqrt{3}+\sqrt{{\mathrm{\Delta }}^2-4}+\sqrt{d_T^2(y_1)-d_T^2(y_2)}\\ \mathit{ }-\sum _{\mathit{i}=2}^{\mathrm{\Delta }}\sqrt{{\mathrm{\Delta }}^2-d_T^2(x_i)}-\sqrt{d_{T^{\ast }}^2(z_{\mathit{s}})-d_{T^{\ast }}^2(y_2)}-\sqrt{{\mathrm{\Delta }}^2-1}\\ =& \sqrt{3}+\sqrt{{\mathrm{\Delta }}^2-4}+\sqrt{d_T^2(y_1)-d_T^2(y_2)}-\sqrt{d_{T^{\ast }}^2(z_{\mathit{s}})-d_{T^{\ast }}^2(y_2)}\\ \mathit{ }-\sqrt{{\mathrm{\Delta }}^2-1}.\end{array}$

If t = 2, then

$\sqrt{d_{T^{\ast }}^2(z_{\mathit{s}})-d_{T^{\ast }}^2(y_2)}=\sqrt{d_T^2(y_1)-d_T^2(y_2)}=\sqrt{3},$

and if $\mathit{t}\ge 3$, then

$\sqrt{d_{T^{\ast }}^2(z_{\mathit{s}})-d_{T^{\ast }}^2(y_2)}=\sqrt{d_T^2(y_1)-d_T^2(y_2)}=0.$

Therefore

$\begin{array}{ll}\mathit{IS}{O}_1(\mathit{T})-\mathit{IS}{O}_1(T^{\ast })=& \sqrt{{\mathrm{\Delta }}^2-4}+\sqrt{3}-\sqrt{{\mathrm{\Delta }}^2-1}>0.\end{array}$

This completes the proof.

Now we ready to prove the main theorem of this paper.

Theorem 3.

For any tree $\mathit{T}\in {\mathcal{T}}_{\mathit{n},\mathrm{\Delta }}$ of order $\mathit{n}\ge 3$,

$\mathit{IS}{O}_1(\mathit{T})⩾\{\begin{array}{ll}(\mathrm{\Delta }-1)\sqrt{{\mathrm{\Delta }}^2-1}+\sqrt{{\mathrm{\Delta }}^2-4}+\sqrt{3}& \mathrm{if}\mathrm{\Delta }<\mathit{n}-1,\\ \mathrm{\Delta }\sqrt{{\mathrm{\Delta }}^2-1}& \mathrm{if}\mathrm{\Delta }=\mathit{n}-1.\end{array}$

The equality holds if and only if T is a starlike with at most one leg of length greater than one.

Proof.

Let $T^{\prime }\in {\mathcal{T}}_{\mathit{n},\mathrm{\Delta }}$ be a tree with $\mathit{IS}{O}_1(T^{\prime })\le \mathit{IS}{O}_1(\mathit{T})$ for every $\mathit{T}\in {\mathcal{T}}_{\mathit{n},\mathrm{\Delta }}$. Assume x be a root node of T^ʹ such that $d_{T^{\prime }}(\mathit{x})=\mathrm{\Delta }$. If $\mathrm{\Delta }=2$, then T is a path and

$\mathit{IS}{O}_1(\mathit{T})=2\sqrt{3}=(\mathrm{\Delta }-1)\sqrt{{\mathrm{\Delta }}^2-1}+\sqrt{{\mathrm{\Delta }}^2-4}+\sqrt{3},$

as desired. Let $\mathrm{\Delta }\ge 3$. By the selection of T^ʹ and Lemma 1, T^ʹ is a starlike with center x. By Lemma 2, T^ʹ has at most one leg of length greater than one. If T^ʹ be a star, then $\mathit{IS}{O}_1(T^{\prime })=\mathrm{\Delta }\sqrt{{\mathrm{\Delta }}^2-1}$. Now let T^ʹ have only one leg of length greater than one. Thus

$\mathit{IS}{O}_1(T^{\prime })=(\mathrm{\Delta }-1)\sqrt{{\mathrm{\Delta }}^2-1}+\sqrt{{\mathrm{\Delta }}^2-4}+\sqrt{3}.$

This completes the proof.

See Figure 4, three trees of orders $\mathit{n}=5,6,7$, maximum degree 4 and with minimum first irregularity Sombor index.

Figure 4. Trees with $\mathit{n}=5,6,7\text{and}\mathrm{\Delta }=4$.

Author contribution statement

Nasrin Dehgardi: Conceptualization; Investigation; Methodology; Validation; Writing original draft. Yilun Shang: Visualization; Investigation; Validation; Resources; Funding acquisition; Writing review and editing.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Data availability statement

The paper does not include or use any datasets.

Supplementary material

Supplemental data for this article can be accessed online at https://doi.org/10.1080/27684830.2023.2291933