Load parameter identification of wind turbine rotor involving probability and interval variables

ABSTRACT

Knowledge of the load parameters of wind turbine rotor is the key problem to eliminate the misalignment of wind turbine. In this paper, an inverse method for identifying the load parameters with imprecise information is investigated by using the probability and interval variables. The interval variables are dealt with interval analysis, only the bounds of the structure response are needed avoiding time-consuming inner loop for structure response prediction. The probability variables are dealt with a proposed iteration method combined micro genetic algorithm with the search interval advance and retreat method. Firstly, at the midpoint of the interval variables, the mean of the load parameters is identified based on the proposed iteration method; secondly, the first-order Taylor expansion is employed to gain the boundary of rotor dynamic response from predicting structure response strip derived from the existence of interval variables; thirdly, the interval of the load parameters is identified via the boundary of rotor dynamic response based on the proposed iteration method. Eventually, the accuracy and efficiency of the proposed inverse method are verified by one numerical example.

KEYWORDS:

• Wind turbine rotor
• load parameter
• uncertain parameter identification
• maximum likelihood method
• probability and interval variables

MATHEMATICS SUBJECT CLASSIFICATIONS:

• 93B30
• 93B40

1. Introduction

The knowledge of load parameters that lead to the misalignment of the wind turbine rotor is always required to eliminate the fan misalignment [1–3]. However, its measurement with force actuators is a difficult task in many instances. Instead, vibration responses can be conveniently measured. The technique of load parameters identification, an important indirect method aimed at estimating load parameters via measured vibration responses, is often preferred in many mechanical engineering practices [4]. Most of the existing load parameters identification is executed for deterministic problems, where the structure parameters and measured vibration responses are completely known. However, due to manufacturing errors, measurement inaccuracy, the discreteness of thin silicon steel sheet material and incomplete knowledge, this information is only partly known in the real wind turbine rotor. Namely, the measured vibration responses are also variable and random mostly corrupted by the measurement errors; meanwhile, the vibration responses are a distribution strip rather than a single distribution because of the existence of the uncertain structure parameters. This kind of problem is unable to be sorted as in traditional deterministic load parameters identification. We term them as mixed uncertainty problems in this study. Due to uncertainties, the identified load parameters via vibration response strip are a distribution strip rather than a single distribution, where the inner loop is uncertain structure response prediction and the outer loop is an inverse calculation in the solving process. The accuracy of identified results can hardly be evaluated using traditional deterministic methods. Therefore, uncertainty-based load parameters identification is an emerging research topic and a more computationally challenging exercise as well.

As the most popular uncertainty modelling strategy, interval method, probability method and evidence theory method [5–7] have been widely applied in engineering for uncertain parameter identification. Hang Wei [8] developed a probability and interval estimation method to assess the probability distributions of unknown parameters through the Monte Carlo Markov Chain method (MCMC) in Bayesian theory [9–11] considering their prior information. The maximum likelihood estimation method [12,13] also has been successfully developed to identify the probability distributions of unknown parameters without considering the prior information. The maximum likelihood estimation method is to determine the unknown parameters through the relationship between the calculated and the measured response of investigated structure by the iteration method, the parameters corresponding to the maximum likelihood function are taken as the identified results, and the corresponding confidence interval is calculated [12]. Compared to MCMC, the maximum likelihood estimation method has a good prospect in the wind turbine rotor system, where the misalignment fault is the coupling influence of multiple load parameters [14], it is difficult for engineers to understand the prior information of load parameters based on experience. However, a commonly encountered difficulty in the maximum likelihood estimation method is that the phenomenon of iterative divergence rather than convergence often occurs because of the sensitivity of the initial value [13]. Therefore, the iterative method should be proposed for identifying the load parameters with probabilistic uncertainty.

Uncertain parameters are mainly described by interval or probability. Structural response strip coming from the interval uncertainty makes the nested solution of the load parameters identification problem have a large amount of computation. The maximum likelihood method to deal with the probability uncertainty is often faced with low efficiency due to the complexity of the likelihood function. Meanwhile, in practical engineering, only the bounds of load parameters are needed to eliminate the fan misalignment. In order to solve the above problems, the load parameters identification under uncertainty is improved in this paper. An inverse method is presented to identify the load parameters of the wind turbine rotor system involving probability and interval variables. The upper and lower bound of structure response coming from interval uncertainty are predicted by the Taylor expansion method and the interval analysis method; A proposed iteration method based on the search interval advance and retreat method (ARM) [15] and micro genetic algorithm (uGA) [16] is used to deal with the probabilistic uncertainty in load parameter identification of the wind turbine rotor system. In the proposed iteration method, the initial load parameter starts from zero, the iterative increment is obtained by the sensitive matrix method and maximum likelihood method, the search space is obtained by ARM, and uGA is used to minimize the deviation between the measured and calculated structure response in the corresponding search space. If the deviation is within the predefined toleration, the set of load parameters is considered to be the total solution to the load parameter identification problem, and the solution procedure ends. The proposed iteration method avoids the stringent requirements of the traditional iterative method on the search space and improves the identification accuracy of the maximum likelihood method.

2. The basic idea of load parameter identification with uncertainty

The dynamic equation of a wind turbine rotor system with misalignment fault [17] is (1) $\mathbf{\text{M}}\ddot{q}+\mathbf{\text{C}}\dot{q}+\text{(}{\mathbf{\text{K}}}_{\mathbf{\text{z}}}\mathbf{\text{+ }}{\mathbf{\text{K}}}_{\mathbf{\text{1}}}\text{)}q=\mathbf{\text{Q + }}{\mathbf{\text{F}}}_{\mathbf{\text{r}}}\mathbf{\text{+ G}}$(1) where q, $\dot{q}$, $\ddot{q}$ are the displacement, velocity and acceleration response vectors, M, ${\mathbf{\text{K}}}_Z$ and C respectively represent the whole structural mass, stiffness and damping matrix which can be established by using the Euler–Bernoulli beam theory in [18]; ${\mathbf{\text{K}}}_1$ denotes the equivalent stiffness matrix of the coupling misalignment; G denotes the Gravity vector; Q denotes the unbalanced force vector and ${\mathbf{\text{F}}}_r$ denotes the misaligned load vector.

If the model-related matrix $\left(\mathbf{\text{M}},{\mathbf{\text{K}}}_Z,{\mathbf{\text{K}}}_1,\mathbf{\text{C}}\right)$ and force-related vector $\left(\mathbf{\text{Q}},\mathbf{\text{G}}\right)$ are complete known constant; ${\mathbf{\text{F}}}_r=[F_{r1},F_{r2,}\cdots ,F_{rn}]$ is a n-dimensional vector of input parameters representing the external causes; $\mathbf{\text{q}}=[q_1,q_2,\dots ,q_m$ is an m-dimensional vector of output parameters representing the effects. A structural mechanics problem among the input ${\mathbf{\text{F}}}_r$ and the output $\mathbf{\text{q}}$ in Equation (1) can be conceptually expressed as follows [19]: (2) $\mathbf{\text{q}}=\mathbf{\text{H}}\left({\mathbf{\text{F}}}_r,\mathbf{\text{MK}},\mathbf{\text{QG}}\right){\mathbf{\text{F}}}_r$(2) where $\mathbf{\text{MK}}$ represents the model-related matrix $\left(\mathbf{\text{M}},{\mathbf{\text{K}}}_Z,{\mathbf{\text{K}}}_1,\mathbf{\text{C}}\right)$; $\mathbf{\text{QG}}$ represents force-related vector $\left(\mathbf{\text{Q}},\mathbf{\text{G}}\right)$; $\mathbf{\text{H}}\left({\mathbf{\text{F}}}_r\text{,}\mathbf{\text{MK}}\text{,}\mathbf{\text{QG}}\right)$ is an m × n system characteristics matrix representing the translation process from input ${\mathbf{\text{F}}}_r$ to output q. It is derived from the physical laws underlying the problem under consideration. Matrix $\mathbf{\text{H}}$ may be dependent on the input ${\mathbf{\text{F}}}_r$ for the wind turbine rotor system with misalignment fault.

That is, a specific input load parameter ${\mathbf{\text{F}}}_r$ corresponds to a corresponding output response $\mathbf{\text{q}}$. According to the type of information be sought in the solution procedure from Equation (2), we traditionally treated the structural mechanics problem among the input ${\mathbf{\text{F}}}_r$ and the output q as either a forward problem or an identification problem. The forward problem is to find out the effect ($\mathbf{\text{q}}$) from the given cause (${\mathbf{\text{F}}}_r$) combined with the known model-related matrix $\mathbf{\text{MK}}$ and force-related vector $\mathbf{\text{QG}}$ utilizing dynamic analysis solution techniques including FEM [20], generalized differential quadrature method [21], transfer matrix method [22], etc. The identification problem is to determine the unknown cause (${\mathbf{\text{F}}}_r$) from the given effect ($\mathbf{\text{q}}$) combining with the known model-related matrix $\mathbf{\text{MK}}$ and force-related vector $\mathbf{\text{QG}}$ utilizing computational reverse techniques including optimization method [23], regularization method [24], etc. However, a commonly encountered difficulty in solving identification problems is that it is often unable to provide a complete known $\mathbf{\text{q}}$, model-related matrix $\mathbf{\text{MK}}$ and force-related vector $\mathbf{\text{QG}}$ because of the existence of measurement noise and model uncertainty. That is, the effect ($\mathbf{\text{q}}$) and the model-related matrix $\mathbf{\text{MK}}$ and force-related vector $\mathbf{\text{QG}}$ are only partly known. We term the problem is treated as a mixed uncertainty problem in this study. A deterministic identification method in a traditional sense is difficult to quantitatively evaluate the credibility of the identified results. Thus, the identified result should also present a certain extent of uncertainty.

To deal with these difficulties in identifying the load parameters ${\mathbf{\text{F}}}_r$ of the wind turbine rotor, a mixed uncertainty analysis framework is suggested to deal with the uncertain parameters coming from the model-related matrix $\mathbf{\text{MK}}$, force-related vector $\mathbf{\text{QG}}$ and the effect ($\mathbf{\text{q}}$) in this paper. This brings up a new approach to solve the mix uncertainty problem, where the probability and interval theory is introduced to deal with the uncertain parameters, all the uncertain parameters in the model-related matrix $\mathbf{\text{MK}}$, force-related vector $\mathbf{\text{QG}}$ and the effect ($\mathbf{\text{q}}$) are as either probability or interval variables. Referring to the mathematical expression of the forward problem in [25], Equation (2) involving probability and interval variables, aimed at estimating the displacement response vectors $\mathbf{\text{q}}$ via a given vector ${\mathbf{\text{F}}}_r$, can be expressed as follows: (3) $\{\begin{array}{rl}\mathbf{\text{q}}& =\mathbf{\text{Y}}({\mathbf{\text{F}}}_r,\mathbf{\text{E}},\mathit{\eta }){\mathbf{\text{F}}}_r\overline{\mathbf{\text{q}}}=\mathbf{\text{q}}+{\mathbf{\text{e}}}_r\\ q_i& =y_i\left({\mathbf{\text{F}}}_r,\mathbf{\text{E}},\mathit{\eta }\right){\mathbf{\text{F}}}_r{\overline{q}}_i=q_i+e_{ri}\end{array}$(3) where $\mathbf{\text{E}}$ and $\mathit{\eta }$ respectively represent a vector that collects all interval and probabilistic uncertain parameters from the model-related matrix $\mathbf{\text{MK}}$ and force-related vector $\left(\mathbf{\text{Q}},\mathbf{\text{G}}\right)$. Probabilistic uncertain parameters obey a zero-mean Gaussian distribution with a variance ${\sigma }_k^{xi}$; Y is a characteristics matrix representing the uncertainty translation process from input ${\mathbf{\text{F}}}_r$ to output $\mathbf{\text{q}}$ for a wind turbine rotor system with interval and probabilistic uncertain parameters. $\mathbf{\text{q}}$ denotes the calculated structure response from the given input ${\mathbf{\text{F}}}_r$ and the established matrix Y, the $\mathbf{\text{q}}$ will be a response strip because of the interval uncertain parameters $\mathbf{\text{E}}$; $\overline{\mathbf{\text{q}}}$ denotes the measured response in the experiment with noise vector ${\mathbf{\text{e}}}_r$ drawn from a zero-mean Gaussian distribution with a variance ${\sigma }^2$, the measurement noise from an experiment is described by probabilistic variables. $q_i\in \mathbf{\text{q}},{\overline{q}}_i\in \overline{\mathbf{\text{q}}},e_{ri}\in {\mathbf{\text{e}}}_r$ respectively denote calculated structure response, the measured response and measurement noise at the $i\text{th}$ specific measurement location. $y_i\left({\mathbf{\text{F}}}_r,\mathbf{\text{E}},\mathit{\eta }\right)$ is a characteristics matrix representing the uncertainty translation process from input ${\mathbf{\text{F}}}_r$ to output $q_i$ at the $i\text{th}$ specific measurement location.

Referring to Bayesian identification [8] for uncertain structures with Gaussian distribution, the general Bayesian identification for Equation (3), aimed at estimating the ${\mathbf{\text{F}}}_r$ via giving the m-point measured response $\overline{\mathbf{\text{q}}}=[{\overline{q}}_1,{\overline{q}}_{2,}\cdots ,{\overline{q}}_m]$ can be written as follows: (4) $p\left({\mathbf{\text{F}}}_r|\overline{\mathbf{\text{q}}}\right)\propto p\left({\mathbf{\text{F}}}_r\right)p(\overline{\mathbf{\text{q}}}|{\mathbf{\text{F}}}_r,\mathbf{\text{E}},\mathit{\eta },{\sigma }^2)=\frac{p\left({\mathbf{\text{F}}}_r\right)}{{\left(2\pi {\sigma }^2\right)}^{m/\phantom{m2}2}}\exp \left(-\frac{1}{2{\sigma }^2}\cdot \sum _{i=1}^m{({\overline{q}}_i-q_i)}^2\right)$(4) where ${\mathbf{\text{F}}}_r=[F_{r1},F_{r2,}\cdots ,F_{rn}]$ is n-unknown load parameters, which would be determined; $p\left({\mathbf{\text{F}}}_r\right)$ denotes the prior probability density of ${\mathbf{\text{F}}}_r$, and is often considered as constants in given prior parameter spaces; $p(\overline{\mathbf{\text{q}}}|{\mathbf{\text{F}}}_r,\mathbf{\text{E}},\mathit{\eta },{\sigma }^2)$ is defined as the data likelihood, and can be regarded as a measure of how well fit the measured response data $\overline{\mathbf{\text{q}}}$; $p\left({\mathbf{\text{F}}}_r|\overline{\mathbf{\text{q}}}\right)$ is the joint posterior probability density distribution (PPDF) of ${\mathbf{\text{F}}}_r$; m denotes the number of the measured point.

As the mechanism of the Bayesian identification approach, the prior knowledge of $p\left({\mathbf{\text{F}}}_r\right)$ is updated with the data likelihood of $p(\overline{\mathbf{\text{q}}}|{\mathbf{\text{F}}}_r,\mathbf{\text{E}},\mathit{\eta },{\sigma }^2)$ to achieve the current knowledge of $p\left({\mathbf{\text{F}}}_r|\overline{\mathbf{\text{q}}}\right)$. In the present engineering practice, we are typically interested in the marginal probability density distribution (PPDF) of each unknown load parameter. Theoretically, this would require integrating Equation (4) over the other j−1 load parameters. The marginal PPDF $p\left(F_{rj}|\overline{\mathbf{\text{q}}}\right)$ of the $j\text{th}$ unknown load parameters $F_{rj}$ is (5) $p\left(F_{rj}|\overline{\mathbf{\text{q}}}\right)={\int }_{R^{n-1}}p\left({\mathbf{\text{F}}}_r|\overline{\mathbf{\text{q}}}\right)d{\mathbf{\text{F}}}_{r-j}\propto {\int }_{R^{n-1}}a\cdot \exp \left(-\frac{1}{2{\sigma }^2}\cdot \sum _{i=1}^m{({\overline{q}}_i-q_i)}^2\right)d{\mathbf{\text{F}}}_{r-j}$(5) where ${\int }_{R^{n-1}}p\left({\mathbf{\text{F}}}_r|\overline{\mathbf{\text{q}}}\right)d{\mathbf{\text{F}}}_{r-j}$ denotes the multidimensional integral over all parameters other than ${\mathbf{\text{F}}}_{r-j}$; a is constant.

Equation (5) show that the uncertainty-based load parameter identification is a double-loop computational procedure, where the inner loop is executed for uncertain response prediction, the outer loop is to determine the load parameter ${\mathbf{\text{F}}}_r$ via response $\overline{\mathbf{\text{q}}}$. But there are three main problems in this solution procedure. First, the marginal PPDF $p\left(F_{rj}|\overline{\mathbf{\text{q}}}\right)$ will form a distribution strip rather than a single distribution due to the response strip resulting from the existing interval parameters $\mathbf{\text{E}}$. Second, the multidimensional integral cannot be done directly in an implicit form due to the complexity of the likelihood function. Third, the prior probability density $p\left({\mathbf{\text{F}}}_r\right)$ is often unable to be provided as required in a traditional Bayesian approach. The traditional MCMC of the Bayesian approach to determine the load parameter ${\mathbf{\text{F}}}_r$ by solving Equation (4) will involve a complex multi-layer nesting solution affecting the computational efficiency. Therefore, an appropriate inverse method should be developed to deal with these difficulties.

3. A proposed inverse method with mixed uncertainty

According to the interval mathematics theory, due to the existence of interval uncertain parameters $\mathbf{\text{E}}$, the marginal posterior distribution $p\left(F_{rj}|\overline{\mathbf{\text{q}}}\right)$ will be formed the following interval vector instead of a real number vector, the marginal PPDF in Equation (5) can be written as follows: (6) $p(F_{rj}|\overline{\mathbf{\text{q}}}{)}^s=\left[p^l\left(F_{rj}|{\overline{\mathbf{\text{q}}}}^l\right),p^r\left(F_{rj}|{\overline{\mathbf{\text{q}}}}^r\right)\right],\mathbf{\text{E}}\in \left[{\mathbf{\text{E}}}^l,{\mathbf{\text{E}}}^r\right]$(6) where $p(F_{rj}|\overline{\mathbf{\text{q}}}{)}^s$ denotes a closed bounded set of real numbers, the superscript s denotes an interval, the superscripts l and r denote the lower and upper bounds of interval, respectively. $p^l\left(F_{rj}|{\overline{\mathbf{\text{q}}}}^l\right)$ and $p^r\left(F_{rj}|{\overline{\mathbf{\text{q}}}}^r\right)$ are the lower and upper bounds of $p(F_{rj}|\overline{\mathbf{\text{q}}}{)}^s$, respectively. ${\overline{\mathbf{\text{q}}}}^l$ and ${\overline{\mathbf{\text{q}}}}^r$ respectively denote the lower and upper response bounds caused by all possible structural responses because of interval uncertain parameters $\mathbf{\text{E}}$ in terms of Equation (3); ${\mathbf{\text{E}}}^l$ and ${\mathbf{\text{E}}}^r$ respectively represent the lower and upper bounds of interval uncertain parameters $\mathbf{\text{E}}$.

In this situation, the mean ${\mathbf{\text{F}}}_r^c$ of the unknown load parameters is no longer the only value but has a variety of possible results, and all the results are concentrated in the interval vector. Similarly, the confidence interval of unknown load parameters is no longer the only interval but has a variety of possible results, and all the interval results are concentrated in the interval vector. The mean value and confidence interval of unknown load parameters obtained by Bayesian parameter identification are interval forms. According to the Bayesian parameter identification method, in order to obtain the maximum and minimum values of mean and confidence interval of unknown load parameters, all possible values of interval uncertain parameters $\mathbf{\text{E}}$ should be selected sequentially, and, the MCMC method is used to sample in the joint PPDF strip, and the maximum and minimum values of mean and confidence interval are searched in the identification results. The process of Bayesian parameter identification will involve complex multi-layer nesting solution, and the forward problem calculation in Equation (2) needs to be called repeatedly, which will inevitably lead to low efficiency of solution.

In this paper, a proposed inverse method combined with rotor dynamic response prediction and a proposed iteration method is introduced to improve the Bayesian parameter identification method, and the boundary of structural response strip coming from interval uncertain parameters $\mathbf{\text{E}}$ is predicted by Taylor expansion and interval mathematical theory. Combining the predicted structure response bound together with the probability uncertain parameters $\mathit{\eta }$ into the proposed iteration method to calculate the corresponding mean and interval of the unknown load parameters.

3.1. The boundary of rotor dynamic response prediction with interval uncertainty

The interval uncertain parameters $\mathbf{\text{E}}$ is described in the form of midpoint ${\mathbf{\text{E}}}^c$-radius ${\mathbf{\text{E}}}^w$ [26]. Which means that the possible values of each interval parameter belong to an interval. Thus, for a specific ${\mathbf{\text{F}}}_r$, the possible values of the output vector $\overline{\mathbf{\text{q}}}$ will form the following interval vector instead of a single vector: (7) $\overline{\mathbf{\text{q}}}\in {\overline{\mathbf{\text{q}}}}^s=[{\overline{\mathbf{\text{q}}}}^l,{\overline{\mathbf{\text{q}}}}^r]$(7) where response strip ${\overline{\mathbf{\text{q}}}}^s$ is an interval vector. ${\overline{\mathbf{\text{q}}}}^l$ and ${\overline{\mathbf{\text{q}}}}^r$ are the lower bound and the upper bound of response strip ${\overline{\mathbf{\text{q}}}}^s$. Equation (7) created a new deterministic relation between the input load parameters ${\mathbf{\text{F}}}_r$ and the output interval vector ${\overline{\mathbf{\text{q}}}}^s$, namely a specific ${\mathbf{\text{F}}}_r$ corresponds to a deterministic interval vector ${\overline{\mathbf{\text{q}}}}^s$ In other words, the unknown load parameters ${\mathbf{\text{F}}}_r$ can be identified via interval vector ${\overline{\mathbf{\text{q}}}}^s$.

When the level of uncertainty is small, the lower bound ${\overline{\mathbf{\text{q}}}}^l$ and the upper bound ${\overline{\mathbf{\text{q}}}}^r$ can be predicted directly and explicitly by first-order Taylor expansion at the midpoint ${\mathbf{\text{E}}}^c$ of the interval uncertain parameters $\mathbf{\text{E}}$ (8) $\{\begin{array}{rl}{\overline{\mathbf{\text{q}}}}^c& =\mathbf{\text{Y}}({\mathbf{\text{F}}}_r^c\mathbf{\text{,}}{\mathbf{\text{E}}}^c,\mathit{\eta }){\mathbf{\text{F}}}_r^c+{\mathbf{\text{e}}}_r\\ {\overline{\mathbf{\text{q}}}}^l& =\underset{\mathbf{\text{E}}\in \mathbf{\Gamma }}{min}\overline{\mathbf{\text{q}}}={\overline{\mathbf{\text{q}}}}^c-\sum _{h=1}^o\left|\frac{\mathrm{\partial }{\overline{\mathbf{\text{q}}}}^c}{\mathrm{\partial }\mathbf{\text{E}}{}_h}\right|\delta {\mathbf{\text{E}}}_h\\ {\overline{\mathbf{\text{q}}}}^r& =\underset{\mathbf{\text{E}}\in \mathbf{\Gamma }}{max}\overline{\mathbf{\text{q}}}={\overline{\mathbf{\text{q}}}}^c+\sum _{h=1}^o\left|\frac{\mathrm{\partial }{\overline{\mathbf{\text{q}}}}^c}{\mathrm{\partial }\mathbf{\text{E}}{}_h}\right|\delta {\mathbf{\text{E}}}_h\end{array}$(8) where ${\mathbf{\text{E}}}_h$ denotes the $h\text{th}$ interval uncertain parameters, o denotes the number of interval uncertain parameters $\mathbf{\text{E}}$. The response ${\overline{\mathbf{\text{q}}}}^c$ can be obtained directly combining the mean ${\mathbf{\text{F}}}_r^c$ together with the midpoint ${\mathbf{\text{E}}}^c$ of the interval uncertain parameters and the established matrix Y according to Equations (8). The partial differential equation $\mathrm{\partial }{\overline{\mathbf{\text{q}}}}^c/\mathrm{\partial }\mathbf{\text{E}}{}_h$ is transformed into an algebraic equation $\mathrm{\partial }{\overline{\mathbf{\text{q}}}}^c/\mathrm{\partial }\mathbf{\text{E}}{}_h=\mathrm{\Delta }{\overline{\mathbf{\text{q}}}}^c/\mathrm{\Delta }\mathbf{\text{E}}{}_h$ using the difference method, the response increment $\mathrm{\Delta }{\overline{\mathbf{\text{q}}}}^c$ is obtained by a small disturbance $\mathrm{\Delta }\mathbf{\text{E}}{}_h$ at the midpoint ${\mathbf{\text{E}}}^c$. The output vector ${\overline{\mathbf{\text{q}}}}^l$, ${\overline{\mathbf{\text{q}}}}^r$ is predicted through Equations (8) based on the interval analysis, which avoids the problem of time-consuming inner loop for structure response prediction.

According to the monotonicity analysis theory [27], the maximum and minimum values of the mean value of the unknown load parameters must correspond to the boundary of the uncertain parameters $\mathbf{\text{E}}$ in the interval of the model. Namely, the MCMC method is used to sample and solve the boundary of $p(F_{rj}|\overline{\mathbf{\text{q}}}{)}^s$ corresponding to the structural response boundary and the mean ${\mathbf{\text{F}}}_r^c$ of the unknown load parameters obtained by MCMC sampling corresponding to the midpoint ${\mathbf{\text{E}}}^c$ can be used as the midpoint of the mean interval. The improved framework of the Bayesian identification method based on the interval analysis can obviously reduce the computational burden. However, the problem of mass sampling also exists to obtain a high-precision joint PPDF space in the sampling process of MCMC due to probability distribution coming from the probabilistic uncertain parameters $\mathit{\eta }$. The maximum likelihood method can transform the Bayesian identification method into an iterative method by introducing the sensitivity matrix method that explicitly dealing with the relation between the input unknown parameter vector ${\mathbf{\text{F}}}_r$ and the probabilistic uncertain parameters $\mathit{\eta }$. The explicit method avoids the mass sampling process of MCMC, but the iterative efficiency is low coming from the unknown priori information of load parameters and the sensitivity of the initial value. Therefore, the iterative method should be proposed for the identifying the load parameters with probabilistic uncertainty.

3.2. A proposed iteration method with the probabilistic uncertainty

To overcome this iterative efficiency, a proposed iteration method combined with uGA and ARM is introduced, where the initial value starts from zero; The increment $\mathbf{\text{B}}$ of load parameters ${\mathbf{\text{F}}}_r$ is obtained based on the sensitivity matrix method, which can transform the probability uncertain parameters into explicit solvable form avoiding MCMC sampling; The search interval in each iterative step is obtained by ARM; uGA is used to gradually correct the solution of load parameters ${\mathbf{\text{F}}}_r$ in an iterative procedure until the error between the measured response and calculated response is within the specified toleration.

Assume the variation $\mathrm{\Delta }{\mathbf{\text{F}}}_r$ and $\mathrm{\Delta }\mathit{\eta }$, combining them together with ${\mathbf{\text{E}}}^c$ into Equations (3) to calculate the variation $\mathrm{\Delta }{\overline{\mathbf{\text{q}}}}_k$ and $\mathrm{\Delta }{\overline{\mathbf{\text{q}}}}_u$ of the output response of the corresponding k-measured point and u-concern point. Calculate the sensitivity matrix $\mathbf{\text{S}}$ centering on the present parameters $\left\{\mathrm{\Delta }{\mathbf{\text{F}}}_r,\mathrm{\Delta }\mathit{\eta },\mathrm{\Delta }{\overline{\mathbf{\text{q}}}}_k,\mathrm{\Delta }{\overline{\mathbf{\text{q}}}}_u\right\}$ using the sensitivity matrix-based method [19], draw the sensitivity matrix $\left\{{\mathbf{\text{S}}}_{11},{\mathbf{\text{S}}}_{12},{\mathbf{\text{S}}}_{21},{\mathbf{\text{S}}}_{22}\right\}$ from the sensitivity matrix $\mathbf{\text{S}}$ according to Equation (9). The increment $\mathbf{\text{B}}$ of the unknown load parameter ${\mathbf{\text{F}}}_r$ is obtained according to the maximum likelihood method shown in Equation (10). (9) $\left[\begin{array}{c}\mathrm{\Delta }{\overline{\mathbf{\text{q}}}}_u\\ \mathrm{\Delta }{\overline{\mathbf{\text{q}}}}_k\end{array}\right]=\left[\begin{array}{cc}{\mathbf{\text{S}}}_{\text{11}}& {\mathbf{\text{S}}}_{\text{12}}\\ {\mathbf{\text{S}}}_{\text{21}}& {\mathbf{\text{S}}}_{\text{22}}\end{array}\right]\left[\begin{array}{c}\mathrm{\Delta }{\mathbf{\text{F}}}_r\\ \mathrm{\Delta }\mathit{\eta }\end{array}\right]$(9) where the subscripts k and u denote the number of measured points and concern points; $\mathrm{\Delta }{\overline{\mathbf{\text{q}}}}_k$ and $\mathrm{\Delta }{\overline{\mathbf{\text{q}}}}_u$ denote the variation of the output response ${\overline{\mathbf{\text{q}}}}_k$ and ${\overline{\mathbf{\text{q}}}}_u$ corresponding to the measured point and concern point, respectively. $\mathrm{\Delta }{\mathbf{\text{F}}}_r$ is the variation of the unknown load parameter ${\mathbf{\text{F}}}_r$; $\mathrm{\Delta }\mathit{\eta }$ is the variation of the known probability uncertain parameter $\mathit{\eta }$. (10) $\mathbf{\text{B}}=({\mathbf{\text{A}}}_w^T{\mathbf{\text{A}}}_w{)}^{-1}{\mathbf{\text{A}}}_w^T{\mathbf{\text{D}}}_w$(10) where ${\mathbf{\text{A}}}_w=\mathbf{\text{WA}}$, $\mathbf{\text{A}}=\left[\begin{array}{cc}\mathbf{\text{I}}& \mathbf{\text{- }}{\mathbf{\text{S}}}_{11}\\ \mathbf{\text{O}}& {\mathbf{\text{S}}}_{21}\end{array}\right]$, ${\mathbf{\text{D}}}_w=\mathbf{\text{WD}}$, $\mathbf{\text{D}}=\left[\begin{array}{c}{\mathbf{\text{S}}}_{12}\mathrm{\Delta }\mathit{\eta }\\ {\overline{\mathbf{\text{q}}}}_k\text{ - }{\mathbf{\text{S}}}_{22}\mathrm{\Delta }\mathit{\eta }\end{array}\right]$ $\mathbf{\text{W}}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(1\text{/}{\sigma }_{\text{1}},1\text{/}{\sigma }_{\text{2}}\right)$, ${\sigma }_1^2,{\sigma }_2^2$ are variances, and ${\sigma }_k^{xi},{\sigma }_k^{yi}$ are the deviations of the $i^{th}$ parameter in the known probability uncertain parameter $\mathit{\eta }$ and measured response ${\overline{\mathbf{\text{q}}}}_k$. ${\sigma }_1^2={\mathbf{\text{S}}}_{12}^2({\sigma }_k^{xi}{)}^2$, ${\sigma }_2^2=({\sigma }_k^{yi}{)}^2+{\mathbf{\text{S}}}_{12}^2({\sigma }_k^{xi}{)}^2$. $\mathbf{\text{I}}$ and $\mathbf{\text{O}}$ denotes the unit matrix and zero matrix, respectively.

Taking the increment $\mathbf{\text{B}}$ of the unknown load parameter value ${\mathbf{\text{F}}}_{r,f}$ as the step size in the $f\text{th}$ iterative step, the corresponding search interval $[{\mathbf{\text{F}}}_{r,f}^l,{\mathbf{\text{F}}}_{r,f}^r]$ is obtained by using the ARM shown in Equation (11). In the $f\text{th}$ iterative step, ${\mathbf{\text{H}}}_{\mathbf{\text{0}}}$ is the initial step size, and ${\mathbf{\text{F}}}_{r1}$, ${\mathbf{\text{F}}}_{r2}$, ${\mathbf{\text{F}}}_{r3}$ is the initial point, intermediate point and end point taken by the unknown load parameter ${\mathbf{\text{F}}}_r$, respectively. ${\mathrm{e}\mathrm{y}}_1,{\mathrm{e}\mathrm{y}}_2,{\mathrm{e}\mathrm{y}}_3$ is the mean square deviation between the output response ${\overline{\mathbf{\text{q}}}}_{mp}$ (the measured rotor dynamic response ${\overline{\mathbf{\text{q}}}}_k$ or predicted ${\overline{\mathbf{\text{q}}}}^l$, ${\overline{\mathbf{\text{q}}}}^r$) in the measured point and the corresponding calculated result ${\mathbf{\text{q}}}_{rp}$ through Equation (11). ${\mathbf{\text{F}}}_{r,f}^l$ and ${\mathbf{\text{F}}}_{r,f}^r$ are the lower and upper bounds of the obtained search interval, respectively.

The uGA is used to search the unknown load parameter value ${\mathbf{\text{F}}}_{r,f+1}$ corresponding to the minimum error between the calculated and measured response in the search interval $[{\mathbf{\text{F}}}_{r,f}^l,{\mathbf{\text{F}}}_{r,f}^r]$. If the error is within the predefined toleration, the set of load parameters ${\mathbf{\text{F}}}_{r,f+1}$ is considered to be the total solution to the problem, and the solution procedure ends. Otherwise, the load parameter value ${\mathbf{\text{F}}}_{r,f+1}$ enters the next iteration as the update of the new unknown load parameter value, and the solution procedure continues. (11) $\{\begin{array}{c}{\mathbf{\text{H}}}_{\mathbf{\text{0}}}=\mathbf{\text{B}},{\mathbf{\text{F}}}_{r2}={\mathbf{\text{F}}}_{r1}+{\mathbf{\text{H}}}_{\mathbf{\text{0}}}\\ {\mathbf{\text{q}}}_{rp}=\mathbf{\text{Y}}({\mathbf{\text{F}}}_{rp}\mathbf{\text{,}}{\mathbf{\text{E}}}^c,\mathit{\eta }){\mathbf{\text{F}}}_{rp},p=1,2,3\\ {\text{ey}}_{\mathbf{\text{1}}}=\text{norm}({\mathbf{\text{q}}}_{r1}-{\overline{\mathbf{\text{q}}}}_{mp}),\\ \text{e}{\text{y}}_{\mathbf{\text{2}}}=\text{norm}({\mathbf{\text{q}}}_{r2}-{\overline{\mathbf{\text{q}}}}_{mp})\\ if{\text{ ey}}_{\mathbf{\text{1}}}>\text{e}{\text{y}}_{\mathbf{\text{2}}}\text{ Move to the right}\\ {\mathbf{\text{F}}}_{r3}={\mathbf{\text{F}}}_{r2}+2{\mathbf{\text{H}}}_{\mathbf{\text{0}}}\\ else{\text{ ey}}_{\mathbf{\text{1}}}<\text{e}{\text{y}}_{\mathbf{\text{2}}}\text{ back to the left}\\ {\mathbf{\text{F}}}_{r2}={\mathbf{\text{F}}}_{r1},{\text{ ey}}_{\mathbf{\text{2}}}=\text{e}{\text{y}}_1\\ {\mathbf{\text{F}}}_{r3}={\mathbf{\text{F}}}_{r2}-2{\mathbf{\text{H}}}_{\mathbf{\text{0}}}\\ {\text{ey}}_3=\text{norm}({\mathbf{\text{q}}}_{r3}-{\overline{\mathbf{\text{q}}}}_{mp})\\ while{\text{ ey}}_3>\text{e}{\text{y}}_{\mathbf{\text{2}}}\\ {\mathbf{\text{F}}}_{r,f}^l=min({\mathbf{\text{F}}}_{r1},{\mathbf{\text{F}}}_{r3})\\ {\mathbf{\text{F}}}_{r,f}^r=max({\mathbf{\text{F}}}_{r1},{\mathbf{\text{F}}}_{r3})\end{array}$(11)

4. Load parameter identification process

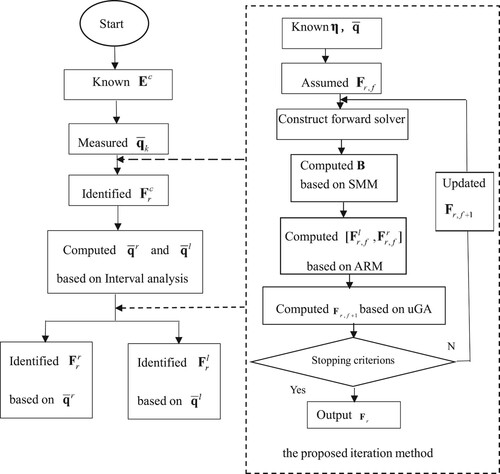
Based on the above discussion, the proposed inverse method combining rotor dynamic response prediction together with the proposed iteration method can calculate the load parameter of the wind turbine rotor with interval and probability uncertainty according to the deterministic load parameter identification method. The solution procedure is described in Figure 1.

Figure 1. Identification of load parameters with mixed uncertainty.

Step 1: The dynamic response of the wind turbine rotor system is measured. Determine the midpoint ${\mathbf{\text{E}}}^c$-radius ${\mathbf{\text{E}}}^w$ of the interval uncertain parameters $\mathbf{\text{E}}$, the probability uncertain parameter $\mathit{\eta }$, the Gaussian distribution of the measurement error and the unknown load parameter ${\mathbf{\text{F}}}_r$.

Step 2: Combining the midpoint ${\mathbf{\text{E}}}^c$ of the interval uncertain parameters together with the measured rotor dynamic response ${\overline{\mathbf{\text{q}}}}_k$ into the proposed iteration method to calculate the mean ${\mathbf{\text{F}}}_r^c$

Step 3: According to the interval analysis method, the upper bound ${\overline{\mathbf{\text{q}}}}^r$ and the low bound ${\overline{\mathbf{\text{q}}}}^l$ of the dynamic response of the wind turbine rotor are predicted by solving Equations (8).

Step 4: Combining the lower bound ${\mathbf{\text{E}}}^l$ of the interval uncertain parameters together with the predicted ${\overline{\mathbf{\text{q}}}}^l$ into the proposed iteration method to calculate the lower bound ${\mathbf{\text{F}}}_r^l$ of the load parameters. similarly, obtain the upper bound ${\mathbf{\text{F}}}_r^r$ by combining the upper bound ${\mathbf{\text{E}}}^r$ together with the predicted ${\overline{\mathbf{\text{q}}}}^r$. As a result, the mean range of unknown load parameters $[{\mathbf{\text{F}}}_r^l,{\mathbf{\text{F}}}_r^r]$ is obtained.

5. Identification of load parameters of the wind turbine rotor

5.1. Recognition model

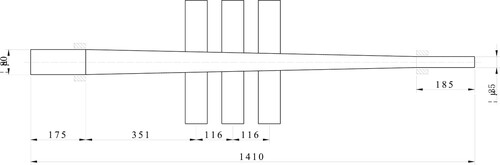
The rotor system of the wind turbine is given in this section to validate the proposed method. The parameters of the conical rotor model with three equivalent disk and two sliding bearings are shown in Figure 2 and Table 1.

Figure 2. Structural parameter model of the wind turbine rotor system.

Table 1. The parameters of the conical rotor system.

	Elastic modulus $E_r$	Shear elastic modulus $G_r$		Density $\rho$	Minimum outer diameter	Maximum outer diameter $L$		Conical length
Rotor	210 GPa	80 GPa		7850 kg/m^3	35 mm	80 mm		1050 mm
	Outer diameter				Thickness
	394 mm				185 mm
Disk	Stiffness coefficient (MN m^−1)				Damping coefficient (kN s m^−1)
Bearing	Kxx	Kxy	Kyx	Kyy	Cxx	Cxy	Cyx	Cyy
Front	66.981	366.84	−321.17	117.89	170.35	28.195	28.195	158.18
Rear	65.626	365.41	−321.70	115.88	169.83	27.713	27.713	158.01

In this case, the axial load and torque load parameters $\left(F,T\right)$ are the unknown load parameters to be determined. The rotor elastic modulus $\left(E_r,G_r\right)$ is an interval uncertain parameter. The length and density of the conical rotor (L, ) are probabilistic uncertain parameters with Gaussian distribution. The number of the measured point is 2, and the dynamic response (d₁, d₂) of the front and rear bearings can be measured with Gaussian measurement errors, and denote the output response ${\overline{\mathbf{\text{q}}}}_k$ corresponding to the measured point. The dynamic response (d₃, d₄) of the front and rear disc is not easy to arrange the sensor and cannot be measured, denote the output response ${\overline{\mathbf{\text{q}}}}_u$ corresponding to the concern point. Namely, there are both measurement noise and model uncertainty, the identification of load parameters $\left(F,T\right)$ is a mixed uncertainty problem.

5.2. Recognition process

The interval uncertainty level is assumed as 3%, that is, ${\mathbf{\text{E}}}_r=\left[203.7,216.3\right]\text{GPa}$, ${\mathbf{\text{E}}}_r=\left[77.6,82.4\right]\text{GPa}$ According to the identification process, the midpoint of the interval uncertain parameters ${\mathbf{\text{E}}}^c=\left[210\text{GPa},80\text{GPa}\right]$. It is assumed that the true value of load parameters $\left(F,T\right)=\left(530\text{kN},655\text{kN}\text{m}\right)$ are given, respectively. Based on Equation (2), therefore, the true rotor dynamic response $\left(d_1,d_2\right)=\left(25.68\text{μ}\mathrm{m},14.40\text{μ}\mathrm{m}\right)$ can be easily obtained. In order to simulate the measured responses, noise-contaminated response ${\overline{\mathbf{\text{q}}}}_k$ is used to identify the mean ${\mathbf{\text{F}}}_r^c$ of load parameters. It is assumed that the all-measurement results and probability uncertain parameter have Gaussian noise and obey the normal distribution with a deviation of 3%, namely, the probability uncertain parameter $\mathit{\eta }$ are expressed as $L\sim N\left(1050,{31.5}^2\right)\text{mm}$, $\rho \sim N\left(7850,{235.5}^2\right)\text{kg/}{\text{m}}^{\text{3}}$, the noise contaminated response ${\overline{\mathbf{\text{q}}}}_k$ are expressed as $d_1\sim N\left(25.68,{0.77}^2\right)um$, $d_2\sim N\left(14.40,{0.43}^2\right)um$. In this case, five individuals are selected in the uGA, the crossover factor is 0.5, the gene mutation rate is 0.003, and the maximum iterative step is 300.

5.2.1. Identification of the mean ${\mathbf{\text{F}}}_r^c$ of load parameters

Table 2 shows the calculation process of load parameter identification. The stop criterion constant is set to 2e-5, and the initial value of the given load parameter is $\text{{ }0\text{kN},0\text{kN}\text{m}\}$ The load parameter increment $\mathbf{\text{B}}$ is calculated from the sensitivity matrix, and the corresponding load parameter search interval is obtained according to the ARM. The axial load parameter interval is $\left[64.47,259.41\right]\text{kN}$ and the torque parameter interval is $\left[51.60,207.61\right]\text{kN}\text{m}$. In this interval, the load parameter $\left\{82.44\text{kN},207.61\text{kN}\text{m}\right\}$ is obtained corresponding to the minimum error of 3.36 by the uGA, as shown in the first row of Table 2, and the error 3.36 is greater than the predefined toleration 2e-5, then take $\{82.44\text{kN},207.61\text{kN}\text{m} }$ as the updated initial value of the load parameter in the next iteration, and continue to run according to the proposed iteration method, as shown in the second row of Table 2. After 34 iterations, the error is 1.54e-05, which is within the predefined toleration and the calculation is over. The identified load parameter is $\left\{\text{529}\text{.94}\text{ kN},\text{654}\text{.99 }\text{kN}\text{m}\right\}$. The mean square deviation between the identified value and the real value is 0.06. As shown in Table 3, the proposed iteration method is feasible to identify the load parameters of the wind turbine rotor system with probabilistic uncertainty.

Table 2. Identification iterative process of load parameter ${\mathbf{\text{F}}}_r^c$ with ${\mathbf{\text{E}}}^c$ involving probability uncertainty.

	Initial value		Increment B		Search interval		Identified value
No. of iteration	Axial load F (kN)	Torque T (kN m)	Axial load F (kN)	Torque T (kN m)	Axial load F (kN)	Torque T (kN m)	Axial load F (kN)	Torque T (kN m)	Error
1	0	0	0.51	0.41	[64.47, 259.41]	[51.60, 207.61]	82.44	207.61	3.36
2	82.44	207.61	0.27	0.06	[90.91, 117.14]	[207.80, 208.40]	90.91	208.40	3.35
3	90.91	208.40	0.76	0.49	[187.63, 480.08]	[270.69, 459.06]	187.63	458.97	1.64
…	…	…			…	…	…	…	…
32	529.23	654.89	0.68	0.66	[528.55, 529.91]	[654.23, 655.55]	529.86	654.98	3.99e-5
33	529.86	654.98	0.54	0.51	[529.31, 530.40]	[654.47, 655.49]	529.69	654.96	8.46e-5
34	529.69	654.96	0.71	0.49	[528.98, 530.41]	[654.47, 655.45]	529.94	654.99	1.54e-5
Target					530		655

Table 3. Identified ${\mathbf{\text{F}}}_r^c$ with ${\mathbf{\text{E}}}^c$ involving probability uncertainty.

	Identified ${\mathbf{\text{F}}}_r^c$ with ${\mathbf{\text{E}}}^c$
Gaussian noise deviation	Axial load F (kN)	Torque T (kN m)	Relative error to the target
1%	530.25	655.03	0.25
3%	529.94	654.99	0.06
5%	530.00	655.00	0

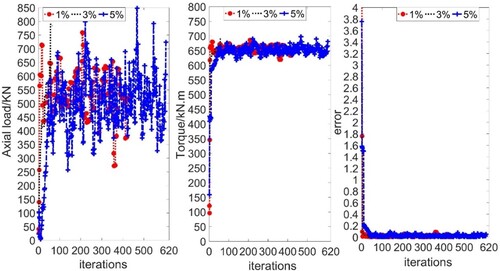
To demonstrate the robustness of the proposed iteration method to probabilistic uncertainty, the load parameters identification results are compared with the Gaussian noise deviations of 1%, 3% and 5%. As shown in Figure 3 and Table 3. It is known that the identification result is less affected by the Gaussian noise deviation, that is, the robustness of the proposed iteration method is good. Figure 3 shows that the local optimal solution of the corresponding interval can gain in 350 iterative steps. The maximum iterative step of uGA in each interval (it is 300 in the case) is the main factor affecting the convergence speed of the proposed iteration method. However, according to the Bayesian approach, MCMC sampling with10⁶ samples [8] must be carried out to compute all possible marginal PPDF in each interval in order to validate the accuracy of the identified results. So, the proposed iteration method improves its efficiency.

Figure 3. Iterative process of $F_r^c$ with ${\mathit{E}}^c$ involving three kinds of probability uncertainty.

5.2.2. Identification of mixed uncertain load parameters

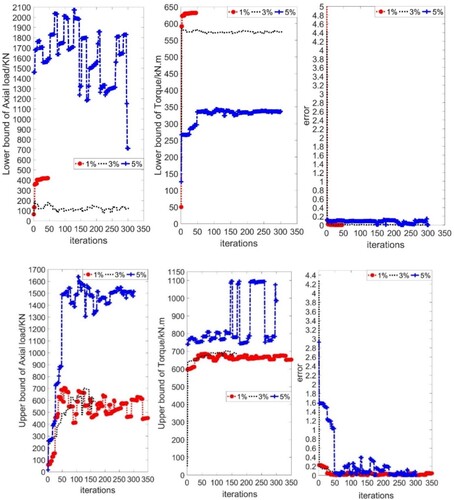
When the probabilistic Gaussian noise deviation is 3%, the interval parameters are considered to identify the load parameters of the wind turbine rotor system under three intervals uncertain levels. The upper and low bound of rotor dynamic response ${\overline{\mathbf{\text{q}}}}^r$ and ${\overline{\mathbf{\text{q}}}}^l$ are predicted by the interval analysis method as shown in Table 4, and the load parameters identification intervals based on ${\overline{\mathbf{\text{q}}}}^r$ and ${\overline{\mathbf{\text{q}}}}^l$ are shown in Table 4. The identification iteration process is shown in Figure 4. The interval uncertain level affects the recognition result. The interval of load parameters identification results expands with the increase of the interval uncertain level.

Figure 4. Iterative process of load parameter identification involving mixed uncertainty.

Table 4. Load parameter identification result involving mixed uncertainty.

	Rotor dynamic response				Identification parameter
	${\overline{\mathbf{\text{q}}}}_k$ (um)		${\overline{\mathbf{\text{q}}}}_u$ (um)		Axial load	Torque
Interval uncertainty level	d1	d2	d3	d4	F (kN)	T (kN m)
1%	[25.4766, 25.8727]	[14.3617, 14.4340]	[5.7034, 5.7259]	[5.7009, 5.7229]	[419.7825, 583.4185]	[631.6624, 670.1147]
3%	[25.0866, 26.2627]	[14.2894, 14.5063]	[5.6809, 5.7485]	[5.6788, 5.7450]	[123.2075 590.0631]	[574.8661, 686.5828]
5%	[24.7144, 26.6350]	[14.2174, 14.5783]	[5.6580, 5.7713]	[5.6564, 5.7673]	[711.8892, 1513.7714]	[336.6242, 985.8635]

6. Conclusions

In order to reduce complex multi-layer nesting solutions coming from the interval and probability parameters, this paper proposes a new inverse analysis framework for load parameter identification in wind turbine rotor systems. A numerical example is given to demonstrate the efficiency and accuracy. Based on this study, the following conclusion can be drawn:

1. The uncertain parameters are characterized as interval and probability variables; the measurement noise and model uncertainty are easy to implement.

2. For conducting the wind turbine rotor response strip coming from the interval uncertain parameters, an interval analysis method is presented to predict the upper and lower bounds of the responses based on the first-order Taylor expansion.

3. For conducting the problem of mass sampling coming from the probability uncertain parameters in the Bayesian approach, the load identification problem is transformed into a parameter optimization problem to deal with probability variables. A proposed iteration method combined ARM with uGA is presented to determine the mean and interval of load parameters via the obtained response.

4. The level of uncertainty has a great influence on the identification results. It can be used as a reference for the uncertainty inverse problem in engineering.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Conflict of interest statement

The authors declared that they have no conflicts of interest to this work. We declare that we do not have any commercial or associative interest that represents a conflict of interest in connection with the work submitted.

Additional information

Funding

This work was supported by National Natural Science Foundation of China: [Grant Number 51775180,51875193]; Hunan Provincial Natural Science Foundation of China: [Grant Number 2021JJ50101]; Hunan Provincial Natural Science Foundation of China: [Grant Number 2019JJ60036].