Groundwater flow in karstic aquifer: analytic solution of dual-porosity fractional model to simulate groundwater flow

ABSTRACT

Karst aquifers have a very complex flow system because of their high spatial heterogeneity of void distribution. In this manuscript, flow simulation has been used to investigate the flow mechanism in a fissured karst aquifer with double porosity, revealing how to connect exchange and storage coefficients to the volumetric density of the highly permeable form of media. The governing space-time differential equations of the dual-porosity model are modified by using the Caputo–Fabrizio fractional derivative operator for time memory. The sensitivity of exchange and storage coefficients has been demonstrated using numerical studies with theoretical karst systems in this hybrid system. When dealing with highly heterogeneous systems, it is demonstrated that porosity storage and exchange coefficients are required. The analytical model could possibly reveal some of the karstic network's essential structural features.

KEYWORDS:

• Karst aquifer
• dual-porosity model
• Caputo–Fabrizio fractional operator
• Laplace transform

2010 MATHEMATICS SUBJECT CLASSIFICATIONS:

• Primary 34A08
• Secondary 26A33

1. Introduction

An aquifer is a geological structure of rocks, fractured rocks and sands, that occur at different levels in groundwater and can store and transmit the groundwater. Karst aquifers are a particular category of broken rock aquifer (calcareous, dolomite or magnesite) in which comparatively fragile rock are dissolved by the water in the cracks, greatly expanding the size of the fractures. These solution cavities can be tens of metres broad in some areas, and form underground cave systems. In karst aquifers, groundwater flow is more intense and higher than in other types of aquifers.

In general, the fissured karstic aquifers are schematized into an unknown high permeability channel network associated with low permeability fractured limestone to a discharge field. The structure of channel network has an important role in hydraulic reaction in such carbonate aquifers, assimilated to the dual porosity model, but a priori is never well understood [1,2]. Karstic aquifer with a dual-porosity system has divided into porosity systems, one is primary porosity which has low permeability (matrix volume) and secondary porosity which has high permeability channel network (karstic network). In the hydraulic channel, these two components are then associated with duality.

In the literature, Cornaton et al. [3] derived one-dimensional analytical porosity-weighted solutions of the dual-porosity model using the integral transform technique, and Warren et al. [4] developed an idealized model for the purpose of studying the characteristic behaviour of a permeable medium of naturally fractured or vugular reservoir and investigated unsteady-state flow in reservoir analytically. Kazemi [5] devised an ideal mathematical framework of a naturally fractured reservoir with a uniform fracture distribution, consisting of a finite circular reservoir with a centrally positioned well and two separate porous sectors, matrix and fracture, respectively. Steady-state exchange models are less complex than transient exchange models in view of mathematical or physical points. Moench [6] studied the pseudo steady-state block/fracture exchange model and showed that the hydraulic behaviour of aquifer lies in only a high permeability aquifer and doesn't require a low permeability aquifer (block).

Barenblatt et al. [7] defined the flux exchange as $q_{ef}=\pm \alpha (h_m-h_f)$, where $h_m$ is the mean hydraulic head in matrix continua, $h_f$ is the average hydraulic head in fractured continua and α being the exchange coefficient which is related to fractured geometry [4].

The dual-porosity approach is a powerful technique to simulate groundwater flow in a fractured aquifer. Lang et al. [8] modelled dual-porosity approach for acoustic propagation through heterogeneous porous structures in the fractured aquifer. It consists of two continua, one is more permeable and the other is less permeable. Moutsopoulos et al. [9] obtained a numerical solution using dual-porosity approach, qualitative behaviour is also described. Pride et al. [10] constructed the governing equations of linear acoustics of composites comprising dual porous constituents isotropic in nature, using volume-averaging arguments. Agarwal et al. [11] examined the concept of miscible flow in porous media with longitudinal dispersion and evaluated the solution of governing differential equation employing the Caputo–Fabrizio fractional derivative operator that has a non-singular kernel.

Many authors have applied the fractional derivatives without singular kernels such as Atangana et al. [12] proposed a novel formulation of the idea of fractional-order derivatives, which he used to calculate the flow of water inside a leaking aquifer. In [13], Atangana established the properties of the Caputo–Fabrizio fractional derivative and used the valuable tools for solving the nonlinear Fisher's reaction-diffusion problem. Baleanu et al. [14] showed that four fractional integro-differential inclusions have solutions. Under certain conditions, the set of solutions for the second fractional integro-differential inclusion problem is infinite dimensional. Atangana et al. [15] proposed a model of the subsurface water movement via aquifer and extended using an alternative definition of Caputo–Fabrizio fractional derivative.

Yavuz et al. [16–18] proposed and investigated fractional order models described by a fractional operator and found analytical/numerical solutions to the constructed problems by using the Laplace transform method. Baleanu et al. [14,19,20] investigated some new class of hybrid type fractional differential equations and inclusions via some nonlocal three-point boundary value conditions and showed that the dimension of the set of solutions for the second fractional integro-differential inclusion problem is infinite dimensional under some different conditions. A generalized fractional model is also introduced for the COVID-19 pandemic, including the effects of isolation and quarantine. Qureshi et al. [21] numerically approximated the Caputo–Fabrizio fractional derivative operator using the two-point finite forward difference formula for first-order ordinary derivative of the function. Jajarmi et al. [20,22] investigated the complex behaviours of a capacitor microphone dynamical system and the asymptotic behaviour of immunogenic tumour dynamics based on a new fractional model constructed by the concept of general fractional operators. Thabet et al. [23] explored the existence and uniqueness criteria for a new coupled Caputo conformable system of pantograph problems. Matar et al. [24] investigated the motion of a beam on an internally bent nanowire by using the fractional calculus theory.

The solutions of two fractional models of Jeffrey's fluid modelled with Caputo and Caputo–Fabrizio fractional derivatives were compared by Ahmad et al. [25]. Aleem et al. [26] presented the unsteady MHD nanofluid flow travelling through an accelerating infinite vertical plate positioned in porous material involving the above two fractional operators. Asjad et al. [27] compared these two fractional differential operators for the time fractional unsteady flows of a second-grade fluid with Newtonian heating. Yang et al. [28] presented a new fractional derivative and used the Laplace transform to provide an analytical solution for the fractional-order heat flow. In [29], Yang et al. developed the first analytical solution of anomalous diffusion equations combining the general derivatives with the decay exponential kernel using the Laplace transform. In [30], Yang et al. used the Laplace transform to obtain series solutions for the generalized fractional-order diffusion equations.

According to transient-type input boundary conditions, we give one-dimensional analytical solutions to the dual-porosity model of the governing fractional differential equation in this study. In this system, we further discuss the relationship between the exchange coefficient and specific geometrical and/or physical properties of the highly permeable zones. To determine the hydraulic responses of karstic aquifers, numerical models are used.

2. Mathematical preliminaries

The definition of the Caputo–Fabrizio fractional derivative operator [31] is given as (1) ${}_a^{CF}{D}_t^{\alpha }f\left(t\right)=\frac{M\left(\alpha \right)}{1-\alpha }{\int }_a^t{f}^{\mathrm{\prime }}\left(\tau \right)\exp (-\alpha \frac{t-\tau }{1-\alpha })\mathrm{d}\tau ,a<t<b,$(1) where $f\in H^{\mathrm{\prime }}(a,b),b>a$, $0<\alpha \le 1$ and $M\left(\alpha \right)$ is a normalized function defined as (2) $M\left(\alpha \right)=1-\alpha +\frac{\alpha }{\mathrm{\Gamma }\left(\alpha \right)},$(2) s.t. $M\left(0\right)=M\left(1\right)=1$.

Laplace transform of the Caputo–Fabrizio fractional derivative is given as [31] (3) $\mathcal{L}\left[{}_0^{CF}{D}_t^{\alpha }f\right(t);s]=M\left(\alpha \right)\frac{sF\left(s\right)-f\left(0\right)}{s+\alpha (1-s)},0<\alpha \le 1,$(3) if exists.

3. Flow in channel continua

In this section, we will derive the solution of one-dimensional governing differential equation using the dual-porosity approach. Here, the matrix conductivity has been assumed zero, and exchange kinetics between porosities has been assumed to be first order [3]. The governing differential equation for controlling flow in channel continua is given as (4) $K_c\frac{{\mathrm{\partial }}^2{h}_c(x,t)}{\mathrm{\partial }{x}^2}=S_c\frac{\mathrm{\partial }{h}_c(x,t)}{\mathrm{\partial }t}+S_m\frac{\mathrm{\partial }{h}_m(x,t)}{\mathrm{\partial }t},$(4) where $S_c$ and $K_c$ are the storage coefficient and hydraulic conductivity in the high permeability channel continuum, respectively and $S_m$ is the storage coefficient in the low permeability matrix continuum. The term $S_m\frac{\mathrm{\partial }{h}_m(x,t)}{\mathrm{\partial }t}$ acts as the source term.

In the channel continuum, volumetric density is $\theta =\frac{V_c}{V_a}$ and in the matrix continuum it is given as $1-\theta =\frac{V_m}{V_a}$, where $V_c$ is the volume of channel, $V_m$ is the volume of matrix and $V_a$ denotes the total volume. Now, weighting the terms of Equation (4(4) $K_c\frac{{\mathrm{\partial }}^2{h}_c(x,t)}{\mathrm{\partial }{x}^2}=S_c\frac{\mathrm{\partial }{h}_c(x,t)}{\mathrm{\partial }t}+S_m\frac{\mathrm{\partial }{h}_m(x,t)}{\mathrm{\partial }t},$(4) ) with θ and $1-\theta$ gives (5) $\begin{array}{rl}& \theta K_c\frac{{\mathrm{\partial }}^2{h}_c(x,t)}{\mathrm{\partial }{x}^2}=\theta S_c\frac{\mathrm{\partial }{h}_c(x,t)}{\mathrm{\partial }t}+(1-\theta )S_m\frac{\mathrm{\partial }{h}_m(x,t)}{\mathrm{\partial }t}\\ & ⟹K_c\frac{{\mathrm{\partial }}^2{h}_c(x,t)}{\mathrm{\partial }{x}^2}=S_c\frac{\mathrm{\partial }{h}_c(x,t)}{\mathrm{\partial }t}+\text{β}{S}_m\frac{\mathrm{\partial }{h}_m(x,t)}{\mathrm{\partial }t},\end{array}$(5) where (6) $\text{β}=\frac{1-\theta }{\theta }.$(6) When continuum are assimilated into tubes or pipes, then Equation (6(6) $\text{β}=\frac{1-\theta }{\theta }.$(6) ) becomes (7) $\text{β}={\left(\frac{r_m}{r_c}\right)}^2,$(7) where $r_c$ and $r_m$ are the radius of channel and matrix respectively.

The obtained solution of Equation (5(5) $\begin{array}{rl}& \theta K_c\frac{{\mathrm{\partial }}^2{h}_c(x,t)}{\mathrm{\partial }{x}^2}=\theta S_c\frac{\mathrm{\partial }{h}_c(x,t)}{\mathrm{\partial }t}+(1-\theta )S_m\frac{\mathrm{\partial }{h}_m(x,t)}{\mathrm{\partial }t}\\ & ⟹K_c\frac{{\mathrm{\partial }}^2{h}_c(x,t)}{\mathrm{\partial }{x}^2}=S_c\frac{\mathrm{\partial }{h}_c(x,t)}{\mathrm{\partial }t}+\text{β}{S}_m\frac{\mathrm{\partial }{h}_m(x,t)}{\mathrm{\partial }t},\end{array}$(5) ) must satisfy the following initial and boundary conditions: (8) $\begin{array}{rl}& h_c(0,t)=f\left(t\right),\end{array}$(8) (9) $\begin{array}{rl}& h_c(x,0)=h_m(x,0)=0,\end{array}$(9) (10) $\begin{array}{rl}& h_c(\pm \mathrm{\infty },t)=0,\end{array}$(10) (11) $\begin{array}{rl}& -K_c\frac{\mathrm{\partial }{h}_c(0,t)}{\mathrm{\partial }x}=f\left(t\right),\end{array}$(11) where $f\left(t\right)$ is a transient input function.

From Equation (5(5) $\begin{array}{rl}& \theta K_c\frac{{\mathrm{\partial }}^2{h}_c(x,t)}{\mathrm{\partial }{x}^2}=\theta S_c\frac{\mathrm{\partial }{h}_c(x,t)}{\mathrm{\partial }t}+(1-\theta )S_m\frac{\mathrm{\partial }{h}_m(x,t)}{\mathrm{\partial }t}\\ & ⟹K_c\frac{{\mathrm{\partial }}^2{h}_c(x,t)}{\mathrm{\partial }{x}^2}=S_c\frac{\mathrm{\partial }{h}_c(x,t)}{\mathrm{\partial }t}+\text{β}{S}_m\frac{\mathrm{\partial }{h}_m(x,t)}{\mathrm{\partial }t},\end{array}$(5) ), storage in matrix, by considering first-order transfer in porosities is given as (12) $S_m\frac{\mathrm{\partial }{h}_m(x,t)}{\mathrm{\partial }t}=-\alpha (h_m-h_c).$(12) Now, using the non-singular time-Caputo–Fabrizio fractional differential operator in Equations (5(5) $\begin{array}{rl}& \theta K_c\frac{{\mathrm{\partial }}^2{h}_c(x,t)}{\mathrm{\partial }{x}^2}=\theta S_c\frac{\mathrm{\partial }{h}_c(x,t)}{\mathrm{\partial }t}+(1-\theta )S_m\frac{\mathrm{\partial }{h}_m(x,t)}{\mathrm{\partial }t}\\ & ⟹K_c\frac{{\mathrm{\partial }}^2{h}_c(x,t)}{\mathrm{\partial }{x}^2}=S_c\frac{\mathrm{\partial }{h}_c(x,t)}{\mathrm{\partial }t}+\text{β}{S}_m\frac{\mathrm{\partial }{h}_m(x,t)}{\mathrm{\partial }t},\end{array}$(5) ) and (12(12) $S_m\frac{\mathrm{\partial }{h}_m(x,t)}{\mathrm{\partial }t}=-\alpha (h_m-h_c).$(12) ), respectively, we obtain (13) $\begin{array}{rl}{K}_c\frac{{\mathrm{\partial }}^2{h}_c(x,t)}{\mathrm{\partial }{x}^2}& =S_c\frac{{\mathrm{\partial }}^{\eta }{h}_c(x,t)}{\mathrm{\partial }{t}^{\eta }}+\text{β}{S}_m\frac{{\mathrm{\partial }}^{\zeta }{h}_m(x,t)}{\mathrm{\partial }{t}^{\zeta }},\end{array}$(13) (14) $\begin{array}{rl}{S}_m\frac{{\mathrm{\partial }}^{\zeta }{h}_m(x,t)}{\mathrm{\partial }{t}^{\zeta }}& =-\alpha \left(h_m\right(x,t)-h_c(x,t\left)\right),\end{array}$(14) where $0<\eta \le 1$, $0<\zeta \le 1$, t>0 and $x\in {\mathbb{R}}^{+}$.

Applying the Laplace transform with respect to the time derivative on Equations (13(13) $\begin{array}{rl}{K}_c\frac{{\mathrm{\partial }}^2{h}_c(x,t)}{\mathrm{\partial }{x}^2}& =S_c\frac{{\mathrm{\partial }}^{\eta }{h}_c(x,t)}{\mathrm{\partial }{t}^{\eta }}+\text{β}{S}_m\frac{{\mathrm{\partial }}^{\zeta }{h}_m(x,t)}{\mathrm{\partial }{t}^{\zeta }},\end{array}$(13) ) and (14(14) $\begin{array}{rl}{S}_m\frac{{\mathrm{\partial }}^{\zeta }{h}_m(x,t)}{\mathrm{\partial }{t}^{\zeta }}& =-\alpha \left(h_m\right(x,t)-h_c(x,t\left)\right),\end{array}$(14) ) and setting the initial conditions mentioned in (9(9) $\begin{array}{rl}& h_c(x,0)=h_m(x,0)=0,\end{array}$(9) ), we obtain (15) $\begin{array}{rl}& K_c\frac{d^2{\overline{h}}_c(x,p)}{\mathrm{d}{x}^2}=S_c\frac{p{\overline{h}}_c(x,p)}{p(1-\eta )+\eta }+\text{β}{S}_m\frac{p{\overline{h}}_m(x,p)}{p(1-\zeta )+\zeta }\end{array}$(15) (16) $\begin{array}{rl}& S_m\frac{p{\overline{h}}_m(x,p)}{p(1-\zeta )+\zeta }=\alpha \left({\overline{h}}_m\right(x,p)-{\overline{h}}_c(x,p\left)\right).\end{array}$(16) Further, by solving Equations (15(15) $\begin{array}{rl}& K_c\frac{d^2{\overline{h}}_c(x,p)}{\mathrm{d}{x}^2}=S_c\frac{p{\overline{h}}_c(x,p)}{p(1-\eta )+\eta }+\text{β}{S}_m\frac{p{\overline{h}}_m(x,p)}{p(1-\zeta )+\zeta }\end{array}$(15) ) and (16(16) $\begin{array}{rl}& S_m\frac{p{\overline{h}}_m(x,p)}{p(1-\zeta )+\zeta }=\alpha \left({\overline{h}}_m\right(x,p)-{\overline{h}}_c(x,p\left)\right).\end{array}$(16) ), we obtain (17) $\frac{{\mathrm{d}}^2{\overline{h}}_c(x,p)}{\mathrm{d}{x}^2}=M\left(p\right){\overline{h}}_c(x,p),$(17) where (18) $M\left(p\right)=\frac{1}{K_c}[S_c\frac{p}{p(1-\eta )+\eta }+\text{β}{S}_m\alpha \frac{p}{S_{m}p+\alpha p(1-\zeta )+\alpha \zeta }].$(18) The general solution of Equation (17(17) $\frac{{\mathrm{d}}^2{\overline{h}}_c(x,p)}{\mathrm{d}{x}^2}=M\left(p\right){\overline{h}}_c(x,p),$(17) ) is obtained as (19) ${\overline{h}}_c(x,p)=\frac{1}{2}\left(\right[{\overline{r}}_1\left(p\right)+{\overline{r}}_2\left(p\right)]e^{x\sqrt{M\left(p\right)}}+[{\overline{r}}_2\left(p\right)-{\overline{r}}_1\left(p\right)\left]e^{-x\sqrt{M\left(p\right)}}\right),$(19) where ${\overline{r}}_1\left(p\right)$ and ${\overline{r}}_2\left(p\right)$ are boundary conditions.

Now to satisfy the boundary condition (10(10) $\begin{array}{rl}& h_c(\pm \mathrm{\infty },t)=0,\end{array}$(10) ), we have ${\overline{r}}_1\left(p\right)=-{\overline{r}}_2\left(p\right)$, and for the condition (8(8) $\begin{array}{rl}& h_c(0,t)=f\left(t\right),\end{array}$(8) ), ${\overline{r}}_2\left(p\right)=\overline{f}\left(p\right)=\mathcal{L}\left[f\right(t);p]$. Applying these results to Equation (19(19) ${\overline{h}}_c(x,p)=\frac{1}{2}\left(\right[{\overline{r}}_1\left(p\right)+{\overline{r}}_2\left(p\right)]e^{x\sqrt{M\left(p\right)}}+[{\overline{r}}_2\left(p\right)-{\overline{r}}_1\left(p\right)\left]e^{-x\sqrt{M\left(p\right)}}\right),$(19) ), we obtain (20) ${\overline{h}}_c(x,p)=\overline{f}\left(p\right)e^{-x\sqrt{M\left(p\right)}}.$(20) For the function $\overline{f}\left(p\right)=\mathcal{L}\left[\delta \right(t);p]=1$, $\delta \left(t\right)$ being Dirac delta function. For the channel transfer function Equation (20(20) ${\overline{h}}_c(x,p)=\overline{f}\left(p\right)e^{-x\sqrt{M\left(p\right)}}.$(20) ) becomes (21) ${\overline{h}}_c(x,p)=e^{-x\sqrt{M\left(p\right)}},$(21) and Darcy flux is given as (22) ${\overline{q}}_c(x,p)=-K_c\frac{\mathrm{d}{\overline{h}}_c(x,p)}{\mathrm{d}x}=K_c\sqrt{M\left(p\right)}{e}^{-x\sqrt{M\left(p\right)}},$(22) and at x = 0 (23) $-K_c\frac{\mathrm{d}{\overline{h}}_c(x,p)}{\mathrm{d}x}=\mathcal{L}\left[\delta \right(t);p]=1.$(23) Now, in the channel, the transformed hydraulic head becomes (24) ${\overline{h}}_c(x,p)=\frac{e^{-x\sqrt{M\left(p\right)}}}{K_c\sqrt{M\left(p\right)}},$(24) and hence the transformed flux is given by (25) ${\overline{q}}_c(x,p)=e^{-x\sqrt{M\left(p\right)}},$(25) which is equal to the transfer defined in Equation (21(21) ${\overline{h}}_c(x,p)=e^{-x\sqrt{M\left(p\right)}},$(21) ).

One can obtain the inverse Laplace transform of Equation (20(20) ${\overline{h}}_c(x,p)=\overline{f}\left(p\right)e^{-x\sqrt{M\left(p\right)}}.$(20) ) by applying the convolution theorem as (26) $\begin{array}{rl}{h}_c(x,t)& ={\int }_0^t{e}^{-x\sqrt{M(t-\tau )}}f\left(\tau \right)\mathrm{d}\tau \\ & ={\int }_0^{t}G(t-\tau )f\left(\tau \right)\mathrm{d}\tau ,\end{array}$(26) where (27) $G\left(t\right)={\mathcal{L}}^{-1}[e^{-x\sqrt{Mp}};t],$(27) is the Green function.

4. Relationship between channels using transfer function

We assume that (28) $\mathrm{tr}(x,p)=e^{-x\sqrt{M\left(p\right)}},$(28) where $\mathrm{tr}(x,p)$ is the transfer function in the dual permeability approach. Using the flux boundary condition $-K_c\frac{\mathrm{d}{\overline{h}}_c(0,p)}{\mathrm{d}x}=f\left(p\right)$, solution of Equation (17(17) $\frac{{\mathrm{d}}^2{\overline{h}}_c(x,p)}{\mathrm{d}{x}^2}=M\left(p\right){\overline{h}}_c(x,p),$(17) ) reads (29) $\overline{h_c}(x,p)=\frac{f\left(p\right)}{K_c}{\int }_x^{\mathrm{\infty }}\mathrm{tr}(u,p)\mathrm{d}u.$(29) Transformed flux in the channel head is (30) ${\overline{q}}_c(x,p)=f\left(p\right)\mathrm{tr}(x,p),$(30) and (31) $h_m=\frac{\alpha h_c}{\frac{S_m}{1-\zeta }(\frac{1}{t}-\frac{\zeta }{1-\zeta }{e}^{\frac{\zeta t}{1-\zeta }})+\frac{\alpha }{t}},$(31) where $h_m$ is hydraulic head in the matrix and the flow rate is given by (32) $Q_c(x,t)=q_c(x,t)\pi r_c^2.$(32) The flow model in Equation (29(29) $\overline{h_c}(x,p)=\frac{f\left(p\right)}{K_c}{\int }_x^{\mathrm{\infty }}\mathrm{tr}(u,p)\mathrm{d}u.$(29) ) and Equation (30(30) ${\overline{q}}_c(x,p)=f\left(p\right)\mathrm{tr}(x,p),$(30) ) described the dual-porosity transfer function model.

5. Numerical simulation

Let incremental volume in channel continua is $\pi r_c^2\mathrm{d}x$, then exchange flux $q_{ef}$ can be formulated as [3] (33) $q_{ef}=-\alpha [h_m-h_c]\frac{r_c}{2},$(33) and using Darcy's law $q_{ef}$ yields (34) $q_{ef}=-K_m\frac{h_m-h_c}{ϵr_m},$(34) where $K_m$ denotes hydraulic conductivity in matrix and ϵ represents constant distance associated with radius $r_m$. From Equations (33(33) $q_{ef}=-\alpha [h_m-h_c]\frac{r_c}{2},$(33) ) and (34(34) $q_{ef}=-K_m\frac{h_m-h_c}{ϵr_m},$(34) ), we can write (35) $\alpha =\frac{2K_m}{ϵr_c{r}_m},$(35) and from Equation (7(7) $\text{β}={\left(\frac{r_m}{r_c}\right)}^2,$(7) ) (36) ${\alpha }_0=\pi r_c^2\alpha =\frac{2\pi K_m}{ϵ\sqrt{\text{β}}},$(36) where ${\alpha }_0$ is the one-dimensional exchange coefficient.

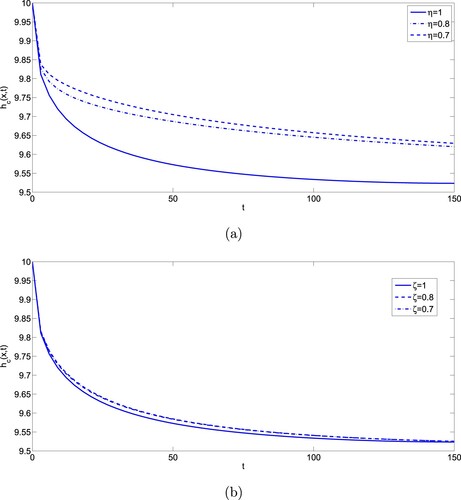
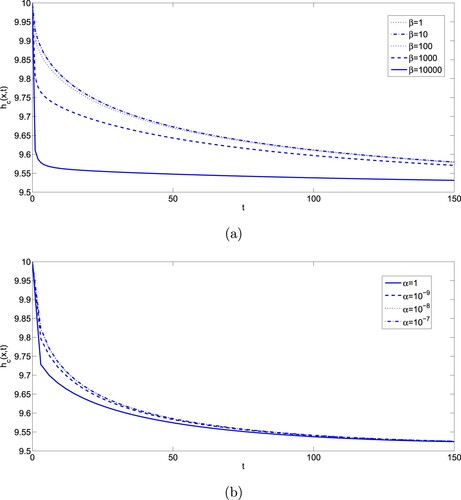
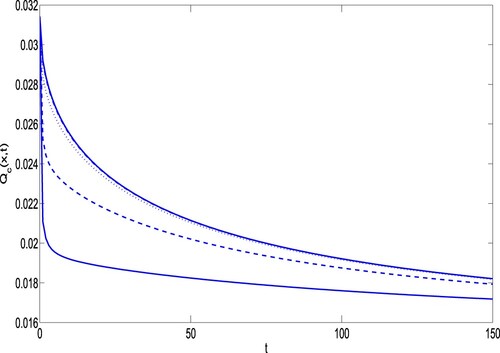
In Figure 1, the behaviour of hydraulic head in channel continua with respect to time variable t is obtained by taking different parameters and fractional order to see the behaviour with integer order derivative. Figure 2 shows the behaviour of hydraulic head with respect to variations of the coefficient β and α. For the increasing values of β taking fixed exchange rate between porosities i.e. for constant α the hydraulic head is decreased. Here β is affected in the same way as the storage coefficient and α does, so coefficient β is very useful in a dual-porosity model to simulate hydraulic head and flow [32]. Similarly, for the decreasing values of coefficient α taking β constant, hydraulic head varies as shown in Figure 3 shows the behaviour of flow rate with respect to time t taking fixed parameters.

Figure 1. Simulated hydraulic head w.r.t. fixed coefficient $K_c=10{\mathrm{m}}^3{\mathrm{s}}^{-1},S_c=5\times {10}^{-2}\mathrm{m},S_m={10}^{-4}\mathrm{m},\alpha ={10}^{-3},x=150\mathrm{m}$ and in (a) for $\zeta =1,\eta =1,0.8,0.7$, in (b) for $\eta =1,\zeta =1,0.8,0.7$.

Figure 2. Simulated hydraulic head w.r.t. fixed coefficient $K_c=10{\mathrm{m}}^3{\mathrm{s}}^{-1},S_c=5\times {10}^{-2}\mathrm{m},S_m={10}^{-4}\mathrm{m},x=150\mathrm{m},\eta =1,\zeta =1$ and in (a) for fixed $\alpha ={10}^{-3},\text{β}=1,10,100,1000,10,000$ and in (b) for fixed $\text{β}=1,\alpha =1,{10}^{-9},{10}^{-8},{10}^{-7}$.

Figure 3. Simulated flow rate w.r.t. fixed coefficient $K_c=10{\mathrm{m}}^3{\mathrm{s}}^{-1},S_c=5\times {10}^{-2}\mathrm{m},S_m={10}^{-4}\mathrm{m},x=150\mathrm{m},\eta =1,\zeta =1$ and for fixed $\alpha ={10}^{-3},\text{β}=1,10,100,1000,10,000$.

6. Conclusion

The dual-porosity approach is used to analyse the hydraulic head in the karst aquifer for the non-integer differential equations by applying the Caputo–Fabrizio fractional operator. We use Laplace transform on the modified governing differential equation to obtain the hydraulic head and connection between the channel and the matrix continua. The dual-porosity approach enables inferences about karstic network structure and its effect on the hydraulic head. The governing differential equation for channel and matrix continua can be used to monitor the karstic structure and are appropriate for any transient boundary state.

The models of dual-porosity transfer function allow inferences to be made about the structure of the karstic network and its impact on the spring hydrograph. The developed analytical models, valid for any transient boundary condition, can be used to investigate the karstic structure, homogeneous/heterogeneous infiltration processes, and parameter distribution impacts on the hydraulic responses of highly heterogeneous systems like karstic aquifers.

Acknowledgments

The authors express their sincere thanks to the reviewers for their careful reading and useful suggestions that helped to improve this paper.

Data availability statement

No data were used to support this study.

Disclosure statement

No potential conflict of interest was reported by the author(s).