Phase-insensitive versus phase-sensitive ultrasound absorption tomography in the frequency domain

ABSTRACT

The sensitivity of phase-sensitive detectors, such as piezoelectric detectors, becomes increasingly directional as the detector element size increases. In contrast, pyroelectric sensors, which are phase-insensitive, retain their omni-directionality even for large element sizes, although they have significantly poorer temporal resolution. This study uses numerical models to examine whether phase-insensitive detectors can be used advantageously in ultrasound tomography, specifically absorption tomography, when the number of detectors is sparse. We present measurement models for phase-sensitive and phase-insensitive sensors and compare the quality of the absorption reconstructions between these sensor types based on relative error and image contrast metrics. We perform the inversion using synthetic data with a Jacobian-based linearized matrix inversion approach.

KEYWORDS:

• Inverse problems
• linear inversion
• ultrasound tomography
• frequency domain ultrasound tomography
• acoustic absorption
• helmholtz equation

MATHEMATICS SUBJECT CLASSIFICATIONS:

• 34A55
• 65L09
• 35J05

1. Introduction

Ultrasound tomography (UST) is an emerging approach for tomographic reconstructions which functions through the measurement of ultrasound waves after interaction with a target of interest. UST has found particular interest in the imaging of soft tissues, such as breasts, where ultrasound transmission tomography has been employed to reconstruct the absorption and sound speed profiles of the interior tissue [1–4], since cancerous breast tissue is known to have different absorption and sound speed properties compared to healthy breast tissue [1, 5]. An important aspect of assessing the performance of UST systems is the detector type, its size and its directional response. In particular, we consider here the possibility of using pyroelectic detectors which are phase-insensitive (PI) [6], versus the better known piezoelectric detectors which are phase-sensitive (PS) [7]. We will consider ultrasound transmission tomography for the purpose of acoustic absorption reconstructions only, as it best enables the comparison of PS and PI detector types in the parallel array geometry, which further allows for comparisons with traditional x-ray tomography approaches.

PI sensors have previously been studied in the context of UST absorption reconstructions with the use of pyroelectric ultrasound detectors [6, 8], which is the detector type that we will use as a reference to model PI sensors in this paper. The key aspect of PI sensors that may prove beneficial in certain scenarios is their much flatter directional response curve due to the lack of phase-cancellation [6, 9], which for PS sensors can lead to false absorption measurements. This is especially true in larger sensors, which have better signal-to-noise ratios but also suffer from strong directionality in PS sensors.

We evaluate the reconstruction qualities of PS and PI sensors for a parallel array geometry with a varying range of array rotation angles and the number of source frequencies, for two choices of sensor width. The quality evaluation is done through the relative error as well as two different contrast metrics: the modulation transfer function (MTF) [10, 11], and the root-mean-square (RMS) contrast [12]. The MTF provides a contrast measure as a function of spatial frequency in the reconstructions, whereas the RMS contrast provides a global contrast measure that is independent of spatial frequencies.

In Section 2, we outline the inverse problem that we are solving in this paper, along with the source–sensor geometry being considered. Then, in Section 3 we describes the models used for the forward problem, consisting of the acoustic field simulation and the detector measurement models. Section 4 covers the theoretical description of the image reconstruction, with a derivation of the Jacobian operator used in our linearized reconstruction approach. Section 5 explains our numerical simulation setup, how the image quality is analysed, followed by the results for our comparison of PS and PI sensors with a focus on sensor size and data sparsity and their affect on reconstruction quality for the two sensor types. Finally, in Section 6 we discuss the results and their implications for UST and future research, in particular the scenarios in which PI sensors may be able to produce better absorption reconstructions than PS sensors. A summary of the symbols and notation used throughout this paper can be found in Table 1.

Table 1. Definitions for symbols used throughout this paper.

Symbol	Definition
χ, $\mathit{x}$	spatial domain, and spatial variable $\mathit{x}\in \chi$
${\chi }_{\theta ,m}\subset \chi$	spatial support of mth sensor at angle θ
$\omega ,\mathrm{\Omega }$	source frequency, set of source frequencies
$\theta ,\mathrm{\Theta }$	array rotation angle, set of array rotation angles
$S_{\omega \theta ,n}$	nth point source for frequency ω at angle θ
${\mathcal{L}}_{\omega }$	Helmholtz operator for source frequency ω
$\mathcal{M}$	pointwise field transformation based on sensor type
${\mathcal{I}}_{\theta ,m}$	measurement sampling operator for mth sensor at angle θ
${\mathit{y}}^{\mathcal{M}},y_{\omega \theta ,nm}^{\mathcal{M}}$	modelled data and its components for sensor type $\mathcal{M}$
${\mathit{g}}^{\mathcal{M}}$	measured data for sensor type $\mathcal{M}$
$\mathit{ϵ}$, ${ϵ}_i$	random noise vector and its components
$\tau ,\alpha$	dimensionless and dimensional absorption distributions
${\tau }_0$	modelled dimensionless absorption distribution
c	sound speed of medium
P	complex-valued pressure field
η	regularization parameter
$L_x,L_y$	pixel dimensions of simulation domain in x and y directions
${\mathbf{A}}_{\mathcal{M}},{\mathit{b}}^{\mathcal{M}}$	augmented forward matrix and data vector for sensor type $\mathcal{M}$
$F_{\mathcal{M}}:L^2\left(\chi \right)\to Y$	forward mapping from solution space $L^2\left(\chi \right)$ to data space Y, for sensor type given by $\mathcal{M}$
${\mathbf{J}}_{F_{\mathcal{M}}}{|}_{{\tau }_0},{\mathbf{J}}_{F_{\mathcal{M}}}{|}_{{\tau }_0}(i,\mathit{x})$, $({\mathbf{J}}_{F_{\mathcal{M}}}{|}_{{\tau }_0}{)}_{ij}$	Jacobian operator of $F_{\mathcal{M}}$ at ${\tau }_0$, its discrete-continuous components, and discretized components
$f_{\left\{i\right\}}\left(\right\{\mathit{z}\};\{a\left\}\right)$	function f with variables $\left\{\mathit{z}\right\}$, experimental parameters $\left\{i\right\}$, and medium parameters $\left\{a\right\}$

2. Inverse problem

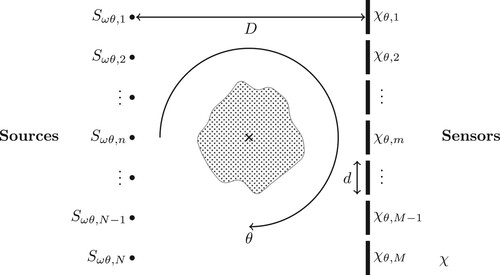
Our goal is to reconstruct the acoustic absorption profile of a region located between an array of ultrasound sources and an array of sensors through transmission UST, using the parallel array geometry shown in Figure 1. This source–sensor geometry can be compared to previous work in both UST as well as traditional x-ray computed tomography. The parallel array consists of a linear array of N point sources $S_{\omega \theta ,n},n\in \{1,\dots ,N\}$ opposing a linear array of M sensors taken to be simply the integral over a finite support function ${\chi }_{\theta ,m}\subset \chi ,m\in \{1,\dots ,M\}$ of width d. We consider an infinite Euclidean domain $\chi ={\mathbb{R}}^2$, so there are no boundary conditions affecting the sound waves. The source and sensor arrays are rotated with respect to their centre point over a range of angles $\theta \in \mathrm{\Theta }$, and the sources are driven at a range of frequencies $\omega \in \mathrm{\Omega }$ in order to capture the full data for the reconstruction problem. The size of the forward model matrix scales linearly with each of the number of sources, sensors, angles, and frequencies.

Figure 1. Parallel array source and sensor geometry where for a rotation of θ the mth sensor occupies a region ${\chi }_{\theta ,m}\subset \chi ={\mathbb{R}}^2$. Each of the M sensors in the array has a diameter of d, and is located at a distance D from the source array which consists of N point sources with continuous-wave signals defined by $S_{\omega \theta ,n}$ for the nth source.

3. Forward models

3.1. Acoustic model

The forward model used in this paper is an acoustic Helmholtz equation with an absorption term implemented through a complex wavenumber, given by the family of equations (1) $S_{\omega \theta ,n}\left(\mathit{x}\right)={\mathcal{L}}_{\omega }(\mathit{x};\tau ,c)P_{\omega \theta ,n}(\mathit{x};\tau ,c),$(1) where $\mathit{x}\in \chi \subset {\mathbb{R}}^2$ is the spatial position, and the equations are parametrized by the source frequency ω, angle θ, and source index n. Parameters which are controlled are written as indices, whereas the absorption and sound speed parameters, τ and c, which are defined by the medium are written in the function argument. Each constant frequency source $S_{\omega \theta ,n}\left(\mathit{x}\right)$ gives rise to a complex acoustic pressure solution $P_{\omega \theta ,n}(\mathit{x};\tau ,c)$ through the differential operator ${\mathcal{L}}_{\omega }(\mathit{x};\tau ,c)$ which has the form (2) ${\mathcal{L}}_{\omega }(\mathit{x};\tau ,c)={\left[\frac{\omega (1+\mathrm{i}\tau (\mathit{x}\left)\right)}{c\left(\mathit{x}\right)}\right]}^2+{\mathrm{\nabla }}^2.$(2) The absorption term τ is dimensionless, but can be related to the usual dimensional absorption coefficient α with units of $\mathrm{d}\mathrm{B}{\mathrm{c}\mathrm{m}}^{-1}$ by the relation (3) $\tau =\frac{100\left[\mathrm{c}\mathrm{m}{\mathrm{m}}^{-1}\right]}{20{\log }_{10}\left(e\right)\left[\mathrm{d}\mathrm{B}{\mathrm{N}\mathrm{p}}^{-1}\right]}\frac{c}{\omega }\alpha ,$(3) which is derived by defining the absorption coefficient to be the imaginary part of the complex wave number in (2(2) ${\mathcal{L}}_{\omega }(\mathit{x};\tau ,c)={\left[\frac{\omega (1+\mathrm{i}\tau (\mathit{x}\left)\right)}{c\left(\mathit{x}\right)}\right]}^2+{\mathrm{\nabla }}^2.$(2) ). This form for the absorption term assumes a linear power law with respect to frequency, $\alpha ={\alpha }_0\omega$, where ${\alpha }_0=\tau /c$.

In this paper, we are only interested in comparing absorption reconstructions, so we assume that the sound speed c is known and has a constant value throughout the medium χ for simplicity. The model does allow for heterogeneous sound speed and absorption, and the effects of a sound speed heterogeneity in the target medium are analysed in Appendix A.

3.2. Measurement model

In this paper, we model the output of each PS sensor as proportional to the integral of the acoustic pressure over the sensor area, for each sensor in the array, and the output of each PI sensor as proportional to the integral of the squared acoustic pressure amplitude over the sensor area. These choices are designed to approximate the behaviour of piezoelectric (PS) sensors, which respond to pressure, and pyroelectric (PI) sensors, which respond to heating. The use of the squared pressure amplitude to model the pyroelectric sensor response follows from the observation that the directional response of a pyroelectric sensor correlates strongly with the directional dependence of the total heat deposition in the sensor with respect to the angle of incidence of an incident ultrasound wave with the sensor [9]. Ultrasonic heat deposition is commonly taken to be proportional to the acoustic pressure amplitude squared [13].

In general we consider the measurement $y_{\omega \theta ,nm}^{\mathcal{M}}$ for $\mathcal{M}$-type sensors at the mth sensor from the nth source at frequency ω and array angle θ to be modelled as the composition of three operators as follows, (4) $y_{\omega \theta ,nm}^{\mathcal{M}}(\tau ,c)=[{\mathcal{I}}_{\theta ,m}\circ \mathcal{M}\circ {\mathcal{L}}_{\omega }^{-1}(\mathit{x};\tau ,c\left)\right]S_{\omega \theta ,n}\left(\mathit{x}\right),$(4) where ${\mathcal{I}}_{\theta ,m}$ is a sampling operator for the mth sensor with rotation θ about the centre, $\mathcal{M}$ is a pointwise field transformation dependent on the type of sensor, and ${\mathcal{L}}_{\omega }^{-1}(\mathit{x};\tau ,c)$ is the inverse Helmholtz operator for an absorption map τ. These operators act as follows: (5) $\begin{array}{rl}{\mathcal{L}}_{\omega }^{-1}(\mathit{x};\tau ,c):S_{\omega \theta ,n}\left(\mathit{x}\right)& \mapsto P_{\omega \theta ,n}(\mathit{x};\tau ,c),\text{by the Helmholtz equation},\end{array}$(5) (6) $\begin{array}{rl}\mathcal{M}:P_{\omega \theta ,n}(\mathit{x};\tau ,c)& \mapsto \{\begin{array}{ll}{P}_{\omega \theta ,n}(\mathit{x};\tau ,c)& \mathrm{p}\mathrm{h}\mathrm{a}\mathrm{s}\mathrm{e}-\mathrm{s}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}\\ |P_{\omega \theta ,n}(\mathit{x};\tau ,c){|}^2& \mathrm{p}\mathrm{h}\mathrm{a}\mathrm{s}\mathrm{e}-\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}\end{array},\end{array}$(6) (7) $\begin{array}{rl}{\mathcal{I}}_{\theta ,m}:\mathcal{M}\left[P_{\omega \theta ,n}\right(\mathit{x};\tau ,c\left)\right]& \mapsto y_{\omega \theta ,nm}^{\mathcal{M}}(\tau ,c)={〈{\mathbf{1}}_{{\chi }_{\theta ,m}},\mathcal{M}\left[P_{\omega \theta ,n}\right(\mathit{x};\tau ,c\left)\right]〉}_{L^2\left(\chi \right)},\end{array}$(7) where ${\mathbf{1}}_{{\chi }_{\theta ,m}}$ is the indicator function on the mth sensor region at rotation θ, and $〈\cdot ,\cdot {〉}_{L^2\left(\chi \right)}$ is the inner product on the Hilbert space of square-integrable functions, $L^2\left(\chi \right)$.

4. Image reconstruction

4.1. Forward problem

We define a forward mappings (8) $\begin{array}{rl}& F_{\mathcal{M}}:L^2\left(\chi \right)\to Y,\end{array}$(8) (9) $\begin{array}{rl}& \tau \mapsto {\mathit{y}}^{\mathcal{M}},\end{array}$(9) which maps the acoustic absorption maps τ to their corresponding measurement vectors ${\mathit{y}}^{\mathcal{M}}$ with components $y_{\omega \theta ,nm}^{\mathcal{M}}$, as described by the measurement model in Equation (4(4) $y_{\omega \theta ,nm}^{\mathcal{M}}(\tau ,c)=[{\mathcal{I}}_{\theta ,m}\circ \mathcal{M}\circ {\mathcal{L}}_{\omega }^{-1}(\mathit{x};\tau ,c\left)\right]S_{\omega \theta ,n}\left(\mathit{x}\right),$(4) ). PS and PI measurements are distinguished by the sensor response mapping $\mathcal{M}$. The absorption maps are described by square-integrable functions over χ, and are thus elements of the Hilbert space $L^2\left(\chi \right)$. The space of data is the complex space $Y={\mathbb{C}}^{|\mathrm{\Omega }||\mathrm{\Theta }|NM}$, where we note that for PI sensors the imaginary part of the measurement is always zero.

4.2. Linear reconstruction scheme

Our reconstructions use a linear inversion scheme using the Fréchet derivative of the measurement model with respect to the parameter of interest, τ [14–16]. The modelled measurement at a desired absorption distribution τ is related to the modelled measurement at a given absorption distribution ${\tau }_0$ through the Taylor expansion of the modelled data at ${\tau }_0$: (10) $\begin{array}{rl}{y}_{\omega \theta ,nm}^{\mathcal{M}}(\tau ,c)& =y_{\omega \theta ,nm}^{\mathcal{M}}({\tau }_0,c)+{\int }_{\chi }\mathrm{d}\mathit{x}{\frac{\delta y_{\omega \theta ,nm}^{\mathcal{M}}}{\delta \tau \left(\mathit{x}\right)}|}_{{\tau }_0}h\left(\mathit{x}\right)\\ & +\frac{1}{2!}{\int }_{\chi }\mathrm{d}{\mathit{x}}^{\prime }{\int }_{\chi }\mathrm{d}\mathit{x}{\frac{{\delta }^2{y}_{\omega \theta ,nm}^{\mathcal{M}}}{\delta \tau \left(\mathit{x}\right)\delta \tau \left({\mathit{x}}^{\prime }\right)}|}_{{\tau }_0}h\left(\mathit{x}\right)h\left({\mathit{x}}^{\prime }\right)+\dots ,\end{array}$(10) where $h\left(\mathit{x}\right)=\tau \left(\mathit{x}\right)-{\tau }_0\left(\mathit{x}\right)$. The first-order linear operator $\frac{\delta y_{\omega \theta ,nm}^{\mathcal{M}}}{\delta \tau \left(\mathit{x}\right)}{|}_{{\tau }_0}=F_{\mathcal{M}}^{\prime }:L^2\left(\chi \right)\to Y$ is the Fréchet derivative for our system evaluated at ${\tau }_0$, i.e. the linearization of the forward mapping from Equation (8(8) $\begin{array}{rl}& F_{\mathcal{M}}:L^2\left(\chi \right)\to Y,\end{array}$(8) ). In the continuous-discrete setting this can be called the Jacobian operator which we can define explicitly as follows: (11) ${{\mathbf{J}}_{F_{\mathcal{M}}}|}_{{\tau }_0}(i,\mathit{x})={\frac{\delta (F_{\mathcal{M}}{)}_i}{\delta \tau \left(\mathit{x}\right)}|}_{{\tau }_0}={\frac{\delta y_{\omega \theta ,nm}^{\mathcal{M}}}{\delta \tau \left(\mathit{x}\right)}|}_{{\tau }_0}={\frac{\delta \left[\right({\mathcal{I}}_{\theta ,m}\circ \mathcal{M}\left)P_{\omega \theta ,n}\right]}{\delta \tau \left(\mathit{x}\right)}|}_{{\tau }_0},$(11) where i indexes over the full set of data parametrized by $\omega ,\theta ,n,$ and m, and the column index is given by the continuum of positions $\mathit{x}\in \chi$. We utilize the adjoint state method to compute the Jacobian operator in Equation (11(11) ${{\mathbf{J}}_{F_{\mathcal{M}}}|}_{{\tau }_0}(i,\mathit{x})={\frac{\delta (F_{\mathcal{M}}{)}_i}{\delta \tau \left(\mathit{x}\right)}|}_{{\tau }_0}={\frac{\delta y_{\omega \theta ,nm}^{\mathcal{M}}}{\delta \tau \left(\mathit{x}\right)}|}_{{\tau }_0}={\frac{\delta \left[\right({\mathcal{I}}_{\theta ,m}\circ \mathcal{M}\left)P_{\omega \theta ,n}\right]}{\delta \tau \left(\mathit{x}\right)}|}_{{\tau }_0},$(11) ) one row at a time by taking the variational derivative of the modelled measurement $y_{\omega \theta ,nm}(\tau ,c)$ with respect to the absorption parameter τ.

We begin by taking an arbitrary variation in the absorption $\tau \left(\mathit{x}\right)\to \tau \left(\mathit{x}\right)+\delta \tau \left(\mathit{x}\right)$ which results in a variation in the pressure $P_{\omega \theta ,n}(\mathit{x};\tau )\to P_{\omega \theta ,n}(\mathit{x};\tau )+\delta P_{\omega \theta ,n}(\mathit{x};\tau )$, where $\delta P_{\omega \theta ,n}(\mathit{x};\tau )=P_{\omega \theta ,n}(\mathit{x};\tau +\delta \tau )-P_{\omega \theta ,n}(\mathit{x};\tau )=\frac{\mathrm{\partial }{P}_{\omega \theta ,n}(\mathit{x};\tau )}{\mathrm{\partial }\tau }\delta \tau \left(\mathit{x}\right)$, and apply this variation to the modelled measurement: (12) $\begin{array}{rl}{y}_{\omega \theta ,nm}^{\mathcal{M}}(\tau +\delta \tau ,c)& =({\mathcal{I}}_{\theta ,m}\circ \mathcal{M})(P_{\omega \theta ,n}+\delta P_{\omega \theta ,n})\\ & ={\mathcal{I}}_{\theta ,m}\left[\mathcal{M}\right(P_{\omega \theta ,n})+{\mathcal{M}}^{\prime }(P_{\omega \theta ,n})\delta P_{\omega \theta ,n}+O(\delta P_{\omega \theta ,n}^2\left)\right]\\ & =({\mathcal{I}}_{\theta ,m}\circ \mathcal{M})P_{\omega \theta ,n}+{\mathcal{I}}_{\theta ,m}\left[{\mathcal{M}}^{\prime }\right(P_{\omega \theta ,n})\delta P_{\omega \theta ,n}+O(\delta P_{\omega \theta ,n}^2\left)\right]\end{array}$(12) Ignoring higher-order terms, we then have that the difference is given by (13) $\begin{array}{rl}\delta y_{\omega \theta ,nm}^{\mathcal{M}}(\tau ,c)& =y_{\omega \theta ,nm}^{\mathcal{M}}(\tau +\delta \tau ,c)-y_{\omega \theta ,nm}^{\mathcal{M}}(\tau ,c)\\ & ={\mathcal{I}}_{\theta ,m}\left[{\mathcal{M}}^{\prime }\right(P_{\omega \theta ,n}\left)\delta P_{\omega \theta ,n}\right]\\ & ={〈{\mathbf{1}}_{{\chi }_{\theta ,m}},\frac{\mathrm{\partial }\left[\mathcal{M}\right(P_{\omega \theta ,n}\left)\right]}{\mathrm{\partial }{P}_{\omega \theta ,n}}\frac{\mathrm{\partial }{P}_{\omega \theta ,n}}{\mathrm{\partial }\tau }\delta \tau \left(\mathit{x}\right)〉}_{L^2\left(\chi \right)}\\ & ={〈{\left(\frac{\mathrm{\partial }\left[\mathcal{M}\right(P_{\omega \theta ,n}\left)\right]}{\mathrm{\partial }{P}_{\omega \theta ,n}}\right)}^{\ast }{\mathbf{1}}_{X_{\theta ,m}},-{\mathcal{L}}_{\omega }^{-1}\frac{\mathrm{\partial }{\mathcal{L}}_{\omega }}{\mathrm{\partial }\tau }{P}_{\omega \theta ,n}\delta \tau \left(\mathit{x}\right)〉}_{L^2\left(\chi \right)}\\ & =-{〈\underset{Z_{\omega \theta ,nm}}{\underbrace{{\left({\mathcal{L}}_{\omega }^{-1}\right)}^{\ast }{\left(\frac{\mathrm{\partial }\left[\mathcal{M}\right(P_{\omega \theta ,n}\left)\right]}{\mathrm{\partial }{P}_{\omega \theta ,n}}\right)}^{\ast }{\mathbf{1}}_{X_{\theta ,m}}}},\frac{\mathrm{\partial }{\mathcal{L}}_{\omega }}{\mathrm{\partial }\tau }{P}_{\omega \theta ,n}\delta \tau \left(\mathit{x}\right)〉}_{L^2\left(\chi \right)}\\ & =-{\int }_{\chi }\frac{\mathrm{\partial }{\mathcal{L}}_{\omega }}{\mathrm{\partial }\tau }{Z}_{\omega \theta ,nm}^{\ast }{P}_{\omega \theta ,n}\delta \tau \left(\mathit{x}\right)\mathrm{d}\mathit{x},\end{array}$(13) where we have used the relation $\frac{\mathrm{\partial }{P}_{\omega \theta ,n}}{\mathrm{\partial }\tau }=-{\mathcal{L}}_{\omega }^{-1}\frac{\mathrm{\partial }{\mathcal{L}}_{\omega }}{\mathrm{\partial }\tau }{P}_{\omega \theta ,n}$, explained in Appendix B. The functional derivative is thus given by (14) $\frac{\delta y_{\omega \theta ,nm}^{\mathcal{M}}(\tau ,c)}{\delta \tau \left(\mathit{x}\right)}=-\frac{\mathrm{\partial }{\mathcal{L}}_{\omega }(\mathit{x};\tau ,c)}{\mathrm{\partial }\tau \left(\mathit{x}\right)}{Z}_{\omega \theta ,nm}^{\ast }(\mathit{x};\tau ,c)P_{\omega \theta ,n}(\mathit{x};\tau ,c).$(14) The left argument of the inner product on the penultimate line of (13(13) $\begin{array}{rl}\delta y_{\omega \theta ,nm}^{\mathcal{M}}(\tau ,c)& =y_{\omega \theta ,nm}^{\mathcal{M}}(\tau +\delta \tau ,c)-y_{\omega \theta ,nm}^{\mathcal{M}}(\tau ,c)\\ & ={\mathcal{I}}_{\theta ,m}\left[{\mathcal{M}}^{\prime }\right(P_{\omega \theta ,n}\left)\delta P_{\omega \theta ,n}\right]\\ & ={〈{\mathbf{1}}_{{\chi }_{\theta ,m}},\frac{\mathrm{\partial }\left[\mathcal{M}\right(P_{\omega \theta ,n}\left)\right]}{\mathrm{\partial }{P}_{\omega \theta ,n}}\frac{\mathrm{\partial }{P}_{\omega \theta ,n}}{\mathrm{\partial }\tau }\delta \tau \left(\mathit{x}\right)〉}_{L^2\left(\chi \right)}\\ & ={〈{\left(\frac{\mathrm{\partial }\left[\mathcal{M}\right(P_{\omega \theta ,n}\left)\right]}{\mathrm{\partial }{P}_{\omega \theta ,n}}\right)}^{\ast }{\mathbf{1}}_{X_{\theta ,m}},-{\mathcal{L}}_{\omega }^{-1}\frac{\mathrm{\partial }{\mathcal{L}}_{\omega }}{\mathrm{\partial }\tau }{P}_{\omega \theta ,n}\delta \tau \left(\mathit{x}\right)〉}_{L^2\left(\chi \right)}\\ & =-{〈\underset{Z_{\omega \theta ,nm}}{\underbrace{{\left({\mathcal{L}}_{\omega }^{-1}\right)}^{\ast }{\left(\frac{\mathrm{\partial }\left[\mathcal{M}\right(P_{\omega \theta ,n}\left)\right]}{\mathrm{\partial }{P}_{\omega \theta ,n}}\right)}^{\ast }{\mathbf{1}}_{X_{\theta ,m}}}},\frac{\mathrm{\partial }{\mathcal{L}}_{\omega }}{\mathrm{\partial }\tau }{P}_{\omega \theta ,n}\delta \tau \left(\mathit{x}\right)〉}_{L^2\left(\chi \right)}\\ & =-{\int }_{\chi }\frac{\mathrm{\partial }{\mathcal{L}}_{\omega }}{\mathrm{\partial }\tau }{Z}_{\omega \theta ,nm}^{\ast }{P}_{\omega \theta ,n}\delta \tau \left(\mathit{x}\right)\mathrm{d}\mathit{x},\end{array}$(13) ) can be understood as the adjoint field $Z_{\omega ,nm}$ through the adjoint equation (15) ${\mathcal{L}}_{\omega }^{\ast }(\mathit{x};\tau ,c)Z_{\omega \theta ,nm}(\mathit{x};\tau ,c)={\left(\frac{\mathrm{\partial }\left\{\mathcal{M}\right[P_{\omega \theta ,n}(\mathit{x};\tau ,c)\left]\right\}}{\mathrm{\partial }{P}_{\omega \theta ,n}(\mathit{x};\tau ,c)}\right)}^{\ast }{\mathbf{1}}_{{\chi }_{\theta ,m}},$(15) where the right-hand side of (15(15) ${\mathcal{L}}_{\omega }^{\ast }(\mathit{x};\tau ,c)Z_{\omega \theta ,nm}(\mathit{x};\tau ,c)={\left(\frac{\mathrm{\partial }\left\{\mathcal{M}\right[P_{\omega \theta ,n}(\mathit{x};\tau ,c)\left]\right\}}{\mathrm{\partial }{P}_{\omega \theta ,n}(\mathit{x};\tau ,c)}\right)}^{\ast }{\mathbf{1}}_{{\chi }_{\theta ,m}},$(15) ) is the adjoint source term. The partial derivative of the Helmholtz operator ${\mathcal{L}}_{\omega }$ with respect to the absorption parameter τ is the imaging condition term, which can be evaluated to be (16) $\frac{\mathrm{\partial }{\mathcal{L}}_{\omega }(\mathit{x};\tau ,c)}{\mathrm{\partial }\tau \left(\mathit{x}\right)}=2\mathrm{i}\frac{{\omega }^2}{c(\mathit{x}{)}^2}[1+\mathrm{i}\tau (\mathit{x}\left)\right].$(16) Once the Jacobian has been computed at some absorption value of ${\tau }_0\left(\mathit{x}\right)$ we can use standard matrix inversion schemes to solve for the absorption $\tau \left(\mathit{x}\right)$ through the linear approximation equation from (10(10) $\begin{array}{rl}{y}_{\omega \theta ,nm}^{\mathcal{M}}(\tau ,c)& =y_{\omega \theta ,nm}^{\mathcal{M}}({\tau }_0,c)+{\int }_{\chi }\mathrm{d}\mathit{x}{\frac{\delta y_{\omega \theta ,nm}^{\mathcal{M}}}{\delta \tau \left(\mathit{x}\right)}|}_{{\tau }_0}h\left(\mathit{x}\right)\\ & +\frac{1}{2!}{\int }_{\chi }\mathrm{d}{\mathit{x}}^{\prime }{\int }_{\chi }\mathrm{d}\mathit{x}{\frac{{\delta }^2{y}_{\omega \theta ,nm}^{\mathcal{M}}}{\delta \tau \left(\mathit{x}\right)\delta \tau \left({\mathit{x}}^{\prime }\right)}|}_{{\tau }_0}h\left(\mathit{x}\right)h\left({\mathit{x}}^{\prime }\right)+\dots ,\end{array}$(10) ) (17) ${\mathit{y}}^{\mathcal{M}}\left(\tau \right)-{\mathit{y}}^{\mathcal{M}}\left({\tau }_0\right)={{\mathbf{J}}_{F_{\mathcal{M}}}|}_{{\tau }_0}(\tau -{\tau }_0)+O\left(h^2\right),$(17) which defines the linearization of our forward model from (8(8) $\begin{array}{rl}& F_{\mathcal{M}}:L^2\left(\chi \right)\to Y,\end{array}$(8) ). For the inverse problem we have data vector ${\mathit{g}}^{\mathcal{M}}$ instead of the modelled data at the true absorption profile, ${\mathit{y}}^{\mathcal{M}}\left(\tau \right)$, so we define our inverse problem through the minimization of the residual in (17(17) ${\mathit{y}}^{\mathcal{M}}\left(\tau \right)-{\mathit{y}}^{\mathcal{M}}\left({\tau }_0\right)={{\mathbf{J}}_{F_{\mathcal{M}}}|}_{{\tau }_0}(\tau -{\tau }_0)+O\left(h^2\right),$(17) ) along with a first-order Tikhonov regulariser term added to better deal with the ill-posedness, (18) $\hat{h}=\underset{h}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}\Vert {{\mathbf{J}}_{F_{\mathcal{M}}}|}_{{\tau }_0}h-[{\mathit{g}}^{\mathcal{M}}-{\mathit{y}}^{\mathcal{M}}({\tau }_0\left)\right]{\Vert }^2+\eta (\Vert {\mathrm{\partial }}_{x}h{\Vert }^2+\Vert {\mathrm{\partial }}_{y}h{\Vert }^2),$(18) where ${\mathit{g}}^{\mathcal{M}}$ is the measured data, ${\mathit{y}}^{\mathcal{M}}\left({\tau }_0\right)$ is the modelled data, $\hat{h}$ is the optimal reconstructed difference in absorption maps $\tau -{\tau }_0$, $\eta \ge 0$ is the regularization parameter, and ${\mathrm{\partial }}_x$, ${\mathrm{\partial }}_y$ are the spatial partial derivatives in the x- and y-directions, respectively, in the domain χ.

If we discretize the domain χ to have $L_x$ pixels in the x-direction and $L_y$ pixels in the y-direction, so that we have a finite collection of position coordinates $\{{\mathit{x}}_j{\}}_{j=1}^{L_x{L}_y}$, then we can express the Jacobian operator from (11(11) ${{\mathbf{J}}_{F_{\mathcal{M}}}|}_{{\tau }_0}(i,\mathit{x})={\frac{\delta (F_{\mathcal{M}}{)}_i}{\delta \tau \left(\mathit{x}\right)}|}_{{\tau }_0}={\frac{\delta y_{\omega \theta ,nm}^{\mathcal{M}}}{\delta \tau \left(\mathit{x}\right)}|}_{{\tau }_0}={\frac{\delta \left[\right({\mathcal{I}}_{\theta ,m}\circ \mathcal{M}\left)P_{\omega \theta ,n}\right]}{\delta \tau \left(\mathit{x}\right)}|}_{{\tau }_0},$(11) ) as a $\left(|\mathrm{\Omega }||\mathrm{\Theta }|NM\right)\times \left(L_x{L}_y\right)$ matrix with discrete components, $({\mathbf{J}}_{F_{\mathcal{M}}}{|}_{{\tau }_0}{)}_{ij}$. We have chosen to use MATLAB's built-in least-squares solver, LSQR, through the augmented matrix ${\mathbf{A}}_{\mathcal{M}}$ and data vector ${\mathit{b}}^{\mathcal{M}}$ given by: (19) ${\mathbf{A}}_{\mathcal{M}}=\left(\begin{array}{c}{{\mathbf{J}}_{{\mathbf{F}}_{\mathcal{M}}}|}_{{\tau }_0}\\ \sqrt{\eta }{\mathrm{\partial }}_x\\ \sqrt{\eta }{\mathrm{\partial }}_y\end{array}\right),{\mathit{b}}^{\mathcal{M}}=\left(\begin{array}{c}{\mathit{g}}^{\mathcal{M}}-{\mathit{y}}^{\mathcal{M}}\left({\tau }_0\right)\\ 0_{L_x{L}_y\times 1}\\ 0_{L_x{L}_y\times 1}\end{array}\right),$(19) to solve the minimization problem in Equation (18(18) $\hat{h}=\underset{h}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}\Vert {{\mathbf{J}}_{F_{\mathcal{M}}}|}_{{\tau }_0}h-[{\mathit{g}}^{\mathcal{M}}-{\mathit{y}}^{\mathcal{M}}({\tau }_0\left)\right]{\Vert }^2+\eta (\Vert {\mathrm{\partial }}_{x}h{\Vert }^2+\Vert {\mathrm{\partial }}_{y}h{\Vert }^2),$(18) ). For each reconstruction $\hat{h}$ we select the regularization parameter η which minimizes the relative error (RE) given by: (20) $\mathrm{R}\mathrm{E}\left(\hat{h}\right)=\frac{\Vert \tau -(\hat{h}+{\tau }_0){\Vert }_2}{\Vert {\tau }_2\Vert }.$(20)

5. Numerical experiments

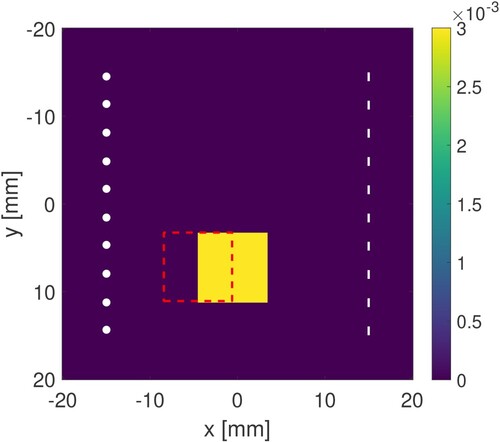
Our modelled absorption profile is homogeneous with a constant dimensionless absorption of ${\tau }_0\left(\mathit{x}\right)=0.003$, whereas the true absorption profile shown in Figure 2 has an equal background value of $\tau \left(\mathit{x}\right)=0.003$ for $\mathit{x}$ outside of the square, and a higher value of $\tau \left(\mathit{x}\right)=0.006$ for $\mathit{x}$ within the square region. The sound speed is set to a constant $c=1540\text{m}{\text{s}}^{-1}$ for both the modelled and measured data, which is a typical sound speed found in human tissue [17, 18]. Hence, we are assuming that the sound speed and background absorption are known exactly. From the absorption transformation Equation (3(3) $\tau =\frac{100\left[\mathrm{c}\mathrm{m}{\mathrm{m}}^{-1}\right]}{20{\log }_{10}\left(e\right)\left[\mathrm{d}\mathrm{B}{\mathrm{N}\mathrm{p}}^{-1}\right]}\frac{c}{\omega }\alpha ,$(3) ) we can see that these dimensionless absorption values correspond to $\alpha \left(\mathit{x}\right)/2\pi \omega =1.06\text{dB}{\text{cm}}^{-1}{\text{MHz}}^{-1}$ for the background, and $\alpha \left(\mathit{x}\right)/2\pi \omega =2.13\text{dB}{\text{cm}}^{-1}{\text{MHz}}^{-1}$ for the square target, which are comparable to the absorption values measured in human tissue [17, 19, 20].

Figure 2. The true absorption difference profile, $\mathrm{\Delta }\tau =\tau -{\tau }_0$, that we wish to reconstruct. Region of interest for contrast analysis is indicated by the dashed red line box with the edge of the square-shaped absorption target acting as the mid-line. The parallel array with 10 point sources (white circles on the left) and 10 line sensors with $1\text{mm}$ diameter (white lines on the right) are shown for the zero rotation case, $\mathrm{\Delta }\theta =0^{\circ }$.

The simulation domain is a $40\text{mm}\times 40\text{mm}$ square which is discretized into a $256\times 256$ pixel grid, so we have that $L_x=L_y=256$ and $\mathrm{d}x=\mathrm{d}y=0.15625\text{mm}$. The square target region in the true absorption profile τ has a side length of 50 pixels or $7.8125\text{mm}$, spanning the range $[100,150]\times [150,200]$ in pixels or $[-4.4706,3.3725]\times [3.3725,11.2157]\text{mm}$ in the spatial domain χ. The perfectly matched layer (PML) is implemented as a quadratic absorbing function [21] spanning 5 pixels ($\approx 0.78\text{mm}$) on all sides of the domain.

Our parallel array consists of 10 point sources spanning a distance of $30\text{mm}$ and an array of 10 sensors of width d spanning the same $30\text{mm}$ distance. The source and sensor arrays are $30\text{mm}$ apart. The point sources each have an amplitude of $1\text{Pa}$, although this choice is arbitrary in the numerical setting as it only affects the scale of the measurements.

Our choices of ${\tau }_0$ and c exhibit rotational symmetry, since they are both spatially constant, and hence we only need to compute the rows of our Jacobian using (14(14) $\frac{\delta y_{\omega \theta ,nm}^{\mathcal{M}}(\tau ,c)}{\delta \tau \left(\mathit{x}\right)}=-\frac{\mathrm{\partial }{\mathcal{L}}_{\omega }(\mathit{x};\tau ,c)}{\mathrm{\partial }\tau \left(\mathit{x}\right)}{Z}_{\omega \theta ,nm}^{\ast }(\mathit{x};\tau ,c)P_{\omega \theta ,n}(\mathit{x};\tau ,c).$(14) ) for a single angle $\theta \in \mathrm{\Theta }$. The rest of the rows can be computed by taking the sensitivity map from the computed row $i\equiv \omega ,\theta ,n,m$, and rotating it by an angle ${\theta }^{\prime }-\theta$ about the centre of the parallel array to get the corresponding sensitivity map for row $i^{\prime }\equiv \omega ,{\theta }^{\prime },n,m$. This reduces the number of forward (P) and adjoint (Z) field computations by a factor of $|\mathrm{\Theta }|$. For media with translation and reflection symmetry, in the case of identical sources and sensors, further optimisations may be made by computing a sensitivity map between source n and sensor m, and then performing the appropriate translation and reflection to get the corresponding sensitivity map between source $n^{\prime }$ and sensor $m^{\prime }$ that have the same, up to a reflection, relative displacement from each other as the original pair. This latter optimization was not done for our computations, but it could further reduce the number of forward and adjoint field computations by a factor of N.

We want to compare the quality of the absorption reconstructions as three parameters are varied for each of the two sensor types: number of angles, number of source frequencies, and sensor size. The number of angles and frequencies control for the amount of data provided by the measurements, and hence give us information about how the reconstruction qualities scale with varying levels of data sparsity. The sensor size affects the directional response of the detector as well as the signal strength, and thus varying this parameter provides us with information about how well each sensor responds to an increase in sensor size.

The sets of angles are constant increment subsets of $\theta \in [0^{\circ },{180}^{\circ })$, for the increments $\mathrm{\Delta }\theta ={7.5}^{\circ }$, ${15}^{\circ }$, ${30}^{\circ }$, and ${60}^{\circ }$. The source frequencies are an odd number of constant increment frequencies centred around $2\text{MHz}$; we consider the two sets of frequencies $\mathrm{\Omega }/\text{MHz}=\left\{2\right\}$ and $\mathrm{\Omega }/\text{MHz}=\{1.5,1.75,2,2.25,2.5\}$. Sensors of width $1\text{mm}$ and $5\text{mm}$ are considered, arranged into a linear array of 10 sensors spanning a distance of $30\text{mm}$. The $5\text{mm}$ sensor array contains overlapping sensors, which can be realized physically by spatially translating a non-overlapping sensor array. Key simulation parameters are summarized in Table 2.

Table 2. Model parameters used for simulations.

Parameter (units)	Value(s)
Source frequency $\omega /2\pi$ (MHz)	1.5, 1.75, 2, 2.25, 2.5
Diameter of sensor d (mm)	1, 5
Rotation increment $\mathrm{\Delta }\theta$ (degrees)	7.5, 15, 30, 60
Source amplitude (Pa)	1
Source – sensor array separation D (mm)	30
Source array length (mm)	30
Sensor array length (mm)	30
Domain spatial dimensions x, y (mm)	40, 40
Domain pixel dimensions $L_x,L_y$ (pixels)	256, 256
Domain spatial increment dx = dy (mm)	0.15625
PML pixel width (pixels)	5

Both noise-free and noisy data are used for reconstructions. For noisy data, additive Gaussian noise scaled by a factor of $1\mathrm{\%}$ of the maximum sensor signal has been applied. This assumes that the noise originates from the sensor devices themselves in such a way that the noise-level is proportional to the maximum signal response of the sensor: (21) ${\mathit{g}}^{\mathcal{M}}\mapsto {\mathit{g}}^{\mathcal{M}}+0.01\cdot max|{\mathit{g}}^{\mathcal{M}}|\cdot \mathit{ϵ},$(21) where ${\mathit{g}}^{\mathcal{M}}$ is the measured data for sensor type $\mathcal{M}$, and $\mathit{ϵ}$ is a vector of random numbers with the same size as the measured data vector ${\mathit{g}}^{\mathcal{M}}$, and components ${ϵ}_i\in \mathcal{N}(0,1)$ that follow the standard normal distribution.

5.1. Contrast analysis

In order to quantitatively judge the quality of the reconstructions, we use two different contrast metrics: the modulation transfer function (MTF), and the weighted root mean square (RMS) contrast weighted by the maximum value of the reconstruction. See Appendix C for more details on these contrast metrics. To make the computation of these contrast metrics as easy as possible, the reconstruction target under consideration here is a square of constant absorption, shown in Figure 2.

The MTF full width at half maximum (FWHM) for the true absorption difference profile is infinite, since the edge is a perfect step function in theory. The maximum weighted RMS contrast is 0.5 for the true absorption difference profile in a region of interest where half the region consists of the background profile, and the second half consists of the target profile, as indicated by the dashed-line box in Figure 2.

5.2. Results

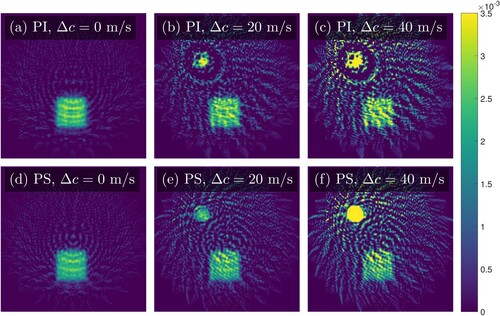
We find that in the noise-free cases the PS sensors are typically dominant in MTF FWHM, RMS contrast, and relative error, except for some of the 3-angle reconstructions. In particular, PI sensors outperform PS sensors in the noise-free case for all metrics when the sensor array has $5\text{mm}$ sensors and only one frequency is measured for 3 angles of the parallel array. There is also an outlier case of PI sensors outperforming PS sensors with $1\text{mm}$ sensors for 5 frequencies and 3 angles. When 1% noise is added, the PI sensors perform closer to the PS sensors under these metrics, and outperform them for more cases than in the noise-free case. Now, PI sensors outperform PS sensors for all three metrics when the sensor array has $5\text{mm}$ sensors for both 1 or 5 frequencies and for 3 angles for the parallel array; the RE and MTF FWHM metrics are also superior for the PI sensors in the case of 6 angles for the previous conditions. For $1\text{mm}$ sensors with 1% noise added, the cases where PI sensors outperform PS sensors it less ordered, but still mostly limited to the sparse data regime. With $1\text{mm}$ sensors and only one frequency, all three metrics are better for PI sensors for the case of 3 angles, with RE remaining better for PI sensors in the case of 6 angles as well, and MTF FWHM remaining better for PI sensors for the case of 5 frequencies. The RMS contrast favours PI sensors in the 5 frequency case for 3, 6, and 12 angles. 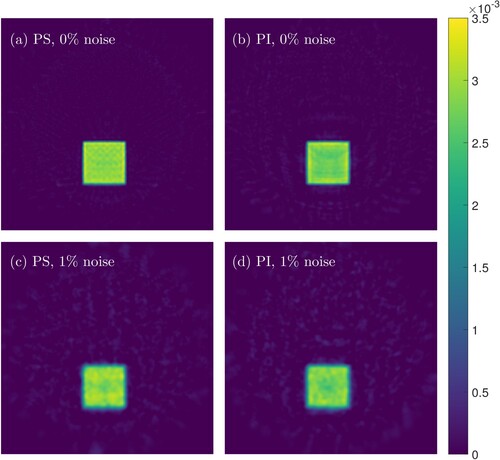We can see examples of these sparse data reconstructions for $5\text{mm}$ sensors in Figure 3. In the full data regime, where we have 24 angles and 5 frequencies, the PS sensors beat or match the PI sensors in all metrics. The full data reconstructions for the $1\text{mm}$ sensors can be seen in Figure 4.

Figure 3. Reconstructions for PS and PI sensor types with 3 angles, 1 frequency ($\mathrm{\Omega }/\text{MHz}=\left\{2\right\}$), and $d=5\text{mm}$ sensors. (a) PS reconstruction with 0% noise. (b) PI reconstruction with 0% noise. (c) PS reconstruction with 1% noise. (d) PI reconstruction with 1% noise.

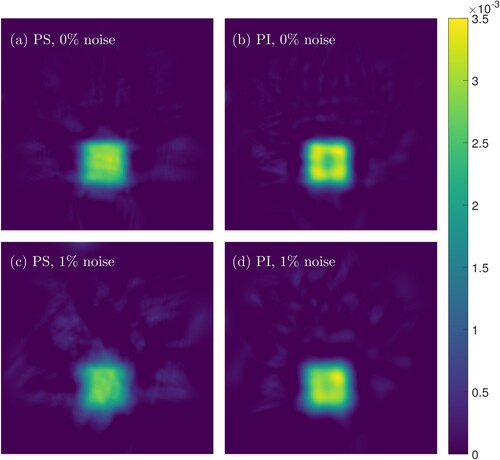
Figure 4. Reconstructions for PS and PI sensor types with 24 angles, 5 frequencies ($\mathrm{\Omega }/\text{MHz}=\{1.5,1.75,2,2.25,2.5\}$), and $d=1\text{mm}$ sensors. (a) PS reconstruction with 0% noise. (b) PI reconstruction with 0% noise. (c) PS reconstruction with 1% noise. (d) PI reconstruction with 1% noise.

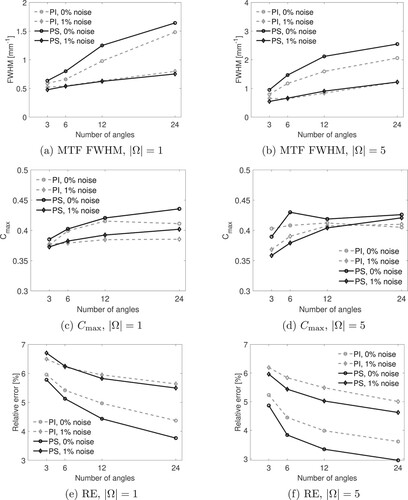
The contrast metrics for the different cases are summarized in Figures 5 and 6. The greatest advantage for PI sensors is achieved with noisy data when the sensor is large in the sparse data regime, which we can see visually in Figure 5(a), (c), and (e). In these sparse data scenarios it is likely that the phase-cancellations arising from the summing of the relative phases across the sensor for PS sensors leads to a loss of information that cannot be corrected due to the lack of enough data, leading to a loss of quality in the reconstruction. This idea is supported by the observation that all three of the considered quality metrics are much closer between the PI and PS sensors in the sparse data regime when using $1\text{mm}$ sensors, as seen in Figure 6(a), (c), and (e), which will cause less phase-cancellation compared to the larger $5\text{mm}$ sensors. When the data has been sampled sufficiently densely, then the PS sensors overcome the phase-cancellation issue and are able to surpass the PI sensors due to having access to both amplitude and phase data, rather than only amplitude data.

Figure 5. Contrast analysis and error curves for $5\text{mm}$ sensors. The plots on the left column show quantities for single-frequency reconstructions, whereas the right column shows the same quantities for 5-frequency reconstructions. (a)–(b) show the MTF FWHM, (c)–(d) show the maximum normalized contrasts, and (e)–(f) show the relative errors. The solid curves correspond to PS reconstructions whereas the dashed curves correspond to the PI reconstructions. The markers along the curves correspond to the noise-free (l) and noisy (♦) cases. (a) MTF FWHM, $|\mathrm{\Omega }|=1$, (b) MTF FWHM, $|\mathrm{\Omega }|=5$, (c) $C_{\mathrm{m}\mathrm{a}\mathrm{x}}$, $|\mathrm{\Omega }|=1$, (d) $C_{\mathrm{m}\mathrm{a}\mathrm{x}}$, $|\mathrm{\Omega }|=5$, (e) RE, $|\mathrm{\Omega }|=1$ and (f)RE, $|\mathrm{\Omega }|=5$.

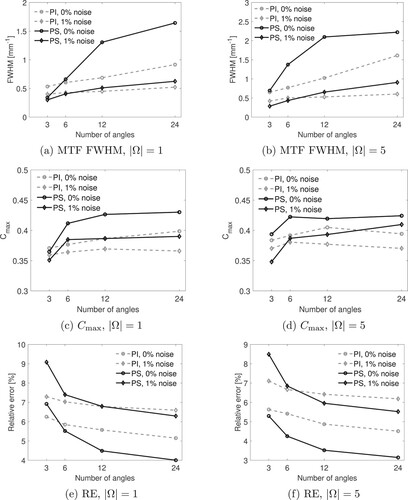
Figure 6. Contrast analysis and error curves for $1\text{mm}$ sensors. The plots on the left column show quantities for single frequency reconstructions, whereas the right column shows the same quantities for 5-frequency reconstructions. (a)–(b) show the MTF FWHM, (c)–(d) show the maximum normalized contrasts, and (e)–(f) show the relative errors. The solid curves correspond to PS reconstructions whereas the dashed curves correspond to the PI reconstructions. The markers along the curves correspond to the noise-free (l) and noisy (♦) cases. (a) MTF FWHM, $|\mathrm{\Omega }|=1$. (b) MTF FWHM, $|\mathrm{\Omega }|=5$. (c) $C_{\mathrm{m}\mathrm{a}\mathrm{x}}$, $|\mathrm{\Omega }|=1$. (d) $C_{\mathrm{m}\mathrm{a}\mathrm{x}}$, $|\mathrm{\Omega }|=5$. (e) RE, $|\mathrm{\Omega }|=1$ and (f)RE, $|\mathrm{\Omega }|=5$.

6. Conclusion

We have shown that phase-insensitive ultrasound sensors can outperform traditional phase-sensitive sensors in limited data situations, especially with large sensors – producing superior contrast in absorption reconstructions both globally and across different spatial frequencies, and having a smaller relative error in the reconstruction compared to the ground truth absorption profile.

Some uncertainty does arise from the choice of regulariser as well as regularization parameter for the reconstructions. We chose a standard Tikhonov regulariser that penalizes higher magnitude gradients, which does a good job of making the reconstructions stable especially with the presence of noise. However, the amount of regularization needs to be carefully balanced in order to make fair comparisons across different reconstructions. Greater regularization smooths out the reconstruction which improves global contrast at the cost of losing edge sharpness, and hence reducing the MTF FWHM. Similarly, lower regularization leaves more artifacts in the reconstruction which decrease contrast, but generally leaves the edge profile more sharp, leading to a better MTF FWHM measure. The relative error minimizer approach was quite effective at picking a regularization parameter that balanced these factors quite well. Selecting the regularization parameter as the maximizer of the global contrast produced marginal improvements in that particular measure, while generally decreasing the MTF FWHM metric as well as the relative error of the reconstruction.

There is also a possibility that our simple linear inversion approach leaves one of the sensor types at a comparative disadvantage in certain situations. Nonlinear inversion schemes could be tested in select cases to see if notable relative differences in these contrast measures arise.

Acknowledgments

We thank Antonio Stanziola for being the primary developer and tester for the Helmholtz equation solver code used in this paper. We thank Bajram Zeqiri, Christian Baker, and David Sinden for helpful discussions regarding pyroelectric ultrasound sensors. We also thank Nathaniel J. Smith, Stefan van der Walt, and Eric Firing for the development of the viridis colourmap used in this paper.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was supported by the National Physical Laboratory UK [grant number 551235 F48 UCT].

Appendices

Appendix 1. Jacobian robustness to sound speed heterogeneity

For the purpose of contrast analysis the Jacobians corresponding to the linearized forward problem are computed with the assumption of a homogeneous medium in both sound speed and acoustic absorption. Inverting measurements from mediums that deviate significantly from the linearization point leads to errors in the reconstruction, the magnitude of which depends on the degree of deviation. Here we investigate the robustness of the Jacobian approach by considering a simple circular perturbation in sound speed in the true medium with a radius of $3.91\text{mm}$ (25 pixels), and we attempt to reconstruct the square-shaped absorption region with this additional perturbation in sound speed. The profile for the acoustic medium is shown in Figure A1.

Figure A1. Profile for acoustic medium used for testing Jacobian robustness for sound speed heterogeneities. (a) Binary image of disk-shaped sound speed and square-shaped absorption perturbations in the acoustic medium and (b) Disk-shaped sound speed perturbation for the case of a sound speed deviation $\mathrm{\Delta }c=30$ [m/s] from the background value.

For brevity, we consider only the single frequency Jacobians for 3 and 12 angles corresponding to a source frequency of $2\text{MHz}$, with a sensor array with $1\text{mm}$ width sensors. The Jacobians have been computed with a homogeneous background medium in both absorption and sound speed. We ignore noise and perform reconstructions for two regularization cases: where the regularization parameter minimizes the relative error, and where it is set to zero. Both PI and PS sensors are tested in all cases. 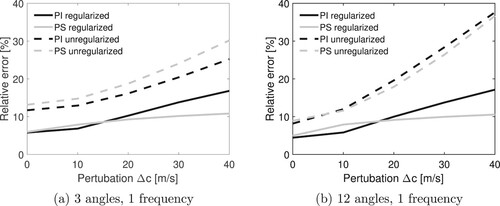We consider sound speed perturbations of varying magnitude, $\mathrm{\Delta }c/\left[\text{m/s}\right]\in \{0,10,20,30,40\}$, and compute the relative error of the corresponding reconstructions to get the error curves shown in Figure A2.

Figure A2. Relative ${\ell }_2$ error for reconstructions with increasing sound speed perturbation magnitude for a disk-shaped sound speed perturbation with a radius of $3.91\text{mm}$ (25 pixels). (a) 3 angles, 1 frequency and(b) 12 angles, 1 frequency

The reconstructions for PI and PS sensors for perturbations of $\mathrm{\Delta }c=0,20$, and $40\text{m/s}$ are shown in Figure A3 for the case of 3 angles with optimal regularization parameter, Figure A4 for 12 angles with optimal regularization parameter, Figure A5 for 3 angles without regularization, and Figure A6 for 12 angles without regularization.

Figure A3. 3 angle minimum error reconstructions for the square-shaped absorption perturbation for varying magnitudes of the disk-shaped sound speed perturbation.

Figure A4. 12 angle minimum error reconstructions for the square-shaped absorption perturbation for varying magnitudes of the disk-shaped sound speed perturbation.

Figure A5. 3 angle unregularised reconstructions for the square-shaped absorption perturbation for varying magnitudes of the disk-shaped sound speed perturbation.

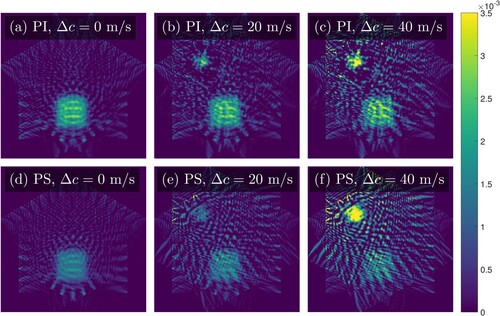
Figure A6. 12 angle unregularised reconstructions for the square-shaped absorption perturbation for varying magnitudes of the disk-shaped sound speed perturbation.

We see that the relative error in the reconstruction is quite small for small sound speed perturbation magnitudes, but the false absorption reconstruction becomes apparent even for the small perturbations when the Jacobian has been computed with the assumption of a homogeneous sound speed distribution.

Appendix 2

Operator derivative relation

The differential operator ${\mathcal{L}}_{\omega }$ is linear, and we assume the boundary conditions allow for unique solutions such that the operator inverse ${\mathcal{L}}_{\omega }^{-1}$ exists and is well-defined. We can then write the following for the derivative with respect to $\tau \left(\mathit{x}\right)$: (A1) $\begin{array}{rl}0& =\frac{\mathrm{\partial }{\mathrm{I}\mathrm{d}}_{L^2\left(\chi \right)}}{\mathrm{\partial }\tau \left(\mathit{x}\right)}=\frac{\mathrm{\partial }\left\{{\mathcal{L}}_{\omega }^{-1}\right(\mathit{x};\tau ,c\left){\mathcal{L}}_{\omega }\right(\mathit{x};\tau ,c\left)\right\}}{\mathrm{\partial }\tau \left(\mathit{x}\right)}\end{array}$(A1) (A2) $\begin{array}{rl}& =\frac{\mathrm{\partial }{\mathcal{L}}_{\omega }^{-1}(\mathit{x};\tau ,c)}{\mathrm{\partial }\tau \left(\mathit{x}\right)}{\mathcal{L}}_{\omega }(\mathit{x};\tau ,c)+{\mathcal{L}}_{\omega }^{-1}(\mathit{x};\tau ,c)\frac{\mathrm{\partial }{\mathcal{L}}_{\omega }(\mathit{x};\tau ,c)}{\mathrm{\partial }\tau \left(\mathit{x}\right)}.\end{array}$(A2) By rearranging this expression we get the following: (A3) $\frac{\mathrm{\partial }{\mathcal{L}}_{\omega }^{-1}(\mathit{x};\tau ,c)}{\mathrm{\partial }\tau \left(\mathit{x}\right)}=-{\mathcal{L}}_{\omega }^{-1}(\mathit{x};\tau ,c)\frac{\mathrm{\partial }{\mathcal{L}}_{\omega }(\mathit{x};\tau ,c)}{\mathrm{\partial }\tau \left(\mathit{x}\right)}{\mathcal{L}}_{\omega }^{-1}(\mathit{x};\tau ,c).$(A3) It thus follows from (1(1) $S_{\omega \theta ,n}\left(\mathit{x}\right)={\mathcal{L}}_{\omega }(\mathit{x};\tau ,c)P_{\omega \theta ,n}(\mathit{x};\tau ,c),$(1) ) that since the sources $S_{\omega \theta ,n}\left(\mathit{x}\right)$ are independent of the absorption distribution τ, that (A4) $\begin{array}{rl}\frac{\mathrm{\partial }{P}_{\omega \theta ,n}(\mathit{x};\tau ,c)}{\mathrm{\partial }\tau \left(\mathit{x}\right)}& =\frac{\mathrm{\partial }\left[{\mathcal{L}}_{\omega }^{-1}\right(\mathit{x};\tau ,c\left)S_{\omega \theta ,n}\right(\mathit{x}\left)\right]}{\mathrm{\partial }\tau \left(\mathit{x}\right)}=\frac{\mathrm{\partial }{\mathcal{L}}_{\omega }^{-1}(\mathit{x};\tau ,c)}{\mathrm{\partial }\tau \left(\mathit{x}\right)}{S}_{\omega \theta ,n}\left(\mathit{x}\right)\end{array}$(A4) (A5) $\begin{array}{rl}& ={\mathcal{L}}_{\omega }^{-1}(\mathit{x};\tau ,c)\frac{\mathrm{\partial }{\mathcal{L}}_{\omega }(\mathit{x};\tau ,c)}{\mathrm{\partial }\tau \left(\mathit{x}\right)}{P}_{\omega \theta ,n}(\mathit{x};\tau ,c).\end{array}$(A5)

Appendix 3

Contrast analysis

We use the MTF definition from [10], given as the normalized Fourier transform of the line spread function (LSF), (A6) $\mathrm{M}\mathrm{T}\mathrm{F}\left(k\right)=\frac{|{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\mathrm{L}\mathrm{S}\mathrm{F}\left(x\right){\mathrm{e}}^{2\pi \mathrm{i}kx}\mathrm{d}x|}{{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\mathrm{L}\mathrm{S}\mathrm{F}\left(x\right)\mathrm{d}x},$(A6) where the LSF is defined as the spatial derivative of the edge spread function (ESF), $\mathrm{L}\mathrm{S}\mathrm{F}\left(x\right)=\frac{\mathrm{d}}{\mathrm{d}x}\mathrm{E}\mathrm{S}\mathrm{F}\left(x\right)$ in the axial direction.

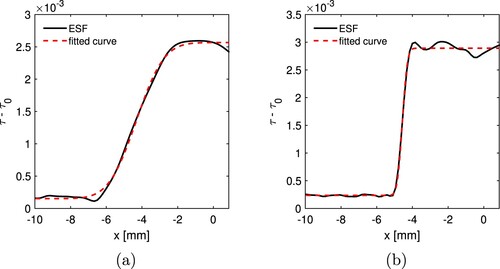
We compute the MTF by fitting an error function to the ESF, defined by the expression (A7) $f\left(x\right)=\frac{B}{2}\mathrm{e}\mathrm{r}\mathrm{f}\left(\frac{x-\mu }{\sqrt{2}\sigma }\right)+r,$(A7) where B, μ, σ, and r are the fitting parameters. We fit f to the ensemble average of the ESFs comprising the interface between the background medium and the square target in the absorption reconstruction, as seen in Figure A7. By fitting an error function to the ESF we are assuming that the LSF is Gaussian, and hence by (A6(A6) $\mathrm{M}\mathrm{T}\mathrm{F}\left(k\right)=\frac{|{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\mathrm{L}\mathrm{S}\mathrm{F}\left(x\right){\mathrm{e}}^{2\pi \mathrm{i}kx}\mathrm{d}x|}{{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\mathrm{L}\mathrm{S}\mathrm{F}\left(x\right)\mathrm{d}x},$(A6) ) the MTF is a Gaussian of the form (A8) $\mathrm{M}\mathrm{T}\mathrm{F}\left(k\right)=\exp (-2{\pi }^2{\sigma }^2{k}^2).$(A8) The full width at half maximum (FWHM) of the MTF function in (A8(A8) $\mathrm{M}\mathrm{T}\mathrm{F}\left(k\right)=\exp (-2{\pi }^2{\sigma }^2{k}^2).$(A8) ) gives us a single number that can quantify how well a given reconstruction can recover the target across multiple levels of detail, and it is given by the equation (A9) $\mathrm{F}\mathrm{W}\mathrm{H}\mathrm{M}\left(\sigma \right)=\frac{2\ln 2}{\pi \sigma },$(A9) which means that we can compute the FWHM directly from the σ parameter of the fitted error function in (A7(A7) $f\left(x\right)=\frac{B}{2}\mathrm{e}\mathrm{r}\mathrm{f}\left(\frac{x-\mu }{\sqrt{2}\sigma }\right)+r,$(A7) ).

Figure A7. Error function f (red dashed line) fitted to the ensemble average of ESFs (solid black line) for the cases of (a) $d=5\text{mm}$ PS sensors with 3 angles, 1 frequency, and $1\mathrm{\%}$ noise, and (b) $d=1\text{mm}$ PS sensors with 24 angles, 5 frequencies, and $1\mathrm{\%}$ noise.

The weighted RMS contrast is defined as the standard deviation in the weighted pixel intensities of the reconstruction $\hat{h}$ in a region of interest. Two examples of constant weights are the mean value, $w_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}=〈\hat{h}\left(\mathit{x}\right){〉}_X$, and the maximum value, $w_{\mathrm{m}\mathrm{a}\mathrm{x}}=\underset{X}{max}\hat{h}\left(\mathit{x}\right)$. In this paper we use $w_{\mathrm{m}\mathrm{a}\mathrm{x}}$. With both choices of weighting the weighted RMS contrast is given by: (A10) $C_w=\sqrt{\frac{1}{L_x{L}_y}\sum _{i=1}^{L_x}\sum _{j=1}^{L_y}\frac{{({\hat{h}}_{ij}-〈\hat{h}〉)}^2}{w^2}}.$(A10)