Optimizing disaster relief goods distribution and transportation: a mathematical model and metaheuristic algorithms

Abstract

The effective distribution of relief goods is critical in mitigating the impact of natural disasters and preserving human life. This study addresses a relief goods distribution problem, assuming the existence of multiple relief orders that must be delivered to various disaster-stricken regions from a network of warehouses using a fleet of diverse vehicles. The objective is to identify the most suitable warehouse for each relief order, allocate relief orders to vehicles, batch the orders in the designated vehicles, and devise routing plans to minimize the total delivery time. A mixed-integer linear programming model is formulated to tackle this problem. Owing to the problem’s NP-hard nature, a metaheuristic algorithm, known as the Multiple League Championship Algorithm, is developed. Furthermore, two innovative variants of the MLCA , namely the League Base Multiple League Championship Algorithm (L- MLCA) and the Playoff Multiple League Championship Algorithm (P-MLCA), are introduced.Experimental results indicate that the P-MLCA outperforms the other two algorithms. The solutions derived from the P-MLCA are compared with the optimal solutions obtained by a commercial solver for small-scale problems. This comparative analysis demonstrates the promising performance of the P-MLCA in finding the optimal distribution of relief goods.

KEYWORDS:

• Disaster-stricken regions
• mixed-integer linear programming
• multiple league championship algorithm
• order batching
• routing planning

MATHEMATICS SUBJECT CLASSIFICATIONS:

• 90C05
• 90C11
• 90B06
• 90B80
• 62P30
• 90C90

1. Introduction

Natural and man-made disasters have always had profound impacts on human lives. The frequency of such disasters is on the rise globally, significantly increasing the number of people affected and the associated costs [1]. In the twentieth century, the world experienced 22,000 natural and man-made disasters resulting in approximately 8 million deaths [2]. Moreover, many tragic disasters have occurred in the current century, such as the Nepal earthquake in 2015, which led to 8569 deaths, 100,000 injuries, and 384 missing individuals [3]. The Haiti earthquake in 2010 caused approximately 200,000 fatalities [4], and the Indian Ocean tsunami in 2004 resulted in 225,000 deaths [5]. In addition, the coronavirus pandemic (COVID-19) has led to over 6 million deaths worldwide [6,7]. The unpredictable nature of disasters underscores the necessity for proper planning to effectively encounter them [8–11]. An accurate plan to tackle these situations facilitates immediate action and can save human lives [12], which highlights the importance of Humanitarian logistics (HL).

The HL includes activities such as disaster planning and preparedness, procurement, transportation, and warehousing [13]. The distribution of relief goods is a critical component of HL, involving aspects such as transportation scheduling, vehicle selection, route planning, and the allocation of goods to vehicles. Due to its significance, the relief goods distribution problem (RGDP) has been introduced as an optimization problem in the literature [14]. The RGDP concerns delivering relief goods from warehouses to damaged regions using a fleet of vehicles, assuming each region has a unique relief order. Providing a solution to RGDP requires the identification of appropriate warehouses for each relief order, allocating suitable vehicles to each order, and determining the loading priority for each relief order within the vehicle.

This study addresses a specific variant of RGDP with multiple relief warehouses and several damaged regions in various geographical areas. Additionally, it is presumed that each damaged region requires different relief orders, and various vehicles with distinct capacities and speeds are available to transport relief orders from warehouses to the affected areas. Given this RGDP, this study aims to minimize the total delivery time of relief orders to the damaged regions by optimally assigning the relief orders to warehouses and vehicles and determining the relief orders’ batching and transportation priority.

To address the RGDP, the problem is mathematically formulated as a mixed-integer linear programming (MILP) model. Considering the complex nature of the problem, a metaheuristic algorithm known as the multiple league championship algorithm (MLCA) and two novel variants of it, namely league base MLCA (L-MLCA) and playoff MLCA (P-MLCA), are proposed to solve the problem. The MLCA draws inspiration from league championships, where several teams compete randomly in a national league format. The best national league teams advance to the group stage. The league teams compete again, and the top teams proceed to the playoff stage. Eventually, one team becomes the champion.

The results of this study will assist decision-makers in making effective plans for relief goods distribution. This will be achieved by optimally determining the suitable warehouse to supply each relief order, assigning relief orders to vehicles, creating order batches, and determining vehicle routing, all within a reasonable timeframe while ensuring the minimum delivery time of relief orders. By minimizing the total delivery time of relief orders, the proposed solution in this study could play a pivotal role in mitigating the effects of disasters, such as reducing losses and alleviating suffering.

While this study presents efficient solution approaches to the relief goods distribution problem (RGDP), it has certain limitations. Firstly, the study is based on the assumption of multiple warehouses, multiple vehicle types, and damaged regions in different geographical areas. This assumption may not represent all disaster situations, limiting the generalizability of the findings. Secondly, the formulated mixed-integer linear programming (MILP) model may not always provide optimal solutions due to the inherent complexity of the problem. Thirdly, the MLCA and its variants are heuristic methods; therefore, finding the absolute optimal solution is not guaranteed.

In summary, the novelty of this study lies in its proposed solution approach mathematical formulation of the RGDP. By considering variables such as multiple warehouses, diverse vehicles, and relief order batching, the research aims to align the problem definition more closely with real-world scenarios. A MILP model is developed to optimize the allocation and transportation of relief goods. Additionally, two innovative variants of the MLCA, namely L-MLCA and P-MLCA, are introduced to cope with the problem’s complexity.

The rest of this study is organized as follows. Section 2 provides a review of the relevant studies on the RGDP. The problem description and mathematical formulation are given in Section 3. The MLCA and its two new variants, L-MLCA and P-MLCA, are introduced in Section 4. Computational experiments are discussed in Section 5. Finally, conclusions and suggestions for future research are presented in Section 6.

2. Literature review

This section provides an overview of the most relevant studies on RGDP.

Zheng and Ling [15] proposed a heuristic algorithm to solve the transportation planning problem in relief goods distribution, using a participatory method considering multi-objective optimization and three correlated ranking criteria to reduce uncertainty. Ruan et al. [16] considered helicopters and vehicles as transportation modes in an emergency medical supply chain and presented the mathematical model of the problem. They proposed a fuzzy clustering-based optimization model that takes into account helicopter travel, transfer, and vehicle delivery time to optimize intermodal transportation. Ben Othman et al. [17] considered multiple agents for emergency supply chain management, wherein one agent controls each zone. Their main goal was to obtain an optimal schedule to deliver resources from suppliers to critical zones for responding to emergencies. They developed a mathematical model and a decision support system based on the branch and bound (B&B) algorithm.

Manopiniwes and Irohara [18] proposed a mathematical model for an integrated problem, in which the three main principles of emergency logistics were considered: facilities, transportation, and scheduling. They provided a multi-objective planning model using the normalized weight summation method. Condeixa et al. [19] proposed a mathematical model for pre-positioning, locating, and distributing relief goods in the relief supply chain to minimize operational and risk-related costs. The supply chain considered in their study assumed the existence of some candidate points in establishing distribution centres. They also considered the number of distribution centres within a certain range and assumed that the capacity of each centre for the storage of each relief order is limited. Loree and Aros-Vera [20] provided a mathematical model and a heuristic algorithm to determine the location of distribution points and inventory allocation in the relief supply chain, aiming to minimize the cost of location, logistics, and deprivation of facilities. Sabouhi et al. [21] discussed an integrated transportation and distribution system for the routing and planning of vehicles to transport people and relief goods. They formulated the problem as a linear mathematical model, aiming to minimize the total travel time of vehicles to damaged zones, shelters, and distribution centres. Given the complexity of the problem, they also proposed a genetic algorithm (GA) as a solution method.

Shavarani [22] used a multi-level facility location problem to find the optimal number of relief stations, assuming that demand occurred based on the Poisson distribution. After presenting the mathematical model of the problem, a hybrid GA was proposed to solve the model. The proposed method improved the efficiency and responsiveness of the relief supply chain. Liu and Song [23] proposed a discrete-time mixed integer linear programming (MILP) model to minimize the total response time and operational costs in a blood supply network. Their model aimed at facilitating decisions regarding the amount of blood collection, location of blood collection stations, transport vehicles needed, and storage requirements. Sakiani et al. [24] discussed an inventory-routing problem to redistribute relief goods in a supply chain to minimize the sum of deprivation and operating costs. This research divided the problem into the main problem and a sub-problem. They proposed a simulated annealing algorithm to solve the main problem and used a commercial solver to solve the sub-problem.

Ghaffari et al. [25] presented a mathematical model and particle swarm optimization (PSO) to minimize the total weighted completion times of services at hospitals in an emergency supply chain with multiple resources in disaster relief operations. Wang and Chen [26] discussed a blood supply chain in the context of disasters. In the considered supply chain, blood was transferred from some permanent and temporary collection facilities to some transfusion centres. They proposed a novel robust model for the problem to optimize blood inventory pre-positioning and relief activities Zhong et al. [27] discussed a location-routing problem in a relief supply chain considering stochastic demands. They proposed a genetic algorithm and a non-dominated sorting genetic algorithm to minimize the supply chain’s total waiting times and costs. The total waiting time objective function was defined as the sum of the arrival times of vehicles at the demand points. Moreover, the total costs of the supply chain are composed of the setup cost of establishing a distribution centre, the fixed cost of used vehicles, vehicle travel costs, and expenses of lack and oversupply at demand points.

Ransikarbum and Mason [28] developed a two-criterion model for relief goods distribution. After presenting the mathematical model of the problem, they proposed a hybrid approach based on the Non-dominated Sorting Genetic Algorithm II (NSGA-II) called HNSGA-II to solve the problem. Mosallanezhad et al. [29] discussed a multi-objective, multi-period supply chain design for personal protection equipment during the COVID-19 pandemic, aiming to optimize total cost and reduce time. After presenting the mathematical model of the problem, a hybrid genetic algorithm was proposed to solve the model. Zahedi et al. [12] developed two innovative approaches to designing a relief supply chain using the Internet of Things to address multiple suspicions during an epidemic, such as the SARS-COV-2 outbreak. The main approach, named the prioritization approach, was used to minimize the maximum response time of ambulances. The second approach, named the allocation approach, was used to minimize the total critical response time. A set of meta-heuristics including Simulated Annealing (SA), Social Engineering Optimization (SEO), particle swarm optimization (PSO), hybrid SA and PSO (SAPSO), hybrid SA and SEO (SASEO), and hybrid PSO and SEO (PSOSEO) were developed to optimize the proposed models.

Cao et al. [30] proposed a fuzzy bi-level optimization model for humanitarian supply chains. The upper level of the model aims to minimize the unmet demand rate, potential environmental risks, and emergency costs, while the lower level seeks to maximize survivors’ perceived satisfaction. The researchers utilized data from the Wenchuan earthquake to evaluate the effectiveness of their proposed model. Chen [14] discussed a relief goods supply chain, considering governmental organizations (GO), non-governmental organizations (NGO), and donors as supplying points and some affected areas as demanding points. In the discussed problem, NGOs received relief goods from GO and donors and delivered them to the affected areas. Moreover, donors and GO could deliver relief goods to NGOs or directly to the affected areas. They proposed a mathematical model to maximize the utility of private donors and NGOs, maximize the affected area’s satisfaction rate, and minimize cost. Yuan and Wang [31] developed a super-network theory to propose a regional emergency scheduling model and improve efficiency between first aid and local relief centres. The proposed super-network model covers only the emergency logistics supply chain and presents a decision-making plan for the emergency material delivery plan. After presenting the mathematical model of the problem, they developed a modified projection algorithm to solve the problem.

A summary of the reviewed studies is presented in Table A1 in the Appendix. The literature review reveals that distribution activities are typically planned over a single period, discrete, or continuous time period. While the consideration of a continuous period is computationally more complex, it is considered to be closer to reality [12,20,21,25–27]. Regarding relief goods warehouses, some research focused on a single warehouse [16,17], whereas most studies contemplated multiple warehouses [12,14,15,18–31]. This is because more than one warehouse is typically available for distributing relief goods. Regarding the type of vehicles used for distribution, most prior studies assumed the use of identical vehicles [14,19–23,25,26,28–30] to reduce problem complexity at the cost of deviating from real-world scenarios where multiple types of vehicles are employed for goods distribution [12,15,16,18,24,27,31]. Concerning the objective function, some studies sought to optimize a single objective [12,16,17,21,22,25,31], while others considered multiple objectives [14,15,18–20,23,24,26–30].

The review also shows that previous studies have not taken into account the possibility of reusing the same vehicles for goods distribution. Additionally, the concept of batching assigned orders into different cargos for a single vehicle has not been considered in any of the studies.

In terms of the solution method, most of the studies formulated a mathematical model of the problem. However, due to the problem’s complexity, these studies eventually resorted to heuristic or meta-heuristic algorithms.

This current study aims to bridge the theoretical and practical gap by considering real-world requirements in relief goods distribution. To this end, the RGDP is approached considering time as a continuous parameter, the existence of multiple warehouses and vehicle types, and the possibilities of reusing vehicles and batching assigned orders into different cargos for a single vehicle. As for the solution method, this study presents a mathematical model to provide an in-depth view of the problem specification and its details. Moreover, two new variants of MLCA, inspired by championship matches and named P-MLCA and L-MLCA, are proposed to address the problem’s complexity.

3. Problem description and mathematical formulation

The RGDP addressed in this study can be described as the logistical challenges of delivering relief goods to disaster-stricken regions via a relief supply network. This network comprises a set of warehouses (W), a heterogeneous fleet of vehicles (V), and various damaged regions (D) requiring certain goods. Each damaged region has unique relief orders (RO), which could potentially be supplied by multiple warehouses. Each relief order is demanded by a damaged region and should be delivered to it. In other words, each damaged region is the owner of some relief orders, and the related relief orders should be delivered to it. The RGDP involves making several decisions, including identifying the appropriate warehouse for each relief order, assigning the orders to suitable vehicles, determining the cargo composition within each vehicle, and determining the loading priority for each relief order within its assigned vehicle. Not all vehicles can transport all types of relief orders, and they differ in terms of speed and capacity. Furthermore, the availability and quantities of relief orders vary among warehouses. The RGDP outlined in this study aims to minimize the total delivery time of the relief orders to the damaged regions by optimizing the delivery process while concurrently satisfying multiple constraints such as warehouse inventory levels, vehicle capacities, geographical distances, and more.

The studied RGDP shares several similarities with the supply chain problem. Thus, the mathematical model presented here draws upon ideas from the existing supply chain model proposed by Beheshtinia and Ghasemi [32]. Both models consider a two-stage supply network, linked by transportation vehicles with differing travel speeds and capacities. Moreover, both models treat time as a continuous parameter. However, while Beheshtinia and Ghasemi [32].explore the relationship between suppliers producing orders and their delivery to a multi-site manufacturer, this research investigates the relationship between multiple warehouses and various damaged regions. Additionally, in the present research, the warehouse’s availability to supply an order must be considered when delivering orders. This consideration is absent in Beheshtinia and Ghasemi’s model, which doesn’t make any assumptions about the availability of facilities. Furthermore, this study assumes that some vehicles may not be capable of conveying certain orders, a notion contrasting with Beheshtinia and Ghasemi’s model, which assumes a vehicle could transport any type of order. Finally, the current study assumes that an order could be supplied by multiple warehouses, collecting a portion of the order from different warehouses, as some warehouses might not have all the required relief orders. In contrast, Beheshtinia and Ghasemi’s model presumes that all suppliers have the capacity to process and supply orders.

3.1. Problem assumptions

The key assumptions of the problem are outlined below.

• Damaged regions and warehouses are located in different geographical areas.

• Vehicles possess different capacities and speeds for transporting relief orders.

• Relief orders occupy varying sizes within vehicles.

• At the start of scheduling, all vehicles are located at a central terminal.

• Relief order i may not be available in the warehouses at the beginning of the scheduling problem. Ready_wo indicates the readiness time of relief order o in warehouse w. If a relief order o is available at the start of scheduling in warehouse w, then Ready_wo equals 0.

• A vehicle may be assigned various relief orders to deliver to the damaged regions. If the total size of the assigned relief orders to a vehicle surpasses its capacity, the vehicle will need to deliver them across multiple cargos. In other words, the assigned relief orders to a vehicle are divided into several cargos, with the total size of relief orders in each cargo not exceeding the vehicle capacity.

• Each vehicle can be used multiple times for goods distribution. In each use of the vehicle, a cargo composed of various relief orders is delivered to their respective regions. After the delivery of relief orders in each cargo, the vehicle can be reused to deliver relief orders in the next cargo.

• Orders in a cargo may be collected from different warehouses and delivered to a single damaged region.

• Relief orders assigned to each cargo have different loading priorities. Vehicles must deliver relief orders to their respective damaged regions following these priorities.

• The maximum number of possible cargos equals the number of RO. This corresponds to a special case where all orders are assigned to a single vehicle, with each order allocated to a distinct cargo.

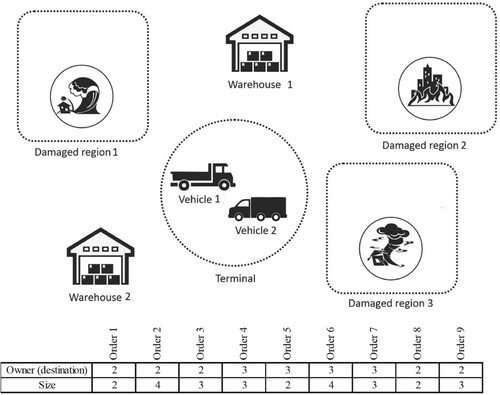
3.2. Illustrate example

To further clarify the problem, this section presents an illustrative example. As depicted in Figure 1, the example relief supply network comprises 3 damaged regions, 2 warehouses, and 2 vehicles. A total of 9 relief orders must be delivered from the warehouses to the damaged regions. The size and the intended destination of each order are also provided. Table 1 outlines the transportation time required between the warehouses, the damaged regions, and the terminal for each vehicle. The capacities of vehicles 1 and 2 are 10 and 8, respectively. It is also assumed that there are no restrictions on the assignment of warehouses and vehicles to the relief orders.

Figure 1. Example of a relief supply network.

Table 1. Traveling times by vehicles 1 and 2.

Terminal	Damaged region 3	Damaged region 2	Damaged region 1	Warehouse 2	Warehouse 1		Terminal	Damaged region 3	Damaged region 2	Damaged region 1	Warehouse 2	Warehouse 1
4	8	6	4	2	0	Warehouse 1	2	4	3	2	1	0	Warehouse 1
6	2	4	4	0		Warehouse 2	3	1	2	2	0		Warehouse 2
6	4	2	0			Damaged region 1	3	2	1	0			Damaged region 1
2	8	0				Damaged region 2	1	4	0				Damaged region 2
2	0					Damaged region 3	1	0					Damaged region 3
0						Terminal	0						Terminal
Vehicle 1							Vehicle 2

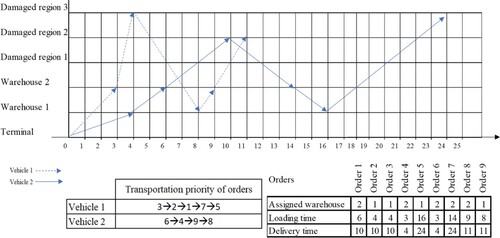
A feasible solution for the problem is depicted in Figure 2. In this solution, orders 1, 2, 3, 5, and 7 are assigned to vehicle 1 with the specified transportation priority shown in Figure 2. Given that the capacity of vehicle 1 is 10 and the total size of the assigned orders is 14, not all the assigned orders can be delivered in a single cargo. Consequently, orders 3, 2, and 1 are assigned to the first cargo, while orders 7 and 5 are assigned to the second cargo.

Figure 2. A feasible solution to the example.

Following the order’s priorities, vehicle 1 begins at the terminal and moves to warehouse 1, the assigned warehouse for order 3, to load this order. As orders 3 and 2 share the same warehouse, their loading times are the same (i.e. 4). The vehicle then moves to warehouse 2 to load order 1. After this, the vehicle progresses to damaged region 2 to deliver orders 3, 2, and 1. It then returns to warehouse 2 to load order 7, and warehouse 1 to load order 5. Finally, the vehicle journeys to damaged region 3 to deliver orders 7 and 5. Figure 2 depicts the loading and delivery times of relief orders.

3.3. Mathematical model

The RGDP considered in this study is formulated as an MILP. The notations, parameters, and decision variables used in the model are presented below.

Sets

Table

OS: o = 1,2, … , RO	Set of orders
DS: d: 1,2, … , D	Set of damaged regions
WS: w = 1,2, … , W	Set of warehouses
VS: v = 1,2, … , V	Set of vehicles

Indexes

Table

q,o	Index of order
D	Index of damaged regions
V	Index of vehicle
$w,w^{\mathrm{\prime }}$	Index of warehouses
C	Index of cargo
P	Index for loading priority of orders in a cargo

Parameters:

Table

RO	Number of relief orders
W	Number of warehouses
V	Number of vehicles
D	Number of damaged regions
$S_o$	Size of relief order i
$V{C}_v$	Capacity of vehicle v
$Read{y}_{wo}$	Ready time of relief order o in warehouse w
$t{D}_v^{wd}=t{D}_v^{dw}$	Time of transportation from warehouse w to damaged region d (vice versa) by vehicle v
$t{T}_v^w$	Time of transportation from the terminal to warehouse w by vehicle v
$t{W}_v^{w{w}^{\mathrm{\prime }}}$	time of transportation from warehouse w to warehouse $w^{\mathrm{\prime }}$ by vehicle v
$destinatio{n}_o^d$	1 if the destination of order o is damaged region d (damaged region d is the owner of order i), else 0
Allowow	1 if relief order o could be supplied by Warehouse w, else 0
Conflictov	1 if vehicle v is proper to load relief order o, else 0
M	A very big positive number

Decision variables

Table

$De{l}_o$	The time that order o is delivered to its related damaged region
$L_o$	The time that relief order o is loaded on by a vehicle
$Availabilit{y}_{vco}$	The time that vehicle v is available to transfer relief order o in cargo c
$W{A}_{wo}$	It is 1, if relief order o is assigned to warehouse w; otherwise, it is 0
$V{A}_{vcop}$	If relief order o has pth loading priority in cth cargo of vehicle v
$J_{oq}$	It is 1, if relief orders o and q have a similar owner; otherwise, it is 0
$L{P}_{vcp}$	It is 1, if the number of assigned orders to cargo c of vehicle v is p; otherwise, it is 0 (in other words, vehicle v should load p orders in its cth cargo)
$Las{t}_{vco}$	It is 1, if order o has the last loading priority in cth cargo of vehicle v; otherwise, it is 0

The mathematical model of the problem is as follows. (1) $MinZ=\sum _{o=1}^{RO}De{l}_o$(1) S.t.: (2) $\sum _{w=1}^{W}W{A}_{wo}=1,o=1,2,\dots ,RO$(2) (3) $\sum _{v=1}^V\sum _{c=1}^{RO}\sum _{p=1}^{RO}V{A}_{vcop}=1,o=1,2,\dots ,RO$(3) (4) $\sum _{o=1}^{RO}V{A}_{vcop}\le 1,\begin{array}{l}v=1,2,\dots ,V,\\ c=1,2,\dots ,RO,\\ p=1,2,\dots ,RO.\end{array}$(4) (5) $\sum _{o=1}^{RO}\sum _{p=1}^{RO}{S}_o\times V{A}_{vcop}\le V{C}_v\begin{array}{l}v=1,2,\dots ,V,\\ p=1,2,\dots ,RO.\end{array}$(5) (6) $J_{oq}=\sum _{d=1}^D(destinatio{n}_o^d\ast destinatio{n}_q^d)o,q=1,2,\dots ,RO.$(6) (7) $\sum _{p=1}^{RO}V{A}_{vcqp}+\sum _{p=1}^{RO}V{A}_{vcop}\le 1+M(J_{oq}),\begin{array}{l}o,q=1,2,\dots ,RO,\\ v=1,2,\dots ,V,\\ c=1,2,\dots ,RO.\end{array}$(7) (8) $\sum _{o=1}^{RO}V{A}_{vco(p+1)}\le \sum _{o=1}^{RO}V{A}_{vcop}\begin{array}{l}v=1,2,\dots ,V,\\ c=1,2,\dots ,RO,\\ p=1,2,\dots ,RO-1.\end{array}$(8) (9) $\sum _{o=1}^{RO}V{A}_{v(c+1)o1}\le \sum _{o=1}^{RO}V{A}_{vco1}\begin{array}{l}v=1,2,\dots ,V,\\ c=1,2,\dots ,RO-1.\end{array}$(9) (10) $L_o\ge Availabilit{y}_{vco}-M\left(1-\sum _{p=1}^{RO}V{A}_{vcop}\right)\begin{array}{l}o=1,2,\dots ,RO,\\ v=1,2,\dots ,V,\\ c=1,2,\dots ,RO.\end{array}$(10) (11) $L_o\ge Read{y}_{w0}-M(1-W{A}_{wo}),o=1,2,\dots ,RO.$(11) (12) $Availabilit{y}_{v1o}\ge t{T}_v^w-M(2-V{A}_{v1o1}-W{A}_{wo})\begin{array}{l}o=1,2,\dots ,RO,\\ v=1,2,\dots ,V,\\ w=1,\dots ,W.\end{array}$(12) (13) $\begin{array}{l}Availabilit{y}_{vco}\ge De{l}_q+t{D}_v^{wd}\\ -M\ast (4-V{A}_{vco1}-V{A}_{v(c-1)q1}-de{s}_q^d-W{A}_{wo}),\end{array}\begin{array}{l}o,q=1,2,\dots ,RO,\\ v=1,2,\dots ,V,\\ w=1,\dots ,W,\\ c=2,\dots ,RO,\\ d=1,2,\dots ,D.\end{array}$(13) (14) $\begin{array}{l}Availabilit{y}_{vco}\ge L_q+t{W}_v^{w{w}^{\mathrm{\prime }}}\\ -M\ast (4-V{A}_{vcqp}-V{A}_{vco(p+1)}-W{A}_{q{w}^{\mathrm{\prime }}}-W{A}_{wo}),\end{array}\begin{array}{l}o,q=1,2,\dots ,RO,\\ v=1,2,\dots ,V,\\ w,w^{\mathrm{\prime }}=1,\dots ,W,\\ c=1,2,\dots ,RO,\\ p=1,2,\dots ,RO-1.\end{array}$(14) (15) $De{l}_o\ge L_o+t{D}_v^{wd}-M\ast (3-de{s}_o^d-Las{t}_{vco}-W{A}_{wo}),\begin{array}{l}v=1,2,\dots ,V,\\ c=1,2,\dots ,RO,\\ o,q=1,2,\dots ,RO,\\ w=1,\dots ,W,\\ d=1,2,\dots ,D.\end{array}$(15) (16) $LS{P}_{vcp}=\sum _{o=1}^{RO}V{A}_{vcop}-\sum _{q=1}^{RO}V{A}_{vcq(p+1)}\begin{array}{l}v=1,2,\dots ,V,\\ c=1,2,\dots ,RO,\\ p=1,2,\dots ,RO-1.\end{array}$(16) (17) $LS{P}_{vc(RO)}=\sum _{o=1}^{RO}V{A}_{vco(RO)},\begin{array}{l}v=1,2,\dots ,V,\\ c=1,2,\dots ,RO.\end{array}$(17) $Las{t}_{vco}\ge (V{A}_{vcop}+LS{P}_{vcp}-1),$ (18) $Las{t}_{vco}\le 0.5\ast (V{A}_{vcop}+LS{P}_{vcp}),\begin{array}{l}v=1,2,\dots ,V,\\ c=1,2,\dots ,RO,\\ o=1,2,\dots ,RO,\\ p=1,2,\dots ,RO.\end{array}$(18) (19) $W{A}_{wo}=0,\begin{array}{l}\begin{array}{l}w=1,2,\dots ,W,\\ o=1,2,\dots ,RO,\end{array}\\ |Allo{w}_{wo}=0.\end{array}$(19) (20) $\sum _{c=1}^{RO}\sum _{p=1}^{RO}V{A}_{vcop}=0,\begin{array}{l}v=1,2,\dots ,V,\\ o=1,2,\dots ,RO,\\ |Conflic{t}_{ov}=0.\end{array}$(20) (21) $Las{t_{vco}}_{\in \{0,1\}},Availabilit{y}_{vco}\ge 0,\begin{array}{l}v=1,2,\dots ,V,\\ c=1,2,\dots ,RO,\\ o=1,2,\dots ,RO.\end{array}{L}_o,De{l_o}_{}\ge 0,o=1,2,\dots ,RO.$(21) $W{A_{wo}}_{\in \{0,1\}},\begin{array}{l}o=1,2,\dots ,RO,\\ w=1,\dots ,W.\end{array},LS{P}_{vcp}\in \{0,1\},\begin{array}{l}v=1,2,\dots ,V,\\ c=1,2,\dots ,RO,\\ p=1,2,\dots ,RO.\end{array}$ $V{A_{vcop}}_{\in \{0,1\}},\begin{array}{l}v=1,2,\dots ,V,\\ c=1,2,\dots ,RO,\\ o=1,2,\dots ,RO,\\ p=1,2,\dots ,RO.\end{array},{J_{oq}}_{\in \{0,1\}},o,q=1,2,\dots ,RO.$

The minimization of total delivery times of orders is considered by Equation (1). Constraint (2) stipulates that each relief order should be supplied by a warehouse. Assigning each relief order to one loading priority of one cargo of one vehicle is ensured by constraint (3). Constraint (4) states that two relief orders cannot have the same loading priority for a cargo. Constraint (5) considers the vehicles’ capacities when assigning relief orders to their cargos. In other words, the sum of the sizes of relief orders assigned to a vehicle should be less than the vehicle’s capacity. Constraint (6) prevents the assignment of two relief orders with different destinations to one cargo. Constraint (7) determines the possibility of joining relief orders in a cargo. Constraint (8) specifies that if there is no assignment to loading priority p of a cargo, it is impossible to assign a relief order to load priority p + 1 of the cargo. Constraint (9) indicates that if there is no assignment to cargo c, it is impossible to assign a relief order to cargo c + 1. Constraint (10) determines the relief orders’ loading time based on the vehicles’ availability time in each cargo. Constraint (11) links the loading time of a relief order to its ready time in the related warehouse. The availability time of the first cargo of vehicles is ensured by constraint (12). Constraint (13) determines a vehicle’s availability time to transport the first relief order of other cargo. Constraint (14) links a vehicle’s availability time for a relief order with the previously assigned relief order’s loading time. Constraint (15) ensures the delivery time of assigned relief orders to cargo is the same. Constraint (16) determines the number of assigned orders in the cth cargo of vehicle v. In other words, this constraint indicates that after assigning the last relief order to the cth cargo of vehicle v, there is no further assignment to this vehicle. Constraint (17) is the same as the previous constraint in the case that all the relief orders are assigned to a cargo of a vehicle (the last assigned relief order to the cth cargo of vehicle v is RO). Constraint (18) determines the relief order with the last loading priority in cargo c of vehicle v. Constraint (19) prevents the assignment of an impermissible warehouse to supply a relief order. Constraint (20) prevents the assignment of an impermissible vehicle to convey a relief order. Constraint (21) indicates the variable types and signs.

4. The proposed solution method

A simplified version of the considered RGDP, where the assignment of orders to warehouses is predetermined and each vehicle has only one batch, is a variant of the vehicle routing problem (VRP). It is known that the VRP problem belongs to the NP-Hard class of complexity [33]. Hence, it can be concluded that the RGDP addressed in this study, being more complex than VRP, is also NP-hard. Consequently, obtaining an optimal solution for this problem within a reasonable time using exact methods for medium and large-scale problems is unattainable. Under such circumstances, heuristics or meta-heuristic algorithms should be proposed to tackle the problem [34]. Among various metaheuristic algorithms, soccer-based algorithms have recently received attention from researchers and have been successfully applied to a variety of optimization problems.

The golden ball (GB) was introduced by Osaba et al. [35] and applied to the travelling salesman and the capacitated vehicle routing problems. Moosavian and Kasaee Roodsari [36] proposed the soccer league competition (SLC) to optimize the design of water distribution networks. The world cup optimization (WCO) algorithm was proposed by Razmjooy et al. [37] and used in the field of cancer detection. Purnomo and Wee [38] presented the soccer games optimization (SGO) algorithm, which was used to solve practical issues such as distribution power flow and distribution generation placement [39]. The league championship algorithm (LCA) was proposed by Husseinzadeh Kashan [40] and applied in various domains such as optimal control problems [41], scheduling a batch processing machine [42], task pattern identification and scheduling [43], world modelling for cooperating robots [44], mechanical engineering design [45], and vehicle-to-vehicle communication [46]. Inspired by the LCA and borrowing ideas from the European champions league, Beheshtinia and Ghasemi [32] proposed the MLCA. They applied the MLCA to the supply chain scheduling problem and demonstrated its superior performance over GB, LCA, and GA.

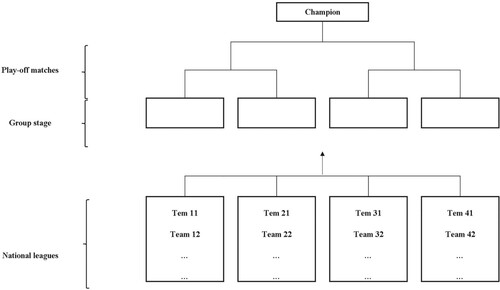
Due to its promising performance, the MLCA is adopted to solve the considered RGDP in this study. Additionally, two novel variants of this algorithm, named L-MLCA and P-MLCA, are also introduced. In the MLCA, each solution is treated as a team, and a set of teams (solutions) are grouped into subsets called national leagues. Teams first compete within their national leagues. The top teams from each league then qualify for the group stage matches. The group stage teams are randomly placed in their leagues, and after the competitions, the best-qualified teams enter the playoff stage. After the playoff games, one team is selected as the champion. The matches allow teams to learn new tactics from each other, identify their strengths and weaknesses, gain new experiences, and improve their quality. In the MLCA, the team structure changes during the matches. After determining a champion, the teams return to their national leagues with a new structure to perform the next iteration, and the process is repeated to determine the subsequent champion.

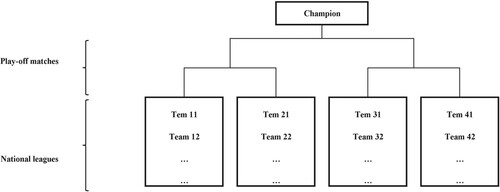
The MLCA and its two new variants, P-MLCA and L-MLCA, have the same structure in the sense that they all have two phases. In the first phase, teams are matched in multiple national leagues, and the best team from each league advances to the second phase, called ‘championship matches’. These algorithms are identical during the first stage (the national leagues’ stage) but vary in the second phase (the championship stage). In MLCA, the qualifying teams are divided into new groups where teams within each group compete against each other. Subsequently, the top teams from these groups face off in a playoff format to determine the champion (Figure 3). In L-MLCA, the qualifying teams from the national leagues stage compete in a unique league to determine the champion (Figure 7). In P-MLCA, the qualifying teams from the national leagues stage compete in playoff mode (Figure 9). Further details about the MLCA, L-MLCA, and P-MLCA are provided in Sections 4.1, 4.2, and 4.3, respectively.

Figure 3. Structure of MLCA.

4.1. Multiple league championship algorithm (MLCA)

In the MLCA, each solution is represented as a team. A set of teams are randomly created and distributed among multiple national leagues. Each team is assigned a label that signifies its national league, and this label remains constant throughout the algorithm solution process. Within each national league, all teams compete against each other, impacting each other’s attributes during these matches. The top-performing teams in each national league qualify for the next stage, referred to as the group stage of the championship matches (the first phase of the championship matches). At this stage, the qualified teams are distributed into various groups to compete with each other. The best teams from each group qualify for the playoff stage (the second phase of the championship matches), and the champion is determined after these playoff matches.

Once the champion has been determined, the teams, now with their new structures, return to their respective national leagues and the process is repeated to determine the next champion. This iterative process continues until a termination criterion is met. An operator is defined to simulate the match between teams, referred to as the match operator. After performing the match operator between two teams, both the team structure and the objective function of its related solution are altered. Figure 3 illustrates the structure of the MLCA. Further details about the algorithm are provided in the subsequent sections.

4.1.1. Structures of the teams

In the MLCA, each team is represented by a string, as illustrated in Figure 4. Each element of the string consists of a random number. This string determines the allocation of relief orders to vehicles, along with their transportation priority. The value of each element is randomly generated from the range (1, Nv +1), where Nv denotes the number of vehicles. The integer part of each number indicates the assigned vehicle. Moreover, the transportation priority of the assigned relief orders to a particular vehicle is determined by sorting them based on their decimal part. Figure 4 depicts a feasible solution assuming 5 relief orders and 3 vehicles. In this solution, relief orders 1 and 5 are assigned to vehicle 1, relief orders 2 and 4 are assigned to vehicle 2, and order 3 is assigned to vehicle 3. Order 1 has a higher transportation priority than order 5 on vehicle 1 because its decimal part is smaller. Similarly, order 4 has a higher transportation priority than order 2 on Vehicle 2. Given that the objective function of the problem is to minimize the total delivery times of relief orders, a team with a lower objective value has a better fitness value. In this study, Equation (22) is utilized to determine the fitness value of each team. (22) $Fitnessvalue=\frac{1}{Objectivefunction}$(22)

Figure 4. Structure of solution representation in the proposed MLCA.

4.1.2. Match operator

This operator simulates a match between two teams. In a match, teams influence each other, become familiar with new tactics and techniques, and identify their strengths and weaknesses. This interaction drives the evolution of techniques and tactics over time. To simulate a match, consider teams A and B as inputs. The operator is implemented through the following steps:

Step 1: Randomly select [Sim_rate*No] elements from team A and replace their values with the values of the corresponding elements in team B. Sim_rate is a real number between 0 and 1 and represents one of the algorithm parameters, indicating the degree of simulation of one team from the other within the match operator.

Step 2: Randomly select [Sim_rate*No] elements from team B and replace their values with those of the corresponding elements in team A.

Step 3: Calculate the objective function value for the newly structured teams A and B.

Step 4: If the original team A (or B) has a better objective function value (fitness value) than the new team A (or B), then retain it. Otherwise, replace it with the new team A (or B). In other words, a greedy selection is performed between each team and its new structure.

For better clarification, a depiction of the match operator between teams A and B is provided in Figure 5.

Figure 5. An example of the match operator.

4.1.3. Termination criteria

The algorithm terminates if the fitness value of the champion team remains unchanged for a specific number of consecutive iterations, denoted by the parameter Ter_num.

4.1.4. MLCA steps

The main steps of the MLCA are summarized below, and its pseudo code is present in Figure 6.

Figure 6. Pseudo-code of MLCA.

Step1: Generate the initial population of teams and randomly scatter them across national leagues. The total number of teams in each national league (NTNL) and the total number of national leagues (NNL) are parameters of the algorithm.

Step 2: Implement the match operator in each national league for each pair of teams. The structure of the teams changes during various matches.

After all the matches have been performed, rank the teams based on their final fitness values. In each league, the teams with better fitness values qualify to play in the next stage (group stage of the championship). The number of qualified teams in each national league (NQNL) to enter the next stage is one of the algorithm’s parameters.

Step 3: Scatter NNL*NQNL qualified teams randomly across the champion league groups. The number of champions league groups (NCLG) is one of the algorithm’s parameters.

Step 4: Perform the match operator between teams in each group. After performing all matches, rank teams based on their fitness values. In each group, the teams with better fitness values qualify to play in the next stage (playoff matches). The number of teams in each group that qualify for the champions league (NQCL) playoff stage is one of the algorithm’s parameters.

Step 5: Conduct a playoff match between NCLG*NQCL qualified teams. After each match, consider the team with the best fitness value as the winner, advance it to the next match, and consider the other team as the loser and eliminate it from the tournament. Only one team remains in the tournament after the losing teams are eliminated in various playoff matches. The remaining team is considered the current champion.

Step 6: If the termination condition is met, stop the algorithm. Otherwise, return the teams to their national league and proceed to step 2.

4.2. League based MLCA

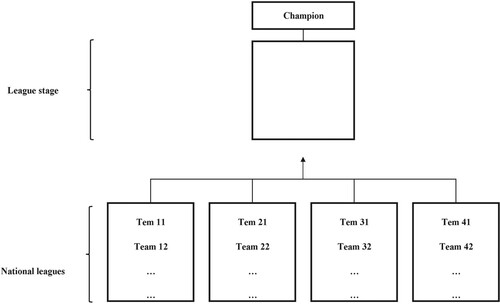
In this section, the first variant of MLCA, named League-based MLCA (L-MLCA) is presented. L-MLCA shares the same structure as MLCA, but the teams that qualify from the national leagues are gathered in a unique league to compete with each other. In other words, there are no group stage or playoff matches; the qualified teams compete directly in a league. After these matches, the team with the best fitness value is considered the champion. The teams, with their new structures, are then reassigned to their national leagues to begin a new algorithm iteration. The steps of L-MLCA are presented below. Figures 7 and 8 illustrate the structure and pseudo code of L-MLCA, respectively.

Figure 7. Structure of L-MLCA.

Figure 8. Pseudo-code of L-MLCA.

Step1: Randomly generate NTNL* NNL teams as the initial population and randomly distribute them across NNL national leagues.

Step 2: Implement the match operator in each national league for each pair of teams. After all the matches have been performed, rank the teams based on their final fitness values. In each league, NQNL teams with the best fitness values qualify for the next stage.

Step 3: Integrate NNL*NQNL qualified teams into a single league, named elite league.

Step 4: Conduct the match operator between each pair of teams in the elite league. After all the matches have been performed, sort the teams based on their fitness values and consider the team with the best fitness value as the current champion.

Step 5: If the termination condition is met, stop the algorithm. Otherwise, return the teams to their national league and proceed to step 2.

4.3. Playoff based MLCA

The Playoff-based MLCA (P-MLCA) is similar to MLCA. However, in P-MLCA, there is no group stage in the champions league matches, and the teams that qualify from each national league proceed directly to the playoff matches. After the losing teams are eliminated in the playoff matches, the remaining team is considered the champion. The steps for P-MLCA are presented below. Figures 9 and 10 illustrate the structure and pseudo code of P-MLCA, respectively.

Figure 9. Structure of P-MLCA.

Figure 10. Pseudo-code of P-MLCA.

Step1: Randomly generate NTNL* NNL teams as the initial population and randomly distribute them across NNL national leagues.

Step 2: Implement the match operator within each national league for each pair of teams. After all the matches have been performed, rank the teams based on their final fitness values. In each league, NQNL teams with the best fitness values qualify for the next stage.

Step 3: Conduct a playoff match between NNL*NQNL qualified teams. After each match, identify the team with the best fitness value as the winner and advance it to the next match. Consider the other team as the loser and remove it from the tournament. After eliminating the losing teams in various playoff matches, only one team will remain in the tournament. Consider this team the current champion.

Step 4: If the termination condition is met, stop the algorithm. Otherwise, return the teams to their respective national leagues and proceed to Step 2.

5. Numerical experiments

In this section, the performance of MLCA, L-MLCA, and P-MLCA are compared by solving some test problems. All three algorithms have been implemented in Python, with the code executed on a Google Colab cloud server equipped with a 2 GHz processor and 12.6 GB of RAM. The performance of the metaheuristic algorithms is known to be significantly affected by the chosen parameter values [47–49]. Consequently, careful parameter tuning was conducted using the Taguchi method. For more information on the Taguchi method, readers are referred to Taguchi et al. [50]. Following the Taguchi method, the parameters were set as follows: NNL = 8, NTNL = 18, NQNL = 2, NCLG = 2NQCL = 2, Sim_rate = 0.2, and Ter_num = 20.

5.1. Test problems

To generate test problems, the parameters of the problem are identified and their corresponding values are determined, as presented in Table 2.

Table 2. Parameters of the problem and their values.

	Low level	Medium level	High level
Number of relief orders	50	100	150
Number of damaged regions	U[1, 5]	U[5, 10]	U[10, 15]
Number of vehicles	U[1, 5]	U[5, 10]	U[10, 15]
Number of warehouses		U[2, 5]
Size of the relief order		U[10, 100]
Traveling times		U[0, 100]
Vehicles capacity		U[500, 2000]
Orders ready times		U[5, 15]

As presented in Table 2, three levels (i.e. low, medium, and high) are considered for three parameters: number of damaged regions, number of vehicles, and number of relief orders. The other parameters each have one level and are randomly generated using the uniform distribution within the range presented in Table 2. Furthermore, it is assumed that there are no restrictions on assigning warehouses and vehicles to supply and transport relief orders. By changing the various levels, 27 test problems have been generated, as detailed in Table 3.

Table 3. Test problems.

Problem	Number of relief orders	Number of damaged regions	Number of vehicles
1	50	U[1,5]	U[1,5]
2	50	U[1,5]	U[5,10]
3	50	U[1,5]	U[10,15]
4	50	U[5,10]	U[1,5]
5	50	U[5,10]	U[5,10]
6	50	U[5,10]	U[10,15]
7	50	U[10,15]	U[1,5]
8	50	U[10,15]	U[5,10]
9	50	U[10,15]	U[10,15]
10	100	U[1,5]	U[1,5]
11	100	U[1,5]	U[5,10]
12	100	U[1,5]	U[10,15]
13	100	U[5,10]	U[1,5]
14	100	U[5,10]	U[5,10]
15	100	U[5,10]	U[10,15]
16	100	U[10,15]	U[1,5]
17	100	U[10,15]	U[5,10]
18	100	U[10,15]	U[10,15]
19	150	U[1,5]	U[1,5]
20	150	U[1,5]	U[5,10]
21	150	U[1,5]	U[10,15]
22	150	U[5,10]	U[1,5]
23	150	U[5,10]	U[5,10]
24	150	U[5,10]	U[10,15]
25	150	U[10,15]	U[1,5]
26	150	U[10,15]	U[5,10]
27	150	U[10,15]	U[10,15]

5.2. Experimental results

All the generated problems are solved by using MLCA, L-MLCA, and P-MLCA. The results obtained are presented in Table 4. Due to the stochastic nature of the algorithms, different runs of an algorithm on a problem may yield different results. Therefore, each problem was solved 30 times using each algorithm, and the mean and standard deviation of the results are reported in Table 4.

Table 4. Results of solving test problems using MLCA, L-MLCA, and P-MLCA.

	MLCA			L-MLCA			P-MLCA
Problem	Mean of results	Variance	Mean of CPU time (Second)	Mean of results	Variance	Mean of CPU time (Second)	Mean of CPU time (Second)	Variance	Mean of results
1	1496.88	639.75	48.29	2035.03	847.13	58.43	61.53	402.09	1287.92
2	930.11	250.03	29.12	1187.04	321.12	32.25	39.67	162.91	896.46
3	697.05	139.14	14.37	821.07	156.23	21.79	28.14	137.72	687.06
4	1982.86	953.06	66.67	2603.32	1355.58	83.15	81.57	388.2	1564.52
5	1038.54	187.17	55.85	1365.88	316.87	61.61	68.18	177.04	1016.28
6	824.64	140.44	21.18	921.27	137.31	31.84	36.63	111.23	741.54
7	1985.53	739.06	95.03	2867.38	1209.88	111.27	113.32	603.79	1933.94
8	1096.31	266.79	69.67	1372.86	313.68	87.13	82.7	194.85	1014.01
9	843.78	124.24	47.23	980.29	152.59	63.67	60.49	112.96	825.3
10	4415.17	1444.79	178.25	8378.28	4415.28	217.68	214.91	1791.88	4350.79
11	2314.17	562.71	113.76	3839.89	1118.47	182.84	135.64	770.66	2140.82
12	1839.24	383.26	86.94	2685.29	693.27	163.99	105.47	424.1	1793.32
13	6696.48	3264.35	282.41	10260.61	4533.35	313.92	307.48	2088.4	6356.45
14	2840.59	743.11	235.19	4355.77	1212.58	256.67	250.15	620.87	2799.15
15	1990.98	287.63	199.47	3169.28	535.71	342.48	308.42	314.84	1965.17
16	8018.81	3709.83	303.22	13229.49	7260.86	324.96	313.17	1917.52	6069.02
17	3523.71	815.51	261.41	4743.32	992.32	312.51	278.9	790.85	2845.43
18	2228.06	389.47	250.23	3166.52	508.42	459.19	310.66	428.73	2212.81
19	10932.09	5269.22	325.1	18543.08	8650.72	545.68	384.87	5846.04	10888.28
20	4586.33	1630.87	319.43	7816.77	2162.36	513.72	370.75	1377.46	4475.9
21	3310.99	818.93	267.56	5882.5	1717.49	487.51	338.15	569.856	2815.99
22	13550.07	7595.63	394.77	22944.86	10808.08	657.29	423.88	3761.05	10944.97
23	5685.56	1739.7	359.24	10236.99	2655.18	637.06	412.73	1135.19	5530.92
24	4008.62	834.86	326.25	6715.92	1621.16	609.33	372.94	526.88	3829.86
25	16238.9	7781.6	498.66	22396.07	11820.5	753.58	532.19	2039.61	10873.09
26	6302.12	1429.7	452.91	10402.19	2780.18	652.59	511.11	1732.81	6099.79
27	4353.38	771.46	409.43	6968.66	1361.85	345.71	492.02	766.49	4120.3

Table 4 demonstrates that P-MLCA yields a better average result than L-MLCA and MLCA. Moreover, MLCA provides a better average result than L-MLCA. To determine whether these advantages are statistically significant, three hypothesis tests are conducted. The null and alternative hypotheses of the first, second, and third tests are presented as equations (23) to (25), respectively. (23) $\begin{array}{l}{H}_0:{\mu }_{P-MLCA}={\mu }_{MLCA}\to {\mu }_{P-MLCA}-{\mu }_{MLCA}=0\\ H_1:{\mu }_{P-MLCA}<{\mu }_{MLCA}\to {\mu }_{P-MLCA}-{\mu }_{MLCA}<0\end{array}$(23) (24) $\begin{array}{l}{H}_0:{\mu }_{P-MLCA}={\mu }_{L-MLCA}\to {\mu }_{P-MLCA}-{\mu }_{L-MLCA}=0\\ H_1:{\mu }_{P-MLCA}<{\mu }_{L-MLCA}\to {\mu }_{P-MLCA}-{\mu }_{L-MLCA}<0\end{array}$(24) (25) $\begin{array}{l}{H}_0:{\mu }_{MLCA}={\mu }_{L-MLCA}\to {\mu }_{MLCA}-{\mu }_{L-MLCA}=0\\ H_1:{\mu }_{MLCA}<{\mu }_{L-MLCA}\to {\mu }_{MLCA}-{\mu }_{L-MLCA}<0\end{array}$(25)

Statistical analysis of the results and the calculation of the P-values for all hypothesis tests led to the rejection of the null hypotheses in all cases, given a significance level of 0.05.

To further assess the performance of P-MLCA, its results are compared with the optimum solution for several randomly generated small-size test problems. Table 5 presents the utilized test problems, each represented by four parameters. The first parameter refers to No, while the others represent Nw, Nv, and Nr, respectively. The remaining parameters for the problems are randomly generated using the uniform distributions presented in Table 2. The optimum solutions are obtained by solving the mathematical model with the LINGO 9 solver. The results reveal that P-MLCA has a significantly lower CPU time than the LINGO 9 solver. Furthermore, in 2 cases, the optimum solution could not be found by LINGO within 5000 s (problems 7 and 8). These results underscore the efficacy of P-MLCA, which identified the optimum solution in 8 out of the 10 test problems for which LINGO also found an optimum solution. Moreover, in the two cases where P-MLCA did not find the optimum solution, the relative deviations of the results were negligible (i.e. 0.0018 and 0.0025).

Table 5. Comparison between P-MLCA results and optimum solutions.

		Optimum solution		P-MLCA
No.	Problem	Result	CPU time (Second)	Result	CPU time (Second)	The relative deviation of the results
1	5 × 2 × 2 × 2	1684	555	1684	18	0
2	5 × 3 × 2 × 2	1591	473	1594	13	0.0018
3	5 × 3 × 2 × 3	1572	362	1576	15	0.0025
4	5 × 4 × 3 × 3	1096	900	1096	17	0
5	5 × 4 × 3 × 2	990	4290	990	19	0
6	6 × 2 × 2 × 1	1325	3259	1325	15	0
7	6 × 3 × 2 × 1	–	>5000	1274	19	–
8	6 × 2 × 3 × 1	–	>5000	1291	14	–
9	4 × 4 × 3 × 3	1062	133	1062	7	0
10	4 × 4 × 3 × 2	834	62	834	9	0
11	3 × 2 × 2 × 1	728	21	728	7	0
12	3 × 3 × 3 × 2	696	34	696	8	0

6. Concluding remarks and future research directions

This study addresses the RGDP, assuming a set of warehouses of relief goods, vehicles, and damaged regions. The relied goods should be delivered to damaged regions based on their demands. The aim is to determine the warehouse that each relief order should be supplied from it, the allocation of relief orders to vehicles, batching of the relief orders, and their priority of transportation by vehicles to minimize the total delivery time of relief orders to damaged regions. The problem is mathematically formulated as a mixed-integer programming model (MILP). Due to the complexity of the problem, the Multiple League Championship Algorithm (MLCA) and two variants of it named League base MLCA (L-MLCA), and Playoff MLCA (P-MLCA) are proposed to cope with the problem. The performance of the algorithms is tested by solving a set of randomly generated test problems. The analysis of the results revealed that P-MLCA performs better than MLCA and L-MLCA. Moreover, the results of P-MLCA have been compared with optimal solutions found by MILP for small-size problems. The comparison underscored the promising performance of the P-MLCA, as it discovered the optimal solution in 80% of the problems solved to optimality by MILP. The optimality gap for the ro indicated a significant difference between the MILP and P-MLCA. The minimum and maxiemaining 20% was remarkably low (i.e. 0.003), making it negligible. The comparison of CPU time also indicated a significant difference between the MILP and P-MLCA. The minimum and maximum CPU time were 7 and 19 s for P-MLCA, whereas for MILP, this span was between 21 and 5000 s.

An analysis of the structure of the P-MLCA discloses a potential reason for its promising performance, which is primarily due to its unique strategy in exploring the solution space and escaping local optima. It is a common issue when using meta-heuristic algorithms that finding a good solution may lead to the algorithm converging on it and getting trapped in a local optimum. The P-MLCA employs a strategy (the concept of national leagues) that divides the solutions into multiple populations. This concept ensures that a good solution only influences other solutions within the same league, reducing the likelihood of entire population convergence. Following this strategy, the impact of teams (solutions) across various national leagues becomes apparent during the championship stage, where the effective solutions from each national league are transferred to it.

This study contributes to the RGDP literature in two significant ways. First, it extends the problem by incorporating some realistic assumptions not considered in previous studies, such as vehicle reuse and order batching. Second, it introduces two new variants of MLCA, L-MLCA and P-MLCA. The possibility of batching helps to reduce transportation costs by combining orders into a batch, and vehicle reuse can enhance the utilization of vehicles by assigning orders based on proximity to each warehouse. Moreover, the proposed algorithms have proven effective at delivering high-quality solutions in a very short amount of time. Therefore, they assist decision-makers in creating efficient disaster response plans and managing diverse disaster scenarios where relief goods must be distributed to affected regions.

As for future work, the uncertain nature of disasters can be considered when formulating the problem. The presented mathematical model can be extended by including stochastic parameters such as transportation time. This will allow more accurately reflecting the complex, real-world logistics in disaster relief operations and provide a framework for decision-making under uncertainty. Another extension opportunely is the introduction of alternative objectives, such as minimizing total transportation costs or tardiness in delivering relief orders that could represent both efficiency and effectiveness measures. Moreover, potential future research could explore the efficiency of the proposed algorithm when hybridizing with local search or other metaheuristic algorithms. Furthermore, while the current research focuses primarily on disaster relief logistics, the proposed algorithm offers significant potential for application in various other topics, such as supply chain, production scheduling, and logistics optimization.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Appendix

Table A1. Summary of the reviewed studies.

	Time			Warehouse		Transportation navigation		Objective function		Reusing the vehicle			Solution method
Article	Single period	Discrete	Continues	Single	Multiple	Identical vehicles	Different vehicles	Single objective	Multi objective	Yes	No	Batching	Mathematical model	Algorithm
Zheng and Ling [15]	√				√		√		√		√			Heuristic
Ruan et al. [16]	√			√			√	√			√		√	Heuristic
Ben Othman et al. [17]	√			√				√			√		√	B&B
Manopiniwes and Irohara [18]	√				√		√		√		√		√	–
Condeixa et al. [19]	√				√	√			√		√		√	–
Loree and Aros-Vera [20]			√		√	√			√		√		√	Heuristic
Sabouhi et al. [21]			√		√	√		√			√		√	GA
Shavarani [22]	√				√	√		√			√		√	GA
Liu and Song [23]		√			√	√			√		√		√	–
Ghaffari et al. [25]			√		√	√		√			√		√	PSO
Zhong et al. [27]			√		√		√		√		√			GA
Wang and Chen [26]			√		√	√			√		√		√	Robust optimization
Sakiani et al. [24]		√			√		√		√		√		√	Simulated annealing
Ransikarbum and Mason [28]	√				√	√			√		√		√	GA
Mosallanezhad et al. [29]		√			√	√			√		√		√	GA
Zahedi et al. [12]			√		√		√	√			√		√	SA, SEO, PSO
Cao et al. [30]		√			√	√			√		√		√	B&B
Chen [14]	√				√	√			√		√		√	–
Yuan and Wang [31]	√				√		√	√			√		√	Heuristic
Current research			√		√		√	√		√		√	√	MLCA