General semi-implicit midpoint approximation for fixed point of almost contraction mapping and applications

Abstract

The objective of this paper is to suggest and construct a general four step semi-implicit iterative scheme involving midpoint rule. We establish and analyse the convergence of the suggested scheme to reckon the fixed point of an almost contraction mapping. Also, we prove the stability of the suggested iterative scheme. Finally, suggested method and our main results are applied to examine a general variational inequality and a nonlinear integral equation.

KEYWORDS:

• Convergence and stability
• general semi-implicit midpoint iteration
• fixed point
• almost contraction mapping
• general variational inequality
• integral equation

2020 MATHEMATICS SUBJECT CLASSIFICATIONS:

• 47H09
• 47H10
• 47H22
• 47H25
• 49J40

1. Introduction

It is evident that nonexpansive mappings are an essential generalization of contraction mappings. These mappings are firmly connected with the monotonicity and exhibits their applications in various problems in nonlinear analysis including variational inequality, optimization, equilibrium and initial value problems. Undoubtedly, the class of nonexpansive mappings has a long history for reckoning fixed points. However, on a complete metric space, a nonexpansive self-mapping need not owns a fixed point. Also, unlike the contraction mappings, the Picard sequence may not converge to a fixed point of a nonexpansive mapping.

Example 1.1

Let $\mathrm{\Omega }=\{\varsigma =({\varsigma }_1,{\varsigma }_2,\dots ):{\varsigma }_k\ge 0,\mathrm{\forall }k,\sum _{k=1}^{\mathrm{\infty }}{\varsigma }_k=1\}$ be a closed and bounded subset of a Banach space of all real absolutely summable sequences $(l^1,\Vert \cdot {\Vert }_1)$. Then the nonexpansive mapping $\mathrm{\Phi }:\mathrm{\Omega }\to \mathrm{\Omega }$ defined by $\mathrm{\Phi }(\varsigma )=(0,{\varsigma }_1,{\varsigma }_2,\cdots )$ does not own a fixed point.

These facts have accelerated the interest in examining the generality of the class of spaces over which fixed points results hold for such mappings. The notion of weak contraction which is also referred to as almost contraction was coined by Berinde [1].

Definition 1.1

A mapping $\mathrm{\Phi }:\mathrm{\Omega }\to \mathrm{\Omega }$ is referred as almost contraction if for some $K\ge 0,\mathrm{\exists }\sigma \in (0,1)$ so that (1) $\Vert \mathrm{\Phi }(\omega )-\mathrm{\Phi }(\varsigma )\Vert \le \sigma \Vert \omega -\varsigma \Vert +K\Vert \omega -\mathrm{\Phi }(\omega )\Vert ,\mathrm{\forall }\omega ,\varsigma \in \mathrm{\Omega }.$(1)

The author established his claim that almost contraction mappings are general than that of Zamfirescu mapping [2] which encompasses Kannan [3], Chatterjea [4] and contraction mapping. In [5], Suzuki introduced modified non-expansive mappings referred as Suzuki's generalized nonexpansive mapping, often referred to as condition (C) and described as follows: (2) $\frac{1}{2}\Vert \omega -\mathrm{\Phi }(\omega )\Vert \le \Vert \omega -\varsigma \Vert \Rightarrow \Vert \mathrm{\Phi }(\omega )-\mathrm{\Phi }(\varsigma )\Vert \le \Vert \omega -\varsigma \Vert ,\mathrm{\forall }\varsigma ,\omega \in \mathrm{\Omega }.$(2) Suzuki [5] pointed out facts with supportive illustrations that the class of mappings referred in (2(2) $\frac{1}{2}\Vert \omega -\mathrm{\Phi }(\omega )\Vert \le \Vert \omega -\varsigma \Vert \Rightarrow \Vert \mathrm{\Phi }(\omega )-\mathrm{\Phi }(\varsigma )\Vert \le \Vert \omega -\varsigma \Vert ,\mathrm{\forall }\varsigma ,\omega \in \mathrm{\Omega }.$(2) ) is general than nonexpansive mapping. The author also reckoned some fixed points by proving some theoretical results.

Example 1.2

[5] Let $\mathrm{\Phi }:[0,3]\to [0,3]$ be a self mapping defined as follows: $\mathrm{\Phi }(\varsigma )=\{\begin{array}{ll}0,& \text{if}\varsigma \ne 3,\\ 1,& \text{if}\varsigma =3.\end{array}$Here Φ is not non-expansive mapping, despite satisfying Suzuki's condition (C).

However, a massive attention has been paid to the fixed -point theory, in recent years and it has become the fastest expanding research field. Numerous real-world problems appearing in science, and engineering, particularly in ODEs, PDEs, VIs, and zeros of monotone operators have been investigated by transforming as a model of fixed-point problem. The fixed point of a nonlinear mapping $\mathrm{\Phi }:\mathcal{B}\to \mathcal{B}$ is expressed as $\mathrm{Fix}(\mathrm{\Phi })=\{\varrho \in \mathcal{B}:\mathrm{\Phi }(\varrho )=\varrho \}$. Owing to the significance of fixed points, numerous new iterative schemes have been designed and tackled over the last few years. The extensively researched and widely used method for determining fixed points is due to Mann [6], which is given as follows: (3) ${\varrho }_{k+1}=(1-t_k){\varrho }_k+t_k\mathrm{\Phi }({\varrho }_k),k\in \mathbb{N},$(3) where $t_k\in [0,1]$ and $\mathrm{\Phi }:\mathrm{\Omega }\to \mathrm{\Omega }$ is a nonexpansive mapping. A few common and widely used iterative techniques include Ishikawa [7], Halpern [8], S-iteration [9]. In view of fruitful outcomes and applicability, many iterative strategies have been created in an effort to improve both the rate of convergence and functionality, see, Noor [10], Abbas and Nazir [11], CR [12], Normal-S [13], Picard-S [14], Thakur et al. [15], and M-iterative scheme [16]. Recently, Ofem and Igbokwe [17] devised a four step iterative method as under (4) $\{\begin{array}{l}{\varrho }_{k+1}=\mathrm{\Phi }({\varsigma }_k),\\ {\varsigma }_k=\mathrm{\Phi }({\vartheta }_k),\\ {\vartheta }_k=\mathrm{\Phi }[(1-t_k){\epsilon }_k+t_k\mathrm{\Phi }{\epsilon }_k],\\ {\epsilon }_k=\mathrm{\Phi }[(1-p_k){\varrho }_k+p_k\mathrm{\Phi }({\varrho }_k)],\end{array}$(4) where $\{t_k\},\{p_k\}\subset [0,1]$. They approximated fixed points for almost contraction mapping and Suzuki's generalized nonexpansive mapping. The authors validated that their scheme is efficient than $K^{\ast }$ iterative scheme [18] for almost contraction mapping and also converges faster than S-iteration process [9], Picard S-iterative method [14] and Thakur's scheme [15] for almost contraction mapping and Suzuki's generalized nonexpansive mapping. Weak and strong convergence results for newly devised scheme are also analysed.

On the other hand, the conception of monotone operators is strongly associated with the initial value problem of ordinary differential equation (5) $\frac{\mathrm{d}\varrho }{\mathrm{d}t}=\psi (\varrho );\varrho (0)={\varrho }_0.$(5) Mathematical model representing initial value problem (5(5) $\frac{\mathrm{d}\varrho }{\mathrm{d}t}=\psi (\varrho );\varrho (0)={\varrho }_0.$(5) ) is a quite significant and substantial tool as numerous physical problems of practical applications can be dealt as a model of the form (5(5) $\frac{\mathrm{d}\varrho }{\mathrm{d}t}=\psi (\varrho );\varrho (0)={\varrho }_0.$(5) ). Solving these kind of models is challenging if the involved function ψ is not continuous. To resolve this issue, one of the alternative way is to set up a sequence of Lipschitz functions whose approximation in some sense is ψ. Numerical solutions of (5(5) $\frac{\mathrm{d}\varrho }{\mathrm{d}t}=\psi (\varrho );\varrho (0)={\varrho }_0.$(5) ) are reported by numerous authors using approximation, see, Mustafa [19], Duffull and Hegarty [20], Khorasani and Adibi [21]. Among these methods, one of the dynamic techniques is implicit midpoint rule (IMR) which approximates the sequence $\{{\varrho }_k\}$ generated as: (6) $\psi \left(\frac{{\varrho }_{k+1}+{\varrho }_k}{2}\right)=\frac{1}{\kappa }({\varrho }_{k+1}-{\varrho }_k),$(6) where $\kappa >0$ is a step-size. It is acknowledged, if $\psi :{\mathbb{R}}^N\to {\mathbb{R}}^N$ is Lipschitz continuous and sufficiently smooth, then $\{{\varrho }_n\}$ produced by the relation (6(6) $\psi \left(\frac{{\varrho }_{k+1}+{\varrho }_k}{2}\right)=\frac{1}{\kappa }({\varrho }_{k+1}-{\varrho }_k),$(6) ) converges to the exact solution of (5(5) $\frac{\mathrm{d}\varrho }{\mathrm{d}t}=\psi (\varrho );\varrho (0)={\varrho }_0.$(5) ) as $\kappa \to 0$ uniformly over $a\in [0,\overline{a})$ for any fixed $\overline{a}>0$, see, [22–25].

Further, the study of the equilibrium is applicable to a great extent, as a number of problems including linear programming, monotone inclusions, convex optimization and elliptic differential equations can be examined as an equilibrium state model. Therefore, the study of variational inclusion or finding $0\in \psi (\varrho )$ is a significant research area as approximate solution of $0\in \psi (\varrho )$ is analogous to the equilibrium state $\frac{\mathrm{d}\varrho }{\mathrm{d}t}=0,\psi (\varrho )=0$, see, Berinde [26], Browder [27], Chidume [28] and the references therein. If $\psi (\varrho ):=g(\varrho )-\varrho$, then the initial value problem (5(5) $\frac{\mathrm{d}\varrho }{\mathrm{d}t}=\psi (\varrho );\varrho (0)={\varrho }_0.$(5) ) coincides with ${\varrho }^{\mathrm{\prime }}=g(\varrho )-\varrho$. Then the equilibrium state of (5(5) $\frac{\mathrm{d}\varrho }{\mathrm{d}t}=\psi (\varrho );\varrho (0)={\varrho }_0.$(5) ) is nothing but the fixed point of g, i.e. $\varrho =g(\varrho )$. As a matter of fact, above discussed fundamental idea impelled [29] to design following implicit iterative method as under (7) ${\varrho }_{k+1}=(1-p_k){\varrho }_k+p_k\mathrm{\Phi }\left(\frac{{\varrho }_{k+1}+{\varrho }_k}{2}\right),$(7) where $\{p_k\}\subset (0,1)$ and $\mathrm{\Phi }:\mathbb{X}\to \mathbb{X}$ is a nonexpansive mapping. Under some appropriate assumptions, weak convergence result was proved. Later, Xu et al. [30] reported a strong convergence result for nonexpansive mapping by employing viscocity implicit midpoint scheme as under (8) ${\varrho }_{k+1}=p_k\psi ({\varrho }_k)+(1-p_k)\mathrm{\Phi }\left(\frac{{\varrho }_{n+1}+{\varrho }_n}{2}\right),$(8) where, ψ and Φ are contraction and nonexpansive mappings, respectively. More precisely, following theorem was encountered.

Theorem 1.1

Let $\mathbb{X}$ be a Hilbert space and $\mathrm{\varnothing }\ne \mathrm{\Omega }$ a closed convex set. Suppose that $\mathrm{Fix}(\mathrm{\Phi })\ne \mathrm{\varnothing }$, where $\mathrm{\Phi }:\mathrm{\Omega }\to \mathrm{\Omega }$ is a nonexpansive mapping and $\psi :\mathrm{\Omega }\to \mathrm{\Omega }$ be a contraction. If the control parameter $\{p_k\}$ fulfils the following preassumptions: $(a_1)\underset{k\to \mathrm{\infty }}{lim}{p}_k=0;(a_2)\sum _{k=0}^{\mathrm{\infty }}{p}_k=\mathrm{\infty };(a_3)\sum _{k=0}^{\mathrm{\infty }}|p_{k+1}-p_k|<\mathrm{\infty }.$Then, the sequence $\{p_k\}$ generated by (8(8) ${\varrho }_{k+1}=p_k\psi ({\varrho }_k)+(1-p_k)\mathrm{\Phi }\left(\frac{{\varrho }_{n+1}+{\varrho }_n}{2}\right),$(8) ) converges to $\varrho \in \mathrm{Fix}(\mathrm{\Phi })$ and ϱ satisfies the variational inequality: $⟨(I-\rho )\psi ,\varrho -\rho ⟩\ge 0,\mathrm{\forall }\varrho \in \mathrm{Fix}(\mathrm{\Phi }).$

The study of Xu et al. [30] was further extended by Luo et al. [31] by obtaining the results in uniformly smooth Banach space instead of real Hilbert space. Following these results, Yao et al. [32] outlined the following midpoint rule for nonexpansive mapping as: (9) ${\varrho }_{k+1}=p_k\psi ({\varrho }_k)+t_k{\varrho }_k+s_k\mathrm{\Phi }\left(\frac{{\varrho }_{k+1}+{\varrho }_k}{2}\right),\mathrm{\forall }k\in \mathbb{N},$(9) where $p_k+t_k+s_k=1$. The authors established the claim that scheme (9(9) ${\varrho }_{k+1}=p_k\psi ({\varrho }_k)+t_k{\varrho }_k+s_k\mathrm{\Phi }\left(\frac{{\varrho }_{k+1}+{\varrho }_k}{2}\right),\mathrm{\forall }k\in \mathbb{N},$(9) ) is efficient than (8(8) ${\varrho }_{k+1}=p_k\psi ({\varrho }_k)+(1-p_k)\mathrm{\Phi }\left(\frac{{\varrho }_{n+1}+{\varrho }_n}{2}\right),$(8) ).

Inspired and impelled by the previously disclosed outcomes and discussions, in this paper, we suggest and construct a general semi-implicit iterative scheme based on four step iterative scheme (4(4) $\{\begin{array}{l}{\varrho }_{k+1}=\mathrm{\Phi }({\varsigma }_k),\\ {\varsigma }_k=\mathrm{\Phi }({\vartheta }_k),\\ {\vartheta }_k=\mathrm{\Phi }[(1-t_k){\epsilon }_k+t_k\mathrm{\Phi }{\epsilon }_k],\\ {\epsilon }_k=\mathrm{\Phi }[(1-p_k){\varrho }_k+p_k\mathrm{\Phi }({\varrho }_k)],\end{array}$(4) ) to regularize the implicit midpoint rule. The order of accomplishment of this paper is as follows: Second section is devoted to the structure of a general semi-implicit mid point approximation method followed by some necessary tools. Convergence of the proposed scheme is reported to reckon a fixed point of an almost contraction mapping, uniqueness of the solution is manifested and the stability of the proposed scheme is incorporated. Next section consists of applications of our proposed scheme. The general nonlinear variational inequality and nonlinear integral equation are examined by implementing the constructed method. Finally, concluding remarks and future research works are discussed.

2. Iterative scheme and convergence

Let $\mathbb{X}$ be a real Hilbert space equipped with norm $\Vert \cdot \Vert$ and inner product $⟨\cdot ,\cdot ⟩$; let $\mathrm{\varnothing }\ne \mathrm{\Omega }\subset \mathbb{X}$ be a closed convex set. Suppose the mapping $\mathrm{\Phi }:\mathrm{\Omega }\to \mathrm{\Omega }$ satisfies (1(1) $\Vert \mathrm{\Phi }(\omega )-\mathrm{\Phi }(\varsigma )\Vert \le \sigma \Vert \omega -\varsigma \Vert +K\Vert \omega -\mathrm{\Phi }(\omega )\Vert ,\mathrm{\forall }\omega ,\varsigma \in \mathrm{\Omega }.$(1) ). Based on the iterative scheme (4(4) $\{\begin{array}{l}{\varrho }_{k+1}=\mathrm{\Phi }({\varsigma }_k),\\ {\varsigma }_k=\mathrm{\Phi }({\vartheta }_k),\\ {\vartheta }_k=\mathrm{\Phi }[(1-t_k){\epsilon }_k+t_k\mathrm{\Phi }{\epsilon }_k],\\ {\epsilon }_k=\mathrm{\Phi }[(1-p_k){\varrho }_k+p_k\mathrm{\Phi }({\varrho }_k)],\end{array}$(4) ), we suggest and examine the following general semi-implicit midpoint approximation method (GSMPA) as under (10) $\{\begin{array}{l}{\varrho }_{k+1}=\mathrm{\Phi }({\varsigma }_k),\\ {\varsigma }_k=\mathrm{\Phi }\left(\frac{{\varsigma }_k+{\vartheta }_k}{2}\right),\\ {\vartheta }_k=\mathrm{\Phi }[(1-t_k)\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)+t_k\mathrm{\Phi }\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)],\\ {\epsilon }_k=\mathrm{\Phi }[(1-p_k)\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)+p_k\mathrm{\Phi }\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)],\end{array}$(10) where $\{p_k\},\{t_k\}\subseteq [0,1]$.

Definition 2.1

[33]

Let $\{{\upsilon }_k\}\subset \mathrm{\Omega }$ is an arbitrary sequence. An iterative scheme ${\varrho }_{k+1}=\psi (\mathrm{\Phi },{\varrho }_k)$ so that $\{{\varrho }_k\}\to \varrho \in \mathrm{Fix}(\mathrm{\Phi })$ is said to be Φ-stable. If for ${ϵ}_k=\Vert {\upsilon }_{k+1}-\psi (\mathrm{\Phi },{\upsilon }_k)\Vert$, we have $\underset{k\to \mathrm{\infty }}{lim}{ϵ}_k=0$ if and only if $\underset{k\to \mathrm{\infty }}{lim}{\upsilon }_k=\varrho$.

Lemma 2.1

[34]

Suppose the non-negative real sequences $\{{\varrho }_k{\}}_{k=1}^{\mathrm{\infty }}$ and $\{{\varsigma }_k{\}}_{k=1}^{\mathrm{\infty }}$ satisfy ${\varrho }_{k+1}\le (1-p_k){\varrho }_k+{\varsigma }_k,$where $p_k\in (0,1),\sum _{k=1}^{\mathrm{\infty }}{p}_k=\mathrm{\infty }$ and $\underset{k\to \mathrm{\infty }}{lim}\frac{{\varsigma }_k}{p_k}=0$. Then $\underset{k\to \mathrm{\infty }}{lim}{\varrho }_k=0$.

Theorem 2.1

Suppose that $\mathrm{\varnothing }\ne \mathrm{\Omega }\subseteq \mathbb{X}$ is a closed convex bounded set. If the mapping $\mathrm{\Phi }:\mathrm{\Omega }\to \mathrm{\Omega }$ satisfies (1(1) $\Vert \mathrm{\Phi }(\omega )-\mathrm{\Phi }(\varsigma )\Vert \le \sigma \Vert \omega -\varsigma \Vert +K\Vert \omega -\mathrm{\Phi }(\omega )\Vert ,\mathrm{\forall }\omega ,\varsigma \in \mathrm{\Omega }.$(1) ) and $\mathrm{Fix}(\mathrm{\Phi })\ne \mathrm{\varnothing }$. Then $\{{\varrho }_k{\}}_{k=1}^{\mathrm{\infty }}$ initiated by GSMPA (10(10) $\{\begin{array}{l}{\varrho }_{k+1}=\mathrm{\Phi }({\varsigma }_k),\\ {\varsigma }_k=\mathrm{\Phi }\left(\frac{{\varsigma }_k+{\vartheta }_k}{2}\right),\\ {\vartheta }_k=\mathrm{\Phi }[(1-t_k)\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)+t_k\mathrm{\Phi }\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)],\\ {\epsilon }_k=\mathrm{\Phi }[(1-p_k)\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)+p_k\mathrm{\Phi }\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)],\end{array}$(10) ) converges strongly to $\varrho \in \mathrm{Fix}(\mathrm{\Phi })$.

Proof.

Suppose that $\varrho \in \mathrm{Fix}(\mathrm{\Phi })$. Then from iterative scheme (10(10) $\{\begin{array}{l}{\varrho }_{k+1}=\mathrm{\Phi }({\varsigma }_k),\\ {\varsigma }_k=\mathrm{\Phi }\left(\frac{{\varsigma }_k+{\vartheta }_k}{2}\right),\\ {\vartheta }_k=\mathrm{\Phi }[(1-t_k)\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)+t_k\mathrm{\Phi }\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)],\\ {\epsilon }_k=\mathrm{\Phi }[(1-p_k)\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)+p_k\mathrm{\Phi }\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)],\end{array}$(10) ), one get $\begin{array}{rl}\Vert {\epsilon }_k-\varrho \Vert & =\Vert \mathrm{\Phi }[(1-p_k)\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)+p_k\mathrm{\Phi }\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)]-\varrho \Vert \\ & =\Vert \mathrm{\Phi }(\varrho )-\mathrm{\Phi }[(1-p_k)\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)+p_k\mathrm{\Phi }\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)]\Vert \\ & \le \sigma \Vert (1-p_k)\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)+p_k\mathrm{\Phi }\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)-\varrho \Vert +K\Vert \varrho -\mathrm{\Phi }(\varrho )\Vert \\ & \le \sigma (1-p_k)\Vert \left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)-\varrho \Vert +\sigma p_k\Vert \mathrm{\Phi }(\varrho )-\mathrm{\Phi }\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)\Vert \\ & \le \sigma (1-p_k)\Vert \left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)-\varrho \Vert +{\sigma }^2{p}_k[\Vert \left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)-\varrho \Vert +K\Vert \varrho -\mathrm{\Phi }(\varrho )\Vert ]\\ & \le \frac{{\iota }_k}{2}(\Vert {\epsilon }_k-\varrho \Vert +\Vert {\varrho }_k-\varrho \Vert ),\end{array}$where ${\iota }_k=\sigma (1-p_k+\sigma p_k)$, which turns into (11) $\Vert {\epsilon }_k-\varrho \Vert \le \frac{{\iota }_k}{2-{\iota }_k}\Vert {\varrho }_k-\varrho \Vert .$(11) Again it follows from iterative scheme (10(10) $\{\begin{array}{l}{\varrho }_{k+1}=\mathrm{\Phi }({\varsigma }_k),\\ {\varsigma }_k=\mathrm{\Phi }\left(\frac{{\varsigma }_k+{\vartheta }_k}{2}\right),\\ {\vartheta }_k=\mathrm{\Phi }[(1-t_k)\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)+t_k\mathrm{\Phi }\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)],\\ {\epsilon }_k=\mathrm{\Phi }[(1-p_k)\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)+p_k\mathrm{\Phi }\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)],\end{array}$(10) ) that $\begin{array}{rl}\Vert {\vartheta }_k-\varrho \Vert & =\Vert \mathrm{\Phi }[(1-t_k)\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)+t_k\mathrm{\Phi }\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)]-\varrho \Vert \\ & =\Vert \mathrm{\Phi }(\varrho )-\mathrm{\Phi }[(1-t_k)\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)+t_k\mathrm{\Phi }\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)]\Vert \\ & \le \sigma \Vert (1-t_k)\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)+t_k\mathrm{\Phi }\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)-\varrho \Vert +K\Vert \varrho -\mathrm{\Phi }(\varrho )\Vert \\ & \le \sigma (1-t_k)\Vert \left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)-\varrho \Vert +\sigma t_k\Vert \mathrm{\Phi }(\varrho )-\mathrm{\Phi }\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)\Vert \\ & \le \sigma (1-t_k)\Vert \left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)-\varrho \Vert +{\sigma }^2{t}_k[\Vert \left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)-\varrho \Vert +K\Vert \varrho -\mathrm{\Phi }(\varrho )\Vert ]\\ & \le \frac{{\varpi }_k}{2}(\Vert {\vartheta }_k-\varrho \Vert +\Vert {\epsilon }_k-\varrho \Vert ),\end{array}$where ${\varpi }_k=\sigma (1-t_k+\sigma t_k)$, which turns into (12) $\Vert {\vartheta }_k-\varrho \Vert \le {\displaystyle \frac{{\varpi }_k}{2-{\varpi }_k}\Vert {\epsilon }_k-\varrho \Vert .}$(12) Using (11(11) $\Vert {\epsilon }_k-\varrho \Vert \le \frac{{\iota }_k}{2-{\iota }_k}\Vert {\varrho }_k-\varrho \Vert .$(11) ) into (12(12) $\Vert {\vartheta }_k-\varrho \Vert \le {\displaystyle \frac{{\varpi }_k}{2-{\varpi }_k}\Vert {\epsilon }_k-\varrho \Vert .}$(12) ), one acquires (13) $\Vert {\vartheta }_k-\varrho \Vert \le \frac{{\varpi }_k{\iota }_k}{(2-{\varpi }_k)(2-{\iota }_k)}\Vert {\varrho }_k-\varrho \Vert .$(13) Also, the second formula of GSMPA (10(10) $\{\begin{array}{l}{\varrho }_{k+1}=\mathrm{\Phi }({\varsigma }_k),\\ {\varsigma }_k=\mathrm{\Phi }\left(\frac{{\varsigma }_k+{\vartheta }_k}{2}\right),\\ {\vartheta }_k=\mathrm{\Phi }[(1-t_k)\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)+t_k\mathrm{\Phi }\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)],\\ {\epsilon }_k=\mathrm{\Phi }[(1-p_k)\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)+p_k\mathrm{\Phi }\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)],\end{array}$(10) ) gives $\begin{array}{rl}\Vert {\varsigma }_k-\varrho \Vert & =\Vert \mathrm{\Phi }\left(\frac{{\varsigma }_k+{\vartheta }_k}{2}\right)-\varrho \Vert \\ & =\Vert \mathrm{\Phi }(\varrho )-\mathrm{\Phi }\left(\frac{{\varsigma }_k+{\vartheta }_k}{2}\right)\Vert \\ & \le \sigma \Vert \left(\frac{{\varsigma }_k+{\vartheta }_k}{2}\right)-\varrho \Vert +K\Vert \varrho -\mathrm{\Phi }(\varrho )\Vert \\ & \le \frac{\sigma }{2}(\Vert {\varsigma }_k-\varrho \Vert +\Vert {\vartheta }_k-\varrho \Vert ),\end{array}$which on simplification yields (14) $\Vert {\varsigma }_k-\varrho \Vert \le \frac{\sigma }{2-\sigma }\Vert {\vartheta }_k-\varrho \Vert ,$(14) and the forthcoming relation along with (13(13) $\Vert {\vartheta }_k-\varrho \Vert \le \frac{{\varpi }_k{\iota }_k}{(2-{\varpi }_k)(2-{\iota }_k)}\Vert {\varrho }_k-\varrho \Vert .$(13) ) and (14(14) $\Vert {\varsigma }_k-\varrho \Vert \le \frac{\sigma }{2-\sigma }\Vert {\vartheta }_k-\varrho \Vert ,$(14) ) becomes (15) $\begin{array}{rl}\Vert {\varrho }_{k+1}-\varrho \Vert & =\Vert \mathrm{\Phi }({\varsigma }_k)-\varrho \Vert \\ & =\Vert \mathrm{\Phi }(\varrho )-\mathrm{\Phi }({\varsigma }_k)\Vert \\ & \le \sigma \Vert {\varsigma }_k-\varrho \Vert +K\Vert \varrho -\mathrm{\Phi }(\varrho )\Vert \\ & \le (1-{\hat{\tau }}_k)\Vert {\varrho }_k-\varrho \Vert ,\end{array}$(15) where (16) ${\hat{\tau }}_k=\frac{(2-\sigma )(2-{\varpi }_k)(2-{\iota }_k)-{\sigma }^2{\varpi }_k{\iota }_k}{(2-\sigma )(2-{\varpi }_k)(2-{\iota }_k)}.$(16) Since ${\iota }_k=\sigma (1-p_k+\sigma p_k),\sigma \in (0,1)$ and $\{p_k\},\{t_k\}\subseteq [0,1]$ yields ${\iota }_k\le \sigma$ and likewise ${\varpi }_k\le \sigma$. Thus, we have $\begin{array}{rl}{\hat{\tau }}_k& \ge \frac{1}{8}[(2-\sigma )(2-{\varpi }_k)(2-{\iota }_k)-{\sigma }^2{\varpi }_k{\iota }_k]\\ & \ge \frac{1}{8}[(2-\sigma )(2-\sigma )(2-\sigma )-{\sigma }^4]\\ & >0,\end{array}$and $1-{\hat{\tau }}_k=\frac{{\sigma }^2{\varpi }_k{\iota }_k}{(2-\sigma )(2-{\varpi }_k)(2-{\iota }_k)}\ge 0$. Furthermore, one can observe that $\sum _{k=0}^{\mathrm{\infty }}{\hat{\tau }}_k=\mathrm{\infty }$ and hence, from (15(15) $\begin{array}{rl}\Vert {\varrho }_{k+1}-\varrho \Vert & =\Vert \mathrm{\Phi }({\varsigma }_k)-\varrho \Vert \\ & =\Vert \mathrm{\Phi }(\varrho )-\mathrm{\Phi }({\varsigma }_k)\Vert \\ & \le \sigma \Vert {\varsigma }_k-\varrho \Vert +K\Vert \varrho -\mathrm{\Phi }(\varrho )\Vert \\ & \le (1-{\hat{\tau }}_k)\Vert {\varrho }_k-\varrho \Vert ,\end{array}$(15) ) and Lemma 2.1, we acquire $\underset{k\to \mathrm{\infty }}{lim}\Vert {\varrho }_k-\varrho \Vert =0$. That is, $\{{\varrho }_k\}$ converges strongly to ϱ. To manifest the uniqueness of ϱ, suppose that $\varrho \ne \hat{\varrho }\in \mathrm{\Omega }$ so that $\varrho ,\hat{\varrho }\in \mathrm{Fix}(\mathrm{\Phi })$. Then (17) $\begin{array}{rl}\Vert \varrho -\hat{\varrho }\Vert & =\Vert \mathrm{\Phi }(\varrho )-\mathrm{\Phi }(\hat{\varrho })\Vert \\ & \le \sigma \Vert \varrho -\hat{\varrho }\Vert +K\Vert \varrho -\mathrm{\Phi }(\varrho )\Vert \\ & =\sigma \Vert \varrho -\hat{\varrho }\Vert .\end{array}$(17) Since $\sigma \in (0,1)$, then subsequently, (17(17) $\begin{array}{rl}\Vert \varrho -\hat{\varrho }\Vert & =\Vert \mathrm{\Phi }(\varrho )-\mathrm{\Phi }(\hat{\varrho })\Vert \\ & \le \sigma \Vert \varrho -\hat{\varrho }\Vert +K\Vert \varrho -\mathrm{\Phi }(\varrho )\Vert \\ & =\sigma \Vert \varrho -\hat{\varrho }\Vert .\end{array}$(17) ) yields $\Vert \varrho -\hat{\varrho }\Vert =0$ and accordingly $\varrho =\hat{\varrho }$.

Theorem 2.2

Suppose that $\mathrm{\varnothing }\ne \mathrm{\Omega }\subseteq \mathbb{X}$ is a closed convex bounded set. If the mapping $\mathrm{\Phi }:\mathrm{\Omega }\to \mathrm{\Omega }$ satisfies (1(1) $\Vert \mathrm{\Phi }(\omega )-\mathrm{\Phi }(\varsigma )\Vert \le \sigma \Vert \omega -\varsigma \Vert +K\Vert \omega -\mathrm{\Phi }(\omega )\Vert ,\mathrm{\forall }\omega ,\varsigma \in \mathrm{\Omega }.$(1) ) and $\varrho \in \mathrm{Fix}(\mathrm{\Phi })$. Then $\{{\varrho }_k{\}}_{k=1}^{\mathrm{\infty }}$ generated by GSMPA (10(10) $\{\begin{array}{l}{\varrho }_{k+1}=\mathrm{\Phi }({\varsigma }_k),\\ {\varsigma }_k=\mathrm{\Phi }\left(\frac{{\varsigma }_k+{\vartheta }_k}{2}\right),\\ {\vartheta }_k=\mathrm{\Phi }[(1-t_k)\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)+t_k\mathrm{\Phi }\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)],\\ {\epsilon }_k=\mathrm{\Phi }[(1-p_k)\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)+p_k\mathrm{\Phi }\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)],\end{array}$(10) ) is Φ-stable.

Proof.

Let ${\varrho }_{k+1}=\psi (\mathrm{\Phi },{\varrho }_k)$ be a sequence initiated by (10(10) $\{\begin{array}{l}{\varrho }_{k+1}=\mathrm{\Phi }({\varsigma }_k),\\ {\varsigma }_k=\mathrm{\Phi }\left(\frac{{\varsigma }_k+{\vartheta }_k}{2}\right),\\ {\vartheta }_k=\mathrm{\Phi }[(1-t_k)\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)+t_k\mathrm{\Phi }\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)],\\ {\epsilon }_k=\mathrm{\Phi }[(1-p_k)\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)+p_k\mathrm{\Phi }\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)],\end{array}$(10) ) so that $\{{\varrho }_k\}\to \varrho \in \mathrm{Fix}(\mathrm{\Phi })$. Suppose that ${ϵ}_k=\Vert {\upsilon }_{k+1}-\psi (\mathrm{\Phi },{\upsilon }_k)\Vert$, where $\{{\upsilon }_k\}\subset \mathrm{\Omega }$ is an arbitrary sequence generated as under (18) $\{\begin{array}{l}{\upsilon }_{k+1}=\mathrm{\Phi }({\eta }_k),\\ {\eta }_k=\mathrm{\Phi }\left({\displaystyle \frac{{\eta }_k+{\theta }_k}{2}}\right),\\ {\theta }_k=\mathrm{\Phi }[(1-t_k)\left({\displaystyle \frac{{\theta }_k+{\omega }_k}{2}}\right)+t_k\mathrm{\Phi }\left({\displaystyle \frac{{\theta }_k+{\omega }_k}{2}}\right)],\\ {\omega }_k=\mathrm{\Phi }[(1-p_k)\left({\displaystyle \frac{{\omega }_k+{\upsilon }_k}{2}}\right)+p_k\mathrm{\Phi }\left({\displaystyle \frac{{\omega }_k+{\upsilon }_k}{2}}\right)].\end{array}$(18) To manifest that the scheme (10(10) $\{\begin{array}{l}{\varrho }_{k+1}=\mathrm{\Phi }({\varsigma }_k),\\ {\varsigma }_k=\mathrm{\Phi }\left(\frac{{\varsigma }_k+{\vartheta }_k}{2}\right),\\ {\vartheta }_k=\mathrm{\Phi }[(1-t_k)\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)+t_k\mathrm{\Phi }\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)],\\ {\epsilon }_k=\mathrm{\Phi }[(1-p_k)\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)+p_k\mathrm{\Phi }\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)],\end{array}$(10) ) is Φ-stable, we substantiate $\underset{k\to \mathrm{\infty }}{lim}{ϵ}_k=0$ if and only if $\underset{k\to \mathrm{\infty }}{lim}{\upsilon }_k=\varrho$. Assume that $\underset{k\to \mathrm{\infty }}{lim}{ϵ}_k=0$. Then (19) $\begin{array}{rl}\Vert {\upsilon }_{k+1}-\varrho \Vert & =\Vert {\upsilon }_{k+1}-\psi (\mathrm{\Phi },{\upsilon }_k)+\psi (\mathrm{\Phi },{\upsilon }_k)-\varrho \Vert \\ & \le \Vert {\upsilon }_{k+1}-\psi (\mathrm{\Phi },{\upsilon }_k)\Vert +\Vert \psi (\mathrm{\Phi },{\upsilon }_k)-\varrho \Vert \\ & \le {ϵ}_k+\Vert {\upsilon }_{k+1}-\varrho \Vert \\ & ={ϵ}_k+\Vert \mathrm{\Phi }({\eta }_k)-\varrho \Vert \\ & \le {ϵ}_k+\Vert \mathrm{\Phi }(\varrho )-\mathrm{\Phi }({\eta }_k)\Vert \\ & \le {ϵ}_k+\sigma \Vert {\eta }_k-\varrho \Vert +K\Vert \varrho -\mathrm{\Phi }(\varrho )\Vert \\ & ={ϵ}_k+\sigma \Vert {\eta }_k-\varrho \Vert .\end{array}$(19) Also, from the second formulation of (18(18) $\{\begin{array}{l}{\upsilon }_{k+1}=\mathrm{\Phi }({\eta }_k),\\ {\eta }_k=\mathrm{\Phi }\left({\displaystyle \frac{{\eta }_k+{\theta }_k}{2}}\right),\\ {\theta }_k=\mathrm{\Phi }[(1-t_k)\left({\displaystyle \frac{{\theta }_k+{\omega }_k}{2}}\right)+t_k\mathrm{\Phi }\left({\displaystyle \frac{{\theta }_k+{\omega }_k}{2}}\right)],\\ {\omega }_k=\mathrm{\Phi }[(1-p_k)\left({\displaystyle \frac{{\omega }_k+{\upsilon }_k}{2}}\right)+p_k\mathrm{\Phi }\left({\displaystyle \frac{{\omega }_k+{\upsilon }_k}{2}}\right)].\end{array}$(18) ), it follows that $\begin{array}{rl}\Vert {\eta }_k-\varrho \Vert & =\Vert \mathrm{\Phi }\left(\frac{{\eta }_k+{\theta }_k}{2}\right)-\varrho \Vert \\ & =\Vert \mathrm{\Phi }(\varrho )-\mathrm{\Phi }\left(\frac{{\eta }_k+{\theta }_k}{2}\right)\Vert \\ & \le \sigma \Vert \left(\frac{{\eta }_k+{\theta }_k}{2}\right)-\varrho \Vert +K\Vert \varrho -\mathrm{\Phi }(\varrho )\Vert \\ & \le \frac{\sigma }{2}[\Vert {\eta }_k-\varrho \Vert +\Vert {\theta }_k-\varrho \Vert ],\end{array}$which turns into (20) $\begin{array}{rl}\Vert {\eta }_k-\varrho \Vert & \le \frac{\sigma }{2-\sigma }\Vert {\theta }_k-\varrho \Vert .\\ \Vert {\theta }_k-\varrho \Vert & =\Vert \mathrm{\Phi }[(1-t_k)\left(\frac{{\theta }_k+{\omega }_k}{2}\right)+t_k\mathrm{\Phi }\left(\frac{{\theta }_k+{\omega }_k}{2}\right)]-\varrho \Vert \\ & =\Vert \mathrm{\Phi }(\varrho )-\mathrm{\Phi }[(1-t_k)\left(\frac{{\theta }_k+{\omega }_k}{2}\right)+t_k\mathrm{\Phi }\left(\frac{{\theta }_k+{\omega }_k}{2}\right)]\Vert \\ & \le \sigma \Vert (1-t_k)\left(\frac{{\theta }_k+{\omega }_k}{2}\right)+t_k\mathrm{\Phi }\left(\frac{{\theta }_k+{\omega }_k}{2}\right)-\varrho \Vert +K\Vert \varrho -\mathrm{\Phi }(\varrho )\Vert \\ & \le \sigma (1-t_k+\sigma t_k)\left(\frac{{\theta }_k+{\omega }_k}{2}\right)-\varrho \Vert ,\end{array}$(20) which turns into (21) $\Vert {\theta }_k-\varrho \Vert \le \frac{{\varpi }_k}{2-{\varpi }_k}\Vert {\omega }_k-\varrho \Vert ,$(21) where ${\varpi }_k=\sigma (1-t_k+\sigma t_k)$ and $\begin{array}{rl}\Vert {\omega }_k-\varrho \Vert & =\Vert \mathrm{\Phi }[(1-p_k)\left(\frac{{\omega }_k+{\upsilon }_k}{2}\right)+p_k\mathrm{\Phi }\left(\frac{{\omega }_k+{\upsilon }_k}{2}\right)]-\varrho \Vert \\ & =\Vert \mathrm{\Phi }(\varrho )-\mathrm{\Phi }[(1-p_k)\left(\frac{{\omega }_k+{\upsilon }_k}{2}\right)+p_k\mathrm{\Phi }\left(\frac{{\omega }_k+{\upsilon }_k}{2}\right)]\Vert \\ & \le \sigma \Vert (1-p_k)\left(\frac{{\omega }_k+{\upsilon }_k}{2}\right)+p_k\mathrm{\Phi }\left(\frac{{\omega }_k+{\upsilon }_k}{2}\right)-\varrho \Vert \\ & \le \sigma (1-p_k+\sigma p_k)\left(\frac{{\omega }_k+{\upsilon }_k}{2}\right)-\varrho \Vert ,\end{array}$which turns into (22) $\Vert {\omega }_k-\varrho \Vert \le \frac{{\iota }_k}{2-{\iota }_k}\Vert {\upsilon }_k-\varrho \Vert ,$(22) where ${\iota }_k=\sigma (1-p_k+\sigma p_k)$. Substituting (20(20) $\begin{array}{rl}\Vert {\eta }_k-\varrho \Vert & \le \frac{\sigma }{2-\sigma }\Vert {\theta }_k-\varrho \Vert .\\ \Vert {\theta }_k-\varrho \Vert & =\Vert \mathrm{\Phi }[(1-t_k)\left(\frac{{\theta }_k+{\omega }_k}{2}\right)+t_k\mathrm{\Phi }\left(\frac{{\theta }_k+{\omega }_k}{2}\right)]-\varrho \Vert \\ & =\Vert \mathrm{\Phi }(\varrho )-\mathrm{\Phi }[(1-t_k)\left(\frac{{\theta }_k+{\omega }_k}{2}\right)+t_k\mathrm{\Phi }\left(\frac{{\theta }_k+{\omega }_k}{2}\right)]\Vert \\ & \le \sigma \Vert (1-t_k)\left(\frac{{\theta }_k+{\omega }_k}{2}\right)+t_k\mathrm{\Phi }\left(\frac{{\theta }_k+{\omega }_k}{2}\right)-\varrho \Vert +K\Vert \varrho -\mathrm{\Phi }(\varrho )\Vert \\ & \le \sigma (1-t_k+\sigma t_k)\left(\frac{{\theta }_k+{\omega }_k}{2}\right)-\varrho \Vert ,\end{array}$(20) )–(22(22) $\Vert {\omega }_k-\varrho \Vert \le \frac{{\iota }_k}{2-{\iota }_k}\Vert {\upsilon }_k-\varrho \Vert ,$(22) ), (19(19) $\begin{array}{rl}\Vert {\upsilon }_{k+1}-\varrho \Vert & =\Vert {\upsilon }_{k+1}-\psi (\mathrm{\Phi },{\upsilon }_k)+\psi (\mathrm{\Phi },{\upsilon }_k)-\varrho \Vert \\ & \le \Vert {\upsilon }_{k+1}-\psi (\mathrm{\Phi },{\upsilon }_k)\Vert +\Vert \psi (\mathrm{\Phi },{\upsilon }_k)-\varrho \Vert \\ & \le {ϵ}_k+\Vert {\upsilon }_{k+1}-\varrho \Vert \\ & ={ϵ}_k+\Vert \mathrm{\Phi }({\eta }_k)-\varrho \Vert \\ & \le {ϵ}_k+\Vert \mathrm{\Phi }(\varrho )-\mathrm{\Phi }({\eta }_k)\Vert \\ & \le {ϵ}_k+\sigma \Vert {\eta }_k-\varrho \Vert +K\Vert \varrho -\mathrm{\Phi }(\varrho )\Vert \\ & ={ϵ}_k+\sigma \Vert {\eta }_k-\varrho \Vert .\end{array}$(19) ) yields (23) $\Vert {\upsilon }_{k+1}-\varrho \Vert \le {ϵ}_k+(1-{\hat{\tau }}_k)\Vert {\upsilon }_k-\varrho \Vert ,$(23) where ${\hat{\tau }}_k$ is same as defined in (16(16) ${\hat{\tau }}_k=\frac{(2-\sigma )(2-{\varpi }_k)(2-{\iota }_k)-{\sigma }^2{\varpi }_k{\iota }_k}{(2-\sigma )(2-{\varpi }_k)(2-{\iota }_k)}.$(16) ). Since $\underset{k\to \mathrm{\infty }}{lim}{ϵ}_k=0$, then by the virtue of Lemma 2.1, $\Vert {\upsilon }_k-\varrho \Vert \to 0$ as $k\to \mathrm{\infty }$, i.e. $\underset{k\to \mathrm{\infty }}{lim}{\upsilon }_k=\varrho$. On the contrary, suppose that $\underset{k\to \mathrm{\infty }}{lim}{\upsilon }_k=\varrho$, then proceeding in the same way as above, one acquires $\begin{array}{rl}{ϵ}_k& =\Vert {\upsilon }_{k+1}-\psi (\mathrm{\Phi },{\upsilon }_k)\Vert \\ & =\Vert {\upsilon }_{k+1}-\varrho +\varrho -\psi (\mathrm{\Phi },{\upsilon }_k)\Vert \\ & \le \Vert {\upsilon }_{k+1}-\varrho \Vert +\Vert \psi (\mathrm{\Phi },{\upsilon }_k)-\varrho \Vert \\ & \le \Vert {\upsilon }_{k+1}-\varrho \Vert +(1-{\hat{\tau }}_k)\Vert {\upsilon }_k-\varrho \Vert .\end{array}$Invoking the hypothesis $\underset{k\to \mathrm{\infty }}{lim}{\upsilon }_k=\varrho$ leads to $\underset{k\to \mathrm{\infty }}{lim}{ϵ}_k=0$. Hence, the scheme (10(10) $\{\begin{array}{l}{\varrho }_{k+1}=\mathrm{\Phi }({\varsigma }_k),\\ {\varsigma }_k=\mathrm{\Phi }\left(\frac{{\varsigma }_k+{\vartheta }_k}{2}\right),\\ {\vartheta }_k=\mathrm{\Phi }[(1-t_k)\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)+t_k\mathrm{\Phi }\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)],\\ {\epsilon }_k=\mathrm{\Phi }[(1-p_k)\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)+p_k\mathrm{\Phi }\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)],\end{array}$(10) ) is Φ-stable.

3. Applications

This section is devoted to the applications of our considered general semi-implicit midpoint approximation method to explore a general variational inequality and a nonlinear integral equation.

3.1. General variational inequality problem

Assume that $\mathrm{\varnothing }\ne \mathrm{\Omega }\subset \mathbb{X}$ is a closed convex set and $\mathrm{\Psi }:\mathrm{\Omega }\to \mathrm{\Omega }$ be a nonlinear mapping. The variational inequality problem (VIP) is to observe a component $\kappa \in \mathrm{\Omega }$ so that (24) $⟨\mathrm{\Psi }(\kappa ),\nu -\kappa ⟩\ge 0,\mathrm{\forall }\nu \in \mathrm{\Omega }.$(24) It is well acclaimed fact that the VIP was set forth by Stampacchia [35]. It is a highly fruitful, productive and applicable tool for analysing issues that arise in all diverse areas of natural sciences. Since its inception, VI has experienced a potential growth and sparkled for many decades. This field has expanded in a number of ways utilizing contemporary techniques which led to tackle previously inaccessible basic and fundamental problems. This evolution have enriched mutually connected areas of mathematical and other applied sciences including nonlinear programming, elasticity, transportation, operations research and economics.

The finite-dimensional VIP is the subsequent expansion of the nonlinear complementarity problem (NCP), which was initially recognized by Cottle [36]. Ever since its establishment, this research area has grown to be quite successful to mathematical programming, providing a fruitful and applicable theory, and connecting a various fields with noteworthy applications in science, engineering and economics such as frictional contact problems, traffic equilibrium, wireless and wireline systems, see, [37–41]. Because of applicability and fruitful outcomes, VIPs have been broadened and diversified in a number of ways, see, [42–48]. We contemplate the inequality to discern an element $\kappa \in \mathrm{\Omega }$ so that (25) $⟨\mathrm{\Psi }(\kappa ),\psi (\nu )-\psi (\kappa )⟩\ge 0,\mathrm{\forall }\nu \in \mathbb{X}:\psi (\nu )\in \mathrm{\Omega },$(25) where $\mathrm{\varnothing }\ne \mathrm{\Omega }\subseteq \mathbb{X}$ is a closed convex set and $\mathrm{\Psi },\psi :\mathbb{X}\to \mathbb{X}$ are nonlinear mappings. We call the inequality (25(25) $⟨\mathrm{\Psi }(\kappa ),\psi (\nu )-\psi (\kappa )⟩\ge 0,\mathrm{\forall }\nu \in \mathbb{X}:\psi (\nu )\in \mathrm{\Omega },$(25) ), the general nonlinear variational inequality $\mathrm{GNVI}(\mathrm{\Omega },\mathrm{\Psi },\psi )$ and its solution set is indicated by $\mathrm{\Xi }(\mathrm{\Omega },\mathrm{\Psi },\psi )$. $\mathrm{GNVI}(\mathrm{\Omega },\mathrm{\Psi },\psi )$ was introduced and examined by Noor [49]. $\mathrm{GNVI}(\mathrm{\Omega },\mathrm{\Psi },\psi )$ is a unified class containing several problems as a particular case. If $\psi =I$ then $\mathrm{GNVI}(\mathrm{\Omega },\mathrm{\Psi },\psi )$ reduces to VIP (24(24) $⟨\mathrm{\Psi }(\kappa ),\nu -\kappa ⟩\ge 0,\mathrm{\forall }\nu \in \mathrm{\Omega }.$(24) ).

As an application of GSMPA (10(10) $\{\begin{array}{l}{\varrho }_{k+1}=\mathrm{\Phi }({\varsigma }_k),\\ {\varsigma }_k=\mathrm{\Phi }\left(\frac{{\varsigma }_k+{\vartheta }_k}{2}\right),\\ {\vartheta }_k=\mathrm{\Phi }[(1-t_k)\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)+t_k\mathrm{\Phi }\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)],\\ {\epsilon }_k=\mathrm{\Phi }[(1-p_k)\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)+p_k\mathrm{\Phi }\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)],\end{array}$(10) ), we construct the implicit scheme to investigate the common solution of $\mathrm{GNVI}(\mathrm{\Omega },\mathrm{\Psi },\psi )$ and fixed point problem of an almost contraction mapping. Next, we recollect the following prominent tools to accomplish the desired goal.

Definition 3.1

[50] A mapping $\mathrm{\Phi }:\mathrm{\Omega }\to \mathbb{X}$ is known as

1. ${\tau }_1$-inverse strongly monotone if $\mathrm{\exists }{\tau }_1>0$ so that $⟨\mathrm{\Phi }(\varrho )-\mathrm{\Phi }(\varsigma ),\varrho -\varsigma ⟩\ge {\tau }_1\Vert \mathrm{\Phi }(\varrho )-\mathrm{\Phi }(\varsigma ){\Vert }^2,\mathrm{\forall }\varrho ,\varsigma \in \mathrm{\Omega };$

2. ${\tau }_1$-Lipschitz continuous if $\mathrm{\exists }{\tau }_2>0$ so that $\Vert \mathrm{\Phi }(\varrho )-\mathrm{\Phi }(\varsigma )\Vert \le {\tau }_2\Vert \varrho -\varsigma \Vert ,\mathrm{\forall }\varrho ,\varsigma \in \mathrm{\Omega }.$

Note that for ${\tau }_2=1$, Φ is nonexpansive and Φ is a contraction if $0<{\tau }_2<1$. ${\tau }_1$-inverse strongly monotone mapping is $\frac{1}{{\tau }_1}$-Lipschitz continuous.

Lemma 3.1

[51] If for any $\nu \in \mathbb{X}$ and $\kappa \in \mathrm{\Omega }$, the projection mapping ${\mathrm{\Pi }}_{\mathrm{\Omega }}:\mathbb{X}\to \mathrm{\Omega }$ satisfies the inequality $⟨\kappa -\nu ,\rho -\kappa ⟩\ge 0$ if and only if ${\mathrm{\Pi }}_{\mathrm{\Omega }}[\nu ]=\kappa$.

Evidently, the projection mapping ${\mathrm{\Pi }}_{\mathrm{\Omega }}$ is nonexpansive. Now by availing Lemma 3.1, we shall set up the following fixed point problem identical to $\mathrm{GNVI}(\mathrm{\Omega },\mathrm{\Psi },\psi )$.

Lemma 3.2

An element $\kappa \in \mathrm{\Xi }(\mathrm{\Omega },\mathrm{\Psi },\psi )$ if and only if $\kappa \in \mathrm{Fix}(\mathrm{{\rm Y}})$, where $\mathrm{{\rm Y}}(\kappa )=\kappa -\psi (\kappa )+{\mathrm{\Pi }}_{\mathrm{\Omega }}[\psi (\kappa )-\mathrm{\Psi }(\kappa )]$.

Proof.

Suppose that $\kappa \in \mathrm{\Xi }(\mathrm{\Omega },\mathrm{\Psi },\psi )$ then $⟨\mathrm{\Psi }(\kappa ),\psi (\nu )-\psi (\kappa )⟩\ge 0,\mathrm{\forall }\nu \in \mathbb{X}:\psi (\nu )\in \mathrm{\Omega }$. By invoking Lemma 3.1, we obtain ${\mathrm{\Pi }}_{\mathrm{\Omega }}[\psi (\kappa )-\mathrm{\Psi }(\kappa )]=\psi (\kappa )$. Thus, $\mathrm{{\rm Y}}(\kappa )=\kappa$. On the contrary, suppose that $\kappa \in \mathrm{Fix}(\mathrm{{\rm Y}})$ then for all $\kappa \in \mathrm{\Omega }$, we get $\mathrm{{\rm Y}}(\kappa )=\kappa$, which turns into $\psi (\kappa )={\mathrm{\Pi }}_{\mathrm{\Omega }}[\psi (\kappa )-\mathrm{\Psi }(\kappa )]$. Again, taking the Lemma 3.1 into account yields $⟨\mathrm{\Psi }(\kappa ),\psi (\nu )-\psi (\kappa )⟩\ge 0,\mathrm{\forall }\nu \in \mathbb{X}:\psi (\nu )\in \mathrm{\Omega }$, i.e. $\kappa \in \mathrm{\Xi }(\mathrm{\Omega },\mathrm{\Psi },\psi )$.

Now, on the basis of scheme (10(10) $\{\begin{array}{l}{\varrho }_{k+1}=\mathrm{\Phi }({\varsigma }_k),\\ {\varsigma }_k=\mathrm{\Phi }\left(\frac{{\varsigma }_k+{\vartheta }_k}{2}\right),\\ {\vartheta }_k=\mathrm{\Phi }[(1-t_k)\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)+t_k\mathrm{\Phi }\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)],\\ {\epsilon }_k=\mathrm{\Phi }[(1-p_k)\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)+p_k\mathrm{\Phi }\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)],\end{array}$(10) ), we shall put forward the following general semi-implicit midpoint approximation method to find an element $\varrho \in \mathrm{\Omega }$ so that $\varrho \in \mathrm{Fix}(\mathrm{\Phi })\cap \mathrm{\Xi }(\mathrm{\Omega },\mathrm{\Psi },\psi )$, where Φ is an almost contraction mapping and $\mathrm{\Psi },\psi :\mathbb{X}\to \mathbb{X}$ are nonlinear mappings.

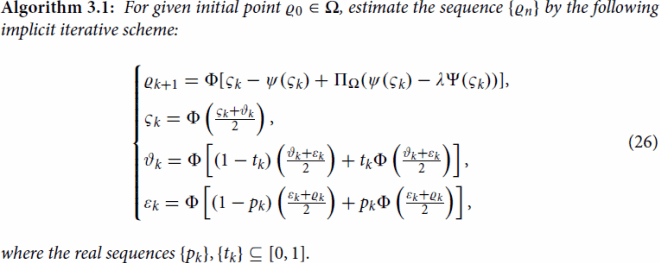
Theorem 3.1

Let $\mathrm{\varnothing }\ne \mathrm{\Omega }\subset \mathbb{X}$ be a closed bounded set. Let the mapping $\mathrm{\Phi }:\mathrm{\Omega }\to \mathrm{\Omega }$ satisfies (1(1) $\Vert \mathrm{\Phi }(\omega )-\mathrm{\Phi }(\varsigma )\Vert \le \sigma \Vert \omega -\varsigma \Vert +K\Vert \omega -\mathrm{\Phi }(\omega )\Vert ,\mathrm{\forall }\omega ,\varsigma \in \mathrm{\Omega }.$(1) ) such that $\mathrm{Fix}(\mathrm{\Phi })\cap \mathrm{\Xi }(\mathrm{\Omega },\mathrm{\Psi },\psi )\ne \mathrm{\varnothing }$. In addition, the following assumptions are fulfilled.

(A1)	The mappings $\mathrm{\Psi },\psi :\mathrm{\Omega }\to \mathrm{\Omega }$ are ${\tau }_1,{\tau }_2$-inverse strongly monotone, respectively.
(A2)	The constant $\lambda >0$ satisfies the relation $|\lambda -{\tau }_1|\le {\tau }_1(1-\mu )$, where $\mu =2(\frac{{\tau }_2-1}{{\tau }_2})$.

Then $\{{\varrho }_k\}$ estimated by (26) converges strongly to $\varrho \in \mathrm{Fix}(\mathrm{\Phi })\cap \mathrm{\Xi }(\mathrm{\Omega },\mathrm{\Psi },\psi )$.

Proof.

Ψ being a ${\tau }_1$-inverse strongly monotone mapping is $\frac{1}{{\tau }_1}$-Lipschitz continuous, then (27) $\begin{array}{rl}& \Vert ({\varsigma }_k-\varrho )-\lambda (\mathrm{\Psi }({\varsigma }_k)-\mathrm{\Psi }(\varrho )){\Vert }^2\\ & =\Vert {\varsigma }_k-\varrho {\Vert }^2-2\lambda ⟨\mathrm{\Psi }({\varsigma }_k)-\mathrm{\Psi }(\varrho ),{\varsigma }_k-\varrho ⟩+{\lambda }^2\Vert \mathrm{\Psi }({\varsigma }_k)-\mathrm{\Psi }(\varrho ){\Vert }^2\\ & \le \Vert {\varsigma }_k-\varrho {\Vert }^2-2\lambda {\tau }_1\Vert \mathrm{\Psi }({\varsigma }_k)-\mathrm{\Psi }(\varrho ){\Vert }^2+{\lambda }^2\Vert \mathrm{\Psi }({\varsigma }_k)-\mathrm{\Psi }(\varrho ){\Vert }^2\\ & \le {\left(\frac{\lambda -{\tau }_1}{{\tau }_1}\right)}^2\Vert {\varsigma }_k-\varrho {\Vert }^2={\mathbb{E}}^2\Vert {\varsigma }_k-\varrho {\Vert }^2.\end{array}$(27) Likewise invoking the ${\tau }_2$-inverse strongly monotone behaviour of ψ yields (28) $\begin{array}{rl}& \Vert ({\varsigma }_k-\varrho )-(\psi ({\varsigma }_k)-\psi (\varrho )){\Vert }^2\\ & =\Vert {\varsigma }_k-\varrho {\Vert }^2-2⟨\psi ({\varsigma }_k)-\psi (\varrho ),{\varsigma }_k-\varrho ⟩+{\lambda }^2\Vert \mathrm{\Psi }({\varsigma }_k)-\mathrm{\Psi }(\varrho ){\Vert }^2\\ & \le \Vert {\varsigma }_k-\varrho {\Vert }^2-2{\tau }_2\Vert \psi ({\varsigma }_k)-\psi (\varrho ){\Vert }^2+\Vert \psi ({\varsigma }_k)-\psi (\varrho ){\Vert }^2\\ & ={\left(\frac{{\tau }_2-1}{{\tau }_2}\right)}^2\Vert {\varsigma }_k-\varrho {\Vert }^2={\mathbb{G}}^2\Vert {\varsigma }_k-\varrho {\Vert }^2.\end{array}$(28) (29) $\begin{array}{rl}\Vert {\varrho }_{k+1}-\varrho \Vert & =\Vert \mathrm{\Phi }[{\varsigma }_k-\psi ({\varsigma }_k)+{\mathrm{\Pi }}_{\mathrm{\Omega }}(\psi ({\varsigma }_k)-\lambda \mathrm{\Psi }({\varsigma }_k))]-\varrho \Vert \\ & =\Vert \mathrm{\Phi }(\varrho )-\mathrm{\Phi }[{\varsigma }_k-\psi ({\varsigma }_k)+{\mathrm{\Pi }}_{\mathrm{\Omega }}(\psi ({\varsigma }_k)-\lambda \mathrm{\Psi }({\varsigma }_k))]\Vert \\ & \le \sigma \Vert {\varsigma }_k-\psi ({\varsigma }_k)+{\mathrm{\Pi }}_{\mathrm{\Omega }}(\psi ({\varsigma }_k)-\lambda \mathrm{\Psi }({\varsigma }_k))-\varrho \Vert +K\Vert \varrho -\mathrm{\Phi }(\varrho )\Vert \\ & =\sigma \Vert {\varsigma }_k-\psi ({\varsigma }_k)+{\mathrm{\Pi }}_{\mathrm{\Omega }}(\psi ({\varsigma }_k)-\lambda \mathrm{\Psi }({\varsigma }_k))-[\varrho -\psi (\varrho )\\ & +{\mathrm{\Pi }}_{\mathrm{\Omega }}(\psi (\varrho )-\lambda \mathrm{\Psi }(\varrho ))]\Vert \\ & \le 2\sigma \Vert ({\varsigma }_k-\varrho )-(\psi ({\varsigma }_k)-\psi (\varrho ))\Vert +\sigma \Vert ({\varsigma }_k-\varrho )-\lambda (\mathrm{\Psi }({\varsigma }_k)-\mathrm{\Psi }(\varrho ))\Vert \\ & \le \sigma (2\mathbb{G}+\mathbb{E})\Vert {\varsigma }_k-\varrho \Vert .\end{array}$(29) Now, putting (12(12) $\Vert {\vartheta }_k-\varrho \Vert \le {\displaystyle \frac{{\varpi }_k}{2-{\varpi }_k}\Vert {\epsilon }_k-\varrho \Vert .}$(12) )–(14(14) $\Vert {\varsigma }_k-\varrho \Vert \le \frac{\sigma }{2-\sigma }\Vert {\vartheta }_k-\varrho \Vert ,$(14) ) together and following the same procedures, (29(29) $\begin{array}{rl}\Vert {\varrho }_{k+1}-\varrho \Vert & =\Vert \mathrm{\Phi }[{\varsigma }_k-\psi ({\varsigma }_k)+{\mathrm{\Pi }}_{\mathrm{\Omega }}(\psi ({\varsigma }_k)-\lambda \mathrm{\Psi }({\varsigma }_k))]-\varrho \Vert \\ & =\Vert \mathrm{\Phi }(\varrho )-\mathrm{\Phi }[{\varsigma }_k-\psi ({\varsigma }_k)+{\mathrm{\Pi }}_{\mathrm{\Omega }}(\psi ({\varsigma }_k)-\lambda \mathrm{\Psi }({\varsigma }_k))]\Vert \\ & \le \sigma \Vert {\varsigma }_k-\psi ({\varsigma }_k)+{\mathrm{\Pi }}_{\mathrm{\Omega }}(\psi ({\varsigma }_k)-\lambda \mathrm{\Psi }({\varsigma }_k))-\varrho \Vert +K\Vert \varrho -\mathrm{\Phi }(\varrho )\Vert \\ & =\sigma \Vert {\varsigma }_k-\psi ({\varsigma }_k)+{\mathrm{\Pi }}_{\mathrm{\Omega }}(\psi ({\varsigma }_k)-\lambda \mathrm{\Psi }({\varsigma }_k))-[\varrho -\psi (\varrho )\\ & +{\mathrm{\Pi }}_{\mathrm{\Omega }}(\psi (\varrho )-\lambda \mathrm{\Psi }(\varrho ))]\Vert \\ & \le 2\sigma \Vert ({\varsigma }_k-\varrho )-(\psi ({\varsigma }_k)-\psi (\varrho ))\Vert +\sigma \Vert ({\varsigma }_k-\varrho )-\lambda (\mathrm{\Psi }({\varsigma }_k)-\mathrm{\Psi }(\varrho ))\Vert \\ & \le \sigma (2\mathbb{G}+\mathbb{E})\Vert {\varsigma }_k-\varrho \Vert .\end{array}$(29) ) yields: (30) $\Vert {\varrho }_{k+1}-\varrho \Vert \le (1-{\hat{\tau }}_n)(2\mathbb{G}+\mathbb{E})\Vert {\varsigma }_k-\varrho \Vert ,$(30) where ${\hat{\tau }}_n=\frac{(2-\sigma )(2-{\varpi }_k)(2-{\iota }_k)-{\sigma }^2{\varpi }_k{\iota }_k}{(2-\sigma )(2-{\varpi }_k)(2-{\iota }_k)}$, which is described in (16(16) ${\hat{\tau }}_k=\frac{(2-\sigma )(2-{\varpi }_k)(2-{\iota }_k)-{\sigma }^2{\varpi }_k{\iota }_k}{(2-\sigma )(2-{\varpi }_k)(2-{\iota }_k)}.$(16) ). Evidently, $(2\mathbb{G}+\mathbb{E})<1$ from the assumption $(A_2)$. Then, (30(30) $\Vert {\varrho }_{k+1}-\varrho \Vert \le (1-{\hat{\tau }}_n)(2\mathbb{G}+\mathbb{E})\Vert {\varsigma }_k-\varrho \Vert ,$(30) ) turns into (31) $\Vert {\varrho }_{k+1}-\varrho \Vert \le (1-{\hat{\tau }}_n)\Vert {\varsigma }_k-\varrho \Vert .$(31) Thus, from (31(31) $\Vert {\varrho }_{k+1}-\varrho \Vert \le (1-{\hat{\tau }}_n)\Vert {\varsigma }_k-\varrho \Vert .$(31) ) and implementing Lemma 2.1, we acquire $\underset{k\to \mathrm{\infty }}{lim}\Vert {\varrho }_k-\varrho \Vert =0$. That is, $\{{\varrho }_k\}\to \varrho$.

Example 3.1

Let $\mathrm{\Omega }=[0,1]$ with norm $\Vert \cdot \Vert =|\cdot {|}_{\mathbb{R}}$ and inner product $⟨\varrho ,\varsigma ⟩=\varrho \cdot \varsigma$. Define $\mathrm{\Phi }(\varrho )=\frac{\varrho }{3},\mathrm{\Psi }(\varrho )=\frac{{\varrho }^2+\varrho }{2}$ and $\psi (\varrho )=\frac{{\varrho }^3+\varrho }{3},\mathrm{\forall }\varrho \in \mathrm{\Omega }$. Clearly, $0\in \mathrm{Fix}(\mathrm{\Phi })$. Firstly, we show that Φ satisfies (1(1) $\Vert \mathrm{\Phi }(\omega )-\mathrm{\Phi }(\varsigma )\Vert \le \sigma \Vert \omega -\varsigma \Vert +K\Vert \omega -\mathrm{\Phi }(\omega )\Vert ,\mathrm{\forall }\omega ,\varsigma \in \mathrm{\Omega }.$(1) ). To manifest this, take $\sigma =\frac{1}{3}$ and for some $K\ge 0$, we express $\begin{array}{rl}& \Vert \mathrm{\Phi }(\varrho )-\mathrm{\Phi }(\varsigma )\Vert -\sigma \Vert \varrho -\varsigma \Vert -K\Vert \varrho -\mathrm{\Phi }(\varrho )\Vert \\ & =\frac{1}{3}|\varrho -\varsigma |-\frac{1}{3}|\varrho -\varsigma |-K|\varrho -\frac{\varrho }{3}|\\ & =-K\left(\frac{\varrho }{3}\right)\le 0,\end{array}$i.e. $\Vert \mathrm{\Phi }(\varrho )-\mathrm{\Phi }(\varsigma )\Vert \le \sigma \Vert \varrho -\varsigma \Vert -K\Vert \varrho -\mathrm{\Phi }(\varrho )\Vert$. Next, we establish the convergence of GSMPA (10(10) $\{\begin{array}{l}{\varrho }_{k+1}=\mathrm{\Phi }({\varsigma }_k),\\ {\varsigma }_k=\mathrm{\Phi }\left(\frac{{\varsigma }_k+{\vartheta }_k}{2}\right),\\ {\vartheta }_k=\mathrm{\Phi }[(1-t_k)\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)+t_k\mathrm{\Phi }\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)],\\ {\epsilon }_k=\mathrm{\Phi }[(1-p_k)\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)+p_k\mathrm{\Phi }\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)],\end{array}$(10) ). Let $t_k=p_k=\frac{3}{4}$ and ${\varrho }_0\in [0,1]$, then $\begin{array}{rl}{\epsilon }_k& =\mathrm{\Phi }[(1-p_k)\left(\frac{{\epsilon }_k+{\varrho }_k}{}\right)+p_k\mathrm{\Phi }\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)]\\ & =\frac{1}{3}[\left(\frac{{\epsilon }_k+{\varrho }_k}{8}\right)+\frac{3}{4}\left(\frac{{\epsilon }_k+{\varrho }_k}{6}\right)]=\frac{1}{11}{\varrho }_k,\\ {\vartheta }_k& =\mathrm{\Phi }[(1-t_k)\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)+t_k\mathrm{\Phi }\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)]\\ & =\frac{1}{3}[\left(\frac{{\vartheta }_k+{\epsilon }_k}{8}\right)+\frac{3}{4}\left(\frac{{\vartheta }_k+{\epsilon }_k}{6}\right)]=\frac{1}{11}{\epsilon }_k,\\ {\varsigma }_k& =\mathrm{\Phi }\left(\frac{{\varsigma }_k+{\vartheta }_k}{2}\right)=\left(\frac{{\varsigma }_k+{\vartheta }_k}{6}\right)=\frac{1}{5}{\vartheta }_k,\\ {\varrho }_{k+1}& =\mathrm{\Phi }({\varsigma }_k)=\frac{{\varsigma }_k}{3}=\frac{1}{1815}{\varrho }_k.\end{array}$Thus, we obtain $\underset{k\to \mathrm{\infty }}{lim}{\varrho }_k=0$. Next, we shall manifest the common fixed point of an almost contraction mapping and a projection mapping which solves $\mathrm{GNVI}(\mathrm{\Omega },\mathrm{\Psi },\psi )$. Now, for all $\varrho ,\varsigma \in \mathrm{\Omega }$, we compute $\begin{array}{rl}⟨\mathrm{\Psi }(\varrho )-\mathrm{\Psi }(\varsigma ),\varrho -\varsigma ⟩& =⟨\frac{{\varrho }^2+\varrho }{2}-\frac{{\varsigma }^2+\varsigma }{2},\varrho -\varsigma ⟩=\frac{(\varrho -\varrho {)}^2}{2}(1+\varrho +\varsigma ),\\ \Vert \mathrm{\Psi }(\varrho )-\mathrm{\Psi }(\varsigma ){\Vert }^2& ={|\frac{(\varrho -\varrho )}{2}(1+\varrho +\varsigma )|}^2=\frac{(\varrho -\varrho {)}^2}{4}(1+\varrho +\varsigma {)}^2.\end{array}$Then, $⟨\mathrm{\Psi }(\varrho )-\mathrm{\Psi }(\varsigma ),\varrho -\varsigma ⟩\ge \frac{2}{3}\Vert \mathrm{\Psi }(\varrho )-\mathrm{\Psi }(\varsigma ){\Vert }^2$. Thus, Ψ is $\frac{2}{3}$-inverse strongly monotone and $\begin{array}{rl}⟨\psi (\varrho )-\psi (\varsigma ),\varrho -\varsigma ⟩& =⟨\frac{{\varrho }^3+\varrho }{3}-\frac{{\varsigma }^3+\varsigma }{3},\varrho -\varsigma ⟩=\frac{(\varrho -\varrho {)}^2}{3}(1+\mathrm{\varrho \varsigma }+{\varrho }^2+{\varsigma }^2),\\ \Vert \psi (\varrho )-\psi (\varsigma ){\Vert }^2& ={|\frac{(\varrho -\varrho )}{3}(1+{\varrho }^2+{\varsigma }^2+\mathrm{\varrho \varsigma })|}^2\\ & =\frac{(\varrho -\varrho {)}^2}{9}(1+{\varrho }^2+{\varsigma }^2+\mathrm{\varrho \varsigma }{)}^2.\end{array}$Thus, $⟨\psi (\varrho )-\psi (\varsigma ),\varrho -\varsigma ⟩\ge \frac{3}{4}\Vert \psi (\varrho )-\psi (\varsigma ){\Vert }^2$, i.e. ψ is $\frac{3}{4}$-inverse strongly monotone. Also, for $\lambda =1$, the constants ${\tau }_1=\frac{2}{3}$ and ${\tau }_2=\frac{3}{4}$ satisfy ($A_2$) of Theorem 3.1. Finally, we show that $0\in \mathrm{\Xi }(\mathrm{\Omega },\mathrm{\Psi },\psi )$. Thus, for $\varrho =0\in \mathrm{\Omega }$ $\begin{array}{rl}⟨\mathrm{\Psi }(\varrho ),\psi (\varsigma )-\psi (\varrho )⟩& =⟨\frac{{\varrho }^2+\varrho }{2},\frac{{\varsigma }^3+\varsigma }{3}-\frac{{\varrho }^3+\varrho }{3}⟩\\ & =\left(\frac{{\varrho }^2+\varrho }{2}\right)(\frac{(\varsigma -\varrho )}{3}(1+{\varsigma }^2+{\varrho }^2+\mathrm{\varsigma \varrho }))\ge 0,\mathrm{\forall }\varsigma \in \mathrm{\Omega }.\end{array}$Thus, we obtain $0\in \mathrm{Fix}(\mathrm{\Phi })\cap \mathrm{\Xi }(\mathrm{\Omega },\mathrm{\Psi },\psi )$.

3.2. Integral equation

Numerous problems appearing in science, engineering, and economics involve integral equations. Integral equations can be employed to deal with broad range of initial and boundary value problems. Models of physical problems, including diffraction, conformal mapping water waves, scattering in quantum mechanics, etc., also contributed to the integral equations. Numerous topics are covered by integral equations, including heat radiation, heat transfer, population growth model, coexisting biological species, see, [52–56]. Some very prominent and significant problems involving electrostatics, low frequency electromagnetism, electromagnetism scattering, and the propagation of elastic and acoustic waves are countered using mathematical models of integral equations. Here, we shall utilize our proposed method to examine a nonlinear integral equation. We consider the nonlinear integral equation as under (32) $\psi (\varrho )=f(\varrho )+\kappa {\int }_0^{1}l(\varrho ,t)g(t,\psi (t))\mathrm{d}t,\mathrm{\forall }\varrho \in I=[0,1],\kappa \ge 0.$(32)

Theorem 3.2

Let $\mathbb{X}=C[0,1]$ be the space of continuous functions on $I=[0,1]$ and $\mathbb{B}\subset \mathbb{X}$ is a closed set. For all $\psi ,\phi \in \mathbb{X}$, the norm $\Vert \cdot \Vert$ on $\mathbb{X}$ is defined as $\Vert \psi -\phi \Vert =\underset{\varrho \in I}{sup}|\psi (\varrho )-\phi (\varrho )|.$Suppose that the assumptions given below are fulfilled.

(a1)	$f:I\to \mathbb{R}$ is continuous;
(a2)	$g:I\times \mathbb{B}\to \mathbb{B}$ is continuous and satisfies the inequality, $|g(a,\psi )-g(a,\phi )|\le \delta |\psi (t)-\phi (t)|,\mathrm{\forall }\psi ,\phi \in \mathbb{B}\mathrm{and}\delta \ge 0;$
(a3)	$l:I\times \mathbb{B}\to \mathbb{R}$ is continuous so that $l(\varrho ,t)\ge 0$ and ${\int }_0^{1}l(\varrho ,t)\le \tau ,\mathrm{\forall }\varrho \in I,t\in \mathbb{B}$;
(a4)	$\mathrm{\kappa \tau \delta }<1$.

If the integral Equation (32(32) $\psi (\varrho )=f(\varrho )+\kappa {\int }_0^{1}l(\varrho ,t)g(t,\psi (t))\mathrm{d}t,\mathrm{\forall }\varrho \in I=[0,1],\kappa \ge 0.$(32) ) admits a solution ϱ, then the sequence $\{{\varrho }_k{\}}_{k=1}^{\mathrm{\infty }}$ estimated by GSMPA (10(10) $\{\begin{array}{l}{\varrho }_{k+1}=\mathrm{\Phi }({\varsigma }_k),\\ {\varsigma }_k=\mathrm{\Phi }\left(\frac{{\varsigma }_k+{\vartheta }_k}{2}\right),\\ {\vartheta }_k=\mathrm{\Phi }[(1-t_k)\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)+t_k\mathrm{\Phi }\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)],\\ {\epsilon }_k=\mathrm{\Phi }[(1-p_k)\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)+p_k\mathrm{\Phi }\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)],\end{array}$(10) ) converges strongly to ϱ.

Proof.

Suppose that $\mathbb{B}\subset \mathbb{X}$ is a closed set. Define $\mathrm{\Phi }:\mathbb{B}\to \mathbb{B}$ by (33) $\mathrm{\Phi }(\psi ):=\mathrm{\Phi }(\psi (\varrho ))=f(\varrho )+\kappa {\int }_0^{1}l(\varrho ,t)g(t,\psi (t))\mathrm{d}t,\mathrm{\forall }\varrho \in I,\kappa \ge 0.$(33) Then, for any $\psi ,\phi \in \mathbb{B}$, one can have (34) $\begin{array}{rl}|\mathrm{\Phi }(\psi )-\mathrm{\Phi }(\phi )|& =|f(\varrho )+\kappa {\int }_0^{1}l(\varrho ,t)g(t,\psi (t))\mathrm{d}t-f(\varrho )-\kappa {\int }_0^{1}l(\varrho ,t)g(t,\phi (t))\mathrm{d}t|\\ & =\kappa |{\int }_0^{1}l(\varrho ,t)(g(t,\psi (t))-g(t,\phi (t)))\mathrm{d}t|\\ & \le \kappa {\int }_0^{1}l(\varrho ,t)|g(t,\psi (t))-g(t,\phi (t))|\mathrm{d}t\\ & \le \kappa {\int }_0^{1}l(\varrho ,t)\delta |\psi (t)-\phi (t)|\mathrm{d}t.\end{array}$(34) After taking the norm, inequality (34(34) $\begin{array}{rl}|\mathrm{\Phi }(\psi )-\mathrm{\Phi }(\phi )|& =|f(\varrho )+\kappa {\int }_0^{1}l(\varrho ,t)g(t,\psi (t))\mathrm{d}t-f(\varrho )-\kappa {\int }_0^{1}l(\varrho ,t)g(t,\phi (t))\mathrm{d}t|\\ & =\kappa |{\int }_0^{1}l(\varrho ,t)(g(t,\psi (t))-g(t,\phi (t)))\mathrm{d}t|\\ & \le \kappa {\int }_0^{1}l(\varrho ,t)|g(t,\psi (t))-g(t,\phi (t))|\mathrm{d}t\\ & \le \kappa {\int }_0^{1}l(\varrho ,t)\delta |\psi (t)-\phi (t)|\mathrm{d}t.\end{array}$(34) ) turns into $\Vert \mathrm{\Phi }(\psi )-\mathrm{\Phi }(\phi )\Vert \le \mathrm{\kappa \tau \delta }\Vert \psi -\phi \Vert \le \Vert \psi -\phi \Vert ,$i.e. Φ satisfies (1(1) $\Vert \mathrm{\Phi }(\omega )-\mathrm{\Phi }(\varsigma )\Vert \le \sigma \Vert \omega -\varsigma \Vert +K\Vert \omega -\mathrm{\Phi }(\omega )\Vert ,\mathrm{\forall }\omega ,\varsigma \in \mathrm{\Omega }.$(1) ). Thus, the sequence generated by (10(10) $\{\begin{array}{l}{\varrho }_{k+1}=\mathrm{\Phi }({\varsigma }_k),\\ {\varsigma }_k=\mathrm{\Phi }\left(\frac{{\varsigma }_k+{\vartheta }_k}{2}\right),\\ {\vartheta }_k=\mathrm{\Phi }[(1-t_k)\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)+t_k\mathrm{\Phi }\left(\frac{{\vartheta }_k+{\epsilon }_k}{2}\right)],\\ {\epsilon }_k=\mathrm{\Phi }[(1-p_k)\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)+p_k\mathrm{\Phi }\left(\frac{{\epsilon }_k+{\varrho }_k}{2}\right)],\end{array}$(10) ) will converge to $\mathrm{Fix}(\mathrm{\Phi })$, which solves (32(32) $\psi (\varrho )=f(\varrho )+\kappa {\int }_0^{1}l(\varrho ,t)g(t,\psi (t))\mathrm{d}t,\mathrm{\forall }\varrho \in I=[0,1],\kappa \ge 0.$(32) ).

4. Concluding remarks

In this article, a general four step semi-implicit iterative scheme involving midpoint rule is suggested. The convergence and stability results are analysed and verified that the suggested general semi-implicit iterative scheme converges to the fixed point of an almost contraction mapping. Furthermore, to examine a general variational inequality, this new scheme is applied to estimate the common fixed point of an almost contraction mapping and a projection mapping associated to the general variational inequality. A nonlinear integral equation is also investigated as an application of the suggested scheme. Further, the implementation of a general four semi-implicit iterative scheme involving midpoint rule to find fixed points of some generalized nonexpansive mappings such as asymptotically quasi-nonexpansive mapping, total asymptotically nonexpansive mapping, Suzuki's generalized non-expansive mapping and solving variational inequalities and inclusions are open questions for worthy future research.

Acknowledgments

This work is funded by Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia under the Researchers supporting project number (PNURSP2024R174).

Disclosure statement

No potential conflict of interest was reported by the author(s).