Primal–dual formulation for parameter estimation in elastic contact problem with friction

Abstract

This work deals with a saddle point formulation of parameter identification in linear elastic contact problems with friction. Using the primal–dual formulation of the constrained minimization problem and given observations, we estimate the Lamé coefficients through the penalization and dualization of the considered inverse problem. By Fenchel duality, we provide the dual energy function associated with the constraint. We prove the existence of a solution to the regularized parameter identification problem as well as the convergence of the penalized problem to the original one. An augmented Lagrangian formulation of the inverse problem and the existence of its saddle point are provided. By means of the alternating direction method of multipliers (ADMM) and a primal–dual active set strategy (PDAS), we solve the problem numerically and illustrate our approach.

KEYWORDS:

• Inverse problem
• identification
• saddle point
• Fenchel duality
• linear elasticity
• contact problem
• friction

2020 MATHEMATICS SUBJECT CLASSIFICATIONS:

• 35J86
• 74B05
• 74P99
• 74S99

1. Introduction

The problem of identifying parameters in elliptic boundary value problems from given measurements has a wide range of interesting applications in various fields, such as tomography [1,2], image processing [3,4], groundwater management [5], crack identification [6,7], Lamé coefficients identification [8], and the general framework of optimization problems [9–11]. A general framework for parameter identification in variational, quasivariational, and hemivariational inequalities and their applications can be found in [12–16].

In [17,18], an augmented Lagrangian was formulated for the identification of a discontinuous coefficient, where the state elliptic boundary value problem was reformulated as an equality constraint. Some applications have been devoted to parameter estimation in linear elastic contact problems [8,19,20]. However, accounting for friction complicates the task significantly due to the presence of a non-differentiable term (associated with the considered friction) in the minimization constraint. Thus, standard numerical methods are neither suitable nor applicable. The commonly used approach involves appropriately smoothing the non-smooth term in the variational inequality, reducing it to an equivalent equation; see [21–24] for example. This technique introduces another parameter in addition to the Tikhonov regularization parameter, leading to further complexities. Numerically, although the penalization method is widely used for frictional contact problems, a small penalty parameter choice results in an ill-conditioned system matrix, while a large choice makes the model deviate from its physical meaning.

In the present paper, we explore a saddle point formulation for parameter identification in elastic contact problems with Tresca friction (with a given slip bound). The theoretical and numerical study of contact problems has become extensive, with various methods employed for the numerical analysis and simulation of these complex problems [25–31]. In [32–36], the dual formulation technique based on Fenchel duality theory [37,38] is employed for studying frictional contact problems. The concept involves transforming the non-differentiable problem into a differentiable one subject to inequality constraints.

We examine a case involving a system of an inverse problem, where the equilibrium state $u\in X$ is obtained by solving a distributed minimization problem of an energy functional ${\mathcal{J}}_q$ over the Hilbert space X. This is referred to as the primal problem: (1) $min{\mathcal{J}}_q\left(u\right),\text{over}u\in X,$(1) where we suppose that the energy functional is sum of differentiable and non-differentiable functions. The energy functional depends on an unknown parameter q that belongs to a set $\mathcal{C}$ of admissible parameters, which is a subset of a reflexive Banach space (or Hilbert space) Y, i.e. $q\in \mathcal{C}\subset Y$. Hence, the identification's problem of $q\in \mathcal{C}$ from a given measurement $z\in \mathcal{B}\left(u\right)$, where the observation operator $\mathcal{B}$ lies in $\mathcal{L}(X,Z)$ and Z is a Hilbert space of observations, can be approximated by penalizing the classical least square formulation for parameter identification problems given by: (2) $\underset{q\in \mathcal{C}}{min}\frac{1}{2}\Vert \mathcal{B}\left(u\right)-z{\Vert }^2,$(2) where $u=u\left(q\right)$ is the solution of the state problem (1(1) $min{\mathcal{J}}_q\left(u\right),\text{over}u\in X,$(1) ) and $\Vert \cdot \Vert$ is an appropriate norm. Or equivalently, one can write the problem as two levels minimization problem: (3) $\underset{q\in \mathcal{C}}{min}\frac{1}{2}\Vert \mathcal{B}\left(u\right)-z{\Vert }^2,s.t.\underset{u\in X}{min}{\mathcal{J}}_q\left(u\right),$(3) where the abbreviation ‘s.t.’ means ‘subject to’.

Since (1(1) $min{\mathcal{J}}_q\left(u\right),\text{over}u\in X,$(1) ) appears in (3(3) $\underset{q\in \mathcal{C}}{min}\frac{1}{2}\Vert \mathcal{B}\left(u\right)-z{\Vert }^2,s.t.\underset{u\in X}{min}{\mathcal{J}}_q\left(u\right),$(3) ) as constraint, solving (1(1) $min{\mathcal{J}}_q\left(u\right),\text{over}u\in X,$(1) ) in first step when the parameter q is still far from its optimal value may be inefficient. Also, one has to make a choice of initialization $q_0$ and this gives a first approximation of state $u\left(q_0\right)$ which may be far from the measurement [39]. The idea is to compute the dual problem associated to the primal problem (1(1) $min{\mathcal{J}}_q\left(u\right),\text{over}u\in X,$(1) ) using the Fenchel duality: (4) $sup{\mathcal{J}}_q^{\ast }\left(u^{\ast }\right),\text{over}{u}^{\ast }\in X^{\ast },$(4) where X and $X^{\ast }$ are placed in topological duality and $J^{\ast }$ is the convex conjugate function associated to J. It is well known that the solution to the primal problem (1(1) $min{\mathcal{J}}_q\left(u\right),\text{over}u\in X,$(1) ) and dual problem (4(4) $sup{\mathcal{J}}_q^{\ast }\left(u^{\ast }\right),\text{over}{u}^{\ast }\in X^{\ast },$(4) ) -if they exist- satisfy the following extremality condition: (5) ${\mathcal{J}}_q\left(\overline{u}\right)+{\mathcal{J}}_q^{\ast }\left({\overline{u}}^{\ast }\right)=0,$(5) where $\overline{u}$ is the solution of (1(1) $min{\mathcal{J}}_q\left(u\right),\text{over}u\in X,$(1) ) and ${\overline{u}}^{\ast }$ is the solutions of (4(4) $sup{\mathcal{J}}_q^{\ast }\left(u^{\ast }\right),\text{over}{u}^{\ast }\in X^{\ast },$(4) ) (see [37] for more details). One can take profit from this relation to get a penalization of the least square problem (3(3) $\underset{q\in \mathcal{C}}{min}\frac{1}{2}\Vert \mathcal{B}\left(u\right)-z{\Vert }^2,s.t.\underset{u\in X}{min}{\mathcal{J}}_q\left(u\right),$(3) ) (see [39]). Then, the penalized least square formulation (see [40]) for parameter identification problem is stated as follows: (6) $\underset{\begin{array}{c}q\in \mathcal{C}\\ \text{s.t.}\left[{\mathcal{J}}_q\right(u)+{\mathcal{J}}_q^{\ast }(u^{\ast }\left)\right]=0\end{array}}{min}\{\frac{1}{2}\Vert \mathcal{B}(u)-z{\Vert }^2+\frac{1}{2ϵ}|{\mathcal{J}}_q\left(u\right)+{\mathcal{J}}_q^{\ast }\left(u^{\ast }\right){|}^2\}.$(6) Once the existence of a solution and the convergences are obtained, by keeping the extremality duality inequality relation as constraint (since weak duality $\left[{\mathcal{J}}_q\right(u)+{\mathcal{J}}_q^{\ast }(u^{\ast }\left)\right]\ge 0$ is always satisfied), we get the following constrained minimization problem (7) $\underset{\begin{array}{c}q\in \mathcal{C}\\ \text{s. t.}\left[{\mathcal{J}}_q\right(u)+{\mathcal{J}}_q^{\ast }(u^{\ast }\left)\right]\le 0\end{array}}{min}\{\frac{1}{2}\Vert \mathcal{B}(u)-z{\Vert }^2+\frac{1}{2ϵ}|{\mathcal{J}}_q\left(u\right)+{\mathcal{J}}_q^{\ast }\left(u^{\ast }\right){|}^2\}.$(7) We state the augmented Lagrangian functional associated with (7(7) $\underset{\begin{array}{c}q\in \mathcal{C}\\ \text{s. t.}\left[{\mathcal{J}}_q\right(u)+{\mathcal{J}}_q^{\ast }(u^{\ast }\left)\right]\le 0\end{array}}{min}\{\frac{1}{2}\Vert \mathcal{B}(u)-z{\Vert }^2+\frac{1}{2ϵ}|{\mathcal{J}}_q\left(u\right)+{\mathcal{J}}_q^{\ast }\left(u^{\ast }\right){|}^2\}.$(7) ), where the quadratic term $\frac{1}{2ϵ}\left|{\mathcal{J}}_q\right(u)+{\mathcal{J}}_q^{(}{u}^{)}{|}^2$ is added to the Lagrangian function. Then, we reformulate the inverse problem as an equivalent saddle point problem. We utilize an ADMM (Alternating Direction Method of Multipliers) to split the problem into several subproblems. Additionally, we employ Fenchel duality and a primal–dual active set strategy (PDAS) to numerically solve the resulting subproblems.

The remainder of this paper is briefly outlined as follows. In Section 2, we formulate the identification problem. Firstly, we reformulate the frictional contact problem as an equivalent minimization problem and compute the associated regularized dual problem. Secondly, we formulate the regularized penalized problem as the least squares identification of Lamé coefficients. We establish the existence of a solution based on a minimizing sequence and demonstrate the convergence of the regularized penalized least squares problem to the original regularized least squares problem based on Sobolev embeddings. In Section 3, we introduce the Lagrangian and augmented Lagrangian formulations of the inverse problem. We demonstrate the existence of Lagrange multipliers. Finally, we provide an equivalent saddle point. Section 4 is devoted to the numerical realization of the problem. We present the algorithms and illustrate the solutions

2. Penalized identification problem formulation

2.1. Elastic contact problem with friction

We are interested in an elastic body occupying in its initial ( non-deformed) configuration a bounded domain $\mathrm{\Omega }\subset {\mathbb{R}}^d,d\in \{2,3\}$, with a smooth boundary $\mathrm{\partial \Omega }=\mathrm{\Gamma }$. We assume that Γ is divided into three disjoint parts, i.e. $\mathrm{\Gamma }={\mathrm{\Gamma }}_D\cup {\mathrm{\Gamma }}_N\cup {\mathrm{\Gamma }}_C$ and $\mathrm{meas}\left({\mathrm{\Gamma }}_D\right)>0$. We assume that the body is clamped on ${\mathrm{\Gamma }}_D$ and a surface traction is applied on ${\mathrm{\Gamma }}_N$. On ${\mathrm{\Gamma }}_C$ the body may come into a frictional contact with a rigid foundation. We assume a linear elasticity, then the strain tensor ε is given by: $ϵ\left(u\right)=\frac{1}{2}(\mathrm{\nabla u}+(\mathrm{\nabla u}{)}^{\mathrm{\top }}),$where u is the displacement field.

The constitutive relation is: $\sigma =\mathcal{A}ϵ\left(u\right)\mathrm{in}\mathrm{\Omega },$where $\mathcal{A}=\left(a_{\mathrm{ijkl}}\right)\in L^{\mathrm{\infty }}\left(\mathrm{\Omega }\right)$ is the (fourth-order) symmetric and coercive elasticity tensor. Let ν be the unit outward normal to Ω on Γ. The displacement field and the stress tensor can be decomposed in normal and tangential components as follows: $\begin{array}{rl}{u}_{\nu }& =u\cdot \nu ,u_{\tau }=u-u_{\nu }\nu ,\\ {\sigma }_{\nu }& =\left(\mathrm{\sigma \nu }\right)\cdot \nu \text{and}{\sigma }_{\tau }=\mathrm{\sigma \nu }-{\sigma }_{\nu }\nu .\end{array}$The mechanical equilibrium equation is given by: (8) $\begin{array}{rl}-\mathrm{div}\left(\sigma \right)& =f\mathrm{in}\mathrm{\Omega },\end{array}$(8) (9) $\begin{array}{rl}\mathrm{\sigma \nu }& =f_s\mathrm{on}{\mathrm{\Gamma }}_N,\end{array}$(9) (10) $\begin{array}{rl}u& =0\text{on}{\mathrm{\Gamma }}_D,\end{array}$(10) where $f\in L^2\left(\mathrm{\Omega }\right)$ and $f_s\in L^2\left({\mathrm{\Gamma }}_N\right)$.

Let $g\in L^{\mathrm{\infty }}\left({\mathrm{\Gamma }}_C\right)$ be the gap between Ω and the rigid foundation. The unilateral contact conditions are then: (11) $u_{\nu }-g\le 0,{\sigma }_{\nu }\le 0\mathrm{and}(u_{\nu }-g){\sigma }_{\nu }=0\mathrm{on}{\mathrm{\Gamma }}_C.$(11) The Coulomb friction is given by: (12) $\{\begin{array}{c}\parallel {\sigma }_{\tau }\parallel \le \mathcal{F}\parallel {\sigma }_{\nu }\left(u\right)\parallel \mathrm{on}{\mathrm{\Gamma }}_C,\\ \parallel {\sigma }_{\tau }\parallel <\mathcal{F}\parallel {\sigma }_{\nu }\left(u\right)\parallel ⟹u_{\tau }=0\mathrm{on}{\mathrm{\Gamma }}_C,\\ \parallel {\sigma }_{\tau }\parallel =\mathcal{F}\parallel {\sigma }_{\nu }\left(u\right)\parallel ⟹\mathrm{\exists \delta }\ge 0\mathrm{such}\mathrm{that}{u}_{\tau }=-\delta {\sigma }_{\tau }\mathrm{on}{\mathrm{\Gamma }}_C.\end{array}$(12) The Tresca friction is given by: (13) $\{\begin{array}{c}\parallel {\sigma }_{\tau }\parallel \le \mathcal{F}S\parallel \mathrm{on}{\mathrm{\Gamma }}_C,\\ \parallel {\sigma }_{\tau }\parallel <\mathcal{F}S⟹u_{\tau }=0\mathrm{on}{\mathrm{\Gamma }}_C,\\ \parallel {\sigma }_{\tau }\parallel =\mathcal{F}S⟹\mathrm{\exists \delta }\ge 0\mathrm{such}\mathrm{that}{u}_{\tau }=-\delta {\sigma }_{\tau }\mathrm{on}{\mathrm{\Gamma }}_C,\end{array}$(13) where $\mathcal{F}$ is the friction coefficient.

There are a major mathematical difficulties inherent in the problem (8(8) $\begin{array}{rl}-\mathrm{div}\left(\sigma \right)& =f\mathrm{in}\mathrm{\Omega },\end{array}$(8) )–(12(12) $\{\begin{array}{c}\parallel {\sigma }_{\tau }\parallel \le \mathcal{F}\parallel {\sigma }_{\nu }\left(u\right)\parallel \mathrm{on}{\mathrm{\Gamma }}_C,\\ \parallel {\sigma }_{\tau }\parallel <\mathcal{F}\parallel {\sigma }_{\nu }\left(u\right)\parallel ⟹u_{\tau }=0\mathrm{on}{\mathrm{\Gamma }}_C,\\ \parallel {\sigma }_{\tau }\parallel =\mathcal{F}\parallel {\sigma }_{\nu }\left(u\right)\parallel ⟹\mathrm{\exists \delta }\ge 0\mathrm{such}\mathrm{that}{u}_{\tau }=-\delta {\sigma }_{\tau }\mathrm{on}{\mathrm{\Gamma }}_C.\end{array}$(12) ). For instance, in general, ${\sigma }_{\nu }$ in (13(13) $\{\begin{array}{c}\parallel {\sigma }_{\tau }\parallel \le \mathcal{F}S\parallel \mathrm{on}{\mathrm{\Gamma }}_C,\\ \parallel {\sigma }_{\tau }\parallel <\mathcal{F}S⟹u_{\tau }=0\mathrm{on}{\mathrm{\Gamma }}_C,\\ \parallel {\sigma }_{\tau }\parallel =\mathcal{F}S⟹\mathrm{\exists \delta }\ge 0\mathrm{such}\mathrm{that}{u}_{\tau }=-\delta {\sigma }_{\tau }\mathrm{on}{\mathrm{\Gamma }}_C,\end{array}$(13) ) is neither pointwise nor almost everywhere defined. Replacing the Coulomb friction in the above model by Tresca friction means replacing $\Vert {\sigma }_{\nu }\left(u\right)\Vert$ by a given friction $S\in L^2\left({\mathrm{\Gamma }}_C\right)$. The resulting system can be then analysed and the existence of a unique solution can be proved. For a review, we refer the reader to [26,41], for example. In the remainder of this work, we will consider the Tresca friction (13(13) $\{\begin{array}{c}\parallel {\sigma }_{\tau }\parallel \le \mathcal{F}S\parallel \mathrm{on}{\mathrm{\Gamma }}_C,\\ \parallel {\sigma }_{\tau }\parallel <\mathcal{F}S⟹u_{\tau }=0\mathrm{on}{\mathrm{\Gamma }}_C,\\ \parallel {\sigma }_{\tau }\parallel =\mathcal{F}S⟹\mathrm{\exists \delta }\ge 0\mathrm{such}\mathrm{that}{u}_{\tau }=-\delta {\sigma }_{\tau }\mathrm{on}{\mathrm{\Gamma }}_C,\end{array}$(13) ) since the problem with (12(12) $\{\begin{array}{c}\parallel {\sigma }_{\tau }\parallel \le \mathcal{F}\parallel {\sigma }_{\nu }\left(u\right)\parallel \mathrm{on}{\mathrm{\Gamma }}_C,\\ \parallel {\sigma }_{\tau }\parallel <\mathcal{F}\parallel {\sigma }_{\nu }\left(u\right)\parallel ⟹u_{\tau }=0\mathrm{on}{\mathrm{\Gamma }}_C,\\ \parallel {\sigma }_{\tau }\parallel =\mathcal{F}\parallel {\sigma }_{\nu }\left(u\right)\parallel ⟹\mathrm{\exists \delta }\ge 0\mathrm{such}\mathrm{that}{u}_{\tau }=-\delta {\sigma }_{\tau }\mathrm{on}{\mathrm{\Gamma }}_C.\end{array}$(12) ) can be obtained by a sequence of problems with the Tresca friction (13(13) $\{\begin{array}{c}\parallel {\sigma }_{\tau }\parallel \le \mathcal{F}S\parallel \mathrm{on}{\mathrm{\Gamma }}_C,\\ \parallel {\sigma }_{\tau }\parallel <\mathcal{F}S⟹u_{\tau }=0\mathrm{on}{\mathrm{\Gamma }}_C,\\ \parallel {\sigma }_{\tau }\parallel =\mathcal{F}S⟹\mathrm{\exists \delta }\ge 0\mathrm{such}\mathrm{that}{u}_{\tau }=-\delta {\sigma }_{\tau }\mathrm{on}{\mathrm{\Gamma }}_C,\end{array}$(13) ) (see [41] for example).

In the following, we introduce the notations and recall some necessary definitions that we will need later. We denote by $W^{1,p}\left(\mathrm{\Omega }\right)$ the usual Sobolev space and $\begin{array}{rl}H& =L^2(\mathrm{\Omega }{)}^d,H_1=H^1(\mathrm{\Omega }{)}^d,\\ \mathcal{H}& =\{\tau =({\sigma }_{\mathrm{ij}})\mid {\sigma }_{\mathrm{ij}}={\sigma }_{\mathrm{ji}}\in L^2(\mathrm{\Omega }\left)\right\}\text{and}{\mathcal{H}}_1=\{\sigma \in \mathcal{H}\mid \mathrm{div}\sigma \in H\},\end{array}$are real Hilbert spaces endowed with the inner products: $(u,v{)}_H={\int }_{\mathrm{\Omega }}{u}_i{v}_i\mathrm{d}x,(\sigma ,\theta {)}_{\mathcal{H}}={\int }_{\mathrm{\Omega }}{\sigma }_{\mathrm{ij}}{\theta }_{\mathrm{ij}}\mathrm{d}x,\sigma \cdot \theta ={\sigma }_{\mathrm{ij}}{\theta }_{\mathrm{ij}},$under summation convention, and $(u,v{)}_{H_1}=(u,v{)}_H+\left(ϵ\right(u),ϵ(v){)}_{\mathcal{H}},(\sigma ,\theta {)}_{{\mathcal{H}}_1}=(\sigma ,\theta {)}_{\mathcal{H}}+(\mathrm{div}\sigma ,\mathrm{div}\theta {)}_{\mathcal{H}}.$The associated norms are $\Vert \cdot {\Vert }_H$, $\Vert \cdot {\Vert }_{H_1}$, $\Vert \cdot \Vert$, $\Vert \cdot {\Vert }_{\mathcal{H}}$ and $\Vert \cdot {\Vert }_{{\mathcal{H}}_1}$, respectively. And we recall the following Rellich Kondrachov compactness theorem [42]:

Theorem 2.1

Assume that Ω is a bounded open subset of ${\mathbb{R}}^d$, and $\mathrm{\partial \Omega }$ is $C^1$. Suppose $1\le p<d$, then: (14) $W^{1,p}\left(\mathrm{\Omega }\right)\subset \subset L^q\left(\mathrm{\Omega }\right)\text{i.e. compact imbedding,}$(14) for each $1\le q<\frac{\mathrm{pd}}{d-p}$. In particular, when p = d, we have (15) $W^{1,p}\left(\mathrm{\Omega }\right)\subset \subset L^p\left(\mathrm{\Omega }\right)\text{i.e. compact imbedding,}$(15) for $1\le p\le +\mathrm{\infty }$.

Keeping in mind the boundary conditions (11(11) $u_{\nu }-g\le 0,{\sigma }_{\nu }\le 0\mathrm{and}(u_{\nu }-g){\sigma }_{\nu }=0\mathrm{on}{\mathrm{\Gamma }}_C.$(11) )–(13(13) $\{\begin{array}{c}\parallel {\sigma }_{\tau }\parallel \le \mathcal{F}S\parallel \mathrm{on}{\mathrm{\Gamma }}_C,\\ \parallel {\sigma }_{\tau }\parallel <\mathcal{F}S⟹u_{\tau }=0\mathrm{on}{\mathrm{\Gamma }}_C,\\ \parallel {\sigma }_{\tau }\parallel =\mathcal{F}S⟹\mathrm{\exists \delta }\ge 0\mathrm{such}\mathrm{that}{u}_{\tau }=-\delta {\sigma }_{\tau }\mathrm{on}{\mathrm{\Gamma }}_C,\end{array}$(13) ), we introduce the closed subspace V of $H_1$ and K the set of admissible displacements defined respectively by: $V=\{v\in H_1|v=0\mathrm{on}{\mathrm{\Gamma }}_D\},\text{and}K=\{v\in V\mid v_{\nu }-g\le 0\mathrm{on}{\mathrm{\Gamma }}_C\}.$Define the following set: $K_s=\{\sigma \in {\mathcal{H}}_1\text{such that}:\{\begin{array}{l}-\mathrm{div}\left(\sigma \right)=f\text{in}\mathrm{\Omega },\\ \mathrm{\sigma \nu }=f_s\text{on}{\mathrm{\Gamma }}_N,\\ {\sigma }_{\nu }\le 0\text{on}{\mathrm{\Gamma }}_C,\\ \left|{\sigma }_{\tau }\right|\le \mathcal{F}S\text{on}{\mathrm{\Gamma }}_C.\end{array}\}$The Hilbert space V is endowed with the inner product given by: (16) $(u,v{)}_V=(u,v{)}_{H_1},\Vert v{\Vert }_V=(v,v{)}_V^{\frac{1}{2}}.$(16) By Korn's inequality, there exists a constant $c_0$ such that: (17) $\Vert ϵ\left(v\right){\Vert }_H\ge c_0\Vert v{\Vert }_{H_1}.$(17) Note that by the Korn's inequality, the norm $\Vert \cdot {\Vert }_{H_1}$ and the usual norm of $H_1$ are equivalent (see [28] for example).

We use the Riesz's representation theorem to consider the element $f\in V^{\ast }$ by: (18) ${〈f,v〉}_{V^{\ast }\times V}={\int }_{\mathrm{\Omega }}f\cdot v\mathrm{d}x+{\int }_{{\mathrm{\Gamma }}_N}{f}_s\cdot v\mathrm{d}\mathrm{\Gamma },\mathrm{\forall }v\in V,$(18) We define the mapping $j:V\to \mathbb{R}$ by: (19) $j\left(v\right)={\int }_{{\mathrm{\Gamma }}_C}\mathcal{F}S\left|v_{\tau }\right|\mathrm{d}\mathrm{\Gamma },\mathrm{\forall }v\in V.$(19) With the above notations, we obtain the following variational formulation of the problem (P):

Problem (PV ). Find a displacement field $u\in K$ such that: (20) $\left(\mathcal{A}ϵ\right(u),ϵ(v)-ϵ(u){)}_{\mathcal{H}}+j(v)-j(u)\ge {〈f,v-u〉}_{V^{\ast }\times V},\mathrm{\forall }v\in K.$(20) The existence of the solution of the problem (PV ) is widely studied [25–31] and the uniqueness depends on the smallness of the friction's coefficient $\mathcal{F}\in L^2\left({\mathrm{\Gamma }}_C\right)$, where $\mathcal{F}\ge 0a.e.$ on ${\mathrm{\Gamma }}_C$ (see [41]).

Now, we are able to give an equivalent minimization problem. To do this, let us introduce the following notations: (21) $\begin{array}{rl}{F}_q\left(u\right)& =\frac{1}{2}(\mathcal{A}u,u{)}_{\mathcal{H}},\end{array}$(21) (22) $\begin{array}{rl}{J}_q\left(u\right)& ={〈f,u〉}_{V^{\ast }\times V},\end{array}$(22) (23) $\begin{array}{rl}{j}_q\left(u\right)& =j\left(u\right).\end{array}$(23) And the linear maps A and B are defined respectively by: $\mathrm{Au}=ϵ\left(u\right),\mathrm{Bu}=u_{\tau }.$Hence, the problem (20(20) $\left(\mathcal{A}ϵ\right(u),ϵ(v)-ϵ(u){)}_{\mathcal{H}}+j(v)-j(u)\ge {〈f,v-u〉}_{V^{\ast }\times V},\mathrm{\forall }v\in K.$(20) ) is equivalent to the following minimization problem, known as primal problem:

Primal Problem: (24) $\text{Find}u\in K\text{such that:}{\mathcal{J}}_q\left(u\right)\le {\mathcal{J}}_q\left(v\right),\mathrm{\forall }v\in K,$(24) where ${\mathcal{J}}_q\left(u\right)=F_q\left(\mathrm{Au}\right)-J_q\left(u\right)+j_q\left(\mathrm{Bu}\right)$. Since the symmetric and bilinear form $(\mathcal{A}\cdot ,\cdot {)}_{\mathcal{H}}$ is coercive, $J_q(\cdot )$ is linear and continuous and $j_q(\cdot )$ is strictly convex and lower semicontinuous, the minimization problem (24(24) $\text{Find}u\in K\text{such that:}{\mathcal{J}}_q\left(u\right)\le {\mathcal{J}}_q\left(v\right),\mathrm{\forall }v\in K,$(24) ) admits a unique solution (see [37]).

Now, we give the dual problem associated to (24(24) $\text{Find}u\in K\text{such that:}{\mathcal{J}}_q\left(u\right)\le {\mathcal{J}}_q\left(v\right),\mathrm{\forall }v\in K,$(24) ) taking into account the separability of cost function into sum of three proper, convex and lower semi continuous functions. For the convex conjugate $J_q^{\ast }$ of $J_q$, one derives that $J_q^{\ast }(A^{\ast }{\ell }^{\ast }+B^{\ast }{k}^{\ast })$ equals $+\mathrm{\infty }$ unless (25) $-\mathrm{div}\left({\ell }^{\ast }\right)=f,{\ell }^{\ast }\nu =f_s\text{on}{\mathrm{\Gamma }}_N\text{and}{\ell }_{\tau }^{\ast }+k^{\ast }=0\text{in}{L}^2\left({\mathrm{\Gamma }}_C\right).$(25) Note that in that in (25(25) $-\mathrm{div}\left({\ell }^{\ast }\right)=f,{\ell }^{\ast }\nu =f_s\text{on}{\mathrm{\Gamma }}_N\text{and}{\ell }_{\tau }^{\ast }+k^{\ast }=0\text{in}{L}^2\left({\mathrm{\Gamma }}_C\right).$(25) ), the regularity $L^2\left({\mathrm{\Gamma }}_C\right)$ for ${\ell }_{\tau }^{\ast }+k^{\ast }=0$ is the best that we can suppose to allow the convergence (see [43,44]).

Further, one obtains (26) $J_q^{\ast }(A^{\ast }{\ell }^{\ast }+B^{\ast }{k}^{\ast })=\{\begin{array}{ll}-〈{\ell }_{\nu }^{\ast },g{〉}_{{\mathrm{\Gamma }}_C},& \text{if}\left(25\right)\text{and}{\ell }_{\nu }^{\ast }\le 0\text{in}{H}^{-\frac{1}{2}}\left({\mathrm{\Gamma }}_C\right)\text{hold,}\\ \mathrm{\infty },& \text{otherwise},\end{array}$(26) and (27) $F_q^{\ast }\left({\ell }^{\ast }\right)=\frac{1}{2}({\mathcal{A}}^{-1}{\ell }^{\ast },{\ell }^{\ast }{)}_{\mathcal{H}}.$(27) Since $S\in L^2\left({\mathrm{\Gamma }}_C\right)$, we have: (28) $j_q^{\ast }\left(k^{\ast }\right)=\{\begin{array}{ll}0,& \text{if}\left|k^{\ast }\right|\le \mathcal{F}S,\\ \mathrm{\infty },& \text{otherwise}.\end{array}$(28) Then, the dual problem is defined as follows: (29) $\underset{\begin{array}{c}({\ell }^{\ast },k^{\ast })\in K_s\times L^2\left({\mathrm{\Gamma }}_C\right)\\ {\ell }_{\tau }^{\ast }+k^{\ast }=0\text{ in }{L}^2\left({\mathrm{\Gamma }}_C\right)\end{array}}{sup}-{\mathcal{J}}_q({\ell }^{\ast },k^{\ast }):=\frac{1}{2}({\mathcal{A}}^{-1}{\ell }^{\ast },{\ell }^{\ast }{)}_{\mathcal{H}}-〈{\ell }_{\nu }^{\ast },g{〉}_{{\mathrm{\Gamma }}_C}.$(29) Evaluating the extremality conditions for the above problems, we obtain the following lemma [36,45]:

Lemma 2.2

The solution $\overline{u}\in K$ of the primal problem (24(24) $\text{Find}u\in K\text{such that:}{\mathcal{J}}_q\left(u\right)\le {\mathcal{J}}_q\left(v\right),\mathrm{\forall }v\in K,$(24) ) and the solution $(\overline{{\ell }^{\ast }},\overline{k^{\ast }})\in K_s$ are related by $\delta \overline{u}=\overline{{\ell }^{\ast }}$ and the existence of $\mathrm{\Lambda }\in H^{-\frac{1}{2}}\left({\mathrm{\Gamma }}_C\right)$ such that: (30) $\begin{array}{rl}(\mathcal{A}\overline{u},v{)}_{\mathcal{H}}-J_q(v)+〈\overline{k^{\ast }},v_{\tau }{〉}_{{\mathrm{\Gamma }}_C}+〈\mathrm{\Lambda },v_{\nu }{〉}_{{\mathrm{\Gamma }}_C}& =0,\text{For all}v\in K,\end{array}$(30) (31) $\begin{array}{rl}〈\mathrm{\Lambda },v_{\nu }{〉}_{{\mathrm{\Gamma }}_C}& \le 0,\text{For all}v\in K,\end{array}$(31) (32) $\begin{array}{rl}〈\mathrm{\Lambda },{\overline{u}}_{\nu }-g{〉}_{{\mathrm{\Gamma }}_C}& =0,\end{array}$(32) (33) $\begin{array}{rl}\delta {\overline{u}}_{\tau }-max(0,\delta {\overline{u}}_{\tau }+\overline{k^{\ast }}-\mathcal{F}S)-min(0,\delta {\overline{u}}_{\tau }+\overline{k^{\ast }}+\mathcal{F}S)& =0,\end{array}$(33) for an arbitrary $\delta >0$.

Following [36,45], we introduce regularized version of the contact problem with Tresca friction, which enable us to apply the semismooth Newton method. To this end, let $\gamma >0$ be a regularization parameter, $\hat{\mathrm{\Lambda }}\in L^2\left({\mathrm{\Gamma }}_C\right)$, $\hat{\mathrm{\Lambda }}\ge 0$ and $\hat{k}\in L^2\left({\mathrm{\Gamma }}_C\right)$. Let us define the functional $D_{\gamma }:L^2\left({\mathrm{\Gamma }}_C\right)\times L^2\left({\mathrm{\Gamma }}_C\right)⟶\mathbb{R}$ by: (34) $D_{\gamma }({\ell }^{\ast },k^{\ast })=\frac{1}{2}(\mathcal{A}{u}_{{\ell }^{\ast },k^{\ast }},u_{{\ell }^{\ast },k^{\ast }})+〈{\ell }^{\ast },g{〉}_{{\mathrm{\Gamma }}_C}+\frac{1}{2\gamma }\Vert {\ell }^{\ast }-\hat{\mathrm{\Lambda }}{\Vert }_{{\mathrm{\Gamma }}_C}^2+\frac{1}{2\gamma }\Vert k^{\ast }-\hat{k}{\Vert }_{{\mathrm{\Gamma }}_C}^2,$(34) where $u_{{\ell }^{\ast },k^{\ast }}\in V$ satisfies: (35) $(\mathcal{A}{u}_{{\ell }^{\ast },k^{\ast }},v)-J_q\left(v\right)+〈{\ell }^{\ast },v_{\nu }{〉}_{{\mathrm{\Gamma }}_C}+〈k^{\ast },v_{\tau }{〉}_{{\mathrm{\Gamma }}_C}=0.$(35) Then, the regularized dual problem with Tresca friction is defined as: (36) $\{\begin{array}{l}{\displaystyle -\underset{\begin{array}{c}({\ell }^{\ast },k^{\ast })\in H^{-\frac{1}{2}}\left({\mathrm{\Gamma }}_C\right)\times L^2\left({\mathrm{\Gamma }}_C\right)\\ {\ell }^{\ast }\ge 0\text{in}{H}^{-\frac{1}{2}}\left({\mathrm{\Gamma }}_C\right)\\ \left|k^{\ast }\right|\le \mathcal{F}S\end{array}}{inf}{D}_{\gamma }({\ell }^{\ast },k^{\ast })}\\ \text{where}{u}_{{\ell }^{\ast },k^{\ast }}\text{satisfies:}(\mathcal{A}{u}_{{\ell }^{\ast },k^{\ast }},v)-J_q\left(v\right)+〈{\ell }^{\ast },v_{\nu }{〉}_{{\mathrm{\Gamma }}_C}+〈k^{\ast },v_{\tau }{〉}_{{\mathrm{\Gamma }}_C}=0.\end{array}$(36) It can be proved (see [36,45]) that the extrimality conditions relating the primal and the regularized dual problem are, for $\gamma >0$: (37) $\begin{array}{rl}& (\mathcal{A}u,v)-J_q\left(v\right)+〈{\ell }^{\ast },v_{\nu }{〉}_{{\mathrm{\Gamma }}_C}+〈k^{\ast },v_{\tau }{〉}_{{\mathrm{\Gamma }}_C}=0,\end{array}$(37) (38) $\begin{array}{rl}& {\ell }^{\ast }-max(0,\hat{\mathrm{\Lambda }}+\gamma (u_{\nu }-g\left)\right)=0,\text{on}{\mathrm{\Gamma }}_C,\end{array}$(38) (39) $\begin{array}{rl}& \{\begin{array}{l}\gamma (\xi -u_{\tau })+k^{\ast }-\hat{k}=0,\\ \xi -max(0,\xi +\theta (k^{\ast }-\mathcal{F}S\left)\right)-min(0,\xi +\theta (k^{\ast }+\mathcal{F}S)=0.\end{array}\end{array}$(39) for any $\theta >0$. Here, ξ is the Lagrange multiplier associated to the constraint $\left|k^{\ast }\right|\le \mathcal{F}S$.

2.2. Primal–dual parameter estimation problem

We are interested in a simple situation of an isotropic elasticity where the elasticity tensor $\mathcal{A}$ depends only on two independent moduli. For instance, $\mathcal{A}$ can be expressed in terms of the Lamé coefficients $(\lambda ,\mu )$ by: (40) ${\mathcal{A}}_{\mathrm{ijkl}}=\lambda {\delta }_{\mathrm{ij}}{\delta }_{\mathrm{kl}}+\mu ({\delta }_{\mathrm{ik}}{\delta }_{\mathrm{jl}}+{\delta }_{\mathrm{jk}}{\delta }_{\mathrm{il}}).$(40) Other commonly used elastic parameters are the Young modulus E and the Poisson ratio ν, which are related to the Lamé constants by: (41) $E={\displaystyle \frac{\mu (3\lambda +2\mu )}{\lambda +\mu }},\nu ={\displaystyle \frac{\lambda }{2(\lambda +\mu )}}.$(41) The following inequality, which holds pointwise in Ω for d = 2, is easy to establish: (42) $2\mathrm{\mu ϵ}\left(v\right)\cdot ϵ\left(v\right)+\mathrm{\lambda tr}\left(ϵ\right(v){)}^2\ge min\{2\mu +2\lambda ,2\mu \left\}ϵ\right(v)\cdot ϵ(v).$(42) From (17(17) $\Vert ϵ\left(v\right){\Vert }_H\ge c_0\Vert v{\Vert }_{H_1}.$(17) ) and (42(42) $2\mathrm{\mu ϵ}\left(v\right)\cdot ϵ\left(v\right)+\mathrm{\lambda tr}\left(ϵ\right(v){)}^2\ge min\{2\mu +2\lambda ,2\mu \left\}ϵ\right(v)\cdot ϵ(v).$(42) ), one can obtain: (43) ${\int }_{\mathrm{\Omega }}2\mathrm{\mu ϵ}\left(v\right)\cdot ϵ\left(v\right)+\mathrm{\lambda tr}\left(ϵ\right(v){)}^2\ge \kappa \Vert v{\Vert }_{H_1}^2.$(43) where $\kappa =c_0^{2}min\{2\mu +2\lambda ,2\mu \}$. For given positive constants ${\lambda }_0$ and ${\mu }_0$ satisfying ${\lambda }_0>{\mu }_0>0$, we define the following subset of $W^{1,1}\left(\mathrm{\Omega }\right)\times W^{1,1}\left(\mathrm{\Omega }\right)$ of elements of the form $q=(\lambda ,\mu )$: $\mathcal{C}:=\{q\in W^{1,1}(\mathrm{\Omega })\times W^{1,1}(\mathrm{\Omega })/min\{2\mu +2\lambda ,2\mu \}\ge {\mu }_0,max\{\mu ,\lambda \}\le {\lambda }_0\text{in}\mathrm{\Omega }\}.$Henceforth, we will assume that a (possibly noisy) measurement z of $u\left(q\right)$ is available, where $u\left(q\right)$ and $q=(\lambda ,\mu )\in \mathcal{C}$ together satisfy (24(24) $\text{Find}u\in K\text{such that:}{\mathcal{J}}_q\left(u\right)\le {\mathcal{J}}_q\left(v\right),\mathrm{\forall }v\in K,$(24) ). The purpose of this paper is to propose and analyse a method for estimating q from z. For this reason, a least squares formulation associated to the estimation of the Lamé parameters $q=(\lambda ,\mu )$ is considered: (44) $\underset{q\in \mathcal{C}}{min}\mathcal{Q}(u,q):=\frac{1}{2}{\int }_{\mathrm{\Omega }}2\mu \left|ϵ\right(u\left(q\right)-z){|}^2+\lambda |\mathrm{div}\left(u\right(q)-z){|}^2,$(44) where $u\left(q\right)$ is the unique solution of (24(24) $\text{Find}u\in K\text{such that:}{\mathcal{J}}_q\left(u\right)\le {\mathcal{J}}_q\left(v\right),\mathrm{\forall }v\in K,$(24) ) corresponding to q.

In principle, it is reasonable to estimate q by minimization problem (44(44) $\underset{q\in \mathcal{C}}{min}\mathcal{Q}(u,q):=\frac{1}{2}{\int }_{\mathrm{\Omega }}2\mu \left|ϵ\right(u\left(q\right)-z){|}^2+\lambda |\mathrm{div}\left(u\right(q)-z){|}^2,$(44) ) over $\mathcal{C}$. However, since the inverse problem under consideration is ill-posed, it is necessary to regularize the cost function.

Therefore, we consider the following minimization regularized problem to estimate q from z. Find $q\in \mathcal{C}$ by solving: (45) $\underset{q\in \mathcal{C}}{min}\mathcal{R}(u,q):=\mathcal{Q}(u,q)+\frac{\rho }{2}R\left(q\right),$(45) where R is a Tikhonov regularization and $\rho >0$ is the Tikhonov's regularization parameter.

Now, we are in position to state the primal–dual formulation for least squares parameter estimation problem: (46) $\underset{\begin{array}{c}q\in \mathcal{C}\\ u\in K\\ ({\ell }^{\ast },k^{\ast })\in K_s\times L^2\left({\mathrm{\Gamma }}_C\right),\\ {\ell }_{\tau }^{\ast }+k^{\ast }=0\text{ in }{L}^2\left({\mathrm{\Gamma }}_C\right).\end{array}}{min}\left\{\mathcal{R}\right(u,q)+\frac{1}{2ϵ}|{\mathcal{J}}_q\left(u\right)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast }){|}^2\}.$(46)

2.3. Convergence results

The first result in this section confirms the existence of at least one solution to the primal–dual problem (46(46) $\underset{\begin{array}{c}q\in \mathcal{C}\\ u\in K\\ ({\ell }^{\ast },k^{\ast })\in K_s\times L^2\left({\mathrm{\Gamma }}_C\right),\\ {\ell }_{\tau }^{\ast }+k^{\ast }=0\text{ in }{L}^2\left({\mathrm{\Gamma }}_C\right).\end{array}}{min}\left\{\mathcal{R}\right(u,q)+\frac{1}{2ϵ}|{\mathcal{J}}_q\left(u\right)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast }){|}^2\}.$(46) ).

Proposition 2.1

For every $ϵ>0$, there exists a solution $(q_{ϵ},u_{ϵ},{\ell }_{ϵ}^{\ast },k_{ϵ}^{\ast })\in \mathcal{C}\times K\times K_s\times L^2\left({\mathrm{\Gamma }}_C\right)$ to (46(46) $\underset{\begin{array}{c}q\in \mathcal{C}\\ u\in K\\ ({\ell }^{\ast },k^{\ast })\in K_s\times L^2\left({\mathrm{\Gamma }}_C\right),\\ {\ell }_{\tau }^{\ast }+k^{\ast }=0\text{ in }{L}^2\left({\mathrm{\Gamma }}_C\right).\end{array}}{min}\left\{\mathcal{R}\right(u,q)+\frac{1}{2ϵ}|{\mathcal{J}}_q\left(u\right)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast }){|}^2\}.$(46) ).

Proof.

Let $\{S_n:=(u_n,q_n,{\ell }_n^{\ast },k_n^{\ast }){\}}_n$ be a minimizing sequence such that for each $n\in \mathbb{N}$ the constraints in (46(46) $\underset{\begin{array}{c}q\in \mathcal{C}\\ u\in K\\ ({\ell }^{\ast },k^{\ast })\in K_s\times L^2\left({\mathrm{\Gamma }}_C\right),\\ {\ell }_{\tau }^{\ast }+k^{\ast }=0\text{ in }{L}^2\left({\mathrm{\Gamma }}_C\right).\end{array}}{min}\left\{\mathcal{R}\right(u,q)+\frac{1}{2ϵ}|{\mathcal{J}}_q\left(u\right)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast }){|}^2\}.$(46) ) are fulfilled, that is: (47) $\{\begin{array}{ll}{q}_n\in \mathcal{C},i.e.& min\{2{\mu }_n+2{\lambda }_n,2{\mu }_n\}\ge {\mu }_0,\\ & max\{{\mu }_n,{\lambda }_n\}\le {\lambda }_0\text{in}\mathrm{\Omega },\\ u_n\in K,i.e.& u_n\in V\text{and}{u}_{\mathrm{n\nu }}\le g,\\ \{\begin{array}{l}({\ell }_n^{\ast },k_n^{\ast })\in K_s\times L^2\left({\mathrm{\Gamma }}_C\right),\\ {\ell }_{\mathrm{n\tau }}^{\ast }+k_n^{\ast }=0\text{in}{L}^2\left({\mathrm{\Gamma }}_C\right),\end{array}i.e.& \{\begin{array}{l}-\mathrm{div}\left({\ell }_n^{\ast }\right)=f\text{in}\mathrm{\Omega },\\ {\ell }_n^{\ast }\nu =f_s\text{on}{\mathrm{\Gamma }}_N,\\ {\ell }_{\mathrm{n\nu }}^{\ast }\le 0\text{on}{\mathrm{\Gamma }}_C,\\ \left|k_n\right|\le \mathcal{F}S\text{on}{\mathrm{\Gamma }}_C,\end{array}\end{array}$(47) and (48) $\alpha \le \mathcal{R}(u_n,q_n)+\frac{1}{2ϵ}\left|{\mathcal{J}}_{q_n}\right(u_n)+{\mathcal{J}}_{q_n}^{\ast }({\ell }_n^{\ast },k_n^{\ast }){|}^2\le \alpha +\frac{1}{n},$(48) here α denotes the infimum of the cost function in (46(46) $\underset{\begin{array}{c}q\in \mathcal{C}\\ u\in K\\ ({\ell }^{\ast },k^{\ast })\in K_s\times L^2\left({\mathrm{\Gamma }}_C\right),\\ {\ell }_{\tau }^{\ast }+k^{\ast }=0\text{ in }{L}^2\left({\mathrm{\Gamma }}_C\right).\end{array}}{min}\left\{\mathcal{R}\right(u,q)+\frac{1}{2ϵ}|{\mathcal{J}}_q\left(u\right)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast }){|}^2\}.$(46) ). Since $\mathcal{R}(u_n,q_n)$ is not negative and $\left[{\mathcal{J}}_{q_n}\right(u_n)+{\mathcal{J}}_{q_n}^{\ast }({\ell }_n^{\ast },k_n^{\ast }\left)\right]$ is coercive and from (48(48) $\alpha \le \mathcal{R}(u_n,q_n)+\frac{1}{2ϵ}\left|{\mathcal{J}}_{q_n}\right(u_n)+{\mathcal{J}}_{q_n}^{\ast }({\ell }_n^{\ast },k_n^{\ast }){|}^2\le \alpha +\frac{1}{n},$(48) ), the sequence $S_n$ is bounded. Hence, there exists a subsequence of $S_n$, which is denoted by the same notation $S_n$, and $S_{ϵ}:=(u_{ϵ},q_{ϵ},{\ell }_{ϵ}^{\ast },k_{ϵ}^{\ast })$ such that (49) $S_n\rightharpoonup S_{ϵ}\text{weakly in}V\times \mathcal{C}\times {\mathcal{H}}_1\times H^{-\frac{1}{2}}\left({\mathrm{\Gamma }}_C\right).$(49) In particular, since ${\ell }_{\mathrm{n\tau }}^{\ast }+k_n^{\ast }=0\text{ in }{L}^2\left({\mathrm{\Gamma }}_C\right)$, we get (50) $(u_n,{\ell }_n^{\ast },k_n^{\ast })⟶(u_{ϵ},{\ell }_{ϵ}^{\ast },k_{ϵ}^{\ast })\text{strongly in}H\times H\times L^2\left({\mathrm{\Gamma }}_C\right).$(50) Moreover (51) $\{\begin{array}{l}-\mathrm{div}\left({\ell }_{ϵ}^{\ast }\right)=f\text{in}\mathrm{\Omega },\\ {\ell }_{ϵ}^{\ast }\nu =f_s\text{on}{\mathrm{\Gamma }}_N,\\ {\ell }_{\mathrm{ϵ\nu }}^{\ast }\le 0\text{on}{\mathrm{\Gamma }}_C,\\ \left|k_{ϵ}\right|\le \mathcal{F}S\text{on}{\mathrm{\Gamma }}_C,\end{array}$(51) also, it follows that (52) $ϵ\left(u_n\right)\rightharpoonup ϵ\left(u_{ϵ}\right)\text{weakly in}{L}^2,$(52) and then (53) ${\mathcal{A}}_nϵ\left(u_n\right)\rightharpoonup {\mathcal{A}}_{ϵ}ϵ\left(u_{ϵ}\right)\text{weakly in}{L}^2.$(53) In the other hand, we have: (54) ${\mathcal{A}}_n^{-1}{\ell }_n^{\ast }\rightharpoonup {\mathcal{A}}_{ϵ}^{-1}{\ell }_{ϵ}^{\ast }\text{weakly in}{L}^2.$(54) Let us prove the following continuity result: (55) $u_n\left(q_n\right)⟶u_{ϵ}\left(q_{ϵ}\right)\text{strongly in}V.$(55) Since $u_n\left(q_n\right)$ and $u_{ϵ}\left(q_{ϵ}\right)$ both satisfy the variational formulation (20(20) $\left(\mathcal{A}ϵ\right(u),ϵ(v)-ϵ(u){)}_{\mathcal{H}}+j(v)-j(u)\ge {〈f,v-u〉}_{V^{\ast }\times V},\mathrm{\forall }v\in K.$(20) ) for $q_n$ and $q_{ϵ}$, respectively, i.e. (56) $\left({\mathcal{A}}_nϵ\right(u_n\left(q_n\right)),ϵ(v)-ϵ(u_n\left(q_n\right)){)}_{\mathcal{H}}+j(v)-j(u_n\left(q_n\right))\ge {〈f,v-u_n\left(q_n\right)〉}_{V^{\ast }\times V},$(56) and (57) $\left({\mathcal{A}}_{ϵ}ϵ\right(u_{ϵ}\left(q_{ϵ}\right)),ϵ(v)-ϵ(u_{ϵ}\left(q_{ϵ}\right)){)}_{\mathcal{H}}+j(v)-j(u_{ϵ}\left(q_{ϵ}\right))\ge {〈f,v-u_{ϵ}\left(q_{ϵ}\right)〉}_{V^{\ast }\times V}.$(57) Taking $v=u_{ϵ}\left(q_{ϵ}\right)$ in (56(56) $\left({\mathcal{A}}_nϵ\right(u_n\left(q_n\right)),ϵ(v)-ϵ(u_n\left(q_n\right)){)}_{\mathcal{H}}+j(v)-j(u_n\left(q_n\right))\ge {〈f,v-u_n\left(q_n\right)〉}_{V^{\ast }\times V},$(56) ) and $v=u_n\left(q_n\right)$ in (57(57) $\left({\mathcal{A}}_{ϵ}ϵ\right(u_{ϵ}\left(q_{ϵ}\right)),ϵ(v)-ϵ(u_{ϵ}\left(q_{ϵ}\right)){)}_{\mathcal{H}}+j(v)-j(u_{ϵ}\left(q_{ϵ}\right))\ge {〈f,v-u_{ϵ}\left(q_{ϵ}\right)〉}_{V^{\ast }\times V}.$(57) ), by adding the resulting inequality, we obtain: (58) $\left({\mathcal{A}}_nϵ\right(u_n\left(q_n\right)),ϵ(u_n\left(q_n\right))-ϵ(u_n\left(q_n\right)){)}_{\mathcal{H}}-({\mathcal{A}}_{ϵ}ϵ\left(u_{ϵ}\right(q_{ϵ}\left)\right),ϵ\left(u_n\right(q_n\left)\right)-ϵ\left(u_{ϵ}\right(q_{ϵ}\left)\right){)}_{\mathcal{H}}\le 0.$(58) Let us set for the sake of simplicity: $\begin{array}{rl}{A}_n+A_{ϵ}& =\left({\mathcal{A}}_nϵ\right(u_n\left(q_n\right))-{\mathcal{A}}_nϵ(u_{ϵ}\left(q_{ϵ}\right)),ϵ(u_n\left(q_n\right))-ϵ(u_{ϵ}\left(q_{ϵ}\right)\left)\right)\\ & +\left({\mathcal{A}}_{ϵ}ϵ\right(u_n\left(q_n\right))-{\mathcal{A}}_{ϵ}ϵ(u_{ϵ}\left(q_{ϵ}\right)),ϵ(u_n\left(q_n\right))-ϵ(u_{ϵ}\left(q_{ϵ}\right)\left)\right),\end{array}$this leads to (59) $\begin{array}{rl}{A}_n+A_{ϵ}& \le \left({\mathcal{A}}_{ϵ}ϵ\right(u_n\left(q_n\right)),ϵ(u_n\left(q_n\right))-ϵ(u_{ϵ}\left(q_{ϵ}\right)\left)\right)\\ & -\left({\mathcal{A}}_nϵ\right(u_{ϵ}\left(q_{ϵ}\right)),ϵ(u_n\left(q_n\right))-ϵ(u_{ϵ}\left(q_{ϵ}\right)\left)\right),\end{array}$(59) which is equivalent to (60) $\begin{array}{rl}{A}_n+A_{ϵ}& \le {\int }_{\mathrm{\Omega }}{\mu }_{ϵ}ϵ\left(u_n\right)\left\{ϵ\right(u_n)-ϵ(u_{ϵ}\left)\right\}+{\lambda }_{ϵ}\mathrm{div}\left(u_n\right)\left\{\mathrm{div}\right(u_n)-\mathrm{div}(u_{ϵ}\left)\right\}\\ & -{\int }_{\mathrm{\Omega }}{\mu }_nϵ\left(u_{ϵ}\right)\left\{ϵ\right(u_n)-ϵ(u_{ϵ}\left)\right\}+{\lambda }_n\mathrm{div}\left(u_{ϵ}\right)\left\{\mathrm{div}\right(u_n)-\mathrm{div}(u_{ϵ}\left)\right\}.\end{array}$(60) Now, taking v = 0 in (20(20) $\left(\mathcal{A}ϵ\right(u),ϵ(v)-ϵ(u){)}_{\mathcal{H}}+j(v)-j(u)\ge {〈f,v-u〉}_{V^{\ast }\times V},\mathrm{\forall }v\in K.$(20) ) we deduce the existence of positive constant C, C will be generating constant in the remainder of the paper, such that (61) $\Vert ϵ\left(u\right){\Vert }_{L^2}^2\le C\Vert u{\Vert }_{L^2},$(61) and since $\mathcal{A}$ and u are bounded, there exists a constant C such that (62) $\Vert ϵ\left(u\right){\Vert }_{L^2}\le C.$(62) Also, we have (63) $\Vert \mathrm{div}\left(u\right){\Vert }_{L^2}\le C\Vert ϵ\left(u\right){\Vert }_{L^2}.$(63) From the coercivity of $\mathcal{A}$ and from (60(60) $\begin{array}{rl}{A}_n+A_{ϵ}& \le {\int }_{\mathrm{\Omega }}{\mu }_{ϵ}ϵ\left(u_n\right)\left\{ϵ\right(u_n)-ϵ(u_{ϵ}\left)\right\}+{\lambda }_{ϵ}\mathrm{div}\left(u_n\right)\left\{\mathrm{div}\right(u_n)-\mathrm{div}(u_{ϵ}\left)\right\}\\ & -{\int }_{\mathrm{\Omega }}{\mu }_nϵ\left(u_{ϵ}\right)\left\{ϵ\right(u_n)-ϵ(u_{ϵ}\left)\right\}+{\lambda }_n\mathrm{div}\left(u_{ϵ}\right)\left\{\mathrm{div}\right(u_n)-\mathrm{div}(u_{ϵ}\left)\right\}.\end{array}$(60) ), there exists a positive constant C such that (64) $\Vert u_n\left(q_n\right)-u_{ϵ}\left(q_{ϵ}\right){\Vert }_V\le C\left\{{\int }_{\mathrm{\Omega }}\right|{\lambda }_n-{\lambda }_{ϵ}|+{\int }_{\mathrm{\Omega }}|{\mu }_n-{\mu }_{ϵ}\left|\right\}.$(64) Since $q_n$ converges weakly in $W^{1,1}$ which is compactly embedded in $L^1\left(\mathrm{\Omega }\right)$, then $q_n$ converges strongly in $L^1\left(\mathrm{\Omega }\right)$ and the right side in (64(64) $\Vert u_n\left(q_n\right)-u_{ϵ}\left(q_{ϵ}\right){\Vert }_V\le C\left\{{\int }_{\mathrm{\Omega }}\right|{\lambda }_n-{\lambda }_{ϵ}|+{\int }_{\mathrm{\Omega }}|{\mu }_n-{\mu }_{ϵ}\left|\right\}.$(64) ) tends to zero.

From (52(52) $ϵ\left(u_n\right)\rightharpoonup ϵ\left(u_{ϵ}\right)\text{weakly in}{L}^2,$(52) ), (53(53) ${\mathcal{A}}_nϵ\left(u_n\right)\rightharpoonup {\mathcal{A}}_{ϵ}ϵ\left(u_{ϵ}\right)\text{weakly in}{L}^2.$(53) ) and (64(64) $\Vert u_n\left(q_n\right)-u_{ϵ}\left(q_{ϵ}\right){\Vert }_V\le C\left\{{\int }_{\mathrm{\Omega }}\right|{\lambda }_n-{\lambda }_{ϵ}|+{\int }_{\mathrm{\Omega }}|{\mu }_n-{\mu }_{ϵ}\left|\right\}.$(64) ) we conclude the existence of a solution to (46(46) $\underset{\begin{array}{c}q\in \mathcal{C}\\ u\in K\\ ({\ell }^{\ast },k^{\ast })\in K_s\times L^2\left({\mathrm{\Gamma }}_C\right),\\ {\ell }_{\tau }^{\ast }+k^{\ast }=0\text{ in }{L}^2\left({\mathrm{\Gamma }}_C\right).\end{array}}{min}\left\{\mathcal{R}\right(u,q)+\frac{1}{2ϵ}|{\mathcal{J}}_q\left(u\right)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast }){|}^2\}.$(46) ).

In this subsection, we turn to the convergence of the sequence $(q_{ϵ},u_{ϵ},{\ell }_{ϵ}^{\ast },k_{ϵ}^{\ast })$ to a solution of (45(45) $\underset{q\in \mathcal{C}}{min}\mathcal{R}(u,q):=\mathcal{Q}(u,q)+\frac{\rho }{2}R\left(q\right),$(45) ).

Proposition 2.2

For every $ϵ>0$, let $(u_{ϵ},q_{ϵ},{\ell }_{ϵ}^{\ast },k_{ϵ}^{\ast })$ denote a solution to (46(46) $\underset{\begin{array}{c}q\in \mathcal{C}\\ u\in K\\ ({\ell }^{\ast },k^{\ast })\in K_s\times L^2\left({\mathrm{\Gamma }}_C\right),\\ {\ell }_{\tau }^{\ast }+k^{\ast }=0\text{ in }{L}^2\left({\mathrm{\Gamma }}_C\right).\end{array}}{min}\left\{\mathcal{R}\right(u,q)+\frac{1}{2ϵ}|{\mathcal{J}}_q\left(u\right)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast }){|}^2\}.$(46) ). Then $\left\{\right(u_{ϵ},q_{ϵ},{\ell }_{ϵ}^{\ast },k_{ϵ}^{\ast }\left)\right\}$ contains a weakly convergent subsequence as $ϵ⟶0^{+}$ and every weak cluster point $(\overline{u},\overline{q},\overline{{\ell }^{\ast }},\overline{k^{\ast }})$ is a solution to (45(45) $\underset{q\in \mathcal{C}}{min}\mathcal{R}(u,q):=\mathcal{Q}(u,q)+\frac{\rho }{2}R\left(q\right),$(45) ).

Proof.

Let $(u,q,{\ell }^{\ast },k^{\ast })$ be such that $({\ell }^{\ast },k^{\ast })$ satisfies the constraints in (46(46) $\underset{\begin{array}{c}q\in \mathcal{C}\\ u\in K\\ ({\ell }^{\ast },k^{\ast })\in K_s\times L^2\left({\mathrm{\Gamma }}_C\right),\\ {\ell }_{\tau }^{\ast }+k^{\ast }=0\text{ in }{L}^2\left({\mathrm{\Gamma }}_C\right).\end{array}}{min}\left\{\mathcal{R}\right(u,q)+\frac{1}{2ϵ}|{\mathcal{J}}_q\left(u\right)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast }){|}^2\}.$(46) ). Then, $\left[{\mathcal{J}}_q\right(u)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast }\left)\right]=0$ and for every $ϵ>0$ we have: (65) $\mathcal{R}(u_{ϵ},q_{ϵ})+\frac{1}{2ϵ}\left|{\mathcal{J}}_{q_{ϵ}}\right(u_{ϵ})+{\mathcal{J}}_{q_{ϵ}}^{\ast }({\ell }_{ϵ}^{\ast },k_{ϵ}^{\ast }){|}^2\le \mathcal{R}(u,q).$(65) Since $\left|{\mathcal{J}}_q\right(u_{ϵ})+{\mathcal{J}}_q^{\ast }({\ell }_{ϵ}^{\ast },k_{ϵ}^{\ast }){|}^2\ge 0$ and $\mathcal{R}(u_{ϵ},q_{ϵ})\ge 0$, then, (66) $0\le \left|{\mathcal{J}}_{q_{ϵ}}\right(u_{ϵ})+{\mathcal{J}}_{q_{ϵ}}^{\ast }({\ell }_{ϵ}^{\ast },k_{ϵ}^{\ast }){|}^2\le 2ϵ\mathcal{R}(u,q).$(66) and hence $(u_{ϵ},q_{ϵ},{\ell }_{ϵ}^{\ast },k_{ϵ}^{\ast })$ is bounded in $V\times \mathcal{C}\times {\mathcal{H}}_1\times H^{-\frac{1}{2}}\left({\mathrm{\Gamma }}_C\right)$. It follows that there exists a subsequence of $(u_{ϵ},q_{ϵ},{\ell }_{ϵ}^{\ast },k_{ϵ}^{\ast })$, denoted by $(u_{ϵ},q_{ϵ},{\ell }_{ϵ}^{\ast },k_{ϵ}^{\ast })$, weakly convergent in $V\times \mathcal{C}\times {\mathcal{H}}_1\times H^{-\frac{1}{2}}\left({\mathrm{\Gamma }}_C\right)$ to $(\overline{u},\overline{q},\overline{{\ell }^{\ast }},\overline{k^{\ast }})\in V\times \mathcal{C}\times {\mathcal{H}}_1\times H^{-\frac{1}{2}}\left({\mathrm{\Gamma }}_C\right)$.

As in the proof of Proposition 2.1, taking the limit as $ϵ⟶0$ in (66(66) $0\le \left|{\mathcal{J}}_{q_{ϵ}}\right(u_{ϵ})+{\mathcal{J}}_{q_{ϵ}}^{\ast }({\ell }_{ϵ}^{\ast },k_{ϵ}^{\ast }){|}^2\le 2ϵ\mathcal{R}(u,q).$(66) ) we obtain: (67) $0\le \left|{\mathcal{J}}_q\right(\overline{u})+{\mathcal{J}}_q^{\ast }(\overline{{\ell }^{\ast }},\overline{k^{\ast }}){|}^2\le 0,$(67) and then, we get (68) $\left[{\mathcal{J}}_q\right(\overline{u})+{\mathcal{J}}_q^{\ast }(\overline{{\ell }^{\ast }},\overline{k^{\ast }}\left)\right]=0,$(68) which implies that $(\overline{u},\overline{q},\overline{{\ell }^{\ast }},\overline{k^{\ast }})$ satisfies all constraints in the problem (46(46) $\underset{\begin{array}{c}q\in \mathcal{C}\\ u\in K\\ ({\ell }^{\ast },k^{\ast })\in K_s\times L^2\left({\mathrm{\Gamma }}_C\right),\\ {\ell }_{\tau }^{\ast }+k^{\ast }=0\text{ in }{L}^2\left({\mathrm{\Gamma }}_C\right).\end{array}}{min}\left\{\mathcal{R}\right(u,q)+\frac{1}{2ϵ}|{\mathcal{J}}_q\left(u\right)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast }){|}^2\}.$(46) ). Furthermore, by (65(65) $\mathcal{R}(u_{ϵ},q_{ϵ})+\frac{1}{2ϵ}\left|{\mathcal{J}}_{q_{ϵ}}\right(u_{ϵ})+{\mathcal{J}}_{q_{ϵ}}^{\ast }({\ell }_{ϵ}^{\ast },k_{ϵ}^{\ast }){|}^2\le \mathcal{R}(u,q).$(65) ) we have (69) $\mathcal{R}(\overline{u},\overline{q})\le \mathcal{R}(u,q),$(69) for all $(u,q)$ such that there exists $({\ell }^{\ast },k^{\ast })\in \mathcal{C}$ with $(u,q,{\ell }^{\ast },k^{\ast })$ is admissible for (46(46) $\underset{\begin{array}{c}q\in \mathcal{C}\\ u\in K\\ ({\ell }^{\ast },k^{\ast })\in K_s\times L^2\left({\mathrm{\Gamma }}_C\right),\\ {\ell }_{\tau }^{\ast }+k^{\ast }=0\text{ in }{L}^2\left({\mathrm{\Gamma }}_C\right).\end{array}}{min}\left\{\mathcal{R}\right(u,q)+\frac{1}{2ϵ}|{\mathcal{J}}_q\left(u\right)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast }){|}^2\}.$(46) ). It follows that $(\overline{u},\overline{q},\overline{{\ell }^{\ast }},\overline{k^{\ast }})$ is a solution to (45(45) $\underset{q\in \mathcal{C}}{min}\mathcal{R}(u,q):=\mathcal{Q}(u,q)+\frac{\rho }{2}R\left(q\right),$(45) ).

3. Augmented Lagrangian formulation

In this section, we provide a new inverse problem formulation. Since the relation formulation between the primal and dual problems is given by: (70) $\left[{\mathcal{J}}_q\right(\overline{u})+{\mathcal{J}}_q^{\ast }(\overline{{\ell }^{\ast }},\overline{k^{\ast }}\left)\right]=0,$(70) where $\overline{u}$ is the solution of the primal problem and $(\overline{{\ell }^{\ast }},\overline{k^{\ast }})$ is the solution of the dual problem.

Hence, to provide the Lagrangian formulation of the inverse problem, we retain the above equation as a constraint in (46(46) $\underset{\begin{array}{c}q\in \mathcal{C}\\ u\in K\\ ({\ell }^{\ast },k^{\ast })\in K_s\times L^2\left({\mathrm{\Gamma }}_C\right),\\ {\ell }_{\tau }^{\ast }+k^{\ast }=0\text{ in }{L}^2\left({\mathrm{\Gamma }}_C\right).\end{array}}{min}\left\{\mathcal{R}\right(u,q)+\frac{1}{2ϵ}|{\mathcal{J}}_q\left(u\right)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast }){|}^2\}.$(46) ). Thus, we consider the following constrained problem: (71) $\underset{\begin{array}{c}q\in \mathcal{C}\\ u\in K\\ ({\ell }^{\ast },k^{\ast })\in K_s\times L^2\left({\mathrm{\Gamma }}_C\right),\\ {\ell }_{\tau }^{\ast }+k^{\ast }=0\text{in}{L}^2\left({\mathrm{\Gamma }}_C\right),\\ \left[{\mathcal{J}}_q\right(u)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast }\left)\right]=0.\end{array}}{min}\left\{\mathcal{R}\right(u,q)+\frac{1}{2ϵ}|{\mathcal{J}}_q\left(u\right)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast }){|}^2\}.$(71) By the weak duality, one have: $\left[{\mathcal{J}}_q\right(u)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast }\left)\right]\ge 0,$then, we can replace the equality constraint by the remaining inequality, thus: (72) $\underset{\begin{array}{c}q\in \mathcal{C},\\ u\in K,\\ \left[{\mathcal{J}}_q\right(u)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast }\left)\right]\le 0.\end{array}}{min}\mathcal{R}(u,q)+{\text{𝟙}}_C({\ell }^{\ast },k^{\ast }).$(72) The Lagrangian formulation of (72(72) $\underset{\begin{array}{c}q\in \mathcal{C},\\ u\in K,\\ \left[{\mathcal{J}}_q\right(u)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast }\left)\right]\le 0.\end{array}}{min}\mathcal{R}(u,q)+{\text{𝟙}}_C({\ell }^{\ast },k^{\ast }).$(72) ) is as follows: (73) $\mathcal{L}(q,u,{\ell }^{\ast },k^{\ast };a^{\ast })=\mathcal{R}(u,q)+〈a^{\ast },{\mathcal{J}}_q\left(u\right)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast })〉+{\text{𝟙}}_C({\ell }^{\ast },k^{\ast })-{\text{𝟙}}_{{\mathbb{R}}_{-}}(-a^{\ast }),$(73) where $a^{\ast }$ is the Lagrange multiplier, ${\text{𝟙}}_S\left(\varphi \right)=\{\begin{array}{ll}0,& \varphi \in S,\\ +\mathrm{\infty },& \mathrm{otherwise}.\end{array}$and $C=\left\{\right({\ell }^{\ast },k^{\ast })\in K_s\times L^2({\mathrm{\Gamma }}_C)/{\ell }_{\tau }^{\ast }+k^{\ast }=0\text{ in }{L}^2({\mathrm{\Gamma }}_C\left)\right\}.$In the next, we give a result providing the existence of Lagrange multiplier $a^{\ast }$.

Theorem 3.1

$(\overline{q},\overline{u})\in \mathcal{C}\times K$ is a solution of (45(45) $\underset{q\in \mathcal{C}}{min}\mathcal{R}(u,q):=\mathcal{Q}(u,q)+\frac{\rho }{2}R\left(q\right),$(45) ) if and only if there exists ${\overline{a}}^{\ast }\in {\mathbb{R}}_{-}$ such that $(\overline{q},\overline{u},{\overline{\ell }}^{\ast },{\overline{k}}^{\ast };{\overline{a}}^{\ast })\in \mathcal{C}\times K\times C\times {\mathbb{R}}_{-}$ is a saddle point of the augmented Lagrangian $\mathcal{L}$, i.e. (74) $\mathcal{L}(\overline{q},\overline{u},{\overline{\ell }}^{\ast },{\overline{k}}^{\ast };a^{\ast })\le \mathcal{L}(\overline{q},\overline{u},{\overline{\ell }}^{\ast },{\overline{k}}^{\ast };{\overline{a}}^{\ast })\le \mathcal{L}(q,u,{\ell }^{\ast },k^{\ast };{\overline{a}}^{\ast }),\mathrm{\forall }(q,u,{\ell }^{\ast },k^{\ast };a^{\ast }).$(74)

Proof.

Let $\mathcal{C}={\mathbb{R}}_{-}$ be a closed convex cone in $\mathbb{R}$ defining the natural partial ordering relation $\le$, the dual cone ${\mathcal{C}}^{\circ }=\{y\in {\mathbb{R}}^{\ast }:〈y,x〉\ge 0\text{ for all }x\in \mathcal{C}\}$ and ${\mathcal{C}}^{\ast }:=-{\mathcal{C}}^{\circ }={\mathbb{R}}_{+}$ its polar cone. The following properties are straightforward:

1. The map $(u,{\ell }^{\ast },k^{\ast })⟼{\mathcal{J}}_q\left(u\right)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast })$ is convex with respect to $\le$.

2. For each $a\in \mathbb{R}$ such that $a\ge 0$, the mapping $(u,{\ell }^{\ast },k^{\ast })⟼〈a,{\mathcal{J}}_q\left(u\right)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast })〉$ is lower semi-continuous.

3. The set $\left\{\right(u,{\ell }^{\ast },k^{\ast }\left)/{\mathcal{J}}_q\right(u)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast })\le 0\}$ is not empty since ${\mathcal{J}}_q\left(\overline{u}\right)+{\mathcal{J}}_q^{\ast }(\overline{{\ell }^{\ast }},\overline{k^{\ast }})=0$.

4. The constraint qualification hypothesis (Slater condition): $\begin{array}{rl}& \mathrm{\exists }(u_0,{\ell }_0^{\ast },k_0^{\ast })\text{such that}-{\mathcal{J}}_q\left(u_0\right)-{\mathcal{J}}_q^{\ast }({\ell }_0^{\ast },k_0^{\ast })<0,i.e.-{\mathcal{J}}_q\left(u_0\right)\\ & -{\mathcal{J}}_q^{\ast }({\ell }_0^{\ast },k_0^{\ast })\in \mathrm{int}\mathcal{C}\end{array}$is straightforward since the space H can be identified to its topological dual space and we have the Gelfand triple $V\subset H\subset V^{\ast }$. Then, the weak extremality condition can be strict for an appropriate choice of $u_0$ and $({\ell }_0^{\ast },k_0^{\ast })$ which allows the Slater condition.

Then, the primal problem (45(45) $\underset{q\in \mathcal{C}}{min}\mathcal{R}(u,q):=\mathcal{Q}(u,q)+\frac{\rho }{2}R\left(q\right),$(45) ) stable. Now, following [37], we will consider the problem (45(45) $\underset{q\in \mathcal{C}}{min}\mathcal{R}(u,q):=\mathcal{Q}(u,q)+\frac{\rho }{2}R\left(q\right),$(45) ) as a primal problem and we are looking to define its dual problem using a family of perturbed problems, where the perturbed costs are defined by: $\mathrm{\Phi }(u,a)=\{\begin{array}{ll}\mathcal{R}(u,q),& \mathrm{if}(u,q)\in K\times \mathcal{C}\mathrm{and}{\mathcal{J}}_q\left(u\right)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast })\le a,\\ +\mathrm{\infty },& \mathrm{otherwise}.\end{array}$The dual problem is hence defined by: $-{\mathrm{\Phi }}^{\ast }(0,a^{\ast })=-{\text{𝟙}}_{{\mathcal{C}}^{\ast }}(-a^{\ast })+\underset{(u,q)\in K\times \mathcal{C}}{inf}\{-〈a^{\ast },{\mathcal{J}}_q\left(u\right)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast })〉+\mathcal{R}(u,q\left)\right\},$which is equivalent to (75) $\underset{a^{\ast }\le 0}{sup}\underset{(u,q)\in K\times \mathcal{C}}{inf}\{-〈a^{\ast },{\mathcal{J}}_q\left(u\right)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast })〉+\mathcal{R}(u,q\left)\right\}.$(75) Since $\mathcal{R}(u,q)⟶+\mathrm{\infty }$ as $\Vert (q,u,{\ell }^{\ast },k^{\ast })\Vert ⟶+\mathrm{\infty }$ with 1)-4), then the primal problem and dual problem have at least one solution $(\overline{u},\overline{{\ell }^{\ast }},\overline{k^{\ast }})$ and ${\overline{a}}^{\ast }$, respectively, which satisfy the strong duality. And we have the extrimality condition: (76) $〈{\overline{a}}^{\ast },{\mathcal{J}}_q\left(\overline{u}\right)+{\mathcal{J}}_q^{\ast }(\overline{{\ell }^{\ast }},\overline{k^{\ast }})〉=0.$(76) The proof is achieved with application of [37, Theorem 5.1].

We are interested in the augmented Lagrangian formulation of the inverse problem. Utilizing the dualization and penalization technique, we define the Lagrangian functional for the following penalized constrained problem: (77) $\underset{\begin{array}{c}q\in \mathcal{C}\\ u\in K\\ ({\ell }^{\ast },k^{\ast })\in K_s\times L^2\left({\mathrm{\Gamma }}_C\right)\\ {\ell }_{\tau }^{\ast }+k^{\ast }=0\text{in}{L}^2\left({\mathrm{\Gamma }}_C\right)\\ \left[{\mathcal{J}}_q\right(u)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast }\left)\right]\le 0\end{array}}{min}\left\{\mathcal{R}\right(u,q)+\frac{1}{2ϵ}|{\mathcal{J}}_q\left(u\right)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast }){|}^2\}.$(77) Then the augmented Lagrangian formulation of (77(77) $\underset{\begin{array}{c}q\in \mathcal{C}\\ u\in K\\ ({\ell }^{\ast },k^{\ast })\in K_s\times L^2\left({\mathrm{\Gamma }}_C\right)\\ {\ell }_{\tau }^{\ast }+k^{\ast }=0\text{in}{L}^2\left({\mathrm{\Gamma }}_C\right)\\ \left[{\mathcal{J}}_q\right(u)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast }\left)\right]\le 0\end{array}}{min}\left\{\mathcal{R}\right(u,q)+\frac{1}{2ϵ}|{\mathcal{J}}_q\left(u\right)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast }){|}^2\}.$(77) ) is as follows: (78) $\begin{array}{rl}{\mathcal{L}}_{ϵ}(q,u,{\ell }^{\ast },k^{\ast };a^{\ast })& =\mathcal{R}(u,q)+〈a^{\ast },{\mathcal{J}}_q\left(u\right)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast })〉+\frac{1}{2ϵ}\left|{\mathcal{J}}_q\right(u)\\ & +{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast }){|}^2+{\text{𝟙}}_C({\ell }^{\ast },k^{\ast })-{\text{𝟙}}_{{\mathbb{R}}_{-}}(-a^{\ast }),\end{array}$(78) where $a^{\ast }$ is the Lagrange multiplier.

Finally, the constrained minimization problem (77(77) $\underset{\begin{array}{c}q\in \mathcal{C}\\ u\in K\\ ({\ell }^{\ast },k^{\ast })\in K_s\times L^2\left({\mathrm{\Gamma }}_C\right)\\ {\ell }_{\tau }^{\ast }+k^{\ast }=0\text{in}{L}^2\left({\mathrm{\Gamma }}_C\right)\\ \left[{\mathcal{J}}_q\right(u)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast }\left)\right]\le 0\end{array}}{min}\left\{\mathcal{R}\right(u,q)+\frac{1}{2ϵ}|{\mathcal{J}}_q\left(u\right)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast }){|}^2\}.$(77) ) is equivalent to the following saddle point problem: (79) ${\mathcal{L}}_{ϵ}(\overline{q},\overline{u},{\overline{\ell }}^{\ast },{\overline{k}}^{\ast },a^{\ast })\le {\mathcal{L}}_{ϵ}(\overline{q},\overline{u},{\overline{\ell }}^{\ast },{\overline{k}}^{\ast },{\overline{a}}^{\ast })\le {\mathcal{L}}_{ϵ}(q,u,{\ell }^{\ast },k^{\ast },{\overline{a}}^{\ast }),\mathrm{\forall }(q,u,{\ell }^{\ast },k^{\ast };a^{\ast }).$(79) And it is well known that $(\overline{q},\overline{u},{\overline{\ell }}^{\ast },{\overline{k}}^{\ast },{\overline{a}}^{\ast })$ is saddle point for $\mathcal{L}$ if and only if it is a saddle point for ${\mathcal{L}}_{ϵ}$.

4. Algorithms and numerical examples

This section is devoted to the numerical treatment and realization of Lamé coefficients identification. The saddle point problem is obtained, we proceed by an ADMM to split the problem and we apply different numerical methods as intern solvers.

4.1. Algorithms

We develop a splitting algorithm for the numerical solution to the problem defined by (46(46) $\underset{\begin{array}{c}q\in \mathcal{C}\\ u\in K\\ ({\ell }^{\ast },k^{\ast })\in K_s\times L^2\left({\mathrm{\Gamma }}_C\right),\\ {\ell }_{\tau }^{\ast }+k^{\ast }=0\text{ in }{L}^2\left({\mathrm{\Gamma }}_C\right).\end{array}}{min}\left\{\mathcal{R}\right(u,q)+\frac{1}{2ϵ}|{\mathcal{J}}_q\left(u\right)+{\mathcal{J}}_q^{\ast }({\ell }^{\ast },k^{\ast }){|}^2\}.$(46) ). The splitting algorithm is an ADMM based on an augmented Lagrangian formulation for inequality constraints [46].

The ADMM in Gauss Seidel fashion is stated as follows:

Starting with initial guess $({\ell }^{\ast ,0},k^{\ast ,0};a^{\ast ,0})$, for $n\ge 0$ compute: (80) $\begin{array}{rl}({\overline{q}}^n,{\overline{u}}^n)& \in \mathrm{Arg}\underset{(q,u)}{min}{\mathcal{L}}_{ϵ}(q,u,{\ell }^{\ast ,n-1},k^{\ast ,n-1};a^{\ast ,n-1}),\end{array}$(80) (81) $\begin{array}{rl}({\overline{\ell }}^{\ast ,n},{\overline{k}}^{\ast ,n})& \in \mathrm{Arg}\underset{({\ell }^{\ast },k^{\ast })}{min}{\mathcal{L}}_{ϵ}({\overline{q}}^n,{\overline{u}}^n,{\ell }^{\ast },k^{\ast };a^{\ast ,n-1}).\end{array}$(81) Update the Lagrange multiplier as follows: (82) $a^{\ast ,n}=a^{\ast ,n-1}+\frac{1}{ϵ}max{\{0,{\mathcal{J}}_{{\overline{q}}^n}({\overline{u}}^n)+{\mathcal{J}}_{{\overline{q}}^n}^{\ast }({\overline{\ell }}^{\ast ,n},{\overline{k}}^{\ast ,n}\left)\right\}}^2.$(82) The subproblem (80(80) $\begin{array}{rl}({\overline{q}}^n,{\overline{u}}^n)& \in \mathrm{Arg}\underset{(q,u)}{min}{\mathcal{L}}_{ϵ}(q,u,{\ell }^{\ast ,n-1},k^{\ast ,n-1};a^{\ast ,n-1}),\end{array}$(80) ) is equivalent to a non-smooth minimization problem, with respect to $(q,u)$ over $\mathcal{C}\times K$, whose cost function is the following map: $(q,u)⟼\mathcal{R}(u,q)+〈a^{\ast },{\mathcal{J}}_q\left(u\right)+F_q^{\ast }\left({\ell }^{\ast }\right)〉+\frac{1}{ϵ}\left\{{\mathcal{J}}_q\right(u)+F_q^{\ast }({\ell }^{\ast }\left)\right\},$after neglecting the constant terms.

The non-smoothness of this minimization problem come originally from the terms associated to the friction in the cost function of the state unknown. Furthermore, we need to deal with the contact condition, i.e. the constraint in the admissible subset K. To overcome all of the cited complexities, we iterate the use of the ADMM for splitting the contact and friction.

To do this, let us introduce three auxiliary unknowns to decouple the linear elasticity from contact and friction in (80(80) $\begin{array}{rl}({\overline{q}}^n,{\overline{u}}^n)& \in \mathrm{Arg}\underset{(q,u)}{min}{\mathcal{L}}_{ϵ}(q,u,{\ell }^{\ast ,n-1},k^{\ast ,n-1};a^{\ast ,n-1}),\end{array}$(80) ). Firstly, let us introduce the following subset ${\mathcal{P}}_c=\{{\omega }_c\in L^2({\mathrm{\Gamma }}_C)/{\omega }_c\le g\text{ in }{\mathrm{\Gamma }}_C\}.$The problem (80(80) $\begin{array}{rl}({\overline{q}}^n,{\overline{u}}^n)& \in \mathrm{Arg}\underset{(q,u)}{min}{\mathcal{L}}_{ϵ}(q,u,{\ell }^{\ast ,n-1},k^{\ast ,n-1};a^{\ast ,n-1}),\end{array}$(80) ) becomes: (83) $\begin{array}{rl}& \underset{\begin{array}{c}q\in \mathcal{C},u\in V,\\ u_{\tau }-{\omega }_f=0,\\ u_{\nu }-{\omega }_c=0.\end{array}}{min}\left\{\mathcal{Q}\right(u,q)+\frac{\rho }{2}\Vert q^2+〈a^{\ast },F_q(\mathrm{Au})-J_q(u)+j_q({\omega }_f)+{\text{𝟙}}_{\mathcal{P}}({\omega }_c)+F_q^{\ast }({\ell }^{\ast })〉\\ & +\frac{1}{ϵ}\left[F_q\right(\mathrm{Au})-J_q(u)+j_q({\omega }_f)+{\text{𝟙}}_{\mathcal{P}}({\omega }_c)+F_q^{\ast }({\ell }^{\ast }\left)\right]\}.\end{array}$(83) By setting $\begin{array}{rl}f(u,q)& =\mathcal{Q}(u,q)+\frac{\rho }{2}\Vert q^2+〈a^{\ast },F_q\left(\mathrm{Au}\right)-J_q\left(u\right)+F_q^{\ast }\left({\ell }^{\ast }\right)〉\\ & +\frac{1}{ϵ}\left[F_q\right(\mathrm{Au})-J_q(u)+F_q^{\ast }({\ell }^{\ast }\left)\right].\end{array}$Then, the Lagrangian functional associated to the constrained minimization problem (83(83) $\begin{array}{rl}& \underset{\begin{array}{c}q\in \mathcal{C},u\in V,\\ u_{\tau }-{\omega }_f=0,\\ u_{\nu }-{\omega }_c=0.\end{array}}{min}\left\{\mathcal{Q}\right(u,q)+\frac{\rho }{2}\Vert q^2+〈a^{\ast },F_q(\mathrm{Au})-J_q(u)+j_q({\omega }_f)+{\text{𝟙}}_{\mathcal{P}}({\omega }_c)+F_q^{\ast }({\ell }^{\ast })〉\\ & +\frac{1}{ϵ}\left[F_q\right(\mathrm{Au})-J_q(u)+j_q({\omega }_f)+{\text{𝟙}}_{\mathcal{P}}({\omega }_c)+F_q^{\ast }({\ell }^{\ast }\left)\right]\}.\end{array}$(83) ) is then, for $U:=(u,q,{\omega }_f,{\omega }_c;{\vartheta }_f,{\vartheta }_c)$, $\begin{array}{rl}{\mathcal{L}}_r\left(U\right)& =f(u,q)+(a^{\ast }+\frac{1}{ϵ})\left[j_q\right({\omega }_f)+{\text{𝟙}}_{\mathcal{P}}({\omega }_c\left)\right]+〈{\vartheta }_f,u_{\tau }-{\omega }_f{〉}_{{\mathrm{\Gamma }}_C}\\ & +〈{\vartheta }_c,u_{\nu }-{\omega }_c{〉}_{{\mathrm{\Gamma }}_C}+\frac{r}{2}\Vert u_{\tau }-{\omega }_f{\Vert }_{{\mathrm{\Gamma }}_C}^2+\frac{r}{2}\Vert u_{\nu }-{\omega }_c{\Vert }_{{\mathrm{\Gamma }}_C}^2.\end{array}$The ADMM that is employed, is stated as follows:

Starting with an initial guess $(w^0,{\omega }_f^0,{\omega }_c^0;{\vartheta }_f^0,{\vartheta }_c^0,{\varsigma }^0)$;

Compute in Gauss-Seidel fashion the following sub-problems: (84) $\begin{array}{rl}(u^{i+1},q^{i+1})& \in \mathrm{Arg}\underset{(u,q)}{min}{\mathcal{L}}_r(u,q,{\omega }_f^i,{\omega }_c^i;{\vartheta }_f^i,{\vartheta }_c^i),\end{array}$(84) (85) $\begin{array}{rl}{\omega }_f^{i+1}& \in \arg \underset{{\omega }_f}{min}{\mathcal{L}}_r(u^{i+1},q^{i+1},{\omega }_f,{\omega }_c^i;{\vartheta }_f^i,{\vartheta }_c^i),\end{array}$(85) (86) $\begin{array}{rl}{\omega }_c^{i+1}& \in \arg \underset{{\omega }_c}{min}{\mathcal{L}}_r(u^{i+1},q^{i+1},{\omega }_f^{i+1},{\omega }_c;{\vartheta }_f^i,{\vartheta }_c^i);\end{array}$(86) Update the Lagrange multipliers: (87) $\begin{array}{rl}{\vartheta }_f^{i+1}& ={\vartheta }_f^i+r(u_{\tau }^{i+1}-{\omega }_f^{i+1}),\end{array}$(87) (88) $\begin{array}{rl}{\vartheta }_c^{i+1}& ={\vartheta }_c^i+r(u_{\nu }^{i+1}-{\omega }_c^{i+1}).\end{array}$(88) The sub-problem (84(84) $\begin{array}{rl}(u^{i+1},q^{i+1})& \in \mathrm{Arg}\underset{(u,q)}{min}{\mathcal{L}}_r(u,q,{\omega }_f^i,{\omega }_c^i;{\vartheta }_f^i,{\vartheta }_c^i),\end{array}$(84) ) is equivalent to minimization problem: (89) $\underset{(u,q)}{inf}P(u,q),\text{over}\mathcal{C}\times V,$(89) where the cost function, after neglecting the constant terms, is as follows: $\begin{array}{rl}P(u,q)& =f(u,q)+〈u_{\tau },{\vartheta }_f^i-r{\omega }_f^i{〉}_{{\mathrm{\Gamma }}_C}+〈u_{\nu },{\vartheta }_c^i-r{\omega }_c^i{〉}_{{\mathrm{\Gamma }}_C}\\ & +\frac{r}{2}\Vert u_{\tau }{\Vert }_{{\mathrm{\Gamma }}_C}^2+\frac{r}{2}\Vert u_{\nu }{\Vert }_{{\mathrm{\Gamma }}_C}^2,\end{array}$which is Gâteaux differentiable.

The sub-problem (85(85) $\begin{array}{rl}{\omega }_f^{i+1}& \in \arg \underset{{\omega }_f}{min}{\mathcal{L}}_r(u^{i+1},q^{i+1},{\omega }_f,{\omega }_c^i;{\vartheta }_f^i,{\vartheta }_c^i),\end{array}$(85) ) is equivalent to the minimization problem (90) $\underset{{\omega }_f}{inf}\left\{(a^{\ast }+\frac{1}{ϵ})j_q\right({\omega }_f)-〈{\vartheta }_f^i+r{u}_{\tau }^i,{\omega }_f{〉}_{{\mathrm{\Gamma }}_C}+\frac{r}{2}\Vert {\omega }_f{\Vert }_{{\mathrm{\Gamma }}_C}^2\}.$(90) In order to get the solution of this problem, one can use the Fenchel duality. Following [37], the solution can be explicitly computed, and it is given by: (91) ${\mathrm{\Theta }}^i=|{\vartheta }_f^i+r{u}_{\tau }^{i+1}|,{\omega }_f^{i+1}=\{\begin{array}{cc}{\displaystyle \frac{{\mathrm{\Theta }}^i-S}{r{\mathrm{\Theta }}^i}}({\vartheta }_f^i+r{u}_{\tau }^{i+1})& \text{if}{\mathrm{\Theta }}^i>(a^{\ast }+{\displaystyle \frac{1}{ϵ}})S,\\ 0& \text{if}{\mathrm{\Theta }}^i\le (a^{\ast }+{\displaystyle \frac{1}{ϵ}})S.\end{array}$(91) And the sub-problem (86(86) $\begin{array}{rl}{\omega }_c^{i+1}& \in \arg \underset{{\omega }_c}{min}{\mathcal{L}}_r(u^{i+1},q^{i+1},{\omega }_f^{i+1},{\omega }_c;{\vartheta }_f^i,{\vartheta }_c^i);\end{array}$(86) ) is equivalent to the following minimization problem: (92) $\underset{{\omega }_c}{inf}\left\{(a^{\ast }+\frac{1}{ϵ}){\text{𝟙}}_{\mathcal{P}}\right({\omega }_c)-〈{\vartheta }_c^i+r{u}_{\nu }^i,{\omega }_c{〉}_{{\mathrm{\Gamma }}_C}+\frac{r}{2}\Vert {{\omega }_c}_{{\mathrm{\Gamma }}_C}^2\}.$(92) The solution to the above minimization problem can be explicitly computed by employing KKT condition, and it is given as follows: (93) ${\omega }_c^{i+1}=u_{\nu }^{i+1}+\frac{1}{r}[{\vartheta }_{\nu }^i-({\vartheta }_{\nu }^i+r(u_{\nu }^{i+1}-g){)}^{+}],$(93) where $x^{+}=max(0,x)$. Therefore, the auxiliary unknowns ${\omega }_c^{i+1}$ and ${\omega }_f^{i+1}$ are computed with a negligible cost.

Now, we turn to the sub-problem (81(81) $\begin{array}{rl}({\overline{\ell }}^{\ast ,n},{\overline{k}}^{\ast ,n})& \in \mathrm{Arg}\underset{({\ell }^{\ast },k^{\ast })}{min}{\mathcal{L}}_{ϵ}({\overline{q}}^n,{\overline{u}}^n,{\ell }^{\ast },k^{\ast };a^{\ast ,n-1}).\end{array}$(81) ). This problem is equivalent to a minimization problem for which the cost function, after neglecting the constant terms, is given by (94) $\underset{({\ell }^{\ast },k^{\ast })}{inf}\{〈a^{\ast },D_{\gamma }({\ell }^{\ast },k^{\ast })〉+\frac{1}{ϵ}{D}_{\gamma }({\ell }^{\ast },k^{\ast }\left)\right\}.$(94) In practice, the minimization problem (94(94) $\underset{({\ell }^{\ast },k^{\ast })}{inf}\{〈a^{\ast },D_{\gamma }({\ell }^{\ast },k^{\ast })〉+\frac{1}{ϵ}{D}_{\gamma }({\ell }^{\ast },k^{\ast }\left)\right\}.$(94) ) corresponds exactly to the dual problem (29(29) $\underset{\begin{array}{c}({\ell }^{\ast },k^{\ast })\in K_s\times L^2\left({\mathrm{\Gamma }}_C\right)\\ {\ell }_{\tau }^{\ast }+k^{\ast }=0\text{ in }{L}^2\left({\mathrm{\Gamma }}_C\right)\end{array}}{sup}-{\mathcal{J}}_q({\ell }^{\ast },k^{\ast }):=\frac{1}{2}({\mathcal{A}}^{-1}{\ell }^{\ast },{\ell }^{\ast }{)}_{\mathcal{H}}-〈{\ell }_{\nu }^{\ast },g{〉}_{{\mathrm{\Gamma }}_C}.$(29) ) multiplied by $a^{\ast }+\frac{1}{ϵ}$. This problem involves an inequality-constrained minimization of a quadratic functional, whereas the primal problem deals with a non-differentiable functional. Therefore, solving (94(94) $\underset{({\ell }^{\ast },k^{\ast })}{inf}\{〈a^{\ast },D_{\gamma }({\ell }^{\ast },k^{\ast })〉+\frac{1}{ϵ}{D}_{\gamma }({\ell }^{\ast },k^{\ast }\left)\right\}.$(94) ) is equivalent to solving (37(37) $\begin{array}{rl}& (\mathcal{A}u,v)-J_q\left(v\right)+〈{\ell }^{\ast },v_{\nu }{〉}_{{\mathrm{\Gamma }}_C}+〈k^{\ast },v_{\tau }{〉}_{{\mathrm{\Gamma }}_C}=0,\end{array}$(37) )–(39(39) $\begin{array}{rl}& \{\begin{array}{l}\gamma (\xi -u_{\tau })+k^{\ast }-\hat{k}=0,\\ \xi -max(0,\xi +\theta (k^{\ast }-\mathcal{F}S\left)\right)-min(0,\xi +\theta (k^{\ast }+\mathcal{F}S)=0.\end{array}\end{array}$(39) ). We can utilize a Primal–Dual Active Set Strategy algorithm (PDAS) for this purpose (see [35,36,45]).

Since ${\mathrm{\Gamma }}_C=I_c^{i+1}\bigsqcup {\mathcal{S}}_c^{i+1}$ and ${\mathrm{\Gamma }}_C={\mathcal{I}}_f^{i+1}\bigsqcup ({\mathcal{S}}_{f,+}^{i+1}\cup {\mathcal{S}}_{f,-}^{i+1})$. Then, the variational equation in PDAS algorithm is equivalent to the following equation: $(\mathcal{A}{u}^{\ast ,i+1},v)-J_q\left(v\right)+〈{\ell }^{\ast i+1},v_{\nu }{〉}_{I_c^{i+1}\bigsqcup {\mathcal{S}}_c^{i+1}}+〈k^{\ast i+1},v_{\tau }{〉}_{{\mathcal{I}}_f^{i+1}\bigsqcup ({\mathcal{S}}_{f,+}^{i+1}\cup {\mathcal{S}}_{f,-}^{i+1})}=0,$which is clearly equivalent to: $\begin{array}{rl}& (\mathcal{A}{u}^{\ast ,i+1},v)+〈(\hat{\mathrm{\Lambda }}+\gamma (u_{\nu }^{\ast ,i+1}-g\left)\right){\chi }_{{\mathcal{S}}_c^{i+1}},v_{\nu }{〉}_{{\mathrm{\Gamma }}_C}+〈(\hat{k}+\gamma u_{\tau }^{\ast ,i+1}){\chi }_{{\mathcal{I}}_f^{i+1}},v_{\tau }{〉}_{{\mathrm{\Gamma }}_C}=J_q\left(v\right)\\ & +〈\mathcal{F}S{\chi }_{S_{f,-}^{i+1}},v_{\tau }{〉}_{{\mathrm{\Gamma }}_C}-〈\mathcal{F}S{\chi }_{S_{f,+}^{i+1}},v_{\tau }{〉}_{{\mathrm{\Gamma }}_C},\end{array}$where ${\chi }_Y\left(x\right)=1$ if $x\in Y$ and ${\chi }_Y\left(x\right)=0$ otherwise.

In the Algorithm 2, we presume the solutions of the subproblems (80(80) $\begin{array}{rl}({\overline{q}}^n,{\overline{u}}^n)& \in \mathrm{Arg}\underset{(q,u)}{min}{\mathcal{L}}_{ϵ}(q,u,{\ell }^{\ast ,n-1},k^{\ast ,n-1};a^{\ast ,n-1}),\end{array}$(80) )–(82(82) $a^{\ast ,n}=a^{\ast ,n-1}+\frac{1}{ϵ}max{\{0,{\mathcal{J}}_{{\overline{q}}^n}({\overline{u}}^n)+{\mathcal{J}}_{{\overline{q}}^n}^{\ast }({\overline{\ell }}^{\ast ,n},{\overline{k}}^{\ast ,n}\left)\right\}}^2.$(82) ).

4.2. Finite element discretization

The aim of this section is to present a computer implementation of the proposed theoretical approach and numerical scheme through representative numerical example. For the sake of simplicity, we treat a two-dimensional simple example i.e. we suppose that $\mathrm{\Omega }\subset {\mathbb{R}}^2$ is polygonal domain. Let $V_h$ be the space of continuous and piecewise affine functions, i.e. $V_h=\{v^h\in \mathcal{C}(\overline{\mathrm{\Omega }}{)}^d,\mathrm{\forall }T\in {\mathcal{T}}_h,v_{/T}^h\in {\mathbb{P}}_1(T{)}^d,v^h=0\mathrm{on}{\mathrm{\Gamma }}_1\}$where ${\mathcal{T}}_h$ is a family of polygons forming Ω (mostly triangles) and ${\mathbb{P}}_1\left(T\right)$ is the space of polynomials of global degree is less or equal to one in T (see [47]). Vectorized Matlab codes for linear two-dimensional elasticity [48] are used to the assembly of the matrices associated to the operators in the algorithms.

Let $\{{\xi }_i{\}}_i$ be the system of piecewise global basis functions of $V_h$. For $u^h=(u_1^h,u_2^h)$, we have: (96) $u_k^h\left(x\right)=\sum _i{\xi }_i\left(x\right)u_k^h,k=1,2.$(96) We employ Voigt's representation of the linear strain tensor as in [48,49], on one hand we have: (97) $\gamma \left(u\right)=\left[\begin{array}{c}{\displaystyle \frac{\mathrm{\partial }{u}_1}{\mathrm{\partial }x}}\\ {\displaystyle \frac{\mathrm{\partial }{u}_2}{\mathrm{\partial }y}}\\ {\displaystyle \frac{\mathrm{\partial }{u}_1}{\mathrm{\partial }y}+\frac{\mathrm{\partial }{u}_2}{\mathrm{\partial }x}}\end{array}\right]=\left[\begin{array}{c}{ϵ}_{11}\\ {ϵ}_{22}\\ 2{ϵ}_{12}\end{array}\right],$(97) and then, the elastic constitutive equation is given by: (98) $\left[\begin{array}{c}{\sigma }_{11}\\ {\sigma }_{22}\\ 2{\sigma }_{12}\end{array}\right]=\mathcal{A}\gamma \left(u\right),$(98) where $\begin{array}{rl}\mathcal{A}& =\left[\begin{array}{ccc}\lambda +2\mu & \lambda & 0\\ \lambda & \lambda +2\mu & 0\\ 0& 0& \mu \end{array}\right]=\lambda \left[\begin{array}{ccc}1& 1& 0\\ 1& 1& 0\\ 0& 0& 0\end{array}\right]+\mu \left[\begin{array}{ccc}2& 0& 0\\ 0& 2& 0\\ 0& 0& 1\end{array}\right]\\ & :=\lambda {\mathcal{A}}_1+\mu {\mathcal{A}}_2.\end{array}$Then, we can write $\left(\mathcal{A}ϵ\right(u),ϵ(v){)}_{\mathcal{H}}=(\lambda {\mathcal{A}}_1\gamma \left(u\right),\gamma \left(v\right){)}_{\mathcal{H}}+\left(\mu {\mathcal{A}}_2\gamma \right(u),\gamma (v){)}_{\mathcal{H}}.$On the other hand, let $u^h=[u_1,\dots ,u_6{]}^{\mathrm{\top }}$ be the transpose of the vector of nodal values of $u^h$ on a triangle $T\in {\mathcal{T}}_h$. We have: (99) $\gamma \left(u^h\right)=\frac{1}{2\left|A_T\right|}\left[\begin{array}{cccccc}{\xi }_{1,x}& 0& {\xi }_{2,x}& 0& {\xi }_{3,x}& 0\\ 0& {\xi }_{1,y}& 0& {\xi }_{2,y}& 0& {\xi }_{3,y}\\ {\xi }_{1,y}& {\xi }_{1,x}& {\xi }_{2,y}& {\xi }_{2,x}& {\xi }_{3,y}& {\xi }_{3,x}\end{array}\right]\left[\begin{array}{c}{u}_1\\ ⋮\\ u_6\end{array}\right]$(99) where ${\xi }_{i,\cdot }$ denotes the derivative with respect to ‘·’ and $\left|A_T\right|$ is the area of the triangle T. Then, we can get the matrix associated to strain deformation defined by: (100) $\mathbf{S}:=\frac{1}{2\left|A_T\right|}\left[\begin{array}{cccccc}{\xi }_{1,x}& 0& {\xi }_{2,x}& 0& {\xi }_{3,x}& 0\\ 0& {\xi }_{1,y}& 0& {\xi }_{2,y}& 0& {\xi }_{3,y}\\ {\xi }_{1,y}& {\xi }_{1,x}& {\xi }_{2,y}& {\xi }_{2,x}& {\xi }_{3,y}& {\xi }_{3,x}\end{array}\right].$(100) Then, one may write, for $u^h\in V_h$ and ${\lambda }^h,{\mu }^h\in {\mathrm{\Lambda }}^h$, $\begin{array}{rl}\left(\mathcal{A}ϵ\right(u^h),ϵ(v^h){)}_{\mathcal{H}}& =v^{h\mathrm{\top }}{\mathbf{S}}^{\mathrm{\top }}[{\lambda }^h{\mathcal{A}}_1+{\mu }^h{\mathcal{A}}_2]\mathbf{S}{u}^h\\ & =\left[v^{h\mathrm{\top }}{\mathbf{S}}^{\mathrm{\top }}{\mathcal{A}}_1\mathbf{S}{u}^h{v}^{h\mathrm{\top }}{\mathbf{S}}^{\mathrm{\top }}{\mathcal{A}}_2\mathbf{S}{u}^h\right]\left[\begin{array}{c}{\lambda }^h\\ {\mu }^h\end{array}\right],\end{array}$and $\left(ϵ\right(u^h),ϵ(v^h){)}_{\mathcal{H}}=v^{h\mathrm{\top }}{\mathbf{S}}^{\mathrm{\top }}\mathbf{S}{u}^h.$

4.3. Example

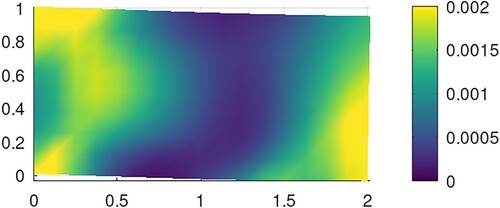
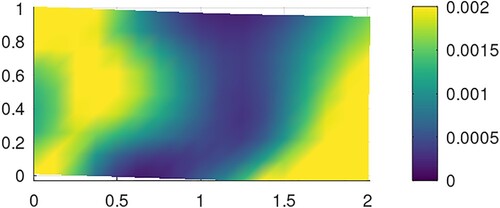
As example, we consider the problem in linear elasticity (under the hypothesis of small deformations). The domain $\mathrm{\Omega }=(0,2)\times \left(0.1\right)\subset {\mathbb{R}}^2$ is discretized using Matlab mesh generator developed in [50]. In Figure 1, we visualize the domain.

Figure 1. The initial configuration.

To compute the observation, we use the following material constants:

• The observed Lamé coefficients are: $\lambda =73.970\mathrm{GPa}$, ${\mu }_o=20.863\mathrm{GPa}$;

• The body is clamped from ${\mathrm{\Gamma }}_D=\left\{0\right\}\times [0,1]$

• The load force is $-2y$ (units of force per unit area) is applied on part ${\mathrm{\Gamma }}_N=[0,2]\times \left\{1\right\}$ of the boundary;

• The gap between the foundation and the contact zone ${\mathrm{\Gamma }}_C=[0,2]\times \left\{0\right\}$ is g = 0.01 (unit area).

• All parameters in the above algorithms are chosen like: $\theta =100$, $\gamma =591.60$, $\rho ={10}^{-2}$, $ϵ=10$ and r = 1.16.

In Figure 2, we illustrate the observed state u, which is computed using ADMM method [32,33] since there is no analytical solution to the considered problem. The colour map shows the von Mises distribution in the domain (von Mises constraint is employed with principal plane stress for which ${\sigma }_3=0$, ${\sigma }_{12}=0$, ${\sigma }_{31}=0$ and ${\sigma }_{23}=0$, then the von Mises criterion is given by $\sqrt{{\sigma }_1^2+{\sigma }_2^2-{\sigma }_1{\sigma }_2}$, where ${\sigma }_1$, $i=1,2$, are the eigenvalues of $\sigma \left(u\right)$). In Figure 3, the computed state computed with the PDAS Algorithm 1. In the same figure, we show both deformation and von Mises distribution (colour map) in the domain. In Table 1, we report different errors ($L^2$ and $H^1$-errors for the error between u and z) between the observations the computed solutions. We note that when the mesh size vanishes, the error between the observed parameter and the computed one becomes bigger, this means that when the mesh size vanishes, the method may diverge. In Table 2, we report the errors with respect to different noises. We note that two different methods are used to compute the observation z and the estimation u. In the other hand the error between u and z showed in Table 1 is of scale ${10}^{-6}$, but taking into account the fact that we have assumed small deformations (see the colour bar on the right of the figures), the $L^2$-error is of scale ${10}^{-3}$ and the $H^1$-error is of scale ${10}^{-1}$.

Figure 2. The observed state and its von Mises distribution.

Figure 3. The estimated state and its von Mises distribution.

Table 1. The errors between the observations and the estimations.

Errors
Mesh size	$\Vert u-z{\Vert }_H^2$	$\Vert u-z{\Vert }_{H_1}^2$	$|\mu -{\mu }_o|$
1/16	1.5016 e–06	3.5947 e–04	1.985 e–04
1/32	1.4600 e–06	3.4619 e–04	8.8177 e–04
1/64	3.5633 e–06	5.3526 e–05	9.7826 e–02

Table 2. The errors between the observations with noise and the estimations.

Errors with mesh size 1/16
Noise	$\Vert u-z{\Vert }_H^2$	$\Vert u-z{\Vert }_{H_1}^2$	$|\mu -{\mu }_o|$
0.001%	5.9516 e–05	1.3383 e–03	3.8153 e–02
0.01%	4.3047 e–04	6.2533 e–02	1.3384 e–02
0.1 %	1.2913 e–02	4.1043 e+00	2.2265 e–02

5. Conclusion

In this paper, we have investigated a primal dual formulation of parameter identification in elastic contact problem with given friction. This approach allows us to reformulate the constrained problem as saddle point problem which will be more useful for the numerical realization of this problem. We have provided a saddle point formulation for the considered inverse problem, the second step was the numerical realization of this problem. This work may be considered as a framework for inverse problems in linear elasticity. Further coming works will be concerned in the employment of this approach for identification of other parameters in frictional contact problem. Considering a regularity weaker than $W^{1,1}$ in admissible set $\mathcal{C}$ will be an important perspective as well as an inverse problem subject to hemi-variational inequalities. Identifying Lamé coefficients for contact problem with elastic-locking or hyperelastic and elastoplastic materials will be an important issue in future works. Nevertheless, there are some important issues to address in order to overcome the limitations of the proposed study:

• An active set strategy method have been used to solve the dual problem. Compared to others methods, it is well known that this method is very slow since the active and inactive sets are updated during the iterations.

• Research alternative function spaces that offer weaker regularity conditions while still providing sufficient structure for solving the problem at hand. For example, Sobolev spaces of lower regularity such as $W^{1,p}$ with p<1, or spaces with less restrictive continuity requirements such as BV (space of functions of bounded variation).

Financial interests

Authors declare they have no financial interests.

Acknowledgments

The authors of this paper express their heartfelt gratitude to the Editorial Office, Editor-in-Chief, Associate Editors, and anonymous reviewers for their valuable and constructive comments and remarks. Their insightful feedback greatly contributed to enhancing the quality and clarity of this work.

Data availability

Data sharing not applicable to this article as no datasets were generated or analysed during the current study.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

No funding was received for conducting this study.