Comparative analysis of FISTA and inertial Tseng algorithm for enhanced image restoration in prostate cancer imaging

Abstract

The Inertial Tseng Algorithm (ITA) and the Fast Iterative Shrinkage-Thresholding Algorithm (FISTA) are well-established methods that provide effective ways to approximate zeros of the sum of monotone operators. In this study, we applied both ITA and FISTA in the restoration process of prostate cancer and osteosarcoma images that were degraded with known blur functions and additive noise. The test images comprised osteosarcoma tumours I and II, prostate fused, and prostate MRI pathology. Both algorithms incorporated the TV-regularizer and $l_1$-regularizer. Numerical simulations revealed that the ITA method consistently outperforms the FISTA method in terms of image quality, despite FISTA's computational efficiency advantage. Additionally, the study found that, for both methods, images restored using the TV-regularizer exhibit higher quality compared to those restored using the $l_1$-regularizer. Overall, the study revealed the effectiveness of the algorithms employed and highlight the significance of integrating mathematical models with well established mechanism in medical image restoration.

Keywords:

• Medical image restoration
• image deblurring
• Tseng algorithm
• prostate cancer
• osteosarcoma

2020 Mathematics Subject Classifications:

• 92-00
• 92-05
• 92B05
• 92B10
• 92F05

1. Introduction

Medical imaging plays a critical role in the diagnosis and treatment of various diseases, offering valuable insight to healthcare professionals. With the advancement of technology in the last decade, medical devices have been developed and become faster, more accurate, and less invasive [1]. Mathematical models are integral to medical image restoration, aiming to obtain high-quality images for clinical purposes and minimize risks and costs associated with patient care. Although data-driven models, especially deep models, are adept at extracting valuable insights from extensive datasets, they often lack solid theoretical foundations [2]. Therefore, mathematical models and data derived from images give an insight in biomedical diagnostics, which are essential components of experimental, clinical, biomedical, and behavioural research. Medical imaging plays a pivotal role in the diagnosis and treatment of various diseases, including cancer, offering valuable guidance to healthcare professionals [3]. Mathematical models are incredibly important in the field of medical image restoration. They allow for the production of high-quality images that can be used for clinical purposes, all while minimizing risks and costs associated with patient care. Data-driven models, especially deep models, are particularly useful in extracting valuable insights from large datasets. However, it is important to note that they may not always have robust theoretical foundations. Nonetheless, mathematical models are vital in the field of biomedical computing, with image data processing playing a critical role in clinical, biomedical, experimental, and behavioural research [4].

Prostate cancer (PC) is the most common form of non-skin cancer found in men across various countries globally, including the United States [5, 6]. Globally, PC ranks as the fifth leading cause of male deaths related to cancer, resulting in approximately 350,000 deaths annually. In the United States, it stands as the second leading cause of cancer-related deaths among men [7]. The vast majority (90–95%) of diagnosed prostate cancer cases belong to the adenocarcinoma category. Adenocarcinoma is distinguished by elevated levels of prostate-specific antigen (PSA), which aids in the diagnostic process. Moreover, this form of cancer entails the expression or activation of the androgen receptor [8]. Approximately, 80% of clinically diagnosed cases of prostate cancer are localized and confined to the prostate gland, with the remaining 20% being metastatic [9]. PC screening is a highly controversial topic and remains one of the most debated issues in healthcare. Those against PSA screening express worries about over diagnosis of non-lethal cancers, which may lead to overtreatment, causing treatment-related side effects, psychological distress, and substantial medical costs [10]. Identifying biomarkers can enhance the diagnosis and treatment of prostate cancer [11]. Measuring PSA concentration can aid in deciding whether a biopsy is necessary, potentially reducing morbidity [12].

Osteosarcoma is a classic primary bone sarcoma that primarily affects children and adolescents, and the typical characteristic of osteosarcoma is the production of immature bone or osteoid tissue by malignant osteoblasts [13]. Individuals diagnosed with osteosarcoma frequently confront the possibility of relapse, with pulmonary metastasis emerging as the predominant site. Despite undergoing aggressive treatment, approximately one-third of patients initially diagnosed with osteosarcoma without metastasis encounter recurrence during follow-up periods [14]. In developing countries, osteosarcoma has an average incidence of 0.0003% and ranks as the most prevalent malignant bone tumour after multiple myeloma, representing 0.2% of malignancies. Its high malignancy often leads to early-stage distant metastasis, with approximately 20% of patients already diagnosed with pulmonary metastasis at the time of diagnosis [15].

Magnetic resonance imaging (MRI) technology is commonly used for imaging examinations related to cancer and other diseases [16]. Diagnosing osteosarcoma and prostate cancer in developing countries presents significant challenges. In many developing nations, healthcare infrastructure is limited, and there is an imbalance in the doctor-to-patient ratio, making it hard to offer personalized and specialized medical services. The process of diagnosing and treating osteosarcoma is time-consuming and financially burdensome. Consequently, many impoverished families may have to forgo treatment due to the prohibitive costs involved [17]. Identifying osteosarcoma manually in MRI images poses a labour-intensive and time-consuming challenge for doctors due to the substantial volume of data and the complexity involved in detection. Moreover, the subjective nature of this process increases the likelihood of missed or misdiagnosed issues [18]. Therefore, there is need to develop a reliable mathematical algorithm that is capable of restoring images and accurately detecting various types of diseases.

Image restoration encompasses various techniques, including image denoising [19], deblurring [20], inpainting [21], dehazing [22], and de-raining [22]. In solving medical imaging analysis problems, numerical simulations are often preferred due to factors like specular noise that can impact image interpretation. Therefore, the study of medical images requires the use of complex mathematical models employing diverse algorithms. In this study, we employed two famous algorithms, the improvement of Fast Iterative Shrinkage-Thresholding Algorithm (FISTA) proposed by Liang et al. [23] and the Inertial Tseng Algorithms (ITA) proposed by Padcharaeon et al. [24], to restore MRI images of PC and osteosarcoma that were degraded with an additive noise and known blur functions. Additionally, We employed established image restoration tools to enhance the quality of the biomedical images and conducted comparisons between the algorithms used and the restored images with their original counterparts.

2. Methodology

The MRI images of PC and osteosarcoma were retrieved from the cancer imaging archive (https://www.cancerimagingarchive.net), which is an open-source licence (https://creativecommons.org/licenses/by/3.0/); they represent various disease conditions and ethical approval is not applicable. Many image restoration problems can be reformulated as convex optimization problems of the form: $\text{find}u\in {\mathbb{R}}^N\text{such that}u=\underset{x}{\arg min}\{\frac{1}{2}\Vert \mathrm{Dx}-\eta {\Vert }^2+\mathrm{\mu G}(x)\},$where D is a degradation function, x is the original image, η is noise, μ is a regularization parameter and G is a regularization function introduced due to the nature of the function (or matrix) D. In the literature, several regularization functions have been considered depending on the objective of the image restoration problem. One of the famous regularizers is the $l_1$-regularizer which usually appears in the $l_1$ regualarization problem, popularly known as least absolute shrinkage and selection operator (LASSO) problem which is to (1) $\text{find}u\in {\mathbb{R}}^N\text{such that}u=\underset{x}{\arg min}\{\frac{1}{2}\Vert \mathrm{Dx}-\eta {\Vert }^2+\mu \Vert x{\Vert }_{l_1}\},$(1) where $\Vert \cdot {\Vert }_{l_1}$ is the usual taxi-cab norm on ${\mathbb{R}}^N$ referred to as the $l_1$ regularization function. The $l_1$-regularizer is a powerful tool in image denoising and deblurring and has been explored by a host of many authors see, e.g. [23–27]

Another regularizer use for image restoration problems is the discrete Total Variation regularizer defined by $\begin{array}{rl}\Vert x{\Vert }_{\mathrm{TV}}& =\sum _{i=1}^{n-1}\sum _{j=1}^{m-1}\sqrt{(x_{i+1,j}-x_{i,j}{)}^2+(x_{i,j+1}-x_{i,j}{)}^2}\\ & +\sum _{i=1}^{m-1}|x_{i,n}-x_{i+1,n}|+\sum _{j=1}^{n-1}|x_{m,j}-x_{m,j+1}|.\end{array}$The TV-regularization problem is defined by (2) $\text{find}u\in {\mathbb{R}}^N\text{such that}u=\underset{x}{\arg min}\frac{1}{2}\Vert \mathrm{Dx}-\eta {\Vert }^2+\mu \Vert x{\Vert }_{\mathrm{TV}}.$(2) This regularizer is known for restoring images with cartooning effects and edge-preserving properties. For more on regularizers used for image restoration problem interested readers may see [22].

All these regularization problems arising from image restoration can be reformulated as follows: (3) $\text{find}u\in {\mathbb{R}}^N\text{such that}u=\underset{x}{\arg min}\{h(x)+g(x)\},$(3) where $h(x):=\frac{1}{2}\Vert \mathrm{Dx}-\eta {\Vert }^2\text{and}g(x):=G(x),\text{a regularization function}.$Through a simple mathematical reformulation, solutions to the minimization problems (3(3) $\text{find}u\in {\mathbb{R}}^N\text{such that}u=\underset{x}{\arg min}\{h(x)+g(x)\},$(3) ) are equivalent to solutions to the inclusion problem: (4) $\text{find}u\in {\mathbb{R}}^N\text{such that}0\in (\mathrm{\nabla f}(u)+\mathrm{\partial g}(u)),$(4) where $\mathrm{\nabla }f$ is the gradient of f and $\mathrm{\partial }g$ is the subdifferential of g, explicitly given as $\mathrm{\nabla }f(x)=D^T(\mathrm{Dx}-\eta )\text{and}\mathrm{\partial g}(x)=\{\begin{array}{ll}{\displaystyle \frac{x}{\Vert x\Vert },}& x\ne 0;\\ \{x:\Vert x\Vert \le 1\},& x=0.\end{array}$In the literature, several algorithms have been introduced to approximate zeros of the sum of two monotone operators, which are frequently utilized to tackle the inclusion problem (4(4) $\text{find}u\in {\mathbb{R}}^N\text{such that}0\in (\mathrm{\nabla f}(u)+\mathrm{\partial g}(u)),$(4) ) (see, e.g. [28–34] and the references therein). We are interested in some recent methods developed based on the famous forward-backwards algorithm used for solving the inclusion problem (4(4) $\text{find}u\in {\mathbb{R}}^N\text{such that}0\in (\mathrm{\nabla f}(u)+\mathrm{\partial g}(u)),$(4) ), namely the ITA proposed by Padcharaeon et al. [24] and improving the FISTA proposed by Liang et al. [23] due to their efficiency in solving image restoration problems. 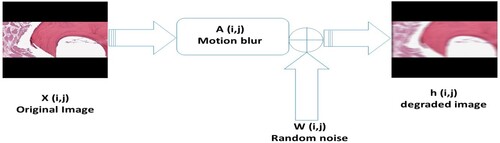We recall that the mathematical formulation for the image restoration problem is given by (5(5) $h=\mathrm{Ax}+w,$(5) ) and illustrated in Figure 1: (5) $h=\mathrm{Ax}+w,$(5) where x is the original image, A is the degradation function, y is the observed image, and w is noise.

Figure 1. Image degradation process.

We will study the performance of the ITA of [23] and a new version FISTA by Liang et al. [23] in the restoration process of postrate cancer images that were initially degraded by random noise and motion blur. We will consider the discrete TV-regularization model (2(2) $\text{find}u\in {\mathbb{R}}^N\text{such that}u=\underset{x}{\arg min}\frac{1}{2}\Vert \mathrm{Dx}-\eta {\Vert }^2+\mu \Vert x{\Vert }_{\mathrm{TV}}.$(2) ) and the $l_1$-regularization model (1(1) $\text{find}u\in {\mathbb{R}}^N\text{such that}u=\underset{x}{\arg min}\{\frac{1}{2}\Vert \mathrm{Dx}-\eta {\Vert }^2+\mu \Vert x{\Vert }_{l_1}\},$(1) ) to solve this problem. For completeness, we will introduce the ITA and FISTA methods here without their respective convergence analysis.

2.1. Convergence analysis

Theorem 2.1

The sequence $\{x_k\}$ generated by Algorithms 1 and 2 converges to a solution of problem (3(3) $\text{find}u\in {\mathbb{R}}^N\text{such that}u=\underset{x}{\arg min}\{h(x)+g(x)\},$(3) ).

Proof.

Since $\mathrm{\nabla }f$ is Lipschitz monotone, and $\mathrm{\partial }g$ is maximal monotone, the convergence analysis follows using a similar argument given in [23, 24], by setting $A=\mathrm{\nabla f}$ and $B=\mathrm{\partial g}$, in these references, respectively.

2.2. Experimental results and discussion

In this section, we will give a comparative study of Algorithms 1 and 2 in the restoration process of some prostate and osteosarcoma cancer images. We will consider four (4) test images, which we label as follows: Images 1, 2, 3 and 4, which are actually the original Osteosarcoma Tumour I, Osteosarcoma Tumour II, Prostate fused, and Prostate MRI pathology, respectively. The performance of Algorithms 1 and 2 in the restoration process of these test images that were initially degraded using ‘MATLAB's built-in motion blur function’ ($P=\mathrm{fspecial}{(}^{\prime }\mathrm{motio}{n}^{\prime },30,60)$) was studied, and Gaussian noise (GN) scaling factor $\sigma =0.001$ was added. Furthermore, TV-regularizer and the $l_1$-regularizer was considered, and the effect of these regularizers when used in Algorithms 1 and 2 is studied. The outcomes of the simulations are shown in Figures 2, 3, 4 and 5 below:

Figure 2. Test images and their restorations via ITA and FISTA using TV-regularizer. (a) original images. (b) images degraded by motion blur and random noise. (c) restored images with ITA and (d) restored images with FISTA.

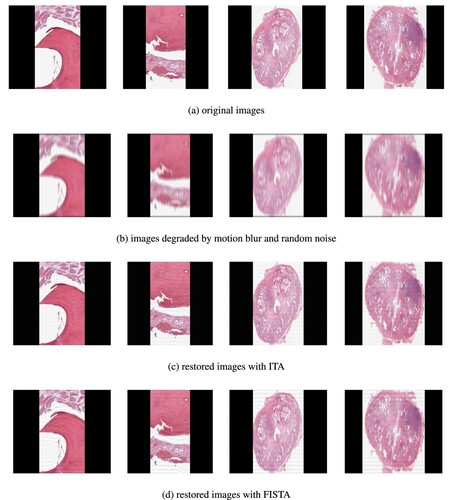
Figure 3. Test images and their restorations via ITA and FISTA $l_1$-regularizer. (a) original images. (b) images degraded by motion blur and random noise. (c) restored images with ITA and (d) restored images with FISTA.

Figure 4. Graphical representation of the results in Table 1, Left: Image 1; Right: Image 2.

Figure 5. Graphical representation of the results in Table 1, Left: Image 3; Right: Image 4.

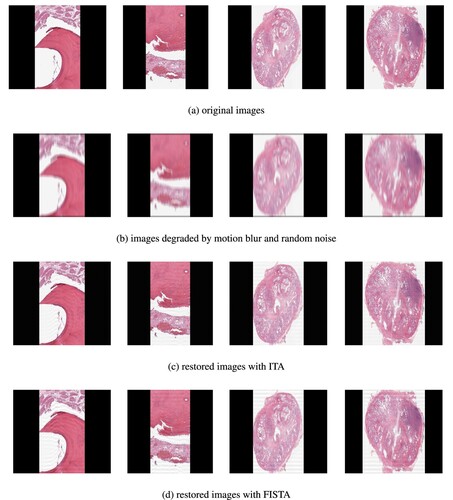
Discussion. Looking at the restored images via ITA and FISTA using TV-regularizer and $l_1$-regularizer (see Figures 2 and 3), we observe that the restored images via TV-regularizer appear to be more closer to the original images compared to the restored images via $l_1$-regularizer. Furthermore, the images restored using the ITA method appear to clearer than those restored using the FISTA method. However, we employed tools to measure the quality of restored images in order to validate the claim. Three different metrics were used for this analysis: Improvement in signal-to-noise ratio (ISNR), peak signal-to-noise ratio (PSNR), and signal-to-noise ratio (SNR). These metrics are expressed as follows: (8) $\begin{array}{r}\mathrm{ISNR}:=10\log \frac{\Vert x-y{\Vert }^2}{\Vert x-x_n\Vert },\mathrm{PSNR}=10{\log }_{10}\left(\frac{{\mathrm{MAX}}^2}{\mathrm{MSE}}\right)\mathrm{and}\mathrm{SNR}:=10\log \frac{\Vert x\Vert }{\Vert x-x_n{\Vert }^2},\end{array}$(8) where y, x, and $x_n$ denote the observed, original, and estimated images at iteration n, respectively, and MAX is the maximum possible pixel value and MSE is the Mean Squared Error between the original and distorted images.

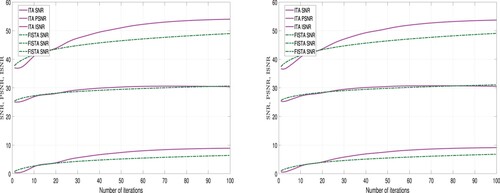
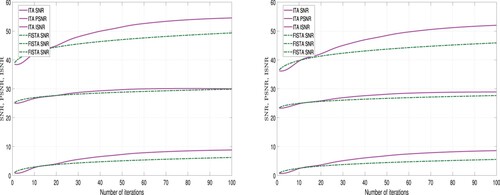
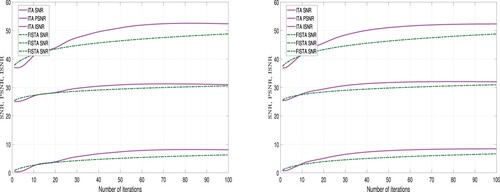
A higher values for ISNR and SNR indicate superior restoration. Also, a higher PSNR value implies lower distortion and better quality. The performance of ITA Algorithm 1 and FISTA Algorithm 2 using these metrics is detailed in Tables 1 and 2 and Figures 4 and 5.

Table 1. Performance metrics for the test images using TV regularizer.

ISNR, PSNR, SNR and CPU time for the test images
	ITA				FISTA
Test images	ISNR	PSNR	SNR	CPU Time	ISNR	PSNR	SNR	CPU time
Image 1	8.91	30.43	54.23	435.22	6.39	30.65	49.00	317.51
Image 2	9.12	30.55	53.72	437.52	6.79	31.08	49.08	319.47
Image 3	8.82	30.02	54.53	437.66	6.24	29.86	49.35	320.28
Image 4	8.6	28.9	51.99	441.9	5.55	27.66	45.91	320.59

Table 2. Performance metrics for the test images using $l_1$-regularizer.

ISNR, PSNR, SNR and CPU time for the test images
	ITA				FISTA
Test Images	ISNR	PSNR	SNR	CPU Time	ISNR	PSNR	SNR	CPU time
Image 1	8.07	30.98	52.38	264.49	6.29	30.56	48.82	141.57
Image 2	8.42	32.01	52.33	249.14	6.65	30.94	48.80	130.13
Image 3	7.92	30.90	52.73	238.05	6.24	29.86	49.35	320.28
Image 4	7.47	29.01	49.75	234.67	5.43	27.54	45.66	133.31

Remark 2.1

From Table 1 and Figures 4 and 5, we observe that using the TV-regularizer, the quality of the restored images using ITA are higher than the quality of the restored images using FISTA. But the computational time required to restore the images using FISTA is less than the computational time required using the ITA method. Hence, we deduce that in terms of quality ITA is better than FISTA and in terms of computational time, FISTA is better than ITA.

Figure 6. Graphical representation of the results in Table 2, Left: Image 1; Right: Image 2.

Remark 2.2

Also, from Table 2 and Figures 6 and 7, we observe that using the $l_1$-regularizer, the quality of the restored images using ITA are higher than the quality of the restored images using FISTA. But the computational time required to restore the images using FISTA is less than the computational time required using ITA method. Hence, we deduce that in-terms of quality ITA is better than FISTA and in terms of computational time, FISTA is better than ITA.

Figure 7. Graphical representation of the results in Table 2, Left: Image 3; Right: Image 4.

3. Conclusion

This study presents a comparative study of two famous Algorithms, namely, the inertial Tseng algorithm (ITA) proposed by Padcharaeon et al. [24] and improving the Fast Iterative Shrinkage-Thresholding Algorithm (FISTA) proposed by Liang et al. [23] in the restoration process of prostate cancer and osteosarcoma images that had been degraded with known blur function and additive noise. Furthermore, the TV-regularizer and $l_1$-regularizers were used in each algorithm. The results of the numerical simulations suggest that the ITA method restores images with higher quality than the FISTA method, even though the FISTA method is less computationally expensive than the ITA method. Furthermore the quality of the images restored using TV-regularizer is higher than the quality of the restored images using $l_1$-regularizer. However, the computational time for TV-regularizer is higher than that for $l_1$-regularizer. Overall, this study successfully restored prostate cancer and osteosarcoma images that had been degraded with additive noise and a known blur. This approach revealed the potential of mathematical models when integrated with established tools in medical image restoration, as well as the efficacy of the algorithms.

Acknowledgments

The authors are grateful for the support provided by their institutions. ‘Operational Research Centre for Healthcare, Near East University, TRNC.’ The author thank the anonymous reviewers for their esteemed comments and suggestions.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Data availability statement

All data used in this study is included in the manuscript.