CALCULATIONS OF OXYGEN TRANSPORT BY RED BLOOD CELLS AND HEMOGLOBIN SOLUTIONS IN CAPILLARIES

Abstract

A theoretical model is developed to investigate the influence of hemoglobin-based oxygen carriers (HBOCs) on oxygen transport in capillary-size vessels. A discrete cell model is presented with red blood cells (RBCs) represented in their realistic parachute shape flowing in a single file through a capillary. The model includes the free and Hb-facilitated transport of O₂ and Hb–O₂ kinetics in the RBC and plasma, diffusion of free O₂ in the suspending phase, capillary wall, interstitium and tissue. A constant tissue consumption rate is specified that drives the simultaneous release of O₂ from RBC and plasma as the cells traverse the capillary. The model mainly focuses on low capillary hematocrits and studies the effect of free hemoglobin affinity, cooperativity and concentration. The results are expressed in the form of cell and capillary mass transfer coefficients, or inverse transport resistances, that relate the spatially averaged flux of O₂ coming out of the RBC and capillary to a driving force for O₂ diffusion. The results show that HBOCs at a concentration of 7 g/dl reduce the intracapillary transport resistance by as much as 60% when capillary hematocrit is 0.2. HBOCs with high O₂ affinity unload most O₂ at the venular end, while those with low affinity supply O₂ at the arteriolar end. A higher cooperativity did not favor O₂ delivery due to the large variation in the mass transfer coefficient values during O₂ unloading. The mass transfer coefficients obtained will be used in simulations of O₂ transport in complex capillary networks.

• Microcirculation
• Capillaries
• Hemoglobin-based oxygen carriers
• Oxygen
• Transport
• Diffusion
• RBC

INTRODUCTION

Hemoglobin (Hb) is the protein in red blood cells (RBCs) responsible for the transport of oxygen. Hemoglobin molecules extracted from RBCs cannot be used without modification as oxygen carriers as the protein molecules break down in the body and are toxic to the kidneys. Over the last decade, advances in biotechnology such as cross-linking, recombinant modification, and encapsulation have overcome this problem and have resulted in the development of hemoglobin-based oxygen carriers (HBOCs) that can temporarily replace whole blood transfusions. Experiments with HBOCs in the plasma have shown an overall improvement in the delivery of O₂ to the tissue, [[1]] particularly in cases where the fraction of RBCs (hematocrit) in the blood is small, in sickle cell anemia, for perioperative uses in surgery, resuscitation after traumatic blood loss, and increased oxygen delivery to ischemic tissues. The main advantages of HBOCs are: 1) the blood substitutes can be sterilized of microorganisms such as those causing AIDS and hepatitis; 2) substitutes do not need to be cross-matched or typed to blood group antigens, thus allowing on-spot transfusions; 3) HBOCs can be lyophilized and stored as stable dry powder for a long time and reconstituted with salt solution just before use; and 4) HBOCs can be made using non-human hemoglobins, e.g. bovine or recombinant Hb. At present, a number of clinical trials are ongoing, but there is no FDA approved blood substitute for use in humans.

Until recently, intraluminal resistance to oxygen transport was neglected in modeling studies under the tacit assumption that the resistance to mass transfer within the tissue was the dominant factor.[[2]] Initial studies that did consider the intraluminal resistance treated blood as a continuum. Later studies using discrete cell models showed that radial convection currents were not important, and that in small capillaries transport of oxygen occurs primarily in the radial direction through the narrow plasma layer between the RBC and the capillary wall via passive diffusion. The discrete cell model was further advanced by studies on the effect of cell spacing related to hematocrit[[3]] and the shape of the RBC.[[4]] A more detailed model that included muscle tissue was presented by Groebe (1995)[[5]] that comprised of three concentric regions. The innermost region represented the RBC, the second, the carrier free region, and the outermost, the muscle region. The carrier free region was a lumped region comprising the plasma layer, the capillary wall, and the interstitial space just outside the wall. Comprehensive reviews are available on the development of mathematical models that predict the distribution of O₂ in tissues.[[2]], [[6]] An accurate computational model of oxygen transport in the presence of HBOCs should help in interpreting results of animal experiments and clinical trials and provide a fundamental understanding of the transport processes in the microvasculature. Past efforts in this area have been focused on arteriolar-sized vessels under in vitro conditions.[[7]] In the microvasculature of the hamster retractor muscle, it has been observed that two-thirds of oxygen is exchanged in the arterioles and the rest in capillaries.[[8]] Measurements in other tissues such as the brain show that cortical capillaries unload about twice the amount of oxygen to the brain tissue as compared to arterioles.[[9]] In the heart under physiological conditions precapillary oxygen losses appear to be small.[[10]] Since the contribution of oxygen from capillaries is found to be fairly substantial in any given tissue, the present paper focuses on this topic by describing the fundamental transport processes associated with RBC/HBOC mixtures in capillaries. We perform simulations on the hamster retractor muscle since most biophysical parameters are available for this tissue and because of our previous calculations under physiological conditions.[[11]], [[12]]

An additional feature of the present model is consideration of relative differences in plasma and RBC velocities. The fluid dynamics of plasma has been extensively investigated via semi-analytical and numerical studies[[13]] and the overall conclusion has been that the effect of plasma motion on local oxygen transport is insignificant. This might be true for cases of high hematocrit where the plasma gaps are small, but for cases of low hematocrit, a frequently encountered clinical condition, the effect of convection cannot be ignored as will be demonstrated by results obtained for the tissue PO₂ distribution. In this paper, we predict the transport of free and bound oxygen in capillaries by considering both diffusion and convection for the low hematocrit cases. Also, the present model uses a parachute shape for the RBC that is based on calculations using an elastic model of the membrane.[[14]] The calculations take into account both the radial and axial drop in oxygen tension for the capillary segment.

This is the first model of capillary transport that includes HBOCs (see Appendix). The calculations consider the full pathway of oxygen transport from its source in the hemoglobin molecule to its sink in the mitochondria of the parenchymal cells. The model uses Krogh-type cylindrical tissue geometry; the goal of the model is calculating capillary mass transfer coefficients that will be used in simulations of O₂ transport in complex capillary networks.

MATHEMATICAL MODEL

Capillary Segment Geometry

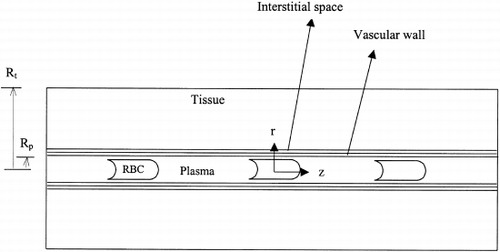
An axisymmetric model of the capillary and the surrounding tissue is used in the present study. The computational domain consisted of five sub-regions: the red blood cell, plasma, vascular wall, interstitium, and the tissue (see Figure 1). The shape of the red blood cell has been selected based on recent numerical simulations[[14]] of RBC flow in capillaries that take into account the deformation of the RBC membrane. Each RBC was represented by a cylinder with a hemispherical leading end and an inverted cap at the trailing end and with smoothed edges. For a single RBC, we define a unit cell with a length, where V _rbc is the volume of the RBC, R _p is the radius of the capillary, and H _c is the capillary (tube) hematocrit. In microcirculatory experiments, it is common to measure lineal cell density, LD=L ⁻¹, the number of RBCs per unit length of capillary; capillary hematocrit can then be expressed in terms of LD using Eq. 1 if capillary diameter and RBC volume are known. A hematocrit range of 0.2 to 0.4 is considered in this work that corresponds to a lineal cell density between 36 and 72 cells/mm. Under normal physiological conditions the average LD=64 cells/mm[[15]] corresponds to a systemic hematocrit H _sys=0.51. Using Eq. 1 we estimate H _c≈0.35. Recent data on hemodilution in hamster retractor muscle from H _sys=0.53 to 0.15 show the decrease of LD from 56 cells/mm to 47 cells/mm.[[16]] Therefore, the range of LD=36–72 cells/mm chosen in this study covers the physiological range of this muscle.

Figure 1. Schematic of computational domain with subregions RBC, plasma, vascular wall, interstitium and tissue.

Model Assumptions

In formulating the model, we make the following major assumptions (a more complete list of assumptions and their discussion can be found in Popel [1989].[[6]]

1. The geometry of the problem as described in the section above.

2. The model considers a train of three equidistant RBCs.

3. The plasma motion is in steady state in the coordinate system moving with the RBCs and is characterized by the velocity components, v _z and v _r.

4. In the tissue, myoglobin and oxygen are assumed to exist in local chemical equilibrium, where S ^Mb is the fractional saturation of Mb, and P ₅₀ ^Mb is the partial pressure of O₂ corresponding to 50% saturation of myoglobin. Although the oxymyoglobin dissociation rate is 66 s ⁻¹[[3]] comparable to that of oxyhemoglobin, the reaction does not lead to a chemical boundary layer region in the muscle fiber, since the flux density of oxygen is distributed over a surface area larger than in the RBC.

5. O₂ consumption in the entire tissue is assumed to be constant. This assumption is appropriate, since P _cr=0.5 Torr, e.g.,[[17]] and since tissue pO₂ does not fall below 3.24 Torr in all the simulations.

Navier–Stokes Equation for Plasma Flow

The equations describing the transient mass transport for free and facilitated oxygen transport in all five sub-regions of the computational domain are presented in Appendix. In order to express the convective component of the intracapillary mass transport equation, it is necessary to know the velocity profile in the plasma. The fluid dynamics of the plasma was described by the equation of continuity or mass balance and the equation of motion, which describes the momentum balance. Plasma was considered to be a Newtonian fluid with a constant density ρ and a constant viscosity μ. These assumptions lead to the Navier–Stokes equation, and for low Reynolds number (Re<0.1) the equation can be simplified to Stokes flow.

The plasma flow has been modeled to take into account the leak back from the individual cells. The amount of leak back depends on the plasma sleeve thickness and the velocity of the red blood cell, v _c. The frame of reference in this study is centered on the middle of the RBC and is moving with the RBC from left to right. Hence, in this reference frame the tissue is moving right to left with a velocity of −v _c. For a capillary hematocrit of 0.2, the calculated pressure drop is approximately 4×10 ⁻³ Torr/μm for the case where no HBOC was present, which is consistent with experimentally measured average pressure drops of 6×10 ⁻³ Torr/μm in the cat mesenteric microcirculation.[[18]], [[19]] Note that explicitly accounting for the endothelial glycocalyx in these calculations leads to significantly higher values of pressure drop.[[14]]

Solution Method

The system of partial differential equations was solved using a finite-element method (FEM) implemented with the finite-element program FLEXPDE© (PdeSolutions, Inc., Antioch, CA). The complete domain was divided into 5 sub-regions: the RBC, plasma, wall, interstitium and the tissue. In order to eliminate possible edge effects due to boundary conditions imposed at the two ends of the domain, a train of 3 RBCs was taken as part of the computational domain.[[4]] Mass transfer coefficients and other transport properties such as wall-average, RBC-average and plasma-average PO₂ were calculated for the middle cell only. The O₂ tension P and normal O₂ flux (−Dα∂P/∂r) were taken to be continuous throughout the domain, while variables S_c ^Hb and S_s^Hb were constrained to the RBC and plasma, respectively. However, to avoid internal boundaries in the computational domain for S_c^Hb and S_s^Hb, all species were taken to be continuous throughout the domain by setting the diffusivities of RBC and plasma hemoglobin to be very small outside their respective domains. The initial value of S_c^Hb was set to zero everywhere except in the RBC, and thus S_c ^Hb≈0 for all time in the plasma, wall, interstitium and tissue regions. Similarly, S_s^Hb≈0 everywhere except in the plasma. The equations for P, S_c^Hb, and S_s ^Hb were solved in the entire cylindrical domain with the conditions of continuity for PO₂ and normal flux of O₂ at the cell-plasma, plasma-wall, wall-interstitium and interstitium-tissue interfaces being satisfied automatically.

The goal of this paper was to study the process of O₂ unloading within a wide range of PO₂ values. Thus, in most of the work presented here we start with an initial PO₂ of 100 Torr and follow the RBCs and plasma until the average RBC saturation has dropped to ~0.1. The length of the “capillary” in this case is unrealistically large and is only used as a means of studying variation of mass transfer coefficients over a wide range of saturation values. Some of the results, especially those of hypoxia are presented for the average capillary length in the hamster retractor muscle. The partial differential equations were solved with an initial time step of 10⁻¹⁰ s that was gradually increased to ~0.2 s during the course of the total simulation time. An isoparametric formulation was used for solving the discretized FEM model of the fluid dynamics in the plasma region with ~1400 triangular elements and nodal v_z, v_r and hydraulic pressure, p_H, being the primary degrees of freedom. For solving the mass transport equations, the isoparametric formulation contained ~9000 triangular elements with primary degrees of freedom being P, S_c^Hb and S_s^Hb. The conjugate-gradient method and a second-order Galerkin time step scheme were used in the calculations. The conjugate-gradient method iterates to a tolerance of 10⁻⁶. The mass balance for the tissue region was satisfied to within 0.1%. The accuracy of the program was validated by comparing numerical and analytical solutions of the axial PO₂ profile calculated using Eqs. A7–A10 14-17 for the case when there was no HBOC in plasma, and for the case where the cooperativities of the HBOC and RBC oxyhemoglobin were the same. In the first case, the numerical and analytical values agreed to within 0.001% of each other and in the second, they agreed to within 0.005% of each other.

Model Parameters

In order to solve the Navier–Stokes equations for the flow of plasma, it is necessary to know the viscosity of the HBOC-plasma solution. The viscosity varies with hemoglobin concentration and can be determined using the fit of Mooney’s relationship to experimental data[[20]] where μ _s=1.2 cP is the viscosity of plasma without hemoglobin,[[21]] and [Hb] _s is the concentration of hemoglobin in the plasma (g/ml). Constants A and B are adjustable parameters of the equation determined from an experimental fit of data, having values of 2.77 ml/g and 1.2 ml/g, respectively, for human tetrameric Hb solution.[[20]]

The values of the parameters used in Eqs. A1–A6 8-13 are summarized in Table 1. A number of these parameters have been discussed in Roy and Popel [1996].[[22]] The vascular wall and the tissue consumption are taken to be 10⁻⁴mlO₂ml⁻¹s ⁻¹[[23]] and 1.58×10 ⁻⁴ mlO₂ml⁻¹s⁻¹,[[15]] respectively. The diffusion coefficient of myoglobin was taken from Wang et al. [1997].[[24]] In Eqs. A3–A6 10-13, we require the diffusion coefficients of the HBOC, D_Hb, and O₂, D_o, as functions of HBOC concentration. For the purposes of this study, we analyzed data for D_Hb and D_o as measured by Spaan et al. [1980],[[25]] Nishide et al. [1997],[[26]] and Bouwer et al. [1997].[[27]] There was an overall agreement in the measurements over a range of 0 to 40 g/dl hemoglobin concentration. The most recent set of diffusion coefficient values[[27]] were used in the paper.

Table 1. List of Model Parameters

Parameter	Value	Units	Source (Ref no.)
Tissue
α	3.88×10 ^−5	mlO 2 cm ^−3 mmHg ^−1	[[31]]
D O	2.41×10 ^−5	cm ^2/s	[[32]]
[Mb]	4×10 ^2	nmole/cm ^3	[[33]]
D Mb	6×10 ^−7	cm ^2/s	[[24]]
P 50 ^Mb	5.3	mm Hg	[[34]]
M t	1.58×10 ^−4	mlO 2ml ^−1s ^−1	[[15]]
Interstitium
α	2.81×10 ^−5	mlO 2 cm ^−3 mmHg ^−1	[[35]]
D O	2.18×10 ^−5	cm ^2/s	[[36]]
R i–R w	0.35×10 ^−4	cm	[[37]]
Wall
α	3.89×10 ^−5	mlO 2 cm ^−3 mmHg ^−1	[[31]]
D O	8.73×10 ^−6	cm ^2/s	[[38]]
M w	1×10 ^−4	mlO 2ml ^−1s ^−1	[[23]]
R w–R p	0.3×10 ^−4	cm	[[37]]
Plasma
[Hb] s	0, 4, 7, 10	g/dl	Model parameter
α	2.81×10 ^−5	mlO 2 cm ^−3 mmHg ^−1	[[39]]
D O		cm ^2/s	[[27]]
D Hb		cm ^2/s	[[27]]
k s	44	s ^−1	[[40]]
P 50,s ^Hb	10, 20, 29.3, 40, 50	mm Hg	Model parameter
n s	1, 2.2, 3.5		Model parameter
μ s	0.012	cP	[[21]]
R p	2.0×10 ^−4	cm	[[15]]
RBC
[Hb] c	34.0	g/dl	Model parameter
α	3.38×10 ^−5	mlO 2 cm ^−3 mmHg ^−1	[[35]]
D O		cm ^2/s	[[27]]
D Hb		cm ^2/s	[[27]]
k c	44	s ^−1	[[40]]
P 50,s ^Hb	29.3	mm Hg	[[15]]
n c	2.2		[[15]]
v c	150×10 ^−4	cm/s	[[41]]
V RBC	6.9×10 ^−11	cm ^3	[[35]]

Definition of Mass Transfer Coefficients

A mass transfer coefficient is calculated as the ratio of the O₂ flux through a surface to the difference in O₂ tension that is the driving force for diffusion. We define two mass transfer coefficients, capillary mass transfer coefficient, k _o, and a cell mass transfer coefficient, k_cell. In a discrete model representation, it is possible to separately calculate the O₂ flux leaving the RBC and the total flux reaching the luminal surface of the capillary. The cell mass transfer coefficient, k_cell, is defined as where is the surface-averaged flux leaving the RBC, is the volume-averaged PO₂ of the RBC, and is the volume-averaged PO₂ of the plasma.

The capillary mass transfer coefficient, k_o, is defined as where is the surface-averaged flux reaching the luminal surface of the capillary and is the surface-averaged plasma-wall interface PO ₂. The mass transfer coefficients are useful in transport studies of vascular networks where it is necessary to quantify the intracapillary transport resistance of O₂ in the presence and absence of HBOCs.

The relative contribution of O₂ flux from the RBC to the total flux at the wall can be represented by the parameter λ. Note that because the tissue consumption rate is constant, the total wall flux is constant by mass balance along the length of the capillary. Thus where A_w is the surface area of the capillary wall within a unit cell and the flux contribution from only the HBOC in the plasma. Therefore where 0≤λ≤1.

RESULTS

The oxygen releasing properties of hemoglobin depend on the affinity to O₂ and its cooperativity. Hence, the parametric study involved changing the values of P_50,s^Hb, n_s, and other model parameters like HBOC concentration [Hb]_s, and cell spacing that are likely to influence the PO₂ distribution in the tissue.

At first, we varied the initial condition by changing the PO₂ value specified on the left side of the capillary domain at t=0. The calculations were terminated when PO₂ values fell below ~10 Torr for a given set of model parameters. The goal of these calculations was to consider the possible effects of different initial PO ₂ values on the mass transfer coefficients. The capillary mass transfer coefficient, k_o, is presented as a function of RBC saturation, S_c^Hb, for P _50,s^Hb=29.3 Torr (Figure 2). After the initial transients, the values of k_o were found to coincide for two simulations that began with PO₂ values of 40 and 100 Torr on the left side of domain. Hence, for a given set of model parameters there is a unique relationship between the capillary mass transfer coefficient and RBC saturation independent of initial conditions. The cell mass transfer coefficient, k_cell, was also found to be insensitive to initial conditions. Consequently, throughout the paper we present k_o and k_cell as a functions of RBC oxyhemoglobin saturation, S_c^Hb.

Figure 2. Comparison of k_o, for different initial PO₂. P_50,c^Hb=P_50,s^Hb=29.3 Torr, n_c=n_s=2.2, [Hb]_s=7g/dl, H_c=0.2.

Effect of HBOC Oxygen Affinities on k _o and k _cell

In the absence 2,3-diphosphoglycerate (2,3-DPG) that cross-links the two β-chains of the hemoglobin molecule in the RBC, the value of P _50,s ^Hb is known to be around 8 Torr, an unfavorably high oxygen affinity that may lead to an insufficient release of oxygen in the body. Hence, in order to improve the oxygen releasing capacity of extracellular hemoglobin, it is necessary to chemically modify the hemoglobin protein.[[1]] Typically, the P _50,s^Hb for these modified hemoglobins ranges between 27 and 38 Torr depending on the site targeted, mode of modification, and in some cases the source of protein. In this paper, we study the dynamics of oxygen unloading for P_50,s ^Hb=10, 20, 29.3, 40 and 50 Torr while P_50,c^Hb is held constant at 29.3 Torr. Thus, it will be possible to understand the variation in the mass transfer coefficients and tissue PO₂ distribution for a wide range of P_50,s^Hb values and RBC oxygen saturation.

The variation of the capillary mass transfer coefficient, k_o, versus RBC saturation, S_c^Hb, for different values of P_50,s^Hb is presented in Figure 3A. The value of k _o varied over a larger range for P_50,s^Hb values less than 29.3 Torr, while remaining nearly constant for values greater than 29.3 Torr. For the case where HBOC concentration is zero, the value of k_o varied in the range 0.97–1.2×10⁻⁶ mlO₂s⁻¹Torr ⁻¹cm ⁻² and was lower than all the HBOC cases for the entire range of S_c^Hb values. For hemoglobin solutions having a P_50,s ^Hb=10 Torr, the capillary mass transfer coefficient, k_o increased monotonically four-fold from a value of 1×10 ⁻⁶mlO₂s⁻¹Torr⁻¹cm⁻², as S_c^Hb decreased from 0.8 to 0.1. For P_50,s^Hb=50 Torr, k _o decreased from 1.7×10⁻⁶ mlO₂s ⁻¹Torr ⁻¹cm⁻² to 1.4×10⁻⁶ mlO₂s⁻¹Torr ⁻¹cm⁻² as S_c^Hb decreased from 0.8 to 0.1.

Figure 3. (A) Comparison of k _o for different values of HBOC oxygen affinities. P _50,c^Hb=29.3 Torr, n_c=n_s=2.2. H_c=0.2, [Hb] _s=7 g/dl. (B) Comparison of k_cell for different values of HBOC oxygen affinities. P_50,c^Hb=29.3 Torr, n_c=n_s=2.2, H_c=0.2, [Hb] _s=7 g/dl.

The variation of k_cell is presented in Figure 3B. For the case where no HBOC is present, k _cell rose from 0.034×10⁻⁶mlO ₂s⁻¹Torr ⁻¹cm⁻² to 0.19×10⁻⁶ mlO₂s⁻¹Torr ⁻¹cm⁻² as S_c^Hb decreased from 0.8 to 0.1. For all HBOCs, k_cell increased as S_c ^Hb decreased, with the maximum change for P _50,s^Hb=10 Torr, where the variation in k_cell was between 0.78 and 1.8×10 ⁻⁶mlO₂s⁻¹Torr ⁻¹cm⁻². The least change in k_cell values was observed for P _50,s^Hb=50 Torr, with the values varying between 0.8 and 1.1×10⁻⁶ mlO₂s⁻¹Torr⁻¹cm ⁻².

Effect of HBOC Cooperativity on k_o and k _cell

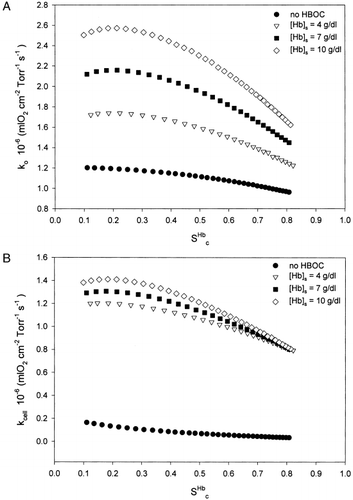
The effect of changing HBOC cooperativity, n _s, is studied by varying the value of n_s at 1.0, 2.2 and 3.5. The variation of the capillary mass transfer coefficient, k_o, versus average RBC oxygen saturation value, S_c^Hb, is presented in Figure 4A. The results are compared to the case where no HBOC is present in plasma. When n_s=1.0 (non-cooperative binding that is encountered in some polymerized hemoglobins), k _o increased monotonically from 1.4×10 ⁻⁶ mlO₂s ⁻¹Torr ⁻¹cm ⁻² to 2.05×10 ⁻⁶ mlO₂s ⁻¹Torr ⁻¹cm ⁻² as S _c ^Hb decreased from 0.8 to 0.1. When n _s=3.5, k _o initially rose from 1.35×10 ⁻⁶ mlO ₂s ⁻¹Torr ⁻¹cm ⁻² to 2.7×10 ⁻⁶ mlO ₂s ⁻¹Torr ⁻¹cm⁻² as S_c ^Hb decreased from 0.8 to 0.44 and thereafter decreased to 1.7×10 ⁻⁶ mlO₂s⁻¹Torr ⁻¹cm ⁻² as S_c ^Hb further decreased to 0.1. The rapid changes in k_o could be attributed to the high degree of non-linearity in the Hill dissociation curve caused by the high value of n _s. The corresponding values of the cell mass transfer coefficient, k _cell, are presented in Figure 4B. For n _s=1, k _cell increased from 0.79×10 ⁻⁶ mlO ₂s ⁻¹Torr ⁻¹cm ⁻² to 1.27×10 ⁻⁶ mlO ₂s ⁻¹Torr ⁻¹cm ⁻². For n _s=3.5, k _cell reached a peak value of 1.41×10 ⁻⁶ mlO ₂s ⁻¹Torr ⁻¹cm ⁻² at S _c ^Hb=0.37 and then decreased to 1.15×10 ⁻⁶ mlO ₂s ⁻¹Torr ⁻¹cm ⁻² as S _c ^Hb decreased to 0.1. Note that the peak values of k _o and k _cell do not occur at the same value of S _c ^Hb.

Figure 4. (A) Comparison of k _o for different values of HBOC oxygen cooperatives. P _50,c ^Hb=P _50,s ^Hb=29.3 Torr, n _c=2.2, H _c=0.2, [Hb] _s=7 g/dl. (B) Comparison of k _cell for different values of HBOC oxygen cooperatives. P _50,c ^Hb=P _50,s ^Hb=29.3 Torr, n _c=2.2, H _c=0.2, [Hb] _s=7 g/dl.

Effect of HBOC Concentration on k _o and k _cell

The amount of oxygen being carried by the plasma will depend on the amount of HBOC present in it and the capillary hematocrit. In order to understand the effect of concentration on the mass transfer coefficients and PO ₂ distribution, we vary the HBOC concentration between 0 and 10 g/dl keeping all other parameters constant.

The results for the capillary mass transfer coefficient for different HBOC concentrations are presented in Figure 5A. As the HBOC concentration increased from 0 to 10 g/dl, the value of k _o was progressively higher at a corresponding value of S _c ^Hb. For the case where no HBOC is present, k _o increased by 25% from a value of 0.97×10 ⁻⁶ mlO ₂s ⁻¹Torr ⁻¹cm ⁻² as S _c ^Hb decreased from 0.8 to 0.1, while for the case where [Hb] _s=10 g/dl, k _o increased by 58% from a value of 1.63×10 ⁻⁶ mlO ₂s ⁻¹Torr ⁻¹cm ⁻² for the same range of S _c ^Hb values. The value of k _cell in Figure 5B followed a trend similar to that of k _o.

Figure 5. (A) Comparison of k _o for different values of HBOC concentrations. P _50,c ^Hb=P _50,s ^Hb=29.3 Torr, n _c=n _s=2.2, H _c=0.2. (B) Comparison of k _cell for different values of HBOC concentrations. P _50,c ^Hb=P _50,s ^Hb=29.3 Torr, n _c=n _s=2.2, H _c=0.2.

Effect of HBOC Affinity, Cooperativity, and Concentration on Tissue Oxygen Distribution

In order to better understand the effect of HBOC properties on tissue oxygenation, the histograms of tissue PO ₂ over the entire capillary length of 417 μm corresponding to the hamster retractor muscle are presented in Figures 6-8. Note, that the calculations were carried out with a low capillary inlet PO ₂ of 35 Torr, reflecting a high degree of precapillary O ₂ transport[[15]] and a higher muscle consumption rate of 2.76×10 ⁻⁴ mlO ₂ml ⁻¹s ⁻¹ for all the runs in order to understand the behavior of HBOCs under conditions of relatively low PO ₂ with the concentration of HBOC [Hb] _s set at 7 g/dl. The mass transfer coefficients k _o and k _cell were higher by 5–10% when compared to the values shown in Figures 3A–B, 4A–B and 5A–B. The most notable differences between the cases are in the spread and peak values of the distribution. The effect of HBOC affinity is shown in Figure 6A, where in the absence of HBOC, the tissue PO ₂ ranged between 3 Torr and 30 Torr with 23% of the tissue having a PO ₂ between 15 and 20 Torr with a mean PO ₂ of 16 Torr. For P _50,s ^Hb=10 Torr, tissue PO ₂ ranged between 10 and 30 Torr with 34% of tissue having PO ₂ between 15 and 20 Torr, similar to the case with no HBOC but with a higher mean PO ₂ of 20 Torr. For P _50,s ^Hb=29.3 Torr, matching that of the hemoglobin in the RBC, tissue PO ₂ was distributed over an even smaller range of 20 and 35 Torr with 36% of the tissue having PO ₂ between 20 and 25 Torr with a mean PO ₂ of 23 Torr. The distributions shift to the right towards higher PO ₂ values as the HBOC oxygen affinities decreases. When P _50,s ^Hb was increased even further to 50 Torr, the PO ₂ spread was between 10 and 35 Torr with a mean PO ₂ of 21 Torr. The increase in the spread of PO ₂ values is due to the early unloading of oxygen by the HBOC having a high P _50,s ^Hb. Also presented in Figure 6B are radial profiles at the arteriolar-end (indicated by B), the middle of the capillary segment (indicated by M), and towards the end of the capillary (indicated by E). The early unloading by the HBOC having P _50,s ^Hb=50 Torr is comparable to that of P _50,s ^Hb=29.3 Torr. Since the HBOC having P _50,s ^Hb=50 Torr unloads most of its oxygen early on while the HBOC having P _50,s ^Hb=10 Torr does not unload its oxygen until PO ₂ values have fallen to very low values, the radial profiles at the venular end for both these HBOCs is much lower than for the case where P _50,s ^Hb=29.3 Torr.

Figure 6. (A) Tissue PO ₂ distribution along capillary length for different HBOC oxygen affinities. P _50,c ^Hb=29.3 Torr, n _c=n _s=2.2, H _c=0.2, [Hb] _s=7 g/dl. (B) Radial tissue PO ₂ distribution profiles for different HBOC oxygen affinities. P _50,c ^Hb=29.3 Torr, n _c=n _s=2.2, H _c=0.2, [Hb] _s=7 g/dl. The vertical line shows the plasma-wall interface. A-arteriolar end, M-midcap, V-venular end. –·–·–·–· P _50,s ^Hb=10 Torr, ------- P _50,s ^Hb=29.3 Torr, ——— P _50,s ^Hb=50 Torr.

Figure 7. Tissue PO ₂ distribution along capillary length for different HBOC oxygen cooperatives. P _50,c ^Hb=P _50,s ^Hb=29.3 Torr, n _c=2.2, H _c=0.2, [Hb] _s=7 g/dl.

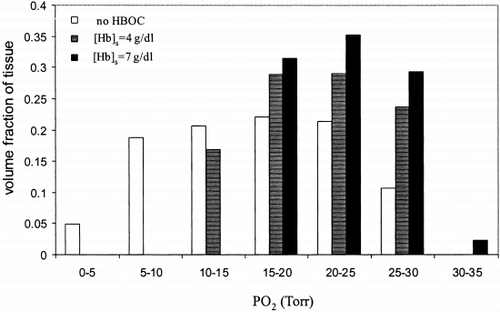
Figure 8. Tissue PO ₂ distribution along capillary length for different HBOC concentrations. P _50,c ^Hb=P _50,s ^Hb=29.3 Torr, n _c=n _s=2.2, H _c=0.2.

Similar to Figure 6A the tissue PO ₂ distributions for different cooperativities with the same inlet capillary PO ₂ of 35 Torr are presented in Figure 7. For n _s=1 the mean PO ₂ is 23.5 Torr with 34% of the tissue having a PO ₂ between 20 and 25 Torr. For n _s=3.5, 47% of the tissue PO ₂ is between 25 and 30 Torr with a mean PO ₂ of 27 Torr.

The effect of HBOC concentration on tissue PO ₂ distribution is presented in Figure 8 for HBOC concentrations of 0, 4 and 7 g/dl. Similar to Figures 6A and 7, the calculations were carried out with the same initial PO ₂ and the results are distinguishable from one another by their range and mean PO ₂ values. In the presence of 4 g/dl HBOC, tissue PO ₂ was spread over a range of 10 to 30 Torr with 60% between 15 and 25 Torr and mean a PO ₂ of 21 Torr. The overall distribution shifted to the right as concentration increased.

Effect of Hematocrit

The results for different hematocrits for the case where [Hb] _s=7 g/dl and with other parameters kept constant are presented in Figures 9A and 9B. The value of k _o in Figure 9A increased at corresponding values of S _c ^Hb as capillary hematocrit increased from 0.2 to 0.4 (lineal cell density, LD, increased from 36 to 72 cells/mm). The largest increase in k _o of 60% was observed for a hematocrit of 0.4, while the smallest change of 50% was observed for a hematocrit of 0.2. The decrease in intracapillary resistance with increase in hematocrit is attributed to the shortening of the plasma gap length. This effect was also found for the case when no HBOC was present in plasma. The cell mass transfer coefficient, k _cell, displayed a trend similar to k _o with the greatest increase observed for a hematocrit of 0.4 and the least for a hematocrit of 0.2.

Figure 9. (A) Comparison of k _o for different values of hematocrits. P _50,c ^Hb=P _50,s ^Hb=29.3 Torr, n _c=n _s=2.2, [Hb] _s=7 g/dl. (B) Comparison of k _cell for different values of hematocrits. P _50,c ^Hb=P _50,s ^Hb=29.3 Torr, n _c=n _s=2.2, [Hb] _s=7 g/dl.

Effect of Oxygen Dissociation Rates on k _o

We also studied the influence of kinetic dissociation rates of hemoglobin. In Figure 10, the capillary mass transfer coefficient, k _o, is presented for the cases of chemical equilibrium and nonequilibrium, in the presence and absence of HBOCs in plasma. Generally, the assumption of instantaneous chemical equilibrium within the RBC is valid as long as the rate of the chemical reaction is much faster than the diffusive transport. Assuming chemical equilibrium greatly simplifies the system of equations being solved and thus speeds up the solution of the problem. However, this assumption breaks down near the RBC membrane because oxygen is permeable to the RBC membrane while the hemoglobin molecule is not thus creating a boundary layer on the inside of the RBC membrane. In the presence of HBOC in the plasma, there are two additional boundary layers formed, one near the RBC-plasma interface and the other near the plasma-wall interface due to the inability of HBOC to diffuse into the RBC and capillary wall. The effect of the additional boundary layers on the plasma side can be seen in values of k _o in Figure 10. In the absence of HBOC, k _o differs by as much as ~20% between equilibrium and non-equilibrium cases, whereas in the presence of HBOCs the corresponding difference is as much as ~55%. Thus, the kinetic effects may play some role in capillary transport. The effect should be more pronounced for hemoglobins with slower kinetics.

Figure 10. Comparison of kinetic parameter values with and without HBOC. P _50,c ^Hb=P _50,s ^Hb=29.3 Torr, n _c=n _s=2.2, [Hb] _s=7 g/dl.

Effect of Plasma Convection and HBOC-Facilitated Diffusion

The effect of plasma convection terms in Eqs. A3 and 10 and A411and A1118 on the numerical solution was studied by estimating the mean tissue PO₂ in the presence and absence of HBOC. In the absence of convection terms, the mean tissue PO ₂ was lower by 0.6 Torr with HBOC (concentration of 7g/dl and hematocrit of 0.2) and by 1.1 Torr in the absence of HBOC when compared to the corresponding cases when convection terms were included in the numerical solution. Thus, the plasma convection plays only a minor role in O₂ delivery to tissue.

The importance of HBOC facilitated O₂ transport in the plasma was studied by varying the value of D _Hb in Eq. A411 between 1×10⁻¹² and 1×10⁻⁶ cm ²/s in the absence of convection terms in Eqs. A3 10 and A411. A comparison of the capillary mass transfer coefficient for all the cases is presented in Figure 11. The capillary mass transfer coefficient was found to decrease as D_Hb is decreased from 1×10 ⁻⁶ cm²/s to 1×10 ⁻¹² cm²/s, indicating an increase in the overall intravascular O ₂ transport resistance. The resistance increased by 8% as D _Hb was lowered from 7.28×10 ⁻⁷ to 1×10 ⁻¹². The capillary mass transfer coefficient is nearly the same for D _Hb=10 ⁻⁹ and 10 ⁻¹² cm ²/s. Hemoglobin tetramers have a diffusion coefficient between 5×10 ⁻⁷ and 8×10 ⁻⁷ cm ²/s, and polymerized hemoglobins have a diffusion coefficient between 5×10 ⁻⁸ and 2×10 ⁻⁷ cm ²/s.[[26]] The value of D _Hb in all our simulations is 7.28×10 ⁻⁷ cm ²/s, and since there is very little change in the capillary mass transport resistance for diffusivities lower than 7.28×10 ⁻⁷ cm ²/s, it is unlikely that changing the diffusivity of the hemoglobin molecule will have a significant effect on the overall transport of oxygen to the tissue thus no effect of facilitated diffusion. As the total flux is constant for all the cases, we observe a corresponding increase in the driving force as D _Hb decreases. The mean tissue PO ₂ for a diffusion coefficient of 1×10 ⁻⁶ was 0.23 Torr more than when diffusion coefficient was 1×10 ⁻¹².

Figure 11. Comparison of overall mass transfer coefficient for different HBOC diffusion coefficients. P _50,c ^Hb=P _50,s ^Hb=29.3 Torr, n _c=n _s=2.2, [Hb] _s=7 g/dl.

DISCUSSION

The capillary mass transfer coefficient, k _o, and the cell mass transfer coefficient, k _cell are consistently higher in the presence of HBOC. In Figure 3A, for high RBC saturation values and P _50,s ^Hb=10 Torr, k _o is nearly equal to the case where there no HBOC is present. As S _c ^Hb falls, k _o increased nearly four-fold due to the delayed unloading of oxygen from the HBOC. This is also evident from the contribution of the average oxygen flux leaving the RBC surface towards the total flux entering the wall. The contribution of the RBC flux, λ (Eq. 7) decreased from 78% to 41% as S _c ^Hb decreased from 0.5 to 0.1. When HBOC P _50,s ^Hb=29.3 Torr, the contribution of the RBC flux stays fairly constant at 60% between S _c ^Hb=0.5 and 0.1, i.e. approximately equal contribution from both the RBC and the HBOC. Hence other parameters being constant, it would be advantageous to use an HBOC with high oxygen affinity when supplying oxygen to tissue regions located towards the end of the capillary, since they can carry the O ₂ for a longer duration. HBOCs with lower oxygen affinity would deliver more oxygen to the arteriolar end of the capillary network and precapillary regions. However, these conclusions may be dependent on a number of factors, including O ₂ consumption rate and inlet PO ₂. A minimal change in tissue PO ₂ distribution can be observed as P _50,s ^Hb value is increased from 29.3 to 50 Torr. The model predictions are in agreement with experimental data and observations dealing with the effect of O ₂ affinity on oxygen delivery[[28]], [[29]] suggesting the use of HBOCs with low P ₅₀ to limit oxygen unloading in arterioles and to target regions with low PO ₂. Mass transfer coefficient values shown in Figure 3A are further supported by the low RBC flux values calculated at low RBC saturations.

The capillary and cell mass transfer coefficients rise monotonically for HBOC cooperativities of 1 and 2.2, while there exists a maximum value for 3.5. The RBC flux contribution decreased from 76% to 62% for n _s=1 and increased from 50% to 70% for n _s=3.5 as S _c ^Hb decreased from 0.5 to 0.1. Combining these results with those in Figure 7, we can conclude that other parameters being constant, HBOCs with a higher cooperativity deliver oxygen more uniformly, leading to a higher average tissue PO ₂ compared to HBOCs with a cooperativity of 1. Despite the large variations in capillary mass transfer coefficient values for n _s=3.5 over the entire range of RBC saturation values, HBOCs with higher cooperativity provide higher oxygenation levels under hypoxic conditions.

We have shown that mass transfer coefficients strongly depend on capillary hematocrit or lineal density, LD, for a range of LD=36–72 cells/mm; this range was based on measurements in the hamster retractor muscle. For comparison, hemodilution experiments under resting conditions in the hamster cremaster muscle have shown that a reduction in H _sys from 0.57 to 0.18 leads to a corresponding decrease in cell density from 94 to 50 cells/mm.[[30]]

Though there is a large variation in k _o for different values of P _50,s ^Hb and n _s, the overall intracapillary resistance is always lower in the presence of HBOCs. This is because the driving force for oxygen is smaller when HBOC is present in plasma, and, given that the luminal flux is constant for all cases, this in turn translates into a higher value of k _o. The extent to which HBOCs improve oxygen transport largely depends on the properties and concentration.

The model predictions are in agreement with theoretical results obtained for small blood vessels without HBOC by Hellums et al. (1996).[[2]] They showed that for vessels with diameter 5.5 μm, the mass transfer coefficient remains approximately constant over an RBC saturation range of 0.8 to 0.1. The mass transfer coefficient for the control case presented in Figure 4 is also nearly constant for the same range of RBC saturation values. The increase in the overall mass transfer coefficient with increasing cell spacing shown by Hellums et al. [1996][[2]] is consistent with the results in Figure 9A and our previous work.[[11]]

CONCLUSIONS

It should be noted that our simulations are limited to consumption remaining constant, i.e., hypoxic conditions are not considered. A detailed analysis of hypoxic conditions is of great importance and should be considered in the future. The present paper is a theoretical study on the effect of HBOCs on oxygen delivery in capillary-size vessels. The only existing theoretical model of oxygen transport with HBOC considers arteriolar size permeable tubes;[[7]] the results are presented in terms of the mean Hb saturation vs. residence time in the tube and the corresponding mass transfer coefficients cannot be readily calculated from the results. Hence, this is the first paper to use a discrete cell model to compute oxygen transport in capillary size vessels in the presence of HBOCs and under conditions of low hematocrit. The mass transfer coefficients calculated in the study can be represented as functions of various model parameters, making it possible to use them in microvascular network calculations where the heterogeneous flow distribution is likely to cause the hematocrit and transport parameters to vary over the entire microvascular network. While the overall conclusion is that HBOCs enhance delivery of oxygen, there are additional findings that follow from our study and are summarized below.

1. The capillary and cell mass transfer coefficients, k _o and k_cell, are strong functions of both average RBC oxyhemoglobin saturation and hematocrit. It is a significant relationship that has not been reported before.

2. Under the conditions considered in this work, lower values of P_50,s^Hb tend to delay oxygen delivery to the venular end of the capillary, while HBOCs with higher P_50,s^Hb values unload more oxygen near the arteriolar end of the capillary, in agreement with previous experimental studies.[[28]], [[29]]

3. Tissue oxygenation improved progressively as HBOC concentration increased from 0 to 10 g/dl.

4. Under resting conditions the effect of convection and Hb-facilitated diffusion of O₂ are not significant.

5. In the presence of HBOCs, substantial deviations from chemical equilibrium can significantly influence tissue PO₂.

ACKNOWLEDGMENTS

This project was supported by the National Institutes of Health Grant HL-18292, American Heart Association Postdoctoral Fellow Grant, and the Johns Hopkins University Center for Advanced Transfusion Practices and Blood Research.

Appendix

MATHEMATICAL MODEL EQUATIONS

Mass Transport in the Tissue

In the tissue, the transport of oxygen takes place via diffusion of free O ₂ and the facilitated diffusion of O ₂ bound to myoglobin (Mb). The frame of reference is moving with the RBC, hence the mass transfer equation in the tissue has the convective term with velocity −v _c. The mass transport equation is expressed as where P is the oxygen tension, α is the solubility coefficient of O ₂, D _o is the diffusion coefficient of O ₂, D _Mb is the diffusivity of Mb in the tissue, [Mb] is the concentration of myoglobin in the tissue, and M _t is the O ₂ consumption in the tissue, which is assumed to be constant for the entire tissue region.

Passive Diffusion in the Interstitium and the Capillary Wall

We assume that there is no extravasation of free Hb from the lumen. Thus, free oxygen is the only species diffusing through the interstitium and capillary wall, where α and D _o are specific to the region, M=0 in the interstitium and M=M _w inside the wall.

Mass Transport in Plasma

In the plasma, free oxygen dissociates from the HBOC. Bound O ₂ in the HBOC is restricted to the plasma region. The oxygen tension and the oxyhemoglobin saturation in plasma, S _s ^Hb, are governed by the transport equations where S _s ^Hb=[HbO ₂]/[Hb] _s, [HbO ₂] is the molar concentration of the oxygenated HBOC in plasma, [Hb] _s the total concentration and D _Hb is the diffusivity of the HBOC in plasma. The last term represents the kinetic reaction between free O ₂ and HBOC, with k _s ^Hb representing the dissociation rate, P _50,s ^Hb the O ₂ tension that corresponds to 50% saturation of the hemoglobin-based solution, and n _s the Hill coefficient of the saturation curve. Both P_50,s ^Hband n_s in Eqs. A411 and A512 are parameters specific to the HBOC present in the plasma. In the absence of HBOC, one solves only Eq. A411 with [Hb]_s=0.

Mass Transport in the Red Blood Cell

In the red blood cell, the free O ₂ diffuses out to the plasma in the direction of the gradient while the oxyhemoglobin is restricted to the red blood cell. Similar to Eqs. A310 and A411, we formulate the transport equations for PO₂ and fractional saturation of oxyhemoglobin in the RBC, S_c^Hb: where [Hb] _c is the total concentration of Hb in the RBC; k _c ^Hb is the kinetic dissociation rate constant; P _50,c ^Hb is the PO ₂ that corresponds to 50% saturation of the hemoglobin; and n _c is the corresponding Hill coefficient of the O ₂ dissociation curve. The values of P _50,c ^Hb and n _c are kept the same for all simulations. Note that since the frame of reference is moving with the RBC, there are no convective terms in Eqs. A512 and A613. The values of the model parameters used in the simulations for all the sub-regions in the computational domain are presented in Table 1.

Initial and Boundary Conditions

In order to solve the set of nonlinear partial differential Eqs. A1–A6 8-13, we need to prescribe initial and boundary conditions for the domain. The present model focuses on a specific section of the capillary containing several red blood cells. For a given segment with constant vascular wall and tissue oxygen consumption rates, the average flux leaving the capillary is constant by mass balance over all the cells. A Krogh-type solution is used to prescribe the initial and boundary conditions as follows. The simplified continuum transport equation for RBC–HBOC mixture is formulated for the capillary with a mass transport coefficient, k_o, at the lumen of the capillary wall. This set of equations can be solved if k_o is known in order to determine the distributions of PO ₂ and SO ₂ in the capillary and tissue. Initially, a constant value of k _o is chosen based on previous calculations.[[11]] The obtained Krogh-type solution is used as the initial condition for the moving region containing three RBCs and also as the boundary conditions as described below. From the numerical solution of Eqs. A1–A68-13, the function k_o(z) is calculated. This function is substituted into the Krogh-type solution, and the process continues iteratively until the convergence of k_o(z) is achieved. For the present model parameters, two iterations were sufficient to achieve convergence.

To obtain the Krogh-type solution (denoted by subscript k), we express O ₂ flux leaving the capillary wall per unit length (F_{O 2}) as where is the average plasma velocity, S _ck(P _ck) and S _sk(P _sk) are the mixing-cup oxyhemoglobin saturations in the cell and plasma phases, respectively, with P _ck and P _sk the PO ₂ values in the red blood cell and plasma, respectively. We assume that P _ck=P _sk, and we neglect dissolved oxygen while solving Eq. A714 since its concentration is much smaller than that of oxygen bound to the heme protein in both the RBC and plasma. Note that Eq. A815 is written in the frame of reference of the tissue unlike Eqs. A1–A68-13 where the frame of reference is located on the RBC. The O₂ balance is completed by equating the longitudinal loss in O₂ in Eq. A714 with the flux leaving the capillary wall in the radial direction

At the plasma-wall interface the boundary condition is where is the O ₂ flux at the wall calculated from Eq. A815 with known values of tissue and wall O₂ consumption rates, k _o(z) is the initial value of the intracapillary mass transfer coefficient as defined in Eq. 5, and P _wk is the PO ₂ at the wall computed using Eq. A916. P _ck is calculated from Eqs. A7–A914-16 and is then used with the value of P_wk to calculate the O₂ distribution in the radial direction for the wall, interstitium and tissue by solving where P _k is the PO ₂ outside the capillary, D _o is O ₂ diffusivity, α is the O ₂ solubility coefficient, and M is the O ₂ consumption rate of either the tissue or the vascular wall as listed in Table 1. It was possible to obtain an analytical solution for Eqs. A7–A1014-17 when no HBOC is present in the plasma and in the case where the HBOC cooperativity in the plasma, n _s, is equal to that of the RBC Hb cooperativity, n _c. For the case when n _s≠n _c, Eqs. A7–A1014-17 were solved numerically.

The Krogh-type solution is also used for prescribing the boundary conditions at each end of the domain. The coordinate system of the domain was centered about the middle cell with the leftmost node (the trailing edge) at z=−(3L/2) and the rightmost node (the leading edge) at z=−(3L/2). The boundary condition at the trailing edge was

The boundary condition at the leading edge (i.e. z=3L/2) is the same except for a negative sign on the right hand side of Eqs. A11–A13 18-20. Because of the condition of axisymmetry

At the outer edge of the tissue

The above set of boundary conditions satisfied the mass balance in the tissue region with the average flux leaving from all the cells being equal to the consumption rate of the tissue. The capillary mass transfer coefficient k _o(z) was obtained by solving Eqs. A1–A68-13 iteratively with value of k_o(z) computed at the end of each iteration using Eq. 5 being used in Eq. A9 16 for the subsequent iteration.