Influence of Process Conditions During Impulsed Electrostatic Droplet Formation on Size Distribution of Hydrogel Beads

Abstract

In the medical applications of microencapsulation of living cells there are strict requirements concerning the high size uniformity and the optimal diameter, the latter dependent on the kind of therapeutic application, of manufactured gel beads. The possibility of manufacturing small size gel bead samples (diameter 300 µm and below) with a low size dispersion (less than 10%), using an impulsed voltage droplet generator, was examined in this work. The main topic was the investigation of the influence of values of electric parameters (voltage U, impulse time τ and impulse frequency f)on the quality of obtained droplets. It was concluded that, owing to the implementation of the impulse mode and regulation of τ and f values, it is possible to work in a controlled manner in the jet flow regime (U> critical voltage U_C). It is also possible to obtain uniform bead samples with the average diameter, d_eff, significantly lower than the nozzle inner diameter d_I (bead diameters 0.12–0.25 mm by d_I equal to 0.3 mm, size dispersion 5–7%). Alterations of the physical parameters of the process (polymer solution physico-chemical properties, flow rate, distance between nozzle and gellifying bath) enable one to manufacture uniform gel beads in the wide range of diameters using a single nozzle.

• Alginate
• Microencapsulation
• Electrostatic droplet formation
• Impulsed mode

Introduction

Among many application fields for bioencapsulation (biotechnology, health care, pharmacy, the food industry, cosmetics, environmental protection) the stringent requirements concerning capsule quality should be met in medicine and, in particular, in microencapsulated cell transplantation (Hunkeler et al., [[2001]]). In addition to the many conditions connected with mass transport properties, mechanical resistance, and biocompatibility, the average capsule size and size distribution is also of importance. Concerning the immunoisolation of cells and tissue fragments, the small size in the range between 0.3 and 0.7 mm and the uniformity of capsules (size dispersion up to 10%) are especially desirable to avoid the physical effects of incorporation of encapsulated cells into the capsule membrane or protrusion out of the beads. These effects cause the direct activation of the immunological system of the host and microencapsulated graft rejection (Chang and Prakash, [[1999]]; Wong and Chang, [[1991]]). The classical example is the Langerhans islets microencapsulation, where a capsule of diameter below 0.1 mm cannot completely encapsulate an islet with an average diameter of 150 µm. Therefore, the methods of droplet formation, used in this application, must guarantee the manufacture of beads with adequate size distribution parameters.

One of the techniques applied for the microencapsulation of living cells (tissues) is the electrostatic method (Nedovic et al., [[2002]]; Rokstad et al., [[2001]]). Electrostatic droplet formation utilizes a special type of physical process and takes advantage of electrohydrodynamical effects occurring in flowing conductive liquids after introduction of an electric charge. When an electrostatic voltage is applied to the metal nozzle and an electric charge is induced in the liquid flowing through the nozzle, the size of droplet detaching from the nozzle tip decreases relative to its size during free flow without electrostatics (Poncelet et al., [[1999]]). In the absence of an electric field, the diameter of the released droplet, d₀, can be approximately determined assuming equilibrium between gravity and surface tension forces:where: ρ—liquid density, g—gravitation constant, d₀—detached droplet diameter, d_s—outer nozzle diameter, and γ—surface tension.

In high electric fields, taking into account the decrease of surface tension due to induced surface charge and neglecting the attracting electrostatic force between charged droplet and gellification bath (Poncelet et al., [[1999]]), the diameter of released droplet d can be found from the relationship:where: U—electric voltage, U_C—critical voltage value.

This kind of droplet formation can be called the electrostatic dripping regime. According to the above description, the droplet diameter d continuously decreases with increasing voltage U, from the initial value d₀ in the absence of an electrostatic field (at U=0, d₀ usually larger than 2.0 mm for water solutions), until the smallest diameter is reached at the critical voltage U_C. The critical voltage corresponds to the situation when surface tension becomes negligible and can be approximated by the relationship:where: ε₀—air dielectric constant.

After surpassing the critical voltage value U_C, the liquid starts to flow as a jet. Stable and unstable jets of various shapes (e.g., conical or half-ellipsoidal) are formed at the nozzle tip at different voltages above the critical value, with droplets generated from the jet end. In this jet flow regime the detached droplet size is, generally, always smaller than the inner nozzle diameter d_I.

If the electric voltage U is applied to the nozzle in an impulse mode, the droplet, being formed at the nozzle tip, oscillates between two physical states: the state of electrostatic dripping, described by Eq. (2), and the state of free dripping, described by Eq. (1). Concerning the impulsed electrostatic dripping regime, the effective droplet diameter d_eff should depend on temporary contributions of both states to the process of droplet formation, and could be generally described according to the following relationship:where: f—frequency of voltage impulses (Hz) and τ—impulse duration time (ms).

The actual value of the coefficient α (in the range 0–1) describes a temporary contribution of the electrostatic dripping state to the entire process of droplet formation.

The quality of each microencapsulation method can be considered with respect to two factors:

• overall size dispersion of manufactured spherical capsules, evaluated by calculating the ratio of standard deviation of diameters in the sample to the average diameter value (in percent),

• presence of the satellite fraction of smaller capsules in the sample and its quantitative contribution to the entire sample content.

In this work, the quality of bead manufacture using an impulsed voltage electrostatic droplet formation device was evaluated. The main point was to investigate the influence of electric parameters (voltage, impulse time, and impulse frequency) on bead sample size uniformity and average diameter.

Materials and Methods

Characteristics of Device

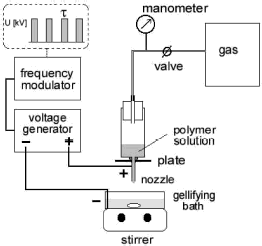
An electrostatic droplet generator with impulsed voltage, of own construction, is schematically presented in Fig. 1. Polymer solution is forced, under regulated gas pressure, to flow through a stainless steel nozzle. Droplets are formed at the nozzle tip and detach to the gellifying bath below. The nozzle is connected with the positive end of a high voltage supply, supplied by a frequency modulator, whereas the gellifying bath is grounded. This setup enables one to apply pulsed electric voltages to the nozzle and, thus, to charge flowing solution in a controlled manner. The nozzle is additionally equipped with a thin stainless steel plate (diameter about 4 cm) to increase the uniformity of the static electric field between nozzle tip and gellifying bath.

Figure 1. A schematic view of the electrostatic droplet generator with the impulsed voltage.

Regulated electric parameters include: the applied voltage value U (in the range 0–25 kV, stepwise), duration time of the voltage impulse τ (in the range 1–9 ms, stepwise) and frequency of impulse application f (in the range 1–100 Hz, stepwise).

Microcapsule Preparation

Sigma alginate (medium viscosity, 3500 cps for 2% solution) 1.5% solution in 0.9% NaCl was used for droplet formation, with droplets subsequently gellified to beads in 1.1% CaCl₂.

All experiments were performed with the following constant parameters: inner nozzle parameter d_I=0.3 mm, outer nozzle diameter d_s=0.5 mm, nozzle length—25 mm, the distance between nozzle tip and gellifying bath—40 mm, applied gas pressure—0.04 At.

Variable parameters included: the applied voltage value U in the range 0–21 kV, frequency f in the range 10–100 Hz and impulse duration time τ in the range 1–9 ms.

Microcapsule Size and Size Distribution Analysis

The average diameter and standard deviation of size were evaluated from sample images, collected using a Sony video camera mounted on a stereo optical microscope (PZO, Poland). For the purpose of comparison, selected samples were analyzed in parallel, using a crystallographic type optical microscope. Bead sizes were evaluated after equilibration in 1.1% calcium chloride water solution (15 min).

Determination of the Critical Voltage Value U_C

Experimental points of droplet diameter–voltage characteristics were fitted by the theoretical curves of Eq. (4) with U_C being the unknown parameter. The fitting procedure was performed with the help of a computer program, and enabled one to determine the values of U_C using the minimalization criterion according to a χ² test.

Results

Influence of Applied Voltage U on Droplet Size

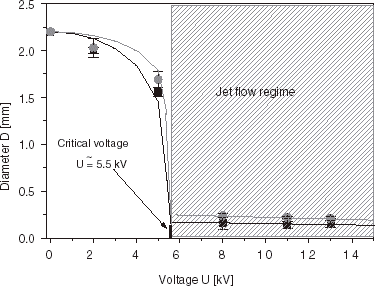
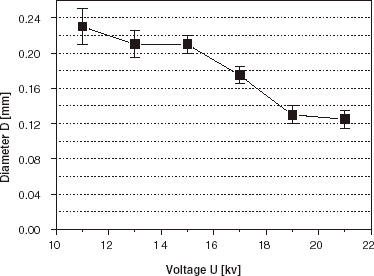
Experimentally, a decrease of droplet size with increasing voltage can be demonstrated both in the electrostatic dripping regime and in the jet flow regime. A typical example of such behavior for the impulse frequency f = 80 Hz is shown in Fig. 2. By inspecting the diameter–voltage characteristics it is evident that slightly larger beads are obtained with the impulse duration time τ=5 ms than with τ=9 ms. Experimental points can be adequately fitted by the theoretical curves of Eq. (4) with the coefficients α equal to 0.72 (for τ = 9 ms) and 0.40 (for τ = 5 ms). The determined value of the critical voltage U_C is equal to 5.5 kV on average. After crossing-over the U_C value it is possible to decrease further the bead diameters with the increasing voltage. Working in the jet flow regime enables one to obtain beads with the average diameter well below the inner diameter of the nozzle (d_I = 0.3 mm). In the voltage range between 11 and 21 kV the average diameter of beads can go down from 0.24 to 0.12 mm (Fig. 3, Table 1), at the working frequency 100 Hz and impulse time 9 ms (conditions close to the situation in a constant voltage device, α = 0.9). The beads are formed from droplets generated from jet tips and are characterized by a very low size dispersion (Table 1).

Table 1. Size distribution of droplets generated at frequency 100 Hz and impulse time 9 ms

Applied voltage U (kV)	Average diameter (mm)	Standard deviation (mm)	Size dispersion (%)
11	0.230	0.020	8.7
13	0.205	0.015	7.3
15	0.204	0.009	4.4
17	0.175	0.009	5.1
19	0.135	0.009	6.7
21	0.128	0.010	7.8

Figure 2. Dependence of the bead size on applied voltage for two different impulse duration times: τ=5 ms (upper curve, gray circles) and τ=9 ms (lower curve, black squares) at the same impulse frequency f=80 Hz.

Figure 3. Dependence of the bead size on applied voltage (above the critical voltage value) in the jet flow regime for the impulse duration time τ=9 ms at the impulse frequency f=100 Hz.

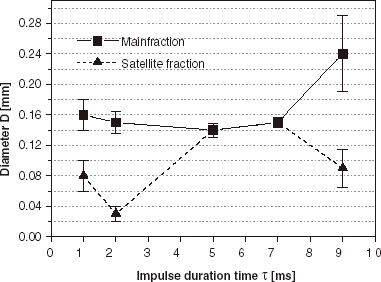
Influence of Impulse Time τ on Sample Homogeneity

The most important problem in the application of electrostatic devices is the presence of the satellite fractions of small beads with average diameters below 100 µm in the obtained samples. This is especially important in cell or tissue encapsulation. As mentioned in the introduction, to avoid an acute immunological reaction after transplantation of encapsulated cells or tissues, the cells must be completely covered by capsule material. Therefore the dimension of the capsule must be greater than the encapsulated biological material. For example, in the case of Langerhans islets the diameter of capsules cannot be smaller than 150 µm.

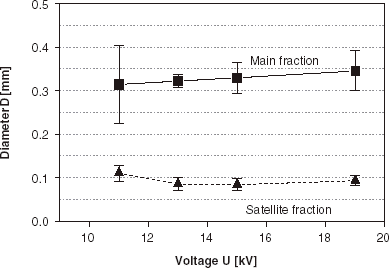
The occurrence of satellite fractions is also observed in the impulsed mode device as Fig. 4 shows. The use of low impulse frequency (10 Hz) and short impulse duration time (1 ms) favors the formation of the satellite fraction in the entire range of applied voltages (from 11 to 19 kV). The impulse duration time τ plays a crucial role in droplet formation as can be seen from Figs. 3 and 4. Therefore the sample uniformity was tested for different impulse duration times in the range of 1–9 ms (Fig. 5), at the impulse frequency 100 Hz and U=11 kV. Homogeneous samples, without any contribution of satellite fraction, were obtained for the impulse duration times in the range 5–7 ms (α values between 0.5 and 0.7) with the average diameters and size dispersions 0.14 mm, 6% and 0.15 mm, 7%, respectively. At other impulse duration times bimodal size distributions were observed in the samples for this impulse frequency, with main and satellite bead fractions present.

Figure 4. Dependence of the bead size on applied voltage (above the critical voltage value) in the jet flow regime for the impulse duration time τ=1 ms at the impulse frequency f=10 Hz. Main fraction—squares, satellite fraction—triangles.

Figure 5. Absence and presence of the satellite fraction in the bead samples in dependence on impulse duration time (f=100 Hz). Main fraction—squares, satellite fraction—triangles.

Discussion and Conclusions

Among many different techniques of cell microencapsulation (Dulieu et al., [[1999]]) one of the most precise methods is electrostatic droplet formation (Bugarski et al., [[1994]]). This process enables one to manufacture spherical and uniform bead fractions with sizes from 4.0 mm down to 0.3 mm (dependent on the viscosity of applied polymer solution and nozzle diameter) (Klokk and Melvik, [[2002]]). It is a feasible, fully controlled and reproducible technique. Nevertheless, similarly to other methods, the manufacture of small size beads and the appropriate selection of process parameters (including non-electrical), avoiding the occurrence of satellite fractions, are often problematic. According to the preliminary results, presented in this work, it seems that these problems can be solved by application of the impulsed electrostatic droplet formation device. Use of the impulsed voltage generator enables one to control and regulate additional process parameters, namely the impulse frequency f and the impulse time τ. The results of conducted investigations evidence that both these parameters play a crucial role in the process of droplet formation. A proper selection of the parameters makes possible the manufacture of the highly uniform beads with diameters in the range between 0.12 and 2.5 mm, using a single nozzle (inner diameter d_I = 0.3 mm). High τ and f values favor the formation of small droplets (Fig. 3). As τ and f decrease, larger droplets are formed. At low τ and f values (and voltages over the critical voltage threshold) the droplets are formed with diameters comparable to the nozzle diameter (Fig. 4), but they are accompanied by the satellite fraction at all applied voltage values. The main point is that small, homogeneous beads (average diameter around 0.15 mm, size dispersion around 7%), without the satellite fraction, can be formed by a proper choice of τ and f parameters (5–7 ms and 100 Hz).

Concerning the mechanism of droplet formation, and the relationship between droplet and nozzle size, a significant dependence on the applied voltage is observed. In the low voltage range the impulsed electrostatic device works like a constant voltage device (Fig. 2, left side of voltage range 0–5 kV). Below the critical voltage value (U < U_C) the droplet forms and detaches directly from the nozzle and its diameter d_eff depends (according to Eq. 2) on the outer diameter of the nozzle d_s. Therefore the generated droplets cannot be smaller than (or even equal to) the nozzle size (Klokk and Melvik, [[2002]]). Surpassing of the critical voltage and working at high voltages (U > U_C) enables the formation of droplets with diameters d_eff smaller than d_s but causes increased size dispersion and occurrence of satellite fraction. The transition to the jet flow regime is accompanied by a significant change in the mode of droplet formation. In the voltage range for U > U_C the liquid jet appears at the nozzle outlet and droplets are generated at the jet tip. The shapes and dimensions of such jets (and thus also size and uniformity of generated droplets) are differentiated and depend on electrical conditions, physico-chemical properties of the liquid and flow conditions (Camelot et al., [[1999]]; Hartman et al., [[1999]]).

The jet evolution in time and droplet generation are very sensitive to, even minor, changes in electrical field and flow rate (Hartman et al., [[1999]]). In such situations the preparation of uniform bead samples demands careful control of electrical parameters, especially concerning quantity of charge and duration of charged state. The impulsed droplet formation device is equipped with extended regulation possibilities which enable one to manufacture beads with optionally adjusted diameters and of high sample uniformity. Varying not only electrical parameters but also electrode distance, flow rate and nozzle diameter makes it possible to obtain high quality bead samples from polymers of different molecular mass and at different concentrations.

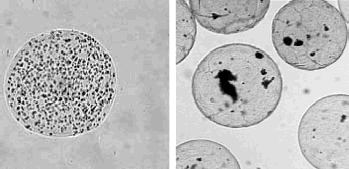
As the encapsulated cells are exposed to high electric voltages during the electrostatic microencapsulation process, it is important to know how this procedure influences the cell viability and function. In our research practice the impulsed voltage droplet formation device of the described construction was used for the microencapsulation of two different kinds of mammalian cells. For the series of six consecutive electrostatic microencapsulations of WEHI-3B cell line (for U = 8 kV, f = 80 Hz, τ = 7 ms), alginate beads with the average diameter and SD of 0.51 ± 0.07 mm (size variation 14%) and the average cell concentration of 2.3 × 10³ cells/microbead were obtained (Lewińska et al., [[2002]]). In the other application, human parathyroid cells were microencapsulated in similar conditions in the alginate beads with the average diameter and SD of 0.42 ± 0.02 mm (size variation 5%) at the average cell concentration of 1.2 × 10³ cells/microbead (Rosiński et al., [[2002]]). Typical examples of microbead samples with entrapped cells are presented in Fig. 6. In both cases cell viability and function were well preserved after microencapsulation (Lewińska et al., [[2002]]; Rosiński et al., [[2002]]).

Figure 6. Samples of microbeads with entrapped WEHI-3B cells (left) and human parathyroid cells (right).

In conclusion it is noteworthy to point out that the impulsed voltage droplet generator offers good control of the bead formation process for different voltage values (in both electrostatic dripping and jet flow modes). Owing to this the manufacture of uniform beads in a wide range of diameters, using the same nozzle, is possible and convenient.