Approaches and Recommendations for Estimating Minimally Important Differences for Health-Related Quality of Life Measures

Abstract

We describe currently available approaches for estimating the minimally important difference (MID) and their associated strengths and weaknesses. Specifically, we show that anchor-based methods should be the primary method of estimating the MID because of the limitations of distribution-based methods. In addition, we provide recommendations for estimating the MID in future research.

• Minimally important difference
• Health-related quality of life
• Anchor-based methods
• Recommendations

Introduction

Health-related quality of life (HRQOL) measures assess multiple domains of functioning and well-being such as physical functioning, role functioning, social functioning, anxiety, depression, positive well-being, pain, and general health perceptions [[1]]. HRQOL measures are essential ingredients in the assessment of outcomes of health care. Accompanying the increased emphasis on HRQOL is a growing recognition of the need to provide mechanisms to help with interpretation of score differences. This paper conducts an evaluation of different approaches for estimating the threshold for the size of difference in HRQOL scores that is minimally important (i.e., the minimally important difference or MID). We discuss anchor-based methods of estimation as the primary methodology. The limitations of distribution-based methods are also noted. We provide recommendations for estimating the MID in the future.

The significance of difference in HRQOL change between two or more groups is typically used to evaluate the effect of alternative interventions. Patients might be randomized to control versus treatment groups and the treatment leads to significantly greater improvement in HRQOL over time. It could then be concluded that the treatment had a statistically significant positive effect on HRQOL. However, it is important to consider the magnitude of the difference between the groups. With a large enough sample size, even very small differences in HRQOL could lead to a statistically significant difference. It is possible that a difference could be so small that it would be considered trivial clinically and unimportant, even if statistically significant.

Estimating the MID

Estimating the MID is a special case of examining responsiveness to change. Responsiveness refers to the ability of a measure to reflect underlying change [[2]]. Underlying change can be defined by change in clinical status, intervening health events, interventions of known or expected efficacy, and retrospective reports of change by patients or providers. The value of these anchors depends on how well they reflect underlying change.

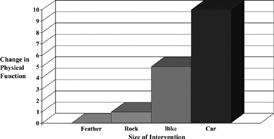
In estimating the MID, the best anchors (retrospective measure of change, knowledge about the course of health overtime and clinical parameters) are ones that identify those who have changed but not too much. In other words, it is important to identify the subset of people who have experienced minimal change. Figure 1, for example, shows a hypothetical plot of the impact on physical function of four life interventions. The change from pre-intervention to post-intervention is displayed on the y-axis. Changes in physical function for getting hit by a feather, rock, bike, and car are 0,1,5, and 10, respectively. Assuming the physical function scale has a standard deviation of 10, the getting hit by a car “intervention” results in a substantial impact on physical function (1 SD). At the other extreme, the feather has no detectable impact on physical function. The bike impacts physical function by 0.50 SD and the rock impacts it by about 0.10 SD. If one was to pick an anchor for estimating the MID in physical function upon, the car, bike, and feather interventions would not be good choices because they would be expected to produce changes in physical function that are either non-existent (feather) or too large (bike or car). One might argue, however, that getting hit by a rock could be an anchor that might be useful for estimating minimal difference or change in physical function.

Figure 1.

Those who have changed by a minimal amount might be identified by asking study participants at follow-up to report how much they changed since baseline of a study using a multiple categorical response scale such as got a lot better; got a little better; stayed the same; got a little worse; got alot worse. People who reported either getting a little better or a little worse could constitute the minimal change subgroup. The change in HRQOL reported by this subgroup of people would then be the estimate of the MID as perceived by the patient. One might decide to look at change for those getting worse versus getting better separately or pool them together after accounting for the difference in the direction of change (e.g., multiplying the change for those who got a little worse by negative one to account for the direction difference).

Retrospective self-reports are known to be subject to recall bias [[3]]. When retrospective change items are used as anchors, it is useful to determine if they reflect the baseline (pre-test) and present (post-test) status equally. In theory, retrospective change items should correlate positively with the post-test and have a negative correlation of equal magnitude with the pre-test as illustrated in the following formulas: r(x, y − x) = r(x,y) and r(y, y − x) = r(y, − x) = − r(x,y), where r (.,. ) is the correlation, x is the pre-test, and y is the post-test. In reality, retrospective self-reports tend to correlate more strongly with the post-test than they do with the pre-test because current status unduly influences the retrospective perception of change. For example, Walters and Brazier [[4]] found moderate correlations (mean 0.45, range: 0.18 to 0.57) between responses to a retrospective measure of global change and the SF-6D at follow-up across nine studies. Correlations with initial assessment were systematically lower (mean 0.22, range: 0.01 to 0.41). Thus, these correlations should be interpreted with flexibility and allowance for lack of equality.

Alternatively, study participants might be asked to compare themselves with other people that they know something about. Patients in one study of COPD were asked to respond relative to other patients with COPD. For example, “Compared to Jack, my ability to walk is:” much better, somewhat better, about the same, a little bit worse, somewhat worse, or much worse [[5]]. The investigators then calculated the difference in walking distance between respondents and the people for whom the respondents rated themselves as walking either a little bit better or a little bit worse. This difference (adjusted for direction) was used to estimate the walking distance MID.

For a clinical parameter, it is also necessary to establish the amount of change on the anchor that is a reasonable indicator of minimal. Hence, estimating the MID requires agreement about what constitutes a minimal change in the anchor. Kosinski et al. [[6]] defined minimal improvement on their clinical measures as 1–20% improvement in the number of swollen and tender joints in a study of 693 patients with rheumatoid arthritis. Although this may be a reasonable threshold, other investigators might argue for another threshold (e.g., 1–10% improvement).

Any anchor that is chosen should have a “non-trivial” association with change in HRQOL. If the correlation between the anchor and HRQOL change is zero, then the anchor is not useful for establishing the MID. While a non-trivialcorrelation is important, an anchor cannot “hope to capture the richness and variation of the construct of HRQOL” [[7]]. Using Cohen's [[8]] rules of thumb, we recommend 0.371 as a correlation threshold to define a noteworthy (large effect) association (Table 1).

Table 1.  Cohen's [[8]] Rules of Thumb for the Magnitude of Effect Sizes and Correlations.

	Effect size	Correlation
Large effect	0.80	0.371
Medium effect	0.50	0.243
Small effect	0.20	0.100

The variety of possible anchors and uncertainty in the anchor cut point that defines a minimal difference makes a single estimate of MID problematic. Using the retrospective report anchor as an example, the recall item might refer globally to change in “health,” “health-related quality of life,” or “quality of life.” Moreover, the anchor might be worded more specifically such as “physical functioning,” “pain,” “getting along with family,” etc. The choice of words could lead to variability in the performance of the anchor. Any specific anchor may be more or less appropriate for different HRQOL domains. For example, an energy/fatigue scale might be expected to change more than a pain scale in response to change in hematocrit [[9]]. Interpreting change in response to a particular anchor should take into consideration the fact that not all domains should change or change equally in tandem with the anchor. Other factors that can lead to variation in the estimation of the MID include whether the people being evaluated are high or low on the measure at baseline, whether they improve or decline in HRQOL over time, and whether they have similar demographic, clinical, and other characteristics [[10]].

The effect sizes (change divided by baseline standard deviation) for the SF-36 scales and summary scores for five different anchors used in a clinical trial of 693 persons with rheumatoid arthritis [[6]] are shown in Table 2. One of the anchors was a self-report about how the patients was doing, considering all the ways that rheumatoid arthritis affects him/her: very good (asymptomatic and no limitation of normal activities), good (mild symptoms and no limitation of normal activities), fair (moderate symptoms and limitation of normal activities), poor (severe symptoms and inability to carry out most normal activities), and very poor (very severe symptoms that are intolerable and inability to carry out normal activities). Another anchor paralleled the self-report anchor but was based on clinician report. The minimally important change for both of these anchors was defined as improvement of one level from time 1 to time 2. The third anchor was a global report of pain on a 10 centimeter visual analog scale. The fourth and fifth anchors were clinician assessments of the number of swollen and tender joints. Minimally important change on the last three anchors was defined by 1–20% improvement from time 1 to time 2.

Table 2.  Effects Sizes for SF-36 Changes Related to Minimal Changes in Five Anchors for Rheumatoid Arthritis [[6]].

Scale	Self-R	Clin.-R	Pain	Swell	Tender	Average
PF	0.35	0.33	0.34	0.26	0.32	0.32
Role-P	0.56	0.52	0.29	0.35	0.36	0.42
Pain	0.83	0.70	0.47	0.69	0.42	0.62
Gen. H	0.20	0.12	0.09	0.12	0.04	0.12
EWB	0.39	0.26	0.25	0.18	0.05	0.23
Role-E	0.41	0.28	0.18	0.38	0.26	0.30
SF	0.43	0.34	0.28	0.29	0.38	0.34
EF	0.50	0.47	0.22	0.22	0.35	0.35
PCS	0.49	0.48	0.34	0.29	0.36	0.39
MCS	0.42	0.27	0.19	0.27	0.20	0.27

Self-R = Self-report; Clin.-R = Clinician report; Pain = Global report of pain; Swell = Number of swollen joints.

Tender = Number of tender joints; PF = Physical functioning; Role-P = Role limitations due to physical health problems.

Pain = Bodily Pain; Gen. H = General Health; EWB = Emotional well-being; Role-E = Role limitations due to emotional problems; SF = Social functioning; EF = Energy/fatigue; PCS = Physical Component Summary.

MCS = Mental Component Summary.

Expressed as effect sizes, these estimates range from 0.04 (joint tenderness anchor for general health perceptions) to 0.83 (self-report anchor for pain). The size of these estimates range from a small to large effect according to Cohen's [[8]] rules of thumb in which 0.20 is considered a small effect, 0.50 is a medium effect, and 0.80 or above a large effect (Table 1).

Should One Include a Placebo or No Change Group?

Whenever possible it is a good idea to compare the change in HRQOL for persons that have been deemed to change by a minimal amount with the change observed for those who are deemed to have stayed the same (not changed). If it turns out that the change for the no-change group is similar to that of the minimally changed group, then the MID estimate is suspect. However, if the MID change exceeds that of the no-change group, the MID estimate is useful and does not need to be adjusted by the HRQOL change observed in the no-change group. For example, ifthe minimally important change group is found to have an average change in HRQOL of 4 points versus 2 points for the no-change group, then the 4 points is the estimated MID. This means that 2 points is not enough to constitute a MID (because this difference is reported by people who have not changed), and it takes a bigger change (4 points) to constitute a MID.

Distribution-Based Methods of “Estimating” MID

A distinction has been drawn between anchor-based and distribution-based methods for determining the MID. Distribution-based methods include the effect size (ES), standardized response mean (SRM), and the responsiveness statistic (RS). For all of these indices, the numerator is the mean change and the denominators are the standard deviation at baseline (ES), the standard deviation of change for the sample (SRM), and the standard deviation of change for people who are deemed to have not changed according to an external standard (RS).

The distribution-based indices provide no direct information about the MID. These indices are simply a way of expressing the observed change in a standardized metric. This makes it possible to compare change observed for measures that have a different raw metric and the degree of deviation (individual and group level) within the sample, but it does not provide new information about the size of change in a measure that is minimally important. ES estimates can be compared to Cohen's guidelines about the magnitude (Table 1), but anchor-based methods are the only way to estimate the MID directly. The standard error of measurement (SEM) has been proposed as another method of relevance to MID estimation. This suggestion is based on anecdotal observations that the SEM was approximately equal to the estimated MID [[11]]. Norman et al. [[12]] note that 1 SEM is approximately the same as a 0.5 difference on a 7-point scale and 1 SEM is approximately 0.5 SD when the reliability is 0.75. But why should one SEM have anything to do with the MID? The SEM is estimated by the product of the standard deviation and the square root of 1 − reliability of the measure. The SEM is used to set the confidence interval around an individual score. Specifically, the observed score plus or minus 1.96 SEMs constitutes the 95% confidence interval. In fact, the reliable change index proposed earlier by Jacobson and Truax [[13]] is based on defining change using the statistical convention of exceeding two standard errors. Hence, one SEM is not inherently any more meaningful than 0.90 SEM, 0.80 SEM, 1.4 SEM, or any other value.

Recommendations

MID estimates should be reported in unstandardized units so that users of the measure will be able to interpret differences in the raw metric. In addition, these estimates can be reported in standardized units (e.g., ES) to make it possible to compare the magnitude of MID estimates for different measures. This will help researchers and others explore the extent to which MID estimates are similar or vary across instruments.

Choice of anchors is critical in estimating the MID. Anchors that represent an unknown quantity of change are problematic. Because the size of the observed HRQOL difference should match the true underlying change, anchors that do not represent minimal change are inappropriate for estimating the MID. In addition, the correlation between anchors and prospectively measured change in HRQOL should be reported whenever possible.

The inherent uncertainty in estimating the MID belies the importance of including multiple and preferably different kinds of anchors (e.g., a mix of retrospective reports and clinical anchors). We recommend that effort be directed at providing reasonable bounds around the MID rather than forcing the MID to be a single value. Specifically, it is important to report a bounded rather than a point estimate. The bounds can be estimated using the range, inter-quartile range (IQR), and confidence intervals (CI). The range and IQR have the advantage that they are robust to possibly asymmetric distributions of MID estimates. CIs can be estimated through large sample theory with the assumption of asymptotically normal distribution of MID estimates. Given the complexity in combining MID across studies, closed form solutions (i.e., exact mathematical expression, not approximation) are likely not available. To obtain bounded estimates of MID, a bootstrap approach can be applied to simulate the distribution of parameters related to MID, such as standard errors in the calculation of effect sizes [[14]]. The sampling process should be staged before obtaining parameter estimates to preserve the sampling variation of the raw data.

Acknowledgments

Drs. Hays and Liu were supported in part by the UCLA/DREW Project EXPORT, National Institutes of Health, National Center on Minority Health and Health Disparities, (P20-MD00148-01) and the UCLA Center for Health Improvement in Minority Elders/Resource Centers for Minority Aging Research, National Institutes of Health, National Institute of Aging, (AG-02-004). Ms. Farivar was supported by a National Research Services Award (T32-HS00046) from the Agency for Health Care Research Quality.