The Relation Between the Minimally Important Difference and Patient Benefit

Abstract

A critical issue in the examination of the effects of treatments on health-related quality of life is how to determine whether a particular change is clinically relevant. One approach is the so-called anchor-based method derived from patient or clinician estimates of minimal change (the Minimally Important Difference or MID). At issue, however, is whether this criterion provides a meaningful way to differentiate between beneficial and ineffective treatments. In this paper, I show that the likelihood that a patient will benefit from treatment, or alternatively, the number of patients in a given cohort who will benefit from treatment, can be predicted with considerable precision from the Effect Size, and the particular choice of MID bears almost no relation to the projected benefit. To examine the relation between the threshold of minimal difference, the effect size of treatment, and the likelihood that a patient will benefit from treatment, a simulation based on a normal distribution was used to compute the proportion of patients benefiting for various values of the ES and the MID. The agreement of the simulation with empirical data from four studies of asthma and respiratory disease was examined. The simulation showed a near-linear relationship between ES and the likelihood of benefit, which was nearly independent of the value of the MID. Agreement of the simulation with the empirical data was excellent. Introducing moderate skew into the distributions had minimal impact on the relationship. The proportion of patients who will benefit from treatment can be directly estimated from the effect size, and is nearly independent of the choice of MID. Effect size- and anchor-based approaches provide equivalent information in this situation. There appears to be little utility in the notion of the MID as an absolute indicator of clinically important treatment effects.

• Health related quality of life
• MID
• NNT

Introduction

The interpretation of changes in health-related quality of life (HRQL) has been a research focus for over a decade. More recently, researchers have been devising methods to identify a minimal level of change consistent with real, as opposed to statistically significant, benefit [[1]]. This appears to be a critical issue for interpretation; in contrast to mortality or morbidity, judgments of important change on HRQL scales, which may have arbitrary scores, is not straightforward. Yet, if HRQL is to be used as a meaningful endpoint for clinical trials, methods must be derived to ascertain just how much difference in response to treatment is clinically important.

It is the thesis of the present paper that estimates of the likelihood that an individual patient will benefit from treatment, and consequently, estimates of the number of patients needed to in order to benefit one (NNT) are directly and nearly linearly related to the average treatment effect expressed as an Effect Size (Average Change/Standard Deviation of Baseline Scores) and are insensitive to the choice of a minimal threshold (MID). As a consequence, use of the MID as an absolute standard of treatment effectiveness is inappropriate.

These analyses have been reported previously in recent articles [2&3]. In the present paper the methods and results of the two studies are reviewed, then some general conclusions are drawn.

Estimates of the MID from Anchor-Based and Distribution-Based Approaches

Perhaps the earliest criterion for identifying important change was devised by Cohen [[4]], who expressed differences as an effect size (the average change divided by the baseline standard deviation). This is simply a way to express a treatment effect on a standard scale, so that different measures can be compared. The effect size is widely accepted, and is the standard unit of treatment used in systematic reviews. In the context of comparing group averages, Cohen stated that a small effect size was 0.2; a medium was 0.5; and a large effect size was 0.8. His primary intent was to provide some basis for sample size calculations. However although Cohen did indicate the criteria were just a convention, they have frequently been referred to in health sciences literature to decide whether a change is important or unimportant, including the assertion that a medium effect size of half a standard deviation is important.

By contrast, anchor-based methods explicitly examine the relationship between an HRQL measure and an independent criterion (or anchor) to elucidate the meaning of a particular degree of change. The most popular anchor-based approach uses an estimate of the Minimally Important Difference or MID, defined as “the smallest difference in score in the domain of interest which patients perceive as beneficial and which would mandate, in the absence of troublesome side-effects and excessive cost, a change in the patient's management” [[1]].

Typically, methods used to assess the MID from patients are based on a retrospective judgment about whether they have improved, stayed the same, or worsened over some period of time. The methods then establish a threshold based on the change in HRQL in patients who report minimal change, either for better or for worse.

Distribution and anchor-based methods appear to be conceptually very different [[5]]. Typically it is argued that effect sizes are based entirely on statistical criteria and are thus are dependent on the standard deviation, which might conceivably change from one sample to another. By contrast, most anchor-based approaches are based on an external criterion like retrospective judgment of change, and hence are presumed to be sample independent. Despite these apparent differences between methods, it is not clear that they will lead to radically different estimates of small, moderate, or large change. Further, as we will see, the MID does not have a straightforward relationship to patient benefit. While it is tempting to think that a treatment effect below the MID will result in no one achieving an important treatment benefit and an average effect falling above the MID will result in everyone benefiting, this is far from the actual situation.

In order to develop the argument, we must establish two conditions:

1. We must obtains some indication of the approximate magnitude of the MID when expressed as an effect size, so that we can locate the MID within a reasonable range against the distribution of changes.

2. We will then use hypothetical normal distributions to explore the relation between the treatment effect (expressed as an Effect Size), the MID, expressed as an effect size, and the proportion of patients showing clinically important benefits (i.e., changes in HRQL greater than the MID).

Condition 1—Estimating the Magnitude of the MID as an Effect Size

In this study [[3]], we systematically reviewed the HRQL literature to identify studies that developed and/or used MID thresholds to evaluate change over time and included data for the baseline standard deviation of the HRQL measure(s), comprehensive computerized literature search of the Medline database of published articles from 1966 to April 2002 was assembled, which was then supplemented with papers from the authors' files. In the end there were 38 studies and a total of 56 effect sizes, because many studies containing more than one instrument.

The most common condition studied was COPD, with heart failure, asthma, and various cancers as other commonly studied conditions. Three studies looked at arthritis, two at GI disease, one examined carpal tunnel syndrome, and one, multiple sclerosis. Response scales were dominated by 7-point and 5-point scales, but a number of other methods (Visual Analog Scale, Time Tradeoff, Symptom checklists) were also used (Figure 1).

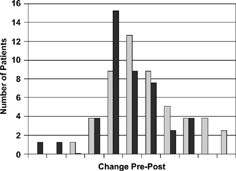
Figure 1. Change in CRQ dyspnea domain for patients randomized to inpatient rehab program or conventional therapy. (Reproduced from J Clin Epidemiol 1999; 52:187–192).

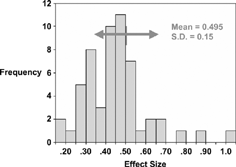
The mean effect size across all measures was 0.495, SD = 0.15. The overall distribution of effect sizes is shown in Figure 2, which shows a reasonably normal distribution. Three studies with effect size > 0.90 resulted from the use of a clinical endpoint to subdivide groups, and thus cannot be assumed to represent a minimal value. Thus, the studies resulted in estimates of a threshold of important change thatare consistently close to approximately one half of the SD (baseline). In the original paper, the argument was advanced that this remarkable consistency was a natural consequence of the stability of the limit of human discrimination to about 1 part in 7, as shown by Miller [[6]] over 50 years ago.

Figure 2. Distribution of 56 observed MID's shown as effect sizes. (Reproduced from Med Care 2000; 41:582–592).

Further analysis examined some factors within the studies that might influence the magnitude of the minimal difference. The first factor examined was the method used to obtain the MID, basically in the two broad classes of Minimally Detectable (MDD) (using the Jaeschke [[1]] or similar method) or Clinically Important (CID) (using some clinical endpoint to develop different classes). While the CID mean was marginally higher (0.53 vs. 0.47), this was not significant (t(54) = 1.12, p = 0.27). We then examined the nature of the scale response to determine whether the uniformity of the MID was, in some way, related to the use of a 7-point scale. Comparing 7-point scales to all others, the mean effect sizes were both close to 0.5 (0.53 for 7-point scales; 0.47 for other scales, t(54) = 1.10, p = 0.27. Finally we examined generic vs. disease-specific scales. The mean effect size for disease-specific scales was 0.48 vs. 0.50 for generic scales (t(54) = 0.49, p = 0.62). Thus, all the factors examined showed relatively small impact on the computed effect size. The mean for all 6 subgroups remained with the range 0.49 to 0.56, consistently close to 1/2 a standard deviation.

To conclude, this analysis has shown that under many circumstances, when patients with a chronic disease are asked to identify minimal change, the estimates fall very close to half a standard deviation, with a plausible range (± 1 SD) from 0.35 to 0.65.

Condition 2—Relation Between Effect Size and Likelihood of Benefit

The underlying rationale for the identification of a “minimal difference” threshold is to separate those changes which, while statistically significant, are of no clinical consequence, from those changes that amount to real perceived benefit to the patient. However, simply establishing such a threshold is not sufficient, because of variability in response. Some patients in a placebo group may receive benefit above threshold and conversely, even with efficacious treatment, some patients may fall below the threshold or even get worse.

A potentially beneficial application of the MID is to determine, based on the overall treatment effect and the MID, the prior likelihood that a particular patient may benefit. In this study [[2]], hypothetical normal distributions were used in order to systematically investigate the relation between effect size (ES), Minimal Important Difference threshold (MID), and proportion benefiting from treatment p(B). The original paper investigated both parallel group and crossover designs. In the present paper, we confine ourselves to parallel group designs (i.e., randomized trials). Further, in the original paper, there was a good fit with experimental data; this will not be discussed in detail here.

To create the simulation data, hypothetical normal distributions were constructed using a spreadsheet program. The difference between treatments was systematically varied in standard deviation units from 0 to 1.5 in steps of 0.25 (i.e., effect sizes ranging from 0 to 1.5 in steps of 0.25). Based on the findings of the earlier analysis that showed that MIDs are typically in the range of 0.5 standard deviations, four values for the MID—0.0, 0.25, 0.5, and 0.75 were chosen.

For each combination of MID and ES, we first computed the proportion of the distribution of the treatment group, p(TI), and the control group, p(CI), which fell to the right of the MID (i.e., the proportion in the treatment and control groups who experienced a clinically important improvement). The net proportion who improved from treatment, p(I), is then the difference between these two probabilities.Next, similar values for the proportions of the treatment and control groups, which were to the left of—MID, p(TW) and p(CW) were calculated; that is, the proportions of patients in the treatment and control groups who worsened. Finally, we computed the net benefit, p(B). The calculations involve consideration of six different marginal proportions—improved, about the same and worsened in the treatment and control groups, and a resulting 3 × 3 table (Proportion Improved, Same and Worsened in the Treat group × Proportion Improved, Same and Worsened in the Control group). The formula from Guyatt, Juniper, and Walter [[7]], which is derived from estimating the proportions in each of the nine cells in this table from the marginal distributions, assuming independence of responses in the two treatments was used. This can be showed to simplify to:Finally, a spreadsheet was used to compute the areas of the treatment and control groups to the right and left of the MID, then applied formulas [1] and [2].

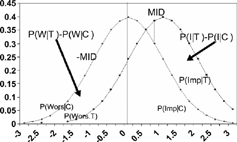
The situation is shown graphically in Figure 3. P(I) is simply the difference between the two shaded areas to the right of the MID; p(B) is approximately this difference minus the difference between the shaded areas to the left of (-MID), with the correction factor in Equation 2.

Figure 3. Distribution of changes in treatment and control groups showing net proportion improved and worsening. (Reproduced from Med Care 2001; 39:1039–1047).

The simulation results and empirical data from 3 studies [8-10] are shown in Figure 4 for probability of improvement (p(I)). The relation between p(I) and effect size was nearly linear, with very small dependence on the choice of MID, particularly for values of effect size in the moderate range (< 1.0) (Figure 5). Examining overall benefit, p(B), individual curves were slightly curvilinear but still showed only minimal dependence on MID. Empirical data, indicated as asterisks on the graphs, were consistent with the theoretical curves.

Figure 4. Net proportion improved related to treatment effect size and MID, with 3 observed points. (Reproduced from Med Care 2001; 39:1039–1047).

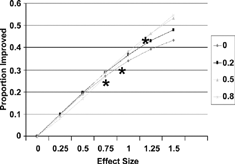
Figure 5. Net proportion benefiting related to treatment effect size and MID (legend at right) with 3 observed points. (Reproduced from Med Care 2001; 39:1039–1047).

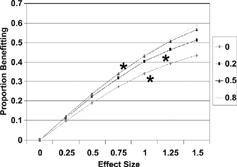
In the original paper, the analysis was repeated with positively skewed distributions (Skewness = 1.0). Although the absolute vales of benefit were slightly lower, the shape of the curves was almost identical.

Discussion

The results of these studies have shown that, within plausible ranges of treatment effects and threshold values, there is a very weak relationship between the choice of a minimally important difference and the proportion of patients who will benefit from treatment. In a sense, this should not come as a surprise; a significant proportion of patients benefit from a placebo. Rather, the result reflects the variability in treatment response that is inherent in many clinical situations. In doing so, it underscores the futility of any attempt to establish some fixed threshold below which a treatment is viewed as ineffective and above which it is effective.

Further, not only is the impact of the choice MID small, but a closer inspection of Figure 4 and 5 yields what is, at first inspection, a paradoxical result. We might expect that, as the MID is increased, proportionally fewer patients will show a benefit, so that the curves for higher MID will fall consistently below those for smaller MID, and the curve for MID = 0 will show a consistently greatest benefit. However, inspection of the graphs shows that this is not the case. In general, the largest p(B) is present with the largest MID. That is, the proportion showing a large benefit of treatment (MID > 0.8) is greater than the proportion showing any benefit of treatment (MID > 0), and this difference is particularly evident with larger overall treatment effects (ES > 1).

How can this be? The answer lies in a detailed reflection on how the differences come about. The “proportion improved” is the difference between the proportion showing a change in HRQL above the MID in the treatment group and the same proportion in the control group. For large ES, the distribution of the treatment group falls far to the right of the MID. Consequently, changing the MID has a relatively small impacton the proportion of the treatment group above the threshold, and a relatively large impact on the proportion in the control group. The net result is a negative relationship between MID and p(I) at high ES. The relation with p(B) is more complex, since both sides of the distributions are involved, as shown in Equation [3], however similar factors are operative.

This creates a paradox. When we are considering patients in the treatment group, it is straightforward to consider that the distribution of changes in HRQL represents the sum of real benefit from treatment and random error, and the area to the right of the MID represent largely real benefit of treatment. But this argument does not apply to the control group, where, from a statistical perspective, the net real benefit of treatment for any patient is zero. In these circumstances, all variation in change is, in some sense, error, and the imposition of an MID on these changes, to separate out change due to random error that is “important” from change that is unimportant is illogical. That is, even though some of the changes in the control group may fall to the right of the MID, this does not, in any sense, make them real. Note that, in this argument, we are not considering the real placebo, but have, without loss of generality, set the average treatment effect of the control group to zero. In this sense, then, all variation in indivdual treatments is error superimposed on an average treatment effect of zero.

A similar argument was made by Norman, Regehr, and Stratford [[11]] in considering methods to compute responsiveness coefficients. They showed that a retrospective calculation of responsiveness derived from the MID shows consistently positive values, even when the overall treatment effect was zero. In both cases, imposing a criterion above which the variation in treatment response is viewed as real, clinically important change, and below which the variation is viewed as error, leads to paradoxical conclusions. The argument was revisited more recently by Senn [[12]], in his critique of a previous paper by Guyatt, Juniper, Walter, and Griffith [[13]], where he argued that these forms of study design cannot distinguish real individual change from other sources of variation, and “nothing from the two clinical trials … is inconsistent with the theory that all patients benefited equally.”

Conclusions

The solution, we believe, lies in abandoning the use of the MID as a criterion to distinguish changes that are important from others that are not, and reconceptualising the information derived from the distributions. Clearly, more patients will benefit from a highly effective treatment than from a minimally effective treatment. Instead of thinking that a position on a curve represents the benefit accrued to a particular patient, we can view the curve as a probability distribution, expressing the likelihood that a patient will obtain a particular level of observed benefit in a circumstance when the true benefit is ES (for the treatment group) or 0 (for the control group). Thus, the proportion of the treatment group curve falling to the right of control curves is the overall probability that a particular patient will show greater change on the treatment regimen than the control regimen.

This conceptual transformation is consistent with the underlying logic of statistical inference. It is also close to the interpretation of the Number Needed to Treat, which rests on the notion that we cannot predict in advance who will benefit from treatment, but the greater the likelihood of benefit, the fewer patients need be treated for one to benefit.

What, then, is the role of the MID? At an individual patient level, the MID may be a useful criterion to decide retrospectively whether the observed change is, or is not, clinically important (although asking the patient may be equally illuminating!). However, in examining group differences, with a view to determining whether of not a treatment is beneficial, the present findings suggest that this conclusion can be derived almost wholly from the effect size, and the MID adds little to interpretation.