Abstract
This paper offers a practical approach to process qualification based on estimating the impact on the fraction nonconforming and the sensitivity of the nonconformance rate to changes in the mean or standard deviation of the process. The methodology makes certain assumptions regarding the magnitude of the changes that might be expected in the process parameters and then computes the effect that these changes might be expected to have on the nonconformance probability and its variability. If the impact is within acceptable limits, then the process is considered robust enough to be released to production.
Introduction
In performing a process qualification study, the practitioner seeks to understand the performance of the process and its sensitivity to changes in key parameters such as the mean and/or standard deviation. The goal of such studies is to determine if the risk of moving a process from development to production is acceptable. The risk associated with producing a product or service is the potential cost of failure (both internal and external) (Citation1). In this paper, the authors propose an approach to risk assessment based on process modeling of the fraction nonconforming and the possible variation in the fraction nonconforming (called net sensitivity) (Citation2).
Curve-fitting techniques (Citation3) are used to model the observed data distribution and then to evaluate the effect of changes in the process parameters on the fraction nonconforming (i.e., tail probabilities). Two real-world cases are examined using this risk analysis technique. In the first example, the Weibull model is used to predict failure probabilities for a highly skewed population to quantify the potential product quality risks associated with a customer cost reduction initiative. In the second example, the Johnson model is used to predict the potential failure probability risk associated with a critical process parameter during a new product introduction evaluation.
Methodology
Estimating the impact of a change in the mean and/or standard deviation on the fraction nonconforming requires that the practitioner either have sufficient data or a model must be used. To make the modeling approach as simple as possible, both Johnson and Weibull curve-fitting techniques are illustrated in this paper. An additional advantage of using a Johnson curve to model the observed distribution is that it allows the practitioner to use the Normal probability distribution to estimate the tail probabilities.
The procedure for estimating the effect of a shift in the mean or variation with the resulting decision criteria is outlined below:
| 1. | Determine the current process left and right tail nonconformance (NC) probabilities and the 90% upper confidence limits for each. | ||||
| 2. | Determine the effect of a shift in the mean of dx units and/or a change of kσ in the standard deviation from the process distribution model for both fraction nonconforming and net sensitivity (Citation2). Net sensitivity (NS) is a measure of the average rate of change in the fraction nonconforming with respect to a change in the input variable (mathematically, NS=∂NC/∂x). The NS for a Normally distributed process is given by: | ||||
| 3. | The results of steps 1 and 2 are compared with the previously agreed upon (by engineering, manufacturing, and quality) NC and NS transfer acceptance criteria. If the results satisfy the criteria, then the process is considered robust enough to be released to production. | ||||
Table 1. Estimated fraction nonconforming in defects per million (DPM)
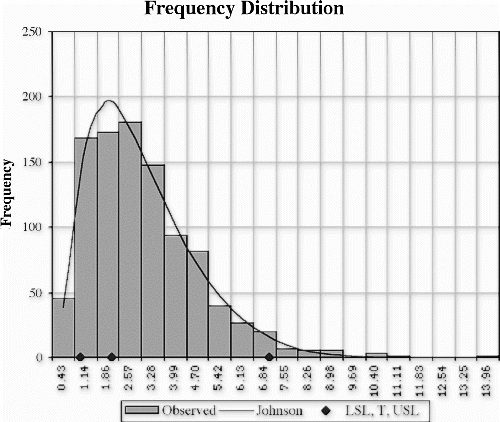
For example, consider the following 1000 data points drawn at random from a gamma (3,1) distribution. The equation for this distribution is f(x;a,b)=b a x a−1 e −bx /Γ(a), which equals x 2 e −x /2 when a=3 and b=1. A histogram of the randomly generated data and a Johnson curve approximation to this distribution are shown in Fig. . This distribution was chosen for illustrative purposes because many real-world processes have a similar shape.
Figure 1. Original (—) and shifted distribution (—).
Figure 2. Original (—) and increased variance distribution (—).
Figure 3. Observed and Johnson distribution.
Table 2. The effect of parameter changes on the nonconformance rate and net sensitivity
If the upper specification limit (USL) is 7 and the lower specification limit (LSL) is 1, then the estimates of the fraction nonconforming can be generated based on various process models (see Table 1).
The practitioner needs to be cognizant of both the nonconformance probability and the effect of changes in the distribution parameters on these estimates (i.e., their sensitivity to change). This is the basis of the risk analysis technique covered in the next section.
Analysis
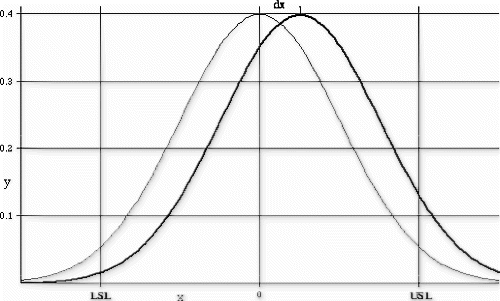
To demonstrate the effect of a change in the process parameters on the Johnson tail probabilities, a mean shift of one half standard deviation (i.e., dx=s/2=.87) and/or a 1.5 times sigma increase in variation (i.e., k=1.5) will be applied to the gamma distribution data (see Table ).
If the qualification team thinks the process might experience changes in the parameters of this magnitude, then there is a risk of a 50% nonconformance rate occurring. Also, the large value of the net sensitivity indicates that the process is potentially very unstable. Given either of these two conditions, the process would fail qualification and it would then be returned to engineering for further improvement before making another attempt at qualification.
Now that the approach to process qualification based on risk modeling has been presented, two case studies are provided that illustrate the application of this methodology.
Case Study 1
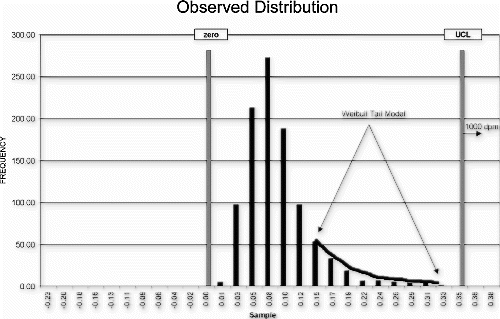
A computer component manufacturer was asked to define the potential quality impact of a reduced test process associated with a customer cost-savings initiative. Because it was known that the tested defect distribution was heavily skewed toward zero, the Weibull model was selected to analyze the upper tail failure probabilities. The critical underlying assumption was that the customer's new product could manage the full defect distribution associated with the manufacturer's typical manufacturing population. Eliminating test altogether was not an option. If the supplier's process were to deteriorate significantly over time, the customer's product risk would be unacceptable.
The task then became to define an audit test control system, that could reliably detect an upward shift in the untested tail population and to estimate the observed and 3-sigma shift in the process failure probabilities that could occur as a result of reduced testing. This 3-sigma mean shift was considered the worst-case situation.
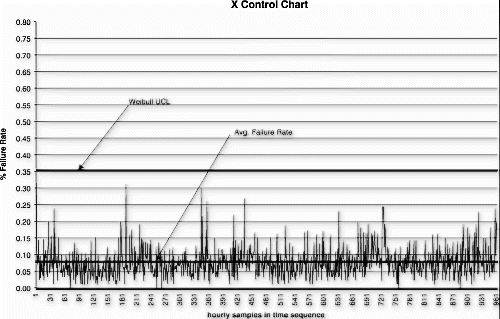
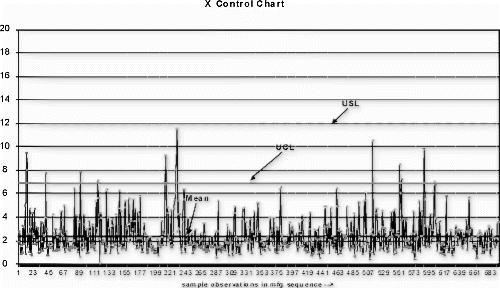
An individuals (x) control chart (see Fig. ) using detection rule one (i.e., one point outside μ±3σ) was selected as the audit test detection system (see Citation4 for plotting p data on an x-chart). The sampling frequency was once per hour with a lot size of 500 and sample size of 100. A power function curve for periodically collected data was used to estimate the probability of detecting a shift in mean using this control scheme. In this case, the probability for detecting a three standard deviation upward shift in the process mean, given two observations after the shift, was approximately 0.74.
Figure 4. Individuals control chart with Weibull UCLp (95%) one-tail.
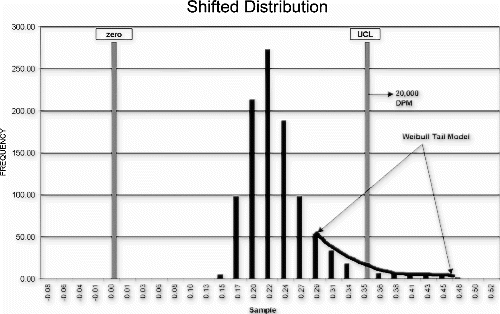
A Weibull curve fit was used to model the observed data distribution (Fig. ). The distribution model was shifted by the maximum expected amount (Fig. ) and the maximum (worst-case) failure rate estimated from the area in the tail of the shifted distribution.
Figure 5. Observed distribution and estimated failure rate.
Figure 6. The 3-sigma “worst-case” mean shift failure rate.
As a result of this risk analysis, the manufacturer was able to demonstrate that the process could be audited on an hourly basis, using the individuals control chart detection system. The audit test could reliably detect an actual upward mean shift of three standard deviations within 2 hours of the actual population shift with 0.74 probability. In addition, the product quality degradation for this degree of process shift is estimated to be approximately 2% worse than normal product. Given this dynamic process performance model, the cost savings associated with the proposed reduced test level could be reasonably compared to the product quality impact.
Case Study 2
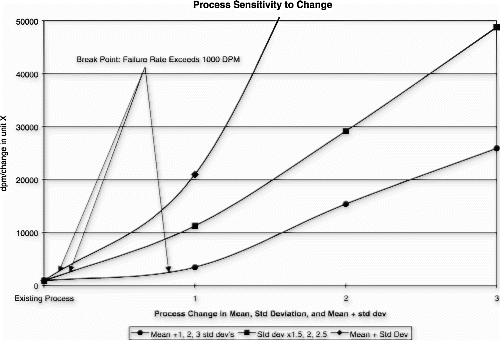
As part of the new product introduction process at this same manufacturer, each critical process parameter is analyzed over a 3 to 4-week manufacturing ramp period. Control charts are generated to measure process centering and stability, and the observed process distribution is modeled to predict the expected nonconformance probability. In addition, the Johnson curve fit risk analysis is used to determine how sensitive the process mean and/or standard deviation is with respect to the maximum nonconformance probability requirement. This is defined as the process break point. A process change model is then constructed to visualize process deterioration and improvement curves.
Successful process transfer requires that the process be reasonably on target with a minimum number of detection rule infractions (i.e., points beyond the control limits). In addition, there must be reasonable margin for the process mean and/or standard deviation to change before the failure rate exceeds 1000 DPM.
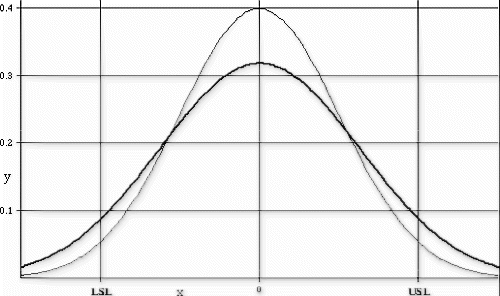
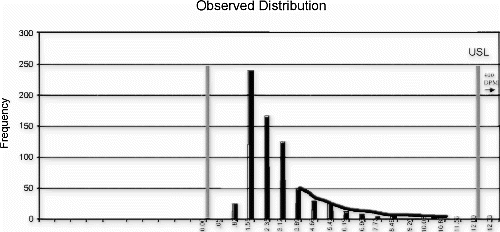
The following new product introduction (NPI) process example is bounded by zero and has no minimum requirement. Therefore, only the target, upper control limit, and upper specification limit are evaluated. The process variation and upper limit conditions are shown in the Fig. control chart, and Fig. depicts the observed process distribution with respect to the USL. The Johnson curve fit analysis for process sensitivity is provided in Table , and the process break points are shown in the process change model in Fig. .
Figure 7. Process control chart.
Figure 8. Observed process distribution vs. the USL.
Figure 9. Process change model.
Table 3. The effect of parameter changes on the production process performance
This process met the transfer requirements for stability and tolerance margin, but it was clearly shown that the mean and standard deviation provided little room for movement before the nonconformance probabilities could be expected to exceed the targeted 1000 DPM ceiling. The standard deviation exhibited the steepest sensitivity curve, exceeding 1000 DPM with as little as a 12% increase (assuming the mean remained fixed). The mean location could increase by almost one standard deviation, or 70% (assuming the standard deviation remained fixed), before exceeding 1000 DPM.
The critical risk associated with the transfer of this process was the nonconformance probability sensitivity to slight changes in the process standard deviation and mean location. This process will require continuous scrutiny; and if left unchecked, it could rapidly deteriorate into one that produces a large amount of nonconforming product.
Reducing the standard deviation was shown to have the most effect on the failure probability sensitivity or variability. It should be noted that the classic process capability indices, Cpk, Cpl, or Cpu, when solely relied upon as go/no go criteria for measuring process capability, can be remarkably insensitive to the true marginality of a given process. In this example, the target (2.50) and USL (12), when compared to the process, yielded a Cpu of 2.09, which is usually considered indicative of a fairly robust process.
Summary
Process modeling provides a way of assessing the possible impact of changes in the process distribution parameters or specification limits on the risks associated with transferring a product to production. As one author warned in a previous paper (Citation2), the practitioner must exercise caution and good sense. The fact that a theoretical change in a process variable generates a more robust process does not imply that a real shift will generate the same results.
Not withstanding the above warning, the practitioner involved in process qualification should:
| 1. | Develop acceptance criteria (i.e., the maximum allowable nonconformance probability and net sensitivity). | ||||||||||||||||
| 2. |
| ||||||||||||||||
| 3. | Generate a control chart to determine the stability of the process. | ||||||||||||||||
| 4. | Find an acceptable model of the observed process distribution. | ||||||||||||||||
| 5. | Determine the effect of possible changes in process parameters (i.e., mean and/or standard deviation). | ||||||||||||||||
| 6. | Compare the worst-case model projections with the acceptance criteria and make a decision on the acceptability of the process. | ||||||||||||||||
Conclusion
The objective of the paper was to illustrate with real-world examples the use of nonconformance and net sensitivity modeling techniques and their application to process qualification. This is a very important activity in the product life cycle, and the tools illustrated here can significantly improve the probability that the transition will be successful.
Acknowledgment
The authors thank Dr. Samuel Kotz and Dr. Harrison Wadsworth for their valuable suggestions, which have contributed to a much better paper.
References
- Bernstein , P. The new religion of risk management . Harvard Business Rev. , March–April 47–52
- in press .
- in press .
- in press .