Minimizing Cost of Multiple Response Systems by Probabilistic Robust Design

Abstract

In the design of products and processes, a methodology that helps adjust the means and tolerances of the design variables to both improve conformance and lower costs is a valuable tool. In this paper, the cost of a product at the manufacturing stage is the sum of the production cost, which includes known costs for tolerances, inspection, and so forth, plus any cost for scrapping or reworking products that do not conform to specifications. We call this added cost the so-called loss-of-quality cost and evaluate it as the probability of nonconformance (of the responses) times established scrap or rework costs. Accurate probability estimates are obtained using full distributions, limit-state functions, and first-order reliability methods (FORM). Probabilities are adjusted through probabilistic robust design. The production costs and the loss-of-quality cost are competing costs and thus their sum provides a single objective function in terms of the means and tolerances of the design variables. The need to satisfy the equations in both the product model and the workings of FORM introduce nonlinear equality constraints. The minimum of the objective function, hence the minimum cost, is obtained by solving a nonlinear, constrained, optimization problem. The design of a mechanism for controlling a grating diffraction spectroscope serves as a case study using the presented method. A minimum cost, the probability of conformance, and the respective parameter settings are found for both complete and zero inspection strategies.

Keywords:

• Quality
• Minimum cost
• Probability
• FORM
• Multiple responses

Introduction

It is essential in the design of a product, or the tuning of a process, to have a methodology that helps adjust the settings of the means and tolerances of the design variables to provide high conformance of the responses (within their specifications) at the lowest possible cost (1 2 3). Herein the means and tolerances of the design variables are together called the design parameters and given the symbol p. The manifestation of such a methodology as a computer program requires a number of mathematical relations. These comprise (1) product models that relate responses to design parameters, and (2), cost models that relate costs to design parameters.

Mathematical models of a product that relate responses to design parameters are formed by first developing either mechanistic models or empirical models that arise from response surface methodology, such that the q responses Z are written as functions of the m design variables V, in the form:

Then, to complete the relation, the design variables V are assigned probability distributions that contain the d design parameters p. In a feasible design, the means of the responses must be positioned appropriately between upper and lower specifications or on the correct side of a single bound. This can be accomplished by properly adjusting the design parameters in the model. The variability of the responses, hence the sense of conformance when specifications are included, can be adjusted via the design parameters as well.

The cost–design parameter relations comprise both the production cost and the so-called loss-of-quality cost (4 5 7). Although the production cost arises from a number of factors, this cost depends mainly on the choices of tolerances for the design variables. For example, as tolerances are tightened the production cost increases, owing to longer set-up times, instruments with higher precision, and more skilled labor. Mathematical formulae can be established to relate costs to design parameters using collected data from experiments and past records: the production cost is denoted as C _P (p). The loss-of-quality cost arises from scrap and reworking costs when the product's responses exceed specifications due in part to the excess variability of the design variables. That is, as the tolerances of the design variables are tightened, the variability of any response decreases, the number of nonconforming products lessens, and the loss-of-quality cost decreases—opposite to the trend in the production cost. In general, the production cost and the loss-of-quality cost are competing costs. If we let the total product cost be defined as the sum of the production cost and the loss-of-quality cost, then to find p to give a minimum total cost we require a loss-of-quality cost relation, analogous to C _P (p), denoted herein as C _LQ (p).

The evaluation of C _LQ (p) is complex, however, since there is no immediate relation between cost and design parameters as there is for production costs. The most common method to provide C _LQ (p) invokes the concept of expected loss and is expressed as:

where f is the probability density function of a response Z, and L(Z) is the loss function. Although the loss function may be general, Taguchi's quadratic loss function, comprising a response Z and its target value τ, has become the standard and is written as:

where k converts units of response to units of cost. Note that all products off target invoke a cost. Then for Z with a normal distribution N[μ,σ], the expected loss from Eq. (2) is:

For multiple responses, a reasonable expression for the loss-of-quality cost is obtained from the sum of like terms in Eq. (4), although there are many variations, as suggested by others (8). The means and variances of the responses in Eq. (4) are obtained through moment transfer relations using the requisite derivatives from Eq. (1) and the first and second moments of the design variables V, which of course are the design parameters p. We now have C _LQ (p). However, this loss-of-quality cost has a few shortcomings. Specifically, the “higher/lower is best” metric typically requires a subjective estimate of some representative target and there is no precise evaluation of the cost because of the way the conversion factor k is evaluated.

A Binary Loss Function

We now present an alternative approach for providing the loss-of-quality cost that alleviates the above difficulties. Let us consider the following costing rules for a batch of a manufactured product with well-defined specifications: (1) any products that conform to specifications introduce no extra costs and (2) all products that exceed any of the specifications are treated uniformly and introduce the same additional costs. This costing philosophy applies particularly well to, for example, over-specification machined products that are reworked, nonconforming electronic integrated circuits that are scrapped, and out-of-conformance instruments that are recalibrated. Thus, the loss function L(Z) is binary, in the sense that a single, nonzero cost C _S is added to the production cost of only nonconforming products. Now, for upper and lower response specifications, H and L, respectively, L(Z) becomes:

and the expected loss from Eq. (2) for an arbitrary density function becomes:

Further, if we define the integrals in Eq. (6) to be the nonconformance probabilities Pr{F_L} and Pr{F_H}, we have:

For multiple responses and their N nonconformance regions F _i , the expected loss, or the loss-of-quality cost, is an extension of Eq. (7) for all N regions and we write:

This loss-of-quality cost is specification oriented and handles the “higher/lower is best” metrics naturally: it includes the traditional target objective by invoking complementary “higher/lower is best” metrics on the respective response.

Evaluating The New Loss-of-quality Cost

The keys to the evaluation of this loss-of-quality cost are (1) a rational evaluation of costs that make up C _S , (2) the use of limit-state functions to relate responses to specifications, and (3) the use of reliability methods to estimate probability quickly (3 6 7). These issues are discussed next.

The value of C _S , which essentially serves the purpose of k in Eq. (4), comprises rework, scrap, or recalibration costs: these costs are product dependent and must be established rationally.

Limit-state functions are written as:

where v denotes samples of the random design variables, z is the response, and z _o is a higher or lower specification. (For an upper specification, the negative of the right side of Eq. (9) is used.) We define the safe, or conforming region, to occur when g(v)>0 and the failure or nonconforming region to occur when g(v)<0. We define the limit-state surface to be the m−1 dimensional surface where g(v)=0.

Probabilities for regions on either side of the limit-state surface are obtained as follows. It is standard practice to transform the limit-state surface from v-space to standard normal space, or u-space. This can be done mathematically by solving the set of equations that describe the transformation. The mapping has the form:

where, in each mapping, the design parameters p are fixed. When all of the limit-state surfaces are considered, the nonconformance probability of the system is expressed as:

It is not obvious, but when the design parameters are altered, the limit-state surfaces move and nonconformance probabilities change. Then, with reference to Eq. (8), we have the connection between the loss-of-quality cost and the design parameters, and this gives us, indirectly, C _LQ (p).

To make the calculations of probabilities in Eq. (11) tractable, it is expedient to approximate a general limit-state surface with a simpler shape such as a hyper plane. Examples are shown in Fig. 1. This approximation provides the first-order reliability method (FORM). The hyper plane is located at the so-called most likely failure point (MLFP) denoted as u ^*, which is the point (1) on the limit-state surface and (2) closest to the origin in u-space. That is, mathematically for a MLFP, g(u)=0 and the vector to u ^* is collinear with the outward normal gradient vector α ^→ of the limit-state function. The distance to the MLFP is the 2-norm of u ^* and is given the symbol β. Because u-space is rotationally symmetrical, we may rotate each of the linearized failure surfaces to be perpendicular to any single negative axis. Then for the i^th limit-state function, the probability of nonconformance is found via the one-dimensional Normal CDF and written as Φ(−β _i ).

Figure 1. Nonconformance regions for two linearized limit-state surfaces.

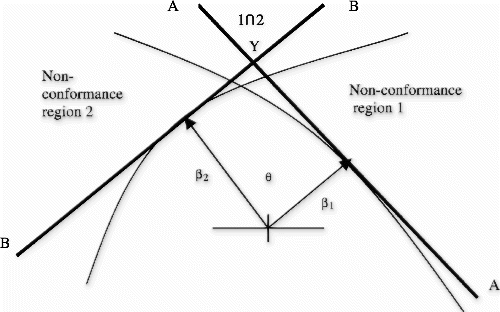
The probability of nonconformance for the system is calculated using relative positions of the N limit-state surfaces. More specifically, when all nonconformance regions are mutually exclusive, or intersections of failure regions are far removed from the origin, the probability of nonconformance for the system is taken as the sum of the N individual nonconformance probabilities. However, for limit-state surfaces close to the origin, the probability in the intersections of any pair (or higher order) of nonconformance regions may be relatively large and must be calculated (8 9 10) to ensure the loss-of-quality cost in Eq. (8) is correct. The geometry in Fig. 1 is used to calculate the intersection probability of any two arbitrary hyper plane limit-state surfaces. The two planes of interest are identified as AA and BB and their respective MLFPs are located at distances β ₁ and β ₂ from the origin with an angle θ separating the vectors to each respective MLFP. The correlation between planes is ρ=cos(θ), and the probability in the region AYB is obtained via the bivariate cumulative function as follows:

The numerical evaluation of this integral is taken from 11. For all pairs of intersection regions F _i,j , the system intersection probability is:

and this value is subtracted from the sum of the individual probabilities of nonconformance to provide a corrected value.

The Optimization Problem

The single objective function used herein is the total cost. This is the sum of the production cost and the loss-of-quality cost and is written as C _T (p)=C _P (p)+C _LQ (p). The optimization problem then is posed as the following nonlinear constrained minimization problem:

The first and second equality constraints in Eq. (14) have been addressed above. The third and fourth equality constraints locate each MLFP, as defined, to ensure a legitimate probability evaluation. The fifth constraint is an inequality constraint and provides ranges for the design parameters. The first four constraints are non linear (the fifth is linear) and thus the solution requires a nonlinear constrained optimization package. Further, the fourth constraint requires gradients of the limit-state functions. Both issues are resolved by invoking (1) the optimization tool box and (2) the symbolic tool box, respectively, in the matrix programming language MATLAB (12). As an added note, it has been found that the optimization proceeds quicker if it is performed in a number of logical steps. That is, it is convenient to find a feasible solution first such that responses meet specifications before entering the formal minimization process (7).

Case Study: Multi-link Diffraction Mechanism

In a grating spectroscope, a wavelength λ is visualized, if present, by the angular position of a viewing piece (13). In a particular design, the angle is related to a displacement through a multi-link mechanism. The displacement S is set by a stepping motor subsystem. The mechanism has two geometrical constants C and L and two adjustable options—an off-set distance and a grating angle-denoted as K ₁ and K ₂ , respectively. To calibrate the mechanism, it is necessary to designate two step positions S ₁ and S ₂ for two respective wavelengths λ ₁ and λ ₂ and then adjust K ₁ and K ₂ to visualize these wavelengths. Once calibrated, any of the hundreds of selected step positions manifests the corresponding wavelength. The responses are the wavelengths λ ₁ and λ ₂ and the design variables are the off-set distance K ₁ , the grating angle K ₂ , step positions S ₁ and S ₂ , and the geometrical constants C and L. The relationships of the two responses to the six design variables are specifically:

with d=600 lines/mm. For specific wavelengths, deterministic geometrical constants, and deterministic step positions, the settings for the off-set distance and the grating angle can be determined by solving the two nonlinear equations in Eq. (15) to give the nominal values of K ₁ and K ₂ . However, the overall uncertainty of the six design variables deems that the problem be posed as a probabilistic problem. Now, the problem is to find means and tolerances for the off-set distance and grating angle to provide sufficient conformance of the responses at best cost. It is suspected that the two responses are highly correlated because of the similarity of the expressions. Consequently, the calculations of probabilities of intersection regions, as discussed previously, will be important.

The distributions for the design variables are determined as follows. The adjustments K ₁ and K ₂ are assigned individual uniform distributions to model the way they are set in the course of production. The dimensions of C and L are uncertain because of the particular machining process and follow a Normal distribution. The step positions S ₁ and S ₂ are uncertain as a result of bearing and screw tolerances and distributions are Normal. Further, S ₁ and S ₂ are set by the same mechanism and are therefore fully correlated. The specific transformation equations in the form of Eq. (10) are:

Specific distribution information is given in Table 1 .

Table 1. Distribution information for control and noise variables

Design variables	Distribution	Parameters
Off-set setting K1 (V1)	Uniform	n1, tol1
Grating angle K2 (V2)	Uniform	n2, tol2
Dimension C (V3)	Normal	μ3=51.00 mm, tol3=±0.050 mm
Dimension L (V4)	Normal	μ4=211.25 mm, tol4=±0.050 mm
Step position S1 (V5)	Joint normal	μ5=34.5325 mm, tol5=±0.001 mm
Step position S2 (V6)	Joint normal, ρ=0.99	μ6=47.4150 mm, tol6=±0.001 mm

The four design parameters to be determined are the means and tolerances of K ₁ and K ₂ , thus:

and from practical considerations there are two minimum tolerance constraints: and

Costs for the mechanism are established as follows. Production costs increase as tolerances are reduced. A model that matches the cost of setting the off-set distance and the grating angle within tolerance is reciprocal and has the form cost=a+b/tol. Values for a and b are obtained by fitting the function to complementary pairs of tolerance and cost. The production cost of the stepping motor subsystem depends on the designated tolerance and presents a cost C _step . The cost for machining the dimensions C and L to a selected tolerance is given as C _CL . The cost for inspection of the assembled mechanism is denoted as C _I . The overall production cost is:

In the analyses, we set a ₁ =10, a ₂ =−2, b ₁ =0.5 $‐mm, and b ₂ =1.0 $‐degree. The latter three costs in Eq. (18) are given specifically in each analysis. The loss-of-quality cost arises from the need to recalibrate any out-of-specification mechanisms, and the unit cost C _S depends on whether recalibration is performed locally, in the factory, or later, on-site, after shipment. Specific costs are given for each analysis.

The wavelengths, or responses, have tolerances of ±1 nm and the two target values used for calibration are λ ₁=532 nm and λ ₂=1064 nm. These targets and specifications give rise to the four limit-state functions:

Initial conditions for the means and tolerances of K ₁ and K ₂ are provided as follows. The means are obtained by solving the two response functions in Eq. (15) with nominal values for λ ₁, λ ₂, C, L, S ₁ , and S ₂ and this gives initial conditions of 230.6 mm and 76.0°, respectively. The initial tolerances are best-case estimates of 0.0085 mm and 0.0120 degrees, respectively.

Results

We now apply the nonlinear constrained optimization process discussed above to find the means and tolerances of K ₁ and K ₂ to achieve minimum total cost. We perform analyses using the following two inspection strategies: In case I, we inspect every unit after assembly by checking wavelengths against step positions using test samples. In case II, we forego inspection and ship the mechanisms as is. Further, for both inspection strategies, we examine (1) how a tighter tolerance and the higher cost for machining dimensions C and L affect the design, and (2) how a looser tolerance and the lower cost for the stepping motor subsystem affect the design.

Case I—Design with 100% Inspection

In this analysis, we inspect every unit after factory assembly for a cost of C _I =$50 and, if required, perform an in-factory re calibration for the unit cost C _S =$500. The results are shown in Table 2.

Table 2. Design for total inspection with C _I =$50 and C _S =$500

Results/case	Case I-A TolStep=0.001 mm TolCL=0.050 mm CStep+CCL=$450	Case I-B TolStep=0.001 mm TolCL=0.005 mm CStep+CCL=$550	Case I-C TolStep=0.005 mm TolCL=0.005 mm CStep+CCL=$520
Off-set n1 mm tol1 mm β1U,1L	230.60006 0.0123 (0.75, 0.75)	230.5999 0.0079 (2.16, 2.16)	230.6002 0.0079 (2.04, 2.04)
Angle n2 deg. tol2 deg. β2U,2L	76.0012 0.0173 (0.73, 0.73)	76.0004 0.0118 (2.23, 2.23)	76.0007 0.0117 (2.10, 2.10)
Pr{conformance}	0.4999	0.9673	0.9564
Pr{intersection}	0.4202	0.0242	0.0330
CP	607	756	727
CLQ	250	16	22
CT	857	772	749

For case I-A, we use the standard tolerances for both the stepping motor subsystem and the machining of dimensions C and L as given in Table 1. The costs for the stepping motor subsystem and machining are $110 and $340, respectively. In case I-B, we tighten the tolerance for the dimensions C and L and the cost increases to $440 because of a higher precision process. The results show a vastly improved design since conformance improves and cost decreases. Finally, we keep the tighter tolerance for dimensions C and L and select a less expensive stepping motor subsystem with a looser tolerance and a lower cost of $80. The results in case I-C show a mechanism design that gives a further cost reduction with slightly lower conformance. In all three analyses, the tolerances for the off-set and angle are well above minimum values and the mean values remain close to initial conditions.

Case II—Design with Zero Inspection

In this analysis, we forego any inspection after assembly and hence the associated cost now is C _I =$0. However, recalibration work combined with travel to site increase the loss-of-quality cost factor to C _S =$2000. The results for pairs of machining and stepping motor tolerances and their costs, as used in case I, are shown in Table 3.

Table 3. Design for zero inspection with C _I =$0 and C _S =$2000

Results/case	Case II-A TolStep=0.001 mm TolCL=0.050 mm CStep+CCL=$450	Case II-B TolStep=0.001 mm TolCL=0.005 mm CStep+CCL=$550	Case II-C TolStep=0.005 mm TolCL=0.005 mm CStep+CCL=$520
Off-set n1 mm tol1 mm β1U,1L	230.6007 0.0067 (0.90, 0.90)	230.6002 0.0068 (2.78, 2.78)	230.6007 0.0064 (2.62, 2.62)
Angle n2 deg. tol2 deg. β2U,2L	76.0013 0.01 (0.86, 0.86)	76.0007 0.0102 (2.84, 2.84)	76.0007 0.01 (2.67, 2.67)
Pr{conformance}	0.5819	0.9940	0.9903
Pr{intersection}	0.3386	0.0040	0.0067
CP	632	729	707
CLQ	836	12	19
CT	1468	741	726

We note in all three analyses that the tolerance for the grating angle has decreased to, or very close to, the minimum value, while in each analysis the tolerance for the off-set remains comfortably above its minimum value. Again, in all three analyses, the mean values remain close to initial conditions. It is clear that case II-C presents the lowest cost of all the designs in Tables 2, 3 and with a very acceptable conformance level of 99%. Further analysis provides an interesting insight. Suppose we wish to achieve the conformance in case II-C and yet inspect each mechanism. In this scenario, the production cost increases by the $50 inspection fee, but the loss-of-quality cost decreases from $19 to $5 because the in-house recalibration cost is only $500. Total cost increases by $36 to become $762. Interestingly, this cost is $13 more than the cost of $749 in case I-C with its lower conformance. A cost-benefit analysis is required to justify the increased cost.

Conclusions

In this paper, a methodology for minimum cost design of multi-response systems has been described. The unique features of the methodology are a probabilistic loss-of-quality cost and a nonlinear constrained optimization algorithm. The underpinnings of the methodology have presented (1) a way for rational costing of both production and loss-of-quality and (2) a way for comparing inspection strategies and choices of noise tolerances. The case study has highlighted a number of important results. First, the algorithm produces a centered, or balanced, design. That is, the program adjusts the design parameters so that respective pairs of β magnitudes are equal, indicating that responses have no preferential nonconforming regions. This provides the sense of positioning responses “on target.” Next, the binary nature of responses (conformance or nonconformance) makes the loss-of-quality cost easy to implement conceptually for multiple response systems since only the probability of nonconformance for the system (and a single cost factor) is required. In practice, this probability is calculated using FORM methods and locating the MLFPs is computationally intensive, although the computation time for an analysis of the mechanism on a Celeron PC under Windows was, on average, 4 minutes. Finally, the inclusion of the intersections of pairs of nonconformance regions has improved probability estimates for highly correlated responses. Indeed, in the case study, the accuracy of the estimates has been verified by Monte-Carlo simulation using 100,000 samples, for an accuracy of 0.3%. Specifically, in case II-C the Monte-Carlo probability of conformance is 0.9934 and our result is 0.9903.

Further work is ongoing to investigate the cost–quality problem. That is, if we define quality as the probability of conformance, then, for a minimum quality, we need to find the design parameters to minimize total cost.

Acknowledgments

We express our utmost appreciation to Dr. J.A. Smith and Mr. J. Domm for providing detailed cost data for the case study, to Dehui Tong for her instructive comments on the manuscript, and to the National Science and Engineering Research Council of Canada for financial support.