Characterizing Performance Variation of Product Designs

Abstract

Quality and reliability design practitioners have utilized Taguchi's methodology of matrix experimentation to generate computer simulation data for characterizing performance variation of product designs. However, the sampling strategy employed renders computer implementation of matrix experimentation cumbersome and statistically invalid. Weaknesses of this approach also include sample size limitation and overestimation of performance variation. An alternative approach that combines Monte Carlo simulation with the strategies of independent sampling across runs and correlated sampling between runs is presented. An application case study shows that the proposed approach constitutes an improvement on the matrix approach with respect to statistical validity and estimation accuracy.

Keywords:

• Matrix experimentation
• Monte Carlo sampling
• Correlated sampling
• Robust product design

Introduction

Manufacturing tolerances and operational noise induce performance variations that adversely affect the quality and reliability of designed systems. Techniques such as statistical quality control, product inspection, and accelerated life testing have been utilized to detect and remove the causes of poor product quality and reliability. As a post-production measure, this approach adds to production cost and development cycle time. In recent years, there has been a concerted effort in industry to replace this iterative process of “design–test–modify” with a preproduction approach that concurrently considers product design and quality and reliability assurance.

In his classic two-volume work, 1 2 presents his pioneering methodologies for the robust design of products and processes. Robustness refers to the capability of maintaining designed performance in the presence of noise. Noise is broadly defined as production and operational conditions that are uncontrollable or expensive to control. Examples of noise include factors such as operator variability, environmental variations, and manufacturing tolerances. Taguchi's methodology provides a mechanism, through the use of designed experiments, for optimizing the design parameters of a product or the control parameters of a process over a domain of operational noise that cause poor quality and unreliability. The standard experimental layout in Taguchi's classical approach to robust product design consists of two orthogonal arrays, which are referred to as inner and outer matrices (2 3). The inner matrix specifies factor-level combinations of process control or product design parameters, while the outer matrix specifies factor-level combinations of noise factors. Depending on cost considerations, these arrays may be full or fractional factorial designs. The inner and outer matrices are also referred to as design and noise matrices, respectively. It is worthwhile to note that the use of the outer matrix is a numerical equivalent of “forced-noise design.”

In physical experimentation, the matrix approach provides statistically valid data as random experimental errors are generated in the conduct of the experiment. Indeed, the majority of applications of the matrix approach involved parameter optimization of industrial processes (2 3 4 5). Nonetheless, the imperative of “quality at the source” requires the implementation of quality and reliability assurance to product designs. Computer simulation is a suitable tool provided that there is a closed-form mathematical model, such as a transfer function, that relates product performance characteristics to product design parameters. Published works by 6 7 8 are examples of application of the matrix approach to robust product design. However, implementing the matrix approach as a template for computer experimentation leads to statistically invalid and inaccurate estimates of product performance variation (9). This paper presents an approach that remedies these problems. This approach, named correlated Monte Carlo simulation (CMCS), is based on designed experiments and correlated Monte Carlo sampling.

As a way of defining the problem addressed in this paper, the variation reduction concept related to reliability and the case for accurate estimation of product performance variation are presented in the following section. This are followed by a presentation of computer implementation of the matrix approach and its shortcomings. Subsequent sections present CMCS and its comparison with the matrix approach.

A Case For Accurate Estimation Of Variation

Depending on the criticality of the mission or the required function, adequate performance is traditionally assured through parallel and redundant reliability structures. It is also a common practice to select components with tighter tolerances to improve system reliability. The latter practice is based on the knowledge that tighter component tolerances lead to reduced product or system performance variations and, hence, improved system reliability.

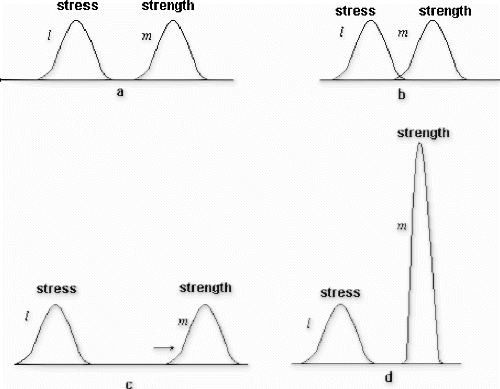
To illustrate the relationship between variation and reliability, we proceed from a conceptual definition that failure occurs when the stress level on a product exceeds its strength. A product's or system's strength is characterized by variation, simply because the parameters of its subcomponents exhibit variation. Similarly, the stress on a product or system may also be characterized by variation because it is caused by uncontrollable internal and external “noise” factors such as deterioration and environmental conditions. Figure 1(a) depicts the spatial separation between stress and strength distributions of a reliable system. Failure occurs when the stress and strength distributions intersect [Fig. 1(b)]. A sudden increase in stress level, a decrease in strength, or a sudden increase in the variability of both, or a combination thereof, might cause this event. Reliability enhancement via implementation of redundant structure amounts to moving the center of the strength distribution to the right to prevent such intersections [Fig. 1(c)]. This may become a costly proposition.

Figure 1. Stress and strength depicted as probability distributions.

In general, a less costly alternative to reliability improvement is to prevent the intersection of the two distributions by reducing “strength” variation, as depicted in Fig. 1(d). In this context, overestimating performance (“strength”) variation may also lead to costly reliability designs as components with tighter tolerance, and therefore being more costly may be specified for reducing performance variation (7). It therefore follows that methodologies for evaluating performance variation affect the economics of quality and reliability assurance. As explained in the following section, the matrix approach overestimates performance.

Matrix Experimentation For Robust Design

Consider the design of an R-C circuit where the output voltage, V, which is a function of resistor (R) and capacitor (C), is of interest:

Let us suppose that R and C each have three admissible design levels: R₁, R₂, R₃ and C₁, C₂, C₃, respectively. A full factorial design consists of nine (3²) factor-level combinations constituting nine design alternatives. The central proposition in robust product design is that although any one of the design alternates may yield specified (nominal) average performance level, there exists a subset (one or more) of the design alteratives that minimizes performance variation. As shown below, factor levels and tolerance limits are used to construct design and noise matrices, respectively.

Suppose Δr and Δc are the manufacturing tolerance limits of R and C, respectively. A two-level noise structure, say for R₁ and C₁ (R and C at level 1), is determined as:

where, for instance, R₁₁=R₁ at noise level 1, and R₁₂=R₁ at noise level 2.

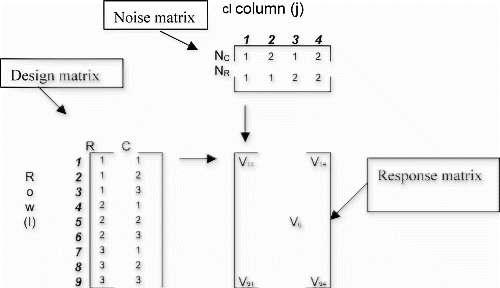
Nominal and noise levels for R and C are shown in Table 1, and the corresponding layout for matrix experimentation is shown in Fig. 2. It is noted that although noise is uncontrollable, specifying noise levels implies controllability during experimentation. The design matrix constitutes a full factorial design for two factors, each at three levels. The noise matrix constitutes a full factorial design for two noise factors, N_C and N_R, each at two levels.

Figure 2. Experimental layout for matrix experimentation.

Table 1. Factor and noise levels

Design factors	Nominal levels	Noise level 1	Noise level 2
	R1	R11	R12
R	R2	R21	R22
	R3	R31	R32
	C1	C11	C12
C	C2	C21	C22
	C3	C31	C32

Each of the nine rows of the control matrix specifies feasible nominal design. Each row of the design matrix is evaluated under the entire noise factor-level combination as specified by the noise matrix, resulting in four responses per row of the design matrix. An element V _ij of the response matrix is calculated using the following computational guide:

The argument f is a specific noise vector corresponding to column j(j=1,2,3,4) of the noise matrix n _j , given the nominal values of row i(i=1,2,…,9) of the design matrix.

For example, to calculate V ₈₂, the factor-level combinations are determined by row 8 (i=8) of the design matrix and the noise levels are determined by column 2 ( j=2) of the noise matrix. Thus:

The response matrix [R_ij ] is utilized to select a nominal design that is least sensitive to noise (see 1 3 5 for approaches to robust design.) This paper is limited to issues related to simulation data generation. Issues of statistical validity, estimation accuracy, and sample size associated with matrix experimentation are presented next.

Statistical Validity And Accuracy Problems In Matrix Experimentation

Since [V _ij ] is generated using deterministically determined sampling points (see Eq. 1), the normal linear statistical model: V _ij =R _i +C _j + (RC) _ij + e _ij is not valid as Σe_ij≠0. Therefore, it follows that in the absence of normally distributed random experimental errors, e_ij, analysis of variance (ANOVA) can not be conducted. Suspending statistical validity, 2 3 utilize several approaches to concoct a sum of squares of errors for conducting ANOVA. One such approach is to combine smaller magnitudes of factor sum of squares into a single sum, which in turn is used as error sum of squares. Nevertheless, this amounts to conducting ANOVA on deterministic data; it does not solve the problem of statistical validity.

The proponents of this approach point to Taguchi's methodology itself as justification. Taguchi's approach for robust design may be viewed as a four-stage sequential process consisting of experimental design, data generation (collection), optimization, and confirmation. Optimality of the predicted robust design parameters is tested by a confirmation experiment. If not confirmed, then the predicted parameters are rejected as optimal. Thus, the argument that if a set of parameters are confirmed to be optimal (in the sense of improving product quality or/and reliability,) then the fact that the process is not statistically valid is inconsequential. It is the sort of case where the end justifies the means.

Second, the way the noise matrix is structured can only permit the assumption that noise is uniformly distributed over a finite set. This limitation adversely affects estimation precision, as the operational noise of many circuit elements is characterized by distributions other than discrete uniform.

Third, the column dimensions of the design and noise arrays limit the size of the experimental data, respectively. In our case, the total number of observations is 36 (9×4). Because of deterministic sampling points, the number of observations can not be increased via replication. Therefore, statistical analysis including distribution characterization of the response variables is severely impaired. The proposed approach, described in the following section, solves the problems of distribution integrity, statistical validity, and estimation accuracy.

Proposed Approach: Correlated Monte Carlo Simulation

Monte Carlo sampling renders statistical validity to experimental data as random errors that sum to zero are generated. Furthermore, distribution integrity is maintained by sampling from within the specification limits of each product design factor (component) based on the factor's unique probability distribution. This would require a priori estimation of the distribution parameters of design factors. For instance, assuming normal distribution for a component with a ± Δ tolerance limit, the standard deviation (σ) may be estimated as Δ/3. Many simulation softwares have in-built random variate generators. For instance, in SIMAN (10), given μ and σ, a corresponding random variate X is generated by using the “NORM” function:

Parameter estimation methods for a range of probability distributions are given in 11. The experimental layout for CMCS is shown in Fig. 3. As in the matrix layout, the inner array represents the experimental design for the control (design) parameters. The similarity ends here. For each factor-level combination there are k replications. Each replication is independently and randomly generated by sampling factors R and C at specified levels. Consider the following:

Figure 3. Experimental layout for the CMCS approach.

Let R_n and C_n represent the values of R and C at the n^th experiment (factor-level combination). The index k is used as a replication of sampling counter. The experimental response for the k^th replication of the n^th experiment is generated as:

Specifically, for k=2:

(Note: At Experiment # 8, R=R₃ and C=C₂; see Fig. 3.)

Since each observation is a function of noise (σ), there is no need for an outer (noise) matrix as a mechanism for inducing “variation” in the observed data. Without the dimensional constraints of the noise matrix, the experiment is replicated as needed.

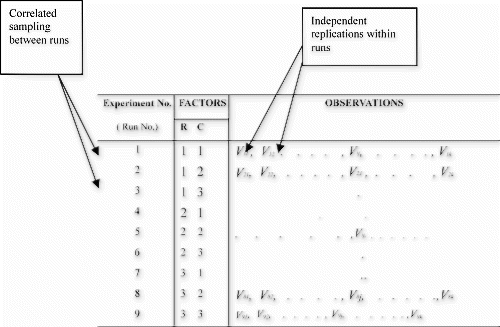
Simulation data are generated by utilizing independent sampling across runs and correlated sampling between runs. Correlated sampling is a variance reduction technique that is implemented by using identical random number seed for each run or design alternative (11). It is similar to blocked-design, as each design alternative is evaluated under identical extraneous sources of variation. As the cycle length of random number generators is large [approximately 2³¹ (10)], for all practical purposes the replications within runs are independent. Sampling from probability density functions and using correlated sampling improve the accuracy and precision of estimates. These two approaches, matrix and CMCS, are compared in the following section.

Comparisons Of The Two Approaches

A published robust design case of a comparator circuit (7) is used as a basis for comparing the matrix approach to CMCS. The case consisted of two designs and six noise factors. With two design factors, each at three levels, full factorial design matrix consists of nine (3²) factor-level combinations. The corresponding two-level full factorial noise matrix consists of 64·(2⁶) factor-level combinations. The layout for matrix experimentation, therefore, is a 9×64 (read as 9 by 64) response matrix, resulting in a total of 576 experimental observations (data points).

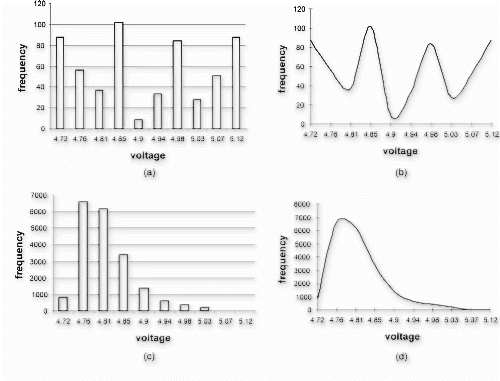
The CMCS implementation uses the same full factorial design matrix. As there is no outer (noise) matrix limiting the number of replications (compare Fig. 2 and Fig. 3), each row of the design matrix is replicated 1000 times, resulting in 9000 (9×1000) data points for the entire experiment. Frequency plots for matrix and CMCS approaches are shown in Fig. 4. Absolute and relative measures of variation, as shown in Table 2, support the central proposition of this paper that the matrix approach overestimates performance variation. The gain in accuracy is a direct attribute of the sampling strategy used by the CMCS approach.

Figure 4. Voltage distribution: (a) and (b) matrix; (c) and (d) CMCS.

Table 2. Estimates of output voltage variation

Approach	Average performance (volts)	Standard deviation	Coefficient of variation (CV)	CV percent reduction
Matrix	4.7390	0.3569	0.0753
CMCS	4.7420	0.2282	0.0403	53.51

Distribution shapes similar to log normal, Weibull, and gamma probability distributions generally characterize performance measures of electronic products (12). As can be seen from Figs. 4(a) and 4(b), matrix experimentation mischaracterizes the distribution of output voltage. On the other hand, as shown in Figs. 4(c) and 4(d), the distribution shape of output data generated by CMCS is in conformance with established norms for electronic products. The distributional clarity thus gained serves the purpose of rigorous statistical characterization by providing a basis for forming reasonable hypotheses.

Conclusion

Compared to matrix experimentation, CMCS is a computationally less cumbersome approach that yields statistically valid and accurate estimates of product performance variation. The noise matrix imposes sample size limitation as well as deterministic sampling points that render the matrix approach statistically invalid. Utilizing end points of tolerance limits as bases for sampling noise tends to overestimate performance variation. By doing away with the outer matrix and utilizing Monte Carlo sampling, CMCS simultaneously solves the problems of sample size limitation and statistical validity of the matrix approach. In CMCS, noise is sampled from within the specification limits of each product design factor (component) based on the factor's unique probability distribution.

By overestimating performance variation, the matrix approach overestimates product failure rate. This in turn may lead to an overly “hardened” and costly product quality and reliability design specification. By improving the accuracy of the estimate of performance variation, CMCS helps lower the cost of reliability and quality assurance design.

Acknowledgments