Crystal growth nucleation and Fermi energy equalization of intrinsic spherical nuclei in glass-forming melts

Abstract

The energy saving resulting from the equalization of Fermi energies of a crystal and its melt is added to the Gibbs free-energy change ΔG_2ls associated with a crystal formation in glass-forming melts. This negative contribution being a fraction ε _ls(T) of the fusion heat is created by the electrostatic potential energy −U₀ resulting from the electron transfer from the crystal to the melt and is maximum at the melting temperature T_m in agreement with a thermodynamics constraint. The homogeneous nucleation critical temperature T₂, the nucleation critical barrier ΔG_2ls∗/k_BT and the critical radius R∗_2ls are determined as functions of ε_ls(T). In bulk metallic glass forming melts, ε_ls(T) and T₂ only depend on the free-volume disappearance temperature T_0l, and ε_ls(T_m) is larger than 1 (T_0l>T_m/3); in conventional undercooled melts ε_ls(T_m) is smaller than 1 (T_0l>T_m/3). Unmelted intrinsic crystals act as growth nuclei reducing ΔG_2ls∗/k_BT and the nucleation time. The temperature-time transformation diagrams of Mg₆₅Y₁₀Cu₂₅, Zr_41.2Ti_13.8Cu_12.5Ni₁₀Be_22.5, Pd₄₃Cu₂₇ Ni₁₀P₂₀, Fe₈₃B₁₇ and Ni melts are predicted using classic nucleation models including time lags in transient nucleation, by varying the intrinsic nucleus contribution to the reduction of ΔG_2ls∗/k_BT. The energy-saving coefficient ε _nm(T) of an unmelted crystal of radius R_nm is reduced when R_nm ≪R∗_2ls; ε_nm is quantified and corresponds to the first energy level of one s-electron moving in vacuum in the same spherical attractive potential −U₀ despite the fact that the charge screening is built by many-body effects.

• metallic glasses
• intrinsic growth nuclei
• crystal nucleation
• Fermi energy effects
• unmelted intrinsic crystals
• glass-forming melts

Introduction

Transformations such as liquid–solid or solid–liquid always induce changes in the conduction electron number per unit volume and sometimes per atom. The equalization of Fermi energies of a tiny particle having a radius smaller than a critical value and its melt produces an unknown energy saving −ε_v equal to a fraction ε_ls of the fusion heat per unit volume. All crystal nucleation models describe the crystallization without taking account of ε _v in metallic alloys [1–3]; they have predicted that unmelted crystals are absent above the melting temperature T_m and that the solidification is governed by a homogeneous nucleation if extrinsic nuclei are absent. The unknown contribution −ε _v has recently been added to the Gibbs free-energy change ΔG_2ls(θ) associated with a nucleus formation in 38 liquid elements; the new critical energy barrier and the new surface energy are compatible with ε _ls0=ε_ls(θ=0) =0.217, where θ=T/T_m −1; in this model, tiny intrinsic crystals can survive above the melting temperature and act as heterogeneous nuclei for crystallization of a melt above a unique homogeneous nucleation critical temperature T₂=T_m/3 or θ₂=−2/3. The thermal variation of ε _ls is an even function of θ having a maximum value ε_ls0 for T=T_m; ε_ls is equal to zero for θ=−2/3 or T=T_m/3 in agreement with the disappearance temperature T_0l=T_m/3 or θ_0l=−2/3 of the free volume in liquid elements [4–6].

The same analysis is applied to metallic glass-forming melts because large values of ε_ls0 induced by large relative changes ΔE_F/E_F of the Fermi energy E_F are expected for two reasons: (i) a solidified eutectic alloy is composed of solid particles having compositions, densities and Fermi energies different from that of the melt [7] and (ii) conduction-electron weak-localization effects are stronger in undercooled melts than in crystallized alloys [8–10].

The θ² dependence of the electronic energy saving coefficients ε_ls(θ) of crystals reaching the critical size is determined on the basis of a thermodynamic constraint at the melting temperature. The glass-forming ability of any metallic melt is determined on the basis of the amplitude of ε_ls0.

The unmelted crystal contribution ΔG_nm to the free-energy change associated with crystal formation is dependent on its radius R_nm and on its own energy saving coefficient ε_nm0; ΔG_nm reduces the critical energy barrier and is used as an adjustable parameter to calculate a temperature-time transformation (TTT) diagram in agreement with the experimental results in Mg₆₅Y₁₀Cu₂₅, Zr_41.2Ti_13.8Cu_12.5Ni₁₀ Be_22.5, Pd₄₃Cu₂₇ Ni₁₀P₂₀ and Fe₈₃B₁₇ taking account of time lags in transient nucleation [11–18]. Direct observations of mean range order (MRO) regions in a conventional glass Fe₈₃B₁₇ are also used to test the model validity by assuming that these regions correspond to unmelted crystals. At low radius R_nm≪R_2ls, ε_nm0 is much smaller than ε_ls0.

The free-electron transfer e·n·Δz creates a crystal charge screened by conduction electrons moving around spherical crystals and by an electrostatic potential energy −U₀, n being the number of atoms in the crystal and Δz the charge number excess per atom. Quantum effects are expected to reduce the electronic energy saving as compared with the potential energy. The first quantified energy level of a conduction electron moving in vacuum in the same spherical attractive potential well −U₀ is compared with the experimental energy saving ε_v obtained in a metallic melt despite the fact that, in a metal, the charge screening is built by many-body effects.

Metallic glasses are quenched with cooling rates R_c varying from 10⁶ to 0.004 K s⁻¹ and depending on the elements involved in their composition [7, 10–12, 19]. Above the glass temperature T_g, the first crystallization at a temperature T_x is produced in the undercooled liquid region using a heating rate R_h (K s⁻¹) from the glass state; the transformation curves T (t) have a nearly parabolic behavior with a nose temperature T_n(t_n). The critical cooling rate applied to the melt without crystallization and the heating rate R_h(K s⁻¹) strongly depend on the presence of heterogeneous nuclei as recently confirmed for some Pd–Ni–Cu–P alloys; R_cc can be decreased by three orders of magnitude [17, 20] during temperature cycling of samples from the glass state to a liquid state far above T_m.

Main results of a revisited crystal nucleation model

The classic growth nucleation model, in its present state, cannot be used to calculate the TTT curves because it predicts a large increase and a divergence of the energy barrier when T approaches the melting temperature [1, 2, 11, 12, 21]. The new analysis of liquid undercooling experiments leads to the following formulae (1–6) [4–6]; the Gibbs free-energy change for a crystal formation given by (11 ) takes account of the energy saving ε_v related to the equalization of the particle Fermi energy to that of the melt 1 Here R is the crystal radius; the surface energy σ_2ls [1], ΔG_v and ε_v are as expressed as follows 2 Here ΔH_m is the fusion enthalpy per mole, V_m is the molar volume, α_2ls is defined by (66 ), ln[K_ls(θ)]90±2 or (K_ls10^39±1 m⁻³ s⁻¹); corresponds to the free-volume disappearance temperature T_ol; the fraction ε_ls of the fusion heat per unit volume is an even function of θ as observed in many liquid elements and shown in figure 1. It has a maximum ε_ls0 at the melting temperature (θ=0) is equal to zero for θ= θ_0l or T=T_0l regardless of the ε_ls0 amplitude [4–6]. The electronic energy coefficient ε_ls(θ) being related to the free-electron density difference is expected to disappear with the free volume, ε_ls=0 when ΔV_m/V_m=0 for θ=θ_0l and is maximum for ε_ls=ε_ls0 when ΔV_m/V_m is maximum for θ=0; the derivative has to be positive and equal to the fusion entropy per unit volume at the equilibrium temperature θ=0 (T=T_m) of a bulk sample; this condition is met by (22 ) because The contribution O(θ⁴) to (22 ) is neglected.

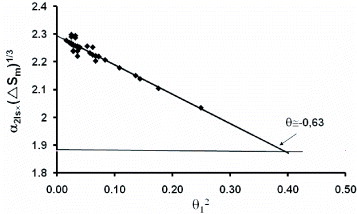
Figure 1 The quantities α_2ls×ΔS_m^1/3 deduced in [4] from α_1ls×ΔS_m^1/3 assembled in [3] for 38 elements are plotted as a function of θ²=θ²₁= (T₁−T_m)²×T_m⁻², θ₁ or T₁ being the temperature of the maximum undercooling of 38 liquid elements; α_1ls has been determined in the past assuming that each element has its own homogeneous nucleation critical temperature T₁ instead of T₂=T_m/3 and using the classic nucleation growth model (ε_ls = 0). A θ² variation is observed and ε_ls tends to be zero for θ ₀≅−0.63. The quantity 1.88 is deduced from (66 ) for ε_ls=0 and ln K_ls. The error bar on θ_0l and ln K_ls is of the order of 5%.

As already shown [4–6], the new critical radius R∗_2ls(θ) and the new critical energy barrier given by (33 ) are calculated setting d(ΔG_2ls)/dR=0 and assuming that the surface energy independent of the radius for or is negligible: 3 Here k_B is the Boltzmann constant and N_A is the Avogadro number. Typical values of R∗_2ls(T_m) extend from 1.8 nm for Si to 3.36 nm for Pb among 38 liquid elements [4] and from approximately 0.6 to 0.8 nm among bulk metallic glass-forming melts (see table 3).

The nucleation rate J per unit volume and per second [1–3] in a homogeneous undercooled liquid is given by (44 ) as a function of the critical barrier ΔG₂∗(T)/k_BT, 4 ln[K_ls(T)]90±2 or (K_ls10^39±1 m⁻³ s⁻¹ is temperature dependent; J attains a maximum equal to 1 when 5 θ₂ is the homogeneous nucleation critical temperature that does not depend on ln[K_ls(θ)] values because ΔG∗_2ls/k_BT ln(K_ls)=g(θ=θ₂)=1 regardless of the ε_ls value as shown by (44 ) and its derivative For θ=θ₂, g(θ₂)=1 and in addition is equal to zero [4]; then ; ln J is maximum for θ=θ₂ or T=T₂. The relation (66 ) results from g(θ₂)=1. 6 The relation (33 ) shows that tiny spherical crystals can survive above T_m up to θ=ε_ls, i.e. θ=0.46 for T_0l/T_m=1/3 and ε_ls0=1. Their radii cannot increase because the critical barrier ΔG_2ls∗ is diverging when θ tends to be θ=ε_ls and is in fact reduced to a value smaller than the critical radius of liquid-droplet homogeneous nucleation [5]; these subnanometer-sized crystals of radius R govern the crystallization for 0θθ₂ because the homogeneous nucleation energy barrier is reduced by the free-energy saving shown by (11 ) and due to the previous solidification of unmelted crystals of radius R=R_nm.

Assuming that the intrinsic nuclei are very numerous regardless of the sample volume v, the steady-state nucleation rate J per unit volume and per second [1–3, 11, 21] is given by: 7 Here v is the sample volume, t_sn is the steady-state nucleation time and DG_nm is the free-change associated with the previous solidification of unmelted crystals. The steady-state homogeneous nucleation time necessary to observe a first crystallization would be equal to 10⁹ with a sample volume v = 1 mm³ .

Much larger J values are obtained in the presence of heterogeneous nuclei at higher temperatures; in this case, t_sn is the steady-state nucleation time necessary to observe the first crystallization induced by one heterogeneous intrinsic nucleus at a temperature T when J⋅v⋅t_sn=1 with J≫1. The nucleation rate J in the presence of unmelted crystals will be maximum at a temperature T_2nm larger than T₂ because d(ln J)/dθ now depends on the derivative of d(ΔG_nm/kT)/dθ; T_2nm can be determined at the minimum value of the steady-state nucleation time.

The steady-state nucleation rate is not only dependent on the critical energy barrier but also on the K_ls value as shown by (77 ); K_ls(θ) is equal to a quantity Aη₀ weakly varying with T divided by the viscosity η given by the Vogel–Fulcher–Tammann (VFT) equation [11, 22] as shown by (88 ) and (99 ) 8 The free-volume disappearance temperature T_0l is chosen in (88 ) to be equal to the VFT temperature T_VFT of Mg₆₅Y₁₀Cu₂₅, Zr_41.2Ti_13.8Cu_12.5Ni₁₀Be_22.5, Pd₄₃Cu₂₇Ni₁₀P₂₀ and equal to T_m/3 in Fe₈₃B₁₇. Note that combining the VFT equation (88 ) with the Doolittle relation defining the viscosity as a function of the free volume leads to T_0l=T_VFT [11, 23, 24]. This equality is proved with a free-volume measurement of a Pd₄₃Cu₂₇Ni₁₀P₂₀ melt and a viscosity measurement of a Pd₄₀Ni₁₀Cu₃₀P₂₀ melt; the VFT temperature is equal to 447 K [14, 15]; a linear extrapolation of the Pd₄₃Cu₂₇Ni₁₀P₂₀ glass volume to the crystal volume leads to T_0l=452.3 K [25].

All the free volumes would tend to be zero at T=T_0l or θ=θ_0l in the absence of a glass transition; the temperature T_0l of the undercooled melt is extrapolated below T_g by using (88 ) for the thermal variation of the melt viscosity [11, 22, 23]; D∗ is the glass-fragility parameter; ln(K_ls) is chosen equal to 9 The numerical constant ln A90 or A10^39±1 m⁻³ s⁻¹ in (99 ) can be slightly changed for alloys [21]; the viscosity of pure liquid elements is of the order of 0.002 Pa s and of η₀; ln(K_ls) is not strongly varying among many liquid elements and is equal to ln A=90±2 [3, 4]. The values of T_m, ΔH_m, V_m, T_g, θ_g, T_0l, θ_0l, D∗, θ₂ and ε_ls0^l of some undercooled melts are given in table 1.

Table 1 The melting temperature T_m, fusion heat ΔH_m per mole, molar volume V_m, glass transition temperatures T_g and θ_g=(T_g−T_m)/T_m, Vogel–Fulcher–Tammann temperature T_0l of the undercooled melt, θ_0l=(T_0l−T_m)/T_m, glass fragility D∗ ln A as defined by (99 ), electronic energy-saving coefficient ε _ls0 at T=T_m associated with a crystal formation and θ₂ are given for various melts with some references; the alloys no. 1 and no. 2 are Zr_41.2Ti_13.8Cu_12.5Ni₁₀Be_22.5 and Pd₄₃Ni₁₀Cu₂₇P₂₀, respectively.

	1-PdCuNiP	2-ZrTiCuNiBe	3-Mg65Y10Cu25	4-Nickel	5-Fe83B17
Tm(K)	802	937	739	1725	1447
ΔHm(J)	7010	6184	8650	17500	13 250
Vm(cm^3)	8	9.75	13.3	7.43	6.55
Tg(K)	585	625	420	425	675
θg	−0.271	−0.333	−0.432	−0.754	−0.534
T0l(K)	452.3	412.5	260	575	482
θ0l	−0.436	−0.56	−0.648	−0.666	−0.666
D∗	9.14	18.5	22.1	0	10.4
ln A	84	86	90	90	90
εls0	1.76	1.54	1.23	0.217	0.3
θ2	- 0.162	- 0.305	- 0.510	- 0.666	- 0.666
References	[13, 25–29]	[18, 26]	[27]	[4, 19]	[34, 35]

Metallic glass-forming melts classified on the basis of an electronic energy saving coefficient ε_ls0 smaller or larger than 1

It is possible to calculate ε _ls0 of each alloy only knowing T_0l or θ_0l. Equation (1010 ) is obtained applying (22 ) and (55 ) for θ=θ₂ 10 There are two solutions for θ₂ when ε_ls0 is larger than a minimum value corresponding to the minimum electronic energy saving as described in figure 2; the relations (1111 ) between ε_ls0, θ₂ and θ_0l² are met when ε_ls0 is minimum and larger than 1 11 The second relation in (1111 ) is obtained by equalizing the derivatives of (22 ) and (55 ). The knowledge of θ_0l and the use of (1111 ) determine ε _ls0 and θ₂ of any alloy having ε_ls0>1 as given in table 1 for several glass-forming melts; θ₂ is always larger than −2/3 for ε_ls0>1 or for θ_0l>−2/3 as shown in figure 2; θ₂=θ_0l=−2/3 for ε_ls01.

Figure 2 The electronic energy saving coefficients ε_ls0(T=T_m) larger than 1 of Pd₄₃Cu₂₇Ni₁₀P₂₀, Zr_41.2Ti_13.8Cu_12.5Ni₁₀Be_22.5 and Mg₆₅Y₁₀Cu₂₅ are plotted as a function of θ₂using (1111 ), the homogeneous nucleation critical temperature T₂ being defined as θ₂=(T₂−T_m)/T_m. The minimum value of ε_ls0 given in table 1 is a linear function of θ₂ that fits the relation ε_ls0=1.5θ₂+ 2.

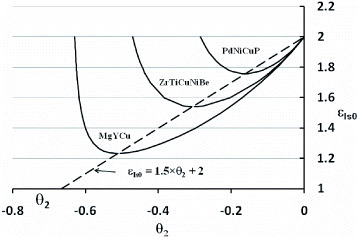
The existence of two glass-former classes is then predicted. The bulk metallic glasses correspond to ε_ls0>1 and θ_0l>−2/3 and conventional glasses to ε_ls0<1 and θ_0l=−2/3. The glass-forming ability of bulk metallic glass-forming melts satisfying T_0l>T_m/3 can be defined using values of ε_ls0 larger than one, ε_ls0 being calculated using (1111 ) from the knowledge of the free-volume disappearance temperature T_0l. The isothermal structural relaxation tends to reduce the free-volume excess frozen by rapid cooling [7]; out-of-equilibrium values of ε _ls0 are then obtained by quenching and are relaxing down to a minimum value given by (1111 ). There is no minimum value of ε _ls0 below 1 except ε_ls(θ₂)=0.

The free-volume disappearance temperature T_0l is observable in spite of its freezing at T=T_g because a Pd₄₃Cu₂₇Ni₁₀P₂₀ specific-heat slope change in the glass state can be observed at this temperature T_0l (see figure 2 of [13]) when the glass specific heat becomes equal to the crystal one; this temperature is also deduced as being equal to T_VFT from measurements of the equilibrium viscosity of the undercooled melt using (88 ).

Temperature-time-transformation diagrams

The calculation of the first-crystallization nucleation time t has to take into account not only the steady-state nucleation time t_sn but also the time lag τ _ns in transient nucleation [11] with 12 13 The time lag τ_ns is proportional to the viscosity η while the steady-state nucleation rate J is proportional to η⁻¹; the coefficient of Jτ_ns in (1313 ) is not dependent on η [11, p 270]; Γ is the Zeldovich factor, a₀∗=π²/6, N the number of atoms per unit volume, j_c the number of atoms in the critical sphere; K_ls is defined by (99 ); equation (1212 ) will also be applied when t_sn is small compared with the time lag τ _ns; a very small value of t/τ_ns undervalues the time t by a factor 2 or 3 and has a negligible effect in a logarithmic scale [11]. The first crystallization occurs when J= (vt_sn)⁻¹ in the presence of an intrinsic growth nuclei, v being the sample volume. The critical energy barrier is obtained using (33 ) and the values of ε_ls as a function of θ²; t_sn is deduced from (77 ) with ln(K_ls) given by (99 ). The various parameters used in these calculations are given in table 1. The energy barrier ΔG_nm of intrinsic nuclei is calculated using (11 ); the radius R_nm is temperature-independent down to the growth temperature; ε_nm (θ ) is assumed to vary as ε_ls(θ) given by (22 ).

The crystal of radius R_nm can act as a growth nucleus at any temperature TT_m when ΔG_eff/k_BT is equal to ln[K_ls(θ)vt]. The intrinsic unmelted crystals also induce the crystallization at the melting temperature T_m when the melt has been weakly overheated [4]. The free-energy change definition could be criticized when the cluster is so small that it mainly contains surface atoms [2]. In this case, the calculation of the TTT diagrams will show that the energy-saving coefficient ε_nm(θ= 0) of very small unmelted crystals is strongly weakened compared with ε_ls0 for n=8–9 atoms; this reduction shows that ε_nm(θ=0) depends on the radius R_nm; the use of ε_ls0 to calculate R_nm in Fe₈₃B₁₇ and in pure liquid elements when R_nm is a large fraction of the critical radius [4–6] is nevertheless successful.

The time lag is easily obtained when t_sn has been determined. The effect of τ_ns in (1212 ) is very important below the nose temperature of the TTT diagram and near the glass transition. It tends to stabilize the nose temperature somewhere between T_m and T_g and to protect the undercooled melt from crystallization; it determines a large fraction of the first-crystallization nucleation time between the nose temperature and the glass transition. The steady-state nucleation time t_sn is minimum at temperatures much lower than the nose temperature T_n; then, T_n results from the competition between the increase in the time lag τ_ns and the decrease in t_sn with decreasing temperature.

Zr_41.2Ti_13.8Cu_12.5Ni₁₀Be_22.5

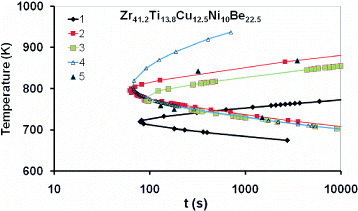
The TTT diagram has been studied using a containerless electrostatic levitation technique [18]. The nose temperature and nose time are 800 K and 70 s, respectively. The TTT curves represented in figure 3 are calculated using the parameters given in table 1 with a sample volume v= 2.5 mm³ [18, 26]. The value of ln A determines the nose temperature; the nose temperature no. 1 calculated with ln A=90 is much smaller than the others calculated with ln A=86. The TTT diagram no. 3 calculated with ln A=86, ε_ls0=1.54, ε_nm0=1.54 and R_nm=0.404 nm is too wide compared with the experimental ones (figure 4 in [18]). The black triangles are experimental points well represented by the curve 4 calculated with ln A= 86, ε_ls0=1.54, ε_nm0= 0.91 and R_nm=0.32 nm. The electronic energy saving ε_nm0 is strongly reduced compared with ε_ls0; such crystals could contain 8.5 atoms on average. The TTT diagrams below the nose temperature do not depend on various contributions ΔG_nm of heterogeneous nuclei to the critical barrier because the time lags become much larger than the steady-state nucleation times.

Figure 3 The first crystallization temperature of a Zr_41.2Ti_13.8Cu_12.5Ni₁₀Be_22.5 melt is plotted versus the nucleation time t. The temperature was calculated using parameters given in table 1 assuming v=2.5 mm³ and ε_ls0=1.54 [18, 26]; Curve 1 (♦) ln A =90, ε_nm0=0.58 and R_nm=0.404 nm, curve 2 (×) ln A=86 ε_nm0=0.91 and R_nm=0.32 nm, curve 3 (▪) ln A=86, ε_nm0=0.83 and R_nm=0.335 nm, curve 4 (▵) ln A=86, ε _nm0 = 1.54, R_nm=0.225 nm. Curve 2 (×) having a nose temperature of 795 K has to be compared with figure 4 in [18]. The black triangles (dataset 5) are experimental points from [18].

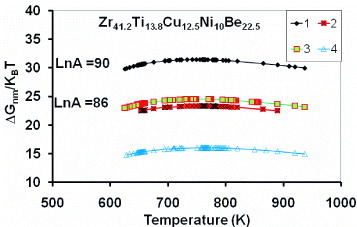
The values of ΔG_nm/k_BT corresponding to the TTT curves in figure 3 are represented in figure 4 by a diagram ΔG_nm/k_BT (T). The TTT diagram width becomes narrower using series 4 calculated points with ε_nm0=0.91 and in good agreement with the experimental results of [18]; it is only modified by the variation of ΔG_nm/k_BT, R_nm and ε_nm being hidden variables.

Figure 4 The contribution ΔG_nm/k_BT of intrinsic heterogeneous nuclei to the effective critical energy barrier ΔG_eff∗/k_BT is calculated with (11 ) and is weakly varying with the temperature. The Zr_41.2Ti_13.8Cu_12.5Ni₁₀Be_22.5 TTT diagrams of figure 3 use these contributions corresponding to various R_nm and ε_nm values: Curve 1 (♦) 0.404 nm and 0.58, curve 2 (×) 0.32 nm and 0.91, curve 3 (▪) 0.335 nm and curve 4 (Δ) 0.225 nm and 1.54.

These unmelted solid particles would have to melt when ε_ls(θ)=0.91×(1−3.189 θ²); this disappearance is expected for θ=0.41 or T=1.41×T_m or 1.41×T_l, T_m=937 K and T_l=993 K being the liquidus temperature. This event would occur in the range of 1321–1400 K. An abrupt increase in the crystallization time has been observed at 830 K after an overheating in the range of 1250–1300 K [18]; all unmelted clusters do not disappear above this temperature range because near-eutectic compositions contain several compounds that have melting temperatures higher than T_m; the model developed here uses a mean composition and a unique melting temperature.

Mg₆₅Y₁₀Cu₂₅

The glass transition T_g and the crystallization temperature of Mg₆₅Cu₂₅Y₁₀ alloy were measured in differential scanning calorimetry (DSC) scans with various heating rates R_h(K s⁻¹) and cooling rates R_c(K s⁻¹); T_g is slightly increased from 400 to 420 K with R_h(K s⁻¹)varying from 0.002 to 10 K s⁻¹ [27] while the glass-undercooled melt transformation extends from 420 to 453 K. The alloy melting occurs between 730 and 739 K. The sample weights vary from 4 to 50 mg. Calculations are made using the parameters indicated in table 1 and ln A=90 in two experiments. The TTT diagrams are indicated in figure 5 by T[R_c(K s⁻¹)] above the nose temperature T_n and T[R_h(K s⁻¹)] below T_n, R_c and R_h being the cooling and heating rates, respectively, given by (T_m−T)/t and (T−T_g)/t and t being the nucleation calculated time at the temperature T. The series 2 curve is calculated with ln A=90, ε_nm0=1.23, R_nm=0.225 nm, v=16.4 mm³; its width is still very broad and the crystal would only contain 3 atoms. In contrast, the series 1 curve is obtained with ε_ls0=1.23, ε_nm0=0.75, R_nm=0.36 nm, v=2.7 mm³; the only change in the series 3 curve is the sample volume v equal to 16.4 mm³; the increase in v moves the nose to a higher critical cooling rate R_cc without changing its width.

Figure 5 The first crystallization temperature of Mg₆₅Y₁₀Cu₂₅ is plotted above the nose temperature versus the cooling rate R_c (K s⁻¹) equal to (T_m−T)/t and below the nose temperature versus the heating rate (T−420)/t, t being the calculated nucleation time at temperature T. All the curves are calculated with ln A=90, ε_ls0=1.23 and the parameters given in table 1; curve 1 is calculated with R_nm=0.235 nm, ε_nm0=1.23 and a sample volume v=16.4 mm³; for the curves 2 and 4, ε _nm0= 0.75, R_nm=0.36 nm and the sample volume, respectively, varying from 2.7 to 16.4 mm³. The best agreement with experimental points (curve 3) extracted from [27] is obtained with curve 4 having T_n=590 K and R_cc=10 450 K s⁻¹; this curve has to be compared with figure 6 of [27].

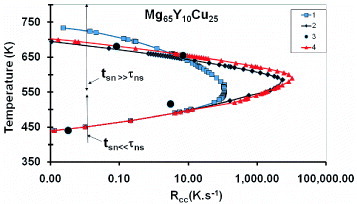
Several experimental points extracted from [27] represented in figure 5 by series 5 are in good agreement with the series 3 curve; T_n=590 K and t_n=10450 K s⁻¹ are obtained. A particle having a radius R_nm=0.36 nm contains 8.8 atoms on average. The nose is more pointed than expected in [27]; the nose time and cooling rate are modified using the same factor when the volume is changed. Here, too, the TTT curves below the nose temperature do not depend on the contribution of heterogeneous intrinsic nuclei to the critical barrier because the time lag τ_ns becomes much larger than the steady-state nucleation time t_sn. The calculated TTT diagrams can be compared with the experimental ones represented in figure 8 of [27].

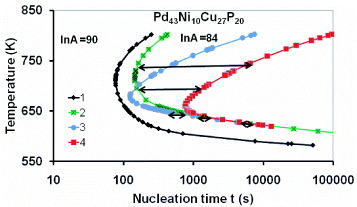
Pd₄₃Ni₁₀Cu₂₇P₂₀

The DSC thermograms of this glass have been studied by isothermal crystallization at various temperatures using a few milligrams of samples processed in B₂O₃ [16, 17, 28–31]. The first growth event corresponding to 1% crystallization is not reproducible above 700 K; a large dispersion of times has been observed as shown in refs. [14, 15, 17, 20] and indicated in figure 7 by horizontal bars. The points measured below 700 K are much less dispersed and used to evaluate ln A and the contribution ΔG_nm/k_BT of heterogeneous intrinsic nuclei to the reduction of the critical energy barrier given by (77 ). Four TTT diagrams are plotted with the same sample volume v=0.32 mm³ chosen by experimentalists [18] and calculated with parameters given in table 1; the first curve on the left corresponds to ln A=90, ε_ls0=ε_nm0=1.76, R_nm=0.194 nm and a nose temperature of 714 K. The only change in the second one is ln A=84. These two TTT diagrams have a very broad temperature width compared with the experimental results indicated by horizontal bars. The dispersion above 700 K is due to changes in the heterogeneous nuclei contribution depending on the temperature cycling of samples [20]. Various values of t are obtained each time that a new sample is studied at the same temperature [17]. This phenomenon has been viewed as being due to impurity nuclei governing the nucleation above 700 K; in particular, the T (t) noses are translated along the t axis when fluxed and unfluxed materials are compared [32]. This could be due to the fact that the contribution of intrinsic nuclei to the reduction of the critical energy barrier above T_n would be smaller than the impurity one.

The first TTT narrow curve on the left of figure 6 having T_n=680 K and t_n=125 s has been calculated with a radius R_nm=0.295 nm, ln A= 84 and ε_nm0=0.6_; the last one on the right having T_n=660 K, t_n=764 s, ln A=84, R_nm=0.295 nm, and ε_nm0=0.5 corresponds to longer times experimentally observed above T_n [16, 17] as well as in Pd_43.2Cu₂₈Ni_8.8P₂₀ and Pd₄₀Cu₃₀Ni₁₀P₂₀ [20, 30, 31]. An unmelted crystal would contain about 7.9 atoms on average for R_nm=0.295 nm. There is a large uncertainty on ε_nm0 because 0.56<ε_nm0<0.6 is determined on the basis of an experimental width of the TTT curve that is not reproducible as a function of ln t.

Figure 6 The first crystallization temperature of Pd₄₃Cu₂₇Ni₁₀P₂₀ plotted versus the crystallization time logarithm; calculations were performed with v=0.32 mm³ and the parameters given in table 1 [13, 28, 29]: Curve 1 (♦) ln A=90, ε_ls0=1.76, ε_nm0=1.76, T_n=714 K, R_nm=0.194 nm; Curve 2 (×) ln A=84 ε_ls0=1.76, ε_nm0=1.76, T_n=714 K, R_nm=0.194 nm; Curve 3 (•) ln A=84, ε_ls0=1.76, ε_nm0=0.6, T_n=680 K, t_n=125 s, R_nm=0.295 nm; Curve 4 (▪) ln A=84, ε_ls0= 1.76, ε_nm0=0.5, T_n=660 K, t_n=764 s, R_nm=0.29 nm. The double arrows correspond to the experimental spread [17, 20].

Nickel

The nucleation rate J in pure liquid elements has a maximum value for θ=θ₂=−2/3 [4]. The time lag is negligible. The glass transition would occur at T=0.246T_m as indicated in [19]; the heating rate used to determine the glass transition would be 12 orders of magnitude smaller than the critical cooling rate [19]. The TTT diagrams calculated with parameters given in table 1 are represented as a function of v·t in figure 7 for different values of R_nm/R_2ls(θ=0); v being the sample volume. The energy-saving coefficient is equal to zero and the critical radius becomes constant for θ<−0,666. There is a good agreement with expectations [19]; the glass state could be obtained using R_cc=3×10¹⁰ K s⁻¹ corresponding to a nose time equal to 38 ns. The unmelted crystal would have to only contain 59 or 102 nickel atoms; such small number of atoms could be obtained by overheating the melt above 2072 K [4]; the sample volume would have to be of the order of 2.6 mm³ when R_nm/R∗_2ls(θ=0)=0.11 and to be much smaller for larger values of R_nm/R∗_2ls(θ=0).

Figure 7 The product of the sample volume and nucleation time of a nickel melt is plotted versus θ=(T−T_m)/T_m; ln A=90 has been previously determined [3, 4]. The sample volumes are 1.0×10⁻¹², 1.0×10⁻¹¹ and 1.0×10⁻¹⁰ m³ from bottom to top. The calculation parameters are given in table 1. The kink at θ₂=−2/3 corresponds to ε_ls=0 [4]. The first crystallization temperature T_x would occur below T₂=T_m /3 at T_x=T_g.

Calculated TTT diagram of Fe₈₃B₁₇ and the direct observations of ‘medium range order’ regions in as-quenched amorphous ribbons

The density of nuclei in the glass state is typically of the order 10²³ to 10²⁴ m^{− 3} far above the density of homogeneous nuclei calculated using the classic nucleation model [33]. The magnetic field texturing obtained after application of a very low cooling rate still produces about 10²¹–10²² crystals per m³ as deduced from crystal radii equal to about 50 nm [4, 5]. Evaluations of their initial size in metallic glasses have been made after quenching Fe₈₆B₁₄, Fe₈₃B₁₇ and Fe₈₆B₂₀ ribbons and by studying their microstructure by high-resolution transmission electron microscopy (HRTEM) and other techniques. Local cluster structures of bcc-Fe and Fe boride having diameters of 1.5–2 and 1 nm diameter are directly observed and are a strong indication of a “nanoscale phase separation” in the amorphous phase [33]. These regions are observed at room temperature with a very diffuse interface. They could have a sharper interface in the undercooled melt above the glass transition. It is suggested that these clusters could be the unmelted crystals surviving above the melting temperature.

Fe₈₃B₁₇ is a eutectic having a melting temperature of 1447 K leading to a conventional glass obtained by melt spinning. Ribbons could have a thickness of 30 μm. The disappearance of the glass state depends on the heating rate R_h and is accompanied by crystallization. T_g=T_x=625 K when R_ch=0.016 K s⁻¹ and T_g=T_x=675 K when R_h= 0.33 K s⁻¹ [34]. The TTT diagram can be calculated with ln A=90 when the fragility D∗ and T_VFT are known; T_VFT and D∗ are, respectively, chosen to be equal to T_m/3=482 K and D∗=7.4 because the dynamic viscosity has been measured at T=T_m equal to 0.0014 Pa s and η₀=N_Ah/V_m=6.1× 10⁻⁵ Pa s where h is the Planck constant [27–29, 35]. The molar volume is 6.55 cm³, the density 7.360 g cm⁻³ and the fusion entropy is assumed to be equal to 9.16 JK⁻¹. The TTT diagram shown in figure 8 is calculated using R∗_nm=0.9 nm in agreement with the experimental observations of bcc-Fe spheres having a 2 nm maximum diameter and ε_ls0=ε_nm0= 0.3. Such unmelted crystal contains 281 atoms. The derivative dT/dt is equal to 1 K s⁻¹ at T=654 K and equal to 0.014 K s⁻¹ at 646 K. These results are very close to the experimental ones despite the fact that the overheating temperature and R_nm are probably different for various samples used by different authors in HRTEM studies, in resistivity and DSC measurements. The nose temperature is T_n=1320 K and the nose time t_n=680 ns for the TTT diagram represented in figure 8. The nose time has to be compared with the ribbon square thickness divided by the thermal conductivity and multiplied by the specific heat per unit volume; this quantity, of the order of 40 μs, corresponds to the time necessary to decrease the ribbon temperature down to 1025 K. In fact, the cooling time has to be only counted in a narrow window of less than 20 K above T_n because the strong divergence of t above 1290 K has no effect on the efficient time. Under these conditions, the model predicts that the glass state is just at the limit for obtaining it by melt spinning.

Figure 8 The calculated TTT diagram of the conventional glass Fe₈₃B₁₇ (□) is plotted as a function of time using parameters given in table 1 and assuming ln A=90, ε_nm0=ε_ls0=0.3. The time t (s) is the sum of the time lag τ_ns and the steady-state nucleation time t_sn. The nose temperature is equal to 1320 K; t_sn(▵) is the minimum at T_2nm=1050 K. The derivative dT/dt is equal to 0.014 K s⁻¹ at T_x≅ 646 K and 1 K s⁻¹ at T_x=654 K. In a conventional glass, the first crystallization temperature occurs below T_2nm at T_g=T_x for about the same heating rates dT/dt.

Fermi energy equalization of a spherical crystal and its melt induced by electron transfer

Formulation of the electrostatic potential induced by a charged crystal

The electrostatic energy saving ε_v is associated with the Fermi-energy equalization of crystal nuclei and their melt. There are nΔz electrons transferred from the solid to the melt when the crystal contains n atoms. The Fermi-energy difference ΔE_F between the solid and its melt is given by (1414 ) in a free-electron model and depends on the free-electron number ν per atom; Δ z is the excess of free electrons per atom above the Fermi level of the melt; it depends on the variation Δν of the conduction-electron number ν per atom and on the free-volume variation ΔV_m; 14 Equation (1414 ) is applied to the following liquid elements: Ti, Fe, Co, Ni, Zn, Pd, Cd, Pt, Au, Al, In, Sn and Pb assuming Δν=0; ΔV_m/V_m is extrapolated up to the melting temperature from the thermal variation of the expansion coefficient and given in table 2 [4, 36, 37]. 15 ΔE_F can be calculated if ν is known: the ultrasound velocity a₀ in liquid elements at T=T_m is related to νE_F as shown by (1616 ), M being the atomic mass [4, 38]. The numerical coefficient 2/3 in (1616 ) has to be seen as a first approximation [39]. This value is corrected and considered as equal to 0.55 using the mean value of the ultrasound velocity a₀ in the following liquid metals at their melting point: Li (ν=1), Na (ν=1), K (ν=1), Cs (ν=1), Mg (ν=2), Ca (ν=2), Sr (ν=2) and Ba (ν=2) [4]. The ν values are calculated using (1616 ) with the numerical coefficient equal to 0.55 instead of 2/3 and are given in table 2 together with ΔE_F deduced from (1515 ) and Δz=Δz_F of the 13 elements deduced from (1414 ), 16 The electrostatic potential energy −U₀ induced by a crystal of large radius R=R_2ls∗ containing n atoms at the melting temperature would have to be nearly equal to E_q, the quantified energy given by (1717 ), because it carries a large charge n·Δz_p⋅e; an analogy is made with clusters carrying electric charges in an inert medium [40–42] with electron correlations being neglected, 17 In a metal, the charge is screened around the crystal surface by the free electrons of the melt; equation (1717 ) contains the vacuum permittivity ε₀=8.85×10⁻¹² C V⁻¹ m⁻¹ and the electron charge e=1.602×10⁻¹⁹ C; it is applied to the 13 liquid elements for T=T_m using R=R_2ls∗(θ = 0) given in table 2 and ε_ls0=0.217 in order to determine Δz_p. 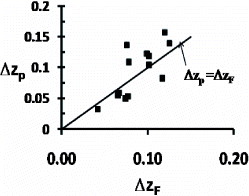The quantities Δz_F determined from (1414 –1616 ) and Δz_p deduced from equation (1717 ) are compared in figure 9 and are nearly equal despite a large dispersion of points mainly due to errors on ΔV_m/V_m; there is no noticeable change when the transition elements are subtracted in figure 9. Equation (1717 ) is then well-founded to relate, in a first approximation, the electronic energy saving ε_ls0 to the number n× Δz of transferred electrons; under these conditions, the potential energy is expected to vary as the radius reverse 1/R_nm because ΔE_F and Δz would not have to be dependent on R_nm. The unmelted crystals in some cases could only contain 9 atoms; ε_nm0 is strongly reduced as shown by the analysis of the TTT diagrams and as compared with the potential energy U₀. This could be due to quantum effects reducing E_q far below the potential energy [40].

Table 2 The following quantities characterizing 13 elements are given at T=T_m from left to right: (11 ) R∗_2ls is the critical radius for crystal growth; (22 ) N_A/V_m is the atomic number per m³; (33 ) Ma₀ ² is the atomic mass multiplied by the ultrasound velocity in the liquid state; (44 ) ν is the number of conduction electrons per atom deduced from (14–16); (5) ΔV_m/V_m is the relative free volume; (66 ) ΔH_m is the fusion heat per mole; (7) Δz_F is the free-electron number difference per atom calculated with (1414 –1616 ); (88 ) Δz_p is the free-electron number per atom transferred from the solid to the liquid and calculated using the electrostatic potential energy (1717 ).

	R∗2ls(θ=0)(nm)		Ma0^2×10^20(J)	ν		ΔHm(kJ)	ΔzF	Δzp
Ti	2.85	5.14	105.2	1.64	0.044	15.4	0.076	0.137
Fe	2.54	7.57	97.2	1.38	0.054	13.8	0.078	0.109
Co	2.35	7.93	109	1.44	0.068	16.2	0.102	0.119
Ni	2.25	8.14	126.6	1.54	0.062	17.5	0.099	0.123
Zn	2.45	6.06	88.7	1.42	0.046	7.3	0.065	0.056
Pd	2.54	5.96	91.8	1.46	0.082	17.6	0.126	0.14
Cd	2.76	4.3	87.6	1.59	0.048	6.2	0.077	0.053
Pt	2.56	5.84	116.1	1.65	0.069	19.7	0.120	0.157
Au	2.66	5.33	121.2	1.74	0.057	12.6	0.102	0.105
Al	2.49	5.33	97.8	1.56	0.074	10.7	0.117	0.083
In	3.21	3.69	102.5	1.81	0.023	3.3	0.042	0.033
Sn	2.7	3.54	123.2	2.01	0.033	7	0.067	0.059
Pb	3.36	3.10	108.6	1.97	0.038	4.8	0.0743	0.050

Figure 9 The transferred free-electron number Δz per atom determined using two independent methods: (1) Δz_F is determined from the ultrasound velocity in 13 liquid elements and from the free-volume change ΔV_m/V_m at T=T_m; (2) Δz_p is calculated with equation (1717 ) taking ε _nm0 = 0.217, and R_2ls∗(θ = 0) and ΔH_m as given in table 2. The line Δz_F ≅ Δz_p is respected despite the experimental spread mainly due to the uncertainty on ΔV_m/V_m.

An analogy with the charged-crystal properties imbedded in an inert medium is proposed in the absence of a model for a metal [40–42]. The charge n·Δz·e cannot be fully screened inside the crystal because there is a deficit of conduction electrons. A tentative is made in 5–2 to calculate a potential energy −U₀ by assuming that the first energy level ε _q in such well is equal to ε_v×4πR³/3 despite the fact that the weakly-bound free electrons of the melt screen the crystal charge instead of only having one electron bound state in the well. It is assumed that this calculated potential energy −U₀ is a good approximation for the potential acting on the melt conduction electrons.

Quantum weakening of the electrostatic energy saving

The potential energy previously defined using (1717 ) is a good approximation for numerous transferred electrons (n× Δz≫1). There is an opportunity to verify if the first-energy levels of an s-state electron moving in vacuum, in a negative spherical potential well −U₀, can describe the quantified values proportional to ε _ls and approximate the true potential energy in the melt even at low radii. 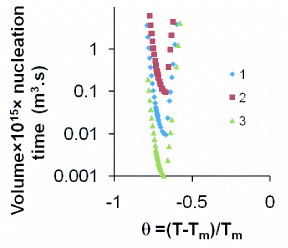The Schrödinger equation has been written with wave functions only depending on the distance r from the potential centre for s states [40], The quantified solutions E_q=nε_qΔH_m/N_A are given by the k value and by (1818 ) as a function of the potential U₀ associated with the crystal radius R=R_nm, n increasing with the cube of R_nm, 18 ε_q is considered as equal to ε_ls(θ) as a function of R∗_2ls(θ). The corresponding quantity for the potential energy ε_ls(θ)×U₀(θ)/E₀(θ) per atom is plotted in figure 10 for Zr_41.2Ti_13.8Cu_12.5Ni₁₀Be_22.5 as a function of R∗_2ls(θ) and compared with ε_ls. The energy saving of a crystal having the critical radius in a metallic melt is slightly reduced by quantum effects as compared with ε_ls×U₀[R∗_2ls(θ)]/E_q[R∗_2ls(θ)], as shown in figure 10. This weakening is stronger for smaller radii.

Figure 10 The potential energies are divided by the fusion heat per mole. The first energy level (▪) per mole ε_ls=ε_q deduced from (22 ); the level induced by the attractive potential associated to a charged crystal (♦) imbedded in vacuum and calculated using (1717 ) and (1818 ). Those energies are plotted as a function of the critical radius R∗_2ls (θ).

Other results of this analysis are given in table 3. The electrostatic potential energy in Zr_41.2Ti_13.8Cu_12.5Ni₁₀Be_22.5 is only 4.7% larger than the quantified energy for R∗_2ls(0)=0.773 nm at T=T_m. The quantified energy ε_q=ε_nm0=0.91 (E₀=7.91×10⁻¹⁹ J) for R_nm=0.32 nm leads to U₀=1.76×10⁻¹⁹ J and Δz=0.110. The weakening of ε_nm0 occurs while Δz remains constant. The same reduction is observed for Mg₆₅Y₁₀Cu₂₅ at very low radius while the potential energy corresponding to the critical radius at T=T_m is only increased by 4.7% as compared with ε_ls0; Δz also remains nearly unchanged. In Pd₄₃Cu₂₇Ni₁₀P₂₀, Δz is still nearly unchanged for ε_nm0=0.5 while the potential energy corresponding to the critical radius at T=T_m is only increased by 8% as compared with ε_ls0. The absence of Δz change in all alloys would correspond to a Fermi energy difference independent of the sphere radius. The energy-saving coefficient ε_ls0 in (1717 ) would be divided by 2 for two s electrons occupying the first energy level; the new value of U₀ deduced from (1818 ) and Δz deduced from (1717 ) would also be divided by a factor of the order of 2. This assumption as well as any change in ε_nm0 would contradict with the observations described in figure 9.

Table 3 The potential energy - U₀ and the charge excess Δz per atom carried by a crystal imbedded in a melt are calculated assuming that the first energy level of an electron moving in vacuum and in a spherical potential −U₀ is equal to the energy saving E_q defined using ε_ls0 and ε_nm0. U₀ is nearly equal to E_q when the crystal radius is equal to its critical value; E_q is strongly reduced by quantum effects when R≪R∗_2ls in very good agreement with the calculated values extracted from the TTT diagrams of several alloys.

Alloys	Radius (nm)	n atoms	εls0	ε nm0	Eq×10^20(J)	U0× 10^20(J)	Δz
Zr41.2Ti13.8Cu12.5Ni10 Be22.5	0.773	119	1.54		189	198	0.111
Zr41.2Ti13.8Cu12.5Ni10 Be22.5	0.32	8.5		0.91	7.91	17.6	0.110
Mg65Y10Cu25	0.805	99	1.23		175	183	0.129
Mg65Y10Cu25	0.36	8.8		0.75	9.52	31.4	0.111
Pd43Cu27Ni10 P20	0.632	80	1.76		163	176	0.121
Pd43Cu27Ni10 P20	0.295	8.1		0.5	4.72	31.8	0.100
Fe83B17	0.9	281		0.3	185	192	0.0525

Table 4 The abbreviations of different physical quantities used in this paper are classified: (11 ) Thermodynamics parameters, (22 ) Physical constants, (33 ) Glass-forming melt and crystal nucleation parameters, (44 ) Crystallized nuclei, (55 ) Temperatures (66 ) Other abbreviations.

	1-Thermodynamic parameters
EF	Fermi energy of the melt
−U0	Crystal electrostatic potential energy in the melt
−Eq	Crystal-quantified electrostatic energy
ε v	Crystal electronic energy saving per unit volume
ε ls (θ)	Equation (22 ), Crystal electronic energy-saving
	coefficient for Rnm=R∗2ls
εnm(θ)	Equation (22 ), value of ε ls(θ) of unmelted crystals
	for Rnm<R∗2ls, εnm(0)=ε nm0
ΔHm	Fusion enthalpy per mole
ΔSm	Fusion entropy per mole
ε q	Crystal-quantified energy saving
	coefficient in vacuum
ΔEF	Fermi energy difference barrier
	=EF(crystal) –EF(melt)
ΔG∗2ls	Critical energy for crystal growth
	(calculated from εls)
ΔGnm	Contribution of unmelted crystals to the
	critical energy barrier reduction
ΔG∗eff	=ΔG∗2ls− ΔGnm
	2-Physical constants
e	Electron charge
m	Electron mass
h, ℏ	Planck constant,
NA	Avogadro number
kB	Boltzmann constant
ε0	Vacuum permittivity
M	Equation (1616 ); Atomic mass
	3-Glass-forming melt and crystal nucleation parameters
ln A	ln A90±2 or A10^39±1 m^−3 s^−1
Kls	Equation (99 ), pre-exponential factor of the
	nucleation rate J
J	Nucleation rate per unit volume per second
tsn	Steady-state nucleation time
τns	Time lag in transient nucleation
t	Equation (1212 ); Crystallization time
tn	Crystallization time at the nose temperature Tn
N	Number of atoms per unit volume N=NA/Vm
Γ	Zeldovich factor
η	Equation (88 ); dynamic viscosity (Pa s)
η0	Equation (88 ); Pre-exponential factor
	of the V–F–T viscosity
D∗	Equation (88 ); Fragility parameter
Rc	Cooling rate (K s^−1)
Rh	Heating rate (K s^−1)
V	Undercooled melt volume (m^3) under processing
	4-Crystallized nuclei
n	Number of atoms in a spherical crystal
R	Crystal radius
R∗2ls	Critical radius for crystal growth (calculated with εls)
Rnm	Unmelted crystal radius (m)
jc	Atom number of the critical size crystal
σ2ls	Surface energy (J m^−2)
α 2ls	Equations (33 ) and (66 )
	5-Temperatures
Tm	Melting temperature
Tl	Liquidus temperature
T, θ	Absolute temperature T, θ = (T−Tm)Tm^−1
T2, θ2	Homogeneous nucleation critical temperature
	θ2= (T2−Tm)Tm^−1
T2nm, θ2nm	Heterogeneous–nucleation critical temperature
	T2nm, θ2nm=(T2nm−Tm)Tm^−1
T0l, θ0l	Free-volume disappearance temperature
	T0l, θ0l=(T0l−Tm)Tm^−1
TVFT	Vogel–Fulcher–Tammann temperature, Equation (1010 )
Tx, θx	Melt crystallization temperature using a
	heating rate of 0.66 K s^−1
Tn	Nose temperature of the TTT diagram
Tg, θg	Glass transition temperature Tg, θg= (Tg−Tm)Tm^−1
	6-Other symbols
ν	Free electron number per atom of the melt
Δv	Variation of ν between solid and melt
Δz	Equation (1414 ), Free-electron excess per atom
	above EF
a0	Equation (1616 ), Ultrasound velocity in the
	melt at T=Tm

The bound state involved in a classic virtual bound state falls in the Fermi Sea [43, 44]. The one-electron bound state energy can be nearly as deep as the potential well far below the free electron band bottom for large radii; these observations could extend the domain of Friedel's virtual bound states to highly charged crystals in metallic melts. There is a need of a theoretical model to determine the true potential energy induced by a crystal in a melt and if the melt electrons screening the charge could lead to an electrostatic energy equal to the observed values of ε_ls0 as expected from this analysis.

The model developed here is nevertheless successful to determine the electrostatic potential energy induced by an intrinsic spherical nucleus in metallic glass-forming melts from the free-volume disappearance temperature. The first energy level of a bound state for one electron moving in a potential well, imbedded in vacuum, could remain unchanged despite the many-body effects screening the giant charge n·Δz·e in the melt. This phenomenon induced by the Fermi-energy equalization between a crystal and its melt could correspond to the formation of a virtual bound state involving at the same time a very large number of weakly bound conduction electrons and inducing a shift of the crystal band bottom as compared with the melt one.

Conclusion

The energy saving ε_v=ε_lsΔH_m/V_m associated with the equalization of Fermi energies of a crystal and its melt cannot be neglected in the Gibbs free energy change related to a crystal formation in bulk metallic glass-forming melts because it can be larger than its fusion heat. The thermal dependence ε_ls=ε_ls0(1−θ/θ²_0l), where θ=T−T_m/T_m is found using a thermodynamics constraint that imposes that the derivative of the free-energy change related to a crystal formation at the melting temperature has to be equal to the fusion entropy; this condition is satisfied because (dε_ls/dT)=0 at T=T_m. This law has already been observed for undercooled liquid elements.

In bulk metallic glass-forming melts, the homogeneous nucleation critical temperature T₂ occurs for θ₂= (ε_ls−2)/3 and the minimum values of ε_ls0 are only determined with the knowledge of the free-volume disappearance temperature T_0l or θ_0l; θ₂ is larger than −2/3 when ε_lsois larger than 1; in this case, the extrapolated temperature T_0l, considered as equal to the Vogel–Fulcher–Tammann temperature (VFT); T_VFT is larger than T_m/3. In conventional glasses, ε_ls0 is smaller than 1 and T_0l=T₂= T_m/3. The glass-forming ability appears as being strongly dependent on ε_ls0 .

The critical radius for crystal growth in glass melts is much smaller than in pure liquid elements. The steady-state heterogeneous nucleation rate is strongly dependent on the unmelted intrinsic crystal contribution to the reduction of the critical energy barrier. The time lag in transient nucleation being proportional to the viscosity protects the undercooled melt against crystallization above the glass transition and below the nose temperature of the TTT diagram. The TTT diagrams of Mg₆₅Y₁₀Cu₂₅, Zr_41.2Ti_13.8Cu_12.5Ni₁₀Be_22.5 and Pd₄₃Cu₂₇Ni₁₀P₂₀ are calculated in agreement with the experimental ones using known thermodynamic properties and varying the intrinsic nucleus contribution ΔG_nm/k_BT to the reduction of growth critical barrier. The nose temperature T_n depends very weakly on ΔG_nm/k_BT because the TTT curves below T_n are very reproducible [17], the time lag τ _ns becoming larger than the steady-state nucleation time t_sn. The experimental TTT diagrams are also used to determine, through ΔG_nm/k_BT, the value of ε_nm0 of intrinsic nuclei and their radii; for radii much smaller than the critical radius, ε_nmo is strongly reduced.

This phenomenon is due to quantum effects associated with electrostatic potentials induced by unmelted spherical crystals in the melt Fermi Sea; the reduced values of ε_nm0 correspond in vacuum to the first energy level of one s-electron moving in the same spherical attractive potential despite the fact that, in a metal, the charge screening is built by many-body effects. Such one-electron bound states become virtual in a metal and are characterized by melt conduction electrons surrounding and screening the crystal giant charges.

The first-crystallization temperature of melts is determined on the basis of the existence of intrinsic heterogeneous nuclei that are not melted. The presence of such nuclei is known for many years despite applying relatively large overheating [45–48]; the model can be used to predict a nucleus melting temperature as a function of ε _ls0 by overheating the glass-forming melts. Nevertheless, this application is limited to homogeneous compositions and cannot be used for all compositions of crystals surviving in a glass melt.

Medium-range regions have been observed for a long time in an as-quenched conventional glass by studying the microstructure of Fe₈₃B₁₇ amorphous ribbons by several techniques and in particular by high-resolution transmission electron microscopy. The TTT diagram has been calculated to predict a first-crystallization temperature equal to T_g; an unmelted crystal radius R_nm equal to 0.9 nm is obtained in agreement with direct observations of the ‘medium range order’ (MRO) region size at room temperature [33]. These regions could be seen as intrinsic unmelted crystals.

Acknowledgments

Thanks are due to Eric Beaugnon, Philippe Odier, Jean-Louis Soubeyroux, to the referees for manuscript review, and to Jacques Friedel for discussions. Commenting on this paper, Yoshihiko Hirotsu considers that intrinsic nuclei could be identified to ‘medium range order’ (MRO) clusters only if the interface cluster-matrix is very diffuse at room temperature. The MRO cluster size depends on the overheating rate and then, these entities exist above the melting temperature even if the cooling rate tends to slightly modify their radii [49]. The Fe₈₅–B₁₅ kinematic viscosity is irreversible between θ = 0 and θ≅0.23 after an overheating up to θ=0.27 in good agreement with our prediction θ≅ε_ls0=0.3 [50] corresponding to the melting temperature of all surviving crystals.